Are the Economically Optimal Harvesting Strategies of Uneven-Aged Pinus nigra Stands Always Sustainable and Stabilizing?
Abstract
:1. Introduction

2. Material and Methods
2.1. Population Dynamics

2.2. Optimization Model

2.3. Input Estimation
2.3.1. Transition Probabilities


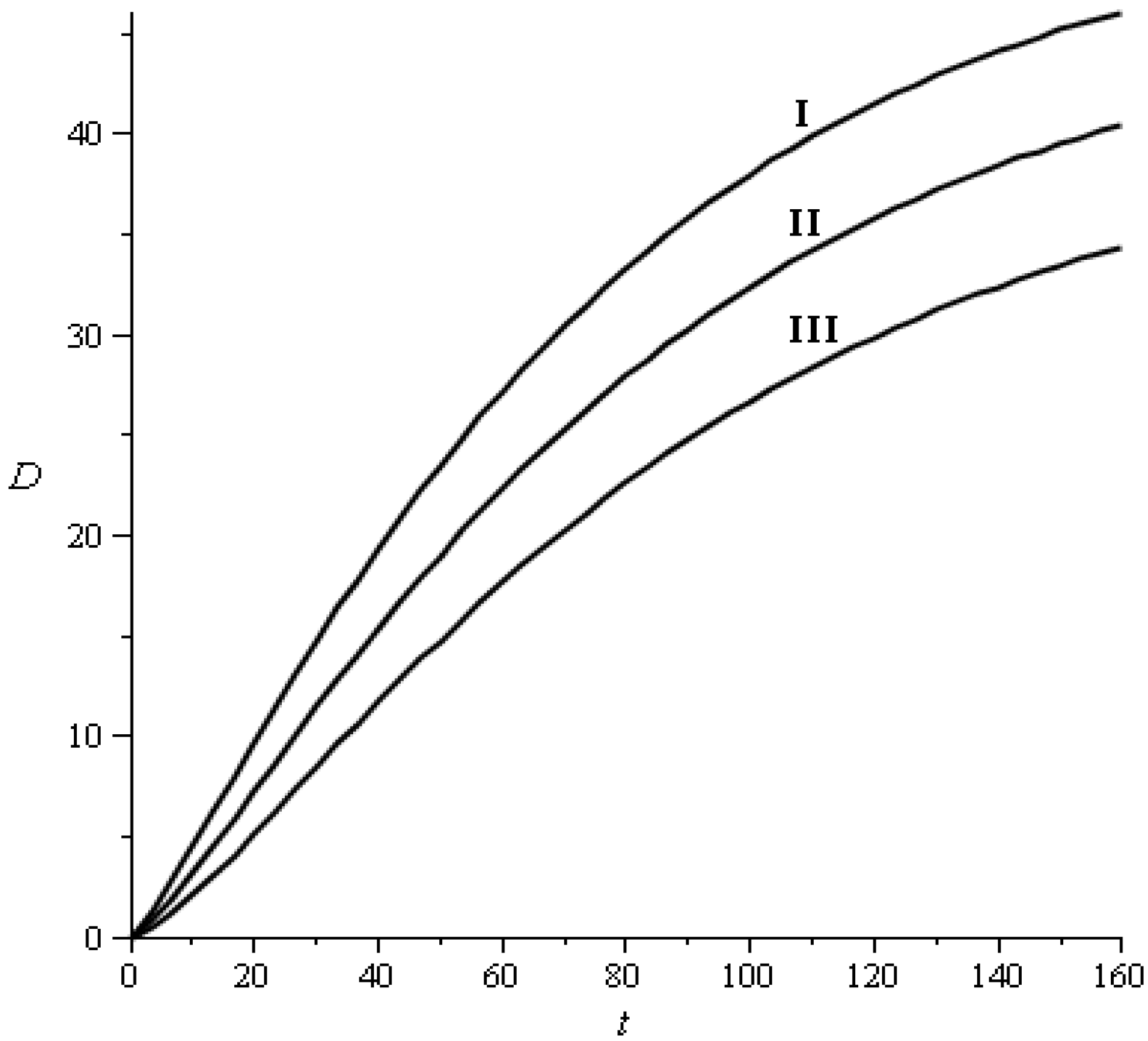
| Quality I | Quality II | Quality III | |
|---|---|---|---|
| (0,6) → (6,12) | p1 = 0.7697 | p1 = 0.5951 | p1 = 0.4564 |
| (6,12) → (12,18) | p2 = 0.8602 | p2 = 0.6824 | p2 = 0.5326 |
| (12,18) → (18,24) | p3 = 0.7913 | p3 = 0.6200 | p3 = 0.4697 |
| (18,24) → (24,30) | p4 = 0.6828 | p4 = 0.5190 | p4 = 0.3692 |
| (24,30) → (30,36) | p5 = 0.5533 | p5 = 0.3971 | p5 = 0.2475 |
| (30,36) → (36,42) | p6 = 0.4106 | p6 = 0.2618 | p6 = 0.1119 |
| (36,42) → (42,48) | p7 = 0.2587 | p7 = 0.1171 | - |
| (42,48) → (48,→) | p8 = 0.1000 | - | - |
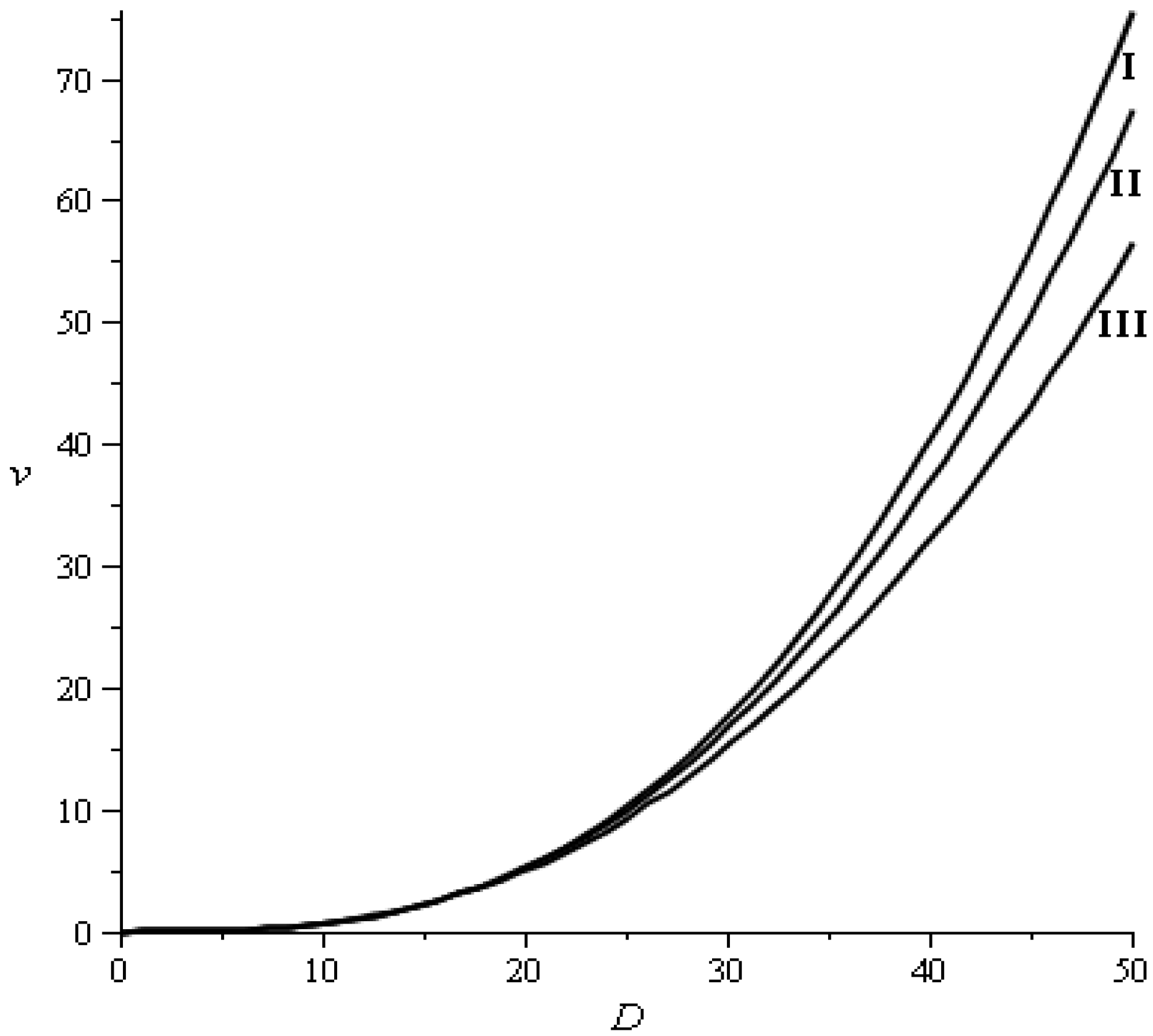
2.3.2. Recruitment and Basal Area
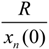 ), which had no influence on the stable diameter distribution of the stand, which is established by transition probabilities, the global amount of recruitment and stand basal area [7].
), which had no influence on the stable diameter distribution of the stand, which is established by transition probabilities, the global amount of recruitment and stand basal area [7].2.3.3. Natural Mortalities
2.3.4. Sustainable/Stable Harvesting Strategy: Stable Diameter Distribution

| R = 200 stem/ha | R = 520 stem/ha | R = 840 stem/ha | |||
|---|---|---|---|---|---|
| Q I | G = 22 | λ0 | 1.305091 | 1.477671 | 1.594240 |
| s | 0.233770 | 0.323259 | 0.372742 | ||
| Gmin | 16.857068 | 14.888296 | 13.799677 | ||
| Est. Dis. | [186.1, 122.9, 96.4, 77.2, 61.4, 47.5, 34.6, 22.1, 7.2] | [416.9, 239.8, 162.6, 110.9, 73.4, 45.7, 25.5, 11.4, 2.4] | [615.9, 325.9, 202.3, 125.4, 74.6, 41.1, 19.8, 7.4, 1.2] | ||
| NPV0 | 5,347.36 | 6,118.03 | 6,383.55 | ||
| G = 24 | λ0 | 1.292499 | 1.458959 | 1.571264 | |
| s | 0.226305 | 0.314580 | 0.363570 | ||
| Gmin | 18.568685 | 16.450081 | 15.274322 | ||
| Est. Dis. | [188.3, 125.7, 99.8, 81.0, 65.4, 51.4, 38.3, 25.3, 8.6] | [423.2, 246.9, 169.9, 117.8, 79.4, 50.5, 28.9, 13.4, 2.9] | [626.4, 336.8, 212.6, 134.2, 81.5, 45.9, 22.7, 8.8, 1.5] | ||
| NPV0 | 5,743.33 | 6,611.13 | 6,918.95 | ||
| G = 26 | λ0 | 1.281305 | 1.442342 | 1.550881 | |
| s | 0.219546 | 0.306683 | 0.355205 | ||
| Gmin | 20.291808 | 18.026241 | 16.764668 | ||
| Est. Dis. | [190.3, 128.3, 102.9, 84.5, 69.1, 55.3, 42.0, 28.5, 10.1] | [429.0, 253.5, 176.8, 124.3, 85.3, 55.3, 32.4, 15.5, 3.5] | [636.1, 347.0, 222.4, 142.6, 88.2, 50.8, 25.7, 10.2, 1.9] | ||
| NPV0 | 6,130.45 | 7,096.29 | 7,447.43 | ||
| Q II | G = 22 | λ0 | 1.262093 | 1.412527 | 1.514472 |
| s | 0.207665 | 0.292049 | 0.339704 | ||
| Gmin | 17.431369 | 15.574919 | 14.526515 | ||
| Est. Dis. | [233.3, 147.0, 113.7, 90.3, 71.1, 53.9, 37.2, 16.6] | [516.1, 280.5, 185.4, 123.4, 79.1, 46.6, 23.0, 6.5] | [757.0, 376.4, 226.4, 135.8, 77.3, 39.6, 16.4, 3.7] | ||
| NPV0 | 4,239.22 | 4,986.61 | 5,284.13 | ||
| G = 24 | λ0 | 1.251140 | 1.396188 | 1.494358 | |
| s | 0.200729 | 0.283764 | 0.330816 | ||
| Gmin | 19.182509 | 17.189656 | 16.060414 | ||
| Est. Dis. | [236.3, 150.7, 118.0, 95.0, 76.1, 58.9, 41.9, 19.5] | [524.6, 289.4, 194.4, 131.7, 86.1, 52.0, 26.5, 7.8] | [771.0, 389.9, 238.8, 146.1, 85.0, 44.7, 19.1, 4.5] | ||
| NPV0 | 4,542.73 | 5,373.95 | 5,710.91 | ||
| G = 26 | λ0 | 1.241406 | 1.381684 | 1.476521 | |
| s | 0.194462 | 0.276245 | 0.322732 | ||
| Gmin | 20.943989 | 18.817621 | 17.608961 | ||
| Est. Dis. | [239.1, 154.0, 122.0, 99.5, 80.9, 63.8, 46.6, 22.6] | [532.4, 297.7, 202.8, 139.6, 93.0, 57.4, 30.1, 9.2] | [783.9, 402.5, 250.5, 156.0, 92.7, 49.8, 22.0, 5.4] | ||
| NPV0 | 4,838.92 | 5,754.14 | 6,131.06 | ||
| Q III | G = 22 | λ0 | 1.220604 | 1.350816 | 1.439536 |
| s | 0.180733 | 0.259707 | 0.305332 | ||
| Gmin | 18.023866 | 16.286454 | 15.282699 | ||
| Est. Dis. | [295.4, 179.0, 138.1, 110.0, 86.7, 64.6, 32.8] | [644.2, 332.8, 216.0, 140.9, 87.0, 46.5, 14.8] | [937.6, 440.2, 257.8, 149.7, 80.5, 36.1, 9.2] | ||
| NPV0 | 3,202.56 | 3,906.48 | 4,224.82 | ||
| G = 24 | λ0 | 1.211164 | 1.336630 | 1.422004 | |
| s | 0.174348 | 0.251850 | 0.296767 | ||
| Gmin | 19.815651 | 17.955611 | 16.877591 | ||
| Est. Dis. | [299.6, 183.8, 143.8, 116.4, 93.7, 71.8, 38.0] | [655.8, 344.3, 227.4, 151.3, 95.6, 52.8, 17.6] | [956.3, 457.2, 273.0, 162.1, 89.4, 41.4, 11.0] | ||
| NPV0 | 3,421.69 | 4,194.95 | 4,548.76 | ||
| G = 26 | λ0 | 1.202780 | 1.324044 | 1.406468 | |
| s | 0.168593 | 0.244738 | 0.288999 | ||
| Gmin | 21.616583 | 19.636810 | 18.486024 | ||
| Est. Dis. | [303.4, 188.3, 149.1, 122.5, 100.4, 79.0, 43.6] | [666.3, 355.0, 238.2, 161.4, 104.2, 59.2, 20.4] | [973.6, 473.1, 287.6, 174.1, 98.3, 46.9, 12.9] | ||
| NPV0 | 3635.05 | 4477.23 | 4866.59 | ||



2.3.5. Stumpage Value Model
| Products | Diameter classes (cm) | ||
|---|---|---|---|
| <20 | 20–40 | >40 | |
| Poles | 0 | 11.85 | 0 |
| Sawlog | 0 | 9.8 | 11.76 |
| High quality sawlog | 0 | 0 | 9.96 |
| Total average price | 6 | 22.85 | 22.32 |
3. Results and Discussion
3.1. Results

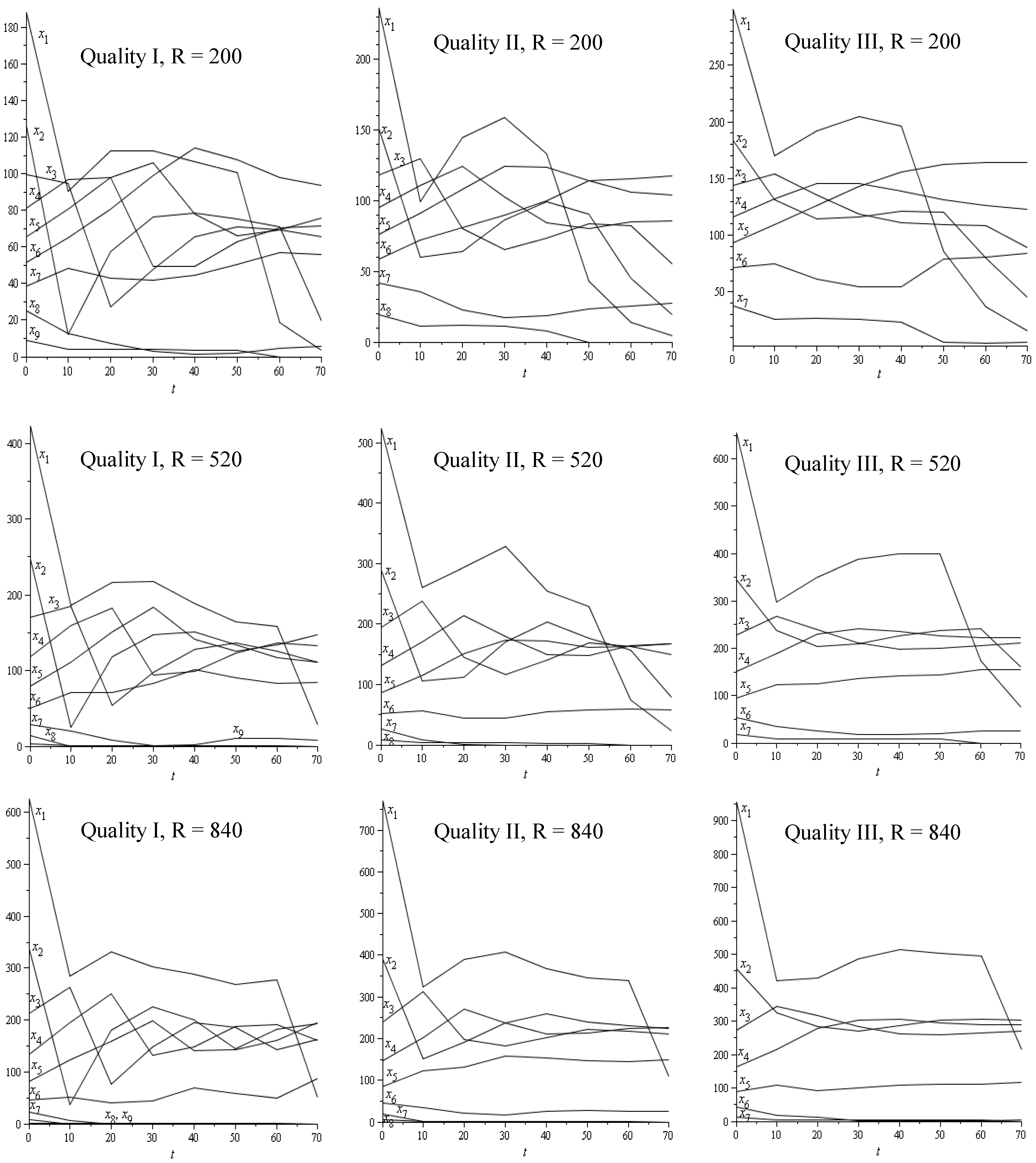
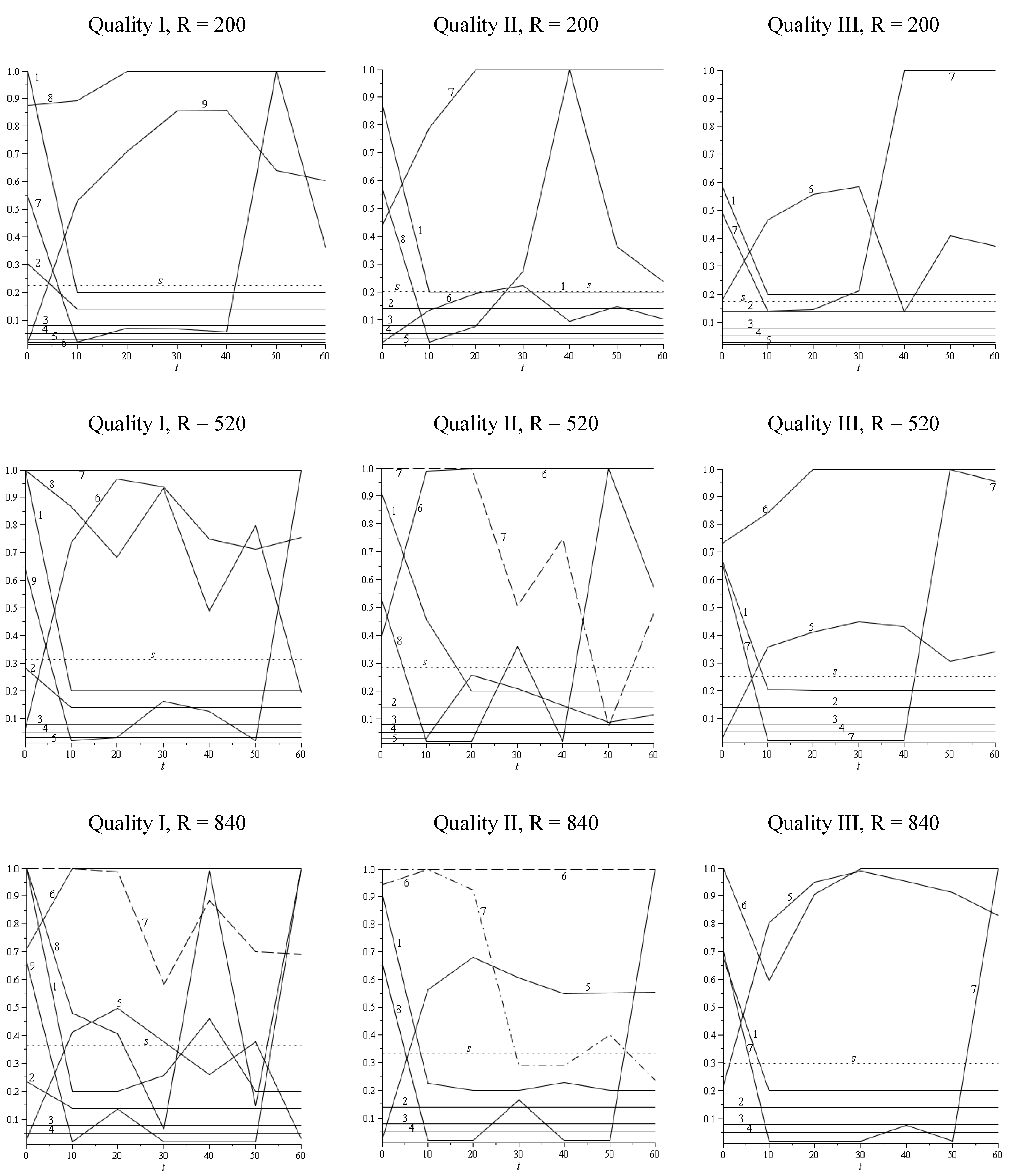
| R = 200 stem/ha | R = 520 stem/ha | R = 840 stem/ha | |||||
|---|---|---|---|---|---|---|---|
| NPV (€/ha) | NPV increase (%) | NPV (€/ha) | NPV increase (%) | NPV (€/ha) | NPV increase (%) | ||
| Q I | G = 22 | 6205.07 | 16.04 | 7188.49 | 17.50 | 7468.18 | 17.00 |
| G = 24 | 6636.65 | 15.55 | 7767.29 | 17.49 | 8095.43 | 17.00 | |
| G = 26 | 7056.80 | 15.11 | 8316.44 | 17.19 | 8718.00 | 17.06 | |
| Q II | G = 22 | 4788.21 | 12.95 | 5754.83 | 15.40 | 6139.05 | 16.18 |
| G = 24 | 5124.07 | 12.80 | 6203.83 | 15.44 | 6623.80 | 15.99 | |
| G = 26 | 5453.96 | 12.71 | 6647.77 | 15.53 | 7098.14 | 15.77 | |
| Q III | G = 22 | 3,502.94 | 9.38 | 4,389.27 | 12.36 | 4,820.65 | 14.10 |
| G = 24 | 3,724.85 | 8.86 | 4,701.48 | 12.07 | 5,185.97 | 14.00 | |
| G = 26 | 3,941.58 | 8.43 | 5,007.24 | 11.84 | 5,529.35 | 13.62 | |
| R = 200 stem/ha | R = 520 stem/ha | R = 840 stem/ha | |||||
|---|---|---|---|---|---|---|---|
| Δ | λT | Δ | λT | Δ | λT | ||
| Q I | G = 22 | 0.450415 | 0.056033 | 0.397311 | 0.002602 | 0.394624 | 0.000226 |
| G = 24 | 0.434304 | 0.178754 | 0.392813 | 0.002866 | 0.390207 | 0.000284 | |
| G = 26 | 0.425244 | 0.210573 | 0.437235 | 0.002866 | 0.387282 | 0.000559 | |
| QII | G = 22 | 0.467745 | 0.310556 | 0.490225 | 0.006628 | 0.361989 | 0.004161 |
| G = 24 | 0.467935 | 0.333705 | 0.487651 | 0.011089 | 0.351967 | 0.004161 | |
| G = 26 | 0.468382 | 0.354182 | 0.478031 | 0.014921 | 0.346997 | 0.004161 | |
| Q III | G = 22 | 0.348297 | 0.604092 | 0.392534 | 0.275817 | 0.335904 | 0.365103 |
| G = 24 | 0.422880 | 0.551102 | 0.385367 | 0.303478 | 0.323309 | 0.336591 | |
| G = 26 | 0.417756 | 0.562400 | 0.378934 | 0.337522 | 0.324559 | 0.312709 | |
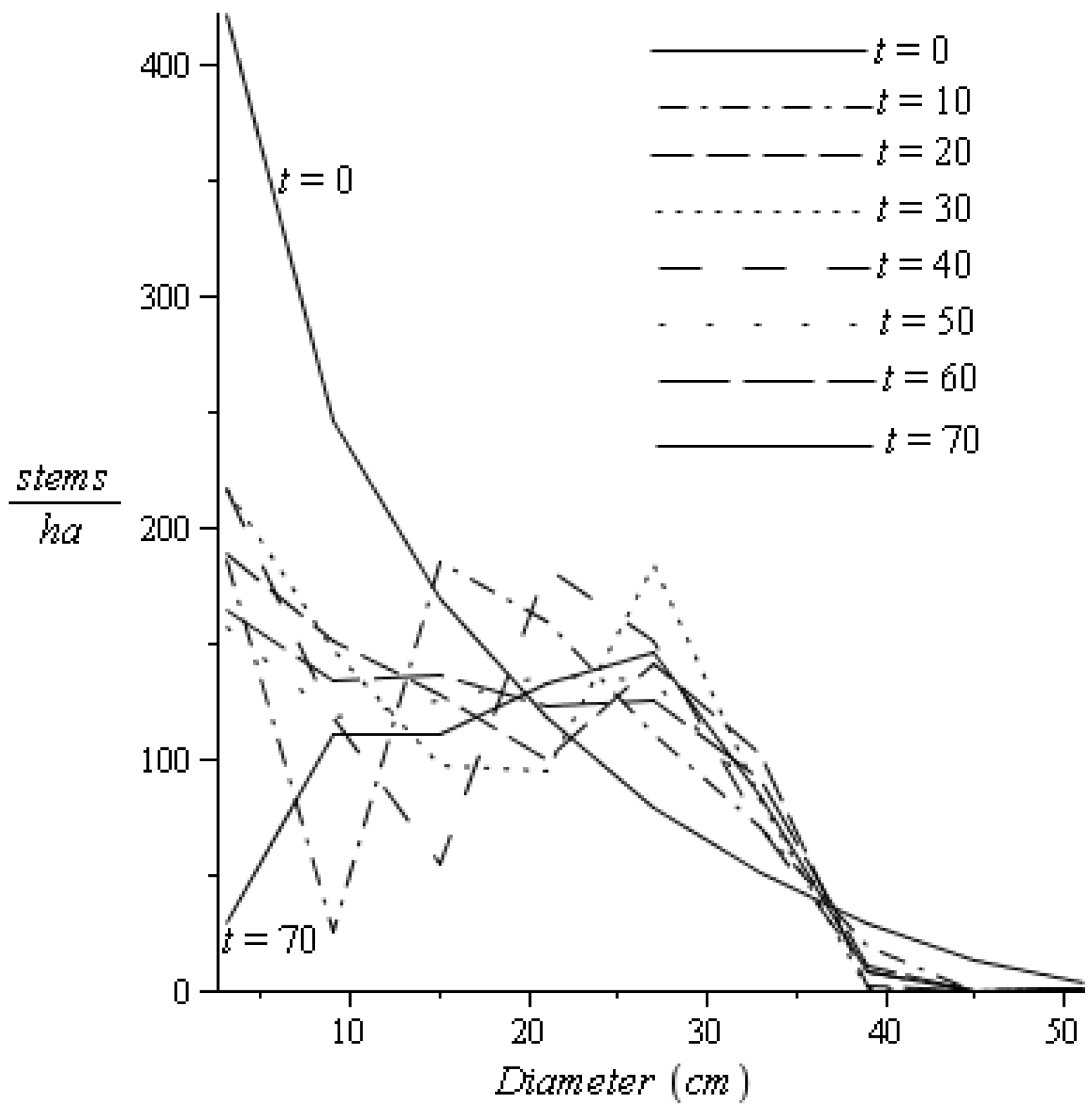
3.2. Discussion and Conclusions
Conflicts of Interest
References
- Buongiorno, J.; Michie, B.R. A matrix model of uneven-aged forest management. For. Sci. 1980, 26, 609–625. [Google Scholar]
- Caswell, H. Matrix Population Models: Construction, Analysis, and Interpretation, 2nd ed.; Sinauer Associates Inc.: Sunderland, MA, USA, 2001; p. 713. [Google Scholar]
- Picard, N.; Ouédraogo, D.; Bar-Hen, A. Choosing classes for size projection matrix models. Ecol. Model 2010, 221, 2270–2279. [Google Scholar] [CrossRef]
- Escalante, E.; Pando, V.; Ordoñez, C.; Bravo, F. Multinomial logit estimation of a diameter growth matrix model of two Mediterranean pine species in Spain. Ann. For. Sci. 2011, 68, 715–726. [Google Scholar] [CrossRef]
- Gotelli, N.J. A Primer of Ecology; Sinauer Associates Inc.: Sunderland, MA, USA, 2001; p. 265. [Google Scholar]
- Schütz, J.P. Modelling the demographic sustainability of pure beech plenter forests in Eastern Germany. Ann. For. Sci. 2006, 63, 93–100. [Google Scholar] [CrossRef]
- López, I.; Ortuño, S.F.; Martín, A.J.; Fullana, C. Estimating the sustainable harvesting and the stable diameter distribution of European beech with projection matrix models. Ann. For. Sci. 2007, 64, 593–599. [Google Scholar] [CrossRef]
- López, I.; Fullana, C.; Ortuño, S.F.; Martín, A.J. Choosing Fagus sylvatica L. matrix model dimension by sensitivity analysis of the population growth rate with respect to the width of the diameter classes. Ecol. Model 2008, 218, 307–314. [Google Scholar] [CrossRef]
- López, I.; Ortuño, S.; García, F.; Fullana, C. Is De Liocourt’s distribution stable? Forest Sci. 2012, 58, 34–46. [Google Scholar] [CrossRef]
- Haight, R.G. A comparison of dynamic and static economic models of uneven-aged stand management. Forest Sci. 1985, 31, 957–974. [Google Scholar]
- Sethi, S.P.; Thompson, G.L. Optimal Control Theory: Applications to Management Science and Economics, 2nd ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Kronrad, G.D.; Huang, C.H. Financially optimal thinning and final harvest schedules for loblolly pine plantations on nonindustrial private forestland in east Texas. South J. Appl. For. 2002, 26, 13–17. [Google Scholar]
- Tahvonen, O. Optimal harvesting of forest age classes: A survey of some recent results. Math Popul. Stud. 2004, 11, 205–232. [Google Scholar] [CrossRef]
- López, I.; Ortuño, S.; Martín, A.J.; Fullana, C. Estimating the optimal rotation age of Pinus nigra in the Spanish Iberian System applying discrete optimal control. For. Syst. 2010, 19, 306–314. [Google Scholar]
- Maple, Version 16.0, Maplesoft: Ontario, Canada, 2012.
- Front Line Systems Solver Premium Platform. Incline Village, NV, USA, 2008. Available online: http://www.solver.com (accessed on 26 July 2013).
- Grande, M.A.; García Abril, A. Los Pinares de Pinus nigra Arn. en España: Ecología, uso y gestión; Fundación Conde del Valle de Salazar (FUCOVASA): Madrid, Spain, 2005; pp. 1–53. [Google Scholar]
- Gómez Loranca, J.A. Modelo de crecimiento y producción para Pinus nigra Arn. en el Sistema Ibérico. Revista Montes 1998, 54, 5–18. [Google Scholar]
- Siegel, W.; Hoover, W.; Haney, H.; Liu, K. Forest Owners’ Guide to the Federal Income Tax; Agriculture Handbook No. 708; United States Department of Agriculture, Forest Service: Washington, DC, USA, 1995; p. 138. [Google Scholar]
- Retana, J.; Espelta, J.M.; Habrouk, A.; Ordóñez, J.L.; Solà-Morales, F. Regeneration patterns of three Mediterranean pines and forest changes after a large wildfire in north-eastern Spain. Ecoscience 2002, 9, 89–97. [Google Scholar]
- Tíscar, P.A. Dinámica de regeneración de Pinus nigra subs. Salzmannii al sur de su área de distribución: etapas, procesos y factores implicados. Inv. Agrar. Sist. Rec. F. 2007, 16, 124–135. [Google Scholar]
- Tíscar Oliver, P.A.; Lucas, M.E.; Tíscar Soria, M.A. La alteración del suelo y la espesura como factores de regeneración de Pinus nigra subs. Salzmannii a lo largo de su área de distribución. Revista Montes 2010, 103, 10–15. [Google Scholar]
- Schütz, J.P. Le régime du jardinage. Document autographique du cours de Sylviculture III; Chaire de Sylviculture; E.T.H. Zürich: Zürich, Switzerland, 1989; p. 55. [Google Scholar]
- Serrada, R.; Domínguez Lerena, S.; Sánchez Resco, M.I.; Ruiz Ortiz, J. El problema de la regeneración natural de Pinus nigra Arn. Revista Montes 1994, 36, 52–57. [Google Scholar]
- Van Mantgem, P.J.; Stephenson, N.T. The accuracy of matrix population model projections for coniferous trees in the Sierra Nevada, California. J. Ecol. 2005, 93, 737–747. [Google Scholar] [CrossRef]
- Misir, M.; Misir, N.; Yavuz, H. Modeling individual tree mortality for Crimean pine plantations. J. Environ. Biol. 2007, 28, 167–172. [Google Scholar]
- Trasobares, A.; Pukkala, T. Optimising the management of uneven-aged Pinus sylvestris L. and Pinus nigra Arn. mixed stands in Catalonia, north-east Spain. Ann. For. Sci. 2004, 61, 747–758. [Google Scholar] [CrossRef]
- Ramula, S.; Lehtilä, K. Matrix dimensionality in demographic analyses of plants: When to use smaller matrices? Oikos 2005, 111, 563–573. [Google Scholar] [CrossRef]
- Zuidema, P.A. Demography of Exploited Tree Species in the Bolivian Amazon; PROMAB Scientific Series 2; Promab: Riberalta, Bolivia, 2000; p. 240. [Google Scholar]
- Keyfitz, N. Introduction to the Mathematics of Population; Addison-Wesley: Reading, MA, USA, 1968; p. 464. [Google Scholar]
- Montero, G.; Rojo, A.; Alía, R. Determinación del turno de Pinus sylvestris L en el Sistema Central. Revista Montes 1992, 29, 42–47. [Google Scholar]
- Boletín Mensual de Estadística 1994–2011; Ministerio de Agricultura, Alimentación y Medio Ambiente: Madrid, Spain, 2011; pp. 29–33.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
López-Torres, I.; Ortuño-Pérez, S.; García-Robredo, F.; Fullana-Belda, C. Are the Economically Optimal Harvesting Strategies of Uneven-Aged Pinus nigra Stands Always Sustainable and Stabilizing? Forests 2013, 4, 830-848. https://doi.org/10.3390/f4040830
López-Torres I, Ortuño-Pérez S, García-Robredo F, Fullana-Belda C. Are the Economically Optimal Harvesting Strategies of Uneven-Aged Pinus nigra Stands Always Sustainable and Stabilizing? Forests. 2013; 4(4):830-848. https://doi.org/10.3390/f4040830
Chicago/Turabian StyleLópez-Torres, Ignacio, Sigfredo Ortuño-Pérez, Fernando García-Robredo, and Carmen Fullana-Belda. 2013. "Are the Economically Optimal Harvesting Strategies of Uneven-Aged Pinus nigra Stands Always Sustainable and Stabilizing?" Forests 4, no. 4: 830-848. https://doi.org/10.3390/f4040830
APA StyleLópez-Torres, I., Ortuño-Pérez, S., García-Robredo, F., & Fullana-Belda, C. (2013). Are the Economically Optimal Harvesting Strategies of Uneven-Aged Pinus nigra Stands Always Sustainable and Stabilizing? Forests, 4(4), 830-848. https://doi.org/10.3390/f4040830




