The Significance of Tree Height as a Predictor of Tree Mortality during Bark Beetle Outbreaks in a Small Catchment
Abstract
1. Introduction
1.1. Bark Beetle Behavior—Endemic and Epidemic Phases
1.2. Spatial Spread of Bark Beetles
1.3. Scales in Bark Beetle Attacks
1.4. Bark Beetles in the Bohemian Forest
1.5. Hypotheses
2. Materials and Methods
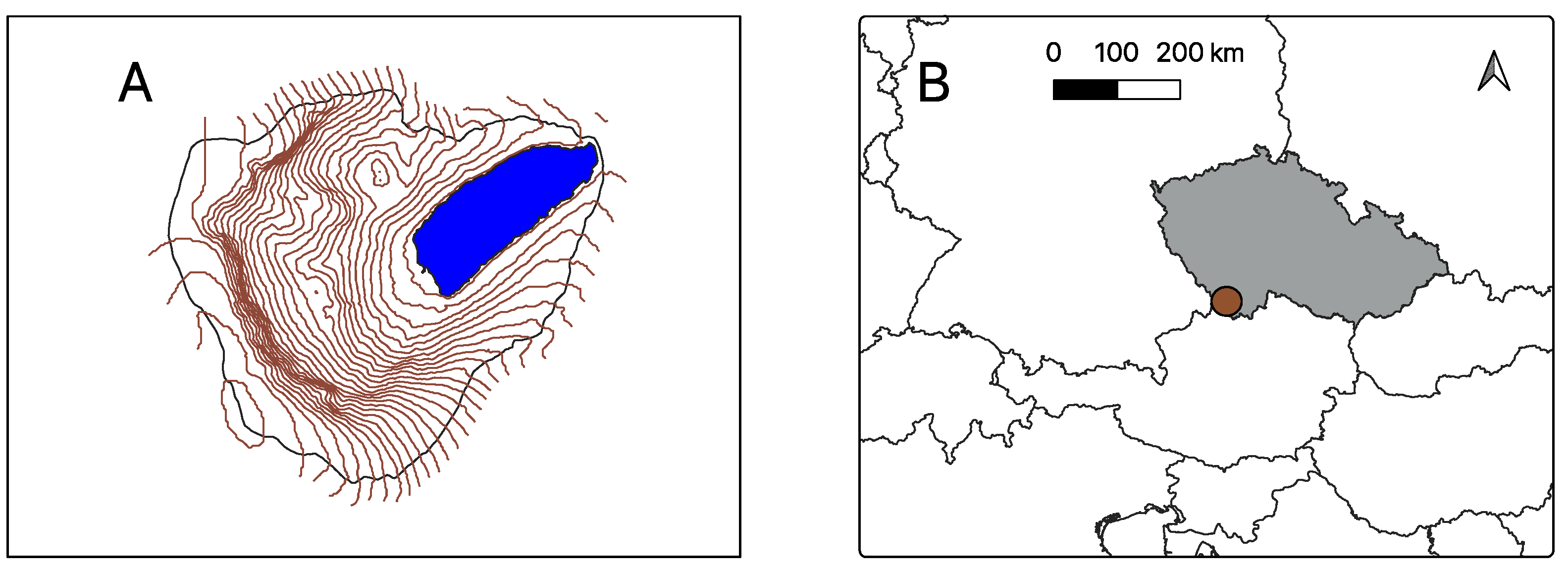
2.1. Study Site
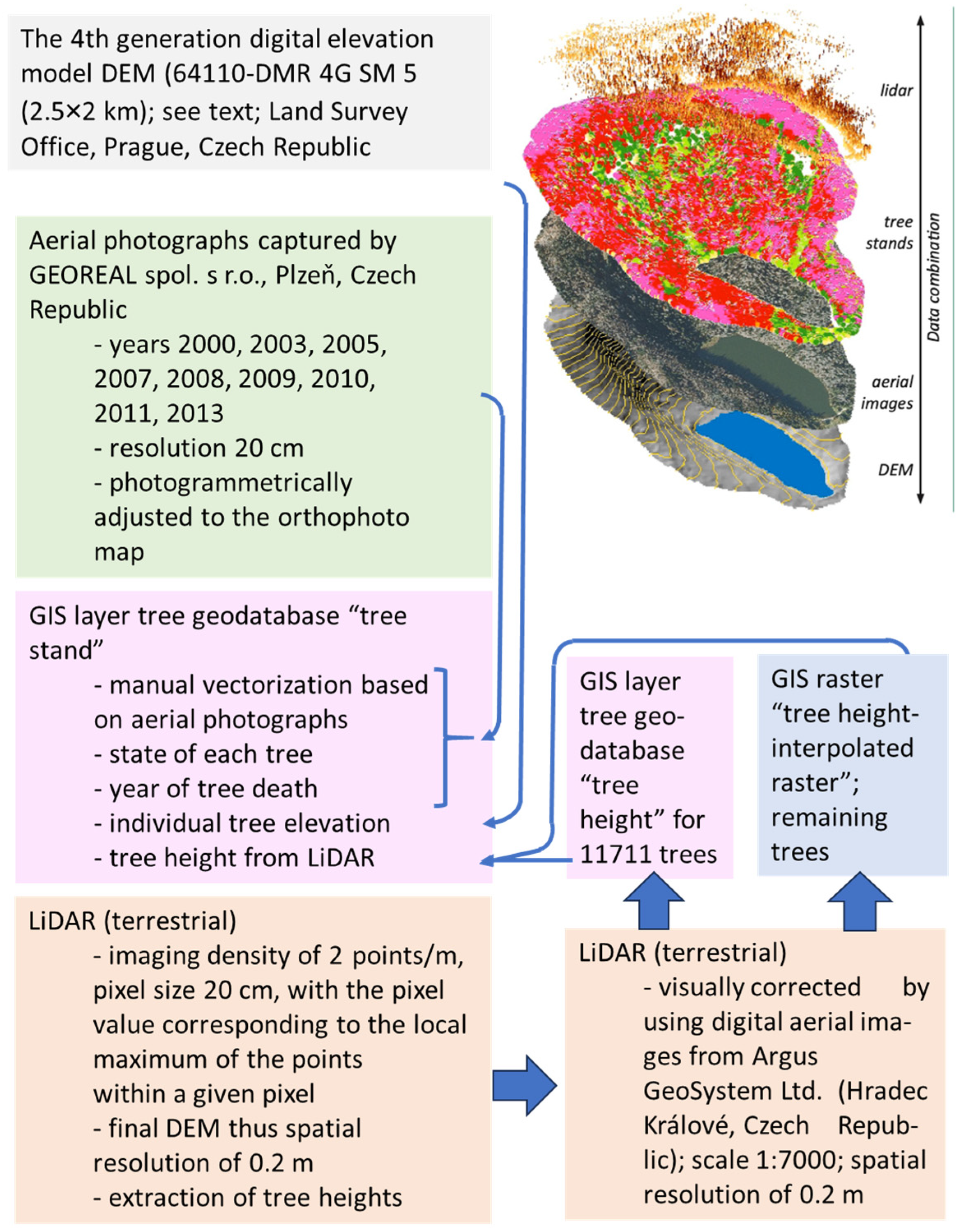
2.2. Elevation, Aspect, and Slope Data
2.3. Tree Mapping and Characteristics
2.4. Geostatistical Analysis—General approach to Spatial Scale Effects
2.5. Geostatistical Analysis—Spatial Kernel Density Smoothing to Calculated Stand Density from the Tree Database by Fluksová et al. [20]
2.6. Forest Damage on the Regional Sale—Czech Data Set of the Šumava National Park Administration
2.7. Forest Damage on the Regional Sale—European Scale
2.8. Statistical Treatment of the Results from Geostatistical Analyses
2.8.1. Spatial Distribution
2.8.2. Gradient Boosting Machine (GBM) Predicting Tree Death
2.8.3. General Additive Models (GAMs) Predicting the Percent of Conifers Killed
3. Results
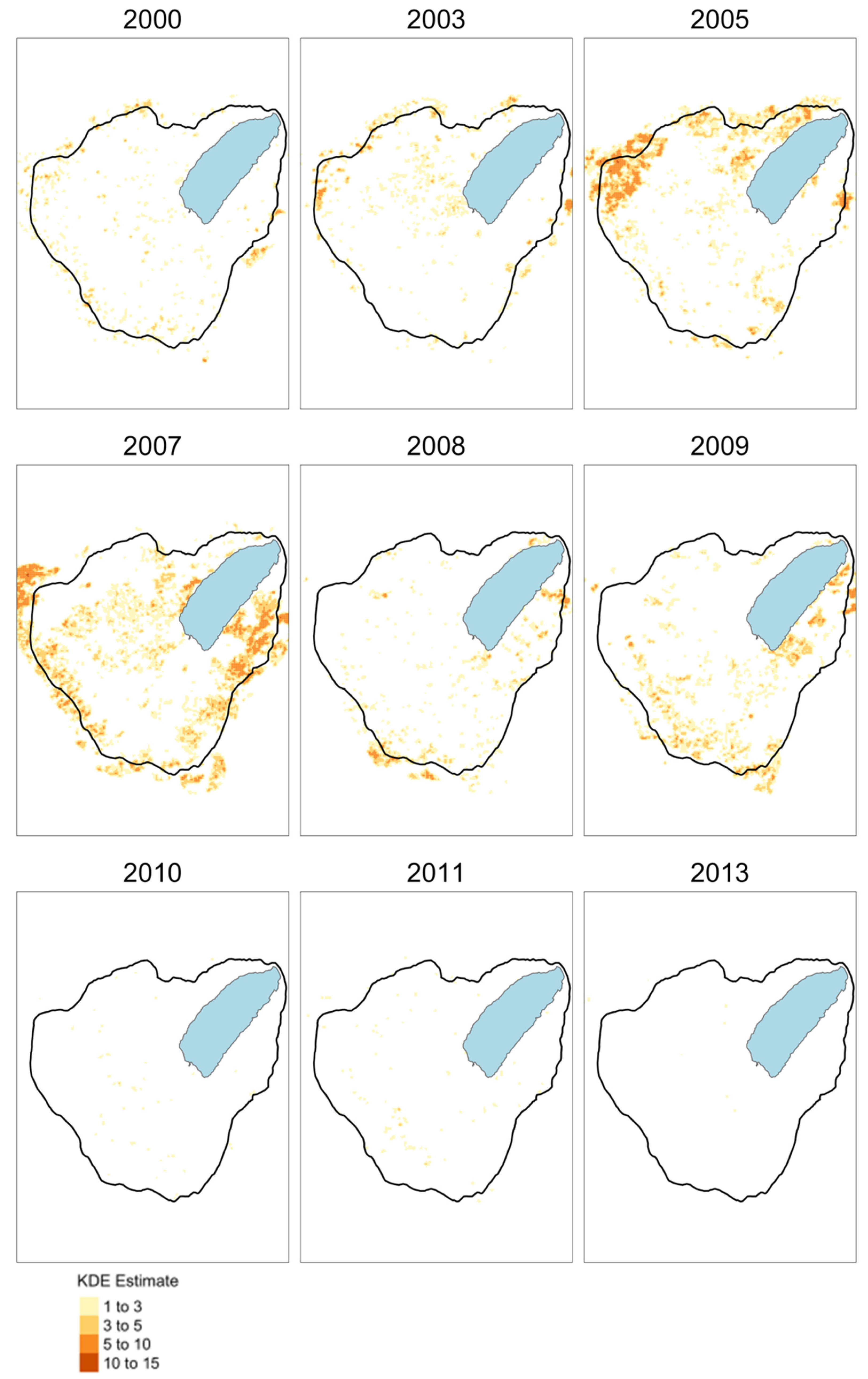
3.1. Spatial-Temporal Dynamics
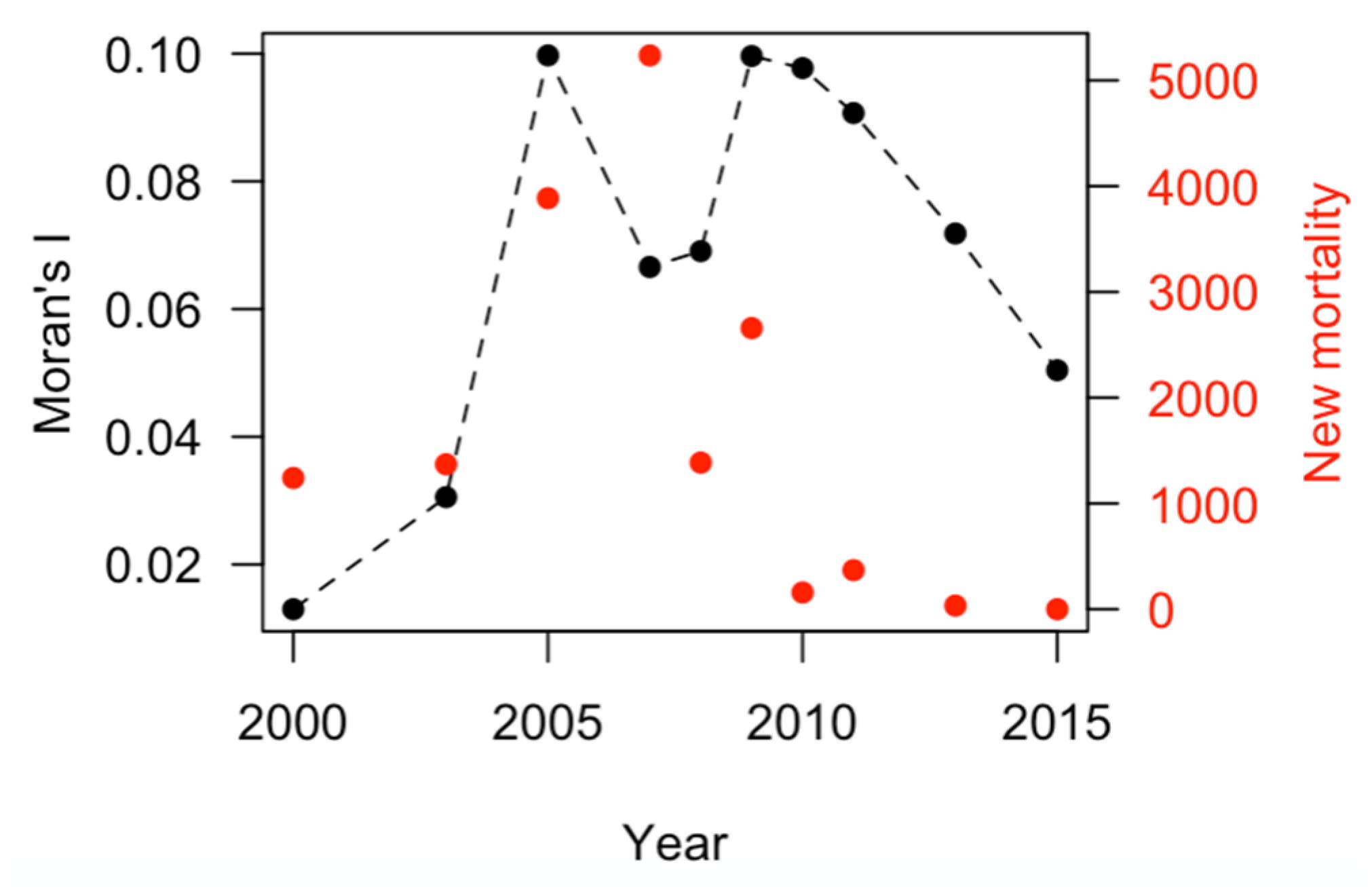
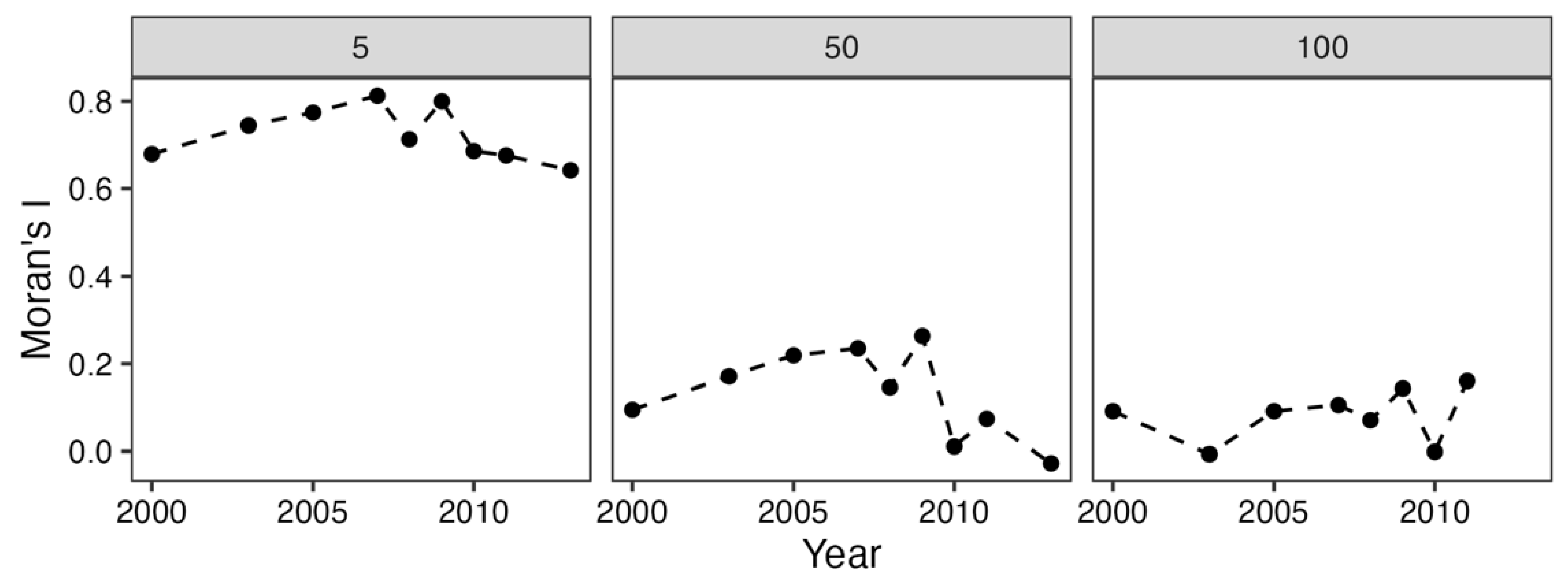
3.2. Spatial Autocorrelation: Moran’s I
3.3. The Most Influential Variables Predicting Tree Death
4. Discussion
4.1. The Importance of Predictors at Different Scales during the Bark Beetle Attack Phases
4.2. Aerial Images Versus Satellite Remote Sensing
4.3. Is the Site Scale the Most Influential Scale?
4.4. Does the Density of Healthy Trees on the Small Scale Protect Trees?
4.5. Are Spatial Scales Useful for Discussing an Ecological Effect?
4.6. Salvage Logging for Managing Bark Beetle Attacks
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeppenfeld, T.; Svoboda, M.; DeRose, R.J.; Heurich, M.; Müller, J.; Čížková, P.; Starý, M.; Bače, R.; Donato, D.C. Response of Mountain Picea abies Forests to Stand-Replacing Bark Beetle Outbreaks: Neighbourhood Effects Lead to Self-Replacement. J. Appl. Ecol. 2015, 52, 1402–1411. [Google Scholar] [CrossRef]
- Dobor, L.; Hlásny, T.; Rammer, W.; Zimová, S.; Barka, I.; Seidl, R. Is Salvage Logging Effectively Dampening Bark Beetle Outbreaks and Preserving Forest Carbon Stocks? J. Appl. Ecol. 2020, 57, 67–76. [Google Scholar] [CrossRef]
- Sommerfeld, A.; Rammer, W.; Heurich, M.; Hilmers, T.; Müller, J.; Seidl, R. Do Bark Beetle Outbreaks Amplify or Dampen Future Bark Beetle Disturbances in Central Europe? J. Ecol. 2021, 109, 737–749. [Google Scholar] [CrossRef] [PubMed]
- Bentz, B.J.; Jönsson, A.M. Chapter 13—Modeling Bark Beetle Responses to Climate Change. In Bark Beetles; Vega, F.E., Hofstetter, R.W., Eds.; Academic Press: San Diego, CA, USA, 2015; pp. 533–553. ISBN 978-0-12-417156-5. [Google Scholar]
- Biedermann, P.H.W.; Müller, J.; Grégoire, J.-C.; Gruppe, A.; Hagge, J.; Hammerbacher, A.; Hofstetter, R.W.; Kandasamy, D.; Kolarik, M.; Kostovcik, M.; et al. Bark Beetle Population Dynamics in the Anthropocene: Challenges and Solutions. Trends Ecol. Evol. 2019, 34, 914–924. [Google Scholar] [CrossRef] [PubMed]
- Morris, J.; Clear, J.; Cottrell, S.; Hansen, W.; Mattor, K.; Seddon, A.; Seppä, H. Social-Ecological Dimensions of Forest Bark Beetle Disturbances: Past, Present, and Future. Past Glob. Chang. Mag. 2015, 23, 74. [Google Scholar] [CrossRef]
- Schroeder, L.M. Colonization of Storm Gaps by the Spruce Bark Beetle: Influence of Gap and Landscape Characteristics. Agric. For. Entomol. 2010, 12, 29–39. [Google Scholar] [CrossRef]
- Raffa, K.F. Mixed Messages across Multiple Trophic Levels: The Ecology of Bark Beetle Chemical Communication Systems. Chemoecology 2001, 11, 49–65. [Google Scholar] [CrossRef]
- Brattli, J.G.; Andersen, J.; Nilssen, A.C. Primary Attraction and Host Tree Selection in Deciduous and Conifer Living Coleoptera: Scolytidae, Curculionidae, Cerambycidae and Lymexylidae. J. Appl. Entomol. 1998, 122, 345–352. [Google Scholar] [CrossRef]
- Tunset, K.; Nilssen, A.C.; Andersen, J. Primary Attraction in Host Recognition of Coniferous Bark Beetles and Bark Weevils (Col., Scolytidae and Curculionidae). J. Appl. Entomol. 1993, 115, 155–169. [Google Scholar] [CrossRef]
- Hedgren, P.O.; Schroeder, L.M.; Weslien, J. Tree Killing by Ips typographus (Coleoptera: Scolytidae) at Stand Edges with and without Colonized Felled Spruce Trees. Agric. For. Entomol. 2003, 5, 67–74. [Google Scholar] [CrossRef]
- Gall, R.; Heimgartner, A. Spatial Patterns of First Spruce Bark Beetle (Ips typographus L.) Infestation of Standing Norway Spruce (Picea abies [L.] Karst.) after Heavy Storm Damage in Switzerland. In Ecology, Survey and Management of Forest Insects; Michael, L.M., Andrew, M.L., Eds.; General Technical Report NE-311; U.S. Department of Agriculture, Forest Service, Northeastern Research Station: Newtown Square, PA, USA, 2003; Volume 311, pp. 132–133. [Google Scholar]
- Becker, T.; Schröter, H. Die Ausbreitung des Borkenkäferbefalls im Bereich von Sturmwurf-Sukzessionsflächen; Forstliche Versuchs- und Forschungsanstalt Baden-Württemberg, Abteilung Waldschutz: Freiburg, Germany, 2001; ISSN 1436-1566. [Google Scholar]
- Hlásny, T.; Zimová, S.; Bentz, B. Scientific Response to Intensifying Bark Beetle Outbreaks in Europe and North America. For. Ecol. Manag. 2021, 499, 119599. [Google Scholar] [CrossRef]
- Stadelmann, G.; Bugmann, H.; Wermelinger, B.; Bigler, C. Spatial Interactions between Storm Damage and Subsequent Infestations by the European Spruce Bark Beetle. For. Ecol. Manag. 2014, 318, 167–174. [Google Scholar] [CrossRef]
- Kautz, M.; Dworschak, K.; Gruppe, A.; Schopf, R. Quantifying Spatio-Temporal Dispersion of Bark Beetle Infestations in Epidemic and Non-Epidemic Conditions. For. Ecol. Manag. 2011, 262, 598–608. [Google Scholar] [CrossRef]
- Wermelinger, B. Ecology and Management of the Spruce Bark Beetle Ips typographus—A Review of Recent Research. For. Ecol. Manag. 2004, 202, 67–82. [Google Scholar] [CrossRef]
- Wichmann, L.; Ravn, H.P. The Spread of Ips typographus (L.) (Coleoptera, Scolytidae) Attacks Following Heavy Windthrow in Denmark, Analysed Using GIS. For. Ecol. Manag. 2001, 148, 31–39. [Google Scholar] [CrossRef]
- Niță, M.D. Testing Forestry Digital Twinning Workflow Based on Mobile LiDAR Scanner and AI Platform. Forests 2021, 12, 1576. [Google Scholar] [CrossRef]
- Fluksová, H.; Grill, S.; Bače, R.; Hais, M. Dynamics of Stand Replacing-Disturbance and Biomass Estimation in the Plešné Lake Basin. Silva Gabreta 2020, 26, 99–116. [Google Scholar]
- Fahrig, L.; Girard, J.; Duro, D.; Pasher, J.; Smith, A.; Javorek, S.; King, D.; Lindsay, K.F.; Mitchell, S.; Tischendorf, L. Farmlands with Smaller Crop Fields Have Higher Within-Field Biodiversity. Agric. Ecosyst. Environ. 2015, 200, 219–234. [Google Scholar] [CrossRef]
- Mey, R.; Temperli, C.; Stillhard, J.; Nitzsche, J.; Thürig, E.; Bugmann, H.; Zell, J. Deriving Forest Stand Information from Small Sample Plots: An Evaluation of Statistical Methods. For. Ecol. Manag. 2023, 544, 121155. [Google Scholar] [CrossRef]
- Seidl, R.; Müller, J.; Hothorn, T.; Bässler, C.; Heurich, M.; Kautz, M. Small Beetle, Large-Scale Drivers: How Regional and Landscape Factors Affect Outbreaks of the European Spruce Bark Beetle. J. Appl. Ecol. 2016, 53, 530–540. [Google Scholar] [CrossRef]
- Seidel, D.; Ehbrecht, M.; Annighöfer, P.; Ammer, C. rom Tree to Stand-Level Structural Complexity—Which Properties Make a Forest Stand Complex? Agric. For. Meteorol. 2019, 278, 107699. [Google Scholar] [CrossRef]
- Zeug, G. Machbarkeitsstudie zur Nutzung von Satellitenfernerkundungsdaten (Copernicus) für Zwecke der Ableitung ökologischer Belastungsgrenzen und der Verifizierung von Indikatoren der Deutschen Anpassungsstrategie an den Klimawandel; Umweltbundesamt: Dessau-Rosslau, Germany, 2019. [Google Scholar]
- Svoboda, M.; Fraver, S.; Janda, P.; Bače, R.; Zenáhlíková, J. Natural Development and Regeneration of a Central European Montane Spruce Forest. For. Ecol. Manag. 2010, 260, 707–714. [Google Scholar] [CrossRef]
- Štursová, M.; Šnajdr, J.; Cajthaml, T.; Bárta, J.; Šantrůčková, H.; Baldrian, P. When the Forest Dies: The Response of Forest Soil Fungi to a Bark Beetle-Induced Tree Dieback. ISME J. 2014, 8, 1920–1931. [Google Scholar] [CrossRef] [PubMed]
- Hlásny, T.; Krokene, P.; Liebhold, A.; Montagné-Huck, C.; Müller, J.; Qin, H.; Raffa, K.; Schelhaas, M.-J.; Seidl, R.; Svoboda, M.; et al. Living with Bark Beetles: Impacts, Outlook and Management Options; From Science to Policy; European Forest Institute: Joensuu, Finland, 2019. [Google Scholar]
- Lobinger, G.; Skatulla, U. Untersuchungen Zum Einfluss von Sonnenlicht Auf Das Schwärmverhalten von Borkenkäfern. Anz. Schädl.Kd. Pflanzenschutz Umweltschutz 1996, 69, 183–185. [Google Scholar] [CrossRef]
- Mattanovich, J.; Ehrenhöfer, M.; Schafellner, C.; Tausz, M.; Führer, E. The Role of Sulphur Compounds for Breeding Success of Ips typographus L. (Col., Scolytidae) on Norway Spruce (Picea abies [L.] Karst.). J. Appl. Entomol. 2001, 125, 425–431. [Google Scholar] [CrossRef]
- Svoboda, M.; Janda, P.; Nagel, T.A.; Fraver, S.; Rejzek, J.; Bače, R. Disturbance History of an Old-Growth Sub-Alpine Picea abies Stand in the Bohemian Forest, Czech Republic. J. Veg. Sci. 2012, 23, 86–97. [Google Scholar] [CrossRef]
- Christiansen, E. Ips/Ceratocystis-Infection of Norway Spruce: What Is a Deadly Dosage? 1. Z. Für Angew. Entomol. 1985, 99, 6–11. [Google Scholar] [CrossRef]
- Wilkinson, R.C.; Haack, R.A. Within-Tree Distribution of Pine Bark Beetles (Coleóptera: Scolytidae) in Honduras. Ceiba 1987, 28, 115–133. [Google Scholar]
- Church, J.E. Evaporation at High Altitudes and Latitudes. Eos Trans. Am. Geophys. Union 1934, 15, 326–351. [Google Scholar] [CrossRef]
- Šantrůčková, H.; Šantrůček, J.; Šetlík, J.; Svoboda, M.; Kopáček, J. Carbon Isotopes in Tree Rings of Norway Spruce Exposed to Atmospheric Pollution. Environ. Sci. Technol. 2007, 41, 5778–5782. [Google Scholar] [CrossRef]
- Kopáček, J.; Fluksová, H.; Hejzlar, J.; Kaňa, J.; Porcal, P.; Turek, J. Changes in Surface Water Chemistry Caused by Natural Forest Dieback in an Unmanaged Mountain Catchment. Sci. Total Environ. 2017, 584–585, 971–981. [Google Scholar] [CrossRef]
- Beudert, B.; Bernsteinová, J.; Premier, J.; Bässler, C. Natural Disturbance by Bark Beetle Offsets Climate Change Effects on Streamflow in Headwater Catchments of the Bohemian Forest. Silva Gabreta 2018, 24, 21–45. [Google Scholar]
- Gdulová, K.; Marešová, J.; Barták, V.; Szostak, M.; Červenka, J.; Moudrý, V. Use of TanDEM-X and SRTM-C Data for Detection of Deforestation Caused by Bark Beetle in Central European Mountains. Remote Sens. 2021, 13, 3042. [Google Scholar] [CrossRef]
- Müller, M. How Natural Disturbance Triggers Political Conflict: Bark Beetles and the Meaning of Landscape in the Bavarian Forest. Glob. Environ. Chang. 2011, 21, 935–946. [Google Scholar] [CrossRef]
- Hlásny, T.; König, L.; Krokene, P.; Lindner, M.; Montagné-Huck, C.; Müller, J.; Qin, H.; Raffa, K.F.; Schelhaas, M.-J.; Svoboda, M.; et al. Bark Beetle Outbreaks in Europe: State of Knowledge and Ways Forward for Management. Curr For. Rep 2021, 7, 138–165. [Google Scholar] [CrossRef]
- Veselý, J. Investigation of the Nature of the Šumava Lakes: A Review. Časopis Národního Muz. Praha Řada Přírodovědná 1994, 163, 103–120. [Google Scholar]
- Kopáček, J.; Čapek, P.; Choma, M.; Cudlín, P.; Kaňa, J.; Kopáček, M.; Porcal, P.; Šantrůčková, H.; Tahovská, K.; Turek, J. Long-Term Changes in Soil Composition in Unmanaged Central European Mountain Spruce Forests after Decreased Acidic Deposition and a Bark Beetle Outbreak. Catena 2023, 222, 106839. [Google Scholar] [CrossRef]
- Kopáček, J.; Bače, R.; Hejzlar, J.; Kaňa, J.; Kučera, T.; Matějka, K.; Porcal, P.; Turek, J. Changes in Microclimate and Hydrology in an Unmanaged Mountain Forest Catchment after Insect-Induced Tree Dieback. Sci. Total Environ. 2020, 720, 137518. [Google Scholar] [CrossRef] [PubMed]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining Tree Height and Crown Diameter from High-Resolution UAV Imagery. Int. J. Remote Sens. 2017, 38, 2392–2410. [Google Scholar] [CrossRef]
- Schmidt, S.I.; Hejzlar, J.; Kopáček, J.; Paule-Mercado, M.C.; Porcal, P.; Vystavna, Y. Relationships between a Catchment-Scale Forest Disturbance Index, Time Delays, and Chemical Properties of Surface Water. Ecol. Indic. 2021, 125, 107558. [Google Scholar] [CrossRef]
- Senf, C. European Forest Disturbance Map; 2021. Available online: https://zenodo.org/record/4570157 (accessed on 15 September 2023).
- Senf, C.; Seidl, R. Mapping the Forest Disturbance Regimes of Europe. Nat. Sustain. 2021, 4, 63–70. [Google Scholar] [CrossRef]
- Pebesma, E. Simple Features for R: Standardized Support for Spatial Vector Data. R J. 2018, 10, 439–446. [Google Scholar] [CrossRef]
- Pebesma, E.; Bivand, R. Spatial Data Science: With Applications in R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2023. [Google Scholar]
- Caha, J. SpatialKDE: Kernel Density Estimation for Spatial Data; R Package Version 0.8.1; 2022. Available online: https://CRAN.R-project.org/package=SpatialKDE (accessed on 15 September 2023).
- Baddeley, A.; Turner, R.; Mateu, J.; Bevan, A. Hybrids of Gibbs Point Process Models and Their Implementation. J. Stat. Softw. 2013, 55, 1–43. [Google Scholar] [CrossRef]
- Hijmans, R. Raster: Geographic Data Analysis and Modeling; R Package Version 3.6-26; 2023. Available online: https://CRAN.R-project.org/package=raster (accessed on 15 September 2023).
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; ACM: San Francisco, CA, USA, 2016; pp. 785–794. [Google Scholar]
- Brown, I.; Mues, C. An Experimental Comparison of Classification Algorithms for Imbalanced Credit Scoring Data Sets. Expert Syst. Appl. 2012, 39, 3446–3453. [Google Scholar] [CrossRef]
- Boehmke, B.; Greenwell, B. Chapter 12 Gradient Boosting. In Hands-On Machine Learning with R; Taylor & Francis Group: Abingdon, UK, 2020; Available online: https://www.taylorfrancis.com/chapters/mono/10.1201/9780367816377-12/gradient-boosting-brad-boehmke-brandon-greenwell (accessed on 15 September 2023).
- Zhang, C.; Liu, C.; Zhang, X.; Almpanidis, G. An Up-to-Date Comparison of State-of-the-Art Classification Algorithms. Expert Syst. Appl. 2017, 82, 128–150. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Integrating Well Log Interpretations for Lithofacies Classification and Permeability Modeling through Advanced Machine Learning Algorithms. J. Pet Explor. Prod. Technol. 2017, 7, 1023–1033. [Google Scholar] [CrossRef]
- Greenwell, B.; Boehmke, B.; Cunningham, J. GBM Developers Package ‘Gbm’ Version 2.1.8.1: Generalized Boosted Regression Models. 2022. Available online: https://CRAN.R-project.org/package=gbm (accessed on 15 September 2023).
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Berthelot, S.; Frühbrodt, T.; Hajek, P.; Nock, C.A.; Dormann, C.F.; Bauhus, J.; Fründ, J. Tree Diversity Reduces the Risk of Bark Beetle Infestation for Preferred Conifer Species, but Increases the Risk for Less Preferred Hosts. J. Ecol. 2021, 109, 2649–2661. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Perperoglou, A.; Sauerbrei, W.; Abrahamowicz, M.; Schmid, M. A Review of Spline Function Procedures in R. BMC Med. Res. Methodol. 2019, 19, 46. [Google Scholar] [CrossRef]
- Wood, S.N. Fast Stable Restricted Maximum Likelihood and Marginal Likelihood Estimation of Semiparametric Generalized Linear Models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 3–36. [Google Scholar] [CrossRef]
- Netherer, S.; Matthews, B.; Katzensteiner, K.; Blackwell, E.; Henschke, P.; Hietz, P.; Pennerstorfer, J.; Rosner, S.; Kikuta, S.; Schume, H.; et al. Do Water-Limiting Conditions Predispose Norway Spruce to Bark Beetle Attack? New Phytol. 2015, 205, 1128–1141. [Google Scholar] [CrossRef] [PubMed]
- Kausrud, K.; Økland, B.; Skarpaas, O.; Grégoire, J.-C.; Erbilgin, N.; Stenseth, N.C. Population Dynamics in Changing Environments: The Case of an Eruptive Forest Pest Species. Biol. Rev. 2012, 87, 34–51. [Google Scholar] [CrossRef] [PubMed]
- Schlyter, F.; Byers, J.A.; Löfqvist, J. Attraction to Pheromone Sources of Different Quantity, Quality, and Spacing: Density-Regulation Mechanisms in Bark Beetle Ips typographus. J. Chem. Ecol. 1987, 13, 1503–1523. [Google Scholar] [CrossRef]
- Schlyter, F.; Löfqvist, J.; Byers, J.A. Behavioural Sequence in the Attraction of the Bark Beetle Ips typographus to Pheromone Sources. Physiol. Entomol. 1987, 12, 185–196. [Google Scholar] [CrossRef]
- Helland, I.S.; Hoff, J.M.; Anderbrant, O. Attraction of Bark Beetles (Coleoptera: Scolytidae) to a Pheromone Trap. J. Chem. Ecol. 1984, 10, 723–752. [Google Scholar] [CrossRef]
- Abdollahnejad, A.; Panagiotidis, D.; Surový, P.; Modlinger, R. Investigating the Correlation between Multisource Remote Sensing Data for Predicting Potential Spread of Ips typographus L. Spots in Healthy Trees. Remote Sens. 2021, 13, 4953. [Google Scholar] [CrossRef]
- Jurc, M.; Perko, M.; Džeroski, S.; Demšar, D.; Hrašovec, B. Spruce Bark Beetles (Ips typographus, Pityogenes chalcographus, Col.: Scolytidae) in the Dinaric Mountain Forests of Slovenia: Monitoring and Modeling. Ecol. Model. 2006, 194, 219–226. [Google Scholar] [CrossRef]
- Blum, J.D.; Klaue, A.; Nezat, C.A.; Driscoll, C.T.; Johnson, C.E.; Siccama, T.G.; Eagar, C.; Fahey, T.J.; Likens, G.E. Mycorrhizal Weathering of Apatite as an Important Calcium Source in Base-Poor Forest Ecosystems. Nature 2002, 417, 729–731. [Google Scholar] [CrossRef]
- Pec, G.J.; Cahill, J.F.J. Large-Scale Insect Outbreak Homogenizes the Spatial Structure of Ectomycorrhizal Fungal Communities. PeerJ 2019, 7, e6895. [Google Scholar] [CrossRef]
- Reininger, V.; Grünig, C.R.; Sieber, T.N. Host Species and Strain Combination Determine Growth Reduction of Spruce and Birch Seedlings Colonized by Root-Associated Dark Septate Endophytes. Environ. Microbiol. 2012, 14, 1064–1076. [Google Scholar] [CrossRef] [PubMed]
- Tellenbach, C.; Grünig, C.R.; Sieber, T.N. Negative Effects on Survival and Performance of Norway Spruce Seedlings Colonized by Dark Septate Root Endophytes Are Primarily Isolate-Dependent. Environ. Microbiol. 2011, 13, 2508–2517. [Google Scholar] [CrossRef]
- Yarwood, S.A.; Myrold, D.D.; Högberg, M.N. Termination of Belowground C Allocation by Trees Alters Soil Fungal and Bacterial Communities in a Boreal Forest. FEMS Microbiol. Ecol. 2009, 70, 151–162. [Google Scholar] [CrossRef] [PubMed]
- Barto, E.K.; Rillig, M.C. Does Herbivory Really Suppress Mycorrhiza? A Meta-Analysis. J. Ecol. 2010, 98, 745–753. [Google Scholar] [CrossRef]
- Schmidt, S.I.; Hejzlar, J.; Kopáček, J.; Paule-Mercado, M.C.; Porcal, P.; Vystavna, Y.; Lanta, V. Forest Damage and Subsequent Recovery Alter the Water Composition in Mountain Lake Catchments. Sci. Total Environ. 2022, 827, 154293. [Google Scholar] [CrossRef] [PubMed]
- Fettig, C.J.; Klepzig, K.D.; Billings, R.F.; Munson, A.S.; Nebeker, T.E.; Negrón, J.F.; Nowak, J.T. The Effectiveness of Vegetation Management Practices for Prevention and Control of Bark Beetle Infestations in Coniferous Forests of the Western and Southern United States. For. Ecol. Manag. 2007, 238, 24–53. [Google Scholar] [CrossRef]
- Leverkus, A.B.; Buma, B.; Wagenbrenner, J.; Burton, P.J.; Lingua, E.; Marzano, R.; Thorn, S. Tamm Review: Does Salvage Logging Mitigate Subsequent Forest Disturbances? For. Ecol. Manag. 2021, 481, 118721. [Google Scholar] [CrossRef]
- Stříbrská, B.; Hradecký, J.; Čepl, J.; Tomášková, I.; Jakuš, R.; Modlinger, R.; Netherer, S.; Jirošová, A. Forest Margins Provide Favourable Microclimatic Niches to Swarming Bark Beetles, but Norway Spruce Trees Were Not Attacked by Ips typographus Shortly after Edge Creation in a Field Experiment. For. Ecol. Manag. 2022, 506, 119950. [Google Scholar] [CrossRef]


| Class | Explanation |
|---|---|
| 0 | future point—there is nothing there at the time of observation, but there will be a sapling/seedling in a later year |
| 1 | tall healthy |
| 2 | small healthy |
| 3 | sapling, seedling |
| 4 | tall dead |
| 5 | small dead |
| 6 | tree stump |
| Predictor | Explanation |
|---|---|
| Individual scale | |
| leaf type | j = coniferous; l = deciduous |
| Tre_hgh | Tree height (m), estimated from LiDAR |
| X | X coordinate |
| Y | Y coordinate |
| Death | Year of death |
| Site scale (including up to 30 m) | |
| pl9_s_1 | Slope (°) |
| plec_4g | Elevation (m) |
| pl3_a_t | Aspect (°) |
| FII_00, FII_03 | Raster cell value from the Forest Infrared Index (UHUL, pers. comm.) for the year 20xx, i.e., FII_00 for the year 2000 |
| c1_30m_j, c2_30m_j, c3_30m_j, c4_30m_j, c5_30m_j, c6_30m_j, c1_30m_l, c2_30m_l, c3_30m_l, c4_30m_l, c5_30m_l, c6_30m_l, c1_10m_j, c2_10m_j, c3_10m_j, c4_10m_j, c5_10m_j, c6_10m_j, c1_10m_l, c2_10m_l, c3_10m_l, c4_10m_l, c5_10m_l, c6_10m_l, c1_5m_j, c2_5m_j, c3_5m_j, c4_5m_j, c5_5m_j, c6_5m_j, c1_5m_l, c2_5m_l, c3_5m_l, c4_5m_l, c5_3m_l, c6_3m_j, c1_3m_j, c2_3m_j, c3_3m_j, c4_3m_j, c5_3m_j, c1_3m_l, c2_3m_l, c3_3m_l, c4_3m_l, c5_3m_l, c6_3m_l, c1_30m, c2_30m, c3_30m, c4_30m, c5_30m, c6_30m, c1_10m, c2_10m, c3_10m, c4_10m, c5_10m, c6_10m, c1_5m, c2_5m, c3_5m, c4_5m, c5_5m, c6_5m, c1_3m, c2_3m, c3_3m, c4_3m, c5_3m, c6_3m | Count of trees of one of six categories (c1, …, c6) within a buffer zone of xx m; if applicable, belonging to tree “species” (l = deciduous; j = coniferous); e.g., “c1_30m_j” stands for the count of trees of category 1, i.e., tall, within 30 m, of “species” coniferous |
| Stand scale (50–100 m) | |
| d_50_00, d_50_03, h_50_00, h_50_03, etc. | Kernel Smoothing-estimated density of d = dead, or h = healthy trees within a raster cell of 50 m or 100 m, in the year 20xx; e.g., d_50_00 = estimated density of dead trees within a 50 m raster cell in the year 2000 |
| subbasn | sub basin; geostatistically calculated; apart from the four known inflows (see, e.g., Kopáček et al. [36]), two more inflows and their subcatchments were identified and used as a variable |
| Regional scale (however, some distances turned out to be less than 30 m, i.e., rather site-scale level) | |
| d_ls_xx | Distance to Czech Šumava National Park-listed damages in year 20xx; only available from year 2006 onwards |
| dm_20xx | Distance to damage in the five years up to 2000, or in the previous years since the last appraisal in the forest state geodatabase; e.g., dm_2000 = damage in the five previous years, i.e., 1996–2000; dm_2003 = damage in the years 2001–2003 according to Senf and Seidl [46,47] which is on a 30 m grain size scale |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, S.I.; Fluksová, H.; Grill, S.; Kopáček, J. The Significance of Tree Height as a Predictor of Tree Mortality during Bark Beetle Outbreaks in a Small Catchment. Forests 2024, 15, 803. https://doi.org/10.3390/f15050803
Schmidt SI, Fluksová H, Grill S, Kopáček J. The Significance of Tree Height as a Predictor of Tree Mortality during Bark Beetle Outbreaks in a Small Catchment. Forests. 2024; 15(5):803. https://doi.org/10.3390/f15050803
Chicago/Turabian StyleSchmidt, Susanne I., Hana Fluksová, Stanislav Grill, and Jiří Kopáček. 2024. "The Significance of Tree Height as a Predictor of Tree Mortality during Bark Beetle Outbreaks in a Small Catchment" Forests 15, no. 5: 803. https://doi.org/10.3390/f15050803
APA StyleSchmidt, S. I., Fluksová, H., Grill, S., & Kopáček, J. (2024). The Significance of Tree Height as a Predictor of Tree Mortality during Bark Beetle Outbreaks in a Small Catchment. Forests, 15(5), 803. https://doi.org/10.3390/f15050803






