Tree Diameter at Breast Height Extraction Based on Mobile Laser Scanning Point Cloud
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Study Area
2.1.2. Mobile Laser Scanning System
2.1.3. Data Acquisition
2.2. Methods
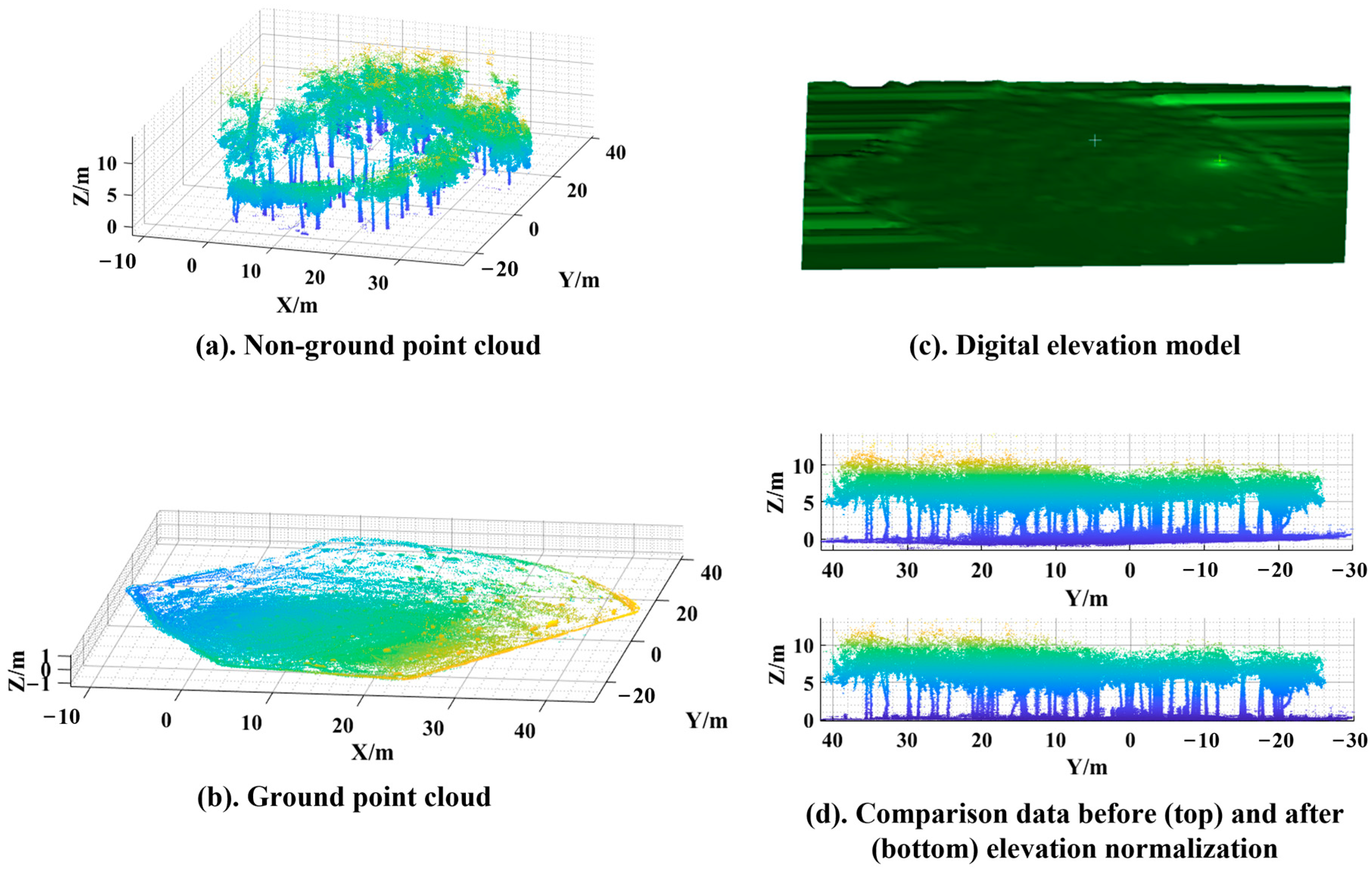
2.2.1. Point Cloud Filtering and Elevation Normalization
2.2.2. Segmentation of Single-Tree Instances Based on Clustering Algorithms
2.2.3. Diameter at Breast Height Extraction Based on Intensity-Weighted Least Squares Circle Fitting
2.2.4. Precision Evaluation
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bonan, G.B. Forests, climate, and public policy: A 500-year interdisciplinary odyssey. Annu. Rev. Ecol. Evol. Syst. 2016, 47, 97–121. [Google Scholar] [CrossRef]
- GB/T 26424-2010; Technical Regulations for Inventory for Forest Management Planning and Design. China National Standardization Administration Committee: Beijing, China, 2011. Available online: https://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=18D1658E2885CD74F5976BEA0A3B2991 (accessed on 6 February 2024).
- Wang, X.; Zhao, Q.; Han, F.; Ma, Y.; Long, X.; Jiang, P. Application of Airborne Multispectral Image Semantic Segmentation Model in Farmland Shelterbelt Extraction. J. Geo-Inf. Sci. 2020, 22, 1702–1713. [Google Scholar]
- Zhao, Q.; Jiang, P.; Wang, X.; Zhang, L.; Zhang, J. Classification of protection forest tree species based on UAV hyperspectral data. Trans. Chin. Soc. Agric. Mach. 2021, 52, 190–199. [Google Scholar]
- Liu, Y.; Zhao, Q.; Wang, X. A tree species classification model based on improved YOLOv7 for shelterbelts. Front. Plant Sci. 2024, 14, 1265025. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Zhao, Q.; Yin, X.; Wang, Y.; Tian, W. Multi-parameter health assessment of jujube trees based on unmanned aerial vehicle hyperspectral remote sensing. Agriculture 2023, 13, 1679. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, Y.E.; de Souza Filho, C.R. Mapping tree species in tropical seasonal semi-deciduous forests with hyperspectral and multispectral data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Srestasathiern, P.; Rakwatin, P. Oil palm tree detection with high resolution multi-spectral satellite imagery. Remote Sens. 2014, 6, 9749–9774. [Google Scholar] [CrossRef]
- Guo, Q.; Liang, X.; Li, W.; Jin, S.; Guan, H.; Cheng, K.; Su, Y.; Tao, S. LiDAR Remote Sensing of Forest Ecosystems: Applications and Prospects. In New Thinking in GIScience; Springer: Berlin/Heidelberg, Germany, 2022; pp. 221–231. [Google Scholar]
- Mielcarek, M.; Kamińska, A.; Stereńczak, K. Digital aerial photogrammetry (DAP) and airborne laser scanning (ALS) as sources of information about tree height: Comparisons of the accuracy of remote sensing methods for tree height estimation. Remote Sens. 2020, 12, 1808. [Google Scholar] [CrossRef]
- Zhang, R.-Y.; Pang, Y.; Li, Z.-Y.; Bao, Y.-H. Canopy closure estimation in a temperate forest using airborne LiDAR and LANDSAT ETM+ data. Chin. J. Plant Ecol. 2016, 40, 102–115. [Google Scholar]
- Kubišta, J.; Surový, P. Individual Tree Identification in ULS Point Clouds Using a Crown Width Mixed-Effects Model Based on NFI Data. Remote Sens. 2022, 14, 926. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, W.; Zhao, X.; Lv, Y.; Feng, W.; Li, Z.; Hu, S. Interactive tree segmentation and modeling from ALS point clouds. J. Graph. 2021, 42, 599. [Google Scholar]
- Brede, B.; Lau, A.; Bartholomeus, H.M.; Kooistra, L. Comparing RIEGL RiCOPTER UAV LiDAR derived canopy height and DBH with terrestrial LiDAR. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef]
- Kuželka, K.; Slavík, M.; Surový, P. Very high density point clouds from UAV laser scanning for automatic tree stem detection and direct diameter measurement. Remote Sens. 2020, 12, 1236. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Liu, L.; Pang, Y.; Li, Z.; Xu, G.; Li, D.; Zheng, G. Retrieving structural parameters of individual tree through terrestrial laser scanning data. J. Remote Sens. 2014, 18, 365–377. [Google Scholar]
- Kuželka, K.; Marušák, R.; Surový, P. Inventory of close-to-nature forest stands using terrestrial mobile laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103104. [Google Scholar] [CrossRef]
- Holopainen, M.; Kankare, V.; Vastaranta, M.; Liang, X.; Lin, Y.; Vaaja, M.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Kaartinen, H. Tree mapping using airborne, terrestrial and mobile laser scanning—A case study in a heterogeneous urban forest. Urban For. Urban Green. 2013, 12, 546–553. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Yu, X. The use of a mobile laser scanning system for mapping large forest plots. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1504–1508. [Google Scholar] [CrossRef]
- Liang, X.; Kukko, A.; Hyyppä, J.; Lehtomäki, M.; Pyörälä, J.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Wang, Y. In-situ measurements from mobile platforms: An emerging approach to address the old challenges associated with forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 143, 97–107. [Google Scholar] [CrossRef]
- Hartley, R.J.; Jayathunga, S.; Massam, P.D.; De Silva, D.; Estarija, H.J.; Davidson, S.J.; Wuraola, A.; Pearse, G.D. Assessing the potential of backpack-mounted mobile laser scanning systems for tree phenotyping. Remote Sens. 2022, 14, 3344. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Nothdurft, A. Forest inventory with long range and high-speed personal laser scanning (PLS) and simultaneous localization and mapping (SLAM) technology. Remote Sens. 2020, 12, 1509. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, W.; Mellado, N.; Wang, N.; Jin, S.; Cai, S.; Luo, L.; Lejemble, T.; Yan, G. SLAM-aided forest plot mapping combining terrestrial and mobile laser scanning. ISPRS J. Photogramm. Remote Sens. 2020, 163, 214–230. [Google Scholar] [CrossRef]
- Fan, Y.; Feng, Z.; Shen, C.; Yan, F.; Su, J.; Wang, W. Design and Experiment of Forest Plot Survey System Based on Improved LOAM. Trans. Chin. Soc. Agric. Mach. 2022, 53, 291–300. [Google Scholar]
- Cabo, C.; Del Pozo, S.; Rodríguez-Gonzálvez, P.; Ordóñez, C.; González-Aguilera, D. Comparing terrestrial laser scanning (TLS) and wearable laser scanning (WLS) for individual tree modeling at plot level. Remote Sens. 2018, 10, 540. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef]
- Duanmu, J.; Xing, Y. Annular neighboring points distribution analysis: A novel pls stem point cloud preprocessing algorithm for dbh estimation. Remote Sens. 2020, 12, 808. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial LiDAR: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Cai, S.; Xing, Y.-Q.; Duanmu, J.-L. Extraction of DBH from filtering out low intensity point cloud by backpack laser scanning. For. Eng. 2021, 37, 12–19. [Google Scholar]
- Duanmu, J.; Xing, Y. Estimating diameter at breast height using personal laser scanning data based on stem surface nodes in polar coordinates. Remote Sens. Lett. 2020, 11, 1051–1059. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 5135–5142. [Google Scholar]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Guenther, M.; Heenkenda, M.K.; Leblon, B.; Morris, D.; Freeburn, J. Estimating Tree Diameter at Breast Height (DBH) Using iPad Pro LiDAR Sensor in Boreal Forests. Can. J. Remote Sens. 2024, 50, 2295470. [Google Scholar] [CrossRef]
- Li, Y.; Da, Z.; Yan, Y. Artificial Platycladus orientalis (L.) Franco Single Wood Segmentation Based on UAV-based Lidar Point Cloud Data. J. Northwest For. Univ. 2023, 38, 171–179. [Google Scholar]
- Wang, P.; Tang, Y.; Liao, Z.; Yan, Y.; Dai, L.; Liu, S.; Jiang, T. Road-side individual tree segmentation from urban MLS point clouds using metric learning. Remote Sens. 2023, 15, 1992. [Google Scholar] [CrossRef]
- Miao, Y.; Li, S.; Wang, L.; Li, H.; Qiu, R.; Zhang, M. A single plant segmentation method of maize point cloud based on Euclidean clustering and K-means clustering. Comput. Electron. Agric. 2023, 210, 107951. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Y.; Xue, Y.; Zhang, H.; Lao, Y. FEC: Fast Euclidean Clustering for Point Cloud Segmentation. Drones 2022, 6, 325. [Google Scholar] [CrossRef]
- Fan, W.; Liu, H.; Xu, Y.; Lin, W. Comparison of estimation algorithms for individual tree diameter at breast height based on hand-held mobile laser scanning. Scand. J. For. Res. 2021, 36, 460–473. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Xie, L. Intensity-slam: Intensity assisted localization and mapping for large scale environment. IEEE Robot. Autom. Lett. 2021, 6, 1715–1721. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point cloud library (pcl). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Gollob, C.; Ritter, T.; Kraßnitzer, R.; Tockner, A.; Nothdurft, A. Measurement of forest inventory parameters with Apple iPad pro and integrated LiDAR technology. Remote Sens. 2021, 13, 3129. [Google Scholar] [CrossRef]





| Species | Phenotypic Features | DBH (cm) | ||
|---|---|---|---|---|
| Min | Max | Mean | ||
| Pinus sylvestris var. mongholica Litv | Crown spire-shaped, grey-brown bark, deep longitudinal fissures | 14.68 | 89.49 | 30.77 |
| Phellodendron amurense Rupr | Crown rounded to broadly ovate, dark grey bark, scale-like fissures | 14.55 | 35.67 | 23.86 |
| Ulmus pumila L. | Crown widely rounded, grey-brown bark, deep longitudinal fissures | 13.06 | 68.47 | 28.98 |
| Betula platyphylla Sukaczev | Crown narrowly tower-shaped, white bark, longitudinally fissured | 11.53 | 56.50 | 24.21 |
| Parameters | Numerical Values |
|---|---|
| Size | 627 mm × 550 mm × 252 mm (L × W × H) |
| Wheel base | 451 mm |
| Wheel track | 450 mm |
| Maximum velocity | 20 km/h |
| Maximum stroke | 10 km |
| Curb weight | 23 kg |
| Rated travelling load | 10 kg |
| Operating temperature | −20 °C–60 °C |
| Parameters | Numerical Values | Parameters | Numerical Values |
|---|---|---|---|
| Size | 103 mm × 72 mm | Scan frequency | 5–20 Hz |
| Maximum distance measured | 100 m | Safety class | Class 1 (human eye-safe) |
| Ranging accuracy | ±3 cm | Weight | 830 g |
| Scan rate | Single echo 300,000 point/s Dual echo 600,000 point/s | Power consumption | 8 W |
| Vertical perspective | −15°–+15° | Voltage | 9–18 V |
| Vertical angular resolution | 2° | Working temperature | −10 °C–+60 °C |
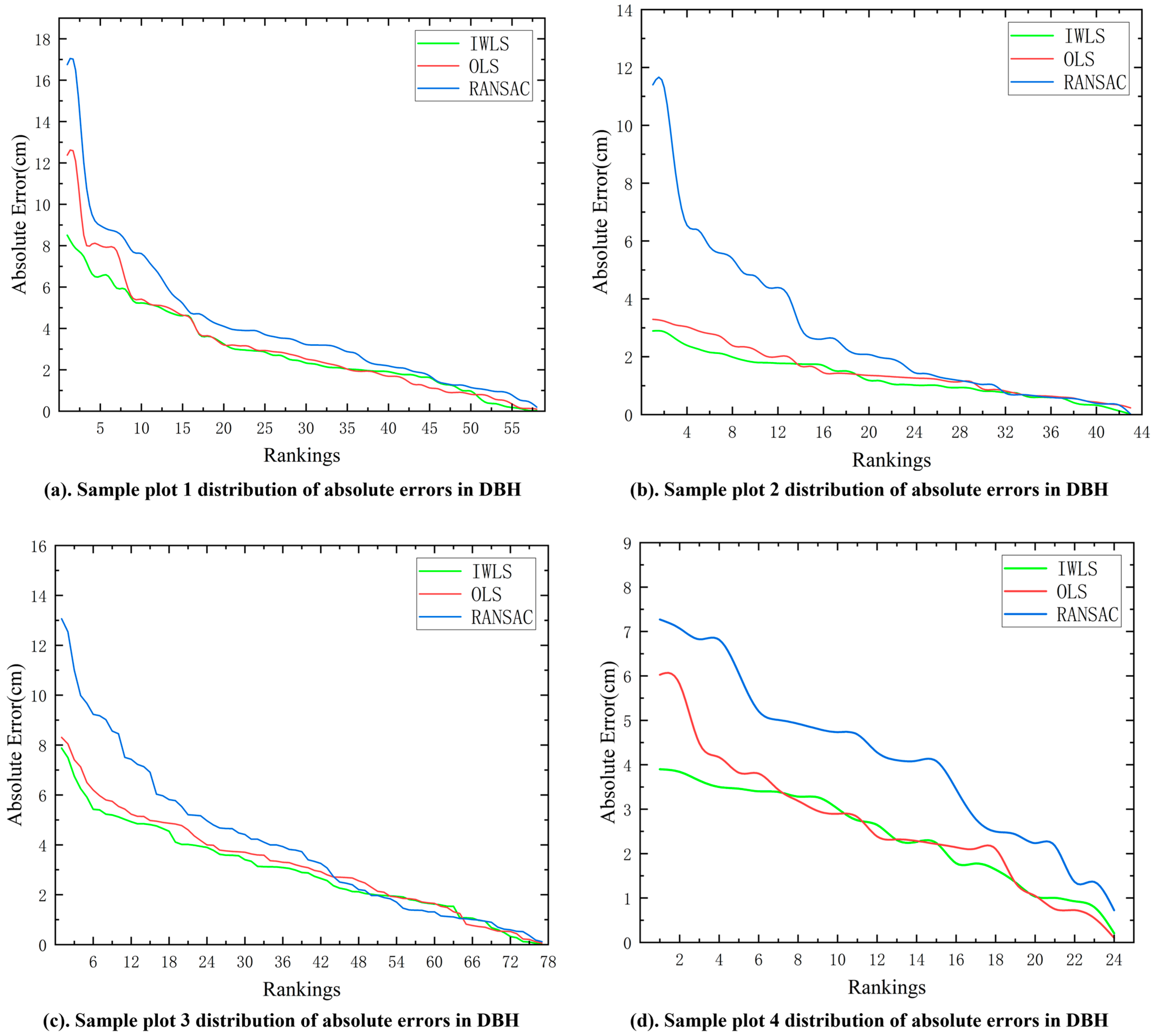
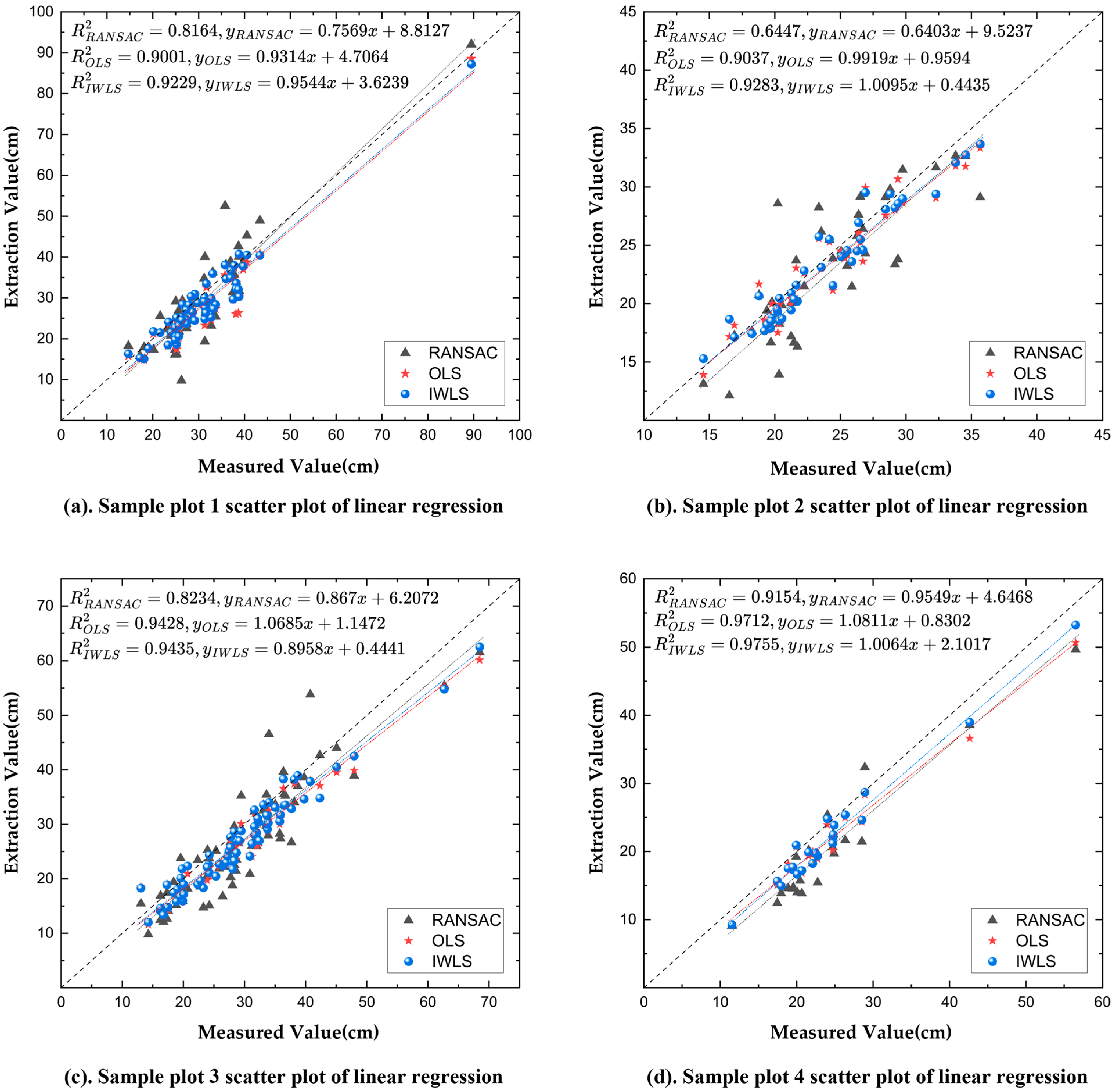
| Plot | Method | Absolute Error (cm) | Root Mean Square Error (cm) | Relative Accuracy (%) | ||
|---|---|---|---|---|---|---|
| Max | Min | Mean | ||||
| 1 | RANSAC | 16.75 | 0.20 | 4.21 | 5.48 | 82.20 |
| OLS | 12.37 | 0.10 | 3.27 | 4.28 | 86.10 | |
| IWLS | 8.51 | 0.03 | 2.99 | 3.65 | 88.12 | |
| 2 | RANSAC | 11.40 | 0.02 | 2.84 | 3.97 | 83.37 |
| OLS | 3.29 | 0.23 | 1.48 | 1.71 | 92.82 | |
| IWLS | 2.89 | 0.02 | 1.28 | 1.48 | 93.80 | |
| 3 | RANSAC | 13.06 | 0.12 | 4.00 | 5.05 | 82.57 |
| OLS | 8.31 | 0.06 | 3.21 | 3.77 | 86.98 | |
| IWLS | 7.88 | 0.00 | 2.98 | 3.48 | 88.00 | |
| 4 | RANSAC | 7.27 | 0.72 | 4.12 | 4.52 | 81.32 |
| OLS | 6.03 | 0.10 | 2.65 | 3.05 | 87.41 | |
| IWLS | 3.90 | 0.21 | 2.39 | 2.63 | 89.15 | |
| Plot | Method | Mean Absolute Error (cm) | Root Mean Square Error (cm) | Relative Accuracy (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | A | B | C | ||
| 1 | RANSAC | 1.96 | 4.93 | 3.74 | 2.37 | 6.35 | 4.29 | 88.26 | 78.20 | 89.96 |
| OLS | 1.80 | 3.22 | 4.46 | 2.33 | 3.85 | 6.08 | 88.47 | 86.79 | 86.77 | |
| IWLS | 1.97 | 3.06 | 3.49 | 2.36 | 3.59 | 4.48 | 88.29 | 87.67 | 89.51 | |
| 2 | RANSAC | 3.46 | 2.12 | - | 1.30 | 2.84 | - | 93.49 | 89.95 | - |
| OLS | 1.25 | 1.75 | - | 1.44 | 1.98 | - | 92.81 | 92.98 | - | |
| IWLS | 1.12 | 1.47 | - | 1.30 | 1.66 | - | 93.49 | 94.14 | - | |
| 3 | RANSAC | 2.80 | 4.49 | 4.71 | 3.36 | 5.44 | 6.26 | 82.48 | 81.86 | 85.76 |
| OLS | 2.60 | 3.28 | 4.15 | 2.95 | 3.77 | 4.95 | 84.62 | 87.43 | 88.73 | |
| IWLS | 2.50 | 2.91 | 4.04 | 2.77 | 3.40 | 4.67 | 85.58 | 88.66 | 89.36 | |
| 4 | RANSAC | 4.13 | 3.79 | 5.45 | 4.54 | 4.17 | 5.62 | 76.89 | 83.86 | 88.66 |
| OLS | 2.48 | 2.12 | 5.92 | 2.64 | 2.61 | 5.92 | 86.53 | 89.89 | 88.05 | |
| IWLS | 2.51 | 1.93 | 3.46 | 2.65 | 2.32 | 3.46 | 86.48 | 91.05 | 93.02 | |
| Overall mean | RANSAC | 3.09 | 3.83 | 4.63 | 2.89 | 4.70 | 5.39 | 85.28 | 83.47 | 88.13 |
| OLS | 2.03 | 2.59 | 4.84 | 2.34 | 3.05 | 5.65 | 88.11 | 89.27 | 87.85 | |
| IWLS | 2.03 | 2.34 | 3.66 | 2.27 | 2.74 | 4.20 | 88.46 | 90.38 | 90.63 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, Y.; Zhao, Q.; Wang, X.; Liu, Y.; Yin, X. Tree Diameter at Breast Height Extraction Based on Mobile Laser Scanning Point Cloud. Forests 2024, 15, 590. https://doi.org/10.3390/f15040590
Sheng Y, Zhao Q, Wang X, Liu Y, Yin X. Tree Diameter at Breast Height Extraction Based on Mobile Laser Scanning Point Cloud. Forests. 2024; 15(4):590. https://doi.org/10.3390/f15040590
Chicago/Turabian StyleSheng, Yuhao, Qingzhan Zhao, Xuewen Wang, Yihao Liu, and Xiaojun Yin. 2024. "Tree Diameter at Breast Height Extraction Based on Mobile Laser Scanning Point Cloud" Forests 15, no. 4: 590. https://doi.org/10.3390/f15040590
APA StyleSheng, Y., Zhao, Q., Wang, X., Liu, Y., & Yin, X. (2024). Tree Diameter at Breast Height Extraction Based on Mobile Laser Scanning Point Cloud. Forests, 15(4), 590. https://doi.org/10.3390/f15040590






