Next Article in Journal
Detection of Forestry Pests Based on Improved YOLOv5 and Transfer Learning
Previous Article in Journal
3PG-MT-LSTM: A Hybrid Model under Biomass Compatibility Constraints for the Prediction of Long-Term Forest Growth to Support Sustainable Management
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 14
Issue 7
10.3390/f14071483
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Tree Size Heterogeneity on the Overall Growth Trend of Trees in Coniferous Forests of the Tibetan Plateau

by
Yuelin Wang
1,†,
Shumiao Shu
2,*,†,
Xiaodan Wang
3,* and
Wende Chen
1
1
College of Tourism and Urban–Rural Planning, Chengdu University of Technology, Chengdu 610059, China
2
Tuojiang River Basin High-Quality Development Research Center, Neijiang Normal University, Neijiang 641000, China
3
Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041, China
*
Authors to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Forests 2023, 14(7), 1483; https://doi.org/10.3390/f14071483
Submission received: 13 June 2023 / Revised: 10 July 2023 / Accepted: 13 July 2023 / Published: 20 July 2023
(This article belongs to the Section Forest Ecology and Management)
Browse Figures
Review Reports Versions Notes

Abstract

:
Tree growth is under the combined influence of abiotic and biotic factors. Trees with different sizes may respond differently to these factors, implying that tree size heterogeneity may also modulate the overall growth trend. To test this hypothesis, we focused on the radial growth trends of natural subalpine forests on the Tibetan Plateau. We first extended the iterative growth model (IGM) to the tree ring scale (IGMR) to test the applicability of the generalized metabolic growth theory to tree growth. As predicted by the IGMR, the radial growth of trees at the aggregate scale is constrained by a unimodal pattern. Using the IGMR, we reconstructed the historical best growth trajectory (HBGT) of trees within the same community based on the tree with the largest radius and/or longest age in the community. From the average difference between the HBGT and the current radial growth rate of trees with different sizes, we constructed an indicator that can measure the overall variation in tree radial growth. Based on this indicator, we found a negative effect of tree size heterogeneity on the overall variability of tree growth across elevations. Further analysis also revealed that the radial growth rate of trees on the Tibetan Plateau has increased significantly compared to the past, where the growing season average temperature and annual minimum temperature were negatively and positively correlated with tree growth below and above the treeline, respectively. Our study not only confirmed that the overall variability of tree growth depends on tree size heterogeneity but also proposed an indicator that reveals net changes in the tree radial growth rate relative to the past. These theoretical advances are highly beneficial for understanding changes in the extent of subalpine forests.

1. Introduction

It has been widely accepted that plant growth follows a “rise-and-fall” unimodal curve [1,2,3]. However, some studies have suggested that very old trees may continue to increase their biomass [4,5,6], which appears to contradict the classical unimodal growth hypothesis. Although further studies have suggested that this may be related to the growth heterogeneity and the mitigation of growth limits [7,8], it is still unclear what pattern the growth trend follows at the community scale and what its variation mechanism is. Furthermore, most growth models assume stable state variables [9], which limits our ability to predict the effects of abiotic and biotic factors on tree growth.
Tree radial growth is an important indicator of tree growth that captures both climate change and intrinsic growth trends. However, it is challenging to determine the overall radial growth trends followed by trees in natural forests. On the one hand, climate, competition, disturbance, and functional traits regulate the unimodal growth trajectory and fluctuate or change over time [10]. On the other hand, trees with different sizes may respond differently to these influence factors and shape different growth trajectories [11]. Metabolic growth theory, also known as the ontogenetic growth model (OGM) [12,13], provides a promising basis for understanding tree growth. This theory dates back to observations of animal metabolism in the early 19th century [14]. Its core can be summarized as follows: the growth rate of an organism is proportional to the difference between its total metabolic rate and maintenance metabolic rate, where the two metabolic terms are proportional to the 0.75 and 1 power of the organism’s size, respectively (see Appendix B). This equation is widely supported by the animal growth [12,13]. However, there is still insufficient evidence to support its applicability to plant growth [3]. We found that this may be related to the incompleteness of its core assumptions. To this end, we introduced the concept of unit tissue “formation time” (T) and thus derived a more comprehensive iterative growth model (IGM) [11,15]. This improvement highlights the second law of thermodynamics constraint on organism growth and reveals the range in which growth trajectories occur [11,15]. Not only that, evidence from plantations with similar tree sizes and stand ages supports this unimodal growth model and suggests that climate can induce changes in the height and length of unimodal radial growth curves [11]. We hypothesize that tree growth trajectories in natural forests are still constrained by the single-peaked model and can be described by the IGM.
Compared to planted forests, natural forests tend to have greater tree size heterogeneity. This means that the overall radial growth trend of trees in natural forests cannot be considered as a simple scale-up of individual growth. In multi-aged stands, the causes of size heterogeneity are related to repeated disturbances or silvicultural interventions that regenerate these new age classes [16,17,18]. In single-aged stands, competition directly drives tree size differentiation [19]. Obviously, to a large extent, tree size heterogeneity may mediate the effects of competition and disturbance on tree growth. Under different climatic conditions, how tree size heterogeneity influences the overall radial growth trend of trees is still unknown.
Ongoing climate warming in mountain areas is amplified with elevation, and its impact on forest distribution is still a major question in global change biology [20]. Range shifts caused by warming have already been observed in some biomes, particularly those subalpine forests close to the treeline [21]. Tree radial growth consists of age-dependent low-frequency and climate-sensitive high-frequency signals. Although the high-frequency signal is a result of the rapid response of tree radial growth to the climate, the age effects and sampling strategies still affect the accuracy of tree growth assessments and climate responses [20]. In fact, studies have found that trees along elevation gradients respond divergently to warming [22,23,24], and the age or size effect profoundly affects tree growth. Exploring the age effect, particularly the radial growth trajectory and its variability at the community scale, will undoubtedly enhance the understanding of forest distribution across different elevations.
The subalpine ecosystem occupies elevations just below the treeline between 2700 and 3500 m. They are not only widely distributed but also sensitive to global climate change [17,25]. The Hengduan and Southern Qinghai Mountains, which run north–south across the Southeastern and Northeastern Tibetan Plateau (TP), are rich in natural subalpine forests, providing invaluable opportunities to study tree growth patterns and variability in natural forests.
The aim of this study was to determine the effect of tree size heterogeneity on the overall radial growth trend of trees in natural forests. The experiment consisted of three steps. First, we extended the IGM to the tree ring scale (IGMR) and evaluated its constraints on community-scale tree growth trends. Second, we developed a model-based measure to assess the overall radial growth variability of trees. Finally, we focused on the effect of tree size heterogeneity in communities under different climatic conditions on this variability across elevations.

2. Materials and Methods

2.1. Study Area and Data Collection

The study focused on coniferous forests in the Hengduan Mountains and South Qinghai Mountains on the Tibetan Plateau (Figure 1). The Hengduan Mountains experience the typical monsoonal climate, influenced by both the South Asian monsoon and the East Asian monsoon [25]. The Southern Qinghai Mountains experience a continental climate with large temperature fluctuations from day to night. The sample sites ranged in altitude from 2500 to 4136 m, with an average annual temperature of 5.04 °C and an average annual precipitation of 486.98 mm. Raw tree ring width data for 7 species were collected from 45 natural forest sample sites distributed throughout the Tibetan Plateau region through the International Tree ring Data Bank (https://www.ncdc.noaa.gov/data-access/paleoclimatologydata/datasets/tree-ring, accessed on 25 May 2023), involving a total of 2500 tree cores (Figure 1 and Table 1).

2.2. Quantification of Tree Radial Growth Pattern and Its Overall Variability

We have extended the IGM to the tree ring scale (IGMR) [11] (See Appendix A). Assuming that f(r)T is the ring width formed during time T, the relationships between the tree growth rate (f(r)), metabolic exponent (b), current radius (r), and potential maximum radius (R) can be expressed as follows:
f ( r ) = 1 T T m r g r r 2 / b R r 2 / b - 2 − 1 + r 2 / b b / 2 − r
where gr is the relatively stable respiration cost required to produce a unit of tissue, and mr is the variable maintenance respiration rate per unit of tissue [26]. The value of T is related to the thermodynamic significance of respiration and ranges between 0 and gr/mr [15]. To counteract natural degradation (entropy increase), organisms must continuously use negative entropy to maintain the complexity, variety, and order of their components. During time T, the growth energy proportional to gr decreases the entropy of a new unit tissue relative to that of their free precursor monomers [27]. Meanwhile, the maintenance energy, which is proportional to Tmr, maintains a low entropy state of an existing unit tissue and indicates its entropy accumulation during this time. Assuming the old and new units of tissue are identical, the synthesis of a new unit of tissue is possible only if Tmr is less than gr; that is, T < gr/mr.
Mathematically, the limits T → 0 and gr/mr provide us with upper and lower boundaries for f(r). Usually, b is considered equal to 0.75 [28,29], but some evidence suggests that it may be equal to 0.85 [30]. Since the following results support the former, we give here only two growth boundaries at b = 0.75:
f r = 3 8 m r g r R 2 / 3 r 1 / 3 − r
f r = m r g r R 1 / 4 r 3 / 4 − r
In theory, the more rapidly a unit of tissue grows (T → 0), the closer f(r) approaches Equation (2). Otherwise, (T → gr/mr), the closer f(r) is to Equation (3) [15]. We termed Equations (2) and (3) as the thermodynamic lower (IGMR-L) and upper (IGMR-U) boundaries of the IGMR. It is worth noting that the mathematical form of extending the OGM (T → 0 and b = 0.75) [17] to the tree ring scale (OGMR) is consistent with Equation (3).
On the basis of Equations (2) and (3), we can establish a historical best growth trajectory (HBGT) based on the maximum radius and ages of the trees in the community, which can be expressed as:
f r H B G T = 2 k + 2 1 − k 1 T G T R 1 − k r k − r
where 1/3 < k < 3/4. Moreover, according to the IGM, the total growth time (TGT) of an organism is gr/mr × (2b + 2)/(1 − b). However, the TGT for Equation (2) is 32/3 × gr/mr. It is also likely that the pattern that tree radial growth follows will shift from Equation (2) to Equation (3) over time, therefore ensuring that the TGT of tree radial growth is consistent with that of biomass growth. We speculated that the k value is closer to 3/4 due to T → gr/mr. This also means that the actual f(r) distributed along the r gradient will be more distributed below Equation (3), as shown in Figure 2. Note that the other case is when b = 0.85 and T → gr/mr, k = 0.85.
Assuming that trees with the largest radius (R) and age (TGT) have the best growth trajectory and are more determined by historical factors, we can further quantify the overall average growth variability (OVG) relative to HBGT for the same community based on Equation (4) as follows:
O V G = ∑ c r i − f r i H B G T ∑ f r i H B G T
where c(ri) and f(ri)HBGT denote the current average growth rate over the past five years and estimate the historical best growth rate, respectively, for the tree i. When the OVG is greater than 0, it means that the overall growth trend of the trees is better than the historical one; otherwise, this trend may decline or maintain the status quo.

2.3. Data Processing and Analysis

We conducted statistics on growth information for each chronology, including the current diameter (rc), age (L), and average growth rate over the past five years (f(r)c), for each tree core. Additionally, we extracted the average tree ring growth rate (f(r)m) for trees of the same species within each site. To ensure the robustness of our findings, we only analyzed chronologies with a minimum of 30 samples. We assumed that tree TGT is the 95th percentile of the L values of all trees of the same species within that site. However, this estimation tends to overestimate TGT for most trees because of growth heterogeneity. Mathematically, we can still assume that TGT is accurate, but f(r)m is overestimated. Therefore, the actual relationship between the normalized tree diameter (r/R) and the normalized growth rate (f(r)c/f(r)m) should be lower than the normalized Equation (4). Note that R here is equal to TGT × f(r)m. The normalized Equation (4) is obtained by assuming R = 1 and mr/gr = 1. Afterwards, we calculated the coefficient of variation of the tree radius (CVR) at each site and tested whether the tree radial growth trajectories conformed to Equation (4) (where k = 0.75). Based on the test results, we estimated the HBGT and CVR of each site using Equations (4) and (5).
After obtaining the current CVR value for each site, we analyzed its relationship with tree size heterogeneity and climate. Tree size heterogeneity is characterized by CVR, and the meteorological factors used, such as the mean annual temperature (MAT) and the mean annual precipitation (MAP), were extracted from WorldClim (2.5 min) (https://www.worldclim.org/data/worldclim21.html#, accessed on 25 May 2023). These meteorological factors were annual averages from 1970 to 2000. The hierarchical partitioning method was employed to determine the individual contribution of climate variables, CVR, and elevation to OVG via the rdacca.hp package in R version 4.0.2 [31]. To analyze the direct and indirect effects of CVR and meteorological factors on OVG, we fitted a structural equation model (SEM). The sample size used here was 45. Since structural equation modeling requires a sample size of at least ten times the number of observed variables [32], we only included five observational variables in this study. The overall fit of the SEM was evaluated using the p-value, GIF, and RMSEA from the SEM package. In addition, we used the Wilcoxon signed-rank test to analyze the differences between the best historical growth rates and the current growth rates of trees at different elevation ranges. The Wilcoxon test is the nonparametric version of the paired t-test, which is appropriate for any distribution of data and especially for small sample sizes.

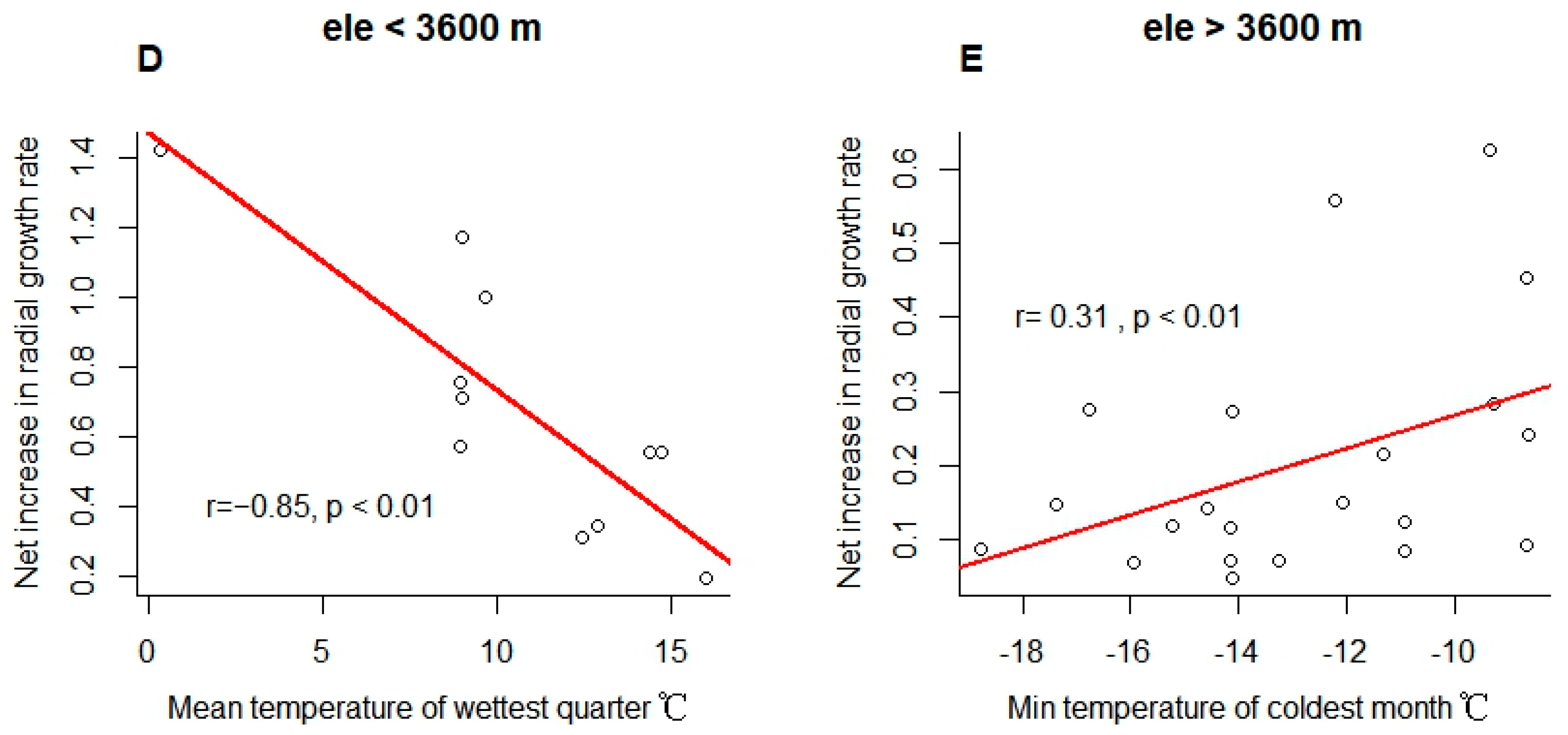
3. Results

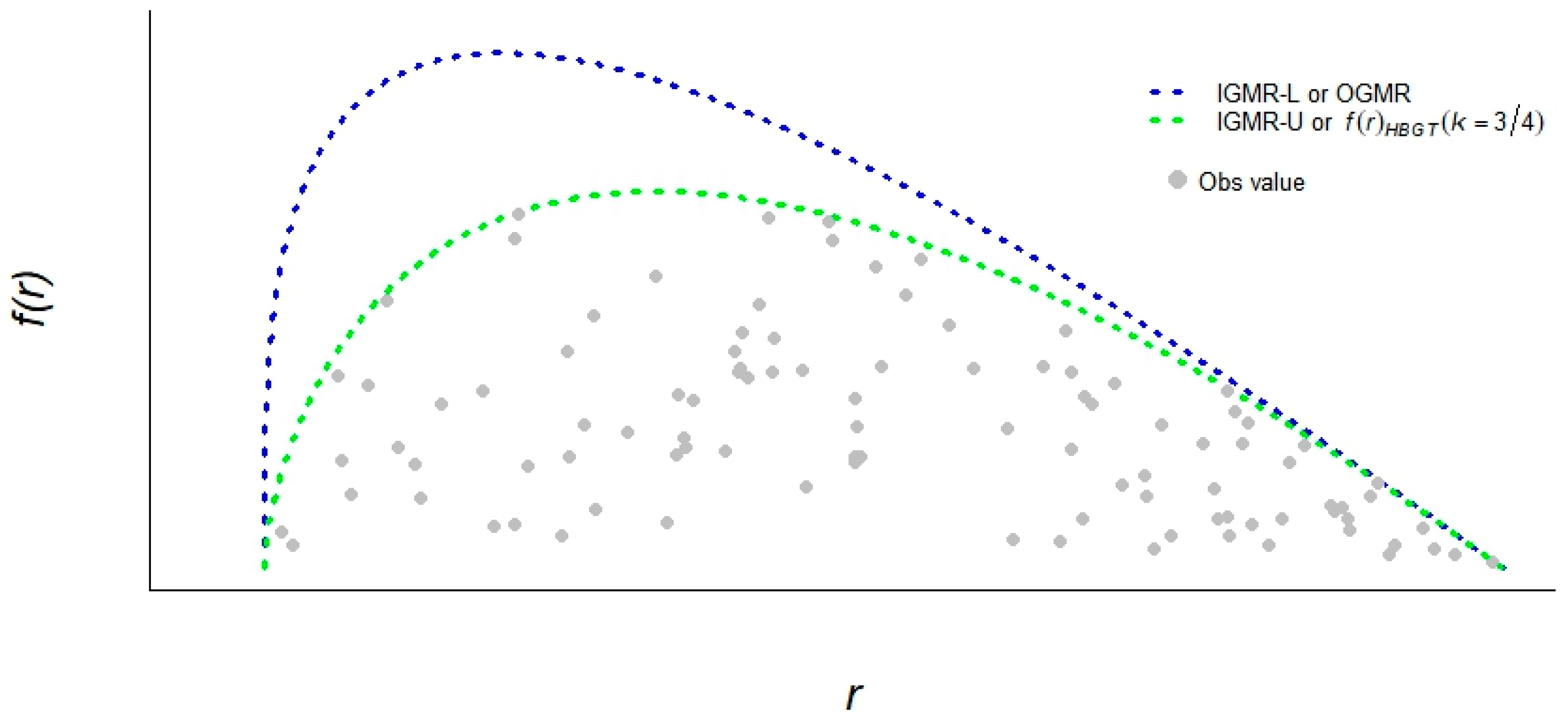
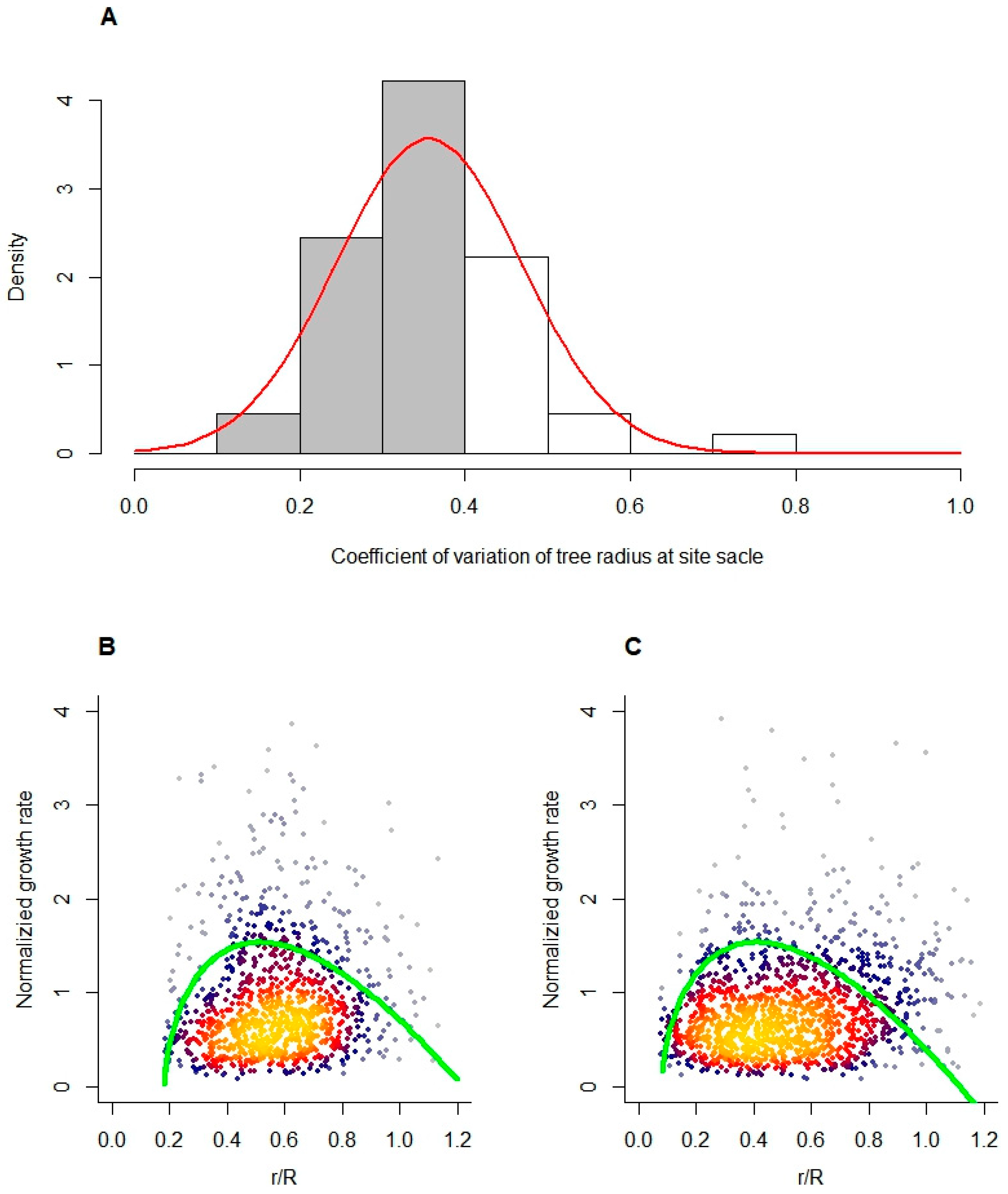
3.1. Tree Radial Growth Follows the IGMR-U

We first determined the distribution of CVR and tested whether the radial growth of trees within different CVR ranges was constrained by the IGMR. The results showed that CVR conforms to a normal distribution with a mean value of 0.375 and a variance of 0.143. Additionally, the tree relative radius (r/R) was normally distributed below CVR < 0.375 (gray bars in Figure 3A and Figure A1). This means that a smaller CVR can filter the effects of competition and disturbance. When CVR < 0.375, the boundary (95th percentile) of the normalized radial growth rate conforms to the normalized Equation (3) (Figure 3B), where the fitted value of k is 0.736 ± 0.10, which supports our theoretical prediction, i.e., k = b = 0.75. On the other hand, the normalized Equation (3) still constrains these growth rates (Figure 3C) when the CVR is larger (CVR > 0.375, white bars in Figure 3A). Not only that, the coefficient of variation of the radial growth rate for the last 5 years is also lower than the average normalized growth trend (i.e., half of the normalized curve) (Figure 3D). Note that the reason for using the average curve here is that the coefficient of variation is determined based on the mean value. From these results, it is evident that unimodal patterns limit tree radial growth following the IGMR-U.

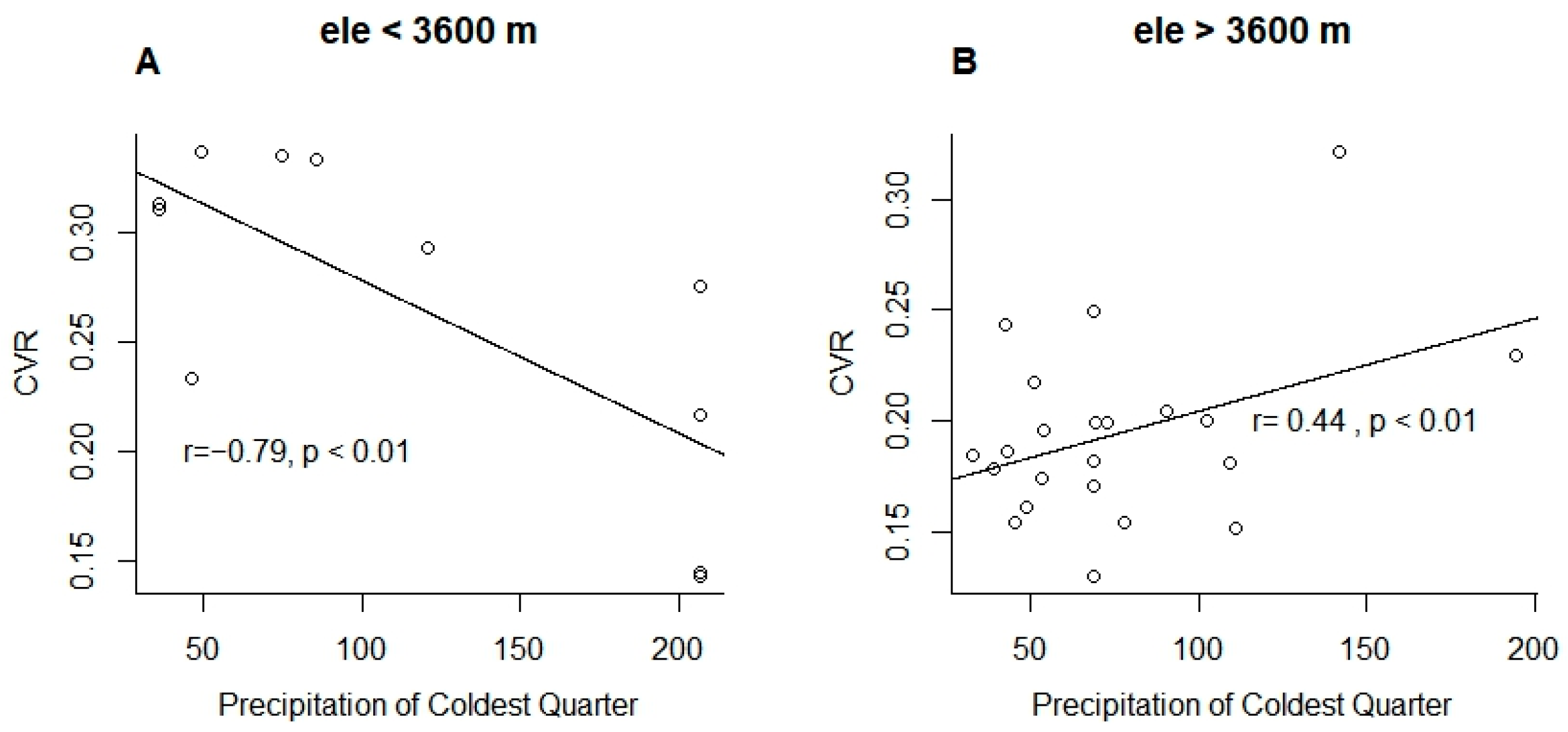
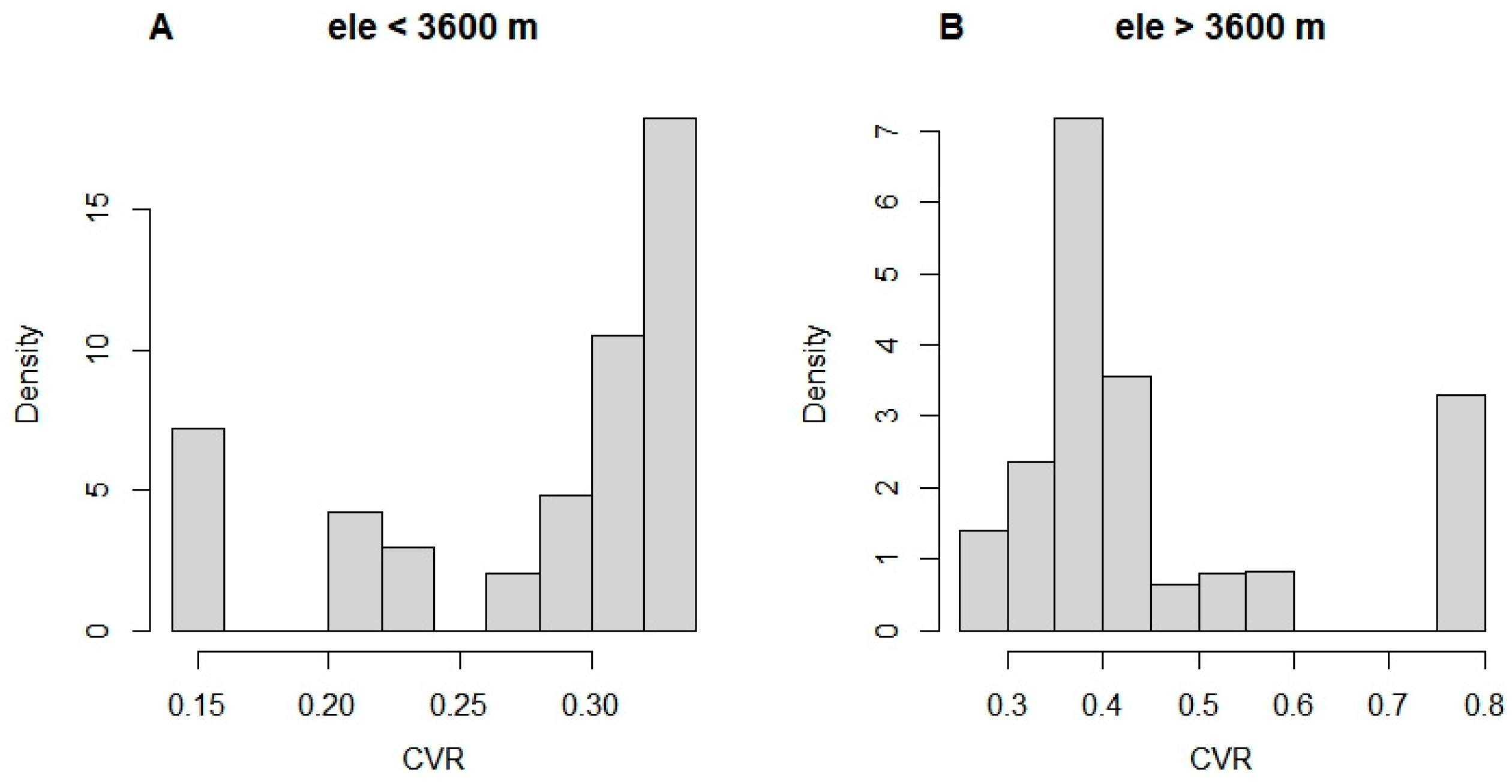
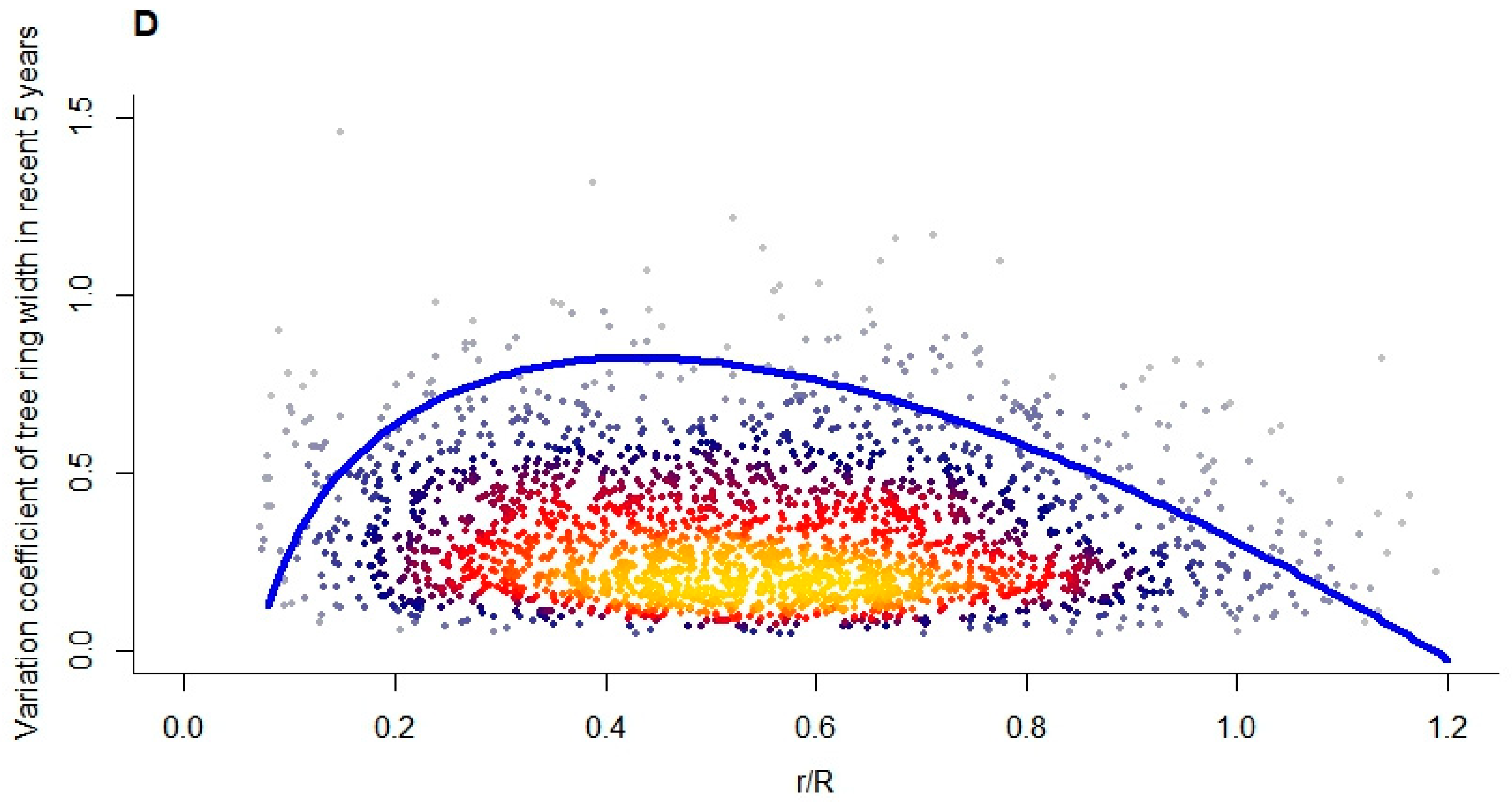
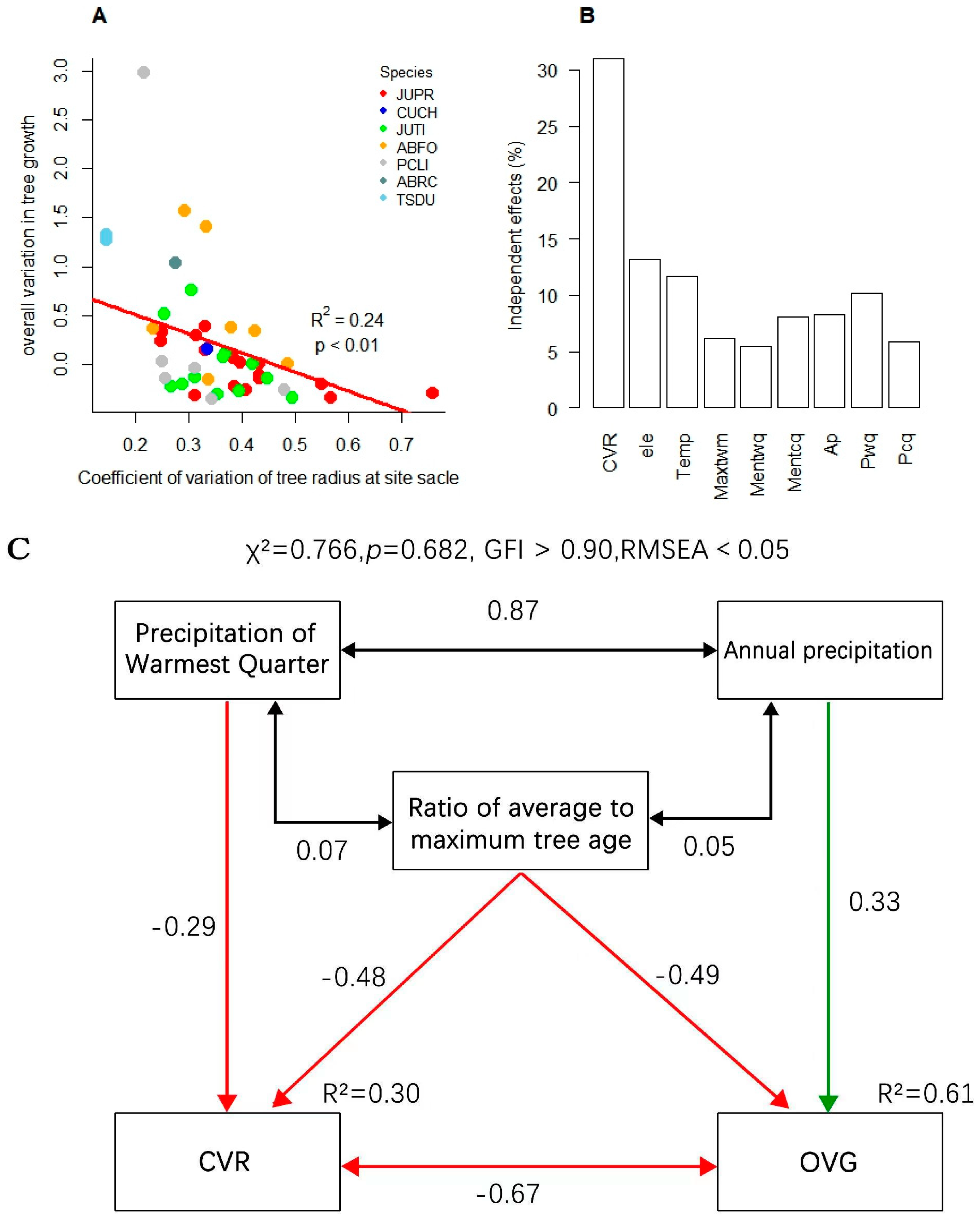
3.2. Effect of Tree Size Heterogeneity on Overall Growth Variability

Using the IGMR-U, we reconstructed the HBGT for each site and assessed the overall variation in the current radial tree growth. The results indicated a significant negative correlation between CVR and OVG (R = 0.24, p < 0.01), as presented in Figure 4A. Furthermore, the hierarchical partitioning analysis suggested that CVR had a higher independent contribution to OVG than climate factors (Figure 4B). To further clarify the direct and indirect effects of climatic variability and/or CVR on OVG, we used SEM to fit the data, as shown in Figure 4C. The SEM indicates that, except for annual precipitation and the ratio of tree average to maximum age, which have certain direct positive and negative effects on OVG (0.33 and −0.52), OVG is mainly mediated by CVR. The precipitation of the warmest quarter and the ratio of tree average to maximum age can indirectly affect OVG through CVR, but they can only explain 31% of the variation in OVG. Most of the variations in OVG are independent of climate and forest age and directly affect OVG. The standardized direct effects of climate, forest development, and CVR on OVG are 0.335, −0.521, and −0.672, respectively. The standardized indirect effects are 0.193, 0.301, and 0, respectively. Collectively, they can explain 61% of the variation in OVG.

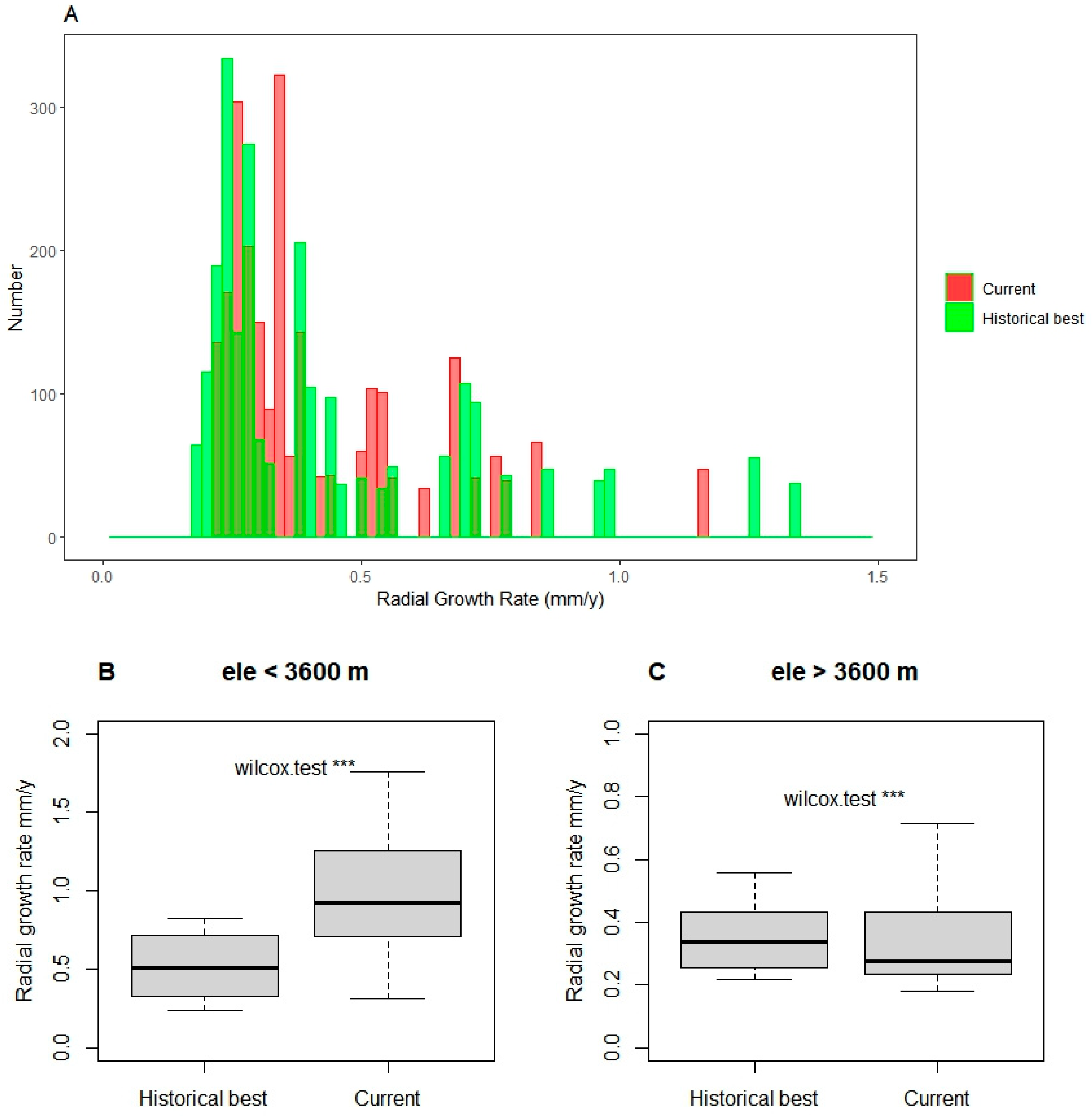
3.3. Tree Radial Growth Assessment

On the basis of OVG, we further assessed the tree radial growth at different elevations. We found that the current growth rate is generally higher than the historical best, calculated by HBGT, when the growth rate is small. However, the opposite is true when the growth rate is large, as shown in Figure 5A. This difference may be related to elevation, as shown in Figure 5B,C. The tree radial growth rates greatly increase at lower elevations. Conversely, the current growth rate of trees situated above the treeline (uppermost elevation of an individual tree, >2 m height, typically >3600 m elevation for TB) [33] is generally lower than the historical best value. If we assume that the average radial growth rate is only half of the ideal, then we can calculate the historical average growth rate. We define the difference between the current average growth rate and the historical average growth rate as the net increase in the radial growth rate. In the low elevation region, there is a strong negative correlation between this net increase rate and the mean temperature of the wettest quarter (Figure 5D). On the other hand, at the upper treeline, the minimum temperature of the coldest month is positively correlated with this net change (Figure 5E).

4. Discussion

4.1. Tree Size or Radius Constrains Its Radial Growth and Growth-Climate Sensitivity

The radial growth of trees is usually considered to be influenced by age (or size) and climatic factors, showing an age-dependent low-frequency (with a stable trend) and a climate-sensitive high-frequency (rapid change) signal [11,34,35]. After removing the modulations of the age effect trend, this signal typically exhibits stable climate sensitivity, termed stationarity assumptions or uniformity principles [34,35]. Based on this principle, it is possible to obtain high-resolution global information on tree species’ responses to global change, forest carbon and water dynamics, and past climate variability and extremes from tree ring dynamics [36]. However, our research indicated that there is no essential difference between high-frequency and low-frequency growth signals. Mathematically, the high-frequency signal is the limited fluctuation of the low-frequency signal, and both are mediated by tree size or radius, mr/gr, and the potential maximum size or radius, where environmental and resource intakes could significantly affect the mr and the maximum size or radius. Some evidence supports this conclusion. For example, age effects and sampling strategy affect the accuracy of a tree growth assessment and its climate response [20,37,38]. Moreover, changes in tree physiological status [34] result in different climate-growth relationships [37,38] and inevitably feed back into the size-to-growth constraint [17,39,40]. In fact, size has a greater effect than cellular senescence on age-related declines in relative growth and net assimilation rates [41]. Our model highlights that tree size, specifically the radius, determines the radial growth trend and climate sensitivity (Figure 3D). That is, the variation coefficient of the radial growth rate still shows a single-peaked pattern on the radius gradient.

4.2. Limited Influence of Climate on Tree Size Heterogeneity of Subalpine Forests

Overall, warm season precipitation contributed to the size convergence of trees in subalpine forests (Figure 4C). Concurrently, forest growth or development can also spontaneously reduce tree size heterogeneity. At lower elevations, increased precipitation can promote radial growth by reducing water stress and accelerating xylem activity during the growing season [42]. This boost will be more pronounced for smaller trees that grow faster, thus reducing CVR. However, at higher elevations with lower temperatures, increased precipitation may cause trees to experience more snowfall events and physical disturbances, resulting in increased CVR. Thus, significant negative (r = −0.79, p < 0.01) and positive (r = 0.44, p < 0.01) correlations were observed between CVR and the precipitation of the coldest quarter at low and high elevations, respectively (see Appendix B, Figure A2). However, the role of precipitation and forest growth or development in regulating size heterogeneity is relatively limited, suggesting the repeated effects of disturbance and competition on forests. These results suggest that precipitation plays a key role in shaping the location and structure of a treeline [43,44].

4.3. Forest Range Response to Tree Size Heterogeneity and Climate Change

Our research suggests that treeline expansion may be related to both tree size heterogeneity and temperature in different seasons. On the one hand, size inequality may cause an overall decrease in tree growth. We found that tree CVR was significantly lower in the low elevation region (<3600 m) than in the high elevation region (>3600 m) (see Appendix B, Figure A3), while the radial growth rate of low elevation trees was also overall higher than the estimated historical best value (Figure 5B,C). This difference can be attributed to the negative effect of CVR on OVG (Figure 4). We speculated that competition and disturbance may be the main causes of increased CVR and decreased OVG. Usually, in natural forests, smaller trees are more vulnerable to asymmetric competition, whereas larger trees are prone to being affected by disturbance [17,39,40]. For subalpine forests, this pattern also broadly applies, but the proportion of large individuals decreases significantly with increasing elevation (see Appendix B and Figure A4), implying that disturbance may be related to treeline formation. On the other hand, net changes in the tree radial growth rates at low and high elevations may be differentially affected by temperature in different seasons. In the subalpine forest belts, precipitation tends to be more abundant during the growing season. Nevertheless, rising temperatures may lead to an increase in respiration rates, which can lead to a decrease in the allocation of photosynthetic products to growth [45]. Consequently, we can observe a significant negative correlation between net changes in tree radial growth rates and the mean temperature of the wettest quarter (Figure 5D). At higher elevations, low temperatures limited tree growth, showing a positive correlation between the minimum temperature and this change (Figure 5E). These results imply that global warming affects tree growth variability differently in the high and low elevation subalpine ranges.

4.4. Tree Growth Assessment Based on Generalized Metabolic Growth Theory

Understanding how abiotic and biotic factors contribute to tree growth has been a longstanding challenge in global ecology. Our study introduces a new indicator for measuring radial growth variability based on a generalized metabolic growth theory. The theoretical framework underlying this indicator not only considers the variability in state variables such as b but also incorporates an iterative growth mechanism, making it highly suitable for modeling and predicting plant growth [17]. The differences in tree lifespan and average growth rate under different environments will be captured by the growth model [11]. Therefore, our method of measuring the overall tree growth variability is highly applicable. However, sampling strategies can affect the accuracy of tree growth assessments and the response to the climate [37,38]. Traditional sampling methods may introduce bias into the growth trend [46]. Therefore, in future studies, it is worth considering the different age classes of the trees at the time of sampling. We recommend choosing as many trees of different sizes as possible so that the overall fit appears as a unimodal trajectory in theory.

5. Conclusions

We revealed a single-peak pattern of radial growth in natural forest trees by expanding the IGM, thereby quantifying the overall average difference in radial growth of trees in subalpine forests relative to the historical best estimate. Further analysis showed that precipitation and tree size heterogeneity have positive and negative effects on this difference, respectively. At lower elevations, precipitation can reduce tree size heterogeneity, but with increasing elevation, precipitation evolves into snowfall disturbance and increases size heterogeneity. In addition, our results suggest a constraining effect of tree size on growth-climate sensitivity.

Author Contributions

Conceptualization: Y.W. and S.S.; Methodology: S.S.; Visualization: Y.W.; Funding acquisition: S.S. and X.W.; Project administration: X.W.; Supervision: X.W.; Writing—original draft: Y.W. and S.S.; and Writing—review and editing: S.S., X.W. and W.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No: 32201374) and by the Second Tibetan Plateau Scientific Expedition and Research Program (Grant No: 2019QZKK0404).

Data Availability Statement

The tree radial growth data are available at https://www.ncei.noaa.gov/products/paleoclimatology/tree-ring, accessed on 25 May 2023.

Conflicts of Interest

The authors declare no conflict of interest.

Glossary

SymbolMeaningUnit
f(r)tree ring growth ratemm/y
TThe formation time of unit tissue is primarily controlled genetically and by physiological activities, with the intrinsic or developmental growth rate independent of organism sizey
RTree maximum radiusmm
rTree current radiusmm
mrRate of maintenance respiration per unit of tissuemg g−1 y−1
grCost of respiration needed to produce a unit of tissuemg g−1
bMetabolic exponent, taken here as 0.751
TGTTotal growth timey
f(r)HGBTGrowth rate of historical best growth trajectorymm/y
OVGoverall average growth variability1
c(ri)current average growth rate over the past five years, for tree i.mm/y
f(ri)HBGTEstimated historical best growth rate for tree imm/y
f(r)caverage growth rate over the past five yearsmm/y
rcStatistical current diametermm
LStatistical tree agey
f(r)mStatistical average tree ring growth ratemm/y
kPending parameter1
CVRcoefficient of variation of the tree radius1

Appendix A. Iterative Growth Model (IGM)

Tree respiration involves the transport, release, and use of energy stored in photosynthetic carbohydrate products. This supports tree growth, maintenance, and longevity. These energy-demanding processes also follow the first and second laws of thermodynamics and the allometric scaling laws of metabolism. Based on these rules, we constructed a general kinetic framework for organism growth [15]:
f ( m ) T = m r g r M 1 − b ( m − o ) b − m + o
where f(m) is the total biomass of new tissue created during the formation time T of a unit of tissue, and hence, f(m)/T represents the average growth rate over this formation time, as well as the growth rate; b is the metabolic scaling exponent, related to a space-filling fractal (self-similar)-like network; gr is the cost of respiration needed to produce a new unit of tissue; and mr is a unit of tissue’s rate of maintenance respiration (per unit of time). Generally, gr is stable, and mr is sensitive to the environment and is driven by temperature, with its trend following the Arrhenius equation. Mathematically, Equation (A1) highlights a growth iterative mechanism. Namely, growth can be described as a series of spontaneously iterated feedbacks, each of length T. At each iteration, the organism moves from the initial biomass m0 (slightly larger than the threshold biomass for growth, o) and approaches the final mass M. Thus, we refer to Equation (A1) as an iterative growth model (IGM). Mathematically, classical metabolic growth theory, also known as the ontogenetic growth model (OGM), is a special case of IGM at b = 0.75 and T → 0.
Moreover, the IGM contains two implicit thermodynamic and mathematical constraints. The first constraint is that T < gr/mr. We derive this from the thermodynamic significance of respiration. To counteract natural degradation (entropy increase), organisms must continuously use negative entropy to maintain the complexity, variety, and order of their components. Usually, organisms obtain useful energy (e.g., chemical energy stored in photosynthetic products or food) from the environment and return equivalent amounts of energy to the environment in less useful forms, such as dissipated energy or heat. In this process, energy provides negative entropy or the required order to organisms. Thus, from an entropy perspective, during time T, the growth energy proportional to gr decreases the entropy of a new unit of tissue relative to that of their free precursor monomers [27], causing free monomers to achieve an appropriate ordered state. At the same time, the maintenance energy proportional to Tmr contributes the negative entropy to maintain the low entropy state of a unit of old tissue, and mr and Tmr are also proportional to the entropy increase rate and entropy accumulation of a unit of old tissue during time T, respectively. Assuming there is no difference between the new and old units of tissue, the new unit tissue can be synthesized only when Tmr must be less than gr, i.e., T < gr/mr. When T → 0 and gr/mr, integrating or iterating Equation (A1) will produce two smooth functions driven by time (t), i.e., the Richards and Gompertz equations [15].
m = M ( 1 − L exp ( − r t ) ) 1 / − b
m = M · m 0 / M b n
where L = 1 − Mb−1 × m01−b, r = mr/gr (1 − b), m0 is the first biomass observed, and n is the number of iterations and is equal to t × mr/gr. These results indicate that the actual growth dynamics lie somewhere between these equations (Equations (A2) and (A3)) and may not be an explicit analytic solution in most cases.
Second, from a mathematical perspective, M maintains a strict relationship with the other parameters.
M = D T g r m r 2 b + 2 1 − b
where D is the average f(m), mainly determined by the ability of plants to absorb resources and the supply of resources, and TM/D or gr/mr × (2b + 2)/(1 − b) represents the total growth time. The basis for this equation is an integral transform from f(m) to M [15].
Due to the tree radius (r) ∝ mb/2 [29], we can then derive Equation (1).

Appendix B

Forests 14 01483 g0a1 550
Figure A1. Distribution of r/R over different CVR intervals. CVR: the coefficient of variation of the tree radius.
Figure A1. Distribution of r/R over different CVR intervals. CVR: the coefficient of variation of the tree radius.
Forests 14 01483 g0a1
Forests 14 01483 g0a2 550
Figure A2. Correlation of the precipitation of the coldest quarter with the coefficient of variation of the tree radius (CVR) at different elevation ranges. The black lines (A,B) are linear regression.
Figure A2. Correlation of the precipitation of the coldest quarter with the coefficient of variation of the tree radius (CVR) at different elevation ranges. The black lines (A,B) are linear regression.
Forests 14 01483 g0a2
Forests 14 01483 g0a3 550
Figure A3. Coefficient of variation of the tree radius (CVR) at different elevation ranges.
Figure A3. Coefficient of variation of the tree radius (CVR) at different elevation ranges.
Forests 14 01483 g0a3
Forests 14 01483 g0a4 550
Figure A4. Radius distribution of trees at different elevation ranges.
Figure A4. Radius distribution of trees at different elevation ranges.
Forests 14 01483 g0a4

References

  1. Karadavut, U.; Kayis, S.; Okur, O. A Growth Curve Application to Compare Plant Heights and Dry Weights of Some Wheat Varieties. Am.-Eurasian J. Agric. Environ. Sci. 2008, 3, 888–892. [Google Scholar]
  2. Ryan, M.G.; Binkley, D.; Fownes, J.H. Age-Related Decline in Forest Productivity: Pattern and Process. In Advances in Ecological Research; Begon, M., Fitter, A.H., Eds.; Academic Press: Cambridge, MA, USA, 1997; Volume 27, pp. 213–262. [Google Scholar]
  3. Shi, P.-J.; Men, X.-Y.; Sandhu, H.S.; Chakraborty, A.; Li, B.-L.; Ou-Yang, F.; Sun, Y.-C.; Ge, F. The “general” ontogenetic growth model is inapplicable to crop growth. Ecol. Model. 2013, 266, 1–9. [Google Scholar] [CrossRef]
  4. Johnson, S.E.; Abrams, M.D. Age class, longevity and growth rate relationships: Protracted growth increases in old trees in the eastern United States. Tree Physiol. 2009, 29, 1317–1328. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Sillett, S.C.; Van Pelt, R.; Koch, G.W.; Ambrose, A.R.; Carroll, A.L.; Antoine, M.E.; Mifsud, B.M. Increasing wood production through old age in tall trees. For. Ecol. Manag. 2010, 259, 976–994. [Google Scholar] [CrossRef]
  6. Stephenson, N.L.; Das, A.J.; Condit, R.; Russo, S.E.; Baker, P.J.; Beckman, N.G.; Coomes, D.A.; Lines, E.R.; Morris, W.K.; Rüger, N.; et al. Rate of tree carbon accumulation increases continuously with tree size. Nature 2014, 507, 90–93. [Google Scholar] [CrossRef]
  7. Sheil, D.; Eastaugh, C.S.; Vlam, M.; Zuidema, P.A.; Groenendijk, P.; Sleen, P.; Jay, A.; Vanclay, J. Does biomass growth increase in the largest trees? Flaws, fallacies and alternative analyses. Funct. Ecol. 2017, 31, 568–581. [Google Scholar] [CrossRef]
  8. Begović, K.; Schurman, J.S.; Svitok, M.; Pavlin, J.; Langbehn, T.; Svobodová, K.; Mikoláš, M.; Janda, P.; Synek, M.; Marchand, W.; et al. Large old trees increase growth under shifting climatic constraints: Aligning tree longevity and individual growth dynamics in primary mountain spruce forests. Glob. Chang. Biol. 2023, 29, 143–164. [Google Scholar] [CrossRef]
  9. Marshall, D.J.; White, C.R. Have We Outgrown the Existing Models of Growth? Trends Ecol. Evol. 2019, 34, 102–111. [Google Scholar] [CrossRef]
  10. Hérault, B.; Bachelot, B.; Poorter, L.; Rossi, V.; Bongers, F.; Chave, J.; Paine, C.E.T.; Wagner, F.; Baraloto, C. Functional traits shape ontogenetic growth trajectories of rain forest tree species. J. Ecol. 2011, 99, 1431–1440. [Google Scholar] [CrossRef]
  11. Yao, Y.; Shu, S.; Wang, W.; Liu, R.; Wang, Y.; Wang, X.; Zhang, S. Growth and carbon sequestration of poplar plantations on the Tibetan Plateau. Ecol. Indic. 2023, 147, 109930. [Google Scholar] [CrossRef]
  12. Zuo, W.; Moses, M.E.; West, G.B.; Hou, C.; Brown, J.H. A general model for effects of temperature on ectotherm ontogenetic growth and development. Proc. R. Soc. B Boil. Sci. 2012, 279, 1840–1846. [Google Scholar] [CrossRef] [PubMed]
  13. Hou, C.; Zuo, W.; Moses, M.E.; Woodruff, W.H.; Brown, J.H.; West, G.B. Energy Uptake and Allocation During Ontogeny. Science 2008, 322, 736–739. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Huxley, J.S.; Teissier, G. Terminology of Relative Growth. Nature 1936, 137, 780–781. [Google Scholar] [CrossRef]
  15. Shu, S.-M.; Zhu, W.-Z.; Kontsevich, G.; Zhao, Y.-Y.; Wang, W.-Z.; Zhao, X.-X.; Wang, X.-D. A discrete model of ontogenetic growth. Ecol. Model. 2021, 460, 109752. [Google Scholar] [CrossRef]
  16. Nepstad, D.C.; Tohver, I.M.; Ray, D.; Moutinho, P.; Cardinot, G. Mortality of large trees and lianas following experimental drought in an amazon forest. Ecology 2007, 88, 2259–2269. [Google Scholar] [CrossRef]
  17. Shu, S.-M.; Zhu, W.-Z.; Wang, W.-Z.; Jia, M.; Zhang, Y.-Y.; Sheng, Z.-L. Effects of tree size heterogeneity on carbon sink in old forests. For. Ecol. Manag. 2019, 432, 637–648. [Google Scholar] [CrossRef]
  18. O’Hara, K.L.; Ramage, B.S. Silviculture in an uncertain world: Utilizing multi-aged management systems to integrate disturbance. For. Int. J. For. Res. 2013, 86, 401–410. [Google Scholar] [CrossRef] [Green Version]
  19. Forrester, D.I. Linking forest growth with stand structure: Tree size inequality, tree growth or resource partitioning and the asymmetry of competition. For. Ecol. Manag. 2019, 447, 139–157. [Google Scholar] [CrossRef]
  20. Wang, W.; Jia, M.; Wang, G.; Zhu, W.; McDowell, N.G. Rapid warming forces contrasting growth trends of subalpine fir (Abies fabri) at higher- and lower-elevations in the eastern Tibetan Plateau. For. Ecol. Manag. 2017, 402, 135–144. [Google Scholar] [CrossRef]
  21. Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraer, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.; Greenwood, G.; Hashmi, M.Z.; Liu, X.D.; et al. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Chang. 2015, 5, 424–430. [Google Scholar] [CrossRef] [Green Version]
  22. Lyu, L.; Deng, X.; Zhang, Q.-B. Elevation Pattern in Growth Coherency on the Southeastern Tibetan Plateau. PLoS ONE 2016, 11, e0163201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Fan, Z.-X.; Braeuning, A.; Cao, K.-F.; Zhu, S.-D. Growth-climate responses of high-elevation conifers in the central Hengduan Mountains, southwestern China. For. Ecol. Manag. 2009, 258, 306–313. [Google Scholar] [CrossRef]
  24. Dang, H.; Zhang, Y.; Zhang, K.; Jiang, M.; Zhang, Q. Climate-growth relationships of subalpine fir (Abies fargesii) across the altitudinal range in the Shennongjia Mountains, central China. Clim. Chang. 2013, 117, 903–917. [Google Scholar] [CrossRef]
  25. Shi, S.; Liu, G.; Li, Z.; Ye, X. Elevation-dependent growth trends of forests as affected by climate warming in the southeastern Tibetan Plateau. For. Ecol. Manag. 2021, 498, 119551. [Google Scholar] [CrossRef]
  26. Thornley, J.H.M.; Cannell, M.G.R. Erratum: Modelling the Components of Plant Respiration: Representation and Realism. Ann. Bot. 2000, 85, 937. [Google Scholar] [CrossRef] [Green Version]
  27. Clarke, A. Energy Flow in Growth and Production. Trends Ecol. Evol. 2019, 34, 502–509. [Google Scholar] [CrossRef]
  28. Mori, S.; Yamaji, K.; Ishida, A.; Prokushkin, S.G.; Masyagina, O.V.; Hagihara, A.; Hoque, A.; Suwa, R.; Osawa, A.; Nishizono, T.; et al. Mixed-power scaling of whole-plant respiration from seedlings to giant trees. Proc. Natl. Acad. Sci. USA 2010, 107, 1447–1451. [Google Scholar] [CrossRef]
  29. West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the structure and allometry of plant vascular systems. Nature 1999, 400, 664–667. [Google Scholar] [CrossRef]
  30. Cheng, D.-L.; Li, T.; Zhong, Q.-L.; Wang, G.-X. Scaling relationship between tree respiration rates and biomass. Biol. Lett. 2010, 6, 715–717. [Google Scholar] [CrossRef] [Green Version]
  31. Lai, J.; Zou, Y.; Zhang, J.; Peres-Neto, P.R. Generalizing hierarchical and variation partitioning in multiple regression and canonical analyses using the rdacca.hp R package. Methods Ecol. Evol. 2022, 13, 782–788. [Google Scholar] [CrossRef]
  32. Jackson, D.L. Revisiting Sample Size and Number of Parameter Estimates: Some Support for the N:q Hypothesis. Struct. Equ. Model. A Multidiscip. J. 2003, 10, 128–141. [Google Scholar] [CrossRef]
  33. Wang, X.; Wang, T.; Xu, J.; Shen, Z.; Yang, Y.; Chen, A.; Wang, S.; Liang, E.; Piao, S. Enhanced habitat loss of the Himalayan endemic flora driven by warming-forced upslope tree expansion. Nat. Ecol. Evol. 2022, 6, 890–899. [Google Scholar] [CrossRef]
  34. Peltier, D.M.P.; Ogle, K. Tree growth sensitivity to climate is temporally variable. Ecol. Lett. 2020, 23, 1561–1572. [Google Scholar] [CrossRef] [PubMed]
  35. Wilmking, M.; Scharnweber, T.; van der Maaten-Theunissen, M.; van der Maaten, E. Reconciling the community with a concept—The uniformitarian principle in the dendro-sciences. Dendrochronologia 2017, 44, 211–214. [Google Scholar] [CrossRef]
  36. Wilmking, M.; van der Maaten-Theunissen, M.; van der Maaten, E.; Scharnweber, T.; Buras, A.; Biermann, C.; Gurskaya, M.; Hallinger, M.; Lange, J.; Shetti, R.; et al. Global assessment of relationships between climate and tree growth. Glob. Chang. Biol. 2020, 26, 3212–3220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  37. Wu, G.; Xu, G.; Chen, T.; Liu, X.; Zhang, Y.; An, W.; Wang, W.; Fang, Z.-A.; Yu, S. Age-dependent tree-ring growth responses of Schrenk spruce (Picea schrenkiana) to climate—A case study in the Tianshan Mountain, China. Dendrochronologia 2013, 31, 318–326. [Google Scholar] [CrossRef]
  38. Sun, J.; Liu, Y. Age-independent climate-growth response of Chinese pine (Pinus tabulaeformis Carrière) in North China. Trees 2015, 29, 397–406. [Google Scholar] [CrossRef]
  39. Coomes, D.A.; Holdaway, R.J.; Kobe, R.K.; Lines, E.R.; Allen, R.B. A general integrative framework for modelling woody biomass production and carbon sequestration rates in forests. J. Ecol. 2012, 100, 42–64. [Google Scholar] [CrossRef]
  40. Pillet, M.; Joetzjer, E.; Belmin, C.; Chave, J.; Ciais, P.; Dourdain, A.; Evans, M.; Hérault, B.; Luyssaert, S.; Poulter, B. Disentangling competitive vs. climatic drivers of tropical forest mortality. J. Ecol. 2018, 106, 1165–1179. [Google Scholar] [CrossRef]
  41. Mencuccini, M.; Martinez-Vilalta, J.; Vanderklein, D.; Abdul-Hamid, H.; Korakaki, E.; Lee, S.; Michiels, B. Size-mediated ageing reduces vigour in trees: Size Reduces Vigour in Tall Trees. Ecol. Lett. 2005, 8, 1183–1190. [Google Scholar] [CrossRef]
  42. Vieira, J.; Nabais, C.; Campelo, F. Extreme Growth Increments Reveal Local and Regional Climatic Signals in Two Pinus pinaster Populations. Front. Plant Sci. 2021, 12, 658777. [Google Scholar] [CrossRef] [PubMed]
  43. Lloyd, A.H.; Graumlich, L.J. Holocene dynamics of treeline forests in the sierra nevada. Ecology 1997, 78, 1199–1210. [Google Scholar] [CrossRef]
  44. Sigdel, S.R.; Wang, Y.; Camarero, J.J.; Zhu, H.; Liang, E.; Peñuelas, J. Moisture-mediated responsiveness of treeline shifts to global warming in the Himalayas. Glob. Chang. Biol. 2018, 24, 5549–5559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  45. Peng, S.; Piao, S.; Ciais, P.; Myneni, R.B.; Chen, A.; Chevallier, F.; Dolman, A.J.; Janssens, I.A.; Peñuelas, J.; Zhang, G.; et al. Asymmetric effects of daytime and night-time warming on Northern Hemisphere vegetation. Nature 2013, 501, 88–92. [Google Scholar] [CrossRef] [PubMed]
  46. Nehrbass-Ahles, C.; Babst, F.; Klesse, S.; Nötzli, M.; Bouriaud, O.; Neukom, R.; Dobbertin, M.; Frank, D. The influence of sampling design on tree-ring-based quantification of forest growth. Glob. Chang. Biol. 2014, 20, 2867–2885. [Google Scholar] [CrossRef]
Forests 14 01483 g001 550
Figure 1. Map of the research area, Tibetan Plateau.
Figure 1. Map of the research area, Tibetan Plateau.
Forests 14 01483 g001
Forests 14 01483 g002 550
Figure 2. Classical metabolic growth theory (OGM) vs. generalized metabolic growth theory (IGM). f(r) and r represent the actual tree ring growth rate and tree radius, respectively. Here, we show the best growth trajectory of trees within the same forest, so we assume that the actual f(r) (gray dots) is below the curve. It is worth noting that the IGMR-U is more common, indicating that the gray dots tend to appear more often below this curve.
Figure 2. Classical metabolic growth theory (OGM) vs. generalized metabolic growth theory (IGM). f(r) and r represent the actual tree ring growth rate and tree radius, respectively. Here, we show the best growth trajectory of trees within the same forest, so we assume that the actual f(r) (gray dots) is below the curve. It is worth noting that the IGMR-U is more common, indicating that the gray dots tend to appear more often below this curve.
Forests 14 01483 g002
Forests 14 01483 g003a 550Forests 14 01483 g003b 550
Figure 3. Distribution of the coefficient of variation in the tree radius (A), the distribution of the normalized growth rate on the relative radius (B,C), and the distribution of the coefficient of variation in the tree ring growth rate along the relative radius over the past 5 years. The test samples in (B,C) are from the data belonging to the gray and white bars in (A), respectively. The green curve in (B) is obtained from the 0.95th quantile fit of the data by Equation (4), where b = k = 0.736 ± 0.10. This curve, along with its half, is also plotted in (C,D). The red curve (A) is the normal distribution curve. (B–D) Dot density is represented by different colors, with warmer colors representing a higher density and cooler colors representing a lower density. The quartiles for the blue, red, and orange borders are 0.95, 0.75, and 0.55, respectively.
Figure 3. Distribution of the coefficient of variation in the tree radius (A), the distribution of the normalized growth rate on the relative radius (B,C), and the distribution of the coefficient of variation in the tree ring growth rate along the relative radius over the past 5 years. The test samples in (B,C) are from the data belonging to the gray and white bars in (A), respectively. The green curve in (B) is obtained from the 0.95th quantile fit of the data by Equation (4), where b = k = 0.736 ± 0.10. This curve, along with its half, is also plotted in (C,D). The red curve (A) is the normal distribution curve. (B–D) Dot density is represented by different colors, with warmer colors representing a higher density and cooler colors representing a lower density. The quartiles for the blue, red, and orange borders are 0.95, 0.75, and 0.55, respectively.
Forests 14 01483 g003aForests 14 01483 g003b
Forests 14 01483 g004 550
Figure 4. Correlation (A), hierarchical partitioning (B), and structural equation model analyses (C) between explanatory variables and OVG. (A) Normalized growth rate: ratio of the average growth rate of tree cores over the past five years to the average growth rate of all tree cores (f(r)c/f(r)m). (B) ele: elevation; Temp: mean annual temperature; Maxtwm: max temperature of warmest month; Mentwq: mean temperature of warmest quarter; Mentcq: mean temperature of coldest quarter; Ap: annual precipitation; Pwq: precipitation of wettest quarter; Pcq: precipitation of driest quarter. (A) Red line is linear regression. (C) Solid red and green arrows represent significant (p < 0.05) positive and negative paths, respectively; double arrow solid lines indicate a correlation. The numbers near the lines indicate the standard path coefficients or correlation coefficients. R2 represents the amount of variation of the variable explained by corresponding paths. The red and green lines indicate negative and positive effects, respectively.
Figure 4. Correlation (A), hierarchical partitioning (B), and structural equation model analyses (C) between explanatory variables and OVG. (A) Normalized growth rate: ratio of the average growth rate of tree cores over the past five years to the average growth rate of all tree cores (f(r)c/f(r)m). (B) ele: elevation; Temp: mean annual temperature; Maxtwm: max temperature of warmest month; Mentwq: mean temperature of warmest quarter; Mentcq: mean temperature of coldest quarter; Ap: annual precipitation; Pwq: precipitation of wettest quarter; Pcq: precipitation of driest quarter. (A) Red line is linear regression. (C) Solid red and green arrows represent significant (p < 0.05) positive and negative paths, respectively; double arrow solid lines indicate a correlation. The numbers near the lines indicate the standard path coefficients or correlation coefficients. R2 represents the amount of variation of the variable explained by corresponding paths. The red and green lines indicate negative and positive effects, respectively.
Forests 14 01483 g004
Forests 14 01483 g005a 550Forests 14 01483 g005b 550
Figure 5. Radial growth rates at the current tree radii vs. model-estimated historical best radial growth rates at the same radii (A) (n = 2500), comparison of their differences at different elevations (B,C) (W-test, *** p < 0.001), and the correlation of this difference with the climatic factors (D,E). The red lines (D,E) are linear regression.
Figure 5. Radial growth rates at the current tree radii vs. model-estimated historical best radial growth rates at the same radii (A) (n = 2500), comparison of their differences at different elevations (B,C) (W-test, *** p < 0.001), and the correlation of this difference with the climatic factors (D,E). The red lines (D,E) are linear regression.
Forests 14 01483 g005aForests 14 01483 g005b
Table
Table 1. Geographic description of the sample sites.
Table 1. Geographic description of the sample sites.
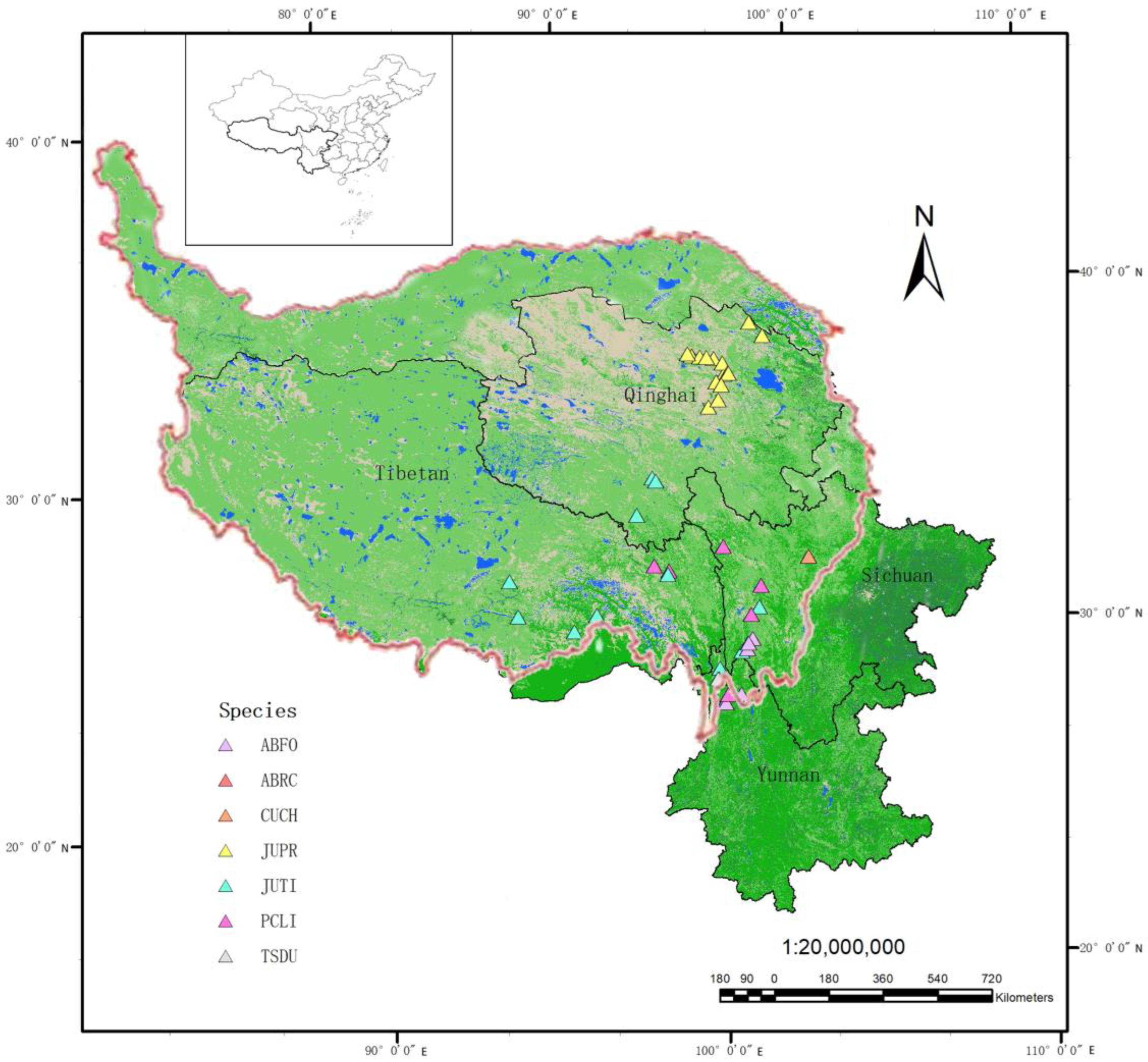
Species NameAbbreviated NameLatitudeLongitudeAverage Elevation (m)Number of Sample Sites/Tree CoresSpecies CompositionAge StructureAverage ± SD/Maximum DBH (mm)Average ± SD/Maximum Age (y)
Abies forestiiABFO27.33–29.2899.27–100.0835217/345single speciesSingle/mixed age202 ± 94/386261 ± 121/463
Abies recurvataABRC28.0499.0232001/18-Single age276 ± 76/394272 ± 88/394
Cupressus chengianaCUCH31.78101.916725001/39single species-218 ± 73/330210 ± 88/358
Juniperus przewalskiiJUPR36.00–38.5797.06–99.87374116/1256-Single/mixed age162 ± 80/294552 ± 288/1046
Juniperus tibeticaJUTI28.37–33.8091.52–100.27413612/549single speciesSingle/mixed age178 ± 81/323407 ± 200/795
Picea likiangensisPCLI27.58–31.9596.48–100.2835206/195--212 ± 83/341232 ± 102/439
Tsuga dumosaTSDU27.88–28.0498.40–98.9831252/63-Single age310 ± 44/362293 ± 82/460
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, Y.; Shu, S.; Wang, X.; Chen, W. Effect of Tree Size Heterogeneity on the Overall Growth Trend of Trees in Coniferous Forests of the Tibetan Plateau. Forests 2023, 14, 1483. https://doi.org/10.3390/f14071483

AMA Style

Wang Y, Shu S, Wang X, Chen W. Effect of Tree Size Heterogeneity on the Overall Growth Trend of Trees in Coniferous Forests of the Tibetan Plateau. Forests. 2023; 14(7):1483. https://doi.org/10.3390/f14071483

Chicago/Turabian Style

Wang, Yuelin, Shumiao Shu, Xiaodan Wang, and Wende Chen. 2023. "Effect of Tree Size Heterogeneity on the Overall Growth Trend of Trees in Coniferous Forests of the Tibetan Plateau" Forests 14, no. 7: 1483. https://doi.org/10.3390/f14071483

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop