Abstract
Formaldehyde emission from cellulosic materials is an important consideration, especially for wood products, which are regulated by many countries in terms of legislation and may affect the health of users. In this study, molecular dynamics simulations were performed at different temperatures using two common wood-modification methods, heat treatment, and acetylation, and the diffusion coefficients of the models as well as the mechanical properties, were discussed. The results showed that the mean square displacement of the common heat treatment model was best at 493 K. The acetylated cellulose model at 483 K was able to achieve four times the diffusion coefficient of the common cellulose model, while the acetylated cellulose material would be weaker than the common heat-treated cellulose material in terms of mechanical properties. These findings provide some reference for formaldehyde pretreatment of wood products.
1. Introduction
Formaldehyde is an important consideration affecting customers’ willingness to purchase wood products, and its carcinogenic properties and irritating odor can affect users’ health to some extent [1], so it is very meaningful to study the mechanism of formaldehyde diffusion influence on wood. Solid wood itself releases a certain amount of formaldehyde, mainly from extractives, polysaccharides, and lignin in the solid wood itself. However, it accounts for a relatively small amount of wood products [2]. For example, Meyer et al. [3] measured the wood in the amount of formaldehyde released, where the highest value of formaldehyde produced by green oak samples was nine parts per billion. A large amount of adhesives is used in the production and processing of wood products. The urea-formaldehyde resin is usually used as a binder for particleboard in Europe, and the free formaldehyde of the adhesives itself will react with the hydroxyl groups of cellulose or hemicelluloses in wood to produce hemiacetal. If the equilibrium conditions change, the reaction will reverse the release of formaldehyde, forming a large amount of formaldehyde detected in wood products [4].
Formaldehyde emissions from wood are related to a variety of factors; formaldehyde emissions from natural solid wood are influenced by wood species, moisture content, outside temperature, and time of storage [2], while formaldehyde emissions from manufactured wood panels are related to the type of panel, wood species, adhesive, overlay, temperature, humidity, air velocity, and air exchange rate [5]. The heat treatment and acetylation of wood as a way of wood modification can affect the density of wood and thus the formaldehyde emission of wood to some extent. Petinarakis et al. [6] designed an experiment on the factors influencing formaldehyde emissions, which mainly took particleboards produced by low formaldehyde emission binders. The experiment showed that the formaldehyde emission of the boards could be influenced by controlling their density, which is inversely proportional to the density. Rowell et al. [7] review the chemical modification of wood by acetylation or furfurylation and how they affect wood properties such as density, dimensional stability, durability, strength, and fire resistance. Mantanis et al. [8] compare different methods of densifying wood, including steaming, acetylation, and furfurylation, and how they influence spring-back and set recovery values. Cao [9] reviews how heat treatment changes the physical, chemical, mechanical, and biological properties of wood, such as color, density, strength, durability, and resistance to decay and insect. Li et al. [10] used confocal laser scanning microscopy (CLSM) to observe the microscopic distribution of polymerized FA resins in the cavities of horsetail pine wood and used nanoindentation to probe the mechanical properties of modified wood cells and finally observed that the indentation modulus and hardness of furfurylated wood cells were greatly improved.
Many methods exist for the detection of formaldehyde. Zhu et al. [11] divided the detection methods for formaldehyde into three categories: total amount detection methods, static emission testing methods, and dynamic emission testing methods. The United States provides three methods for testing formaldehyde: large chamber, small chamber, and desiccator, of which the chamber method is a dynamic emission test method [12]. The EU standard uses the chamber, gas analysis, and perforation method, where the perforation method belongs to the total amount testing method [13]. In the Japanese standard, the desiccator method is used, which belongs to the electrostatic emission method. Regarding the control of formaldehyde regulations, the United States has three product standards and three method standards, the European Union and Japan have four product standards and four method standards, and Japan’s requirements are the most stringent [5]. In addition to this, Jia Shao et al. [14] discussed the use of a desiccator method and a 1 m3 climate chamber method to measure formaldehyde emissions from veneered particle boards, thereby reducing the measurement time of formaldehyde emissions from man-made boards and reducing the cost of quality control processes during industrial furniture production. A. Baldelli et al. [15] used a low-cost detector for formaldehyde emissions from a gross-anatomical laboratory, demonstrating that real-time monitoring is useful for limiting emissions.
For wood, modification treatment can change the density and also change the mechanical properties of the wood. Cao et al. [9] performed heat treatment to reduce the water absorption and swelling of wood by degrading hemicellulose and changing its hydrophilic groups. Heat treatment also improves the biological durability of wood by reducing its nutrient content and increasing its thermal stability. However, heat treatment also decreases the strength and elasticity of wood by breaking down lignin and cellulose bonds. Vasiliki Kamperidou [16] performed wet chemical analysis and Fourier-transform infrared spectroscopy on poplar and black pine wood and found that with increasing intensity of heat treatment, the wood became more hydrophobic and dimensionally stable due to water loss and degradation of volatile compounds, especially at 200 °C when the whole cellulose content was lower in all modified wood categories of both species than in unmodified wood due to strong decomposition of hemicellulose. Esteves et al. [8] concluded that chemical modification of wood by acetylation or furfuralization could effectively improve the durability, dimensional stability, and mechanical properties of wood. In this paper, the role of the corresponding wood treatment is judged by the changes in the mechanical properties of wood after molecular dynamics simulations. This study can be of practical interest as a new method for detecting formaldehyde emissions from wood products, providing a reference for reducing formaldehyde emissions from wood products or other cellulose products by heat treatment and acetylation, which consumes less cost compared to other methods.
2. Experimental
2.1. Model Construction Parameter Setting
In the microscopic experiments, the cellulose chains with a polymerization degree of 20 are adopted to construct the model of the amorphous region of the molecular structure [17]. Since the cellulose molecule content in the cell is extremely high, the model directly used the density of cellulose as the density of cells, which was set to 1.5 g/cm3 for the cellulose–formaldehyde composite model and 1.3 g/cm3 for the cellulose acetate–forma–dehyde composite model in this paper [18]; considering that multiple molecular chains can only play the role of mutual influence and form the physical environment of opening and closing molecular channels, the composite model is therefore composed of three cellulose chains and four formaldehyde molecules. It is important to note that Mazeau et al. [19] showed that the length size of cellulose chains does not affect the simulation experiments; hybrid modeling using the amorphous cell module of Materials Studio software. The composite model is shown in Figure 1, a for the cellulose–formaldehyde model and b for the cellulose–acetate–formaldehyde model.
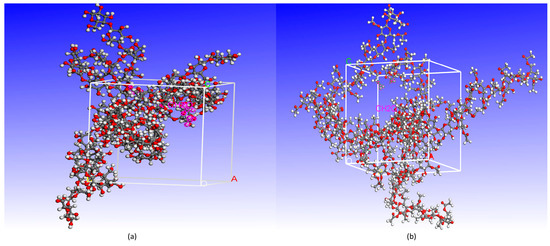
Figure 1.
The composite model: (a) cellulose–formaldehyde model; (b) cellulose–acetate–formaldehyde model.
2.2. Parameter Setting
Molecular dynamics simulations were performed using Materials Studio software (version 2020). Since the model constructed by microscopic experiments is too idealized, the distribution of molecules in the model may not be uniform throughout the cell; in order to make the model construction similar to the real material structure, structural relaxation of the cellulose and two composite models is needed to minimize the energy of the system and find the lowest energy configuration through the annealing module. This treatment can balance the cell structure.
On the basis of the relaxation treatment, the dynamics of the wood are simulated on the compass forcefield, using the NVT system synthesis, with 100,000 kinetic steps and one output at 1000 steps. All simulations use an atom-based approach to calculate the charge and van der Waals forces. The simulated temperatures were 298 K, 453 K, 463 K, 473 K, 473 K, 483 K, and 493 K, representing the average summer temperature of 25 °C, and 180 °C, 190 °C, 200 °C, 210 °C, and 220 °C, commonly used for thermal modification of wood [20], and the same cellulose acetate–formaldehyde model was constructed, by which the experiments of wood acetylation were simulated. After simulation, all data in this paper were calculated by three experiments and then taking the mean value.
3. Results
3.1. System Equilibrium
Molecular dynamics explains the energy changes between molecules from a microscopic perspective. If the model system reaches equilibrium, it proves that the intermolecular is in a stable state, and this equilibrium can be observed by temperature and energy fluctuations in the range of simulation time. Taking the cellulose–formaldehyde model as an example, Figure 2 shows that the temperature quickly reaches a steady state as time changes, while the energy changes in more ways; taking the 453 K temperature experiment with the cellulose–formaldehyde composite model as an example, the energy fluctuations are plotted in Figure 3.
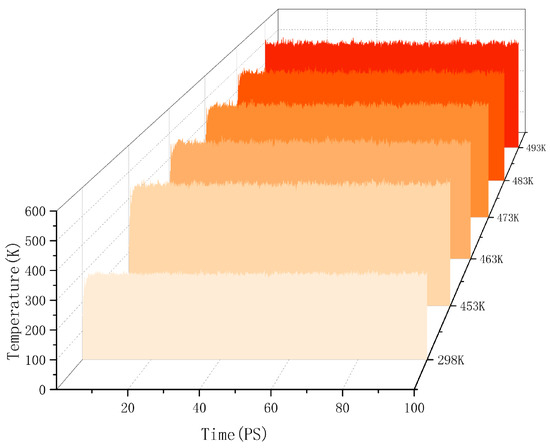
Figure 2.
Temperature fluctuation.
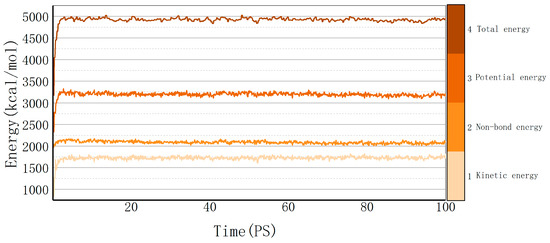
Figure 3.
Energy fluctuation.
The data in both graphs show stable fluctuations after a certain time, and the temperature does not show significant changes greater than 30 K. Therefore, the model can be considered to be in a local optimum, from which the results of subsequent molecular dynamics simulations can be trusted [21].
3.2. Mean Square Displacement Calculation
For the release of formaldehyde in a molecular system, the diffusion of formaldehyde molecules can generally be used to make a determination, and the diffusion coefficient helps to quantify that diffusion. In molecular dynamics, the mean square displacement and Einstein relationship are generally used to calculate the diffusion coefficient. The advantage of molecular dynamics simulations is that the intermolecular interactions and structural changes can be taken into account, resulting in more accurate and detailed results [22]. The mean square displacement is a method in molecular dynamics to describe the distance a particle travels in a finite time, and the diffusion coefficient of a system can be estimated using Einstein’s relation. There has been a wide scientific research base for this calculation method, and the mean square displacement has been used to study different systems in molecular dynamics. For example, Xue Li et al. [23] proposed to use the mean square displacement to calculate the diffusion coefficient of a polymer film based on the polysorbate diffusion coefficient and proton conductivity.
When molecular dynamics is used to calculate the mean-square displacement, it is necessary to first relax the system at different temperatures and perform molecular dynamics simulations for a certain time to record the particle position information, then calculate the vector distance of each particle from the initial position at each time point, then square and average it to obtain the mean-square displacement, and finally fit the diffusion coefficient according to Einstein’s relation, considering the mean square displacement versus time.
The commonly used formula for calculating the mean square displacement is as follows Equation (1):
where N is the total number of particles, <…> is the mean of the system synthesis after equilibrium, and is the vector displacement of particles passing through at moment.
Once the mean square displacement data are obtained, the diffusion coefficient can be derived from the Einstein relationship [24], as shown in Equation (2) below:
where d is the dimension of the motion space. For normal three-dimensional diffusion, we have d = 3. For Brownian motion on the surface of a liquid, we have d = 2. By calculation, the MSD (mean square displacement) curves of the cellulose–formaldehyde model are shown in Figure 4 below, and those of the cellulose–acetate–formaldehyde model are shown in Figure 5 below.
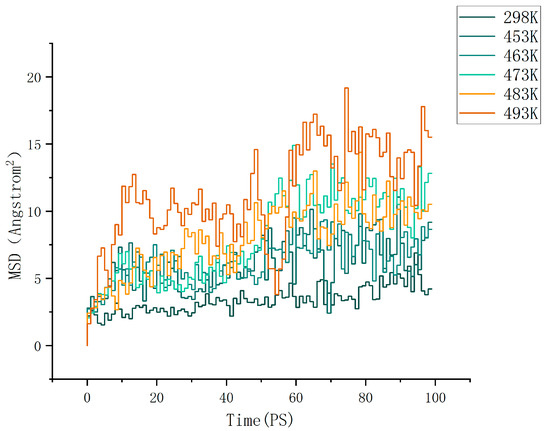
Figure 4.
MSD of cellulose–formaldehyde model.
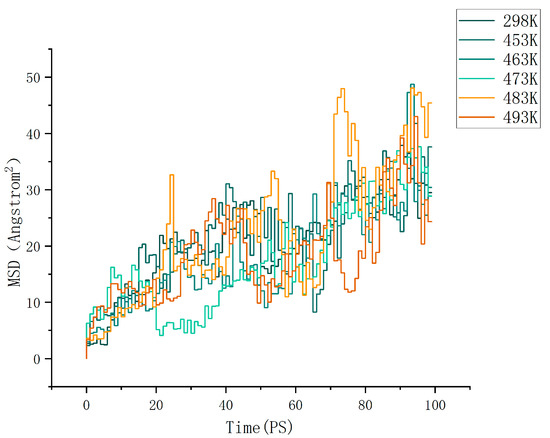
Figure 5.
MSD of cellulose acetate–formaldehyde model.
By calculating the goodness of fit of the regression line of the mean square displacement, we can judge the degree of fit of the regression line of the mean square displacement to the observed values. The formula of the goodness of fit is as follows Equation (3):
where R2 is the goodness of fit, y is the data to be fitted, the mean of is , and the fitted data is .
By calculating the mean square displacement values, we can linearly fit them to obtain the slope of the mean square displacement curve and the diffusion coefficient. As a result, a comparison of the diffusion coefficients of cellulose–formaldehyde model and cellulose–acetate–formaldehyde model at different temperatures was obtained, as shown in Figure 6.
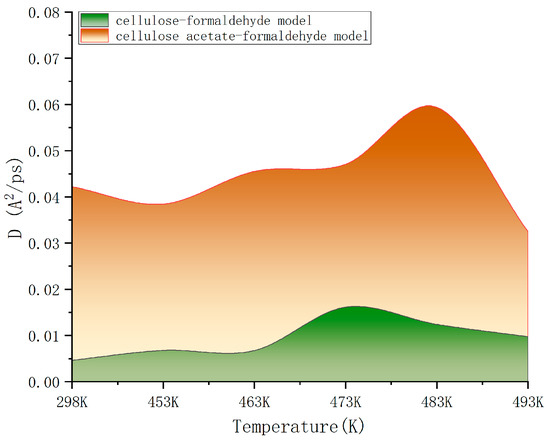
Figure 6.
Comparison of diffusion coefficients.
As can be seen in Figure 6, the diffusion coefficient of the cellulose–acetate–formaldehyde model is always higher than that of the cellulose–formaldehyde model, while they both stand out at 483 K versus 493 K.
3.3. Interaction Energy
The study of the release of formaldehyde molecules in wood can also be judged by the binding energy between formaldehyde molecules and cellulose. Through molecular dynamics simulation, we can obtain the interaction energy between formaldehyde and cellulose and cellulose acetate; when the interaction energy is negative, it represents that energy is being released in this system and there is a binding interaction between the current molecules, while when the interaction energy is a positive sign, it represents that there is a repulsion between the molecules. The absolute magnitude of the interaction energy can determine the strength of the current interaction [25]. The interaction energy is calculated as shown in Equation (4) below:
where represents the final calculated interaction energy, and represent the single-point potential energy of the two substances, and represents the total potential energy, a calculation method validated for use by Dihua Ouyang et al. [26]. With this formula, the compass force field was used to simulate formaldehyde as well as cellulose and cellulose–acetate molecules, and the relevant interaction energies were obtained, as shown in Table 1 below.

Table 1.
Interaction energy of formaldehyde with cellulose and cellulose–acetate molecules in different temperature ranges.
In this table, model a is a cellulose–formaldehyde model, and model b is a cellulose–acetate–formaldehyde model, and it can be seen from the table that both models have negative interaction energies, while model b has lower interaction energy than model a.
3.4. Mechanical Performance Analysis
The mechanical properties of the material can be calculated by Materials Studio, and the mechanical parameters involved can be indicated by this matrix (5).
where λ and μ are important parameters for calculating the relevant mechanical properties, both of which can be derived from the matrix, as shown in Equations (6) and (7).
Young’s modulus is a characterization of the ease of elastic deformation of objects; the greater the value, the greater the stress that makes the wood undergo a certain elastic deformation. That is, the greater the stiffness of the wood when the wood is less prone to elastic deformation, the increase in Young’s modulus contributes to the steel of the wood, which is calculated as shown in Equation (8).
Shear modulus is the modulus of wood when shear deformation occurs and is the ratio of shear stress to strain; the larger the modulus, the more rigid the material. The shear modulus is expressed in the form shown in Equation (9).
When wood undergoes transverse deformation, we usually use Poisson’s ratio (γ) and the ratio of volume and shear variables (K/G) as the elastic constants reflecting the transverse deformation of the material, both of which are expressed as shown in Equations (10) and (11).
The mechanical property indices of the cellulose–formaldehyde model, as well as the cellulose–acetate–formaldehyde model at each temperature, were calculated as shown in Table 2. Where model a is a cellulose–formaldehyde model and model b is a cellulose–acetate–formaldehyde model.

Table 2.
Calculated mechanical properties.
The mechanical property indices of the cellulose–formaldehyde model, as well as the cellulose–acetate–formaldehyde model at each temperature, were calculated as shown in Table 2, where model a is a cellulose–formaldehyde model and model b is a cellulose–acetate–formaldehyde model.
4. Discussion
From the above data, it can be seen that cellulose produces different changes in mechanical properties at different temperatures, while acetylated cellulose will react more than normal cellulose, confirming the important role of acetic anhydride as well as temperature in wood modification.
As can be seen in Figure 6, in terms of improving the ability to release formaldehyde, comparing the ambient environment at 298 K, all other heat treatments of cellulose at different temperatures are effective in improving the diffusion coefficient of the wood, resulting in a better release of formaldehyde. However, the cellulose–formaldehyde model obtains a superior diffusion coefficient performance at 483 K. This is in accordance with the experimental phenomenon performed by de Medeiros et al. [27], who, by analyzing the Qualea paraensis wood at different temperatures, they concluded that the maximum dimensional stability and less strength loss to static bending and parallel compression were obtained for wood treated at 200 °C. The acetylation-modified wood, on the other hand, was able to obtain a diffusion coefficient four times higher than that of the wood obtained by normal heat treatment at the same temperature of 473 K and an even more optimal diffusion coefficient at 483 K.
As for the change of mechanical properties after wood modification, the model performance under ideal environment simulation is consistent with the macroscopic experiments done by many researchers, where Young’s modulus increases at a temperature of 453–473 K and then decreases sharply [28]. This change in the modulus of elasticity is irregularly decreasing with time [29,30]; the acetylation-modified wood produced greater changes in mechanical properties than the wood after heat treatment alone. The reason for these changes in mechanical properties was attributed to chemical reactions occurring within the cell walls, leading to the degradation of hemicellulose in the wood, which in turn reduced the free hydroxyl groups in the wood [31].
The shortcoming of the present experiment is that the simulated temperatures, although they belong to the common temperatures for wood heat treatment, should be designed within the simulation for better observation below 453 K and above 493 K. The temperatures in these two intervals are not commonly used in heat treatment, which might be better to judge the influence range of wood after modification. Nevertheless, this experiment also provides a new direction for the study of formaldehyde diffusion in wood. If acetylation of wood is carried out before wood processing, although it may lead to a reduction of some physical properties of the wood, a more efficient formaldehyde release capacity can be obtained, thus greatly reducing the cost of formaldehyde treatment on the panels for retailers as well as reducing the health risks for customers who purchase wood products.
5. Conclusions
In this study, the cellulose–formaldehyde model and the cellulose–acetate–formaldehyde model were constructed using Materials Studio software to simulate two wood modification methods, namely heat treatment and acetylation treatment of wood, respectively. After structural optimization and kinetic relaxation of the models, the system energy of the models stabilized, the cells reached the equilibrium state, and the kinetic simulations could be performed with high confidence. On this basis, the diffusion behavior of formaldehyde molecules, the interaction energy of formaldehyde molecules with cellulose and cellulose–acetate, and the mechanical properties of the two models at different temperatures were studied, and the following conclusions were drawn:
- (1)
- With the increase in temperature, the diffusion coefficient of formaldehyde molecules in the model increased continuously but reached a peak of around 483 K and 493 K. On the one hand, it showed that the temperature helped to increase the diffusion movement of molecules, and on the other hand, it indicated that the acetylation led to the change of physical properties of cellulose, which created a better environment for the release of formaldehyde in wood;
- (2)
- The interaction energy of formaldehyde with both cellulose and cellulose–acetate was calculated to be negative, which represents the existence of their binding interaction, and the interaction energy of cellulose–acetate–formaldehyde model was lower than that of the cellulose–formaldehyde model, which represents that the binding interaction between formaldehyde and cellulose–acetate is weaker in the cellulose–formaldehyde model and formaldehyde molecules are more easily diffused rather than attracted by cellulose–acetate after acetylation, which proves that the acetylation modification of wood can better promote the release of formaldehyde;
- (3)
- The mechanical property data of the cellulose-amorphous zone produced irregular fluctuations in response to changes in temperature, and the decreases in the modulus of elasticity and Poisson’s ratio indicate that the temperature reduced the stiffness of the wood but increased the ductility of the wood. At the same time, the mechanical property values of the cellulose acetate–formaldehyde model were substantially lower than those of the normal cellulose model, indicating that the wood after acetylation was higher in ductility than the wood after heat treatment only, which may be an important hint for some processors who need high ductility properties of wood. Additionally, the study provides wood companies with an idea of how to detect formaldehyde emissions when pretreating wood. Wood modification methods exist in a variety of ways, and some novel wood modification methods may not be applicable to old formaldehyde detection methods in the future, while software simulations demonstrate a low-cost method for estimating formaldehyde emissions from wood.
Author Contributions
Conceptualization, N.L.; methodology, N.L.; software, N.L.; validation, N.L. and W.W.; formal analysis, N.L.; investigation, J.L.; resources, N.L.; data curation, Y.H.; writing—original draft preparation, N.L.; writing—review and editing, N.L.; visualization, N.L.; supervision, W.W.; project administration, J.W.; funding acquisition, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities, grant number 2572019BL04, and the Scientific Research Foundation for the Returned Overseas Chinese Scholars of Heilongjiang Province, grant number LC201407.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kang, D.S.; Kim, H.S.; Jung, J.-H.; Lee, C.M.; Ahn, Y.-S.; Seo, Y.R. Formaldehyde exposure and leukemia risk: A comprehensive review and network-based toxicogenomic approach. Genes Environ. 2021, 43, 13. [Google Scholar] [CrossRef] [PubMed]
- Salem, M.Z.M.; Bohm, M. Understanding of Formaldehyde Emissions from Solid Wood: An Overview. BioResources 2013, 8, 4775–4790. [Google Scholar] [CrossRef]
- Meyer, B.; Boehme, C. Formaldehyde emission from solid wood. For. Prod. J. 1997, 47, 45–48. [Google Scholar]
- Schäfer, M.; Roffael, E. On the formaldehyde release of wood. Holz als Roh- und Werkst. 2000, 58, 259–264. [Google Scholar] [CrossRef]
- Zhang, J.; Song, F.; Tao, J.; Zhang, Z.; Shi, S.Q. Research Progress on Formaldehyde Emission of Wood-Based Panel. Int. J. Polym. Sci. 2018, 2018, 9349721. [Google Scholar] [CrossRef]
- Petinarakis, J.; Kavvouras, P. Technological factors affecting the emission of formaldehyde from particleboards. Wood Res. 2006, 51, 31–40. [Google Scholar]
- Rowell, R.M.; Dickerson, J.P. Acetylation of Wood. In Deterioration and Protection of Sustainable Biomaterials; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 2014; Volume 1158, pp. 301–327. [Google Scholar]
- Mantanis, G. Chemical Modification of Wood by Acetylation or Furfurylation: A Review of the Present Scaled-up Technologies. BioResources 2017, 12, 4478–4489. [Google Scholar] [CrossRef]
- Cao, S.; Cheng, S.; Cai, J.B. Research Progress and Prospects of Wood High-temperature Heat Treatment Technology. BioResources 2022, 17, 3702–3717. [Google Scholar] [CrossRef]
- Li, W.; Ren, D.; Zhang, X.; Wang, H.; Yu, Y. The Furfurylation of Wood: A Nanomechanical Study of Modified Wood Cells. BioResources 2016, 11, 3614–3625. [Google Scholar] [CrossRef]
- Zhu, H.; Lu, Z.; Li, X.; Zhang, J.; Yuan, M. Analysis on test methods for determining formaldehyde emission from wood-based products. China Wood Ind. 2009, 2009, 37–40. [Google Scholar]
- Zhang, J.; Shaw, C.; Kanabus-Kaminska, J.; MacDonald, R.; Magee, R.; Lusztyk, E.; Weichert, H. Study of Air Velocity and Turbulence Effects on Organic Compounds Emissions from Building Materials/Furnishings Using a New Small Test Chamber; American Society for Testing and Materials: West Conshohocken, PA, USA, 1996. [Google Scholar]
- Carvalho, L.; Magalhães, F.; Ferra, J. Formaldehyde emissions from wood-based panels-Testing methods and industrial perspectives. In Formaldehyde: Chemistry, Applications and Role in Polymerization; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2012; pp. 1–45. [Google Scholar]
- Shao, J.; Chen, Y.; Dong, L.; Yuan, T.; Zhang, Z.; Zhang, J. Correlation between the Desiccator Method and 1 m3 Climate Chamber Method for Measuring Formaldehyde Emissions from Veneered Particleboard. Processes 2022, 10, 1023. [Google Scholar] [CrossRef]
- Baldelli, A.; Jeronimo, M.; Tinney, M.; Bartlett, K.H. Real-time measurements of formaldehyde emissions in a gross anatomy laboratory. SN Appl. Sci. 2020, 2, 769. [Google Scholar] [CrossRef]
- Kamperidou, V. Chemical and Structural Characterization of Poplar and Black Pine Wood Exposed to Short Thermal Modification. Drvna Ind. 2021, 72, 155–167. [Google Scholar] [CrossRef]
- Wang, W.; Cao, Y.; Sun, L.; Wu, M. Effect of Temperature on Formaldehyde Diffusion in Cellulose Amorphous Region: A Simulation Study. BioResources 2021, 16, 3200–3213. [Google Scholar] [CrossRef]
- Onyon, P.F. Polymer Handbook. Nature 1972, 238, 56. [Google Scholar] [CrossRef]
- Mazeau, K.; Heux, L. Molecular Dynamics Simulations of Bulk Native Crystalline and Amorphous Structures of Cellulose. J. Phys. Chem. B 2003, 107, 2394–2403. [Google Scholar] [CrossRef]
- Esteves, B.; Pereira, H. Wood modification by heat treatment: A review. BioResources 2009, 4, 370–404. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Li, X. Molecular Dynamics Study on Mechanical Properties of Cellulose with Air/Nitrogen Diffusion Behavior. BioResources 2018, 13, 7900–7910. [Google Scholar] [CrossRef]
- Liu, X.; Schnell, S.K.; Simon, J.-M.; Krüger, P.; Bedeaux, D.; Kjelstrup, S.; Bardow, A.; Vlugt, T.J.H. Diffusion Coefficients from Molecular Dynamics Simulations in Binary and Ternary Mixtures. Int. J. Thermophys. 2013, 34, 1169–1196. [Google Scholar] [CrossRef]
- Li, X.; Zhao, Y.; Wang, S.; Xie, X. Molecular dynamics simulation study of a polynorbornene-based polymer: A prediction of proton exchange membrane design and performance. Int. J. Hydrogen Energy 2016, 41, 16254–16263. [Google Scholar] [CrossRef]
- Einstein, A. Zur Elektrodynamik bewegter Körper. In Das Relativitätsprinzip: Eine Sammlung von Abhandlungen; Lorentz, H.A., Einstein, A., Minkowski, H., Eds.; Vieweg + Teubner Verlag: Wiesbaden, Germany, 1923; pp. 26–50. [Google Scholar]
- Hanuš, J.; Mazeau, K. The xyloglucan-cellulose assembly at the atomic scale. Biopolymers 2006, 82, 59–73. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, D.; Zhang, L.; Mao, R.; Qin, X.; Pang, W. Application Process of Coating Agent and the Coating Effect Evaluation Based on Molecular Dynamics. Langmuir 2023, 39, 3411–3419. [Google Scholar] [CrossRef] [PubMed]
- Medeiros, D.T.d.; Batista, F.G.; Melo, R.R.d.; Mascarenhas, A.R.P.; Pedrosa, T.D. Alterações físico-mecânicas na madeira de cambará (Qualea paraensis) termorretificada. Madera y Bosques 2021, 27, e2722176. [Google Scholar] [CrossRef]
- Inoue, M.K.; Norimoto, M.; Tanahashi, M.; Rowell, R.M. Steam or Heat Fixation of Compressed Wood. Wood Fiber Sci. 2007, 25, 224–235. [Google Scholar]
- Esteves, B.; Marques, A.V.; Domingos, I.; Pereira, H. Influence of steam heating on the properties of pine (Pinus pinaster) and eucalypt (Eucalyptus globulus) wood. Wood Sci. Technol. 2007, 41, 193–207. [Google Scholar] [CrossRef]
- Mitchell, P.H. Irreversible property changes of small loblolly pine specimens heated in air, nitrogen, or oxygen. Wood Fiber Sci. 1988, 20, 320–335. [Google Scholar]
- Boonstra, M.J.; Tjeerdsma, B. Chemical analysis of heat treated softwoods. Holz als Roh- und Werkst. 2006, 64, 204–211. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).