Assessing Moisture Content and Its Mitigating Effect in an Urban Area Using the Land Surface Temperature–Vegetation Index Triangle Method
Abstract
1. Introduction
2. Materials and Methods
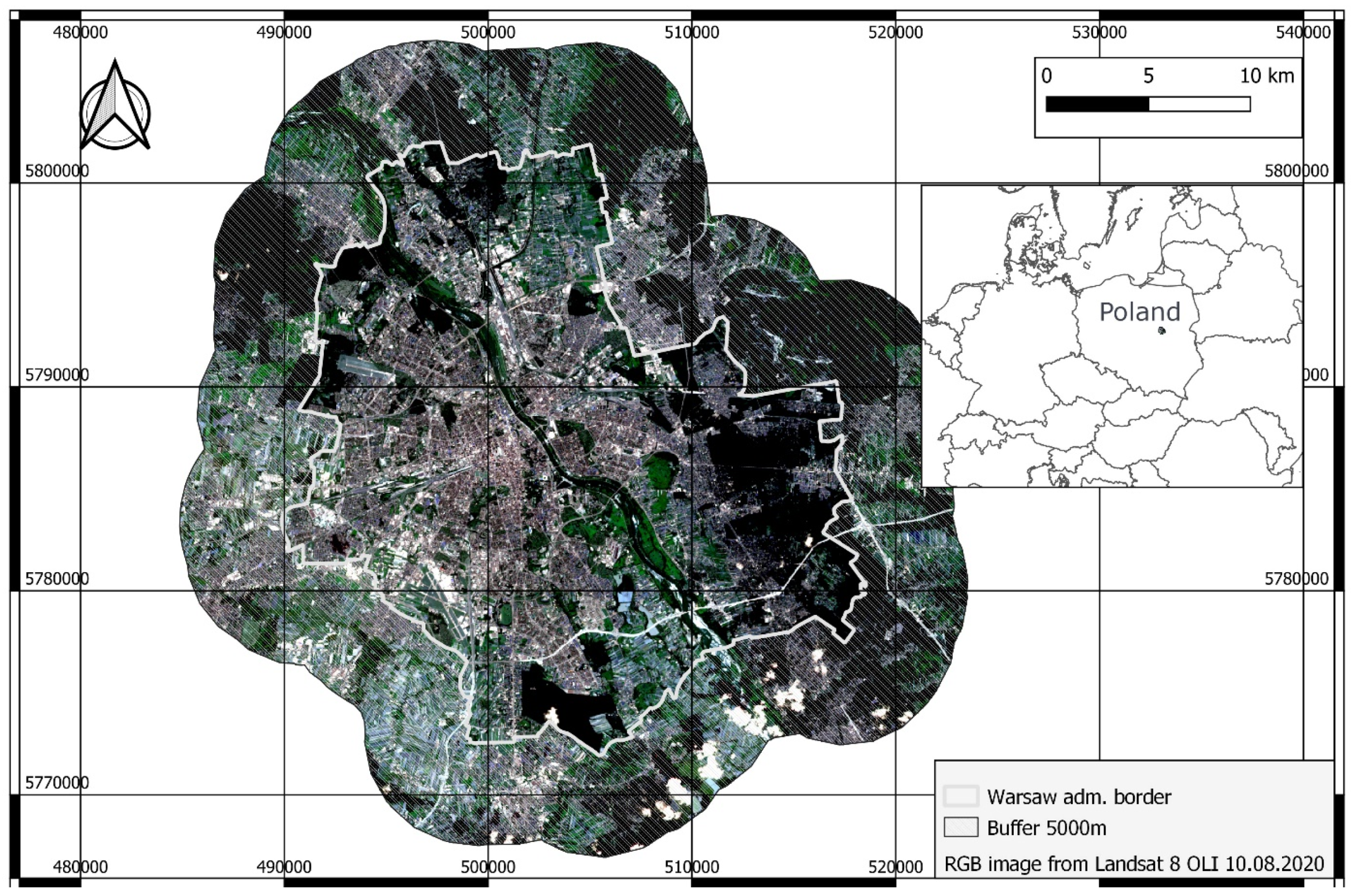
2.1. Research Area
2.2. Data
2.2.1. Landsat 8 OLI and TIRS Imagery
2.2.2. Warsaw Administrative Border
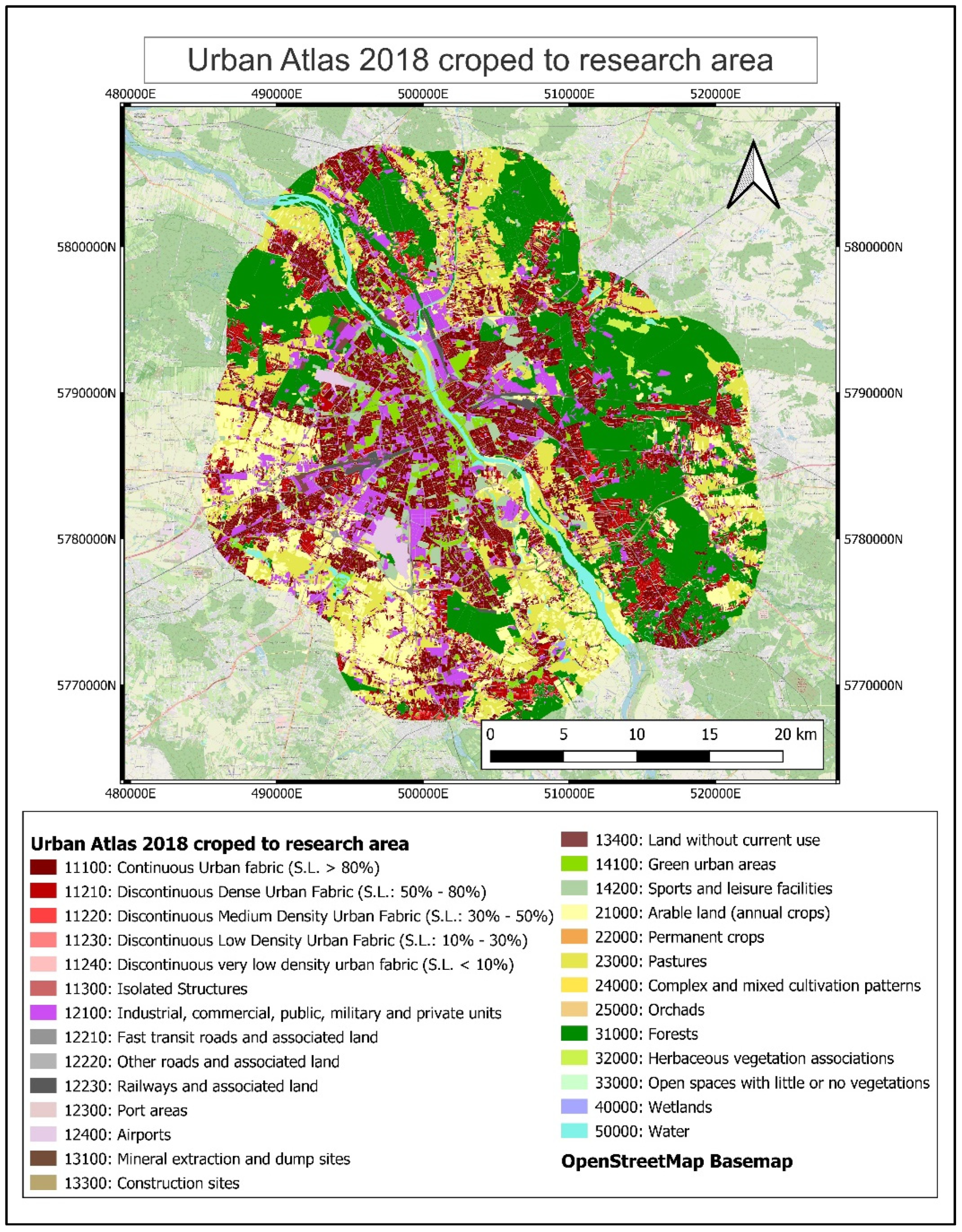
2.2.3. Urban Atlas 2018
2.3. Methods
2.3.1. Satellite Imagery Pre-Processing
2.3.2. TVDI and Quadratic TVDI
2.3.3. Image Standardization and Reclassification
3. Results
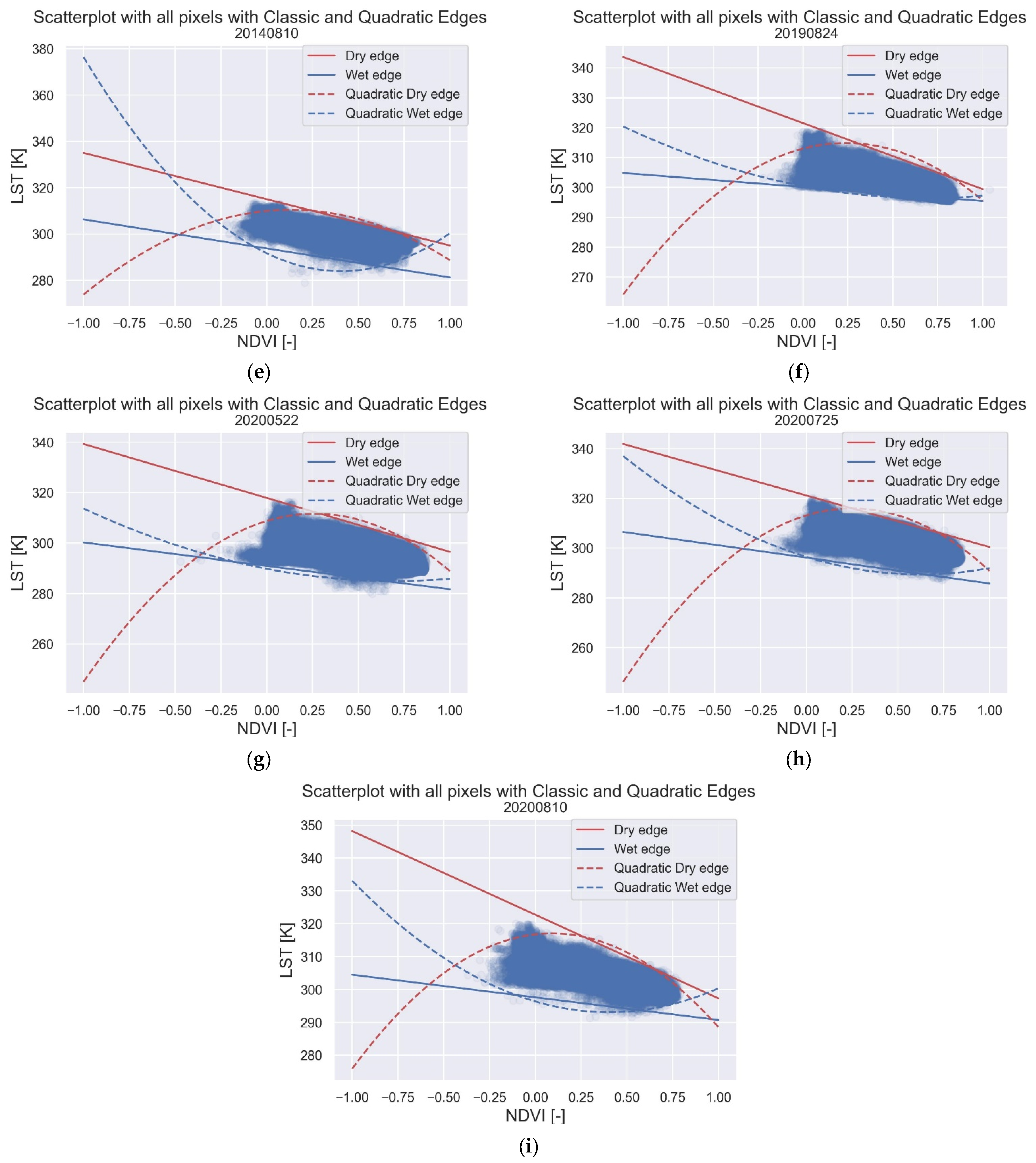
3.1. Edges Estimation
3.2. Analysis of LST-VI Scatterplots
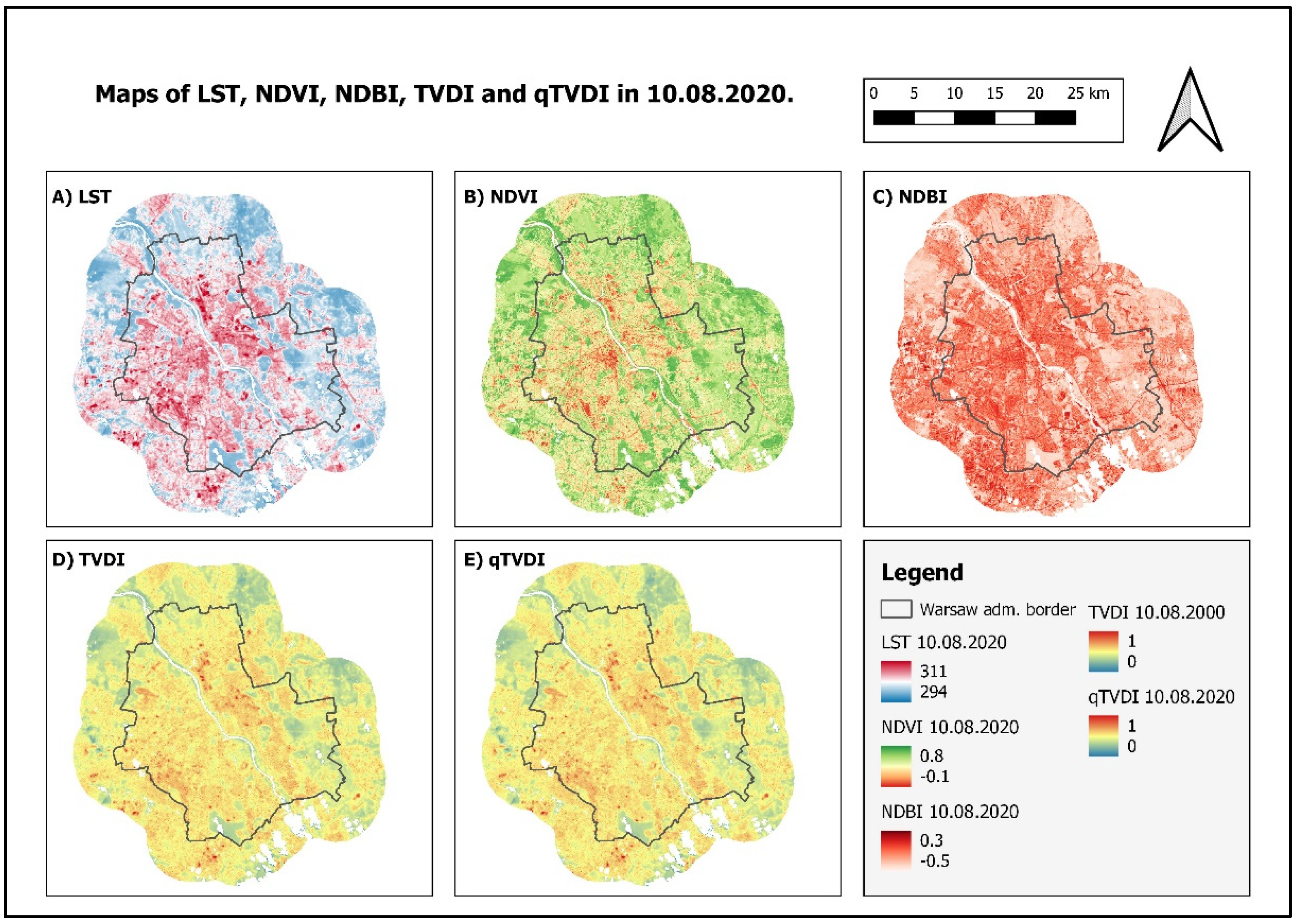
3.3. Spatial Distributions of Studied Satelite Indices over the Studied Area
3.4. Comparison of Different Classes of Coverage on the Basis of Urban Atlas 2018
3.5. Comparing TVDI and qTVDI Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- United Nations. World Population Prospects, The 2019 Revision—Volume I: Comprehensive Tables; UN: New York, NY, USA, 2019; ISBN 978-92-1-004642-8. [Google Scholar]
- Mensah, C.A. Destruction of Urban Green Spaces: A Problem Beyond Urbanization in Kumasi City (Ghana). Am. J. Environ. Prot. 2014, 3, 1. [Google Scholar] [CrossRef]
- Moreno, R.; Ojeda, N.; Azócar, J.; Venegas, C.; Inostroza, L. Application of NDVI for Identify Potentiality of the Urban Forest for the Design of a Green Corridors System in Intermediary Cities of Latin America: Case Study, Temuco, Chile. Urban For. Urban Green. 2020, 55, 126821. [Google Scholar] [CrossRef]
- Mora, C.; Dousset, B.; Caldwell, I.R.; Powell, F.E.; Geronimo, R.C.; Bielecki, C.R.; Counsell, C.W.W.; Dietrich, B.S.; Johnston, E.T.; Louis, L.V.; et al. Global Risk of Deadly Heat. Nat. Clim. Chang. 2017, 7, 501–506. [Google Scholar] [CrossRef]
- Venter, Z.S.; Brousse, O.; Esau, I.; Meier, F. Hyperlocal Mapping of Urban Air Temperature Using Remote Sensing and Crowdsourced Weather Data. Remote Sens. Environ. 2020, 242, 111791. [Google Scholar] [CrossRef]
- Bizjak, M.; Žalik, B.; Štumberger, G.; Lukač, N. Estimation and Optimisation of Buildings’ Thermal Load Using LiDAR Data. Build. Environ. 2018, 128, 12–21. [Google Scholar] [CrossRef]
- Van, T.T.; Tran, N.D.H.; Bao, H.D.X.; Phuong, D.T.T.; Hoa, P.K.; Han, T.T.N. Optical Remote Sensing Method for Detecting Urban Green Space as Indicator Serving City Sustainable Development. Proceedings 2017, 2, 140. [Google Scholar] [CrossRef]
- Haq, S.M.A. Urban Green Spaces and an Integrative Approach to Sustainable Environment. J. Environ. Prot. 2011, 02, 601–608. [Google Scholar] [CrossRef]
- Liu, Y.; Meng, Q.; Zhang, J.; Zhang, L.; Jancso, T.; Vatseva, R. An Effective Building Neighborhood Green Index Model for Measuring Urban Green Space. Int. J. Digit. Earth 2016, 9, 387–409. [Google Scholar] [CrossRef]
- Qiu, G.; Li, H.; Zhang, Q.; Chen, W.; Liang, X.; Li, X. Effects of Evapotranspiration on Mitigation of Urban Temperature by Vegetation and Urban Agriculture. J. Integr. Agric. 2013, 12, 1307–1315. [Google Scholar] [CrossRef]
- Hari, V.; Rakovec, O.; Markonis, Y.; Hanel, M.; Kumar, R. Increased Future Occurrences of the Exceptional 2018–2019 Central European Drought under Global Warming. Sci. Rep. 2020, 10, 12207. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, C.; Ma, X.; Brindha, K.; Han, Q.; Li, C.; Zhao, X. Projected Spatiotemporal Dynamics of Drought under Global Warming in Central Asia. Sustainability 2019, 11, 4421. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Quiring, S.M.; Peña-Gallardo, M.; Yuan, S.; Domínguez-Castro, F. A Review of Environmental Droughts: Increased Risk under Global Warming? Earth-Sci. Rev. 2020, 201, 102953. [Google Scholar] [CrossRef]
- Kong, D.; Gu, X.; Li, J.; Ren, G.; Liu, J. Contributions of Global Warming and Urbanization to the Intensification of Human-Perceived Heatwaves Over China. J. Geophys. Res. Atmos. 2020, 125, e2019JD032175. [Google Scholar] [CrossRef]
- Lemonsu, A.; Viguié, V.; Daniel, M.; Masson, V. Vulnerability to Heat Waves: Impact of Urban Expansion Scenarios on Urban Heat Island and Heat Stress in Paris (France). Urban Clim. 2015, 14, 586–605. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, L.-W.; Shi, J.-J.; Huang, J.-F. Soil Moisture Monitoring Based on Land Surface Temperature-Vegetation Index Space Derived from MODIS Data. Pedosphere 2014, 24, 450–460. [Google Scholar] [CrossRef]
- Farhadi, H.; Faizi, M.; Sanaieian, H. Mitigating the Urban Heat Island in a Residential Area in Tehran: Investigating the Role of Vegetation, Materials, and Orientation of Buildings. Sustain. Cities Soc. 2019, 46, 101448. [Google Scholar] [CrossRef]
- Mariani, L.; Parisi, S.G.; Cola, G.; Lafortezza, R.; Colangelo, G.; Sanesi, G. Climatological Analysis of the Mitigating Effect of Vegetation on the Urban Heat Island of Milan, Italy. Sci. Total Environ. 2016, 569–570, 762–773. [Google Scholar] [CrossRef]
- Chun, B.; Guldmann, J.-M. Impact of Greening on the Urban Heat Island: Seasonal Variations and Mitigation Strategies. Comput. Environ. Urban Syst. 2018, 71, 165–176. [Google Scholar] [CrossRef]
- Czekajlo, A.; Coops, N.C.; Wulder, M.A.; Hermosilla, T.; Lu, Y.; White, J.C.; van den Bosch, M. The Urban Greenness Score: A Satellite-Based Metric for Multi-Decadal Characterization of Urban Land Dynamics. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102210. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal Remote Sensing of Urban Climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A Simple Interpretation of the Surface Temperature/Vegetation Index Space for Assessment of Surface Moisture Status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Wang, C.; Qi, S.; Niu, Z.; Wang, J. Evaluating Soil Moisture Status in China Using the Temperature–Vegetation Dryness Index (TVDI). Can. J. Remote Sens. 2004, 30, 671–679. [Google Scholar] [CrossRef]
- Przeździecki, K.; Zawadzki, J.J. Triangle Method Modification with Second Degree Polynomial Edges Fitting in LST NDVI Scatterplot in Lignite Mine Influence Area. Remote Sens. Appl. Soc. Environ. 2020, 20, 100404. [Google Scholar] [CrossRef]
- Przeździecki, K.; Zawadzki, J.J. Impact of the Variability of Vegetation, Soil Moisture, and Building Density between City. Sustainability 2023, 15, 1274. [Google Scholar] [CrossRef]
- Districts on Land Surface Temperature, Warsaw, Poland. Sustainability 2023, 15, 1274. [CrossRef]
- Bai, J.; Yu, Y.; Di, L. Comparison between TVDI and CWSI for Drought Monitoring in the Guanzhong Plain, China. J. Integr. Agric. 2017, 16, 389–397. [Google Scholar] [CrossRef]
- Kuchcik, M.; Dudek, W.; Błażejczyk, K.; Milewski, P.; Błażejczyk, A. Two Faces to the Greenery on Housing Estates–Mitigating Climate but Aggravating Allergy. A Warsaw Case Study. Urban For. Urban Green. 2016, 16, 170–181. [Google Scholar] [CrossRef]
- Gawuc, L.; Jefimow, M.; Szymankiewicz, K.; Kuchcik, M.; Sattari, A.; Struzewska, J. Statistical Modeling of Urban Heat Island Intensity in Warsaw, Poland Using Simultaneous Air and Surface Temperature Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2716–2728. [Google Scholar] [CrossRef]
- Błażejczyk, K.; Kuchcik, M.; Dudek, W.; Kręcisz, B.; Błażejczyk, A.; Milewski, P.; Szmyd, J.; Pałczyński, C. Urban Heat Island and Bioclimatic Comfort in Warsaw. In Counteracting Urban Heat Island Effects in a Global Climate Change Scenario; Musco, F., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 305–321. ISBN 978-3-319-10424-9. [Google Scholar]
- Holzman, M.E.; Rivas, R.; Piccolo, M.C. Estimating Soil Moisture and the Relationship with Crop Yield Using Surface Temperature and Vegetation Index. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 181–192. [Google Scholar] [CrossRef]
- Department of the Interior U.S. Geological Survey. Landsat 8 (L8) Data Users Handbook; EROS: Sioux Falls, SD, USA, 2019; p. 114.
- Landsat Levels of Processing. Available online: https://www.usgs.gov/land-resources/nli/landsat/landsat-levels-processing (accessed on 8 April 2020).
- Urban Atlas 2018—Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/local/urban-atlas/urban-atlas-2018 (accessed on 30 August 2022).
- Chavez, P.S. Image-Based Atmospheric Corrections—Revisited and Improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1035. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with Erts. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Sobrino, J.A.; Jimenez-Munoz, J.C.; Soria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martinez, P. Land Surface Emissivity Retrieval from Different VNIR and TIR Sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Zha, Y.; Gao, J.; Ni, S. Use of Normalized Difference Built-up Index in Automatically Mapping Urban Areas from TM Imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Bhatti, S.S.; Tripathi, N.K. Built-up Area Extraction Using Landsat 8 OLI Imagery. GIScience Remote Sens. 2014, 51, 445–467. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, L.; Yue, H. Biparabolic NDVI-T s Space and Soil Moisture Remote Sensing in an Arid and Semi Arid Area. Can. J. Remote Sens. 2015, 41, 159–169. [Google Scholar] [CrossRef]
- Lu, Y.; Tao, H.; Wu, H. Dynamic Drought Monitoring in Guangxi Using Revised Temperature Vegetation Dryness Index. Wuhan Univ. J. Nat. Sci. 2007, 12, 663–668. [Google Scholar] [CrossRef]
- Liu, Y.; Yue, H. The Temperature Vegetation Dryness Index (TVDI) Based on Bi-Parabolic NDVI-Ts Space and Gradient-Based Structural Similarity (GSSIM) for Long-Term Drought Assessment Across Shaanxi Province, China (2000–2016). Remote Sens. 2018, 10, 959. [Google Scholar] [CrossRef]


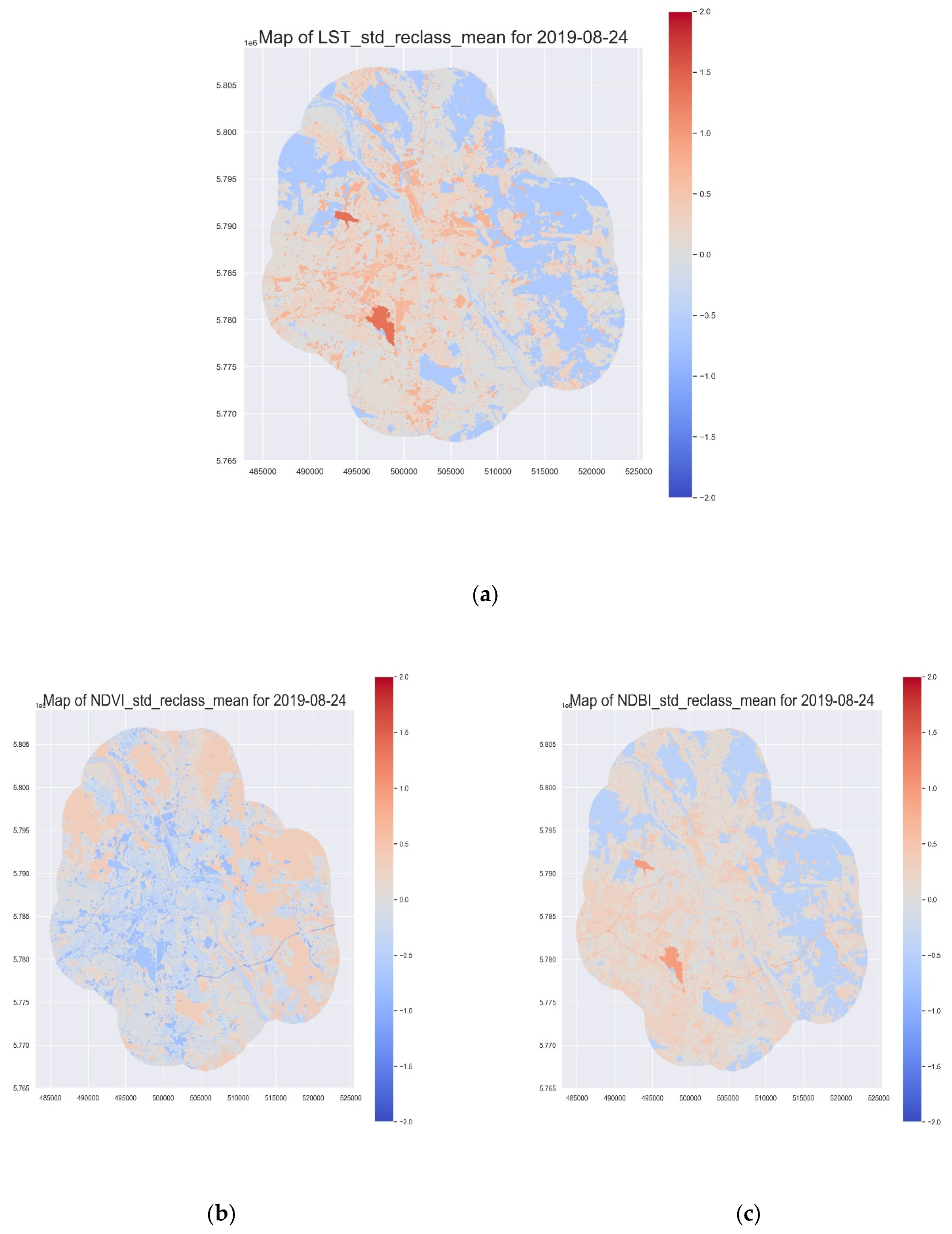
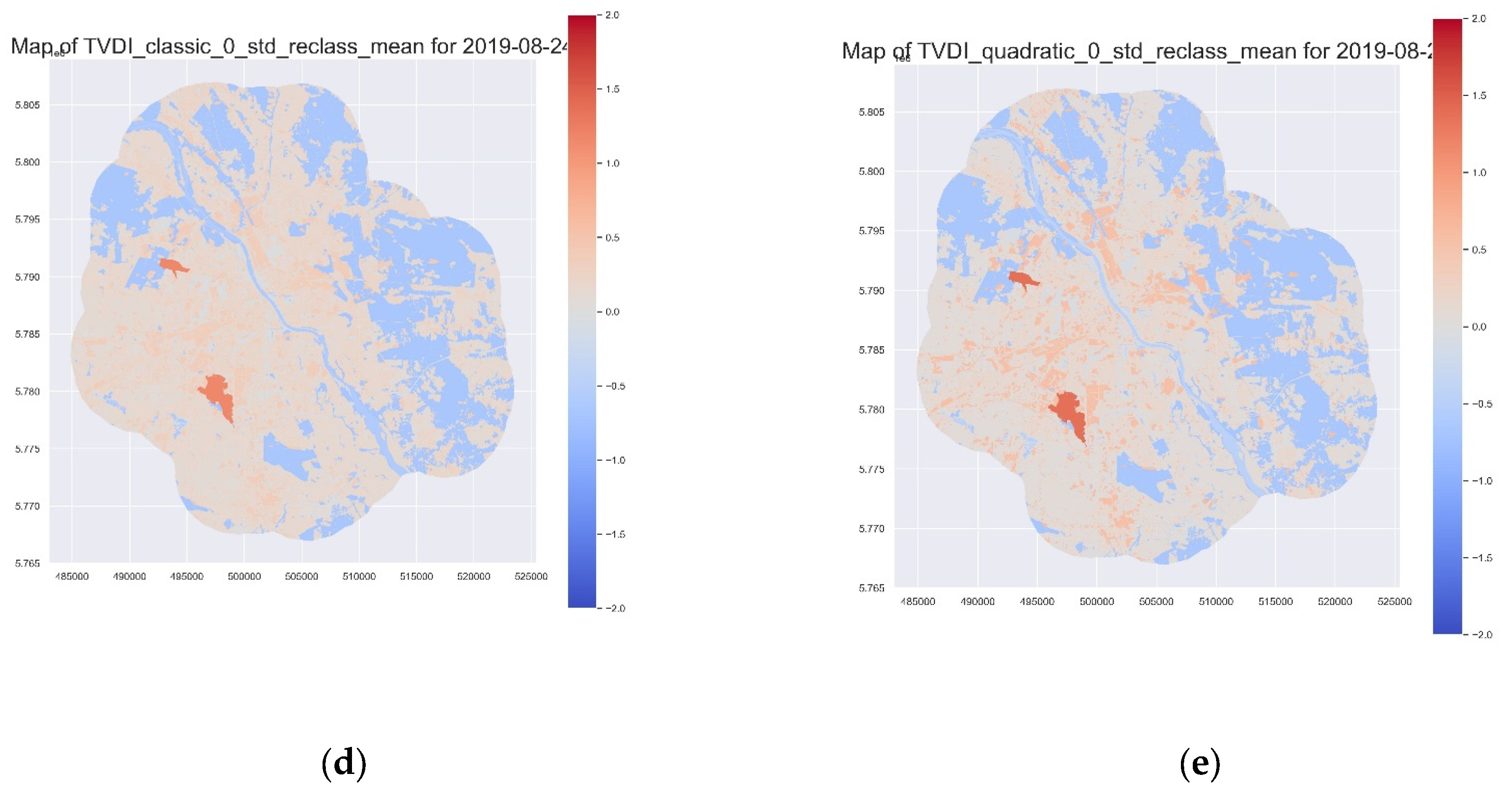
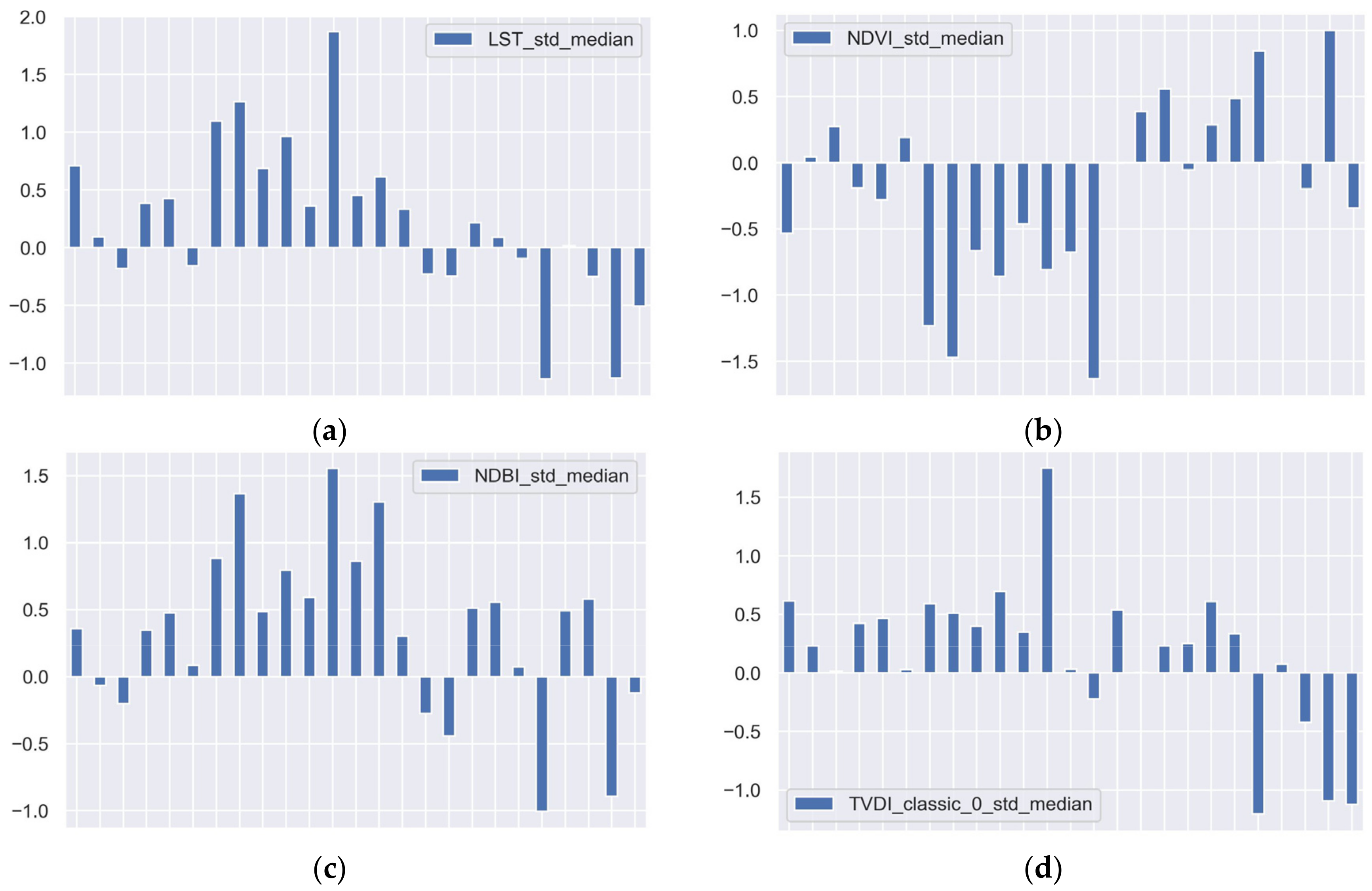
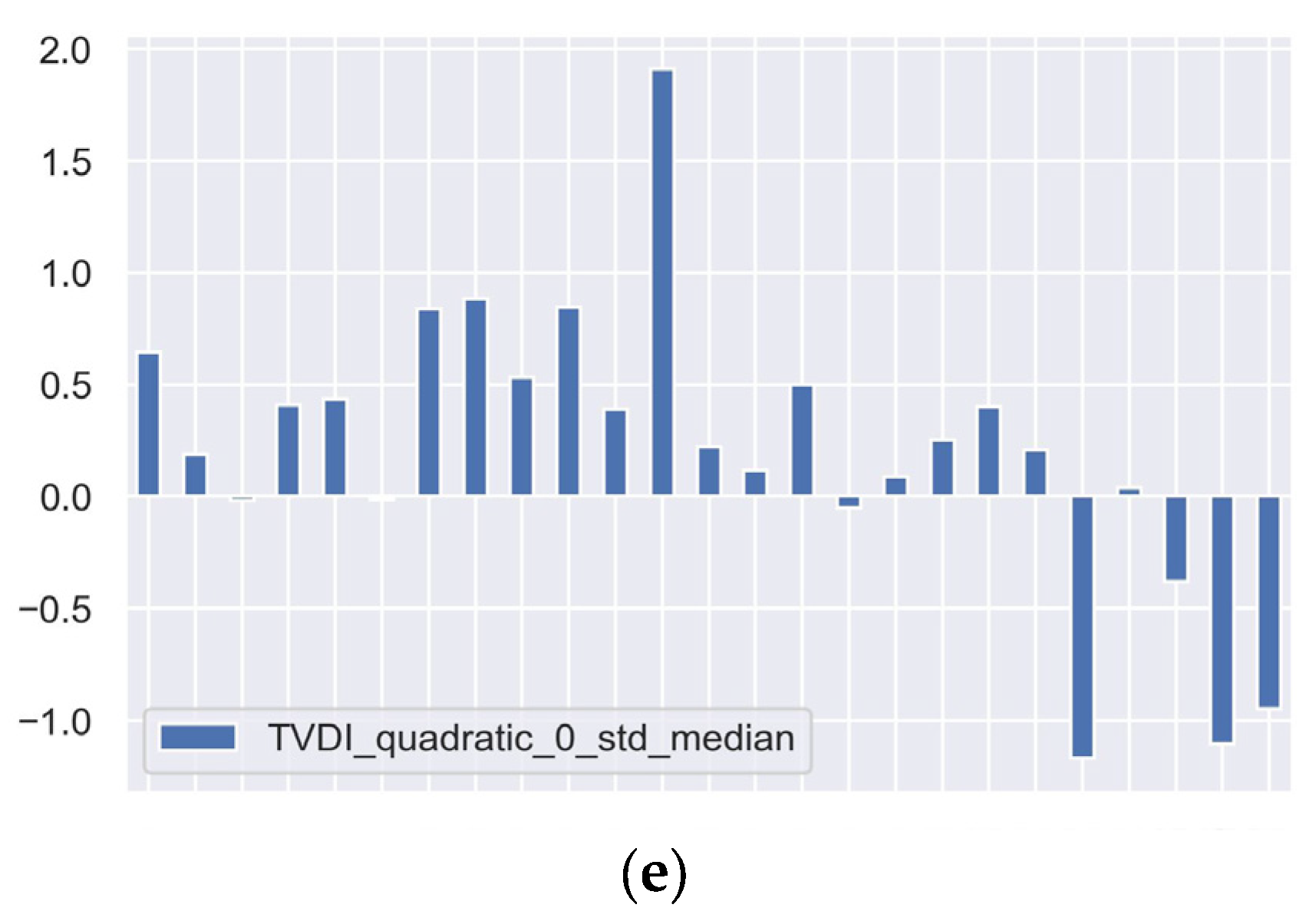

| Z Value | Z Reclassed |
|---|---|
| <−3 | −3 |
| <−3, −2 | −2 |
| <−2, −1 | −1 |
| <−1, 1> | 0 |
| 1, 2> | 1 |
| 2, 3> | 2 |
| >3 | 3 |
| Date | Classic TVDI | Quadratic TVDI | |
|---|---|---|---|
| 20 June 2013 | Dry Edge R2 | 0.88 | 0.78 |
| Wet Edge R2 | 0.97 | 0.97 | |
| 6 July 2013 | Dry Edge R2 | 0.92 | 0.83 |
| Wet Edge R2 | 0.68 | 0.90 | |
| 22 May 2014 | Dry Edge R2 | 0.82 | 0.80 |
| Wet Edge R2 | 0.34 | 0.77 | |
| 7 June 2014 | Dry Edge R2 | 0.92 | 0.80 |
| Wet Edge R2 | 0.87 | 0.90 | |
| 10 August 2014 | Dry Edge R2 | 0.95 | 0.83 |
| Wet Edge R2 | 0.34 | 0.80 | |
| 24 August 2019 | Dry Edge R2 | 0.95 | 0.77 |
| Wet Edge R2 | 0.60 | 0.81 | |
| 22 May 2020 | Dry Edge R2 | 0.91 | 0.82 |
| Wet Edge R2 | 0.53 | 0.62 | |
| 25 July 2020 | Dry Edge R2 | 0.89 | 0.72 |
| Wet Edge R2 | 0.69 | 0.85 | |
| 10 August 2020 | Dry Edge R2 | 0.95 | 0.79 |
| Wet Edge R2 | 0.49 | 0.87 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Przeździecki, K.; Zawadzki, J. Assessing Moisture Content and Its Mitigating Effect in an Urban Area Using the Land Surface Temperature–Vegetation Index Triangle Method. Forests 2023, 14, 578. https://doi.org/10.3390/f14030578
Przeździecki K, Zawadzki J. Assessing Moisture Content and Its Mitigating Effect in an Urban Area Using the Land Surface Temperature–Vegetation Index Triangle Method. Forests. 2023; 14(3):578. https://doi.org/10.3390/f14030578
Chicago/Turabian StylePrzeździecki, Karol, and Jarosław Zawadzki. 2023. "Assessing Moisture Content and Its Mitigating Effect in an Urban Area Using the Land Surface Temperature–Vegetation Index Triangle Method" Forests 14, no. 3: 578. https://doi.org/10.3390/f14030578
APA StylePrzeździecki, K., & Zawadzki, J. (2023). Assessing Moisture Content and Its Mitigating Effect in an Urban Area Using the Land Surface Temperature–Vegetation Index Triangle Method. Forests, 14(3), 578. https://doi.org/10.3390/f14030578







