Application of Temperature and Process Duration as a Method for Predicting the Mechanical Properties of Thermally Modified Timber
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Resources Needed for the Experiment
2.2. Experimental Procedure and Setup
2.3. Polynomial Form of Bending Strength Function
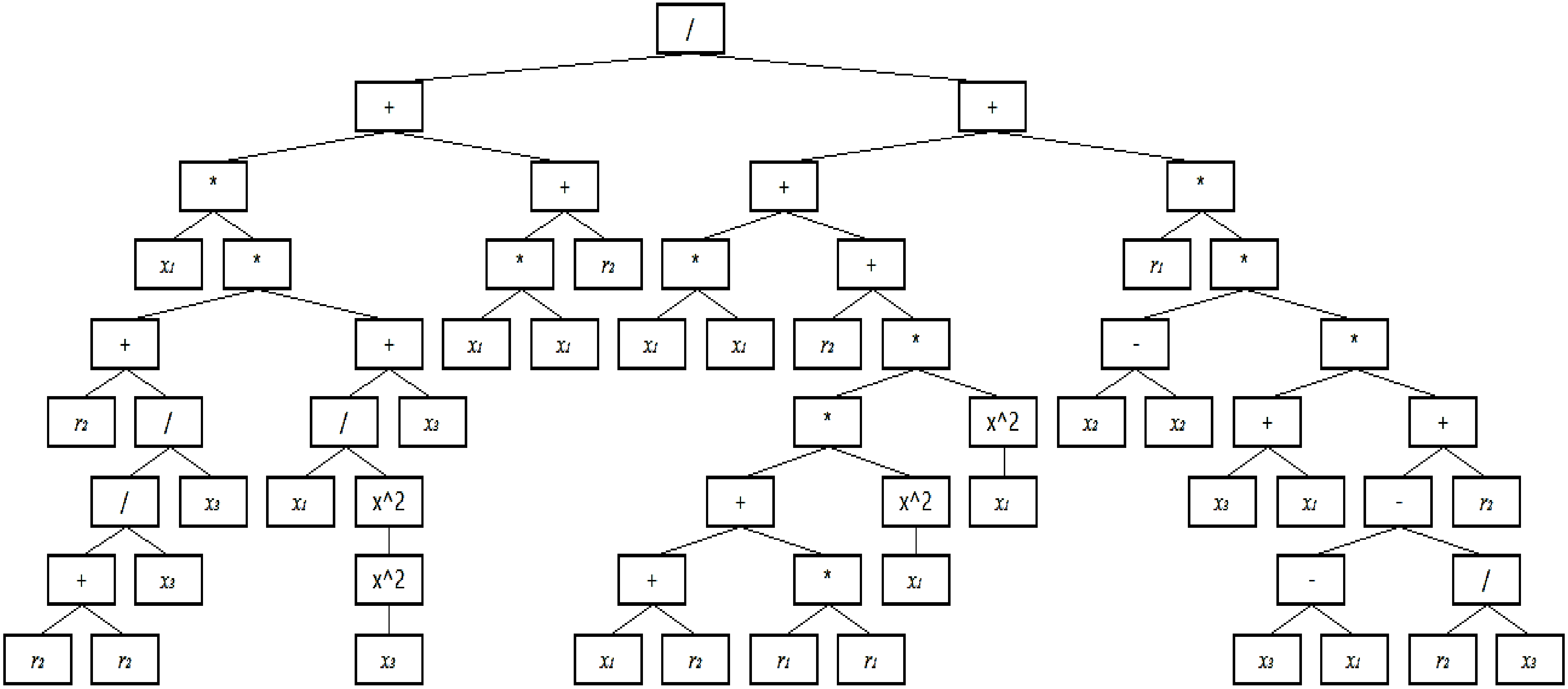
2.4. Modelling by Genetic Programming
- -
- Set of functions F = {+, −, *, /}
- -
- Input variable vectors X1, X2, X3, Set T= {T, t, ρ}—set of terminals, temperature (T), time (s), and density (ρ).
- -
- R-makes a set of randomly generated constants that can be found in the expression (r1 = 0.517009973526; r2 = 0.930670022964478)
- -
- Size of population G = 500,
- -
- Initial depth of binary wood 5,
- -
- Depth of wood at mutation and crossing 8,
- -
- Probability of crossing 90%,
- -
- Probability of mutation 5%,
- -
- Probability of reproduction 20%,
- -
- Selection method, Elite selection,
- -
- Method of initialization of mixed population ‘’ramped half and half’’
- -
- Number of iterations (evolutions).
- -
- The criterion function of chromosome goodness-of-fit testing (computer programs) is defined by multiple regressions, as follows:
2.5. Optimization of Bending Strength of Thermally Modified Wood by Classical Mathematical Analysis Method
2.6. Optimization of Bending Strength of Thermally Modified Wood by Genetic Algorithm
- -
- population size 500,
- -
- number of iterations 272,
- -
- probability of mutation 5%,
- -
- crossing probability 90%,
- -
- probability of reproduction 20%,
- -
- rank selection method.
3. Results and Discussion
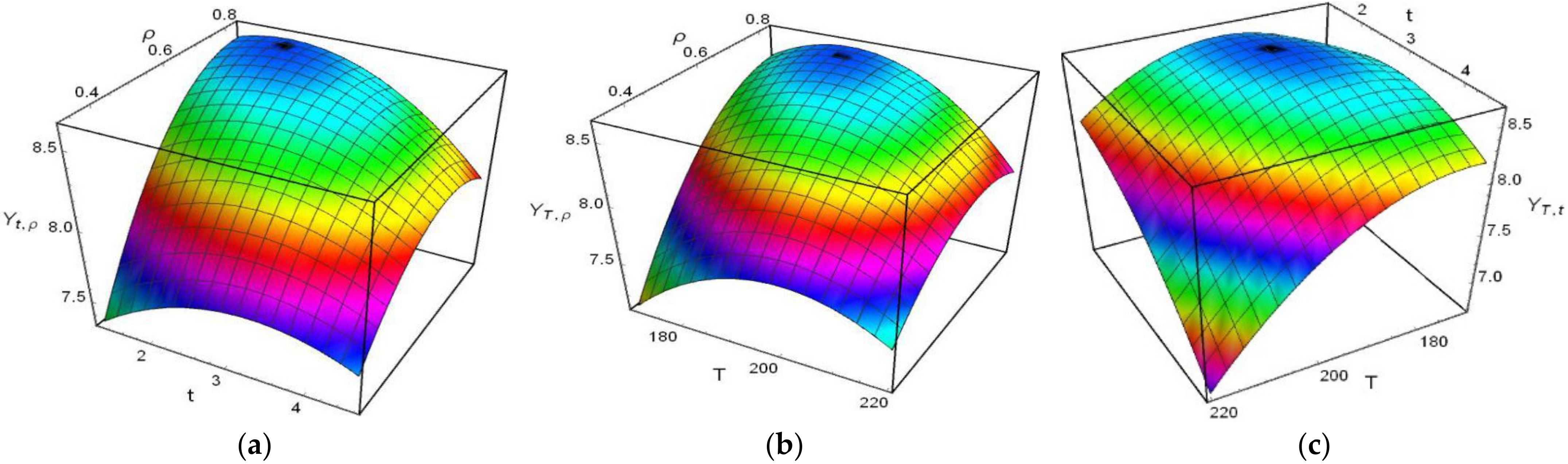
3.1. Comparative Results of Bending Strength Experiment and Modelling
3.2. The Comparison of the Optimal Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kržišnik, D.; Grbec, S.; Lesar, B.; Plavčak, D.; Šega, B.; Šernek, M.; Straže, A.; Humar, M. Durability and Mechanical Performance of Differently Treated Glulam Beams during Two Years of Outdoor Exposure. Drv. Ind. 2020, 71, 243–252. [Google Scholar] [CrossRef]
- Goli, G.; Marcon, B.; Fioravanti, M. Poplar wood heat treatment: Effect of air ventilation rate and initial moisture content on reaction kinetics, physical and mechanical properties. Wood. Sci. Technol. 2014, 48, 1303–1316. [Google Scholar] [CrossRef]
- Jones, D.; Sandberg, D.; Goli, G.; Todaro, L. Wood Modification in Europe: Processes, Products; University of Florence: Florence, Italy, 2018; Volume 41. [Google Scholar]
- Hill, C.A. Wood Modification: Chemical, Thermal and Other Processes, 3rd ed.; John Wiley & Sons, USA: Hoboken, NJ, USA, 2007; pp. 99–100. [Google Scholar]
- Esteves, B.; Carmo, J.; Nunes, L. Commercialisation and production of modified wood. In Proceedings of the European Conference on Wood Modification, Portugal, Lisbon, 10–12 March 2014. [Google Scholar]
- Kržišnik, D.; Lesar, B.; Thaler, N.; Humar, M. Micro and material climate monitoring in wooden buildings in sub-Alpine environments. Constr. Build. Mater. 2018, 166, 188–195. [Google Scholar] [CrossRef]
- Popescu, C.M.; Jones, D.; Kržišnik, D.; Humar, M. Determination of the effectiveness of a combined thermal/chemical wood modification by the use of FT-IR spectroscopy and chemometric methods. J. Mol. Struct. 2020, 1200, 127–133. [Google Scholar] [CrossRef]
- Sandberg, D.; Kutnar, A.; Karlsson, O.; Jones, D. Wood Modification Technologies Principles, Sustainability, and the Need for Innovation, 1st ed.; Taylor & Francis Group: Oxfordshire, UK, 2021. [Google Scholar]
- Reinprecht, L. Wood Deterioration, Protection and Maintenance, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Boonstra, M.J.; Blomberg, J. Semi-isostatic densification of heat-treated radiata pine. Wood Sci. Technol. 2007, 41, 607. [Google Scholar] [CrossRef] [Green Version]
- Hasanagić, R. Thermal modified wood: A critical review. In Proceedings of the RIM 2019—Development and Modernization of Production, Sarajevo, Bosnia and Herzegovina, 10–14 September 2019. [Google Scholar]
- Schmidt, O. Wood and Tree Fungi, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2006; p. 100. [Google Scholar]
- Van den Bulcke, J.; De Windt, I.; Defoirdt, N.; De Smet, J.; Van Acker, J. Moisture dynamics and fungal susceptibility of plywood. Int. Biodeterior. Biodegrad. 2011, 65, 708–716. [Google Scholar] [CrossRef] [Green Version]
- Eaton, R.A.; Hale, M.D.C. Wood: Decay, Pests, and Protection; Chapman & Hall: London, UK; New York, NY, USA,, 1993. [Google Scholar]
- Tjeerdsma, B.F.; Stevens, M.; Militz, H. Durability Aspects of Hydrothermal Treated Wood; International Research Group on Wood Preservation: Stockholm, Sweden, 2000. [Google Scholar]
- Boonstra, M.J.; Tjeerdsma, B. Chemical analysis of heat treated softwoods. Holz Roh- Werkst. 2006, 64, 204–211. [Google Scholar] [CrossRef]
- Hill, C.A.S. Wood modification: An update. BioResources 2011, 2, 918–919. [Google Scholar]
- Zauer, M.; Kowalewski, A.; Sproßmann, R.; Stonjek, H.; Wagenführ, A. Thermal modification of European beech at relatively mild temperatures for the use in electric bass guitars. Eur. J. Wood Wood Prod. 2016, 74, 43–48. [Google Scholar] [CrossRef]
- Korošec, R.C.; Lavrič, B.; Rep, G.; Pohleven, F.; Bukovec, P. Thermogravimetry as a possible tool for determining modification degree of thermally treated Norway spruce wood. J. Therm. Anal. Calorim. 2019, 98, 189–195. [Google Scholar] [CrossRef]
- Tjeerdsma, B.F.; Boonstra, M.; Pizzi, A.; Tekely, P.; Militz, H. Characterisation of thermally modified wood: Molecular reasons for wood performance improvement. Holz Roh- Werkst. 1998, 56, 149–153. [Google Scholar] [CrossRef]
- Brito, A.F.; Calonego, F.W.; Bond, B.H.; Severo, E.T.D. Color changes, EMC, and biological resistance of thermally modified yellow poplar. Wood Fiber Sci. 2018, 50, 439–446. [Google Scholar] [CrossRef]
- Kozakiewicz, P.; Drozdzek, M.; Laskowska, A.; Grześkiewicz, M.; Bytner, O.; Radomski, A.; Zawadzki, J. Effects of thermal modification on selected physical properties of sapwood and heartwood of black poplar (Populus nigra L.). BioResources 2019, 14, 8391–8404. [Google Scholar]
- Meyer-Veltrup, L.; Brischke, C.; Alfredsen, G.; Humar, M.; Flæte, P.O.; Isaksson, T.; Brelid, P.L.; Westin, M.; Jermer, J. The combined effect of wetting ability and durability on outdoor performance of wood: Development and verification of a new prediction approach. Wood Sci. Technol. 2017, 51, 615–637. [Google Scholar] [CrossRef]
- Shuang-Yan, Z.; Fei, B.-H.; Yu, Y.; Cheng, H.-T.; Wang, C.-G. Effect of the amount of lignin on tensile properties of single wood fibers. For. Sci. Pract. 2013, 15, 56–60. [Google Scholar]
- Militz, H. Thermal Treatment of Wood: European Processes and Their Background; International Research Group on Wood Preservation: Stockholm, Sweden, 2000. [Google Scholar]
- Rahimi, S.; Singh, K.; DeVallance, D. Effect of different hydrothermal treatments (steam and hot compressed water) on physical properties and drying behavior of yellow-poplar (Liriodendron tulipifera). For. Prod. J. 2019, 69, 42–52. [Google Scholar] [CrossRef]
- Le, X.P.; Satoshi, S.; Yukie, S. Effects of heat treatment on brittleness of Styrax tonkinensis wood. J. Wood Sci. 2007, 53, 181–186. [Google Scholar]
- Esteves, B.M.; Pereira, M.H. Wood modification by heat treatment: A review. BioResources 2008, 4, 370–404. [Google Scholar] [CrossRef]
- Kaboorani, A.; Englund, K.R. Water sorption and mechanical performance of preheated wood/thermoplastic composites. J. Compos. Mater. 2010, 45, 1423–1433. [Google Scholar] [CrossRef]
- Gokhan, G.; Suleyman, K.; Deniz, A.; Ilter, B. The density, compression strength and surface hardness of heat treated hornbeam (Carpinus betulus L.) wood. Maderas Cienc. Tecnol. 2009, 1, 61–70. [Google Scholar]
- Otávio, J.; Brito, J.; Nivaldo, G.; Geraldo, B.; Júnior, A.; Pessoa, M.; Paulo, M.H. The density and shrinkage behavior of Eucalyptus grandis wood suubmitted to difrent temperatures of termoretification. Cerne 2015, 12, 182–188. [Google Scholar]
- Hasanagić, R.; Sauradipta, G.; Bajramović, E.; Hasanagić, A. Mechanical properties changes in fir wood (abies sp.), linden wood (tilia sp.), and beech wood (fagus sp.) subjected to various thermal modification process conditions. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1208, 012025. [Google Scholar] [CrossRef]
- Bilgin, I.; Abdullah, B. Effects of industrial heat treatment on some physical and mechanical properties of iroko wood. Drvna industrija 2017, 68, 229–2369. [Google Scholar]
- Vasiliki, K.; Barboutis, I.; Vasileios, V. Influence of thermal treatment on mechanical strength of Scots pine (Pinus sylvestris L.) wood. Wood Res. 2014, 59, 373–378. [Google Scholar]
- Jurković, M. Mathematical Modelling and Optimization of Machining Processes, 2nd ed.; Faculty of Engineering, University of Rijeka: Rijeka, Croatia, 2006. [Google Scholar]
- Jurković, M. Matematičko Modeliranje Nžinjerskih Procesa i Sistema, 1st ed.; Univerzitet u Bihaću-Tehnički fakultet: Bihać, Bosnia & Herzegovina, 1999. [Google Scholar]
- Dean, A.; Morris, M.; Stufken, J.; Bingham, D. Handbook of Design and Analysis of Experiments, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2015; p. 591. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- EN 408. In Timber and Glued Laminated Timber-Determination of Some Physical and Mechanical Properties.; Swedish Institute for Standards: Stockholm, Sweden, 1995.
- EN 789; Timber structures—Test methods—Determination of Mechanical Properties of Wood-Based Panels; European Committee for Standardization: Brussels, Belgium, 2004.
- Jenkel, C.; Leichsenring, F.; Graf, W.; Kaliske, M. Engineering Structures, Stochastic modelling of uncertainty in timber engineering. Elsevie 2015, 99, 296–310. [Google Scholar]
- Hodžić, A.; Hasanagić, R. Matematičko modeliranje sile loma na istezanje masivnog drveta produženog sa zupčastim vezom. In Proceedings of the Zbornik Međunarodnog Kongresa o Procesnoj Industriji—Procesing, Beograd, Srbija; 2017. [Google Scholar]
- Hasanagić, R.; Hodžić, A.; Jurković, M. Modelling and optimization of tensile break force of solid wood elements lengthened by finger joint. J. Adhes. Sci. Technol. 2020, 34, 1013–1027. [Google Scholar] [CrossRef]
- Hasanagić, R.; Hodžić, A.; Bjelić, A. Mathematical modelling of the surface roughness in orthogonal cutting of the massive wood. Wood Mater. Sci. Eng. 2019, 16, 74–80. [Google Scholar] [CrossRef]
- Hrnjica, B.; Danandeh, M.A. Optimized Genetic Programming Applications: Emerging Research and Opportunities, 1st ed.; IGI Global: Hershey, PA, USA, 2018; p. 190. [Google Scholar]
- Hasanagić, R. Modeling and prediction of fracture force to tighten solid wood elements by genetic programming. Tehnika 2018, 73, 653–657. [Google Scholar] [CrossRef]
- Gondia, A.; Ezzeldin, M.; El-Dakhakhni, W. Mechanics-guided genetic programming expression for shear-strength prediction of squat reinforced concrete walls with boundary elements. J. Struct. Eng. 2020, 11, 04020223. [Google Scholar] [CrossRef]
- Rep, G.; Pohleven, F.; Kosmerl, S. Development of the Industrial kiln for Thermal Wood Modification by a Procedure with an Initial Vacuum and Commercialisation of Modified Silvapro Wood. In Proceedings of the 6th European Conference on Wood Modification, Ljubljana, Slovenia, 17–18 September 2012; Jones, M.H., Militz, M.P.D., Petrič, H., Pohleven, M.F., Eds.; Slovenia University of Ljubljana: Ljubljana, Slovenia, 2012. [Google Scholar]
- BAS EN 408+A1. In Timber Structures-Structural Timber and Glued Laminated Timber-Determination of Some Physical and Mechanical Properties; Institute for Standardization BIH: Sarajevo, Bosnia and Herzegovina, 2013.
- Altgen, M.; Welzbacher, C.; Humar, M.; Willems, W.; Militz, H. Bestimmung der Behandlungsqualitat von Thermoholz mithilfe von Schnellverfahren. Holztechnologie 2012, 6, 44–49. [Google Scholar]



| Parameters/Levels | Lowest | Low | Centre | High | Highest |
|---|---|---|---|---|---|
| Coding–classical experimental design | −1.682 | −1 | 0 | 1 | 1.682 |
| Temperature (°C) X1 = T | 170 | 180 | 195 | 210 | 220 |
| Process duration (min) X2 = t | 78 | 120 | 180 | 240 | 276 |
| Density (g/cm3) X3 = ρ | 0.330 | 0.430 | 0.580 | 0.730 | 0.830 |
| Coding-orthogonal array (Xi) | −1.682 | −1 | 0 | 1 | 1.682 |
| N Species * | T °C | t min | g/cm3 | X0 | X1 | X2 | X3 | X1X2 | X1X3 | X2X3 | X1X2X3 | X12 | X22 | X32 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 Fir | 180 | 120 | 0.43 | 1 | −1 | −1 | −1 | 1 | 1 | 1 | −1 | 1 | 1 | 1 |
| 2 Fir | 210 | 120 | 0.43 | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | 1 |
| 3 Fir | 180 | 240 | 0.43 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | 1 | 1 |
| 4 Fir | 210 | 240 | 0.43 | 1 | 1 | 1 | −1 | 1 | −1 | −1 | −1 | 1 | 1 | 1 |
| 5 Beech | 180 | 120 | 0.73 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 | 1 | 1 | 1 |
| 6 Beech | 210 | 120 | 0.73 | 1 | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | 1 | 1 |
| 7 Beech | 180 | 240 | 0.73 | 1 | −1 | 1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | 1 |
| 8 Beech | 210 | 240 | 0.73 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9–14 Linden | 195 | 180 | 0.58 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 Linden | 170 | 180 | 0.58 | 1 | −α | 0 | 0 | 0 | 0 | 0 | 0 | (−α)2 | 0 | 0 |
| 16 Linden | 220 | 180 | 0.58 | 1 | α | 0 | 0 | 0 | 0 | 0 | 0 | α2 | 0 | 0 |
| 17 Linden | 195 | 78 | 0.58 | 1 | 0 | −α | 0 | 0 | 0 | 0 | 0 | 0 | (−α)2 | 0 |
| 18 Linden | 195 | 276 | 0.58 | 1 | 0 | α | 0 | 0 | 0 | 0 | 0 | 0 | α2 | 0 |
| 19 Fir | 195 | 180 | 0.33 | 1 | 0 | 0 | −α | 0 | 0 | 0 | 0 | 0 | 0 | (−α)2 |
| 20 Beech | 195 | 180 | 0.83 | 1 | 0 | 0 | α | 0 | 0 | 0 | 0 | 0 | 0 | α2 |
| N * | Experimental Results Y [N] | Standard Deviations | Results Per Models | |
|---|---|---|---|---|
| Stochastic Model(YR) [N] | Genetic Model(GP) [N] | |||
| 1 | 2665 | 2.05 | 2522 | 2569 |
| 2 | 3081 | 4.21 | 2830 | 3146 |
| 3 | 2873 | 3.40 | 2887 | 2928 |
| 4 | 2164 | 4.02 | 2359 | 1889 |
| 5 | 6150 | 6.10 | 5183 | 6438 |
| 6 | 5299 | 4.00 | 4165 | 5053 |
| 7 | 5110 | 7.06 | 4394 | 4880 |
| 8 | 2653 | 6.47 | 2210 | 2977 |
| 9 | 4403 | 5.32 | 4459 | 4283 |
| 10 | 4201 | 4.11 | 4237 | 4461 |
| 11 | 4856 | 5.15 | 4396 | 4621 |
| 12 | 4438 | 4.06 | 4559 | 4161 |
| 13 | 4606 | 3.27 | 4379 | 4282 |
| 14 | 4394 | 5.84 | 4959 | 4299 |
| 15 | 4015 | 3.11 | 3695 | 4054 |
| 16 | 2200 | 5.04 | 2283 | 2602 |
| 17 | 4123 | 3.75 | 4220 | 4628 |
| 18 | 2976 | 4.10 | 2774 | 2905 |
| 19 | 2761 | 5.06 | 2293 | 2897 |
| 20 | 3933 | 6.24 | 4519 | 4502 |
| Method | Optimal TM Parameters | ||
|---|---|---|---|
| T (°C) | t (min) | ρ (g/cm3) | |
| Classic mathematical analysis | 193 | 126 | 0.780 |
| Genetic algorithm (GA) | 197 | 121 | 0.728 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, D.; Hasanagić, R.; Hodžić, A.; Kržišnik, D.; Hodžić, D.; Bahmani, M.; Petrič, M.; Humar, M. Application of Temperature and Process Duration as a Method for Predicting the Mechanical Properties of Thermally Modified Timber. Forests 2022, 13, 217. https://doi.org/10.3390/f13020217
Chu D, Hasanagić R, Hodžić A, Kržišnik D, Hodžić D, Bahmani M, Petrič M, Humar M. Application of Temperature and Process Duration as a Method for Predicting the Mechanical Properties of Thermally Modified Timber. Forests. 2022; 13(2):217. https://doi.org/10.3390/f13020217
Chicago/Turabian StyleChu, Demiao, Redžo Hasanagić, Atif Hodžić, Davor Kržišnik, Damir Hodžić, Mohsen Bahmani, Marko Petrič, and Miha Humar. 2022. "Application of Temperature and Process Duration as a Method for Predicting the Mechanical Properties of Thermally Modified Timber" Forests 13, no. 2: 217. https://doi.org/10.3390/f13020217
APA StyleChu, D., Hasanagić, R., Hodžić, A., Kržišnik, D., Hodžić, D., Bahmani, M., Petrič, M., & Humar, M. (2022). Application of Temperature and Process Duration as a Method for Predicting the Mechanical Properties of Thermally Modified Timber. Forests, 13(2), 217. https://doi.org/10.3390/f13020217










