Hybrid Method for Fitting Nonlinear Height–Diameter Functions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Overview
2.2. Database Structure
2.3. Fitting Approach
2.3.1. Nonlinear Regression Models
| Parameter | ID | Model Reference | Model |
|---|---|---|---|
| 2 | 1 | Meyer 1 | |
| 2 | Burkhart 2 | ||
| 3 | 3 | Monomolecular 1 | |
| 4 | Mitcherlich 1 | ||
| 5 | Gompertz 1 | ||
| 6 | Logistic 3 | ||
| 7 | Chapman-Richards 4 | ||
| 8 | Bailey 2 | ||
| 4 | 9 | Von Bertalanffy 1 | |
| 10 | Bailey 2 | ||
| 11 | Zeide 2 | ||
| 12 | Richards 2 |
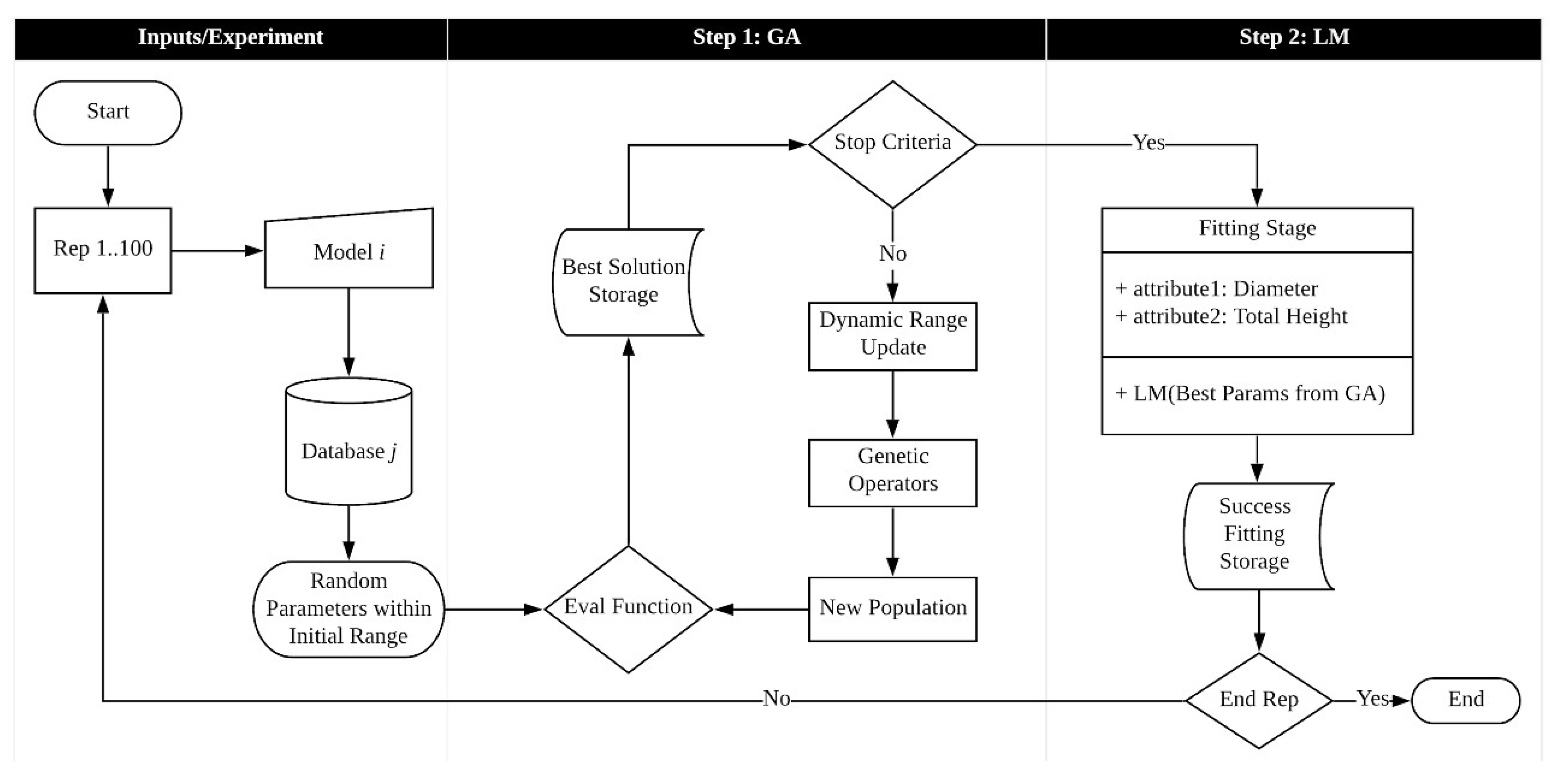
2.3.2. Hybrid Method
- Step 1: Genetic Dynamic Approach
- (1)
- Selection Operator: This operator plays the role of the most adapted individual selector, similar to Darwin’s theory of biological selection, which asserts that the most adapted individual has the greatest probability of survival. Computationally, this is implemented by a random search of the population, creating a new set and selecting individuals according to their fitness values [37]. Tournament selection (Equation (2)) was chosen to control the diversity losses [38], selecting two individuals (f(x*) and f(y*)) from the pool of parents (population). In order to obtain the most adapted parents, this operator chooses the best value of fitness in every defined pair. Thereafter, the best individuals are selected to crossover proceedings.
- (2)
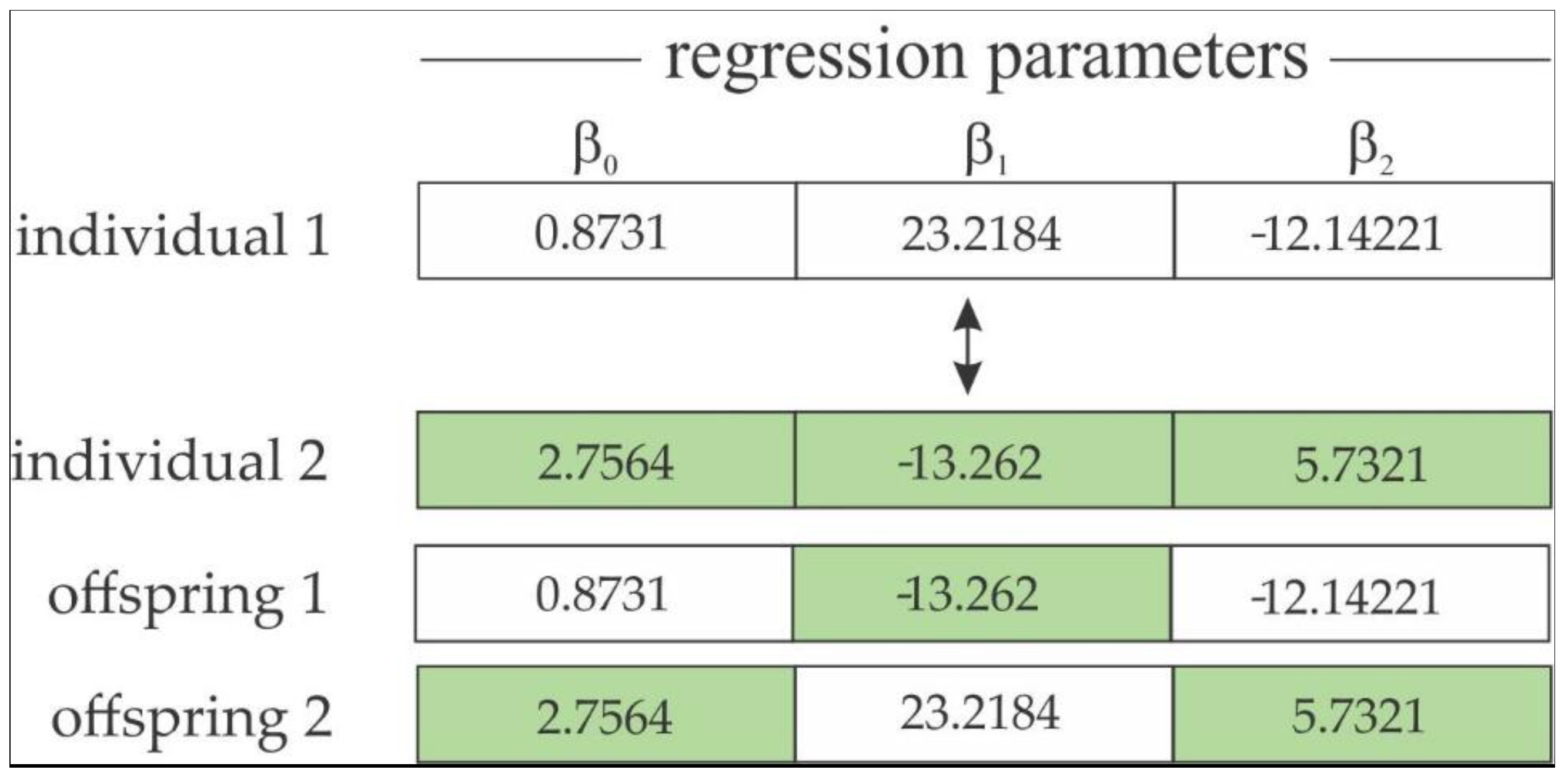
- Crossover Operator: This is an important operator of the GA, providing the exploitation phase of the solution search [55]. Similar to biology, the crossover is responsible for exchanging genes from parents to their offspring, producing phenotypic variability, i.e., a combination of parameter estimates from selected parents with the aim of producing offspring containing characteristics of both best selected individuals in the selection operator. The crossover operator has one swapping gene for each selected pair of parents (Figure 4).
- (3)
- Mutation Operator: According to [55], mutation performs solution exploration, increasing the diversity of the population. This operator imitates biological mutation as described in Darwin’s theory, which says that there are some “random changes” in an individual’s characteristics that if these changes are skill-increasing, they will be passed from parents to offspring, maintaining differences from the other individuals (diversity). Mutation maintains genetic population diversity and provides an escape mechanism from a local optima space [28]. Computationally, mutation works by randomly selecting a parameter and a new value for this parameter according to the interval R described above. We applied a 60% random mutation rate for each iteration. We chose a high mutation rate for this study to account for the lack of previous information about the datasets and the mathematical properties of the loss function (nonlinear models).
- Step 2: Statistical Approach
2.4. Assessment of the Hybrid Approach
3. Results
3.1. Hybrid Modeling Assessment
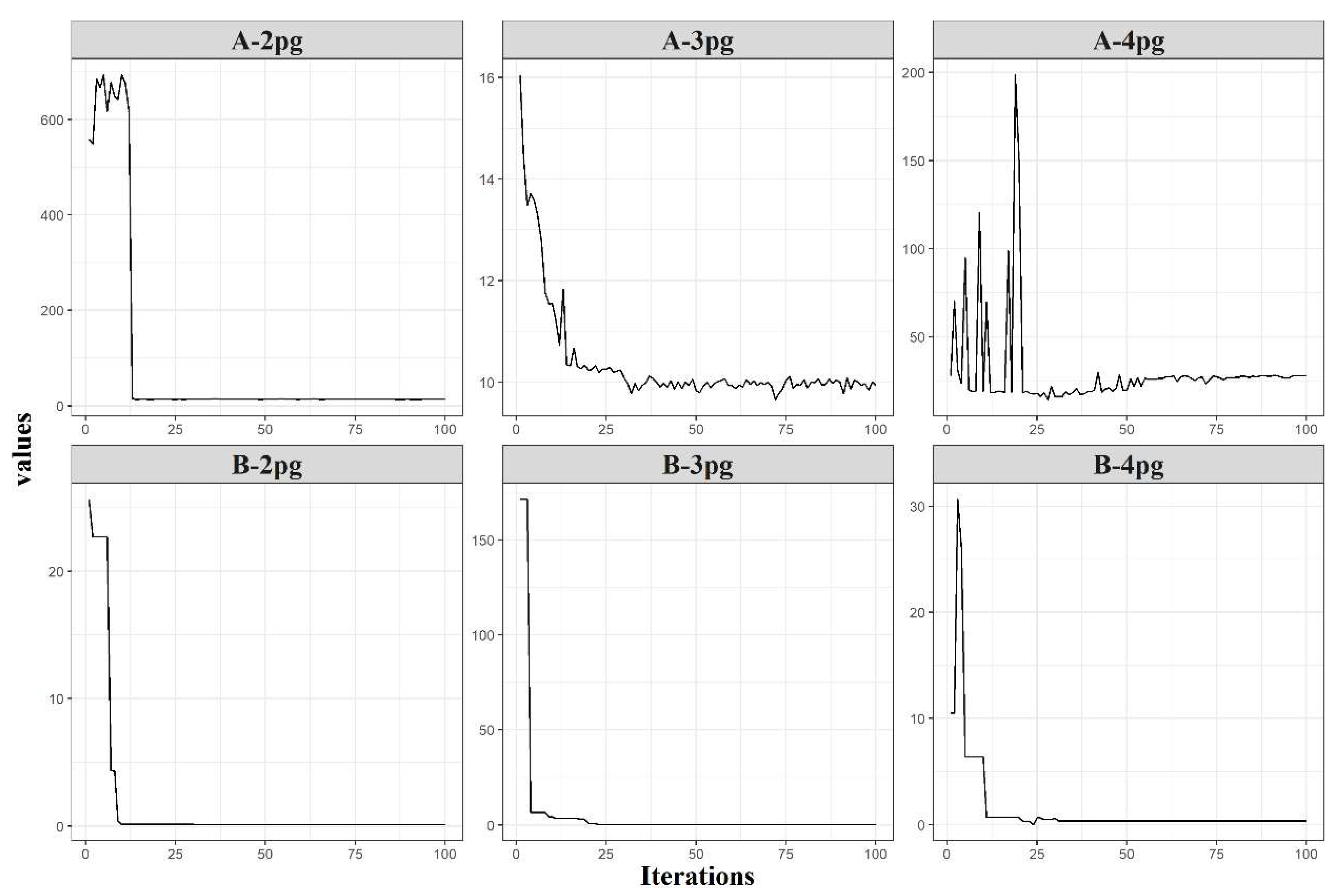
3.1.1. Genetic Algorithm Approach
3.1.2. Hybrid Approach
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fischer, C.; Schönfelder, E. A Modified Growth Function with Interpretable Parameters Applied to the Age–Height Relationship of Individual Trees. Can. J. For. Res. 2017, 47, 166–173. [Google Scholar] [CrossRef]
- Huang, S.; Titus, S.J.; Wiens, D.P. Comparison of Nonlinear Height–Diameter Functions for Major Alberta Tree Species. Can. J. For. Res. 1992, 22, 1297–1304. [Google Scholar] [CrossRef]
- Fang, Z.; Bailey, R.L. Height-Diameter Models for Tropical Forests on Hainan Island in Southern China. For. Ecol. Manag. 1998, 110, 315–327. [Google Scholar] [CrossRef]
- Mehtätalo, L.; de-Miguel, S.; Gregoire, T.G. Modeling Height-Diameter Curves for Prediction. Can. J. For. Res. 2015, 45, 826–837. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Sun, H.; Sharma, R.P.; Lei, Y.; Zhang, H.; Tang, S. Nonlinear Mixed-Effects Crown Width Models for Individual Trees of Chinese Fir (Cunninghamia Lanceolata) in South-Central China. For. Ecol. Manag. 2013, 302, 210–220. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Hao, K.; Tang, S. A Generalized Interregional Nonlinear Mixed-Effects Crown Width Model for Prince Rupprecht Larch in Northern China. For. Ecol. Manag. 2017, 389, 364–373. [Google Scholar] [CrossRef]
- Bianchi, S.; Hale, S.; Cahalan, C.; Arcangeli, C.; Gibbons, J. Light-Growth Responses of Sitka Spruce, Douglas Fir and Western Hemlock Regeneration under Continuous Cover Forestry. For. Ecol. Manag. 2018, 422, 241–252. [Google Scholar] [CrossRef] [Green Version]
- Rayner, M.E. Evaluation of Six Site Classifications for Modelling Timber Yield of Regrowth Karri (Eucalyptus Diversicolor F. Muell.). For. Ecol. Manag. 1992, 54, 315–336. [Google Scholar] [CrossRef]
- Fontes, L. Modelling Dominant Height Growth of Douglas-Fir (Pseudotsuga Menziesii (Mirb.) Franco) in Portugal. Forestry 2003, 76, 509–523. [Google Scholar] [CrossRef] [Green Version]
- Lekwadi, S.O.; Nemesova, A.; Lynch, T.; Phillips, H.; Hunter, A.; Mac Siúrtáin, M. Site Classification and Growth Models for Sitka Spruce Plantations in Ireland. For. Ecol. Manag. 2012, 283, 56–65. [Google Scholar] [CrossRef]
- Shvets, V.; Zeide, B. Investigating Parameters of Growth Equations. Can. J. For. Res. 1996, 26, 1980–1990. [Google Scholar] [CrossRef]
- Mønness, E. The Power-Normal Distribution: Application to Forest Stands. Can. J. For. Res. 2011, 41, 707–714. [Google Scholar] [CrossRef] [Green Version]
- Graybill, F.A.; Iyer, H.K. Regression Analysis: Concepts and Applications; Duxbury Press: London, UK, 1994. [Google Scholar]
- Pienaar, L.V.; Turnbull, K.J. The Chapman-Richards Generalization of Von Bertalanffy’s Growth Model for Basal Area Growth and Yield in Even-Aged Stands. For. Sci. 1973, 19, 2–22. [Google Scholar]
- Paine, C.E.T.; Marthews, T.R.; Vogt, D.R.; Purves, D.; Rees, M.; Hector, A.; Turnbull, L.A. How to Fit Nonlinear Plant Growth Models and Calculate Growth Rates: An Update for Ecologists. Methods Ecol. Evol. 2012, 3, 245–256. [Google Scholar] [CrossRef]
- Tashkova, K.; Šilc, J.; Atanasova, N.; Džeroski, S. Parameter Estimation in a Nonlinear Dynamic Model of an Aquatic Ecosystem with Meta-Heuristic Optimization. Ecol. Modell. 2012, 226, 36–61. [Google Scholar] [CrossRef]
- Pedersen, M.W.; Berg, C.W.; Thygesen, U.H.; Nielsen, A.; Madsen, H. Estimation Methods for Nonlinear State-Space Models in Ecology. Ecol. Modell. 2011, 222, 1394–1400. [Google Scholar] [CrossRef]
- Payandeh, B. Some Applications of Nonlinear Regression Models in Forestry Research. For. Chron. 1983, 59, 244–248. [Google Scholar] [CrossRef] [Green Version]
- Khan, D.M.; Ihtesham, S.; Ali, A.; Khalil, U.; Khan, S.A.; Manzoor, S. An efficient and high breakdown estimation procedure for nonlinear regression models. Pak. J. Stat. 2017, 33, 223–236. [Google Scholar]
- Ratkowsky, D.A. Principles of Nonlinear Regression Modeling. J. Ind. Microbiol. 1993, 12, 195–199. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: New York, NY, USA, 1998; p. 326. [Google Scholar]
- Wright, S.; Nocedal, J. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 1999; Volume 35, p. 7. [Google Scholar]
- Parresol, B.R. Additivity of Nonlinear Biomass Equations. Can. J. For. Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
- Cao, Q.V.; Wang, J. Calibrating Fixed- and Mixed-Effects Taper Equations. For. Ecol. Manag. 2011, 262, 671–673. [Google Scholar] [CrossRef]
- Max, T.A.; Burkhart, H.E. Segmented Polynomial Regression Applied to Taper Equations. For. Sci. 1976, 22, 283–289. [Google Scholar]
- Chumney, E.C.G.; Simpson, K.N. Methods and Designs for Outcomes Research; ASHP: Bethesda, MD, USA, 2006. [Google Scholar]
- Holmström, K.; Petersson, J. A Review of the Parameter Estimation Problem of Fitting Positive Exponential Sums to Empirical Data. Appl. Math. Comput. 2002, 126, 31–61. [Google Scholar] [CrossRef]
- Tomioka, S.; Nisiyama, S.; Enoto, T. Nonlinear Least Square Regression by Adaptive Domain Method with Multiple Genetic Algorithms. IEEE Trans. Evol. Comput. 2007, 11, 1–16. [Google Scholar] [CrossRef]
- Fekedulegn, D.; Mac Siurtain, M.P.; Colbert, J.J. Parameter Estimation of Nonlinear Growth Models in Forestry. Silva Fenn. 1999, 33, 327–336. [Google Scholar] [CrossRef] [Green Version]
- Křivý, I.; Tvrdík, J. The Controlled Random Search Algorithm in Optimizing Regression Models. Comput. Stat. Data Anal. 1995, 20, 229–234. [Google Scholar] [CrossRef]
- Tang, K.; Li, T. Comparison of Different Partial Least-Squares Methods in Quantitative Structure—Activity Relationships. Anal. Chim. Acta 2003, 476, 85–92. [Google Scholar] [CrossRef]
- Imbault, F.; Lebart, K. A Stochastic Optimization Approach for Parameter Tuning of Support Vector Machines. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 26 August 2004; Volume 4, pp. 597–600. [Google Scholar] [CrossRef]
- Pouzol, T.; Kopf, C.; Lévi, Y.; Bertrand-Krajewski, J.-L. Stochastic Modelling of Pharmaceuticals Path from Sales and Deliveries to Wastewater Treatment Plant at Hourly Scale. Proc. SPN 2016, v. 8, 264–265. [Google Scholar]
- Leehter, Y.; Sethares, W.A. Nonlinear Parameter Estimation via the Genetic Algorithm. IEEE Trans. Signal Process. 1994, 42, 927–935. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, S.; Laudato, M.; Lynch, L.A. Genetic Algorithms and Their Statistical Applications: An Introduction. Comput. Stat. Data Anal. 1996, 22, 633–651. [Google Scholar] [CrossRef]
- Karr, C.L.; Weck, B.; Freeman, L.M. Solutions to Systems of Nonlinear Equations via a Genetic Algorithm. Eng. Appl. Artif. Intell. 1998, 11, 369–375. [Google Scholar] [CrossRef]
- Kapanoglu, M.; Koc, I.O.; Erdogmus, S. Genetic Algorithms in Parameter Estimation for Nonlinear Regression Models: An Experimental Approach. J. Stat. Comput. Simul. 2007, 77, 851–867. [Google Scholar] [CrossRef]
- Jin, Y.-F.; Yin, Z.-Y.; Shen, S.-L.; Hicher, P.-Y. Selection of Sand Models and Identification of Parameters Using an Enhanced Genetic Algorithm. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 1219–1240. [Google Scholar] [CrossRef]
- Moin, N.H.; Salhi, S.; Aziz, N.A.B. An Efficient Hybrid Genetic Algorithm for the Multi-Product Multi-Period Inventory Routing Problem. Int. J. Prod. Econ. 2011, 133, 334–343. [Google Scholar] [CrossRef]
- Li, T.-H.; Lucasius, C.B.; Kateman, G. Optimization of Calibration Data with the Dynamic Genetic Algorithm. Anal. Chim. Acta 1992, 268, 123–134. [Google Scholar] [CrossRef]
- Haj Seyed Hadi, M.R.; Gonzalez-Andujar, J.L. Comparison of Fitting Weed Seedling Emergence Models with Nonlinear Regression and Genetic Algorithm. Comput. Electron. Agric. 2009, 65, 19–25. [Google Scholar] [CrossRef]
- Forrest, S. Genetic Algorithms: Principles of Natural Selection Applied to Computation. Science 1993, 261, 872–878. [Google Scholar] [CrossRef] [Green Version]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; De Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s Climate Classification Map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Veloso, H.P.; Rangel-Filho, A.L.R.; Lima, J.C.A. Classificação Da Vegetação Brasileira, Adaptada a Um Sistema Universal; Ibge—Instituto Brasileiro de Geografia e Estatistica: Rio de Janeiro, Brazil, 1991; ISBN 8524003847.
- Temesgen, H.; Monleon, V.J.; Hann, D.W. Analysis and Comparison of Nonlinear Tree Height Prediction Strategies for Douglas-Fir Forests. Can. J. For. Res. 2008, 38, 553–565. [Google Scholar] [CrossRef] [Green Version]
- Özçelik, R.; Diamantopoulou, M.J.; Crecente-Campo, F.; Eler, U. Estimating Crimean Juniper Tree Height Using Nonlinear Regression and Artificial Neural Network Models. For. Ecol. Manag. 2013, 306, 52–60. [Google Scholar] [CrossRef]
- Misik, T.; Antal, K.; Kárász, I.; Tóthmérész, B. Nonlinear Height-Diameter Models for Three Woody, Understory Species in a Temperate Oak Forest in Hungary. Can. J. For. Res. 2016, 46, 1337–1342. [Google Scholar] [CrossRef]
- Wang, Y.; LeMay, V.M.; Baker, T.G. Modelling and Prediction of Dominant Height and Site Index of Eucalyptus Globulus Plantations Using a Nonlinear Mixed-Effects Model Approach. Can. J. For. Res. 2007, 37, 1390–1403. [Google Scholar] [CrossRef]
- Huang, S.; Titus, S.J. Estimating a System of Nonlinear Simultaneous Individual Tree Models for White Spruce in Boreal Mixed-Species Stands. Can. J. For. Res. 1999, 29, 1805–1811. [Google Scholar] [CrossRef]
- Bi, H.; Fox, J.C.; Li, Y.; Lei, Y.; Pang, Y. Evaluation of Nonlinear Equations for Predicting Diameter from Tree Height. Can. J. For. Res. 2012, 42, 789–806. [Google Scholar] [CrossRef]
- Calegario, N. Modeling Eucalyptus Stand Growth Based on Linear and Nonlinear Mixed-Effects Models; University of Georgia: Athens, GA, USA, 2002. [Google Scholar]
- Zeide, B. Analysis of Growth Equations. For. Sci. 1993, 39, 594–616. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing 2022. Available online: https://cran.r-project.org/ (accessed on 20 October 2022).
- Elzhov, T.V.; Mullen, K.M.; Spiess, A.-N.; Bolker, B. Minpack.Lm: R Interface to the Levenberg-Marquardt Nonlinear Least-Squares Algorithm Found in MINPACK, Plus Support for Bounds. 2022. Available online: https://cran.r-project.org/web/packages/minpack.lm/minpack.lm.pdf (accessed on 20 October 2022).
- VanderNoot, T.J.; Abrahams, I. The Use of Genetic Algorithms in the Non-Linear Regression of Immittance Data. J. Electroanal. Chem. 1998, 448, 17–23. [Google Scholar] [CrossRef]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Bates, D.M.; Watts, D.G. Nonlinear Regression Analysis and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 1990; Volume 32. [Google Scholar]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt Algorithm: Implementation and Theory. In Numerical Analysis; Springer: Bern, Switzerland, 1978; pp. 105–116. [Google Scholar]
- Moré, J.J.; Sorensen, D.C. Computing a Trust Region Step. SIAM J. Sci. Stat. Comput. 1983, 4, 553–572. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.B.; Bailey, R.L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. For. Sci. 2001, 47, 311–321. [Google Scholar]
- Araújo, L.A.; Oliveira, R.M.; Dobner, M.; Jarochinski e Silva, C.S.; Gomide, L.R. Appropriate Search Techniques to Estimate Weibull Function Parameters in a Pinus Spp. Plantation. J. For. Res. 2021, 32, 2423–2435. [Google Scholar] [CrossRef]
- Cao, Q.; Strub, M. Evaluation of Four Methods to Estimate Parameters of an Annual Tree Survival and Diameter Growth Model. For. Sci. 2008, 54, 617–624. [Google Scholar]
- Schwaab, M.; Biscaia, E.C., Jr.; Monteiro, J.L.; Pinto, J.C. Nonlinear Parameter Estimation through Particle Swarm Optimization. Chem. Eng. Sci. 2008, 63, 1542–1552. [Google Scholar] [CrossRef]
- Özkan, E.; Šmídl, V.; Saha, S.; Lundquist, C.; Gustafsson, F. Marginalized Adaptive Particle Filtering for Nonlinear Models with Unknown Time-Varying Noise Parameters. Automatica 2013, 49, 1566–1575. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, M.; Egea, J.A.; Banga, J.R. Novel Metaheuristic for Parameter Estimation in Nonlinear Dynamic Biological Systems. BMC Bioinform. 2006, 7, 483. [Google Scholar] [CrossRef] [PubMed]
- Inayat, A.; Nassef, A.M.; Rezk, H.; Sayed, E.T.; Abdelkareem, M.A.; Olabi, A.G. Fuzzy Modeling and Parameters Optimization for the Enhancement of Biodiesel Production from Waste Frying Oil over Montmorillonite Clay K-30. Sci. Total Environ. 2019, 666, 821–827. [Google Scholar] [CrossRef] [Green Version]
- Lacerda, T.H.S.; Miranda, E.N.; E Lopes, I.L.; Fonseca, G.R.; França, L.C. de Jesus França, L.C.; Gomide, L.R. Feature Selection by Genetic Algorithm in Nonlinear Taper Model. Can. J. For. Res. 2022, 52, 769–779. [Google Scholar] [CrossRef]

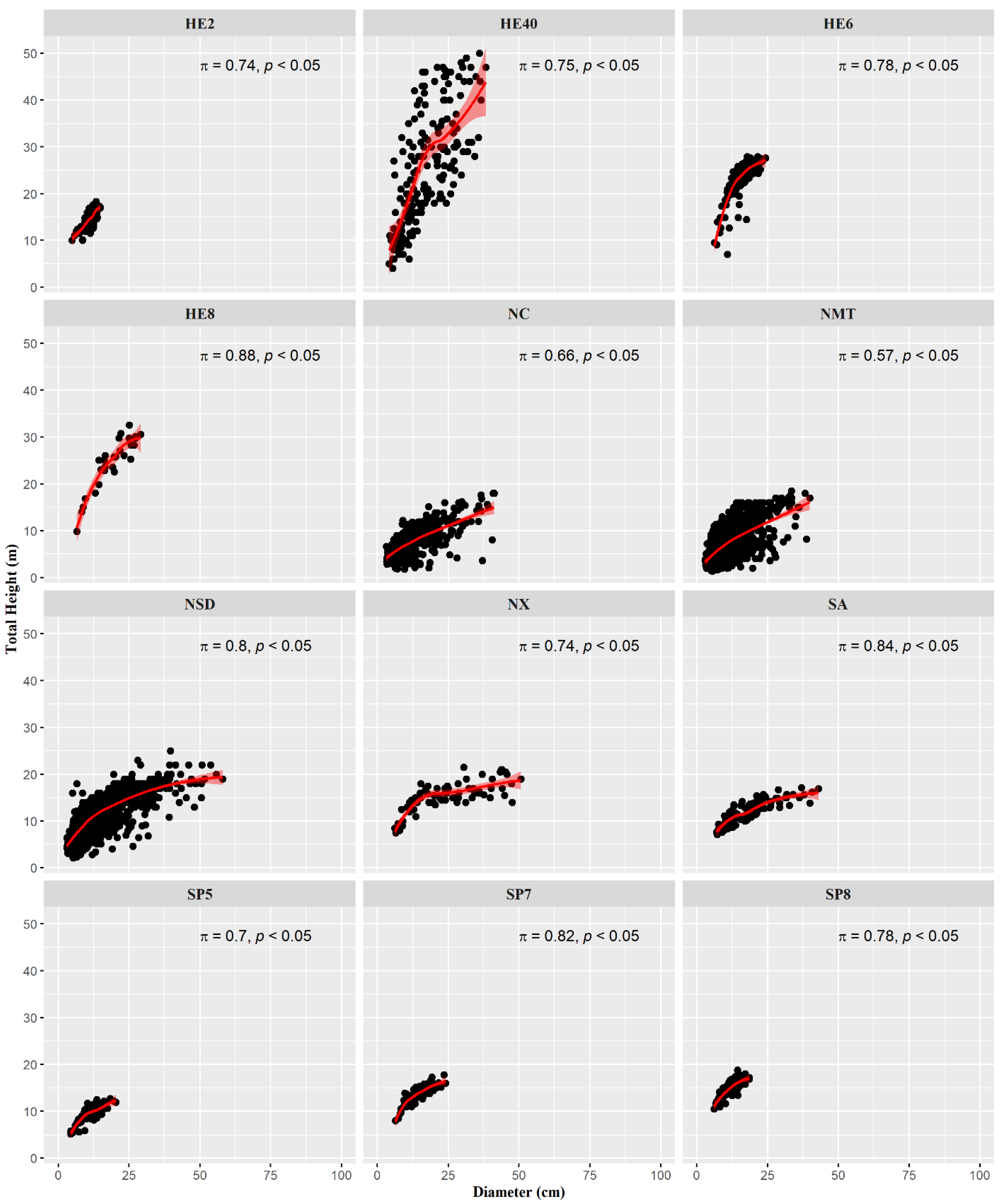

| Database | N | Average | Max | Min | SD | ||||
|---|---|---|---|---|---|---|---|---|---|
| d | h | d | h | d | h | d | h | ||
| SA * | 100 | 19.7 | 12.3 | 43.0 | 17.1 | 7.0 | 7.1 | 80.5 | 22.7 |
| NMT ** | 1975 | 9.6 | 6.5 | 99.0 | 30.0 | 2.9 | 1.4 | 54.8 | 30.2 |
| NX ** | 73 | 24.3 | 15.1 | 50.6 | 21.5 | 6.1 | 7.5 | 126.4 | 33.8 |
| NSD ** | 1975 | 11.7 | 9.7 | 77.4 | 25.0 | 3.0 | 2.1 | 82.5 | 36.0 |
| NC ** | 609 | 11.1 | 7.1 | 56.8 | 20.6 | 3.1 | 1.8 | 71.6 | 28.4 |
| HE2 * | 229 | 11.7 | 15.1 | 14.9 | 40.3 | 4.8 | 10.0 | 15.6 | 22.7 |
| HE6 * | 357 | 16.9 | 24.1 | 24.3 | 27.9 | 6.3 | 7.0 | 30.6 | 29.0 |
| HE8 * | 28 | 19.1 | 24.4 | 29.1 | 32.5 | 6.5 | 9.8 | 63.6 | 56.0 |
| HE40 * | 188 | 17.1 | 25.1 | 38.2 | 50.0 | 2.7 | 4.0 | 84.2 | 121.6 |
| SP5 * | 100 | 11.7 | 9.6 | 20.4 | 12.7 | 4.4 | 5.1 | 31.0 | 15.5 |
| SP7 * | 100 | 14.7 | 13.7 | 24.1 | 17.8 | 6.3 | 7.9 | 35.1 | 16.9 |
| SP8 * | 100 | 14.4 | 14.8 | 23.1 | 18.8 | 7.1 | 10.4 | 30.3 | 15.9 |
| Begin function: dyrange (gk, g*,){ if (gk > g*): r = min {} where j = 1,…, p. else: r = r return range [+r, -r] } End function |
| Model | MAE (SD) | Bias (SD) | RMSE (SD) | |
|---|---|---|---|---|
| Meyer | 1.732 (1.76) | 0.553 (0.233) | −0.113 (0.339) | 0.174 (0.174) |
| Burkhart | 1.736 (1.759) | 0.549 (0.24) | −0.122 (0.341) | 0.173 (0.175) |
| Monomolecular | 1.722 (1.773) | 0.558 (0.236) | −0.098 (0.341) | 0.172 (0.173) |
| Mitcherlich | 1.715 (1.774) | 0.562 (0.235) | −0.098 (0.341) | 0.171 (0.174) |
| Gompertz | 1.724 (1.771) | 0.559 (0.234) | −0.097 (0.341) | 0.172 (0.174) |
| Logistic | 1.733 (1.776) | 0.557 (0.233) | −0.094 (0.341) | 0.173 (0.174) |
| Chapman & Richards | 1.727 (1.772) | 0.558 (0.234) | −0.096 (0.341) | 0.172 (0.174) |
| Bailey1 | 1.719 (1.769) | 0.561 (0.236) | −0.1 (0.342) | 0.172 (0.174) |
| Von Bertalanffy | 1.728 (1.772) | 0.554 (0.237) | −0.094 (0.341) | 0.172 (0.174) |
| Bailey2 | 1.706 (1.774) | 0.561 (0.236) | −0.099 (0.336) | 0.171 (0.174) |
| Zeide | 1.704 (1.763) | 0.562 (0.235) | −0.096 (0.337) | 0.17 (0.172) |
| Richards | 1.723 (1.772) | 0.558 (0.231) | −0.091 (0.33) | 0.172 (0.174) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monti, C.A.U.; Oliveira, R.M.; Roise, J.P.; Scolforo, H.F.; Gomide, L.R. Hybrid Method for Fitting Nonlinear Height–Diameter Functions. Forests 2022, 13, 1783. https://doi.org/10.3390/f13111783
Monti CAU, Oliveira RM, Roise JP, Scolforo HF, Gomide LR. Hybrid Method for Fitting Nonlinear Height–Diameter Functions. Forests. 2022; 13(11):1783. https://doi.org/10.3390/f13111783
Chicago/Turabian StyleMonti, Cassio Augusto Ussi, Rafael Menali Oliveira, Joseph Peter Roise, Henrique Ferraço Scolforo, and Lucas Rezende Gomide. 2022. "Hybrid Method for Fitting Nonlinear Height–Diameter Functions" Forests 13, no. 11: 1783. https://doi.org/10.3390/f13111783
APA StyleMonti, C. A. U., Oliveira, R. M., Roise, J. P., Scolforo, H. F., & Gomide, L. R. (2022). Hybrid Method for Fitting Nonlinear Height–Diameter Functions. Forests, 13(11), 1783. https://doi.org/10.3390/f13111783






