Abstract
Patterns in foliar nitrogen (N) stable isotope ratios (δ15N) have been shown to reveal trends in terrestrial N cycles, including the identification of ecosystems where N deficiencies limit forest ecosystem productivity. However, there is a gap in our understanding of within-species variation and species-level response to environmental gradients or forest management. Our objective is to examine the relationship between site index, foliar %N, foliar δ15N and spectral reflectance for managed Douglas-fir (Pseudotsuga menziesii) and loblolly pine (Pinus taeda) plantations across their geographic ranges in the Pacific Northwest and the southeastern United States, respectively. Foliage was measured at 28 sites for reflectance using a handheld spectroradiometer, and further analyzed for δ15N and N concentration. Unlike the prior work for grasslands and shrubland species, our results show that foliar δ15N and foliar %N are not well correlated for these tree species. However, multiple linear regression models suggest a strong predictive ability of spectroscopy data to quantify foliar δ15N, with some models explaining more than 65% of the variance in the δ15N. Additionally, moderate to strong explanations of variance were found between site index and foliar δ15N (R2 = 0.49) and reflectance and site index (R2 = 0.84) in the Douglas-fir data set. The development of relationships between foliar spectral reflectance, δ15N and measures of site productivity provides the first step toward mapping canopy δ15N for these managed forests with remote sensing.
1. Introduction
To meet demands for food, fuel and fiber, the addition of nitrogenous fertilizer is a common practice in agriculture and forestry, as N often limits productivity in these systems [1]. Increased production of reactive N has resulted in enhanced deposition of N across the landscape, nearly doubling the rate of N input into terrestrial ecosystems [2,3]. Thus, there is an increased risk for adverse environmental impacts such as the acidification of aquatic ecosystems and soils, loss of soil nutrients and accelerated biodiversity losses of both flora and fauna [3]. Further, the relationship between N and soil base cations is complex, and not fully understood. Work in Douglas-fir (Pseudotsuga menziesii) illustrated a coupling between N and calcium in the soil, where increases in N caused a depletion and deficiency of soil calcium [4]. There is a need to better understand ecosystem-level N dynamics, particularly with respect to the capacity of terrestrial forest ecosystems to retain increasing N.
Patterns in natural abundance N stable isotope ratios (δ15N) have been shown to integrate terrestrial N cycling dynamics and can be used to monitor ecosystems where N limits ecosystem production (e.g., loblolly pine and Douglas-fir forests) or identify those that are susceptible to N losses. This is due to the isotopic discrimination, or fractionation, that occurs throughout the N cycle as various processes, such as mineralization and nitrification, which creates products that are depleted and substrates that are enriched in 15N [5]. With high net soil nitrification rates and substantial loss of nitrate from the system, soil and foliar δ15N are gradually elevated due to the loss of the depleted products from the system [6,7,8,9]. For example, Högberg [10] and Högberg and Johannisson [11] found that Scots pine (Pinus sylvestris L.) foliage showed an increase in δ15N when large amounts of added N were lost from the system. The ability to predict foliar δ15N across large spatial and temporal scales would provide a framework to rapidly assess ecosystem N status and susceptibility to N losses. Establishing a relationship between leaf-level reflectance and foliar δ15N is the first step to developing a framework that would provide an efficient and non-destructive method of mapping foliar δ15N.
Spectroscopy data has been used for over 30 years to study vegetation spectral signatures at the leaf-level [12,13,14,15,16,17]. The narrow bandwidth of the data facilitates the study of cell structure, water content and foliar biochemistry by observing slight variations in reflectance at specified wavelengths. Of particular interest in forest ecosystems is the use of reflectance data to quantify foliar N concentrations (%N). In fresh vegetation, the close correlation between N and chlorophyll has led to the use of wavelengths in the visible and red-edge regions of the electromagnetic spectrum to develop regression equations for predicting N concentrations in foliage [18]. Wavelengths in the near-infrared, associated with N absorption features due to the vibration of N-hydrogen bonds in proteins [19], have also been utilized in the prediction of N concentration from leaf-level reflectance [18,20,21].
With the relationship between reflectance and %N well-established at the leaf-level, researchers have successfully scaled observations to the canopy, stand and regional levels using image-level reflectance data obtained from airborne and satellite platforms [22,23,24,25], and top-of-canopy reflectance simulated from radiative transfer models [26]. However, recent research [27,28,29] has demonstrated a decoupling of the relationship between reflectance and %N at the canopy scale due to the influence of canopy structure, which is likely impeding the successful prediction of canopy %N from imaging spectroscopy data.
Several authors have also demonstrated relationships between spectral reflectance and foliar δ15N for grasslands, fields, and shrub species. Wang et al. [30] and Wang et al. [31] demonstrated the ability of foliar spectral reflectance to predict δ15N of fresh vegetation in specific wavelength ranges (i.e., 481–523 nm, 617–703nm, 1098–1319 nm, and 1480–1522 nm), at leaf and canopy scales in grasslands and successional fields. Elmore and Craine [32] also investigated the feasibility of predicting δ15N with hyperspectral data in managed pastures and hay lands, focusing on the use of known absorption features of N and lignin in near-infrared wavelengths. Kleinebecker et al. [33] successfully demonstrated the prediction of foliar δ15N using dried and ground plant tissues of a variety of species found in bog complexes of the Chilean Patagonia using near-infrared spectrometry. Hellman et al. [34] used partial least squares regression to develop predictive models of foliar δ15N for shrub species, and also assesses the relationship between foliar δ15N and examine the relationship between foliar %N and foliar δ15N. If foliar %N and δ15N are strongly correlated, as suggested by Hellman et al. [34], Wang et al. [31], and Hobbie et al. [35] then the previous work done to predict %N at the canopy and stand level could be built upon by simply utilizing the relationship between %N and δ15N. However, if there is evidence of a decoupling between %N and δ15N, the relationship between reflectance and δ15N must first be established at the leaf-level before it can be successfully scaled to coarser spatial resolutions.
Although the above-mentioned efforts do suggest that spectral reflectance can be used to predict foliar δ15N, this has not been well demonstrated for tree species and forested ecosystems. One exception to this is the work of Serbin et al. [36] who predict foliar isotopic nitrogen for several temperate and boreal tree species (R2 = 0.62 for these species). This was done using partial least squares regression, in the spectral region from 1200–2400 nm. Their work demonstrates the potential for spectroscopy to predict isotopic nitrogen for trees across species, but was not designed to examine variations within a species. We begin to address this gap in the literature by exploring the relationship between foliar %N, foliar δ15N, and spectral reflectance for Douglas-fir (Pseudotsuga menziesii) and loblolly pine (Pinus taeda) canopies throughout their geographic ranges in the Pacific Northwest and southeastern United States, respectively. Douglas-fir and loblolly pine have a dominant presence on the landscape, representing nearly half of the standing softwood volume and nearly 20% of the forest cover in the United States [37]. With the establishment of the relationship between reflectance and δ15N, these relatively homogeneous systems should facilitate future efforts to scale from leaf to canopy level observations, as the impact of overstory species diversity on reflectance and δ15N should be minimal. In addition to developing models to predict δ15N from leaf-level reflectance, this research explores the relationship between δ15N and site productivity as well as the relationship between reflectance and site productivity.
2. Materials and Methods
2.1. Study Sites
This research leveraged existing regional trials of the National Science Foundation Center for Advanced Forestry Systems (NSF CAFS) with study sites located within the species’ ranges of Douglas-fir and loblolly pine in the Pacific Northwest and southeastern United States, respectively (Figure 1). Ten sites were located in Washington and Oregon for Douglas-fir (Figure 1A), and 18 sites located in loblolly pine plantations across eleven different states, ranging north to south from Virginia to Florida and east to west from Oklahoma to the coast of North Carolina (Figure 1B). The intent of the NSF CAFS research trials is to examine the ecosystem fate and uptake efficiency of added N in mid-rotation plantations. At each site 100 m2 plots were established. Plantation age varied from 6 to 21 years and density ranged from 2 to 25 trees per plot in loblolly pine. Throughout the Douglas-fir study sites, planation age ranged from 13 to 19 years with number of trees per plot ranging from 7 to 13.
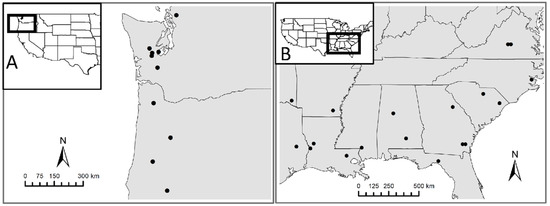
Figure 1.
Map of the NSF CAFS 15N fertilization sites for: (A) Douglas-fir plantations in the Pacific Northwest region of the United States; (B) loblolly pine sites of the southeastern United States.
2.2. Field Data Collection
Fieldwork was conducted throughout the growing season of 2012. Douglas-fir study sites were visited in March and loblolly pine study sites were visited in July through early September. Foliage was collected from one tree of the control plot at each study site to measure natural abundance δ15N and reflectance. Tree branches were collected from the upper one-third of the canopy using a shotgun or pole pruner. Following the approach of Wang et al. [30], foliage was sampled for reflectance using an ASD FieldSpec3 handheld spectroradiometer (ASD Inc., Boulder, CO, USA) equipped with a plant probe containing its own halogen light source and a leaf clip attachment. The FieldSpec3 has a spectral range of 350 to 2500 nm with sampling intervals of 1.4 nm from 350 to 1000 nm and 2 nm from 1000 to 2500 nm. The system was operated by the RS3 Version 6.0 software package ASD Inc., Boulder, CO, USA). Reflectance was measured as the ratio of the energy reflected from the sample to the energy reflected off a white reference standard of known reflectance (i.e., a Spectralon panel; Labsphere, Inc., North Sutton, NH). Within the RS3 software interface, dark current and white reference readings were taken after each sample, or as needed, to recalibrate the FieldSpec3 and ensure quality reflectance data collection. To minimize noise, an average of 10 spectral signatures were collected per foliage sample. The samples were viewed and averaged within the ViewSpec Pro software (ASD Inc., Boulder, CO, USA) and exported as text files for subsequent statistical analysis.
Each foliage sample of Douglas-fir consisted of 12 needles aligned to minimize overlap and maximize field of view coverage. At each Douglas-fir site the spectral signature of 10 separate foliage samples was measured. Loblolly pine foliage samples consisted of 6 to 10 fascicles of needles and varied due to the number needed to cover the entire field of view of the plant probe. Needles were sampled near their center to avoid inclusion of the fascicle sheath. Loblolly pine was sampled during the height of the growing season when foliage from the previous year (2011) and current year (2012) was present. Samples were separated in the field by flush and only foliage from 2011 or, when unavailable, the first flush from 2012 was used in subsequent analysis. The number of foliage samples collected at each loblolly pine site varied due to the amount of foliage available from the desired year and flush.
Though all practical measures were taken to ensure maximum field of view coverage this was not always achieved due to needle length and shape (i.e., the short needle length of Douglas-fir foliage). Therefore, the black background of the leaf clip attachment was used when measuring reflectance of all foliage samples. After the spectral signatures were recorded, each sample was placed in a marked coin envelope and transported to Virginia Tech for δ15N and %N analysis.
Site index is a common measure of site productivity that describes the height of canopy dominant or co-dominant trees at a given base age. It was calculated by relating inventory data (i.e., age, height) with published curves [38,39] that relate current age and height to estimate canopy height at the designated base age. As is common, a base age of 50 was used for Douglas fir [38] and 25 for loblolly pine [39].
2.3. Laboratory Analysis for Foliar %N and δ15N
Foliar samples were dried at 65 °C for a minimum of three days then ground in a ball mill to ensure sample homogeneity. A weighed subsample of foliar material was analyzed for δ15N and %N using an IsoPrime 100 continuous-flow isotope ratio mass spectrometer coupled with an elemental analyzer (EA-IRMS; IsoPrime Ltd., Cheadle Hulme, UK). %N is reported as the mass of N relative to the mass of the subsample (×100). δ15N is reported relative to the accepted standard of atmospheric N in parts per thousand (%) deviation from the standard using the following equation [40]:
Foliar δ15N and %N values were then averaged by site.
2.4. Foliar Spectral Reflectance Data
A second order Savitzky-Golay smoothing filter with a window of five bands was applied to further reduce noise in the signature [41]. Various transformations including first and second derivatives, log 1/reflectance and the first derivative of log 1/reflectance were also calculated. These various transformations highlight features of the vegetation spectral signature that may not be apparent in the original reflectance curve. In particular the log transformation of reflectance (log 1/R), also referred to as pseudoabsorbance, simulates an absorption curve, creating peaks at the absorbing wavelengths [42]. The first derivative has also been utilized to identify features of the reflectance curve such as the location of the red-edge inflection point and the magnitude of reflectance at that wavelength [12,43]. Signatures were averaged by study site resulting in 10 signatures for Douglas-fir and 18 signatures for loblolly pine.
Correlation curves were created by calculating the Pearson correlation coefficient for δ15N and each wavelength of reflectance and its various transformations. The correlation curves were used to assist with feature selection for subsequent multiple linear regression models. Given that our understanding of the relationship between reflectance and foliar δ15N in natural ecosystems is in its infancy, we identified wavelength regions with significant correlations with δ15N (i.e., 3 or more channels), as well as regions known to be well correlated with N. Areas of the electromagnetic spectrum that may be affected by atmospheric water vapor (i.e., ~940, ~1140, 1350–1470, 1800–2000 nm) were excluded from selection as they may compromise the use of resulting models in future remote sensing applications. More than thirty vegetation indices related to various properties of vegetation, such as biochemicals, structure, and physiology, were calculated and included in the best subsets regression (Table 1). Also included were wavelengths previously identified for the prediction of foliar δ15N [30] and %N [37], as were the lignin and N absorption features explored by Elmore and Craine [32] (Table 1).

Table 1.
Vegetation indices and wavelengths of interest included in a best subsets approach to building multiple linear regression models for the prediction of natural abundance foliar δ15N from hyperspectral data in Douglas-fir and loblolly pine. R = reflectance, FDR = 1st derivative of R, L = log of 1/R, FDL = 1st derivative of the log of 1/R.
2.5. Statistical Analysis
Multiple regression analysis was performed using JMP Statistical Discovery Software Version 10.0 (JMP Statistical Discovery LLC, Cary, NC, USA). Multiple linear regression models to predict natural abundance foliar δ15N from spectroscopy data were built using a best subsets approach. In this approach all possible models are compared with a user-defined number of independent variables. A maximum of three variables was chosen, however, the number of independent variables in the final models for each data set varies from one to three based on sample size and strength of the model output. The coefficient of determination (R2) and adjusted R2 were used to initially assess the overall adequacy of the models. To avoid multicollinearity the variable inflation factor (VIF) was limited to 6 [65]. Studentized residuals from each model were tested for normality using the Shaprio-Wilk test [66]. Model validation was performed using a leave-one-out cross validation technique reported as the Press RMSE. The Press statistic can be used to assess how well a model will perform when predicting new data, with smaller Press values being more desirable [65]. If the model with the highest R2 and adjusted R2 did not meet all of the above requirements, the next best model was chosen and the process was repeated until a satisfactory model was selected. The relationship between foliar %N and δ15N was also explored by performing a simple linear regression model with %N as the independent variable and δ15N as the dependent variable. These analyses were performed separately on the Douglas-fir and loblolly pine data sets as well as a combined data set of both species.
In addition, an exploratory analysis of the relationships between reflectance, δ15N and site index was performed using multiple linear regression. A best subsets approach was performed on each data set to ascertain which, if any, of the previously identified wavelengths useful in predicting δ15N may also predict site index. Furthermore, a simple linear regression was performed to explore the relationship between δ15N and site index.
3. Results
3.1. Foliar δ15N and %N
The distributions of δ15N and %N for Douglas-fir and loblolly pine are described in Table 2. All samples across both species had negative δ15N and fell within the range of natural abundance levels for foliage observed in other studies conducted in temperate forest ecosystems [8,67,68]. The loblolly pine data set had a larger range of δ15N (6.3‰ compared to 2.3‰) and foliar %N (0.6% compared to 0.3%) than Douglas-fir (Table 2).

Table 2.
Summary statistics of δ15N (‰) and %N in Douglas-fir and loblolly pine foliage collected during the growing season of 2012.
Results demonstrate that there is no significant relationship between foliar %N and δ15N for Douglas-fir, and only 25% of the variance in δ15 N is explained by %N for loblolly pine (Table 3, Figure 2). Some explanatory power is evident when the datasets are combined, but still less than half of the variance in δ15N is explained by %N. This may suggest an underlying environmental gradient that is partially driving response of both %N and δ15N across the large geographic extent of the study.

Table 3.
Linear regression models using foliar nitrogen concentration (%N) to predict natural abundance foliar δ15N (‰) in Douglas-fir, loblolly pine, and a combined data set of both species. An asterisk (*) indicates model significance at the α = 0.05 level.
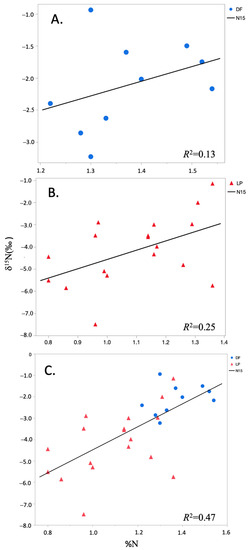
Figure 2.
Relationship between foliar nitrogen concentration (%N) and natural abundance foliar δ15N (‰) in: (A) Douglas-fir; (B) loblolly pine; and (C) a combined data set of both species (Table 3).
3.2. Reflectance and Foliar δ15N
The strong predictive ability of leaf-level spectral reflectance data to quantify natural abundance foliar δ15N is demonstrated in the multiple linear regression models for each of the data sets (Table 4, Figure 3). Wavelengths selected for inclusion in the final models were located in the visible and near-infrared regions of the spectrum. One (R2 = 0.65, RMSE = 0.43) and two (R2 = 0.81, RMSE = 0.35) variable models were selected for Douglas-fir, two (R2 = 0.54, RMSE = 1.11) and three (R2 = 0.68, RMSE = 0.96) variable models were selected for loblolly pine, and a two variable model was selected for the combined data set of both species (R2 = 0.63 RMSE = 1.03). There is a clear species gradient in the δ15N data (Figure 3C), which also corresponds to a latitudinal difference across the species locations, but there were no significant correlations to latitude or longitude within either species (not shown).

Table 4.
Multiple linear regression models selected by a best subsets approach using leaf-level spectroscopy data to predict foliar δ15N (‰) in Douglas-fir, loblolly pine, and a combined data set of both species. R = reflectance, FDR = 1st derivative of R, SDR = 2nd derivative of R, L = log of 1/R, FDL = 1st derivative of the log of 1/R.
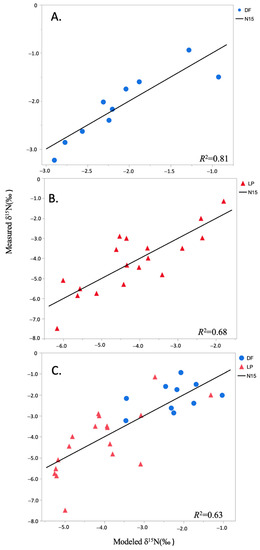
Figure 3.
Multiple linear regression models predicting natural abundance foliar δ15N (‰) from leaf level spectroscopy for: (A) Douglas-fir (two-variable model); (B) loblolly pine (three-variable model); and (C) a combined data set of both species (two-variable model) (Table 4).
Selected wavelengths and vegetation indices varied across each data set. Variables selected for the Douglas-fir models included a wavelength located in the green visible region of the spectrum, specifically the second derivative of reflectance at 543 nm, and the Anthocyanin Reflectance Index (ARI) [46]. The two-variable loblolly pine model included wavelengths located in the green and red-edge regions of the spectrum, specifically the first derivative of reflectance at 587 nm and the log of 1/reflectance at 748 nm. The Pigment Specific Simple Ratio (PSSR) [59] and reflectance at 619 nm, a wavelength previously identified by Wang et al. [30] as being useful in predicting foliar δ15N, were selected for inclusion in the three-variable loblolly pine model. The combined data set model included the log of 1/reflectance at 1167 nm and the second derivative of reflectance at 570 nm located in the near-infrared and green visible regions of the spectrum, respectively.
3.3. Reflectance, Site Index and δ15N
Site index ranged from 37 to 55 m (base age 50) and 16 to 36 m (base age 25) in Douglas-fir and loblolly pine, respectively. In the Douglas-fir data set, a strong positive linear relationship was found between the second derivative of reflectance at 543 nm, the same variable used in the one and two variable models for predicting δ15N, and site index (R2 = 0.84). The use of site index to predict δ15N also yielded interesting results with a correlation of R2 = 0.49.
In the loblolly pine data set, the first derivative of reflectance at 677 nm explained 25% of the variation in site index. This specific wavelength was not chosen for any of the models, but it falls within the visible light region of the spectrum from which many of the selected wavelengths in the models were chosen. The relationship between site index and δ15 N was statistically insignificant in this data set (p = 0.43).
4. Discussion
4.1. Prediction of Foliar δ15N from Spectral Reflectance
The simplest mechanism facilitating the prediction of δ15N from hyperspectral reflectance data would be the relationship between δ15N and %N and the demonstrated ability of hyperspectral data to predict %N. Our results show a decoupling of the relationship between %N and δ15N, most notably in the Douglas-fir data set from which the strongest models were developed (Table 3, Figure 2). There is a moderate correlation between %N and δ15N in the combined data set which may result from the increased range of both variables when the data are pooled (Table 2 and Table 4, Figure 3), however, none of the vegetation indices specific to foliar %N nor any of the wavelengths associated with known N absorption features were selected for use in the regression models. Instead, many of the selected wavelengths and vegetation indices were located in the visible region of the electromagnetic spectrum (400–700 nm), similar to the results of Wang et al. [30], and have been correlated to various vegetation physiological properties and biochemicals. Wavelengths at 543, 570 and 587 nm are located within the green peak of the vegetation reflectance curve which has been correlated with photosynthetic efficiency and seasonal changes in N and chlorophyll content [62]. The wavelength at 619 nm, previously identified by Wang et al. [30] and Wang et al. [31] as being highly correlated to foliar δ15N, is associated with red visible light absorption by chlorophyll. The wavelength at 748 nm is located near the shoulder of the red-edge. The red-edge is a feature of the vegetation spectral signature, specific to hyperspectral data, which is caused by the shift from visible light absorption by pigments to the scattering of near infrared light by plant cellular structure [12]. It is a feature that is highly correlated to total chlorophyll content and has been used to estimate various measures of productivity, such as leaf area index (LAI) and biomass, and vegetation nutritional status such as N concentration and content [12,43,69,70]. The wavelength selected in the near-infrared at 1167 nm may be associated with the vibration of a carbon-hydrogen bond related to lignin located at 1120 nm or the vibration of an oxygen-hydrogen bond associated with water, cellulose, starch and lignin located at 1200 nm [19]. The ARI uses wavelengths in the visible light, specifically in the green and red regions of the spectrum, and was developed to assess foliar anthocyanin content [46]. The PSSR index was developed for the prediction of the accessory pigment chlorophyll b, utilizing wavelengths located in the red and near-infrared regions [59].
Although our experiment was not designed to investigate the relationships between δ15N, chlorophyll and/or other indicators of greenness, our results suggests that these mechanisms, as opposed to %N, are driving the relationships between reflectance and δ15N across our experiment. Additional research investigating the relationships to δ15N, chlorophyll and pigments across large environmental gradients is required.
4.2. δ15. N, Reflectance and Site Index
The use of remote sensing to directly assess aboveground forest productivity has been demonstrated at the canopy scale by developing relationships between reflectance, canopy %N and various measures of productivity such as aboveground net primary production and aboveground wood production [71]. Work by Knyazikhin et al. [27] and Sullivan et al. [29] has demonstrated the strong influence of canopy structure (i.e., LAI and the number of leaves per canopy volume) on reflectance. Their findings suggest that it is canopy structure driving the relationship between reflectance and %N at the canopy-level as opposed to the leaf-level relationships between reflectance and %N. The significant correlations observed between leaf-level reflectance and site index in Douglas-fir and loblolly pine indicate that various physiological properties known to be correlated to reflectance in the green and red visible regions of the spectrum, as previously mentioned, may also be related to measures of site productivity. Additionally, the significant correlation between δ15N and site index observed in Douglas-fir demonstrates a relationship between site nutrient status, leaf-level processes, canopy scale physiology, and overall productivity. This observed relationship may facilitate future efforts for scaling from the leaf to the canopy level as it is increasingly important to identify the driving mechanisms controlling reflectance at both leaf and canopy scales.
As site index is a measure of productivity, sites with higher site index values would be expected to be less resource deficient and specifically, less N deficient. Garten and Van Miegroet [72] observed a strong positive correlation between foliar δ15 N and net N mineralization rates and several regional-scale studies have shown strong positive relationships between N mineralization and productivity [73,74,75]. As N is lost from the system, foliar δ15N has been shown to become more positive over time [6,7]. Therefore, a positive relationship between δ15N and site index would be expected, as observed in Douglas-fir. The lack of a significant relationship between δ15 N and site index in loblolly pine may be due to how this species utilizes N in foliage. Loblolly pine produce 2 to 4 flushes each growing season, and nutrient concentration and weight have been shown to decrease with each subsequent flush [76]. Therefore, a measure of δ15N scaled to the canopy, as opposed to leaf-level observations, may be more appropriate when assessing the relationship between δ15N and measures of site productivity in loblolly pine.
4.3. Moving toward Assessment across Spatial and Temporal Scales
Our study sites span a very large geographic range, covering much of the range of Douglas fir and loblolly pine in the contiguous United States. Examining the data across the scale of the species range versus the entire range does show some spatial patterns. When examining the entire dataset, there is a clear gradient in foliar δ15N that corresponds to both species and latitude (Figure 3C and Figure 1). A within-species assessment found no relationship to either latitude or longitude for either species (not shown), suggesting that the patterns are driven by species. A full assessment of the spatial and temporal drivers of foliar δ15N patterns across the landscape is beyond the scope of this paper, and would require either multiple repeat visits to the site or the use of remote sensing. The active management practices in these plantations, particularly fertilization, add additional management drivers of foliar δ15N patterns that have not been well reported to date. Our study represents a first step in this process for these managed systems—developing relationships between foliar δ15N and reflectance that can be used as a basis for upscaling in future research.
5. Summary and Conclusions
There is a need to assess ecosystem N dynamics across large spatial and temporal scales to address questions related to N limitation and potential N loss following N addition. This has become well recognized—plant foliar stable isotopes for N and carbon are included in routine measurements done by the U.S. National Ecological Observatory Network (NEON, neonscience.org) and other groups. Developing the relationships between foliar spectral reflectance, δ15N, and ecosystem N dynamics would provide a method for the prediction of ecosystem N status using remote sensing.
Our results are drawn from field locations within 13 states, representing much of the geographic range of Douglas fir and loblolly pine and allowing for an assessment of within-species variation. Loblolly pine plantations show a significantly greater range of δ15N and %N than Douglas fir plantations (δ15N = 6.3‰, %N = 0.6 for loblolly pine versus δ15N = 2.3‰, %N = 0.3% Douglas fir). We found no significant relationship between δ15N and %N for Douglas fir (R2 = 0.13), and a very weak relationship between them for loblolly pine (R2 = 0.25). This in an important finding because it means that well-vetted remote sensing indices for canopy nitrogen content should not be used to estimate isotopic nitrogen when examining within-species response in these plantations, unlike what has been shown previously in other ecosystems [31,34,35]. However, we identified specific wavelengths and indices that could robustly predict δ15N within each species and across both species using best subsets multiple linear regression (R2 =0.81,0.68, and 0.63 for Douglas-fir, loblolly pine, and both species). Green, red, and near infrared wavelength ranges were most valuable for these models.
Future research efforts should focus on scaling from leaf to canopy level for managed forests (as has been done in other forest ecosystems), investigating the underlying relationships between foliar δ15N and reflectance and exploring the relationship between natural abundance δ15N and measures of ecosystem N retention or loss of added N. A better understanding of the relationship between reflectance and foliar δ15N may improve predictive capabilities and facilitate the use of reflectance to map foliar δ15N at larger spatial scales and in ecosystems that are more heterogeneous in species composition and land use history.
Author Contributions
This manuscript is part of the MS research of L.B. (formerly L. Lorentz). L.B., V.A.T. and B.D.S. contributed to all stages, including the conceptualization, methodology, formal analysis and writing. T.F. and R.H. contributed to the conceptualization and administration of the NSF CAFS sites, and helped with field-related resources, data acquisition, and writing—review and editing. A.H. and K.L. contributed to data acquisition and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
Funding for this research was provided by the National Council for Air and Stream Improvement, Inc. (NCASI), the USDA National Needs Fellowship Program (grant number 2010-38420-21851), and the Virginia Agricultural Experiment Station/McIntire-Stennis Program of the National Institute of Food and Agriculture, USDA (Project number 1007054 (VA-136633), “Detecting and Forecasting the Consequences of Subtle and Gross Disturbance on Forest Carbon Cycling”).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Jay Raymond and Betsy Vance for their assistance in field data collection as well as Colleen Carlson for providing ancillary data. We also acknowledge the Northwest Advanced Renewables Alliance, the National Science Foundation Center for Advanced Forestry Systems (NSF CAFS), the Forest Productivity Cooperative (FPC) and the Stand Management Cooperative (SMC) for access to and use of their resources and study sites.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Vitousek, P.M.; Howarth, R.W. Nitrogen limitation on land and in the sea: How can it occur? Biogeochemistry 1991, 13, 87–115. [Google Scholar] [CrossRef]
- Galloway, J.N. The global nitrogen cycle: Changes and consequences. Environ. Pollut. 1998, 102, 15–24. [Google Scholar] [CrossRef]
- Vitousek, P.M.; Aber, J.D.; Howarth, R.W.; Likens, G.E.; Matson, P.A.; Schindler, D.W.; Schlesinger, W.H.; Tilman, D.G. Human alteration of the global nitrogen cycle: Sources and consequences. Ecol. Appl. 1997, 7, 737–750. [Google Scholar] [CrossRef]
- Perakis, S.S.; Sinkhorn, E.R.; Catricala, C.E.; Bullen, T.D.; Fitzpatrick, J.A.; Hynicka, J.D.; Cromack, K.J. Forest calcium depletion and biotic retention along a soil nitrogen gradient. Ecol. Appl. 2013, 23, 1947–1961. [Google Scholar] [CrossRef] [PubMed]
- Shearer, G.; Kohl, D.H. N2-Fixation in Field Settings: Estimations Based on Natural 15N Abundance. Funct. Plant Biol. 1986, 13, 699–756. [Google Scholar]
- Cheng, S.L.; Fang, H.J.; Yu, G.R.; Zhu, T.H.; Zheng, J.J. Foliar and soil 15N natural abundances provide field evidence on nitrogen dynamics in temperate and boreal forest ecosystems. Plant Soil 2010, 337, 285–297. [Google Scholar] [CrossRef]
- Högberg, P. Tansley Review No. 95 15N natural abundance in soil-plant systems. New Phytol. 1997, 137, 179–203. [Google Scholar] [CrossRef] [PubMed]
- Martinelli, L.A.; Piccolo, M.C.; Townsend, A.R.; Vitousek, P.M.; Cuevas, E.; McDowell, W.; Robertson, G.P.; Santos, O.C.; Treseder, K. Nitrogen stable isotopic composition of leaves and soil: Tropical versus temperate forests. In New Perspectives on Nitrogen Cycling in the Temperate and Tropical Americas; Townsend, A.R., Ed.; Springer: Cham, The Netherlands, 1999; pp. 45–65. [Google Scholar]
- Pardo, L.H.; Hemond, H.F.; Montoya, J.P.; Fahey, T.J.; Siccama, T.G. Response of the natural abundance of 15N in forest soils and foliage to high nitrate loss following clear-cutting. Can. J. For. Res. 2002, 32, 1126–1136. [Google Scholar] [CrossRef]
- Högberg, P. Forests losing large quantities of nitrogen have elevated 15N:14N ratios. Oecologia 1990, 84, 229–231. [Google Scholar] [CrossRef]
- Högberg, P.; Johannisson, C. 15N Abundance of forests is correlated with losses of nitrogen. Plant Soil 1993, 157, 147–150. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Rem. Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Belward, A.S. Spectral characteristics of vegetation, soil and water in the visible, near-infrared and middle-infrared wavelengths. In Remote Sensing and Geographical Information Systems for Resource Management in Developing Countries; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1991; pp. 31–53. [Google Scholar]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red edge spectral measurements from sugar maple leaves. Int. J. Rem. Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Carter, G.A. Ratios of leaf reflectances in narrow wavebands as indicators of plant stress. Rem. Sens. 1994, 15, 697–703. [Google Scholar] [CrossRef]
- Belanger, M.J.; Miller, J.R.; Boyer, M.G. Comparative relationships between some red edge parameters and seasonal leaf chlorophyll concentrations. Can. J. Rem. Sens. 1995, 21, 16–21. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N.; Lichtenthaler, H.K. Detection of red edge position and chlorophyll content by reflectance measurements near 700 nm. J. Plant Physiol. 1996, 148, 501–508. [Google Scholar] [CrossRef]
- Yoder, B.J.; Pettigrew-Crosby, R.E. Predicting nitrogen and chlorophyll content and concentrations from reflectance spectra (400–2500 nm) at leaf and canopy scales. Rem. Sens. Environ. 1995, 53, 199–211. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Rem. Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Johnson, L.F.; Billow, C.R. Spectrometry estimation of total nitrogen concentration in Douglas-fir foliage. Int. J. Rem. Sens. 1996, 17, 489–500. [Google Scholar] [CrossRef]
- Peterson, D.L.; Aber, J.D.; Matson, P.A.; Card, D.H.; Swanberg, N.; Wessman, C.; Spanner, M. Remote sensing of forest canopy and leaf biochemical contents. Rem. Sens. Environ. 1988, 24, 85–108. [Google Scholar] [CrossRef]
- Coops, N.C.; Smith, M.L.; Martin, M.E.; Ollinger, S.V. Prediction of eucalypt foliage nitrogen content from satellite-derived hyperspectral data. IEEE Trans. Geosci. Rem. Sens. 2003, 41, 1338–1346. [Google Scholar] [CrossRef]
- Martin, M.E.; Aber, J.D. High spectral resolution remote sensing of forest canopy lignin, nitrogen, and ecosystem processes. Ecol. Appl. 1997, 7, 431–443. [Google Scholar] [CrossRef]
- Martin, M.E.; Plourde, L.C.; Ollinger, S.V.; Smith, M.L.; McNeil, B.E. A generalizable method for remote sensing of canopy nitrogen across a wide range of forest ecosystems. Rem. Sens. Environ. 2008, 112, 3511–3519. [Google Scholar] [CrossRef]
- Townsend, P.A.; Foster, J.R.; Chastain, R.A.; Currie, W.S., Jr. Application of imaging spectroscopy to mapping canopy nitrogen in the forests of the central Appalachian Mountains using Hyperion and AVIRIS. IEEE Trans. Geosci. Rem. Sens. 2003, 41, 1347–1354. [Google Scholar] [CrossRef]
- Doughty, C.E.; Asner, G.P.; Martin, R.E. Predicting tropical plant physiology from leaf and canopy spectroscopy. Oecologia 2011, 165, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Mõttus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Carmona, P.L.; Kaufmann, R.K.; Lewis, P.; et al. Hyperspectral remote sensing of foliar nitrogen content. Proc. Nat. Acad. Sci. USA 2013, 110, E185–E192. [Google Scholar] [CrossRef] [PubMed]
- Ollinger, S.V. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, F.B.; Ollinger, S.V.; Martin, M.E.; Ducey, M.J.; Lepine, L.C.; Wicklein, H.F. Foliar nitrogen in relation to plant traits and reflectance properties of New Hampshire forests. Can. J. For. Res. 2013, 43, 18–27. [Google Scholar] [CrossRef]
- Wang, L.; Okin, G.S.; Wang, J.; Epstein, H.; Macko, S.A. Predicting leaf and canopy 15N compositions from reflectance spectra. Geophys. Res. Let. 2007, 34, L02401. [Google Scholar]
- Wang, L.; Okin, G.S.; Macko, S.A. Remote Sensing of Nitrogen and Carbon Isotope Compositions in Terrestrial Ecosystems. In Isoscapes; West, J.B., Bowen, G.J., Dawson, T.E., Tu, K.P., Eds.; Springer: Cham, The Netherlands, 2010; pp. 51–70. [Google Scholar]
- Elmore, A.J.; Craine, J.M. Spectroscopic Analysis of Canopy Nitrogen and Nitrogen Isotopes in Managed Pastures and Hay Land. IEEE Trans. Geosci. Rem. Sens. 2011, 49, 2491–2498. [Google Scholar] [CrossRef]
- Kleinebecker, T.; Schmidt, S.R.; Fritz, C.; Smolders, A.J.P.; Hölzel, N. Prediction of δ13C and δ15N in plant tissues with near-infrared reflectance spectroscopy. New Phytol. 2009, 184, 732–739. [Google Scholar] [CrossRef]
- Hellman, C.; Grobe-Stoletenberg, A.; Laustroer, V.; Oldeland, J.; Werner, C. Retrieving nitrogen isotopic signatures from fresh leaf reflectance spectra: Disentangling δ15N from biochemical and structural leaf properties. Front. Plant Sci. 2015, 6, 307. [Google Scholar] [CrossRef]
- Hobbie, E.A.; Macko, S.A.; Williams, M. Correlations between foliar δ15N and nitrogen concentrations may indicate plant-mycorrhizal interactions. Oecologia 2000, 122, 273–283. [Google Scholar] [CrossRef] [PubMed]
- Serbin, S.; Singh, A.; McNeil, B.; Kingdon, C.; Townsend, P. Spectroscopic determination of leaf morphological and biochemical traits for northern temperate and boreal tree species. Ecol. Appl. 2014, 24, 1651–1669. [Google Scholar] [CrossRef] [PubMed]
- Smith, W.B.; Miles, P.D.; Perry, C.H.; Pugh, S.A. Forest resources of the United States, 2007: A technical document supporting the forest service 2010 RPA Assessment. In General Technical Report—USDA Forest Service, (WO-78); United States Department of Agriculture, Forest Service: Washington, DC, USA, 2009. [Google Scholar]
- King, J.E. Site index curves for Douglas-fir in the Pacific Northwest. In Weyerhauser Forestry Paper No. 8; Weyerhaeuser Company, Forestry Research Center: Centralia, WA, USA, 1996; pp. 36–38. [Google Scholar]
- Amateis, R.L.; Burkhart, H.E. Site Index Curves for Loblolly Pine Plantations on Cutover Site-Prepared Lands. South. J. Appl. For. 1985, 9, 166–169. [Google Scholar] [CrossRef]
- Sulzman, E.W. Stable isotope chemistry and measurement: A primer. In Stable Isotopes in Ecology and Environmental Science; Michener, R.M., Lajtha, K., Eds.; Blackwell Publishers: Oxford, UK, 2007; pp. 1–21. [Google Scholar]
- Cho, M.A.; Skidmore, A.K. A new technique for extracting the red edge position from hyperspectral data: The linear extrapolation method. Rem. Sens. Environ. 2006, 101, 181–193. [Google Scholar] [CrossRef]
- Serrano, L.; Peñuelas, J.; Ustin, S.L. Remote sensing of nitrogen and lignin in Mediterranean vegetation from AVIRIS data: Decomposing biochemical from structural signals. Rem. Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
- Filella, I.; Penuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Rem. Sens. 1994, 15, 1459–1470. [Google Scholar] [CrossRef]
- Van den Berg, A.K.; Perkins, T.D. Nondestructive Estimation of Anthocyanin Content in Autumn Sugar Maple Leaves. HortScience 2005, 40, 685–686. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N.; Chivkunova, O.B. Optical Properties and Nondestructive Estimation of Anthocyanin Content in Plant Leaves. Photochem. Photobiol. 2001, 74, 38–45. [Google Scholar] [CrossRef]
- Kim, M.S. The Use of Narrow Spectral Bands for Improving Remote Sensing Estimations of Fractionally Absorbed Photosynthetically Active Radiation (Fapar). Ph.D. Dissertation, University of Maryland, College Park, MD, USA, 1994. [Google Scholar]
- Gitelson, A.A.; Keydan, G.P.; Merzlyak, M.N. Three-band model for noninvasive estimation of chlorophyll, carotenoids, and anthocyanin contents in higher plant leaves. Geophys. Res. Let. 2006, 33, 11. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Zur, Y.; Chivkunova, O.B.; Merzlyak, M.N. Assessing Carotenoid Content in Plant Leaves with Reflectance Spectroscopy. Photochem. Photobiol. 2002, 75, 272–281. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L.; Sampson, P.H. Vegetation Stress Detection through Chlorophyll a+b Estimation and Fluorescence Effects on Hyperspectral Imagery. J. Environ. Qual. 2002, 31, 1433–1441. [Google Scholar] [CrossRef] [PubMed]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L.; Sampson, P.H. Canopy optical indices from infinite reflectance and canopy reflectance models for forest condition monitoring: Application to hyperspectral CASI data. In Proceedings of the Geoscience and Remote Sensing Symposium, 1999. IGARSS ’99 Proceedings, Hamburg, Germany, 28 June–2 July 1999; Volume 1873, pp. 1878–1881. [Google Scholar]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; van Leeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Rem. Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Gökkaya, K. Prediction of Foliar Biochemistry in a Boreal Forest Canopy Using Imaging Spectroscopy and LiDAR Data. Ph.D. Dissertation, Virginia Tech, Blacksburg, VA, USA, 2012. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Rem. Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Oppelt, N.; Mauser, W. Hyperspectral monitoring of physiological parameters of wheat during a vegetation period using AVIS data. Int. J. Rem. Sens. 2004, 25, 145–159. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K.; Gitelson, A.; Lang, M. Non-Destructive Determination of Chlorophyll Content of Leaves of a Green and an Aurea Mutant of Tobacco by Reflectance Measurements. J. Plant Physiol. 1996, 148, 483–493. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey Iii, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Rem. Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with Erts; NASA Special Publication: Washington, DC, USA, 1974. [Google Scholar]
- Gamon, J.A.; Serrano, L.; Surfus, J.S. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral indices for estimating photosynthetic pigment concentrations: A test using senescent tree leaves. Int. J. Rem. Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plantar. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Gamon, J.A.; Surfus, J.S. Assessing leaf pigment content and activity with a reflectometer. New Phytol. 1999, 143, 105–117. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Rem. Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hobokon, NJ, USA, 2012. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrica 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Emmett, B.A.; Kjonaas, O.J.; Gundersen, P.; Koopmans, C.J.; Tietma, A.; Sleep, D. Natural abundance of 15N in forests across a nitrogen deposition gradient. For. Ecol. Man. 1998, 101, 9–18. [Google Scholar] [CrossRef]
- Pardo, L.H.; Templer, P.H.; Goodale, C.L.; Duke, S.; Groffman, P.M.; Adams, M.B.; Boeckx, P.; Boggs, J.; Campbell, J.; Colman, B.; et al. Regional Assessment of N Saturation using Foliar and Root d15N. Biogeochemistry 2006, 80, 143–171. [Google Scholar] [CrossRef]
- Cho, M.S.; Skidmore, A.K. Hyperspectral predictors for monitoring biomass production in Mediterranean mountain grasslands: Majella National Park, Italy. Int. J. Rem. Sens. 2009, 30, 499–515. [Google Scholar] [CrossRef]
- Lamb, D.W.; Steyn-Ross, M.; Schaare, P.; Hanna, M.M.; Silvester, W.; Steyn-Ross, A. Estimating leaf nitrogen concentration in ryegrass (Lolium spp.) pasture using the chlorophyll red-edge: Theoretical modelling and experimental observations. Int. J. Rem. Sens. 2002, 23, 3619–3648. [Google Scholar] [CrossRef]
- Smith, M.L.; Ollinger, S.V.; Martin, M.E.; Aber, J.D.; Hallett, R.A.; Goodale, C.L. Direct estimation of above ground forest productivity through hyperspectral remote sensing of canopy nitrogen. Ecol. Appl. 2002, 12, 1286–1302. [Google Scholar] [CrossRef]
- Garten, C.T.J.; Van Miegroet, H. Relationships between soil nitrogen dynamics and natural 15N abundance in plant foliage from Great Smokey Mountains National Park. Can. J. For. Res. 1994, 24, 1636–1645. [Google Scholar] [CrossRef]
- Joshi, A.B.; Vann, D.R.; Johnson, A.H.; Miller, E.K. Nitrogen availability and forest productivity along a climosequence on Whiteface Mountain, New York. Can. J. For. Res. 2003, 33, 1880–1891. [Google Scholar] [CrossRef]
- Nadelhoffer, K.J.; Aber, J.D.; Melillo, J.M. Fine Roots, Net Primary Production, and Soil Nitrogen Availability: A New Hypothesis. Ecol. 1985, 66, 1377–1390. [Google Scholar] [CrossRef]
- Pastor, J.; Aber, J.D.; McClaugherty, C.A.; Melillo, J.M. Aboveground Production and N and P Cycling Along a Nitrogen Mineralization Gradient on Blackhawk Island, Wisconsin. Ecology 1984, 65, 256–268. [Google Scholar] [CrossRef]
- Schultz, R.P. Lololly pine: The ecology and culture of loblolly pine (Pinus Taeda L.). In Agriculture Handbook 713; USDA Forest Service: Washington, DC, USA, 1997; 493p. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).