Assessment of Tree Diameter Estimation Methods from Mobile Laser Scanning in a Historic Garden
Abstract
:1. Introduction
2. Materials and Methods
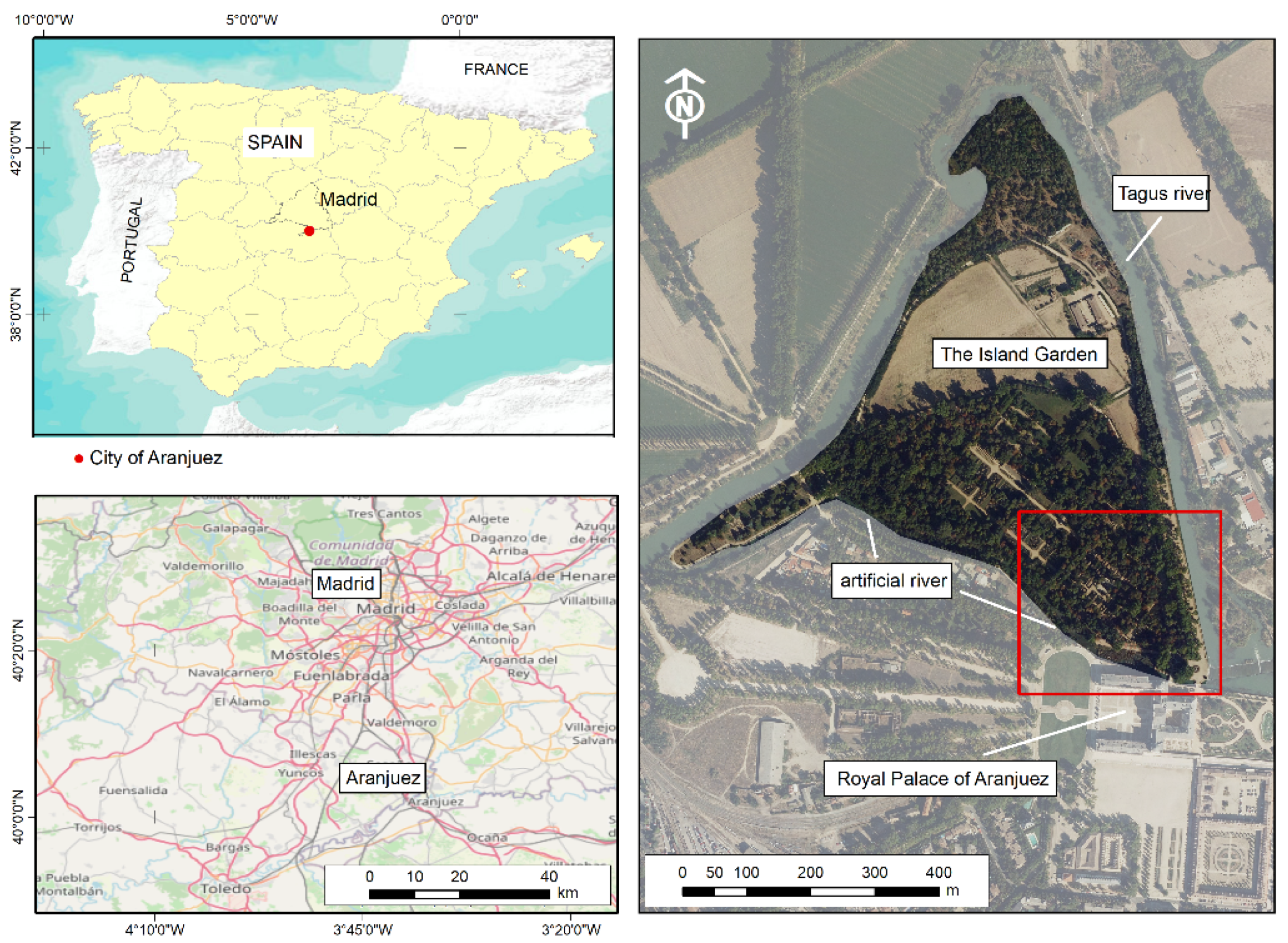
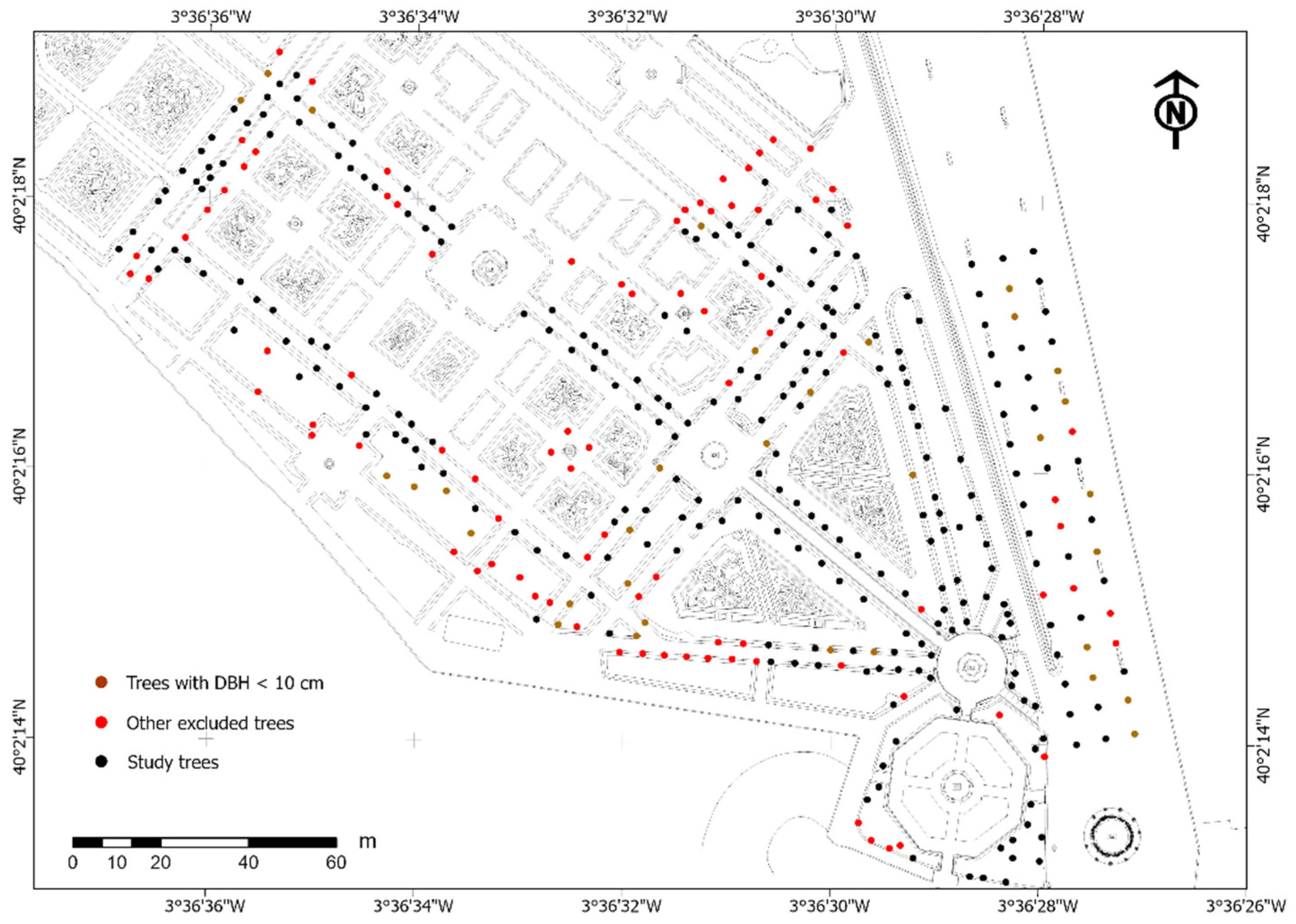
2.1. Case Study Description
2.2. Materials
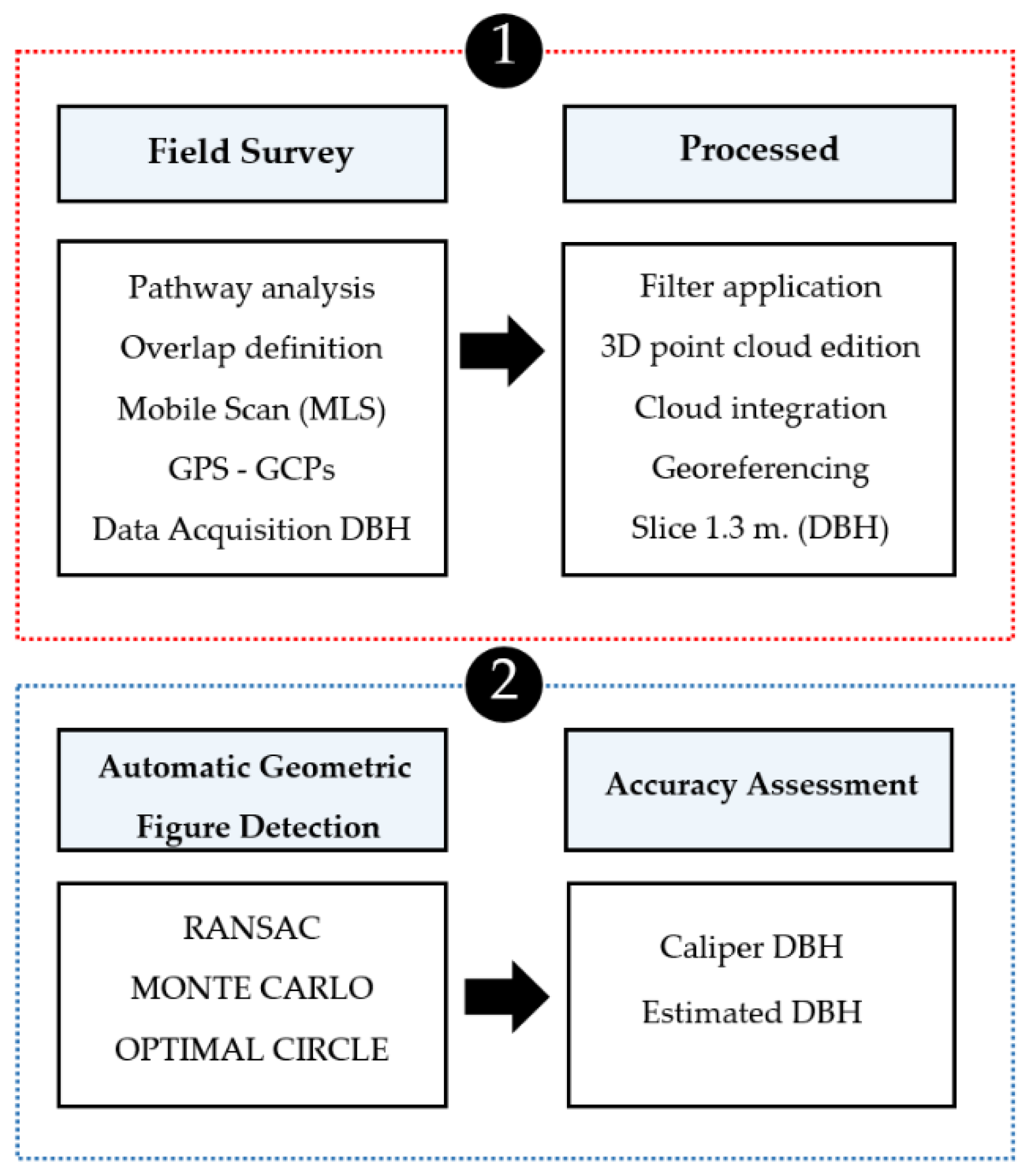
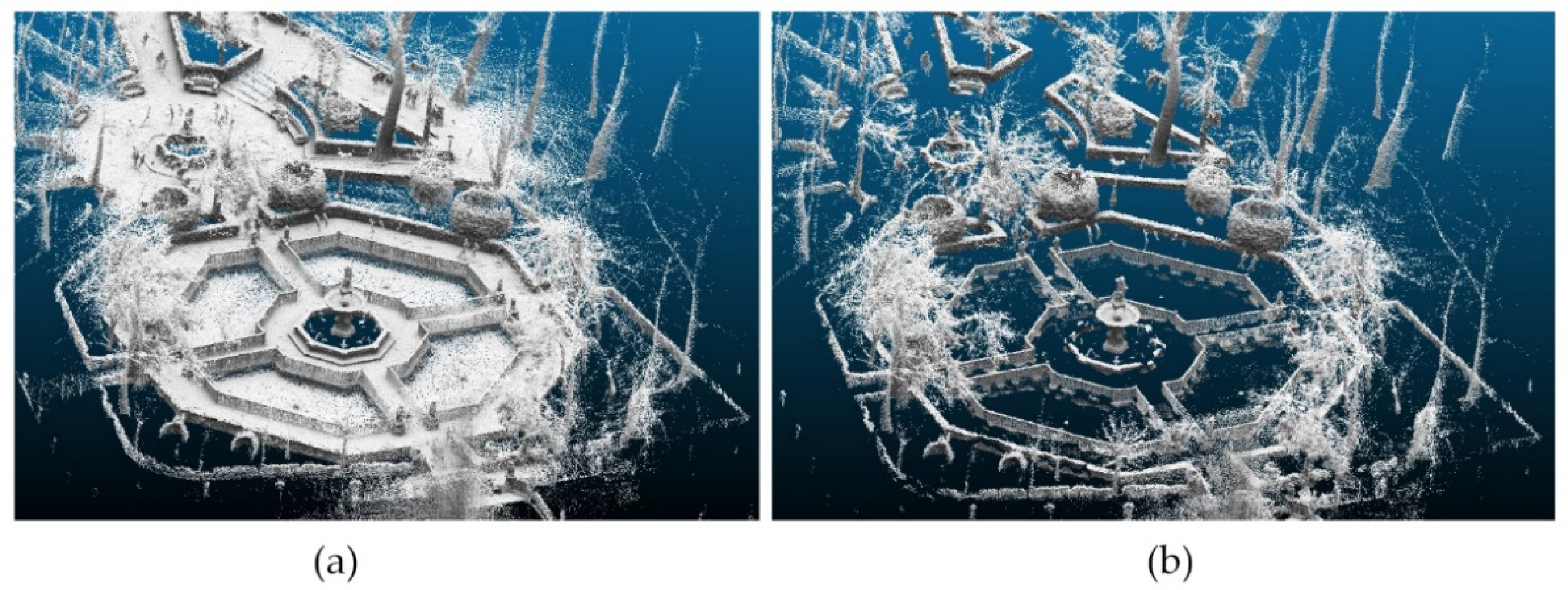
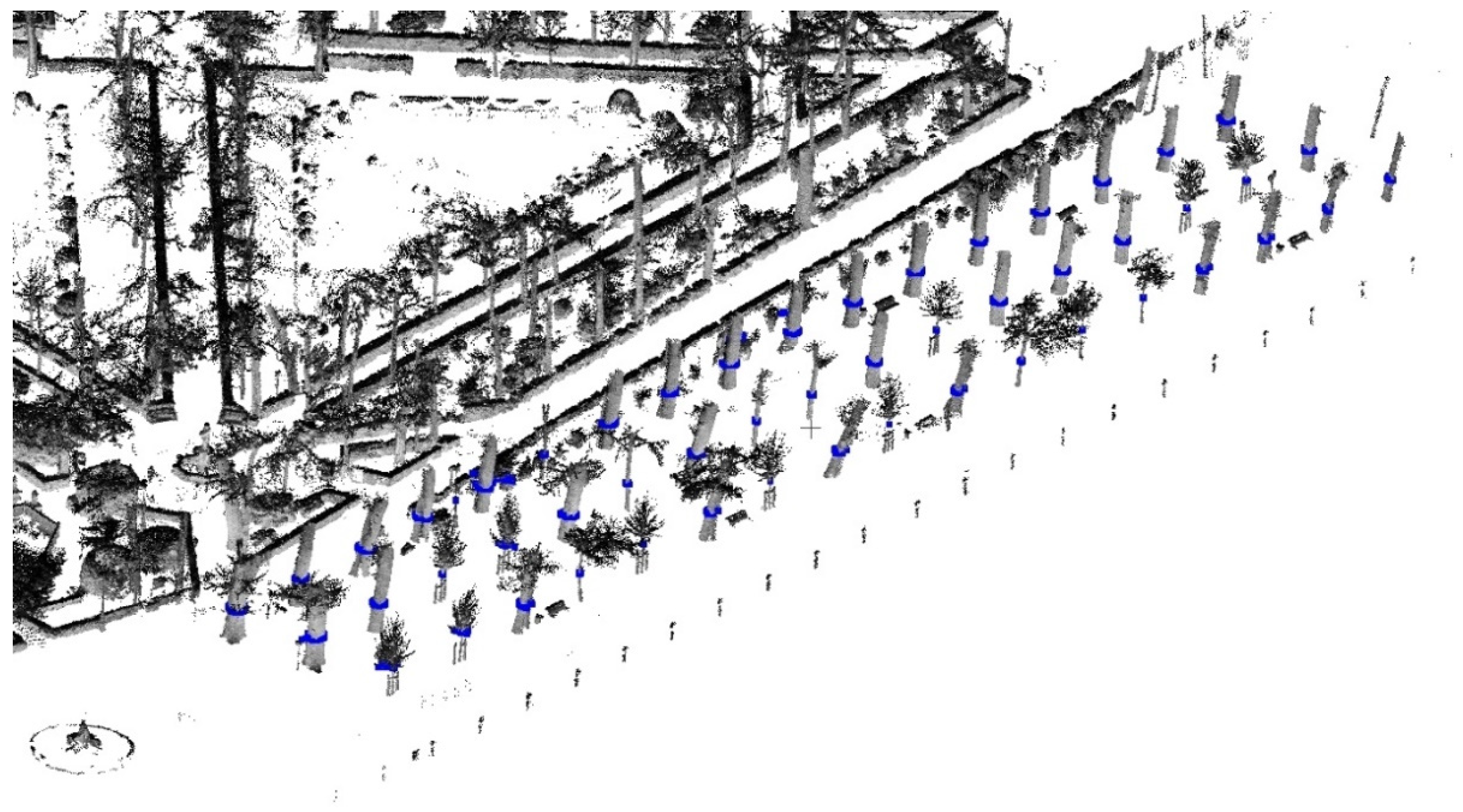
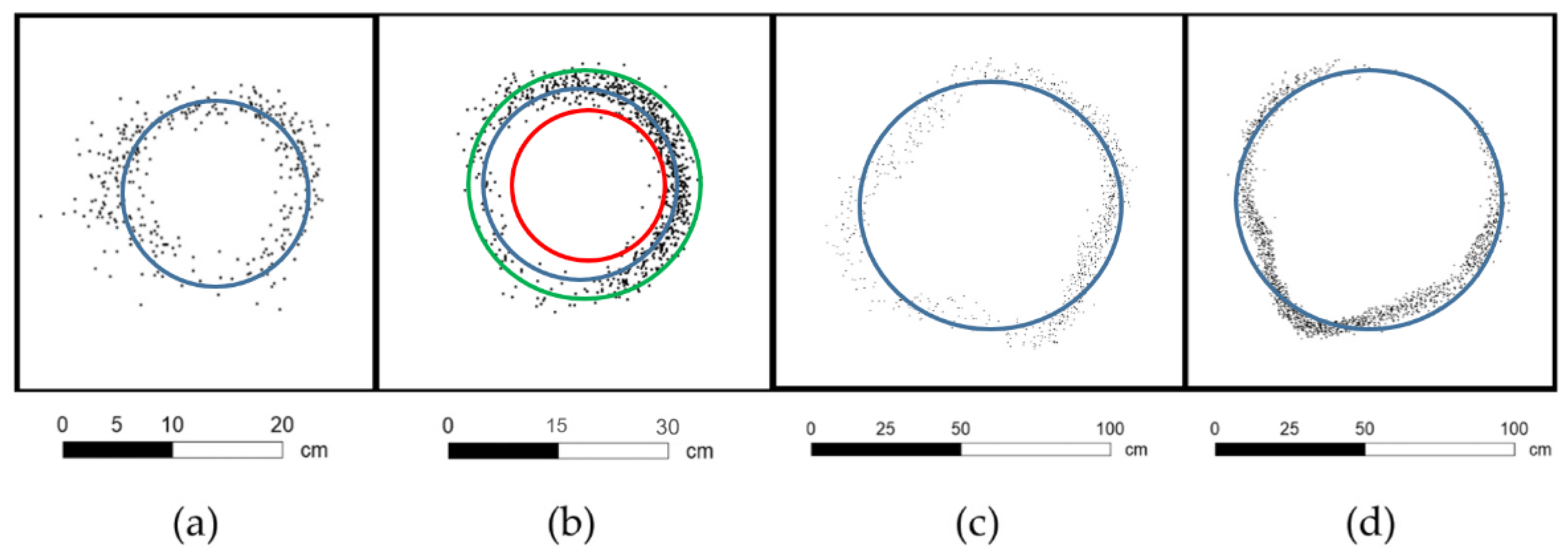
2.3. Methods
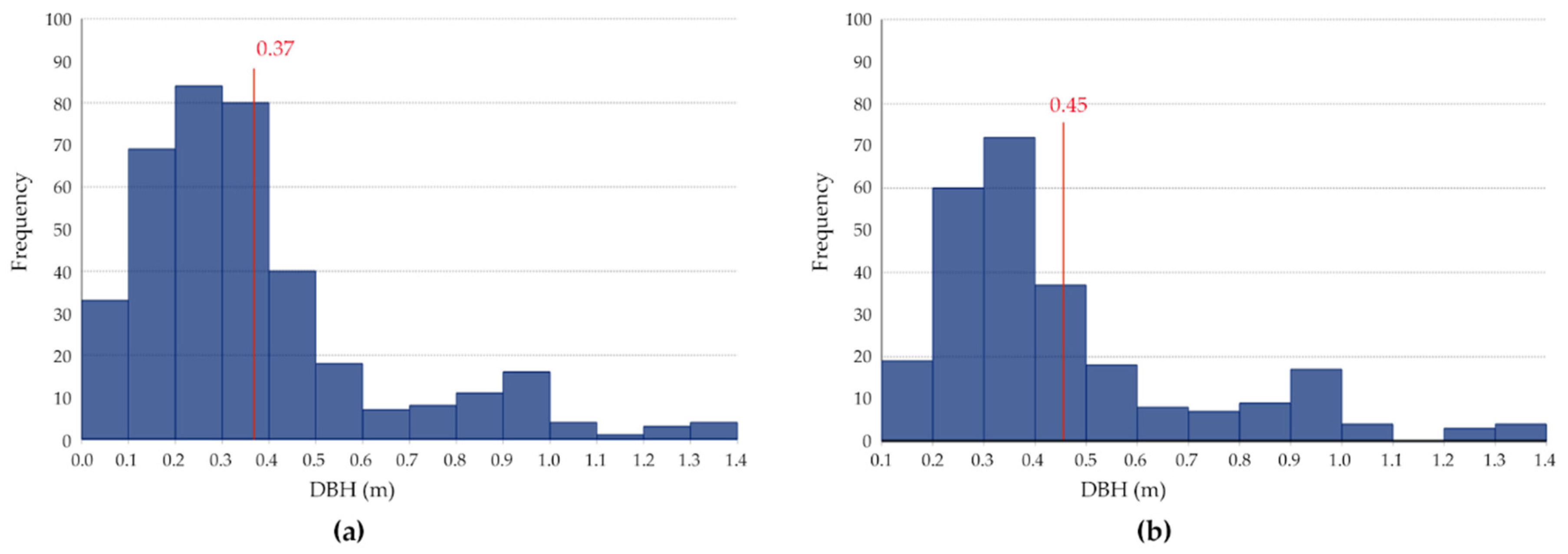
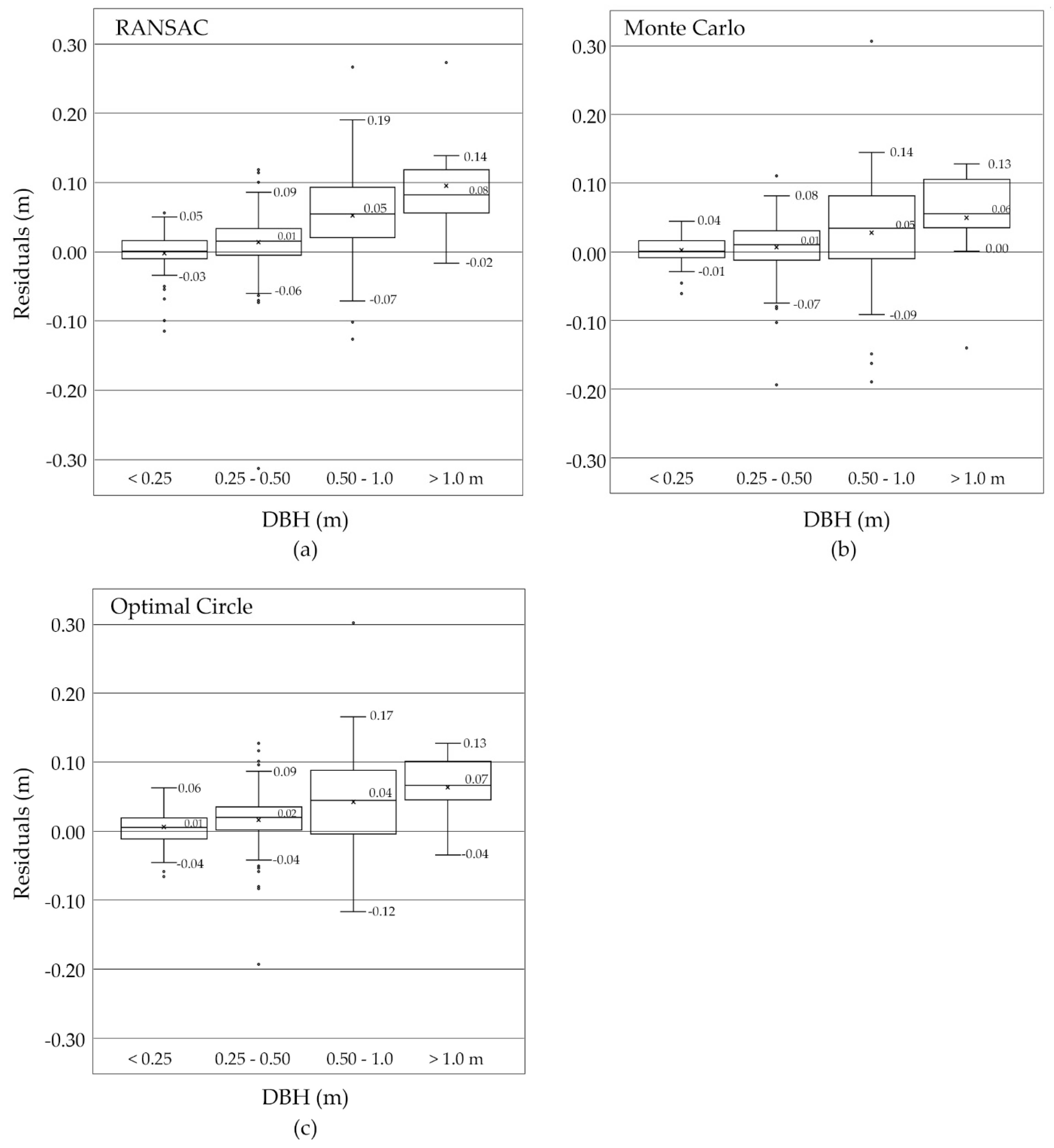
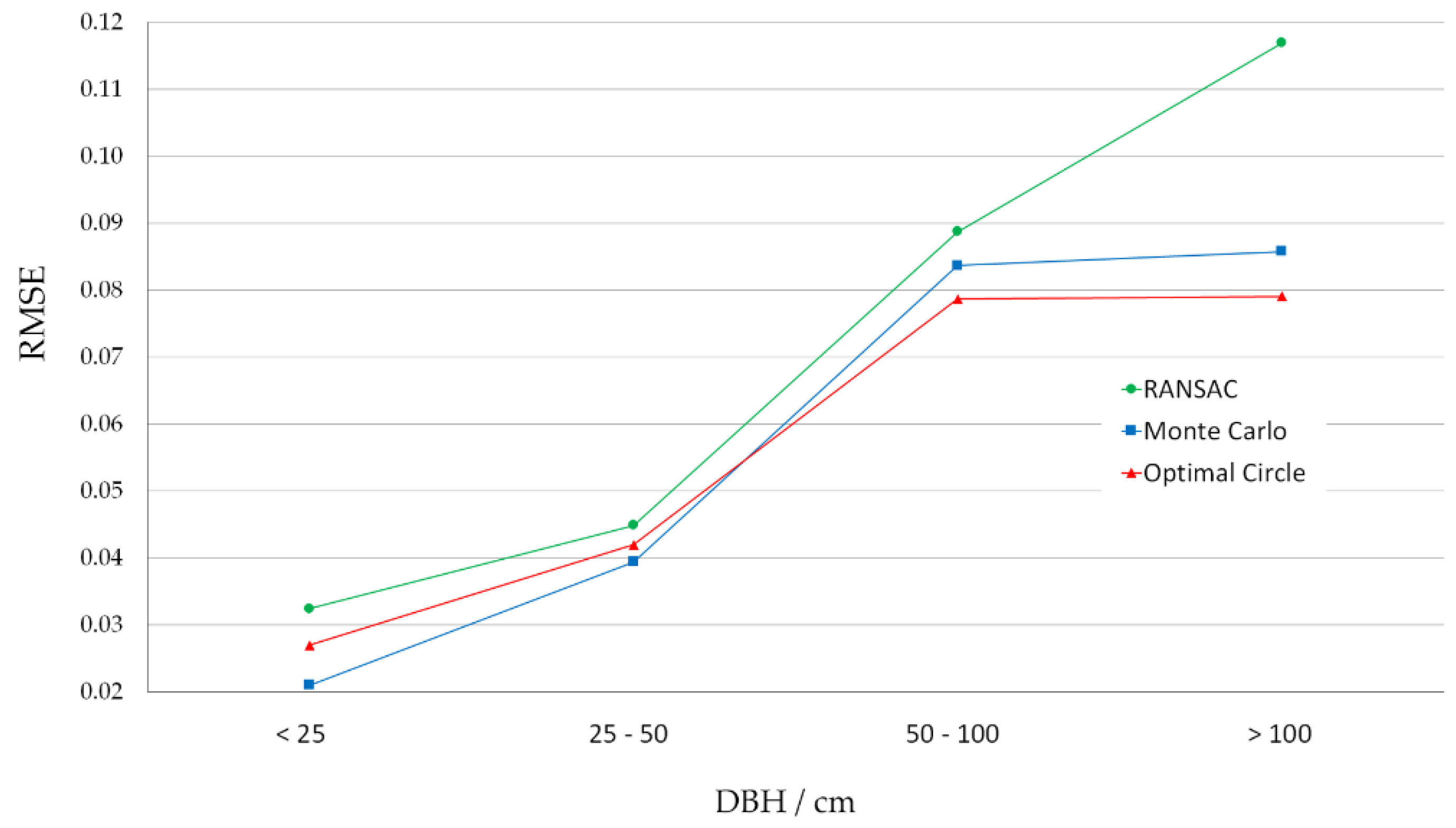
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Merlos Romero, M. Paisaje cultural de aranjuez: Parámetros para un plan de gestión. Am. Patrim. 2013, 5, 24–39. [Google Scholar]
- Herrero-Tejedor, T.R.; Arques Soler, F.; Lopez-Cuervo Medina, S.; Cabrera, M.R.d.l.O.; Martin Romero, J.L. Documenting a cultural landscape using point-cloud 3d models obtained with geomatic integration techniques. The case of the El Encin atomic garden, Madrid (Spain). PLoS ONE 2020, 15, e0235169. [Google Scholar] [CrossRef]
- Liang, X.L.; Hyyppa, J.; Kaartinen, H.; Lehtomaki, M.; Pyorala, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Pirotti, F.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Cazzani, A.; Zerbi, C.M.; Brumana, R. Management Plans and Web-GIS Software Applications as Active and Dynamic Tools to Conserve and Valorize Historic Public Gardens. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W15, 291–298. [Google Scholar] [CrossRef] [Green Version]
- Hackenberg, J.; Morhart, C.; Sheppard, J.; Spiecker, H.; Disney, M. Highly Accurate Tree Models Derived from Terrestrial Laser Scan Data: A Method Description. Forests 2014, 5, 1069–1105. [Google Scholar] [CrossRef] [Green Version]
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial LiDAR technology in forest science: Application fields, benefits and challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Li, L.; Mu, X.; Soma, M.; Wan, P.; Qi, J.; Hu, R.; Zhang, W.; Tong, Y.; Yan, G. An Iterative-Mode Scan Design of Terrestrial Laser Scanning in Forests for Minimizing Occlusion Effects. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3547–3566. [Google Scholar] [CrossRef]
- Kukenbrink, D.; Gardi, O.; Morsdorf, F.; Thurig, E.; Schellenberger, A.; Mathys, L. Above-ground biomass references for urban trees from terrestrial laser scanning data. Ann. Bot. 2021. [Google Scholar] [CrossRef]
- Xia, S.; Chen, D.; Peethambaran, J.; Wang, P.; Xu, S. Point Cloud Inversion: A Novel Approach for the Localization of Trees in Forests from TLS Data. Remote Sens. 2021, 13, 338. [Google Scholar] [CrossRef]
- Watt, P.J.; Donoghue, D.N.M. Measuring forest structure with terrestrial laser scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
- Torralba, J.; Crespo-Peremarch, P.; Ruiz, L.A. Assessing the use of discrete, full-waveform LiDAR and TLS to classify Mediterranean forest species composition. Rev. Teledetec. 2018, 27–40. [Google Scholar] [CrossRef] [Green Version]
- Yrttimaa, T.; Luoma, V.; Saarinen, N.; Kankare, V.; Junttila, S.; Holopainen, M.; Hyyppa, J.; Vastaranta, M. Structural Changes in Boreal Forests Can Be Quantified Using Terrestrial Laser Scanning. Remote Sens. 2020, 12, 2672. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef] [Green Version]
- Gollob, C.; Ritter, T.; Wassermann, C.; Nothdurft, A. Influence of Scanner Position and Plot Size on the Accuracy of Tree Detection and Diameter Estimation Using Terrestrial Laser Scanning on Forest Inventory Plots. Remote Sens. 2019, 11, 1602. [Google Scholar] [CrossRef] [Green Version]
- Pueschel, P.; Newnham, G.; Rock, G.; Udelhoven, T.; Werner, W.; Hill, J. The influence of scan mode and circle fitting on tree stem detection, stem diameter and volume extraction from terrestrial laser scans. ISPRS J. Photogramm. Remote Sens. 2013, 77, 44–56. [Google Scholar] [CrossRef]
- Koren, M.; Mokros, M.; Bucha, T. Accuracy of tree diameter estimation from terrestrial laser scanning by circle-fitting methods. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 122–128. [Google Scholar] [CrossRef]
- Piermattei, L.; Karel, W.; Wang, D.; Wieser, M.; Mokros, M.; Surovy, P.; Koren, M.; Tomastik, J.; Pfeifer, N.; Hollaus, M. Terrestrial Structure from Motion Photogrammetry for Deriving Forest Inventory Data. Remote Sens. 2019, 11, 950. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Feng, Z.; Shen, C.; Khan, T.U.; Mannan, A.; Gao, X.; Chen, P.; Saeed, S. A trunk-based SLAM backend for smartphones with online SLAM in large-scale forest inventories. ISPRS J. Photogramm. Remote Sens. 2020, 162, 41–49. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Nothdurft, A. Forest Inventory with Long Range and High-Speed Personal Laser Scanning (PLS) and Simultaneous Localization and Mapping (SLAM) Technology. Remote Sens. 2020, 12, 1509. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppa, J. Automatic Stem Mapping by Merging Several Terrestrial Laser Scans at the Feature and Decision Levels. Sensors 2013, 13, 1614–1634. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nurunnabi, A.; Sadahiro, Y.; Lindenbergh, R. Robust cylinder fitting in three-dimensional point cloud data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 63–70. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Wang, S.; Li, J.; Ma, L.; Wu, R.; Luo, Z.; Wang, C. Rapid Urban Roadside Tree Inventory Using a Mobile Laser Scanning System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3690–3700. [Google Scholar] [CrossRef]
- Herrero-Huerta, M.; Lindenbergh, R.; Rodriguez-Gonzalvez, P. Automatic tree parameter extraction by a Mobile LiDAR System in an urban context. PLoS ONE 2018, 13, e0196004. [Google Scholar] [CrossRef] [Green Version]
- Duanmu, J.; Xing, Y.Q. Annular Neighboring Points Distribution Analysis: A Novel PLS Stem Point Cloud Preprocessing Algorithm for DBH Estimation. Remote Sens. 2020, 12, 808. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef] [PubMed]
- Király, G.; Brolly, G. Tree height estimation methods for terrestrial laser scanning in a forest reserve. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 36, 211–215. [Google Scholar]
- Bienert, A.; Georgi, L.; Kunz, M.; Maas, H.-G.; von Oheimb, G. Comparison and Combination of Mobile and Terrestrial Laser Scanning for Natural Forest Inventories. Forests 2018, 9, 395. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Kukko, A.; Kaartinen, H.; Hyyppa, J.; Yu, X.; Jaakkola, A.; Wang, Y. Possibilities of a Personal Laser Scanning System for Forest Mapping and Ecosystem Services. Sensors 2014, 14, 1228–1248. [Google Scholar] [CrossRef]
- Smith, A.; Astrup, R.; Raumonen, P.; Liski, J.; Krooks, A.; Kaasalainen, S.; Akerblom, M.; Kaasalainen, M. Tree Root System Characterization and Volume Estimation by Terrestrial Laser Scanning and Quantitative Structure Modeling. Forests 2014, 5, 3274–3294. [Google Scholar] [CrossRef]
- Tang, J.; Chen, Y.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Khoramshahi, E.; Hakala, T.; Hyyppa, J.; Holopainen, M.; Hyyppa, H. SLAM-Aided Stem Mapping for Forest Inventory with Small-Footprint Mobile LiDAR. Forests 2015, 6, 4588–4606. [Google Scholar] [CrossRef] [Green Version]
- Gwenzi, D.; Lefsky, M.A. Plot-level aboveground woody biomass modeling using canopy height and auxiliary remote sensing data in a heterogeneous savanna. J. Appl. Remote Sens. 2016, 10, 016001. [Google Scholar] [CrossRef]
- Forsman, M.; Holmgren, J.; Olofsson, K. Tree Stem Diameter Estimation from Mobile Laser Scanning Using Line-Wise Intensity-Based Clustering. Forests 2016, 7, 206. [Google Scholar] [CrossRef] [Green Version]
- Forsman, M.; Borlin, N.; Olofsson, K.; Reese, H.; Holmgren, J. Bias of cylinder diameter estimation from ground-based laser scanners with different beam widths: A simulation study. ISPRS J. Photogramm. Remote Sens. 2018, 135, 84–92. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree Stem and Height Measurements using Terrestrial Laser Scanning and the RANSAC Algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef] [Green Version]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Ritter, T.; Schwarz, M.; Tockner, A.; Leisch, F.; Nothdurft, A. Automatic Mapping of Forest Stands Based on Three-Dimensional Point Clouds Derived from Terrestrial Laser-Scanning. Forests 2017, 8, 265. [Google Scholar] [CrossRef]
- Liu, C.; Xing, Y.; Duanmu, J.; Tian, X. Evaluating Different Methods for Estimating Diameter at Breast Height from Terrestrial Laser Scanning. Remote Sens. 2018, 10, 513. [Google Scholar] [CrossRef] [Green Version]
- Ravaglia, J.; Fournier, R.A.; Bac, A.; Vega, C.; Cote, J.-F.; Piboule, A.; Remillard, U. Comparison of Three Algorithms to Estimate Tree Stem Diameter from Terrestrial Laser Scanner Data. Forests 2019, 10, 599. [Google Scholar] [CrossRef] [Green Version]
- Brolly, G.; Kiraly, G. Algorithms for stem mapping by means of terrestrial laser scanning. Acta Silv. Lignaria Hung. 2009, 5, 119–130. [Google Scholar]
- UNESCO. New Sites on the World Heritage List. Available online: http://whc.unesco.org/en/news/143/ (accessed on 8 September 2020).
- UNESCO. Aranjuez Cultural Landscape. Available online: http://whc.unesco.org/en/list/1044 (accessed on 8 September 2020).
- Madrid, C.D. Catálogo Regional de Especies Amenazadas de Fauna y Silvestres, y de Árboles Singulares. In Guías de la Naturaleza; Ed. Comunidad de Madrid: Madrid, Spain, 2013; p. 492. [Google Scholar]
- Patrimonio Nacional. Spain. Available online: https://www.patrimonionacional.es/ (accessed on 24 February 2021).
- ZEB. Horizon—GeoSLAM. Available online: https://geoslam.com/solutions/zeb-horizon/ (accessed on 30 September 2020).
- Bailey, T.; Durrant-Whyte, H. Simultaneous localization and mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 108–117. [Google Scholar] [CrossRef] [Green Version]
- Cabo, C.; Ordonez, C.; Lopez-Sanchez, C.A.; Armesto, J. Automatic dendrometry: Tree detection, tree height and diameter estimation using terrestrial laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 164–174. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef] [Green Version]
- LeicaGeoOffice. Available online: https://leica-geosystems.com/es-es/products/total-stations/software/leica-geo-office (accessed on 5 October 2020).
- CloudCompare. Available online: http://www.cloudcompare.org/ (accessed on 2 October 2020).
- Dewez, T.J.B.; Yart, S.; Thuon, Y.; Pannet, P.; Plat, E. Towards cavity-collapse hazard maps with Zeb-Revo handheld laser scanner point clouds. Photogramm. Rec. 2017, 32, 354–376. [Google Scholar] [CrossRef] [Green Version]
- Ryding, J.; Williams, E.; Smith, M.J.; Eichhorn, M.P. Assessing Handheld Mobile Laser Scanners for Forest Surveys. Remote Sens. 2015, 7, 1095–1111. [Google Scholar] [CrossRef] [Green Version]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus—A Paradigm for Model-Fitting with Applications to Image-Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Mokros, M.; Koreň, M. DendroCloud: Free Terrestrial-Based Point Cloud Processing Software for Forestry; Czech University of Life Sciences Prague (Czech Republic): Praha-Suchdol, Czech Republic, 2019. [Google Scholar]
- Sveier, A.; Kleppe, A.L.; Tingelstad, L.; Egeland, O. Object Detection in Point Clouds Using Conformal Geometric Algebra. Adv. Appl. Clifford Algebras 2017, 27, 1961–1976. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Zhang, J.; Chen, X.; Pang, S.; Zeng, H.; Shen, Z. Accuracy assessment and error analysis for diameter at breast height measurement of trees obtained using a novel backpack LiDAR system. For. Ecosyst. 2020, 7, 1–11. [Google Scholar] [CrossRef]
- Cernava, J.; Tucek, J.; Koren, M.; Mokros, M. Estimation of diameter at breast height from mobile laser scanning data collected under a heavy forest canopy. J. For. Sci. 2017, 63, 433–441. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppa, J.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Yu, X. The Use of a Mobile Laser Scanning System for Mapping Large Forest Plots. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1504–1508. [Google Scholar] [CrossRef]
- James, M.R.; Quinton, J.N. Ultra-rapid topographic surveying for complex environments: The hand-held mobile laser scanner (HMLS). Earth Surf. Process. Landf. 2014, 39, 138–142. [Google Scholar] [CrossRef] [Green Version]

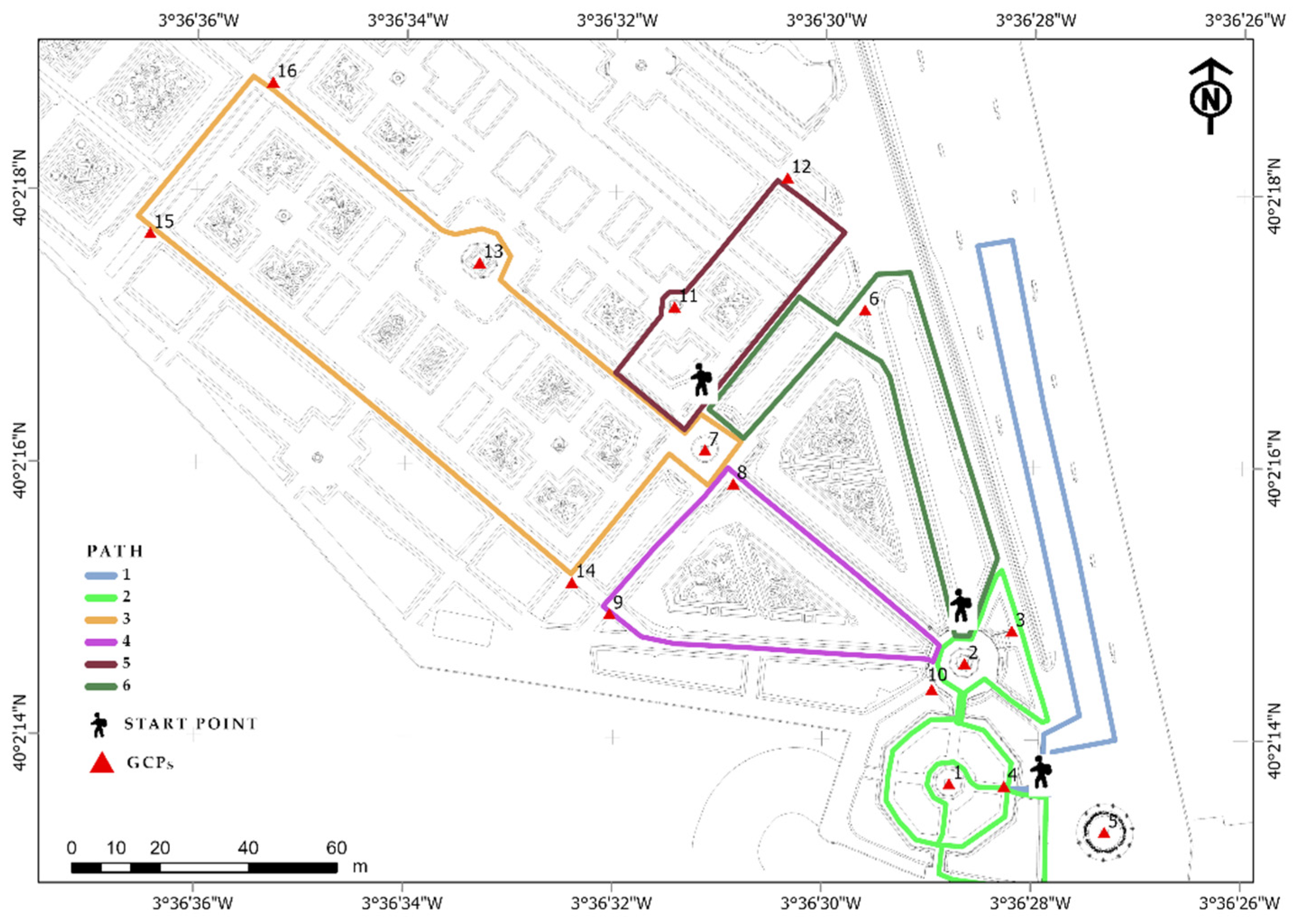


| Path | Distance (m) | Points | Time |
|---|---|---|---|
| 1 | 298 | 5,420,396 | 5 min 11 s |
| 2 | 300 | 5,325,954 | 5 min 27 s |
| 3 | 378 | 3,072,892 | 3 min 14 s |
| 4 | 186 | 5,052,089 | 4 min 48 s |
| 5 | 156 | 3,829,763 | 3 min 49 s |
| 6 | 272 | 5,383,714 | 5 min 08 s |
| Total | 1590 | 28,084,808 | 27 min 37 s |
| RANSAC | Monte Carlo | Optimal Circle | ||||
|---|---|---|---|---|---|---|
| DBH (m) | RMSE (cm) | BIAS (cm) | RMSE (cm) | BIAS (cm) | RMSE (cm) | BIAS (cm) |
| <0.25 m | 3.24 | −0.22 | 2.10 | 0.21 | 2.70 | 0.54 |
| 0.25–0.5 m | 4.48 | 1.34 | 3.94 | 0.65 | 4.20 | 1.54 |
| 0.5–1.0 m | 8.87 | 5.22 | 8.37 | 2.75 | 7.86 | 4.19 |
| >1.0 m | 11.68 | 9.47 | 8.58 | 4.94 | 7.90 | 6.31 |
| total | 6.04 | 2.26 | 5.31 | 1.23 | 5.25 | 2.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Martín, E.; López-Cuervo Medina, S.; Herrero-Tejedor, T.; Pérez-Souza, M.A.; Aguirre de Mata, J.; Ezquerra-Canalejo, A. Assessment of Tree Diameter Estimation Methods from Mobile Laser Scanning in a Historic Garden. Forests 2021, 12, 1013. https://doi.org/10.3390/f12081013
Pérez-Martín E, López-Cuervo Medina S, Herrero-Tejedor T, Pérez-Souza MA, Aguirre de Mata J, Ezquerra-Canalejo A. Assessment of Tree Diameter Estimation Methods from Mobile Laser Scanning in a Historic Garden. Forests. 2021; 12(8):1013. https://doi.org/10.3390/f12081013
Chicago/Turabian StylePérez-Martín, Enrique, Serafín López-Cuervo Medina, Tomás Herrero-Tejedor, Miguel Angel Pérez-Souza, Julian Aguirre de Mata, and Alejandra Ezquerra-Canalejo. 2021. "Assessment of Tree Diameter Estimation Methods from Mobile Laser Scanning in a Historic Garden" Forests 12, no. 8: 1013. https://doi.org/10.3390/f12081013
APA StylePérez-Martín, E., López-Cuervo Medina, S., Herrero-Tejedor, T., Pérez-Souza, M. A., Aguirre de Mata, J., & Ezquerra-Canalejo, A. (2021). Assessment of Tree Diameter Estimation Methods from Mobile Laser Scanning in a Historic Garden. Forests, 12(8), 1013. https://doi.org/10.3390/f12081013









