Analytical and Numerical Verification of Vibration Design in Timber Concrete Composite Floors
Abstract
1. Introduction
2. TCC Floor System Subjected to Footfall Induced Vibration
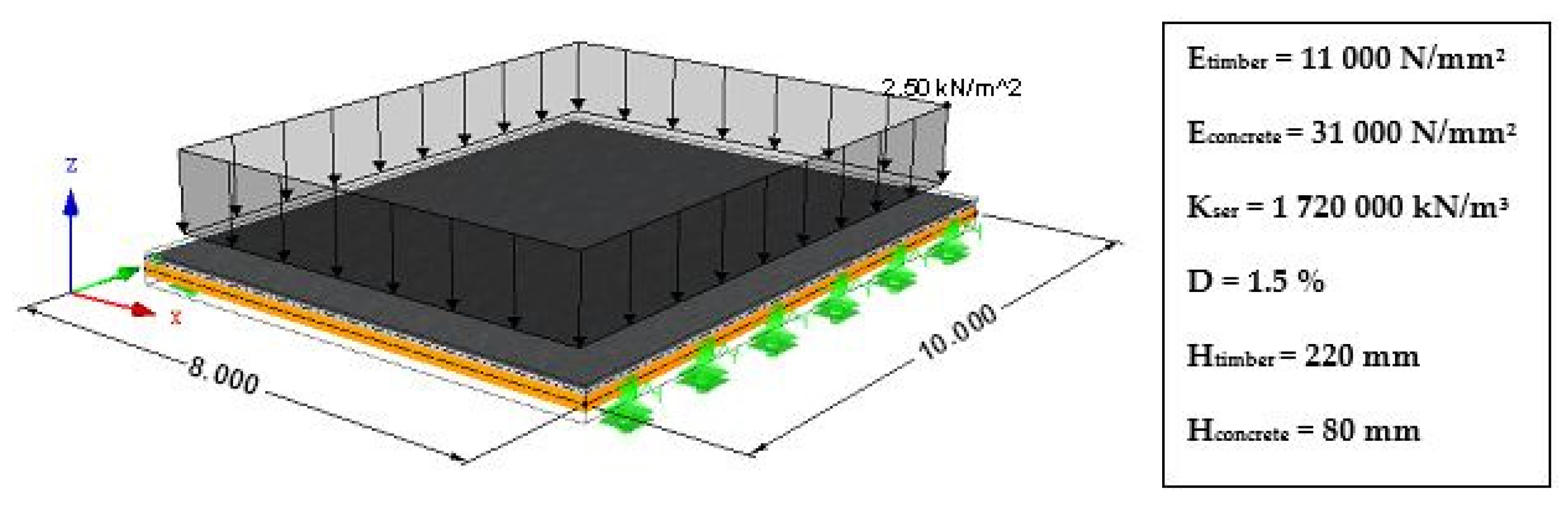
3. FEM Analysis of TCC Floor Slab
3.1. Compliance of the Connection–Kser
3.2. Results
3.3. Stiffness Design
3.4. Connector Design
3.5. Concrete Check
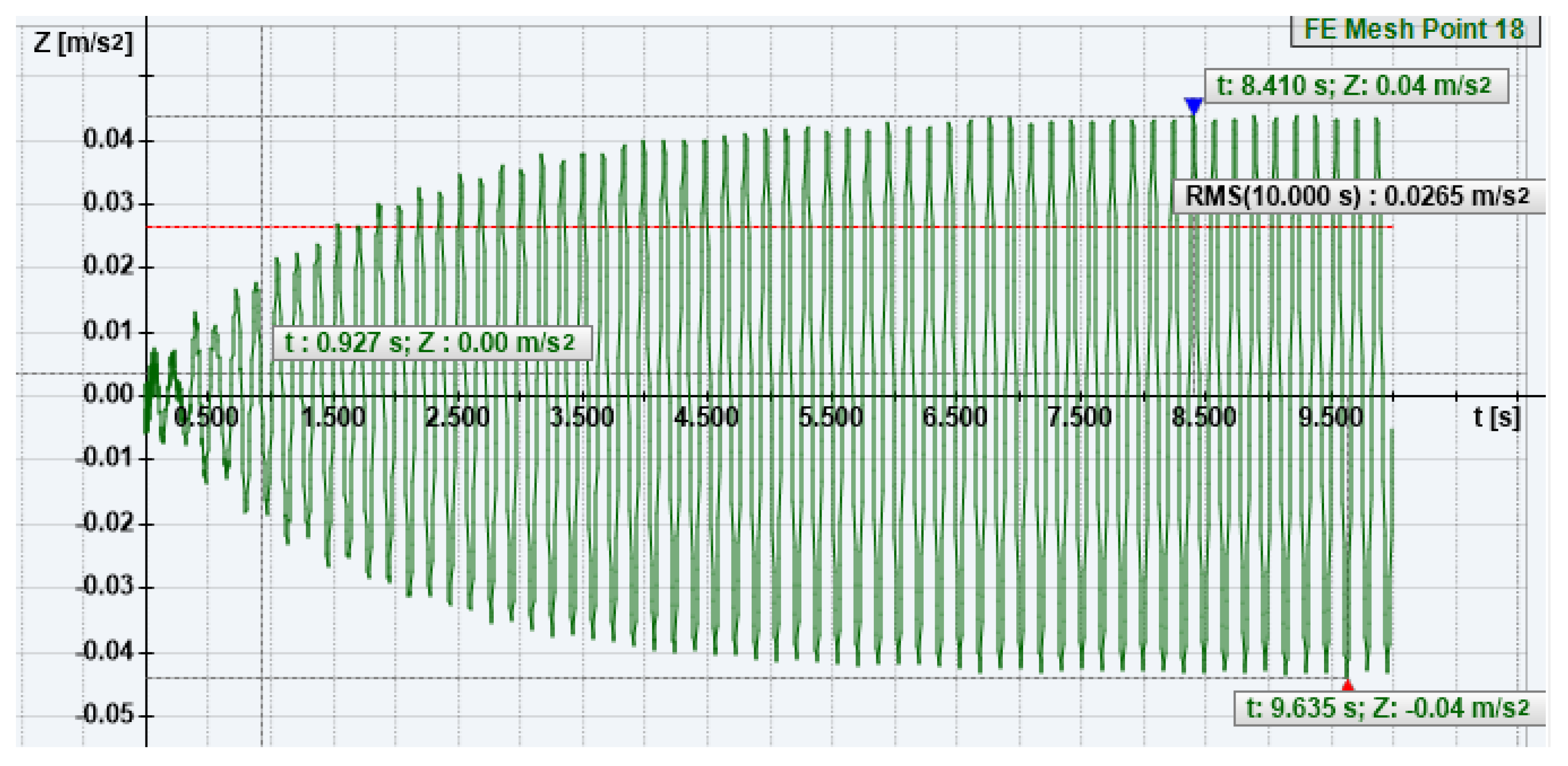
3.6. Acceleration Design
- M—the modal mass of the TCC floor
- 700 N—harmonic part of the force (see [69])
- 0.1—Fourier coefficient
- 0.4—simplification factor (person moves around)
- m—mass (kg)
- l—TCC floor span (m)
- b—the width of the floor (<1.5 l)
3.7. Constructive Design Requirements
3.8. Comparison Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rajčić, V.; Žagar, Z. FEM models of composite timber-lightweight concrete floor systems. In Proceedings of the World Conference on Timber Engineering (WCTE 2000), Whistler, BC, Canada, 31 July–3 August 2000. [Google Scholar]
- Yooh, D.; Fagiacomo, M.; De Franceschi, M.; Boon, K.H. State of the art on timber-concrete composite structures: Literature review. J. Eng. 2011, 137, 1085–1095. [Google Scholar] [CrossRef]
- Klotz, S.; Holschemacher, K.; Köhler, S. Wirtschaftlichkeit von Holz-Beton-Verbunddecken. In Holz-Beton-Verbund: Innovationen im Bauwesen, Beiträge aus Praxis und Wissenschaft; König, G., Holschemacher, K., Dehn, F., Eds.; Bauwerk Verlag: Leipzig, Germany, 2004; pp. 269–279. [Google Scholar]
- Newcombe, M.P.; Carradine, D.; Pampanin, S.; Buchanan, A.H.; Deam, B.L. In-plane experimental testing of timber-concrete composite floor diaphragms. In Proceedings of the NZSEE 2009 Conference, Christchurch, New Zealand, 3–5 April 2009. [Google Scholar]
- Smith, I.; Frangi, A. Use of Timber in Tall Multi-Storey Buildings; IABSE: Zürich, Switzerland, 2014. [Google Scholar]
- Movaffaghi, H.; Pyykkö, J.; Yitmen, I. Value-driven design approach for optimal long-span timber-concrete composite floor in multi-storey wooden residential buildings. Civ. Eng. Environ. Syst. 2020, 37, 100–116. [Google Scholar] [CrossRef]
- Stepinac, M.; Šušteršič, I.; Gavrić, I.; Rajčić, V. Seismic design of timber buildings: Highlighted challenges and future trends. Appl. Sci. 2020, 10, 1380. [Google Scholar] [CrossRef]
- Sebastian, W.; Webb, S.; Nagree, H.S. Orthogonal distribution and dynamic amplification characteristics of partially prefabricated timber-concrete composites. Eng. Struct. 2020, 219, 110693. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, X.; Gong, H.; Zhang, J.; Lv, Z.; Hong, W. Experimental study on the impact sound insulation of cross laminated timber and timber-concrete composite floors. Appl. Acoust. 2020, 161, 107173. [Google Scholar] [CrossRef]
- Dias, A.M.P.G.; Skinner, J.; Crewa, K.; Tannert, T. Timber Concrete composites increasing the use of timber in construction. Eur. J. Wood Wood Prod. 2016, 74, 443–451. [Google Scholar] [CrossRef]
- Dias, A.M.P.G.; Schänzlin, J.; Dietsch, P. Hybrid Structures: State of Art Report; Cost Action FP1402: Brussels, Belgium, 2017. [Google Scholar]
- Knauf, M. Market potentials for timber-concrete composites in Germany’s building construction sector. Eur. J. Wood Wood Prod. 2017, 75, 639–649. [Google Scholar] [CrossRef]
- Andersson, J. A Survey of Multi-Objective Optimization in Engineering Design; LiTH-IKP-R-1097; Department of Mechanical Engineering Linköping University: Linköping, Sweden, 2000. [Google Scholar]
- Weckendorf, J.; Toratti, T.; Smith, I.; Tannert, T. Vibration serviceability performance of timber floors. Eur. J. Wood Wood Prod. 2016, 74, 353–367. [Google Scholar] [CrossRef]
- Dolan, J.D.; Murray, T.M.; Johnson, J.R.; Runte, D.; Shue, B.C. Preventing annoying wood floor vibrations. J. Struct. Eng. 1999, 125, 19–24. [Google Scholar] [CrossRef]
- Talja, A.; Toratti, T. Effect on floating floors on the vibration performance of wood-concrete composite floors. In Proceedings of the World Conference on Timber Engineering (WCTE 2000), Whistler, BC, Canada, 31 July–3 August 2000. [Google Scholar]
- Mertens, C.; Martin, Y.; Dobbels, F. Investigation of the vibration behaviour of timber-concrete composite floors as part of a performance evaluation for the belgian building industry. Build. Acoust. 2007, 14, 25–36. [Google Scholar] [CrossRef]
- Abd Ghafar, N.H.; Deam, B.; Fragiacomo, M.; Buchanan, A. Vibration performance of LV-concrete composite floor systems. In Proceedings of the World Conference on Timber Engineering (WCTE 2008), Miyazaki, Japan, 2–5 June 2008. [Google Scholar]
- Hamm, P.; Richter, A.; Winter, S. Floor vibrations: New results. In Proceedings of the World Conference on Timber Engineering (WCTE 2010), Trento, Italy, 20–24 June 2010. [Google Scholar]
- Rijal, R.; Samali, B.; Crews, K.; Shrestha, R. Dynamic behaviour of timber-concrete composite flooring systems. In Proceedings of the World Conference on Timber Engineering (WCTE 2010), Trento, Italy, 20–24 June 2010. [Google Scholar]
- Skinner, J.; Harris, R.; Paine, K.; Walker, P.; Bregulla, J. The characterisation of connectors for the upgrade of timber floors with thin structural toppings. In Proceedings of the World Conference on Timber Engineering (WCTE 2012), Auckland, New Zealand, 15–19 July 2012. [Google Scholar]
- Omenzetter, P.; Kohli, V.; Desgeorges, Y. Evaluation of timber-concrete floor performance under occupant-induced vibrations using continuous monitoring. Key Eng. Mater. 2013, 569–570, 230–237. [Google Scholar] [CrossRef]
- Fong, L.Y.; Abd Ghafar, N.H.; Abd Rahman, N.; Fragiacomo, M.; Ibrahim, Z.; Buchanan, A. Comparison between the vibration performance of LVL-concrete composite (LCC) flooring system made of Malaysian and New Zealand LVL. Malays. J. Civil Eng. 2015, 27, 68–80. [Google Scholar]
- Dos Santos, P.G.G.; Martins, C.E.J.; Skinner, J.; Harris, R.; Dias, A.M.P.G.; Godinho, L.M.C. Modal frequencies of a reinforced timber-concrete composite floor: Testing and modeling. J. Struct. Eng. 2015, 141, 04015029. [Google Scholar] [CrossRef]
- Kozarić, L. Vibrations of repaired wooden floors caused by human action. Wood Res. 2015, 60, 663–670. [Google Scholar]
- Marshall, E.J.N.; Granello, G.; Palermo, A. Vibration performance of timber-concrete composite floors: A case study. J. Struct. Eng. Soc. N. Z. Inc. 2020, 33, 33–46. [Google Scholar]
- Mushina, J.; Abd Ghafar, N.H.; Yeoh, D.; Mushina, W.; Boon, K.H. Vibration behaviour of natural timber and timber concrete composite deck ystem. Mater. Sci. Eng. 2020, 713, 012023. [Google Scholar]
- Jarnerö, K. Vibrations in Timber Floors: Dynamic Properties and Human Perception. Ph.D. Thesis, Linnaeus University, Växjö, Sweden, 2014. [Google Scholar]
- CEN/TC 250. Technical Specification—Background Document—Eurocode 5: Design of Timber Structures—Vibrations; CEN: Brussels, Belgium, 2020. [Google Scholar]
- ISO. Bases for Design of Structures: Serviceability of Buildings and Walkways against Vibrations; ISO 10137:2007; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- CEN. Eurocode 0: Basis of Structural Design; EN 1990:2002+A1:2005+A1:2005/AC:2010; CEN: Brussels, Belgium, 2010. [Google Scholar]
- Ohlsson, S.V. Svikt, svängningar och styvhet hos bjälklag: Dimensioneringsregler; Rapport T20; BFR: Stockholm, Sweden, 1984. [Google Scholar]
- CEN/TC 250. Technical Specification—Background Document—Eurocode 5: Design of Timber Structures—Structural Design of Timber-Concrete Composite Structures—Common Rules and Rules for Buildings; CEN: Brussels, Belgium, 2020. [Google Scholar]
- CEN. Eurocode 5: Design of Timber Structures—Part 1-1: General-Common Rules and Rules for Buildings; EN 1995-1-1:2004+AC:2006+A1:2008; CEN: Brussels, Belgium, 2008. [Google Scholar]
- Pavic, A.; Reynolds, P. Vibration serviceability of long-span concrete building floors—Part 1: Review of background information. Shock Vib. Dig. 2002, 34, 191–211. [Google Scholar]
- Pavic, A.; Reynolds, P. Vibration serviceability of long-span concrete building floors—Part 1: Review of mathematical modelling approaches. Shock Vib. Dig. 2002, 34, 279–297. [Google Scholar]
- CEN. Eurocode 4: Design of Composite Steel and Concrete Structures—Part 1-1: General Rules and Rules for Buildings; EN 1994-1-1:2004+AC:2009; CEN: Brussels, Belgium, 2009. [Google Scholar]
- CEN. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; EN 1992-1-1:2004+AC:2010; CEN: Brussels, Belgium, 2010. [Google Scholar]
- Rieg, A. Verformungsbezogene mittragende Breite niedriger Verbundträger. Ph.D. Thesis, University of Stuttgart, Institute for Structural Design, Stuttgart, Germany, 2006. [Google Scholar]
- Kuhlmann, U.; Merkle, J.; Schänzlin, J.; Bux, H. Brettstapel-Beton-Verbunddecken mit integrierten Slim-Floor-Profilen; Deutsche Bundesstiftung Umwelt AZ 211682006; Institute for Structural Design, University of Stuttgart: Stuttgart, Germany, 2006. [Google Scholar]
- Xie, Z.; Hu, X.; Du, H.; Zhang, X. Vibration behavior of timber-concrete composite floor under human-induced excitation. J. Build. Eng. 2020, 32, 101744. [Google Scholar] [CrossRef]
- Abd Ghafar, N.H.; Deam, B.; Fragiacomo, M. Vibration susceptibility of multi-span lvl-concrete composite floors. In Proceedings of the World Conference on Timber Engineering (WCTE 2010), Trentino, Italy, 20–24 June 2010. [Google Scholar]
- Skinner, G.J. Short Term Scientific Mission: The Vibration Performance of Round Wood Timber-Concrete Composite floors; Cost Action FP1004: Brussels, Belgium, 2012. [Google Scholar]
- Rijal, R. Dynamic Performance of Timber and Timber-Concrete Composite Flooring Systems. Ph.D. Thesis, Sydney University of Technology, Faculty of Engineering and Information Technology, Sydney, Australia, 2013. [Google Scholar]
- Skaare, M.K. Vibrations in Composite Timber-Concrete Floor Systems. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2013. [Google Scholar]
- Franklin, K.; Hough, R. Modelling and measurement of the dynamic performance of a timber concrete composite floor. In Proceedings of the World Conference on Timber Engineering (WCTE 2014), Quebec City, QC, Canada, 10–14 August 2014. [Google Scholar]
- Rijal, R.; Samali, B.; Shrestha, R.; Crews, K. Experimental and analytical dtudy on dynamic performance of timber-concrete composite beams. Constr. Build. Mater. 2015, 75, 46–53. [Google Scholar] [CrossRef]
- Abd Ghafar, N.H. Dynamic Behaviour of LVL-Concrete Composite Flooring Systems. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2015. [Google Scholar]
- Hu, L.; Auclair, S.C.; Chui, Y.; Ramzi, R.; Gagnon, S.; Mohammad, M.; Ni, C.; Popovski, M. Design method for controlling vibrations of wood-concrete composite floors systems. In Proceedings of the World Conference on Timber Engineering (WCTE 2016), Vienna, Austria, 22–25 August 2016. [Google Scholar]
- Murray, T.M.; Allen, D.E.; Ungar, E.E. Design Guide 11: Vibrations of Steel-Framed Structural Systems Due to Human Activity Second Edition 11 Steel Design Guide, 2nd ed.; American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- CEN. Test Methods—Timber Flooring Systems: Determination of Vibration Properties; EN 16929:2018; CEN: Brussels, Belgium, 2018. [Google Scholar]
- Wyatt, T.A. Design Guide on the Vibration of Floors; Steel Construction Institute: Ascot, UK, 1989. [Google Scholar]
- Murray, T.M.; Allen, D.E.; Ungar, E.E. Steel Design Guide Series 11: Floor Vibrations Due to Human Activity; American Institute of Steel Construction: Chicago, IL, USA, 1997. [Google Scholar]
- Girhammar, U.A. A simplified analysis method for composite beams with interlayer slip. Int. J. Mech. Sci. 2009, 51, 515–530. [Google Scholar] [CrossRef]
- Niederer, A. Grenzen der Anwendung des γ-Verfahrens. Bachelor’s Thesis, HTWG Konstanz, Konstanz, Germany, 2008. [Google Scholar]
- Grosse, M.; Hartnack, R.; Lehmann, S.; Rautenstrauch, K. Modellierung von diskontinuierlich verbundenen Holz-Beton-Verbundkonstruktionen. Bautechnik 2003, 80, 534–541, 693–701. [Google Scholar] [CrossRef]
- Michelfelder, B.C. Trag- und Verformungsverhalten von Kerven bei Brettstapel-Beton-Verbunddecken. Ph.D. Thesis, University of Stuttgart, Institute for Structural Design, Stuttgart, Germany, 2006. [Google Scholar]
- Ceccotti, A.; Fragiacomo, M.; Giordano, S. Long-term and collapse tests on a timber-concrete composite beam with glued-in connection. Mater. Struct. 2007, 40, 15–25. [Google Scholar] [CrossRef]
- Lukaszewska, E.; Fragiacomo, M.; Frangi, A. Evaluation of the slip modulus for ultimate limit state verifications of timber-concrete composite structures. In Proceedings of the CIB-W18 no. 40, Bled, Slovenia, 28–31 August 2007. [Google Scholar]
- Dias, A.M.P.G.; Cruz, H.M.P.; Lopes, S.M.R.; van de Kuilen, J.-W. Stiffness of dowel-type fasteners in timber-concrete joints. Struct. Build. 2010, 163, 257–266. [Google Scholar] [CrossRef]
- Dias, A.M.P.G. Performance of dowel-type fasteners for hybrid timber structures. In Proceedings of the International Conference on Connections in Timber Engineering: From Research to the Standards, Graz, Austria, 13 September 2017. [Google Scholar]
- Turrini, G.; Piazza, M. Una tecnica di recupero statico dei solai in legno. Recuperare 1983, 2, 5–7. [Google Scholar]
- DIBT. HBV-Schubverbinder aus Streckmetall und vorgefertigte Bauteile mit eingeklebten HBV-Schubverbindern für ein Holz-Beton-Verbundsystem; DIBT: Berlin, Germany, 2020. [Google Scholar]
- Kudla, K. Short Term Scientific Mission: Notched Connections for TCC Structures; Cost Action FP1402: Brussels, Belgium, 2017. [Google Scholar]
- Deutsches Institut fur Bauctechnik. Allgemeine Bauaufsichtliche Zulassung; Zulassungsnummer Z-9.1-557; DIBT: Berlin, Germany, 2020. [Google Scholar]
- CEN. Eurocode 1: Actions on Structures—Part 1-1: General Actions—Densities, Self-Weight and Imposed Loads for Buildings; EN 1991-1-1:2002+AC:2009; CEN: Brussels, Belgium, 2009. [Google Scholar]
- Hamm, P. Schwingungsverhalten von decken bei auflagerung auf unterzügen. Holzbau Die Neue Quadriga 2008, 526, 41–46. [Google Scholar]
- Maier, C.; Heger, C.; Neujahr, M.; Stöffler, J. Großversuch zum Einfluss nichttragender Ausbauelemente auf das Schwingungsverhalten weitgespannter Verbundträger: Forschungsbericht; Technical University of Darmstadt: Darmstadt, Germany, 2005. [Google Scholar]
- Bachmann, H.; Ammann, W.J.; Deischl, F.; Eisenmann, J.; Floegl, I.; Hirsch, G.H.; Klein, G.K.; Lande, G.J.; Mahrenholtz, O.; Natke, H.G.; et al. Vibration Problems in Structures: Practical Guidelines, 2nd ed.; Birkhäuser Verlag: Basel, Switzerland, 1997. [Google Scholar]
- SIA. Holzbau—Ergänzende Festlegungen; 265/1; SIA: Zürich, Switzerland, 2018. [Google Scholar]
- Blaß, H.J.; Ehlbeck, J.; Kreuzinger, H.; Steck, G. Erläuterungen zu DIN 1052: 2004-08: Entwurf, Berechnung und Bemessung von Holzbauwerken; DGfH Innovations und Service GmbH: Munich, Germany, 2004. [Google Scholar]
- Collins, L. Timber-Concrete Composite: An Alternative Composite Floor System. Master’s Thesis, Kansas State University, Manhattan, KS, USA, 2020. [Google Scholar]
- Marshall, J. Footfall Vibration Modelling and In-Situ Testing of Timber Concrete Composite Floors. Master’s Thesis, University of Canterbury, Christchurch, New Zealand, 2020. [Google Scholar]
- Al-Sammari, A.T.; Clouston, P.L.; Brena, S.F. Finite-element analysis and parametric study of perforated steel plate shear connectors for wood-concrete composites. J. Struct. Eng. 2018, 144, 04018191. [Google Scholar] [CrossRef]
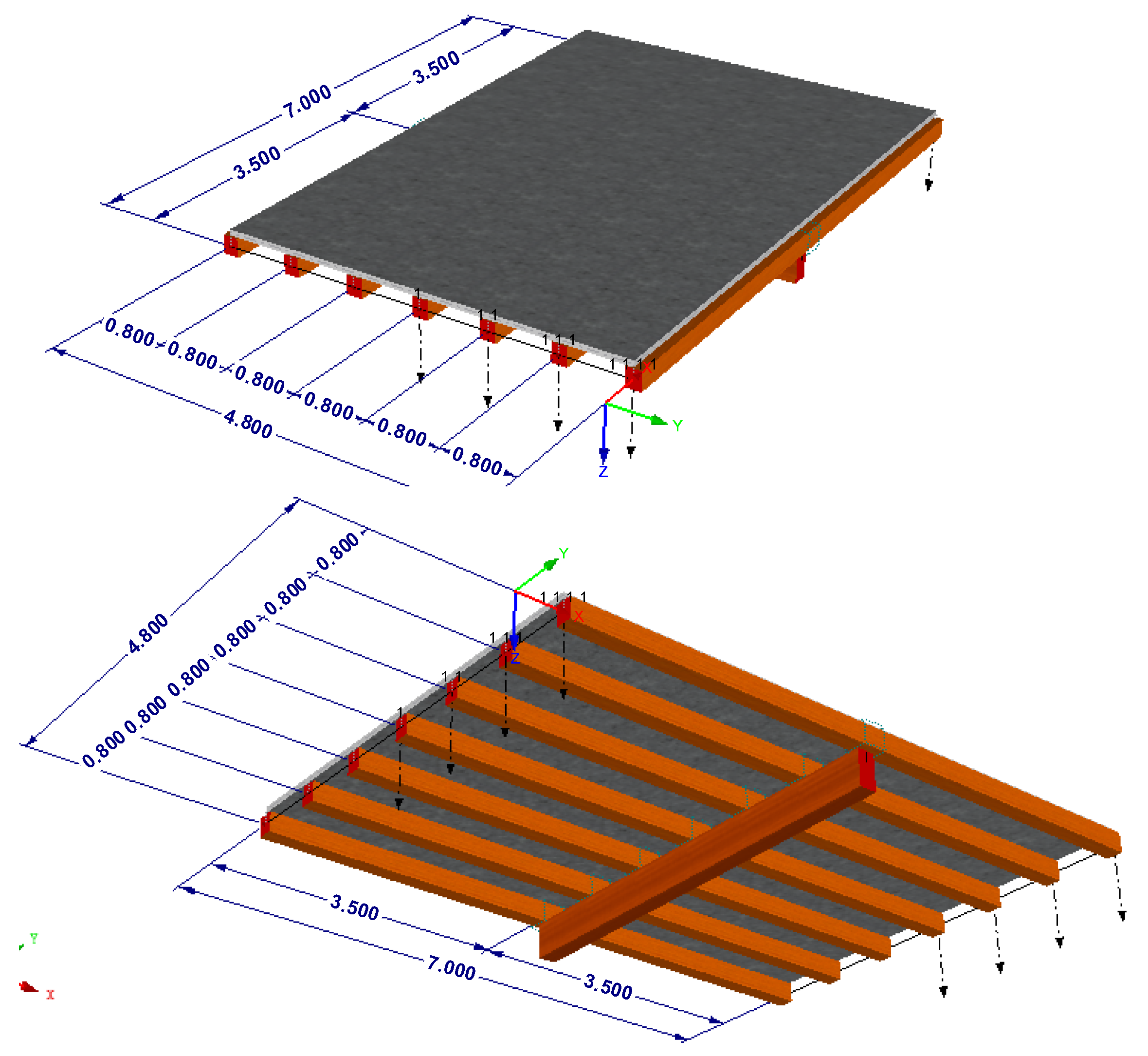
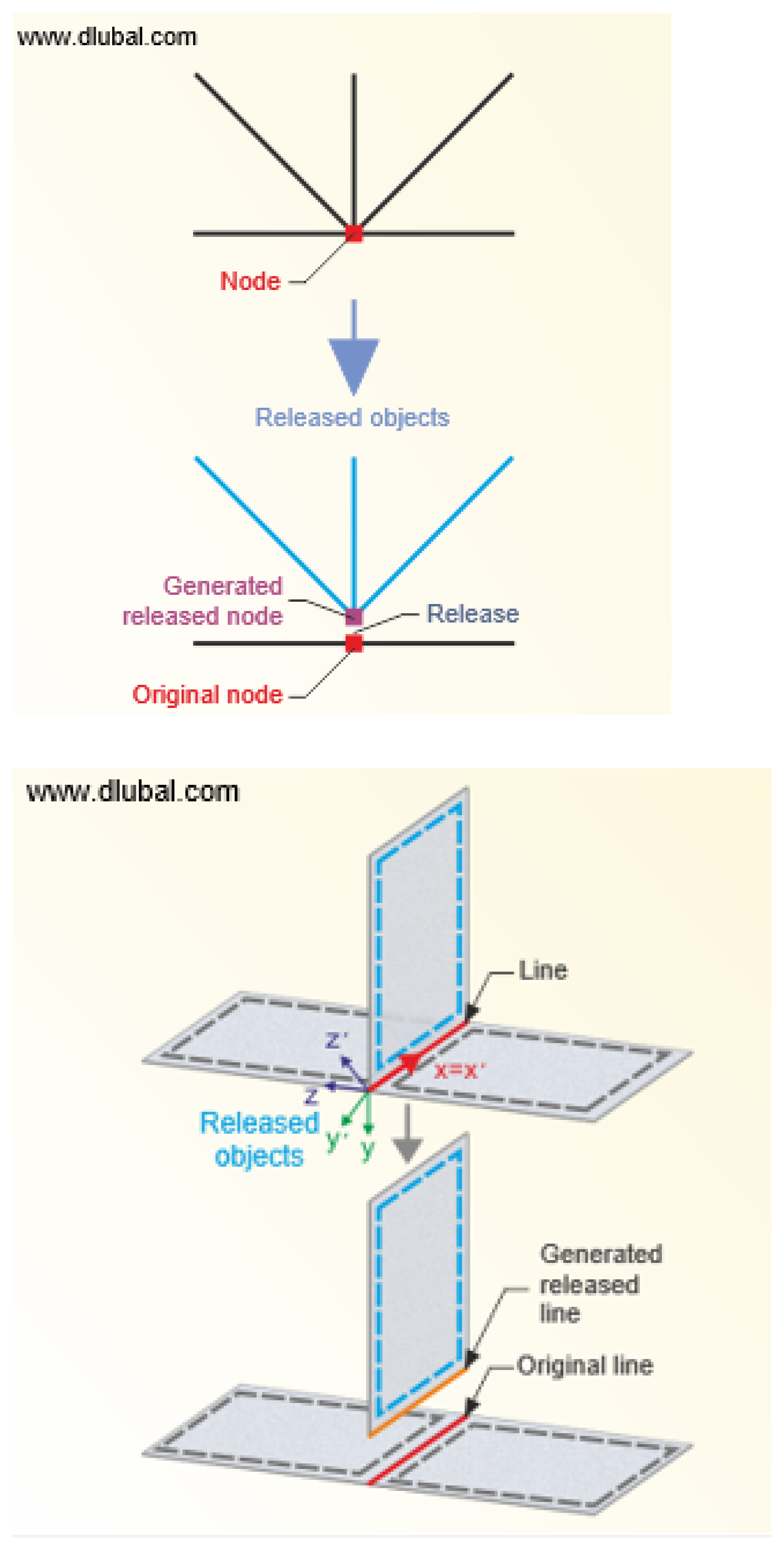




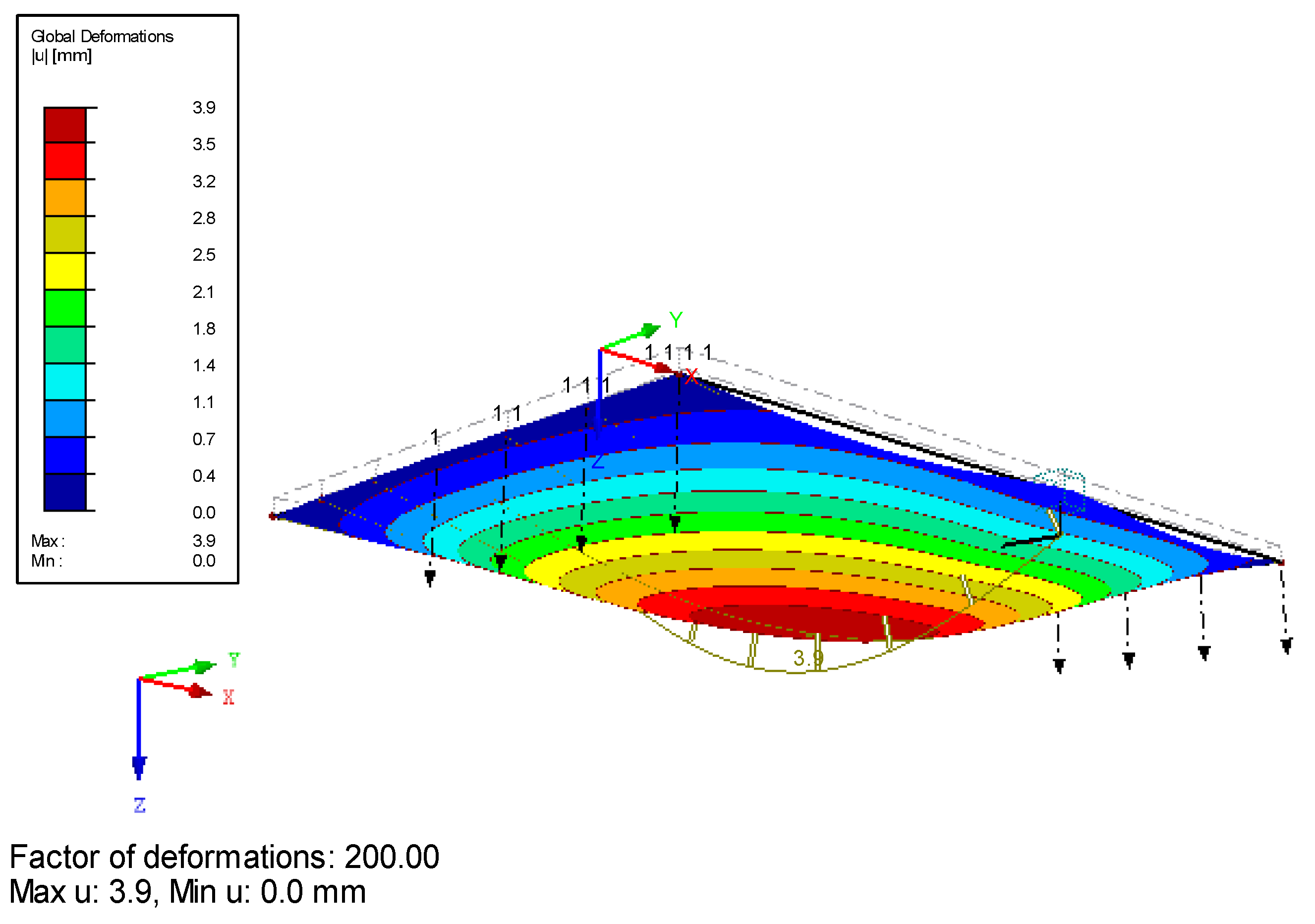
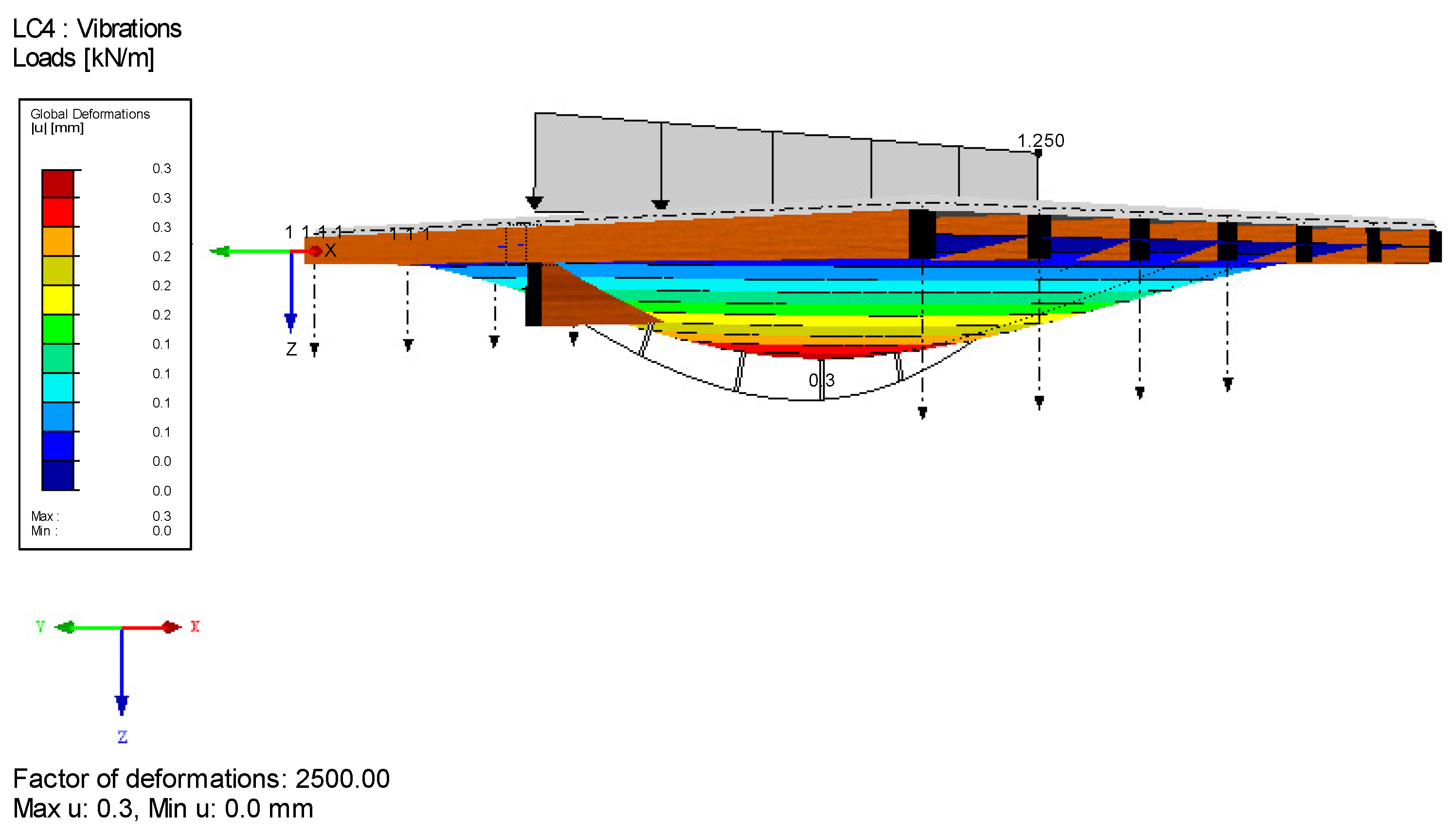
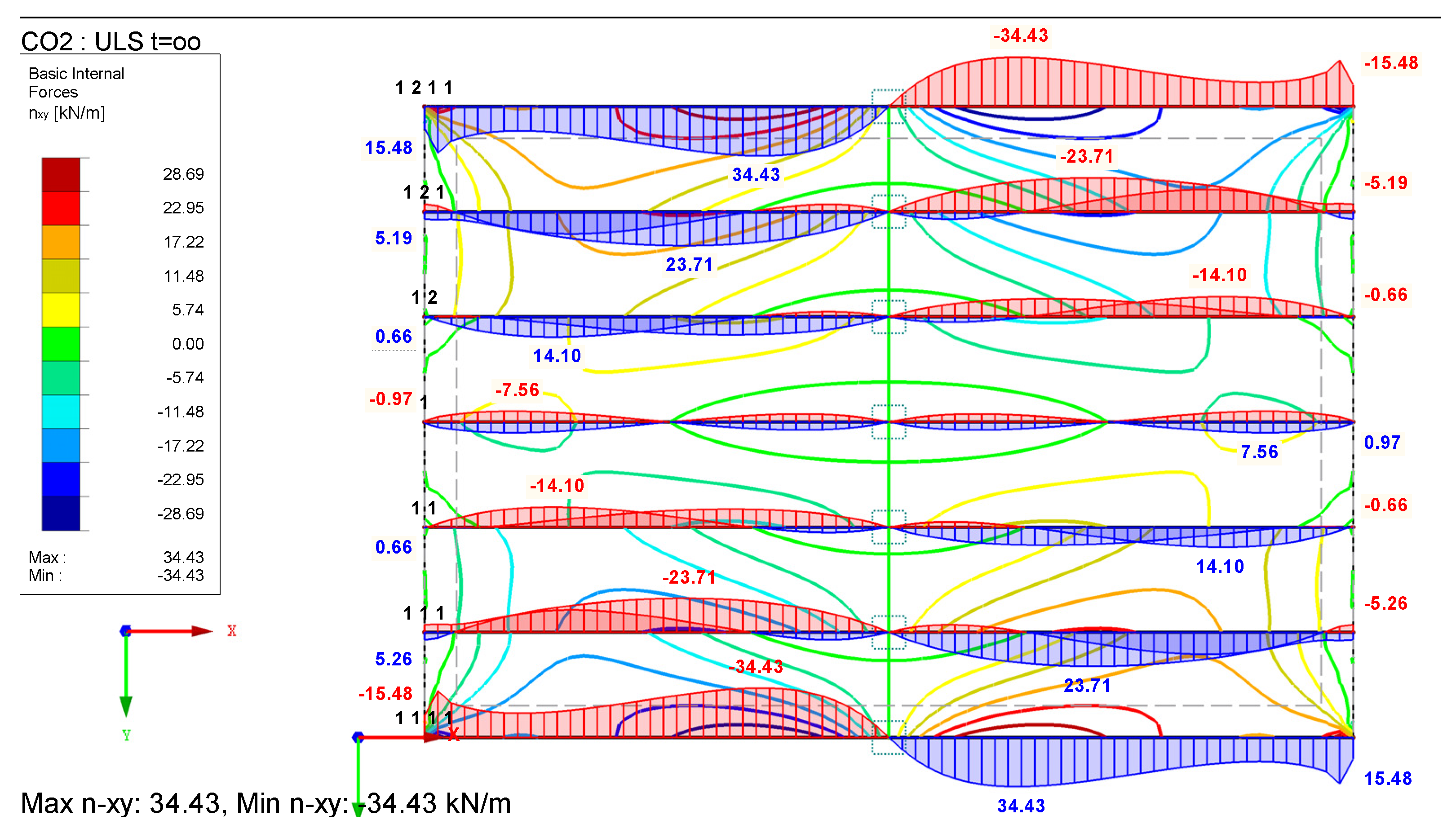
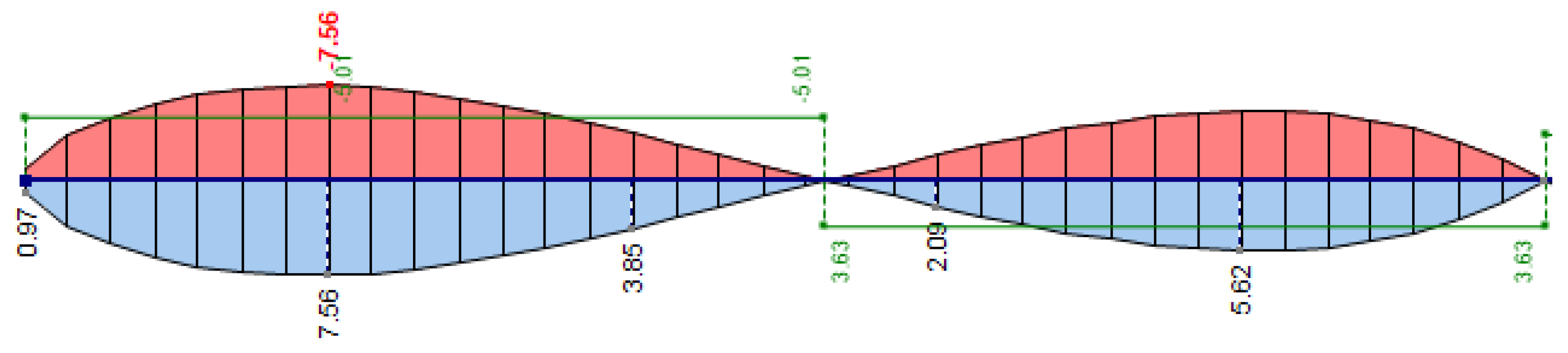
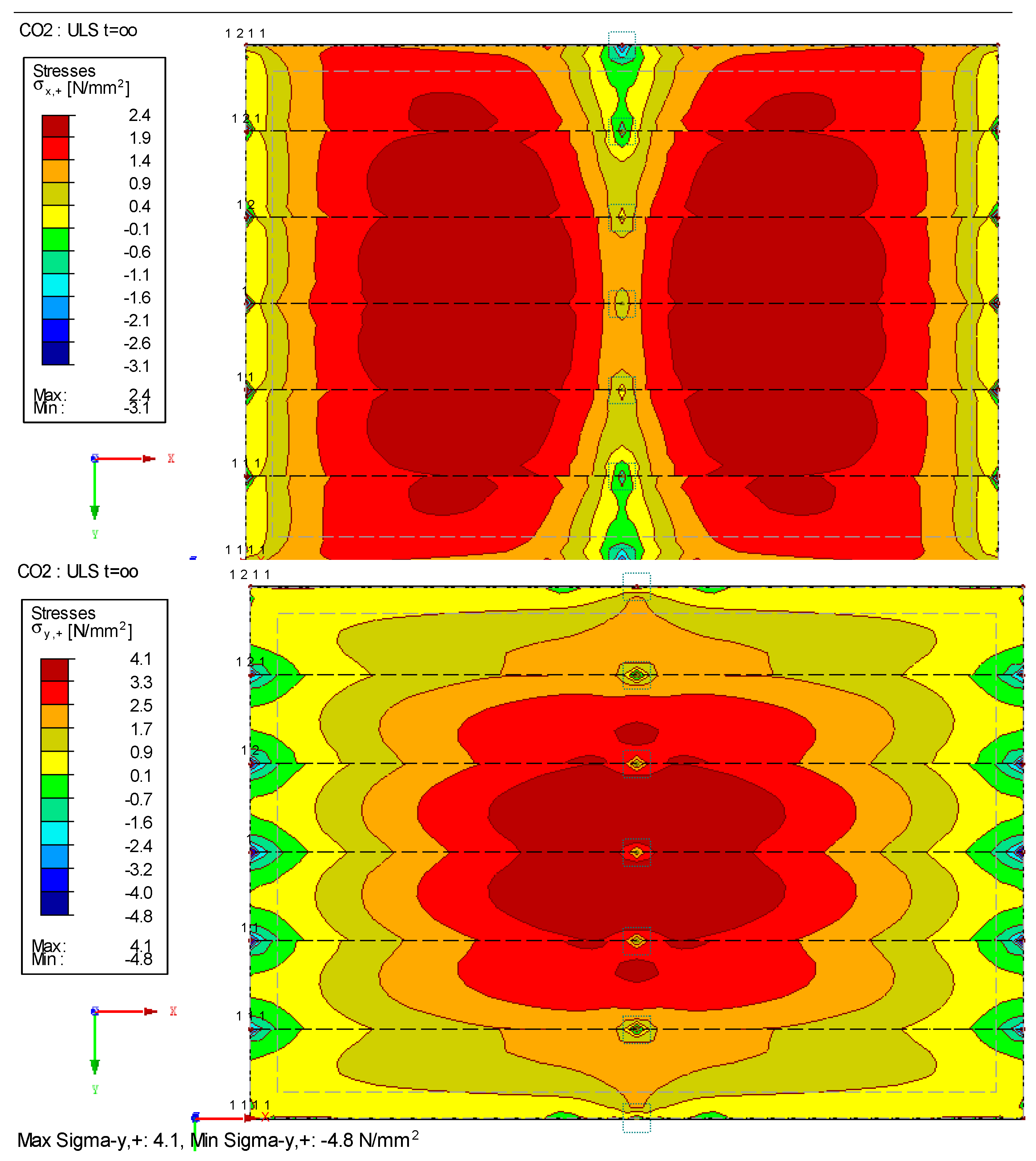
| Criteria | Floor Performance Levels | ||||||
|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VI | |
| stiffnes criteria w1kN [mm] ≤ | 0.25 | 0.25 | 0.50 | 0.80 | 1.20 | 1.60 | no criteria |
| response factor R ≤ | 4 | 8 | 12 | 16 | 24 | 32 | |
| frequency criteria f1 [HZ] ≥ | 4.50 | ||||||
| acceleration criteria arms [m/s2] ≤ | 0.005R | ||||||
| velocity criteria vrms [m/s] ≤ | 0.0001R | ||||||
| Limit State | Time | Timber | Concrete | Connector | LC |
|---|---|---|---|---|---|
| ULS | t = 0 | Emean | Ecm | 2 Kser/3 γM | LC1 |
| t = ∞ | Emean/(1 + kdef) | Ecm/3.5 | 0.5∙(2 Kser)/(3 γM) | LC2 | |
| SLS | t = 0 | Emean | Ecm | Kser | LC3 |
| t = ∞ | Emean/(1 + kdef) | Ecm/3,5 | 0.5∙Kser | LC4, RC1 |
| Material | The Factor for E, G | ||
| Poplar and Softwood Timber C24 | 0.625000 | ||
| Glulam Timber GL32h | 0.625000 | ||
| Concrete C25/30 | 0.285000 | ||
| The Factor for Connector Stiffness | |||
| Cux | Cuy | Cuz | Cφx |
| 0.5 | 1.0 | 1.0 | 1.0 |
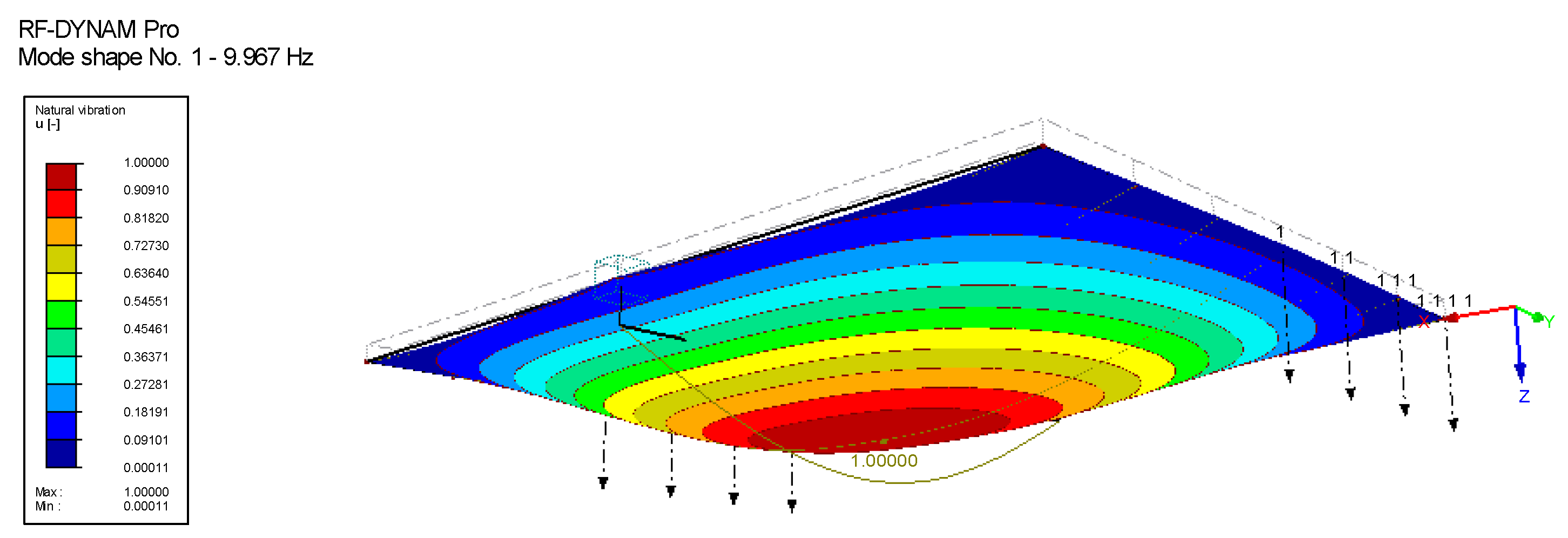
| Mode | Eigenvalue | Angular Frequency | Natural Frequency | Natural Period |
|---|---|---|---|---|
| No. | l [1/s2] | v [rad/s] | f [Hz] | T [s] |
| 1 | 3921.982 | 62.626 | 9.967 | 0.100 |
| 2 | 15,583.944 | 124.836 | 19.868 | 0.050 |
| 3 | 19,639.645 | 140.142 | 22.304 | 0.045 |
| 4 | 21,777.285 | 147.571 | 23.487 | 0.043 |
| Mode | Eigenvalue | Angular Frequency | Natural Frequency | Natural Period |
|---|---|---|---|---|
| No. | l [1/s2] | v [rad/s] | f [Hz] | T [s] |
| 1 | 1561.041 | 39.510 | 6.288 | 0.159 |
| 2 | 1974.294 | 44.433 | 7.072 | 0.141 |
| 3 | 3402.945 | 58.335 | 9.284 | 0.108 |
| 4 | 6336.676 | 79.603 | 12.669 | 0.079 |
| Description | Value | Unit |
|---|---|---|
| LC1—Permanent Load | ||
| Sum of loads in X | 0.00 | kN |
| Sum of loads in Y | 0.00 | kN |
| Sum of loads in Z | 119.27 | kN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perković, N.; Rajčić, V.; Barbalić, J. Analytical and Numerical Verification of Vibration Design in Timber Concrete Composite Floors. Forests 2021, 12, 707. https://doi.org/10.3390/f12060707
Perković N, Rajčić V, Barbalić J. Analytical and Numerical Verification of Vibration Design in Timber Concrete Composite Floors. Forests. 2021; 12(6):707. https://doi.org/10.3390/f12060707
Chicago/Turabian StylePerković, Nikola, Vlatka Rajčić, and Jure Barbalić. 2021. "Analytical and Numerical Verification of Vibration Design in Timber Concrete Composite Floors" Forests 12, no. 6: 707. https://doi.org/10.3390/f12060707
APA StylePerković, N., Rajčić, V., & Barbalić, J. (2021). Analytical and Numerical Verification of Vibration Design in Timber Concrete Composite Floors. Forests, 12(6), 707. https://doi.org/10.3390/f12060707








