A Review of Dynamic Tree Behaviors: Measurement Methods on Tree Sway, Tree Tilt, and Root–Plate Movement
Abstract
1. Introduction
2. The Methodology of the Literature Review
3. Review of Methods and Techniques
3.1. An Overview of the Study Sites
3.1.1. Geographic Coverage
3.1.2. Tree Species and the Physical Attributes
- Location: usually described as (i) urban areas or peri-urban areas and (ii) the latitude, longitude, and exposition of test sites;
- Health status: healthy or with different kinds of defects [28] on stems or roots (wound, diseased, crossed, hollow, etc.).
3.1.3. Selection of Study Period
3.2. Investigation Approaches
3.2.1. High Wind Events
3.2.2. Static Pulling
3.2.3. Wind Tunnel Tests
3.3. Instruments for Tree Behavior Measurement
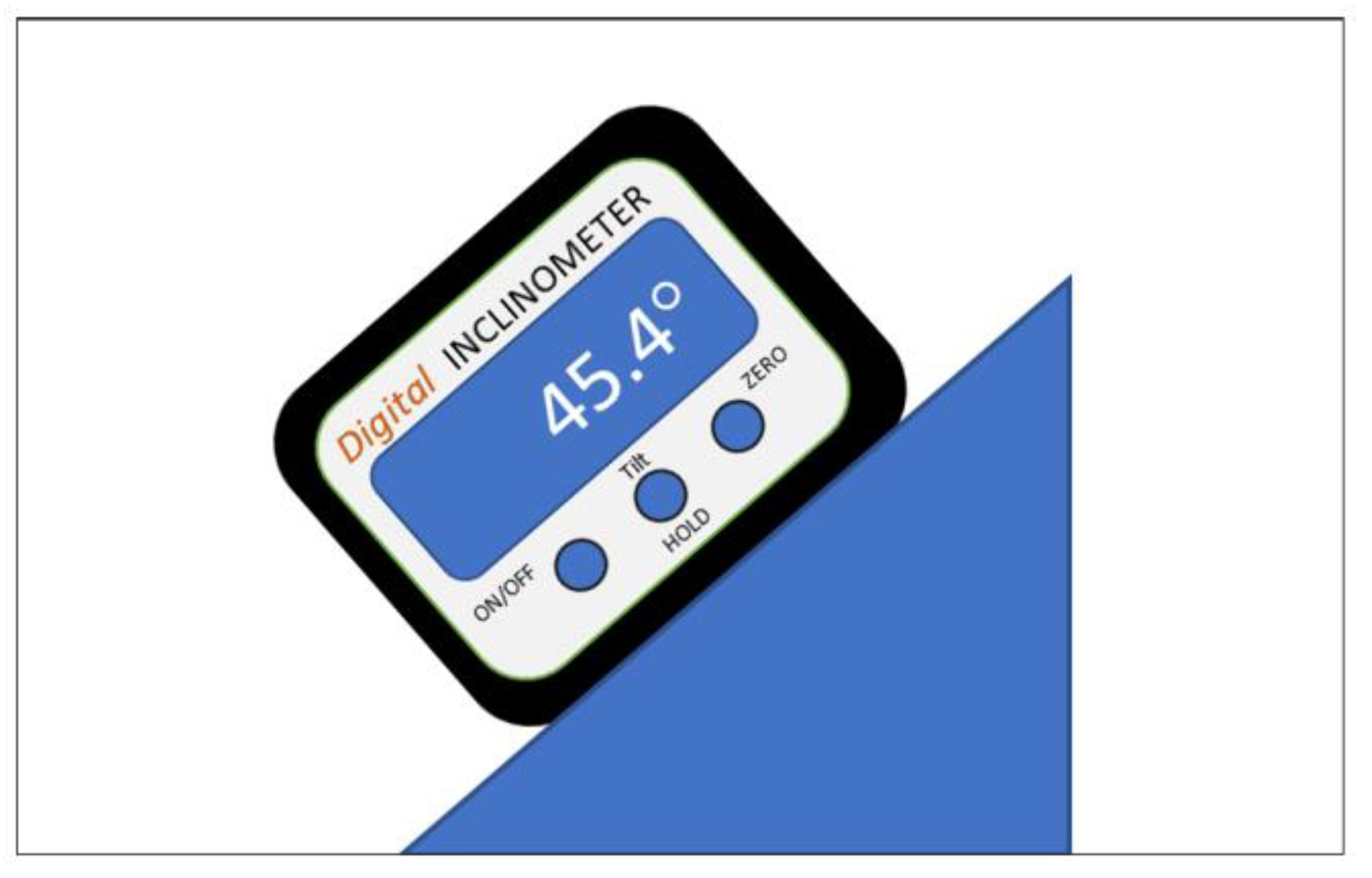
3.3.1. Tilt Measurement
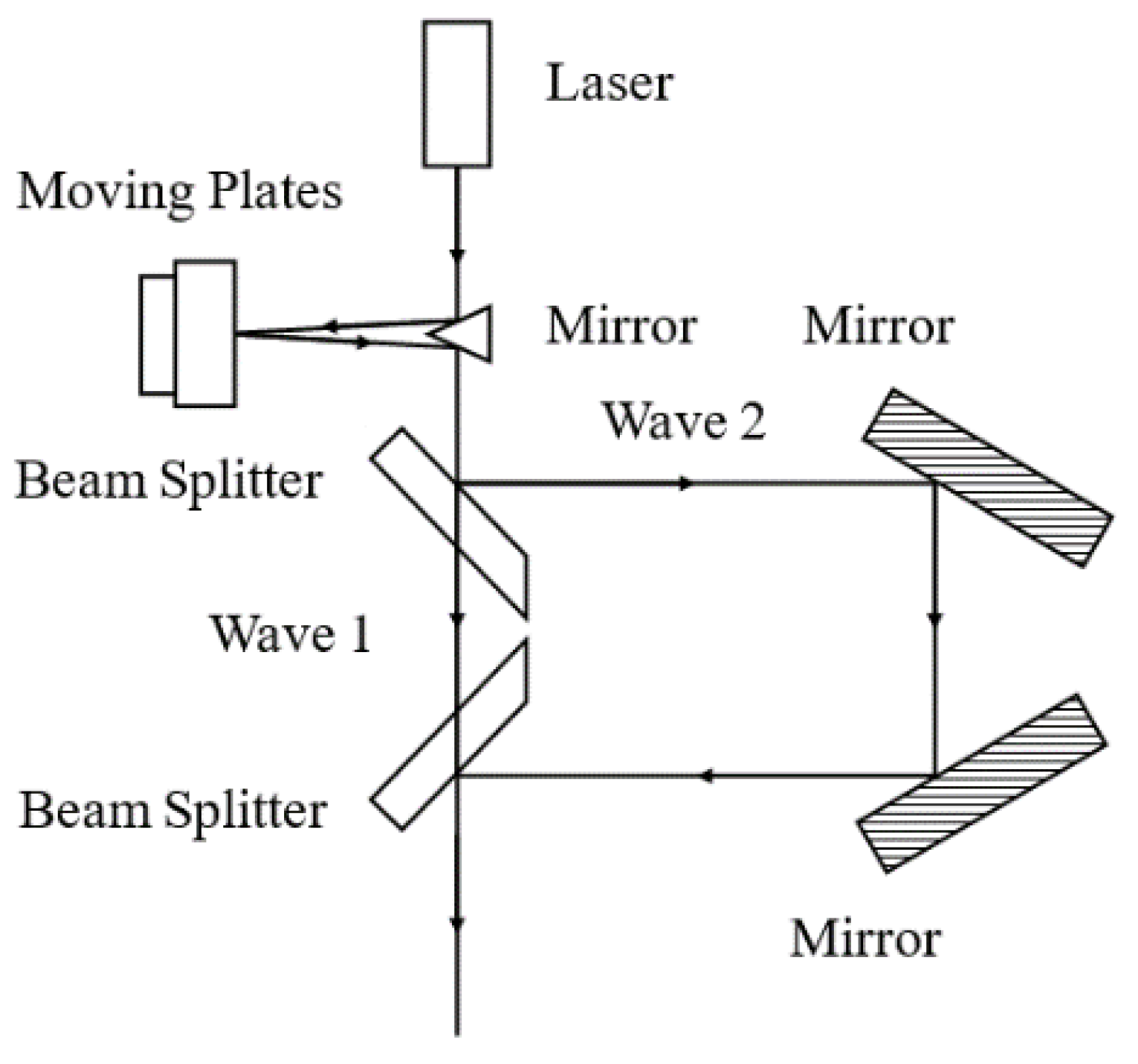
3.3.2. Sway Measurement
3.3.3. Wind Speed Measurement
3.4. Analytical Approaches
3.4.1. Conventional Statistical Analysis
- Fundamental Statistics
- ANOVA Test
- Regression Analysis
3.4.2. Time-Frequency-Based Techniques
- Wavelet Analysis
- Fourier Transform
3.4.3. A Combination of Multiple Analysis
4. Discussion
4.1. Impacting Factors of Tree’s Sway and Tilt Analysis
4.1.1. The Specialty of Inherent Tree Features—Internal Factors
- Wood Elasticity
- Natural Swaying Frequency of Trees
- Damping Ratio
- Diameter at Breast Height (DBH) and Height (H)
4.1.2. Impact of External Forces on Trees
- Wind
- The Root–Soil System
4.2. Four Major Measures for Tree Tilt and Sway Analysis
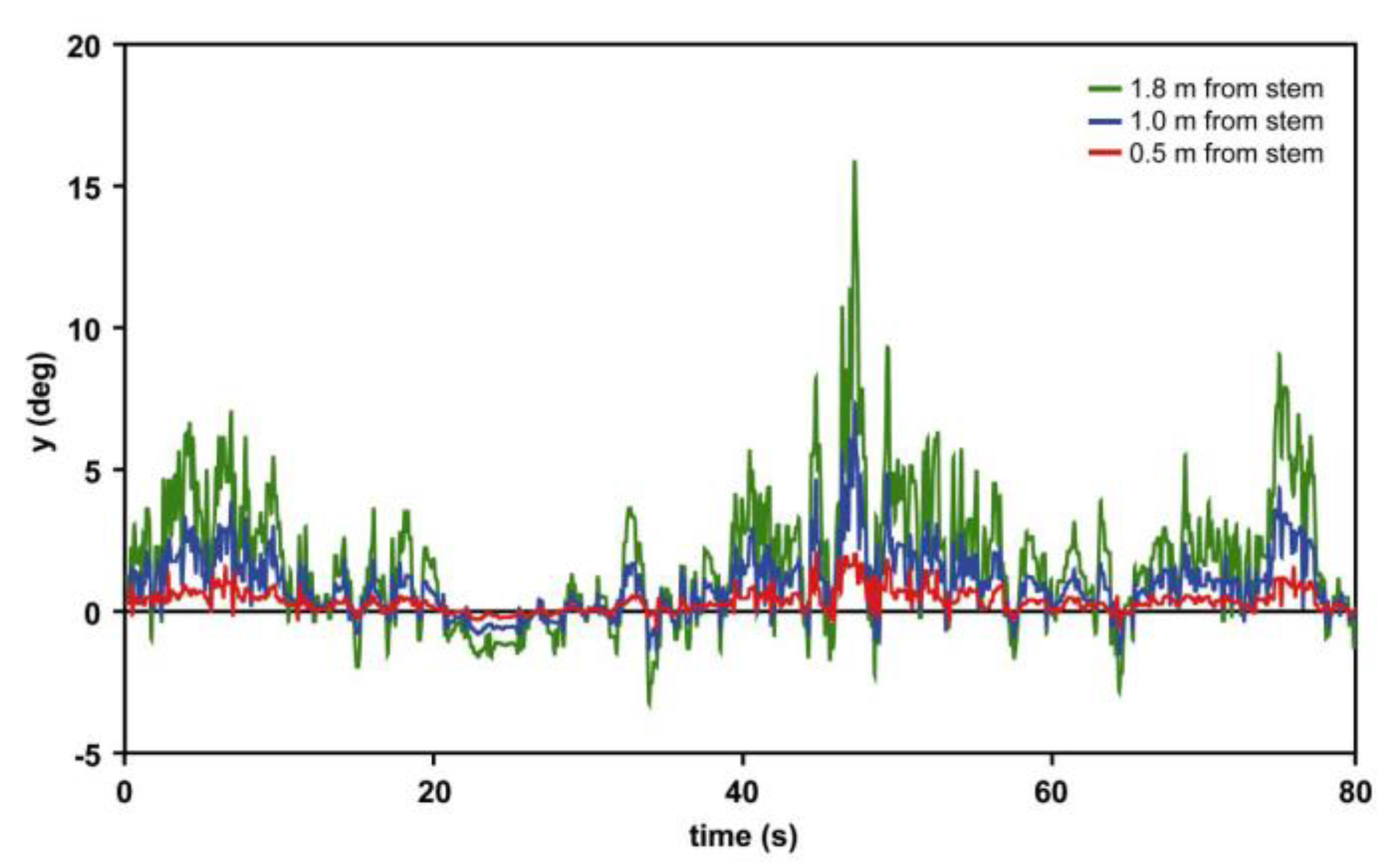
4.3. A Closer Look at Broadleaf Trees
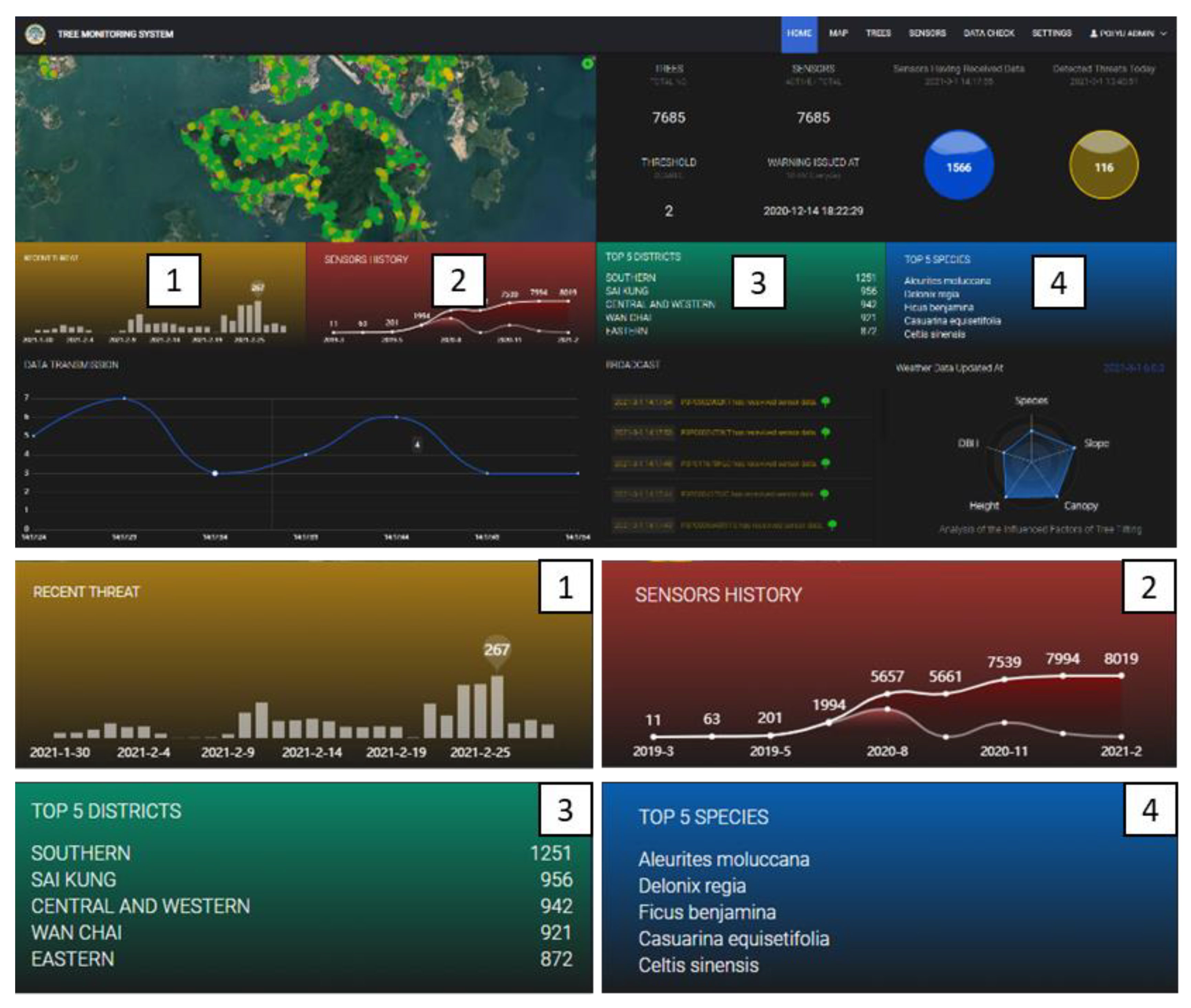
4.4. A Large-Scale Integrated Tree Monitoring System in Hong Kong
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McHale, M.R.; McPherson, E.G.; Burke, I.C. The potential of urban tree plantings to be cost effective in carbon credit markets. Urban For. Urban Green. 2007, 6, 49–60. [Google Scholar] [CrossRef]
- Cariñanos, P.; Calaza, P.; Hiemstra, J.; Pearlmutter, D.; Vilhar, U. The role of urban and peri-urban forests in reducing risks and managing disasters. Unasylva 250 For. Sustain. Cities 2018, 69, 53. [Google Scholar]
- Nagabhatla, N.; Springgay, E.; Dudley, N. Forests as nature-based solutions for ensuring urban water security. Unasylva 250 For. Sustain. Cities 2018, 69, 43. [Google Scholar]
- Endreny, T.A. Strategically growing the urban forest will improve our world. Nat. Commun. 2018, 9, 1160. [Google Scholar] [CrossRef] [PubMed]
- Scholz, T.; Hof, A.; Schmitt, T. Cooling Effects and Regulating Ecosystem Services Provided by Urban Trees—Novel Analysis Approaches Using Urban Tree Cadastre Data. Sustainability 2018, 10, 712. [Google Scholar] [CrossRef]
- Price, C. Quantifying the aesthetic benefits of urban forestry. Urban For. Urban Green. 2003, 1, 123–133. [Google Scholar] [CrossRef]
- Vlachokostas, C.; Michailidou, A.; Matziris, E.; Achillas, C.; Moussiopoulos, N. A multiple criteria decision-making approach to put forward tree species in urban environment. Urban Clim. 2014, 10, 105–118. [Google Scholar] [CrossRef]
- Hostetler, A.E.; Rogan, J.; Martin, D.; DeLauer, V.; O’Neil-Dunne, J. Characterizing tree canopy loss using multi-source GIS data in Central Massachusetts, USA. Remote Sens. Lett. 2013, 4, 1137–1146. [Google Scholar] [CrossRef]
- Cullen, S. Trees and wind: Wind scale and speeds. J. Arboric. 2002, 28, 237–242. [Google Scholar]
- Cullen, S. Trees and wind: A bibliography for tree care professionals. J. Arboric. 2002.
- Šilhán, K. Can tree tilting indicate mechanisms of slope movement? Eng. Geol. 2015, 199, 157–164. [Google Scholar] [CrossRef]
- Ballesteros-Cánovas, J.; Márquez-Peñaranda, J.; Sánchez-Silva, M.; Díez-Herrero, A.; Ruiz-Villanueva, V.; Bodoque, J.; Eguibar, M.; Stoffel, M. Can tree tilting be used for paleoflood discharge estimations? J. Hydrol. 2015, 529, 480–489. [Google Scholar] [CrossRef]
- Jim, C.; Zhang, H. Defect-disorder and risk assessment of heritage trees in urban Hong Kong. Urban For. Urban Green. 2013, 12, 585–596. [Google Scholar] [CrossRef]
- Zhang, H.; Lai, P.Y.; Jim, C. Species diversity and spatial pattern of old and precious trees in Macau. Landsc. Urban Plan. 2017, 162, 56–67. [Google Scholar] [CrossRef]
- Jim, C.Y.; Chen, W.Y. Assessing the ecosystem service of air pollutant removal by urban trees in Guangzhou (China). J. Environ. Manag. 2008, 88, 665–676. [Google Scholar] [CrossRef] [PubMed]
- Kokotovich, A.E.; Zeilinger, A.R. Exploring social and institutional variation across oak wilt risk management programs in Minnesota, USA. Urban For. Urban Green. 2011, 10, 39–45. [Google Scholar] [CrossRef]
- Koeser, A.K.; McLean, D.C.; Hasing, G.; Allison, R.B. Frequency, severity, and detectability of internal trunk decay of street tree Quercus spp. in Tampa, Florida, U.S. Arboric. Urban 2016, 42, 217–226. [Google Scholar]
- Allison, R.B.; Wang, X.; Ross, R.J. Visual and Nondestructive Evaluation of Red Pines Supporting A Ropes Course in the USFS Nesbit Lake Camp, Sidnaw, Michigan. In Proceedings of the 15th International Symposium on Nondestructive Testing of Wood, Duluth, MN, USA, 10–12 September 2007; Forest Products Society: Madison, WI, USA, 2008; pp. 43–48. [Google Scholar]
- Rudnicki, M.; Silins, U.; Lieffers, V.J.; Josi, G. Measure of simultaneous tree sways and estimation of crown interactions among a group of trees. Trees 2001, 15, 83–90. [Google Scholar] [CrossRef]
- Flesch, T.K.; Wilson, J.D. Wind and remnant tree sway in forest cutblocks. II. Relating measured tree sway to wind statistics. Agric. For. Meteorol. 1999, 93, 243–258. [Google Scholar] [CrossRef]
- Stathers, R.J.; Rollerson, T.; Mitchell, S. Windthrow Handbook for British Columbia Forests. Research Program Working Paper No. 9401; Ministry of Forests Research Program: Victoria, BC, Canada, 1994. [Google Scholar]
- Slater, D.; Ennos, R. An assessment of the movement behaviour of bifurcations in hazel (Corylus avellana L.) under dynamic wind loading using triaxial accelerometers. Arboric. J. 2016, 38, 183–203. [Google Scholar] [CrossRef]
- Gardiner, B.; Marshall, B.; Achim, A.; Belcher, R.; Wood, C. The stability of different silvicultural systems: A wind-tunnel investigation. Forestry 2005, 78, 471–484. [Google Scholar] [CrossRef]
- Lopes, A.; Oliveira, S.; Fragoso, M.; Andrade, J.; Pedro, P. Wind risk assessment in urban environments: The case of falling trees during windstorm events in Lisbon. In Bioclimatology and Natural Hazards; Springer: Berlin/Heidelberg, Germany, 2009; pp. 55–74. [Google Scholar] [CrossRef]
- Jan, Č.; Jaroslav, S.; Hana, K.; Soňa, T. Absorptive root areas of large pedunculate oak trees differing in health status along a road in South Bohemia, Czech Republic. Urban For. Urban Green. 2013, 12, 238–245. [Google Scholar] [CrossRef]
- Schindler, D.; Schönborn, J.; Fugmann, H.; Mayer, H. Responses of an individual deciduous broadleaved tree to wind excitation. Agric. For. Meteorol. 2013, 177, 69–82. [Google Scholar] [CrossRef]
- James, K.R.; Haritos, N.; Ades, P.K. Mechanical stability of trees under dynamic loads. Am. J. Bot. 2006, 93, 1522–1530. [Google Scholar] [CrossRef] [PubMed]
- Baker, C. Measurements of the natural frequencies of trees. J. Exp. Bot. 1997, 48, 1125–1132. [Google Scholar] [CrossRef]
- Wang, X.; Allison, R.B. Decay detection in red oak trees using a combination of visual inspection, acoustic testing, and resistance microdrilling. Arboric. Urban For. 2008, 34, 1–4. [Google Scholar]
- James, K.R. A Dynamic Structural Analysis of Trees Subject to Wind Loading; The University of Melbourne: Melbourne, Australia, 2010. [Google Scholar]
- Bunce, A.; Volin, J.C.; Miller, D.R.; Parent, J.; Rudnicki, M. Determinants of tree sway frequency in temperate deciduous forests of the Northeast United States. Agric. For. Meteorol. 2019, 266, 87–96. [Google Scholar] [CrossRef]
- Kane, B.; James, K.R. Dynamic properties of open-grown deciduous trees. Can. J. For. Res. 2011, 41, 321–330. [Google Scholar] [CrossRef]
- Schindler, D.; Vogt, R.; Fugmann, H.; Rodriguez, M.; Schönborn, J.; Mayer, H. Vibration behavior of plantation-grown Scots pine trees in response to wind excitation. Agric. For. Meteorol. 2010, 150, 984–993. [Google Scholar] [CrossRef]
- Stacey, G.; Belcher, R.; Wood, C.; Gardiner, B. Wind flows and forces in a model spruce forest. Bound. Layer Meteorol. 1994, 69, 311–334. [Google Scholar] [CrossRef]
- Jonsson, M.; Foetzki, A.; Kalberer, M.; Lundström, T.; Ammann, W.; Stöckli, V. Root-soil rotation stiffness of Norway spruce (Picea abies (L.) Karst) growing on subalpine forested slopes. Plant Soil 2006, 285, 267–277. [Google Scholar] [CrossRef]
- Moore, J.R.; Maguire, D.A. Natural sway frequencies and damping ratios of trees: Concepts, review and synthesis of previous studies. Trees 2004, 18, 195–203. [Google Scholar] [CrossRef]
- Lin, C.-J.; Huang, Y.-H.; Huang, G.-S.; Wu, M.-L. Detection of decay damage in iron-wood living trees by nondestructive techniques. J. Wood Sci. 2016, 62, 42–51. [Google Scholar] [CrossRef]
- Schindler, D.; Mohr, M. No resonant response of Scots pine trees to wind excitation. Agric. For. Meteorol. 2019, 265, 227–244. [Google Scholar] [CrossRef]
- Schindler, D. Responses of Scots pine trees to dynamic wind loading. Agric. For. Meteorol. 2008, 148, 1733–1742. [Google Scholar] [CrossRef]
- Schindler, D.; Fugmann, H.; Schönborn, J.; Mayer, H. Coherent response of a group of plantation-grown Scots pine trees to wind loading. Eur. J. For. Res. 2012, 131, 191–202. [Google Scholar] [CrossRef]
- Moore, J.R. Mechanical Behavior of Coniferous Trees Subjected to Wind Loading; Oregon State University: Corvallis, OR, USA, 2002. [Google Scholar]
- Lundström, T.; Jonsson, M.J.; Kalberer, M. The root–soil system of Norway spruce subjected to turning moment: Resistance as a function of rotation. Plant Soil 2007, 300, 35–49. [Google Scholar] [CrossRef]
- Jonsson, M.; Foetzki, A.; Kalberer, M.; Lundström, T.; Ammann, W.; Stöckli, V. Natural frequencies and damping ratios of Norway spruce (Picea abies (L.) Karst) growing on subalpine forested slopes. Trees 2007, 21, 541–548. [Google Scholar] [CrossRef]
- Blackwell, P.; Rennolls, K.; Coutts, M. A root anchorage model for shallowly rooted Sitka spruce. For. Int. J. For. Res. 1990, 63, 73–91. [Google Scholar] [CrossRef]
- Vogel, S. Drag and reconfiguration of broad leaves in high winds. J. Exp. Bot. 1989, 40, 941–948. [Google Scholar] [CrossRef]
- Jackson, T.; Shenkin, A.; Kalyan, B.; Zionts, J.; Calders, K.; Origo, N.; Disney, M.; Burt, A.; Raumonen, P.; Malhi, Y. A new architectural perspective on wind damage in a natural forest. Front. For. Glob. Chang. 2019, 1. [Google Scholar] [CrossRef]
- Gardiner, B.; Berry, P.; Moulia, B. Wind impacts on plant growth, mechanics and damage. Plant Sci. 2016, 245, 94–118. [Google Scholar] [CrossRef]
- Ciftci, C.; Brena, S.F.; Kane, B.; Arwade, S.R. The effect of crown architecture on dynamic amplification factor of an open-grown sugar maple (Acer saccharum L.). Trees 2013, 27, 1175–1189. [Google Scholar] [CrossRef]
- Granucci, D.; Rudnicki, M.; Hiscox, A.; Miller, D.; Su, H.-B. Quantifying the effects of freezing on tree sway frequencies. Agric. For. Meteorol. 2013, 168, 10–14. [Google Scholar] [CrossRef]
- Spatz, H.-C.; Theckes, B. Oscillation damping in trees. Plant Sci. 2013, 207, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Peltola, H.; Kellomäki, S.; Hassinen, A.; Lemettinen, M.; Aho, J. Swaying of trees as caused by wind: Analysis of field measurements. Silva Fenn. 1993. [Google Scholar] [CrossRef][Green Version]
- Peltola, H.M. Mechanical stability of trees under static loads. Am. J. Bot. 2006, 93, 1501–1511. [Google Scholar] [CrossRef]
- Schönborn, J.; Schindler, D.; Mayer, H. Measuring vibrations of a single, solitary broadleaf tree. Wind Eff. Trees 2003, 16, 135. [Google Scholar]
- Ciftci, C.; Arwade, S.R.; Kane, B.; Brena, S.F. Analysis of the probability of failure for open-grown trees during wind storms. Probabilistic Eng. Mech. 2014, 37, 41–50. [Google Scholar] [CrossRef]
- Duryea, M.L.; Kampf, E.; Littell, R.C. Hurricanes and the urban forest: I. Effects on southeastern United States coastal plain tree species. Arboric. Urban For. 2007, 33, 83. [Google Scholar]
- Duryea, M.L.; Kampf, E.; Littell, R.C.; Rodriguez-Pedraza, C.D. Hurricanes and the urban forest: II. Effects on tropical and subtropical tree species. Arboric. Urban For. 2007, 33, 98. [Google Scholar]
- Lee, L.S.; Jim, C. Applying precision triaxial accelerometer to monitor branch sway of an urban tree in a tropical cyclone. Landsc. Urban Plan. 2018, 178, 170–182. [Google Scholar] [CrossRef]
- Papesch, A. Wind and Its Effects on (Canterbury) Forests; University of Canterbury: Christchurch, New Zealand, 1984. [Google Scholar]
- Mayhead, G. Sway periods of forest trees. Scot For. 1973, 27, 19–23. [Google Scholar]
- Gardiner, B. Mechanical Characteristics of Sitka Spruce; Forestry Commission: Edinburgh, UK, 1989; Volume 24. [Google Scholar]
- James, K.; Hallam, C.; Spencer, C. Measuring tilt of tree structural root zones under static and wind loading. Agric. For. Meteorol. 2013, 168, 160–167. [Google Scholar] [CrossRef]
- Vollsinger, S.; Mitchell, S.J.; Byrne, K.E.; Novak, M.D.; Rudnicki, M. Wind tunnel measurements of crown streamlining and drag relationships for several hardwood species. Can. J. For. Res. 2005, 35, 1238–1249. [Google Scholar] [CrossRef]
- Rudnicki, M.; Mitchell, S.J.; Novak, M.D. Wind tunnel measurements of crown streamlining and drag relationships for three conifer species. Can. J. For. Res. 2004, 34, 666–676. [Google Scholar] [CrossRef]
- Van Emmerik, T.; Steele-Dunne, S.; Hut, R.; Gentine, P.; Guerin, M.; Oliveira, R.; Wagner, J.; Selker, J.; van de Giesen, N. Measuring tree properties and responses using low-cost accelerometers. Sensors 2017, 17, 1098. [Google Scholar] [CrossRef]
- Gardiner, B.A. Wind and wind forces in a plantation spruce forest. Bound. Layer Meteorol. 1994, 67, 161–186. [Google Scholar] [CrossRef]
- Fisher, R.A. XV.—The correlation between relatives on the supposition of Mendelian inheritance. Earth Environ. Sci. Trans. R. Soc. Edinb. 1919, 52, 399–433. [Google Scholar] [CrossRef]
- Kane, B.; Pavlis, M.; Harris, J.R.; Seiler, J.R. Crown reconfiguration and trunk stress in deciduous trees. Can. J. For. Res. 2008, 38, 1275–1289. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. Siam J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Bochner, S.; Chandrasekharan, K. Fourier Transforms; Princeton University Press: Princeton, NJ, USA, 1949. [Google Scholar]
- Lee, D.T.; Yamamoto, A. Wavelet analysis: Theory and applications. Hewlett Packard J. 1994, 45, 44. [Google Scholar] [CrossRef]
- Aubry, N.; Guyonnet, R.; Lima, R. Spatiotemporal analysis of complex signals: Theory and applications. J. Stat. Phys. 1991, 64, 683–739. [Google Scholar] [CrossRef]
- Jastrzebski, Z.D. Nature and Properties of Engineering Materials; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 1976. [Google Scholar]
- Green, D.W.; Winandy, J.E.; Kretschmann, D.E. Mechanical properties of wood. In Wood Handbook: Wood as an Engineering Material; General Technical Report FPL; GTR-113; USDA Forest SERVICE, Forest Products Laboratory: Madison, WI, USA, 1999; Volume 113, pp. 4.1–4.45. [Google Scholar]
- Sugden, M.J. Tree sway period—A possible new parameter for crown classification and stand competition. For. Chron. 1962, 38, 336–344. [Google Scholar] [CrossRef]
- Hoag, D.; Fridley, R.; Hutchinson, J. Experimental measurement of internal and external damping properties of tree limbs. Trans. Asae 1971, 14, 20–0024. [Google Scholar] [CrossRef]
- Wood, C. Understanding wind forces on trees. Wind Trees 1995, 133–164. [Google Scholar] [CrossRef]
- Feldpausch, T.R.; Banin, L.; Phillips, O.L.; Baker, T.R.; Lewis, S.L.; Quesada, C.A.; Affum-Baffoe, K.; Arets, E.J.; Berry, N.J.; Bird, M. Height-diameter allometry of tropical forest trees. Biogeosciences 2011, 8, 1081–1106. [Google Scholar] [CrossRef]
- Schindler, D.; Mohr, M. Non-oscillatory response to wind loading dominates movement of Scots pine trees. Agric. For. Meteorol. 2018, 250, 209–216. [Google Scholar] [CrossRef]
- Wang, Y.; Titus, S.J.; LeMay, V.M. Relationships between tree slenderness coefficients and tree or stand characteristics for major species in boreal mixedwood forests. Can. J. For. Res. 1998, 28, 1171–1183. [Google Scholar] [CrossRef]
- Quine, C.P.; Gardiner, B.A. Understanding how the interaction of wind and trees results in windthrow, stem breakage, and canopy gap formation. Plant Disturb. Ecol. Process Response 2007, 103–155. [Google Scholar] [CrossRef]
- Coutts, M. Components of tree stability in Sitka spruce on peaty gley soil. For. Int. J. For. Res. 1986, 59, 173–197. [Google Scholar] [CrossRef]
- Niklas, K.J. Computing factors of safety against wind-induced tree stem damage. J. Exp. Bot. 2000, 51, 797–806. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.R.; Maguire, D.A. Natural sway frequencies and damping ratios of trees: Influence of crown structure. Trees 2005, 19, 363–373. [Google Scholar] [CrossRef]
- Uchida, T. Validation testing of the prediction accuracy of the numerical wind synopsis prediction technique RIAMCOMPACT for the case of the bolund experiment: Comparison against a wind-tunnel experiment. Rep. RiamKyushu Univ. 2014, 147, 7–14. [Google Scholar]
- Mekki, K.; Bajic, E.; Chaxel, F.; Meyer, F. A comparative study of LPWAN technologies for large-scale IoT deployment. Ict Express 2019, 5, 1–7. [Google Scholar] [CrossRef]
- Kitchin, R. Big Data, new epistemologies and paradigm shifts. Big Data Soc. 2014, 1, 2053951714528481. [Google Scholar] [CrossRef]
- Wang, S.; Zhong, Y.; Wang, E. An integrated GIS platform architecture for spatiotemporal big data. Future Gener. Comput. Syst. 2019, 94, 160–172. [Google Scholar] [CrossRef]
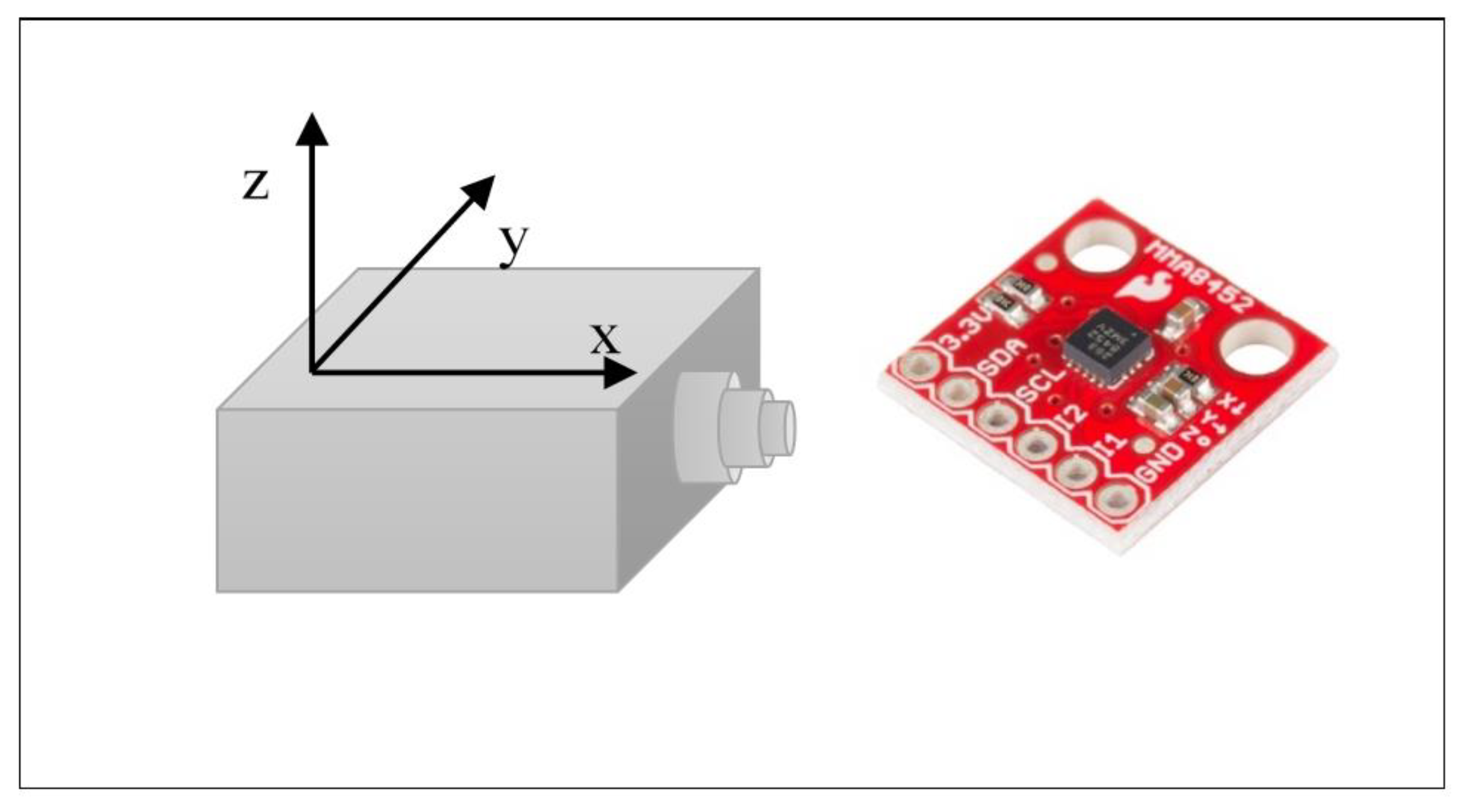
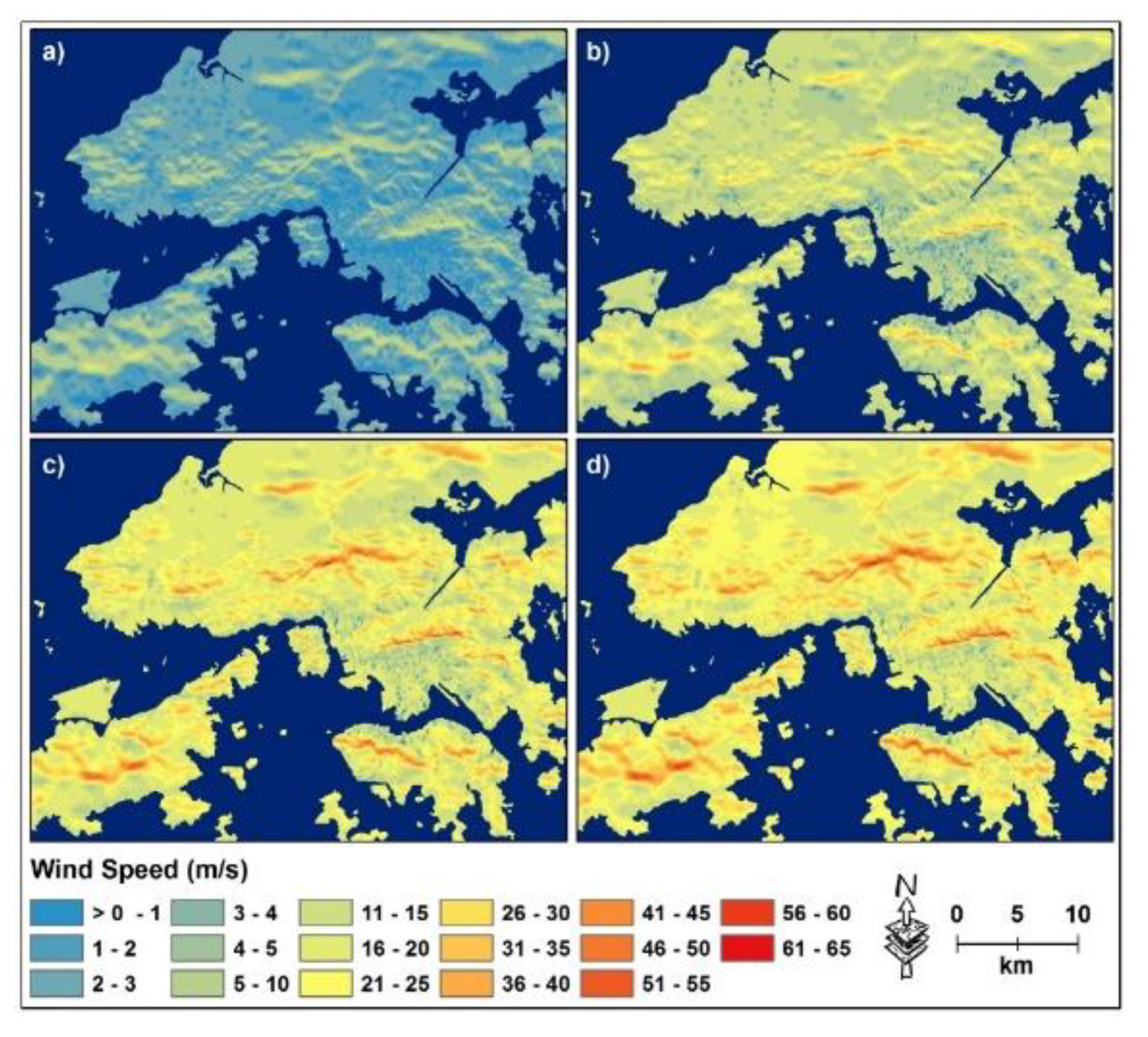
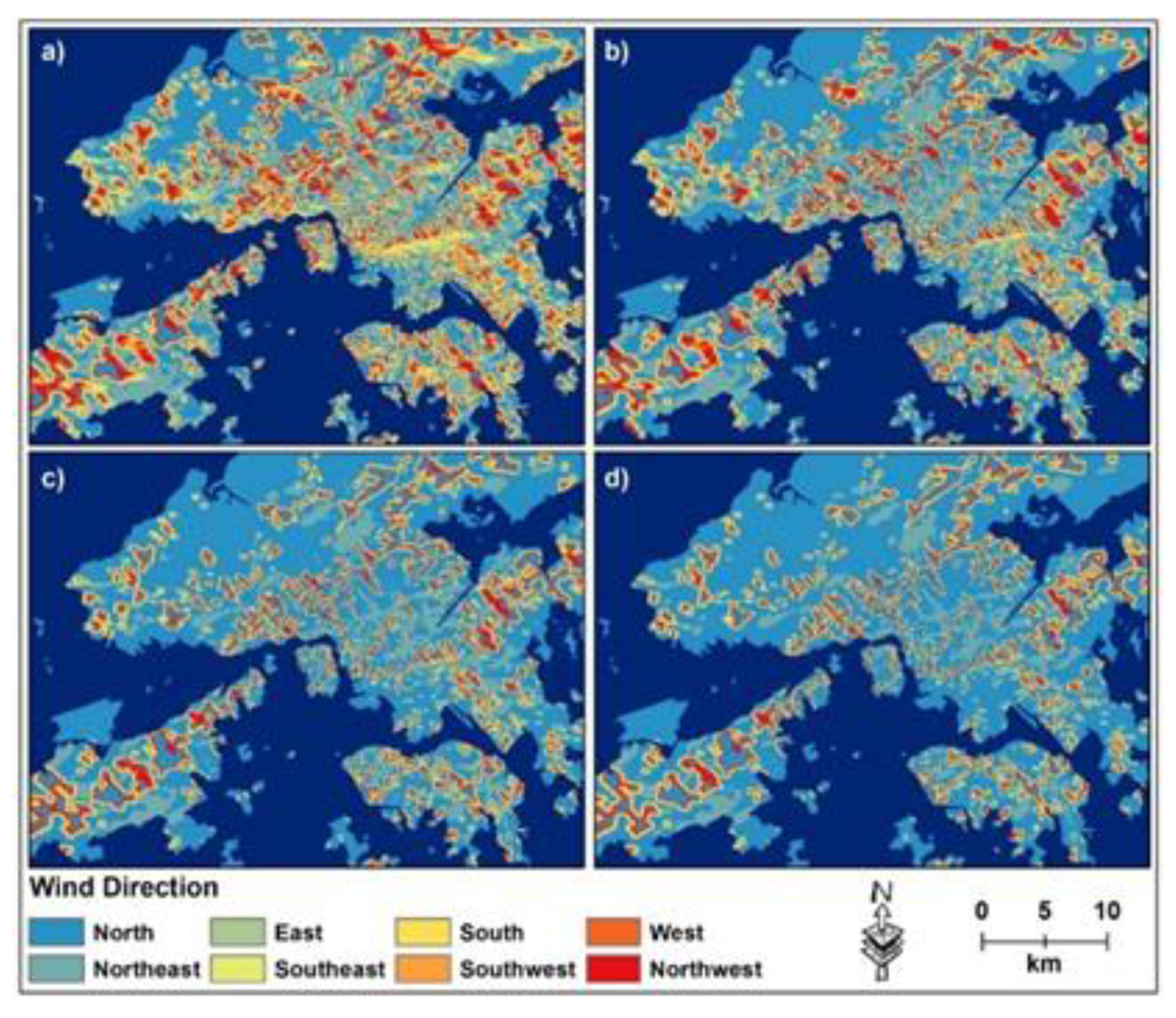

| Measure | Unit | Instrument | Description |
|---|---|---|---|
| Angular Sway Data | Degree | Accelerometer | The tilt angle of a tree recorded as the response of wind loading (the sensor is often attached to the base of the tree) |
| Vertical Displacement | Meter | Inclinometer | Vertical deflection measured from the center of tree mass |
| Sway Frequency | Hz | Calculation | The fundamental frequency peak |
| Critical Wind Speed | Km/h | Anemometer | The wind speed that could cause the tree to snap at 1.3 m |
| Local Area Network (LAN) | Lower Power Wide Area Network (LPWAN) | Cellular Network | |
|---|---|---|---|
| Advantages | Well established standard |
| High coverage |
| |||
| |||
| Disadvantages | Limited area coverage | Emerging standards | Cost of ownership |
| Examples |
| Long-range wide area network (LoRaWAN) | 3G |
| 4G |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Hui, K.W.; Abbas, S.; Zhu, R.; Kwok, C.Y.T.; Heo, J.; Ju, S.; Wong, M.S. A Review of Dynamic Tree Behaviors: Measurement Methods on Tree Sway, Tree Tilt, and Root–Plate Movement. Forests 2021, 12, 379. https://doi.org/10.3390/f12030379
Yang Z, Hui KW, Abbas S, Zhu R, Kwok CYT, Heo J, Ju S, Wong MS. A Review of Dynamic Tree Behaviors: Measurement Methods on Tree Sway, Tree Tilt, and Root–Plate Movement. Forests. 2021; 12(3):379. https://doi.org/10.3390/f12030379
Chicago/Turabian StyleYang, Zi, Ka Wai Hui, Sawaid Abbas, Rui Zhu, Coco Yin Tung Kwok, Joon Heo, Sungha Ju, and Man Sing Wong. 2021. "A Review of Dynamic Tree Behaviors: Measurement Methods on Tree Sway, Tree Tilt, and Root–Plate Movement" Forests 12, no. 3: 379. https://doi.org/10.3390/f12030379
APA StyleYang, Z., Hui, K. W., Abbas, S., Zhu, R., Kwok, C. Y. T., Heo, J., Ju, S., & Wong, M. S. (2021). A Review of Dynamic Tree Behaviors: Measurement Methods on Tree Sway, Tree Tilt, and Root–Plate Movement. Forests, 12(3), 379. https://doi.org/10.3390/f12030379









