Exploring the Potential to Improve the Estimation of Boreal Tree Structural Attributes with Simple Height- and Distance-Based Competition Index
Abstract
1. Introduction
2. Materials and Methods
2.1. Competition Measurements
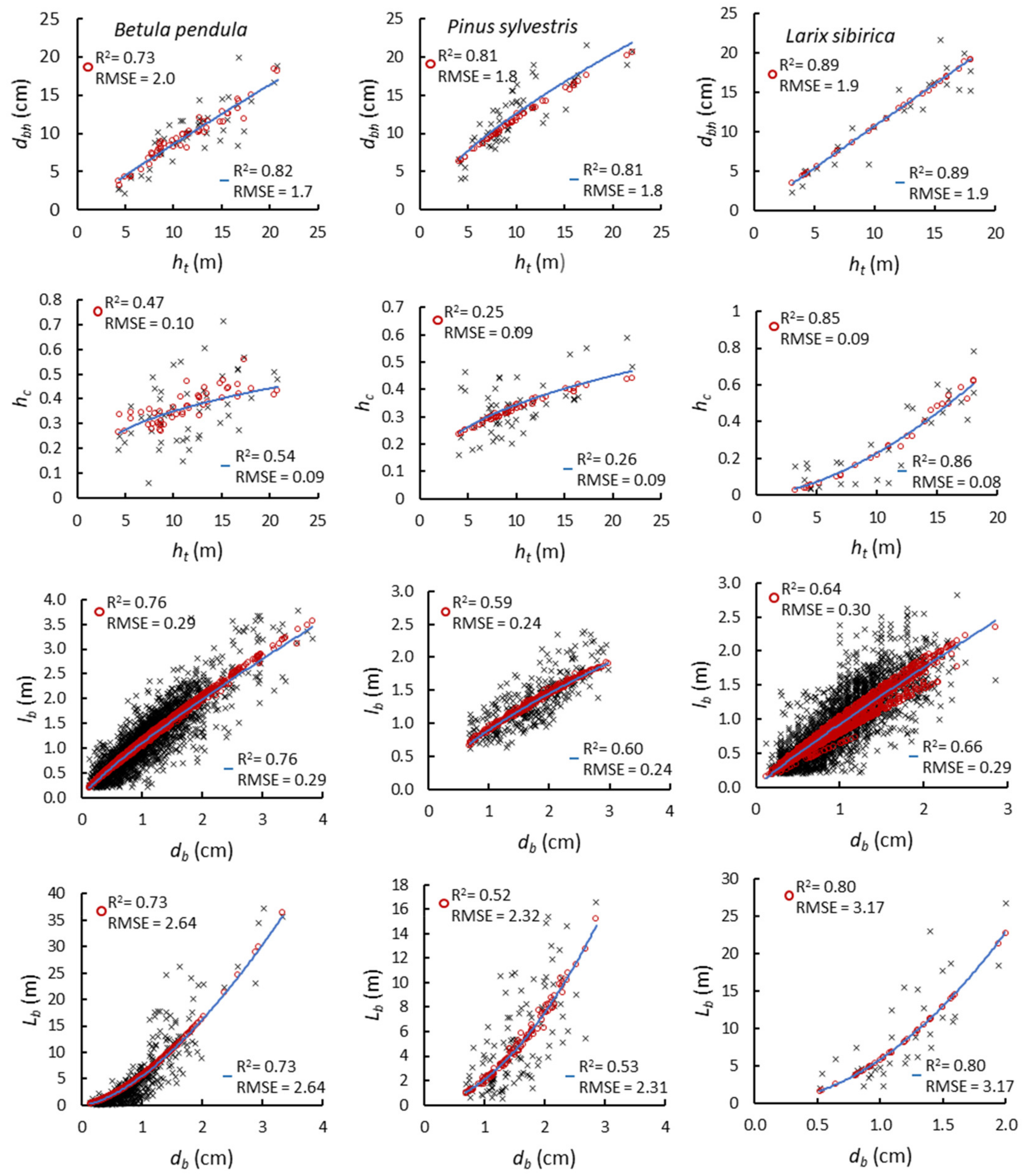
2.2. Allometric Equations
3. Results and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and stem volume equations for tree species in Europe. Silva Fenn. Monogr. 2005, 4, 1–63. [Google Scholar]
- Weiskittel, A.R. Forest Growth and Yield Modeling; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Temesgen, H.; LeMay, V.; Mitchell, S.J. Tree crown ratio models for multi-species and multi-layered stands of southeastern British Columbia. For. Chron. 2005, 81, 133–141. [Google Scholar] [CrossRef]
- Del Río, M.; Bravo-Oviedo, A.; Ruiz-Peinado, R.; Condés, S. Tree allometry variation in response to intra- and inter-specific competitions. Trees 2019, 33, 121–138. [Google Scholar] [CrossRef]
- Daniels, R.F.; Burkhart, H.E.; Clason, T.R. A comparison of competition measures for predicting growth of loblolly pine trees. Can. J. For. Res. 1986, 16, 1230–1237. [Google Scholar] [CrossRef]
- Ilomäki, S.; Nikinmaa, E.; Mäkelä, A. Crown rise due to competition drives biomass allocation in silver birch. Can. J. For. Res. 2011, 33, 2395–2404. [Google Scholar] [CrossRef]
- Newton, P.F. Stand density management diagrams: Review of their development and utility in stand-level management planning. For. Ecol. Manag. 1997, 98, 251–265. [Google Scholar] [CrossRef]
- Saarinen, N.; Calders, K.; Kankare, V.; Yrttimaa, T.; Junttila, S.; Luoma, V.; Huuskonen, S.; Hynynen, J.; Verbeeck, H. Understanding 3D structural complexity of individual Scots pine trees with different management history. Ecol. Evol. 2021, 1–12. [Google Scholar] [CrossRef]
- Kotivuori, E.; Korhonen, L.; Packalen, P. Nationwide airborne laser scanning based models for volume, biomass and dominant height in Finland. Silva Fenn. 2016, 50, 1567. [Google Scholar] [CrossRef]
- Karjalainen, T.; Korhonen, L.; Packalen, P.; Maltamo, M. The transferability of airborne laser scanning based tree-level models between different inventory areas. Can. J. For. Res. 2019, 49, 228–236. [Google Scholar] [CrossRef]
- Lin, C.; Thomson, G.; Popescu, S. An IPCC-compliant technique for forest carbon stock assessment using airborne LiDAR-derived tree metrics and competition index. Remote Sens. 2016, 8, 528. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.; Tao, S.; Guo, Q. Quantifying individual tree growth and tree competition using bi-temporal airborne laser scanning data: A case study in the Sierra Nevada Mountains, California. Int. J. Digit. Earth 2018, 11, 485–503. [Google Scholar] [CrossRef]
- Versace, S.; Gianelle, D.; Frizzera, L.; Tognetti, R.; Garfì, V.; Dalponte, M. Prediction of competition indices in a Norway spruce and silver fir-dominated forest using Lidar data. Remote Sens. 2019, 11, 2734. [Google Scholar] [CrossRef]
- Aubry-Kientz, M.; Dutrieux, R.; Ferraz, A.; Saatchi, S.; Hamraz, H.; Williams, J.; Coomes, D.; Piboule, A.; Vincent, G. A Comparative assessment of the performance of individual tree crowns delineation algorithms from ALS data in tropical forests. Remote Sens. 2019, 11, 1086. [Google Scholar] [CrossRef]
- Pyörälä, J.; Liang, X.; Saarinen, N.; Kankare, V.; Wang, Y.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Assessing branching structure for biomass and wood quality estimation using terrestrial laser scanning point clouds. Can. J. Remote Sens. 2018, 44, 462–475. [Google Scholar] [CrossRef]
- Vanderwel, M.C.; Lopez, E.L.; Sprott, A.H.; Khayyatkhoshnevis, P.; Shovon, T.A. Using aerial canopy data from UAVs to measure the effects of neighbourhood competition on individual tree growth. For. Ecol. Manag. 2020, 461, 117949. [Google Scholar] [CrossRef]
- Kaitaniemi, P.; Lintunen, A. Neighbor identity and competition influence tree growth in Scots pine, Siberian larch, and silver birch. Ann. For. Sci. 2010, 67, 604. [Google Scholar] [CrossRef]
- Lintunen, A.; Sievänen, R.; Kaitaniemi, P.; Perttunen, J. Models of 3D crown structure for Scots pine (Pinus sylvestris) and silver birch (Betula pendula) grown in mixed forest. Can. J. For. Res. 2011, 41, 1779–1794. [Google Scholar] [CrossRef]
- Äijälä, O.; Koistinen, A.; Sved, J.; Vanhatalo, K.; Väisänen, P. Metsänhoidon Suositukset; Metsäkustannus Oy; Publications of Forestry Development Centre Tapio: Helsinki, Finland, 2014. (In Finnish) [Google Scholar]
- Lintunen, A.; Kaitaniemi, P. Responses of crown architecture in Betula pendula to competition are dependent on the species of neighbouring trees. Trees 2010, 24, 411–424. [Google Scholar] [CrossRef]
- Hegyi, F. A simulation model for managing jack-pine stands. In Growth Models for Tree and Stand Simulation; Royal College of Forestry: Stockholm, Sweden, 1974; pp. 74–90. [Google Scholar]
- Kaitaniemi, P.; Lintunen, A.; Sievänen, R. Power-law estimation of branch growth. Ecol. Model. 2020, 416, 108900. [Google Scholar] [CrossRef]
- Kurada, R.R. Fitting Multilevel Hierarchical Mixed Models Using PROC NLMIXED; SAS Global Forum: 2016. Paper SAS4720-2016; SAS Institute Inc.: Cary, NC, USA, 2016. [Google Scholar]
- Niemistö, P. Influence of initial spacing and row-to-row distance on the crown and branch properties and taper of silver birch (Betula pendula). Scand. J. For. Res. 1995, 10, 235–244. [Google Scholar] [CrossRef]
- Mäkelä, A.; Vanninen, P. Impacts of size and competition on tree form and distribution of aboveground biomass in Scots pine. Can. J. For. Res. 1998, 28, 216–227. [Google Scholar] [CrossRef]
- Gradel, A.; Ammer, C.; Ganbaatar, B.; Nadaldorj, O.; Dovdondemberel, B.; Wagner, S. On the effect of thinning on tree growth and stand structure of white birch (Betula platyphylla Sukaczev) and Siberian Larch (Larix sibirica Ledeb.) in Mongolia. Forests 2017, 8, 105. [Google Scholar] [CrossRef]
- Aphalo, P.J.; Rikala, R. Spacing of silver birch seedlings grown in containers of equal size affects their morphology and its variability. Tree Physiol. 2006, 26, 1227–1237. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Uria-Diez, J.; Pommerening, A. Crown plasticity in Scots pine (Pinus sylvestris L.) as a strategy of adaptation to competition and environmental factors. Ecol. Model. 2017, 356, 117–126. [Google Scholar] [CrossRef]
- Hu, M.; Lehtonen, A.; Minunno, F.; Mäkelä, A. Age effect on tree structure and biomass allocation in Scots pine (Pinus sylvestris L.) and Norway spruce (Picea abies L. Karst.). Ann. For. Sci. 2020, 77, 90. [Google Scholar] [CrossRef]
- Van de Peer, T.; Verheyen, K.; Kint, V.; Van Cleemput, E.; Muys, B. Plasticity of tree architecture through interspecific and intraspecific competition in a young experimental plantation. For. Ecol. Manag. 2017, 385, 1–9. [Google Scholar] [CrossRef]
- Lehtonen, A.; Heikkinen, J.; Petersson, H.; Ťupek, B.; Liski, E.; Mäkelä, A. Scots pine and Norway spruce foliage biomass in Finland and Sweden—Testing traditional models versus the pipe model theory. Can. J. For. Res. 2019, 50, 146–154. [Google Scholar] [CrossRef]
- Henry, H.A.L.; Aarssen, L.W. The interpretation of stem diameter-height allometry in trees: Biomechanical constraints, neighbour effects, or biased regressions? Ecol. Lett. 1999, 2, 89–97. [Google Scholar] [CrossRef]
- Forrester, D.I.; Benneter, A.; Bouriaud, O.; Bauhus, J. Diversity and competition influence tree allometric relationships—Developing functions for mixed-species forests. J. Ecol. 2017, 105, 761–774. [Google Scholar] [CrossRef]
| Variable | Description |
|---|---|
| ht | tree height (m) |
| dbh | tree diameter at breast height (cm) |
| hc | relative height of crown base |
| lb | branch axis length as a straight line between the branch base and tip (m) |
| db | branch diameter (cm) |
| Lb | total branch length with all branching orders combined (m) |
| H | competition index (see text for calculation) |
| Model | a (±CL) | b (±CL) | c (±CL) | AICC | R2 | RMSE | N of Trees |
|---|---|---|---|---|---|---|---|
| Betula pendula | |||||||
| dbh = ahtb | 1.01 (±0.51) | 0.93 (±0.21) | 219 | 0.73 | 2.0 cm | 50 | |
| dbh = aHchtb | 1.55 (±1.00) | 0.84 (±0.22) | −0.27 (±0.20) | 213 | 0.82 | 1.7 cm | 50 |
| hc = ahtb | 0.16 (±0.15) | 0.34 (±0.41) | −71 | 0.47 | 0.10 | 50 | |
| hc = aHchtb | 0.08 (±0.09) | 0.52 (±0.39) | 0.35 (±0.30) | −74 | 0.54 | 0.09 | 50 |
| lb = adbb | 1.10 (±0.5) | 0.85 (±0.03) | 653 | 0.76 | 0.29 m | 45 | |
| lb = aHcdbb | 1.18 (±0.08) | 0.84 (±0.04) | −0.08 (±0.06) | 646 | 0.76 | 0.29 m | 45 |
| Lb = adbb | 5.52 (±0.76) | 1.56 (±0.14) | 2789 | 0.73 | 2.64 m | 47 | |
| Lb = aHcdbb | 5.65 (±1.13) | 1.55 (±0.16) | −0.02 (±0.15) | 2791 | 0.73 | 2.64 m | 47 |
| Pinus sylvestris | |||||||
| dbh = ahtb | 0.10 (±0.08) | 0.70 (±0.16) | 242 | 0.81 | 1.8 cm | 55 | |
| dbh = aHchtb | 0.08 (±0.11) | 0.72 (±0.18) | 0.03 (±0.13) | 244 | 0.81 | 1.8 cm | 55 |
| hc = ahtb | 0.14 (±0.07) | 0.39 (±0.21) | −106 | 0.25 | 0.09 | 55 | |
| hc = aHchtb | 0.13 (±0.08) | 0.42 (±0.24) | 0.05 (±0.25) | −104 | 0.26 | 0.09 | 55 |
| lb = adbb | 0.90 (±0.80) | 0.69 (±0.09) | −75.4 | 0.59 | 0.24 m | 34 | |
| lb = aHcdbb | 0.92 (±0.10) | 0.68 (±0.08) | −0.04 (±0.11) | −74.0 | 0.60 | 0.24 m | 34 |
| Lb = adbb | 2.08 (±0.49) | 1.86 (±0.29) | 1053 | 0.52 | 2.32 m | 55 | |
| Lb = aHcdbb | 1.77 (±0.57) | 1.93 (±0.34) | 0.16 (±0.20) | 1051 | 0.53 | 2.31 m | 55 |
| Larix sibirica | |||||||
| dbh = ahtb | 1.10 (±0.66) | 0.99 (±0.23) | 127 | 0.89 | 1.9 cm | 29 | |
| dbh = aHchtb | 1.05 (±0.85) | 1.00 (±0.27) | 0.02 (±0.20) | 130 | 0.89 | 1.9 cm | 29 |
| hc = ahtb | 0.005 (±0.01) | 1.66 (±1.10) | −44 | 0.85 | 0.09 | 29 | |
| hc = aHchtb | 0.005 (±0.02) | 1.70 (±1.12) | −0.16 (±0.39) | −42 | 0.86 | 0.08 | 29 |
| lb = adbb | 0.93 (±0.07) | 0.90 (±0.07) | 676 | 0.64 | 0.30 m | 25 | |
| lb = aHcdbb | 1.07 (±0.08) | 0.88 (±0.06) | −0.20 (±0.08) | 650 | 0.66 | 0.29 m | 25 |
| Lb = adbb | 5.84 (±1.50) | 1.97 (±0.49) | 289 | 0.80 | 3.17 m | 29 | |
| Lb = aHcdbb | 5.81 (±2.45) | 1.97 (±0.51) | 0.01 (±0.39) | 292 | 0.80 | 3.17 m | 29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaitaniemi, P.; Lintunen, A. Exploring the Potential to Improve the Estimation of Boreal Tree Structural Attributes with Simple Height- and Distance-Based Competition Index. Forests 2021, 12, 324. https://doi.org/10.3390/f12030324
Kaitaniemi P, Lintunen A. Exploring the Potential to Improve the Estimation of Boreal Tree Structural Attributes with Simple Height- and Distance-Based Competition Index. Forests. 2021; 12(3):324. https://doi.org/10.3390/f12030324
Chicago/Turabian StyleKaitaniemi, Pekka, and Anna Lintunen. 2021. "Exploring the Potential to Improve the Estimation of Boreal Tree Structural Attributes with Simple Height- and Distance-Based Competition Index" Forests 12, no. 3: 324. https://doi.org/10.3390/f12030324
APA StyleKaitaniemi, P., & Lintunen, A. (2021). Exploring the Potential to Improve the Estimation of Boreal Tree Structural Attributes with Simple Height- and Distance-Based Competition Index. Forests, 12(3), 324. https://doi.org/10.3390/f12030324







