Abstract
Wood is considered one of the most important construction materials, as well as a natural material prone to degradation, with fungi being the main reason for wood failure in a temperate climate. Visual inspection of wood or other approaches for monitoring are time-consuming, and the incipient stages of decay are not always visible. Thus, visual decay detection and such manual monitoring could be replaced by automated real-time monitoring systems. The capabilities of such systems can range from simple monitoring, periodically reporting data, to the automatic detection of anomalous measurements that may happen due to various environmental or technical reasons. In this paper, we explore the application of Unsupervised Anomaly Detection (UAD) techniques to wood Moisture Content (MC) data. Specifically, data were obtained from a wood construction that was monitored for four years using sensors at different positions. Our experimental results prove the validity of these techniques to detect both artificial and real anomalies in MC signals, encouraging further research to enable their deployment in real use cases.
1. Introduction
Wood is a very popular, widespread, and most importantly, renewable construction material, whose physical properties have been praised by many. However, like any other natural or synthetic material, it can deteriorate and eventually fail [1]. These processes are important to maintain the carbon cycle, but when wood is used in commercial applications, it is in our interest to slow them down [2]. Depending on the nature of the specific construction and the severity of the failure, this could lead to a wide variety of negative consequences [3]. In the past, degradation was controlled predominately with biocides and the use of durable tropical timber. However, these options are not acceptable by consumers and are limited by EU legislation as well. Therefore, new strategies need to be developed, which will allow us to use less durable European species in a variety of indoor and outdoor applications. Undoubtedly, the development of a system that could help us prevent or, at least, mitigate the undesired consequences of wood decay in buildings would have numerous benefits.
In order to use less durable wood species, proper protection-by-design measures have to be applied [4]. Protection-by-design is based on the principle that wood has to be kept dry, and if the wood is moistened, the construction has to enable fast drying. The Moisture Content (MC) of wood has to be kept below the threshold required for fungal decay. There are various data available in the literature in this regard. In the first reports, the authors stated that moisture limits are dependent predominantly on fungal species. For example, Reference [5] reported that the minimum MC of wood for the growth of Fibroporia vaillantii and Gloeophyllum trabeum is 30%, while a slightly lower (26%) minimum MC level is reported for Coniophora puteana and Serpula lacrymans. In [6], similar values were reported as well. However, recent findings have shown that moisture limits for fungal growth and decay depend on the fungal species in question and considerably differ among the investigated wood species. For example, the minimum MC for wood decay varied between 16.3% (G. trabeum for Scots pine sapwood) and 52.3% (Donkioporia expansa for Douglas fir) [7]. Wood treatments such as acetylation affect the wood decay processes related to fungi as well. However, the processes that result in reduced decay are not fully understood yet [8]. Common questions are: How fast will decay occur in various wood-based materials, and under what conditions (temperature and MC) will decay become established and cause structural damage?
Although the threshold for moisture content varies by wood species and decay fungi, it has been agreed that wood decay is always associated with an increase in moisture content. Early works such as [9] already linked tree decay and discoloration with lower electrical resistance measured by inserting probes into trees and utility poles. Moisture increase is the first indication of potential problems. The key question, however, is how to develop the methodology to detect these increases. After that, it is still up to the expert to assess the potential threat based on available data.
Currently, as part of the well-known Internet of Things phenomenon, we see an increase in the use—and associated market segment [10]—of systems that provide real-time information about manufacturing processes [11], the status of different types of infrastructure [12], or the consumption of resources such as power or water [13]. In some cases, the capabilities of such systems go beyond simple monitoring, for instance raising alarms when some abnormal measurements are detected, or even locating the possible root causes of failures.
In this paper, we study the application of techniques that would enable the automatic detection of anomalies in time series data captured from wood constructions. After the analysis of the experimental results, we can confirm the usefulness and added value of combining Unsupervised Anomaly Detection (UAD) methods with monitoring systems for wood constructions, enabling the detection not only of the possible malfunctioning of the sensing devices, but also of deviations from normal operating conditions caused by wood decay or deterioration. In addition, these techniques can be applied to surface-coated wood (facade, windows, fences, etc.) to assess the failure of the film on the surface, as well as to monitor possible leakage and condensation at thermal bridges.
2. Related Work
Outlier detection, also referred to as anomaly detection, is a wide field both regarding the variety of techniques it comprises, as well as its potential application to very diverse use cases [14]. Unsupervised anomaly detection techniques for time series, a subset of the former, have seen increasing interest along with the rise in the popularity of the terms Internet of Things (IoT) [15] and Industry 4.0 [16]. One of the main features of these is the presence of a high number of connected sensors, providing big amounts of time series data. Considerable research has already been done on how to effectively exploit the potential that this kind of data offers to automatically detect anomalies in complex systems [17].
Some early works already explored the use of machine learning in combination with industrial monitoring systems, such as [18], in which a neural network was used to provide real-time estimates of the viscosity of produced materials, or [19], which detailed the application of a machine learning algorithm to detect tool breakages. However, the application of time series anomaly detection techniques in industrial environments was studied mostly in more recent works [20,21], also tackling specific applications such as natural gas [22], building power consumption [23], or water management systems [24]. Some authors also proposed generic anomaly detection frameworks [25,26].
On the contrary, not many studies have applied anomaly detection to the monitoring of building structures yet. An overview of the application of machine learning to structural health monitoring can be found in [12], including some examples of outlier detection. One of the most recent works on this topic is [27], in which autoencoders were used to detect anomalies in images of plotted time series data from accelerometers.
Regarding wood constructions specifically, some works have documented the use of monitoring systems, mainly as a means to assess wood performance [28,29,30,31]. Generally, all these works focused on obtaining the data and carrying out diverse analysis afterward, such as decay modeling or correlation analysis. However, none of those placed emphasis on the capabilities of the monitoring system. To the best of our knowledge, this is the first work in which anomaly detection techniques are applied to data from a monitoring system installed on a wooden construction.
3. Methodology
3.1. Data Description
The data used in this work were recorded as part of the WINTHERWAX (https://cordis.europa.eu/project/id/666206) project from 10 June 2016 to 10 June 2020, with a sampling period of 12 h, which makes a total of 2922 records. Specifically, log resistance signals were recorded from 16 different wood samples mounted on a test cube located in Žiri, Slovenia (46.0530, 14.1046). Moisture Content (MC) was determined from measurements of electrical resistance. Insulated electrodes (stainless steel screws) were applied at various positions and depths and linked to electrical resistance measuring equipment (Gigamodule, Scanntronik Mugrauer GmbH, Germany) [32]. The method was validated with samples that were preconditioned at various relative humidity and temperature levels to achieve various target concentrations. This equipment enables accurate wood MC measurements between 6% and 60%. To transform electrical resistance measured inside the wood to MC, wood-species-specific resistance characteristics were developed based on the methodology described in [33]. The results were periodically downloaded to a personal computer, and the systems were periodically checked and had their batteries replaced on the visits. Out of the 16 signals, twelve correspond to wood samples installed on the facade of the test cube, while only 4 of them correspond to wood samples installed on the windows. Additionally, average wood temperature signals were recorded, having four different signals corresponding to outdoor samples and two signals corresponding to indoor samples. The test cube is equipped with an A/C inside, set to a fixed temperature of 25 °C, which affects the indoor measurements, as well as those from the windows. In Table 1, we present a summary of the data used in this study, detailing the different wood materials that composed the test cube.

Table 1.
Summary of the data used in this study. TMT stands for Thermally Modified Timber. For spruce, two different intensities were used, with a higher one used for the facade (TMT facade) and a lower one for the windows (TMT window). Note that a spruce sample to which the “TMT window” modification was applied was installed in the facade for comparison purposes. A thin acrylic coating was applied to the spruce samples installed in the windows.
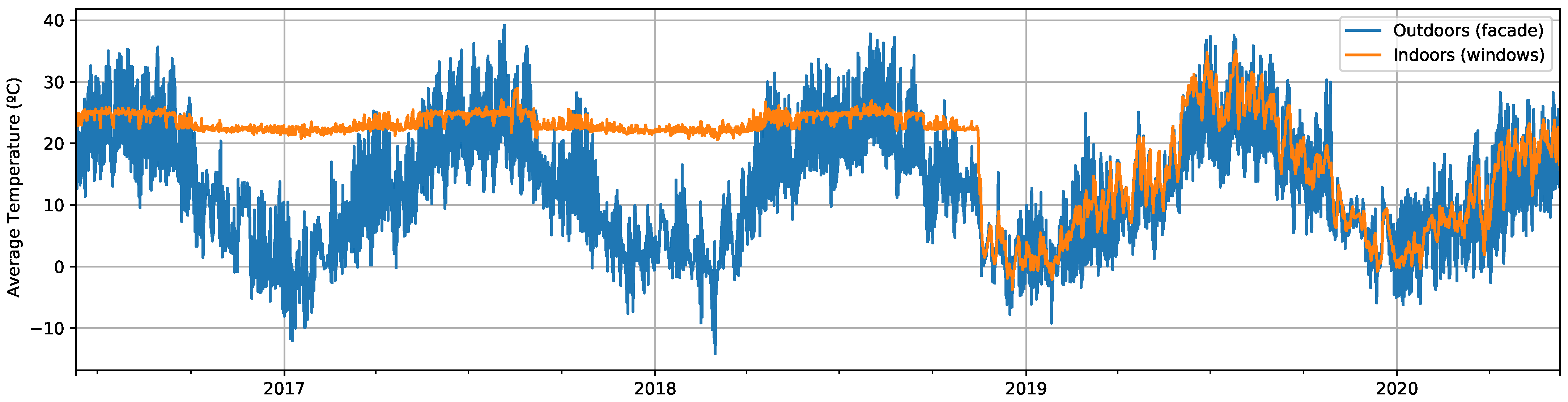
Firstly, we include several plots that will make it easier to understand the signals with which we are working. In Figure 1, we compare the average of all the outdoor and indoor wood temperature signals. While the former follows a clear seasonal variation, the changes of the latter along the year are undoubtedly smaller because of the presence of the A/C system. However, indoor measurements show an abnormal decrease on 15 November 2018, after which they start behaving like the outdoor temperature signal. This was caused by an unexpected failure of the A/C system inside the test cube, which explains the match with the outdoor values afterward.
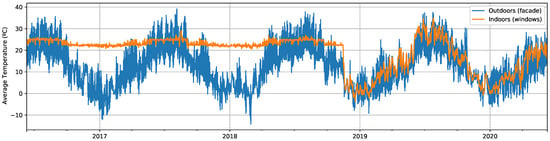
Figure 1.
Average temperature (°C) for the facade (blue) and windows (orange).
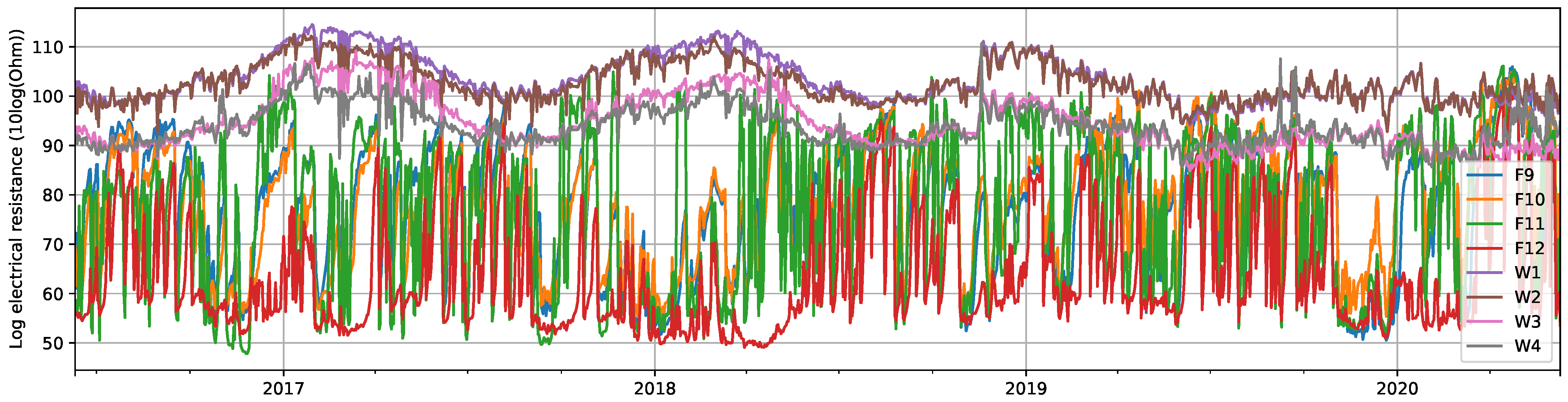
Similarly, in Figure 2, eight of the log resistance signals are plotted, and it is possible to observe that signals corresponding to Facade measurements (i.e., F9 to F12), clearly showing different behavior and average values compared to those taken from the Window samples (i.e., W1 to W4).
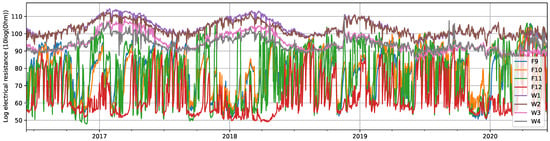
Figure 2.
Log electrical resistance () for four of the Facade signals (F9 to F12) and for the four signals only from the Windows (W1 to W4). Daily averages were taken to facilitate visualization.
Because signals from facade and windows are different regarding both their range of values and their evolution and because there was an unexpected event (the failure of the A/C inside the test cube) that affected only signals from windows, the rest of this study will use both subsets separately. Different transformations and different experiments will be carried out for each of the subsets mentioned above. From this point on, we will refer to them as the facade dataset and the windows dataset.
3.2. Data Preprocessing
3.2.1. Moisture Content
Wood Moisture Content (MC) refers to the percentage of water mass contained in the wood with respect to the wood mass without water. MC levels above certain limits have proven to lead to a variety of wood decay processes. In order to compute wood MC from the log electrical resistance signals (U), we will also use temperature signals from the two datasets. Specifically, we use the formula described in [34], which takes as the input log electrical resistance (U), average temperature (T), and several calibration parameters depending on the wood material ():
3.2.2. Daily Average
Even though daily averaged data were employed in previous works [30], mainly because they were needed in order to compute some values, such as the daily exposure dose received by wood samples, we do not see any advantage in using these in this case. Working with daily averaged data would simply make us lose temporal resolution. Consequently, they were not used in any of the proposed experiments.
3.2.3. Seasonal Decomposition
When carrying out anomaly detection on time series data, several preprocessing steps (e.g., normalization, standardization) can be applied depending on the specific problem. One of them is seasonal decomposition, which basically separates the signal into several components, usually level, trend, season, and noise. Going into further details about signal decomposition techniques is out of the scope of this article. Thus, let us just mention that in this work, we explored the advantages and disadvantages of applying seasonal decomposition as a preprocessing step. The results of this process are included in Section 4.1.
3.3. Unsupervised Anomaly Detection Methods
Unsupervised Anomaly Detection (UAD) methods require only normal data to function, and conceptually, they try to capture the intrinsic characteristics of the signals under normal operating conditions. This process is referred to as training the detection model. A detector, once it has been trained with enough data, will be able to generate an anomaly score for every new signal sample fed to it. This anomaly score is generated taking into account everything that the detector knows about how a normal signal should look like. It tells us how anomalous every sample in the signal is and thus will enable the implementation of an alarm system when, for example, the score is abnormally large. In our experiments, we explored and compared several methods to compute the mentioned anomaly score: isolation forest [35,36], local outlier factor [37], mean linear regression residual (For every signal, we trained one linear regression model using the rest of the signals as variables. Then, we computed the anomaly score as the mean of the residuals for all the trained models.), Cluster-based Local Outlier Factor (CBLOF) [38], PCA reconstruction error (the reconstruction error when transforming back after applying PCA is used as the anomaly score), one-class Support Vector Machine (SVM) [39], Long Short-Term Memory (LSTM) [40,41], and LSTM encoder-decoder [40,42].
3.4. Artificial Anomaly Generation
When studying the application of UAD techniques to solve a problem, even if we just use data obtained under normal operating conditions to train our models, we still need a way to evaluate their performance for the specific use case under study. For that reason, we generated different types of artificial anomalies that were added to the test signals, so that we could then tell if our detectors were able to identify them correctly as anomalies.
Conceptually, one of the key aspects when artificially generating anomalies is that they resemble the anomalies that might arise in reality. With that in mind, we asked field experts and came up with two different anomaly generation methods that introduce artificial anomalies resembling real anomalies seen in wood MC signals. We provide below a detailed description of these methods, namely mask product and trend component addition.
In any case, it is worth pointing out that the ideal conditions for determining which anomaly detection technique works better to solve our problem would imply having enough quality data, which would also include real labeled anomalies. The generation of artificial anomalies is simply a way to overcome the lack of labeled data. Moreover, since the process is randomized, it should be noted that the manipulation of the signals for such a purpose does not guarantee that the specific affected segments will actually look anomalous when compared to the rest of the unmodified signal. Artificial anomalies will only be generated for the facade data, given that the A/C failure that affected the data from the windows constitutes a real anomaly that we aim to detect.
3.4.1. Mask Product
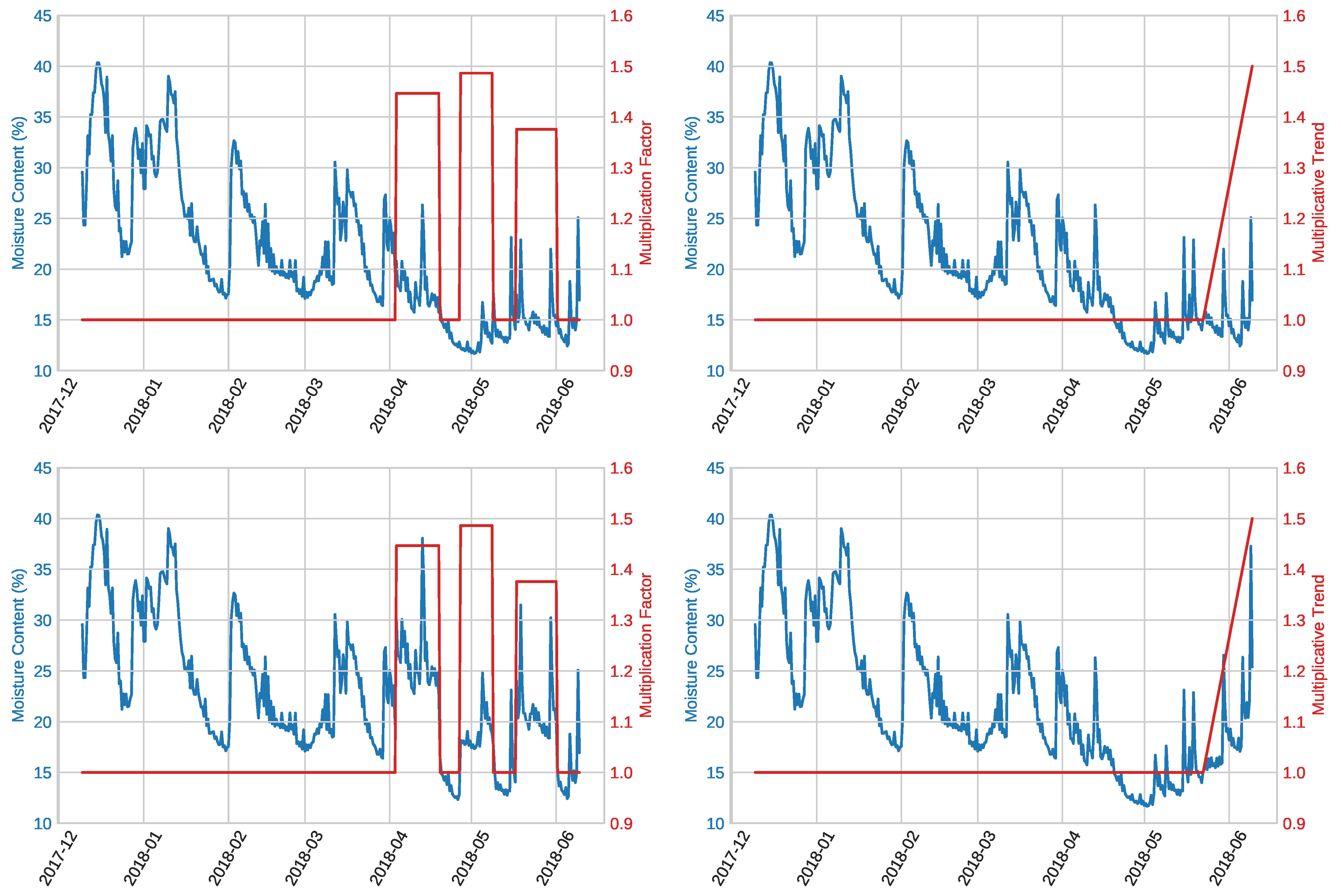
The mask product method generates a random mask according to several tunable parameters and multiplies it with the original signal so that its values increase or decrease accordingly. The method takes as parameters the minimum and maximum length that each anomalous segment can have, the minimum and maximum value for the product operation, the number of segments in the signal to apply the product to, and the minimum samples of separation between segments. An example of the application of the mask product is illustrated in the left column of Figure 3.
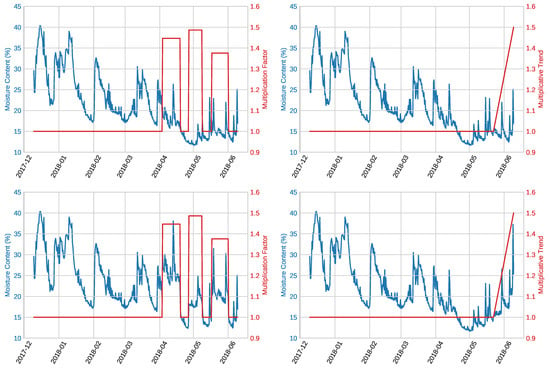
Figure 3.
Examples of the application of the presented artificial anomaly generation methods: mask product (left column) and linear multiplicative trend (right column). The first row depicts the original test sequences, while the second row the resulting modified ones.
3.4.2. Trend Component
This method generates a trend component that is inserted into the signal. The method takes as parameters the trend type (linear or logarithmic), the maximum value that it should reach, the starting and ending timestamps of the trend (alternatively, also the contamination level), and whether to hold or not the maximum value after the ending timestamp. The contamination level refers to the proportion of anomalous samples with respect to the total number of samples. An example of the application of a linear multiplicative trend is illustrated in the right column of Figure 3.
3.5. Experimental Setup
3.5.1. Facade Dataset
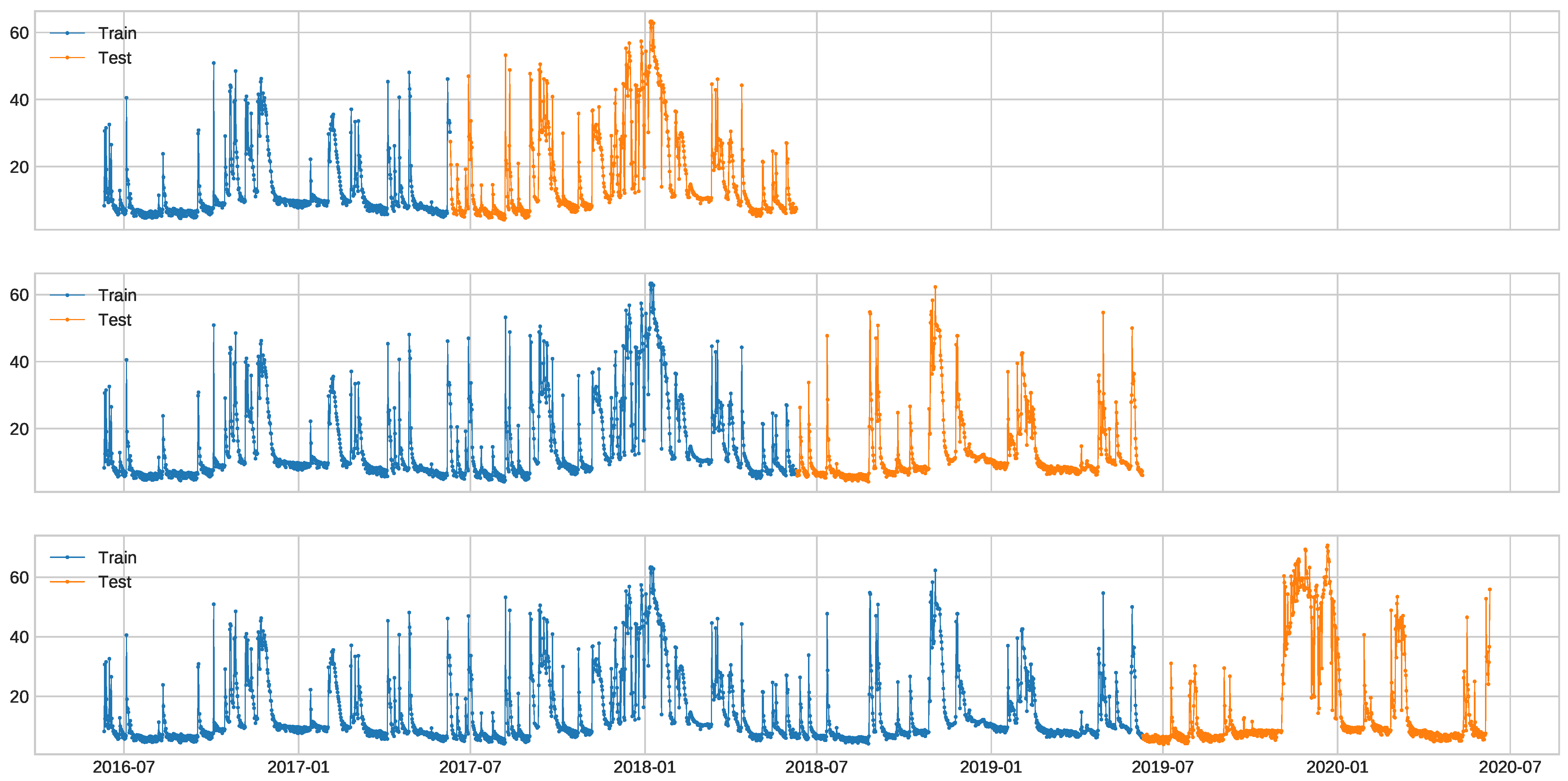
In order to generate training and test splits, we decided to divide our data in a way such that the test set always had the same length, while the training set always started in the first sample of the time series and increased its size for the different setups. This way, we were able to apply the same modification to all the test sets when artificially generating anomalies. In the implementation, a function available as part of the ADTK framework (https://adtk.readthedocs.io/en/stable/api/data.html#adtk.data.split_train_test) was used. The process is illustrated in Figure 4. We decided to divide the signal into four segments, obtaining three different training/test setups. This way, we tested the detection methods in several different conditions regarding the training data availability, thus providing a more complete evaluation.
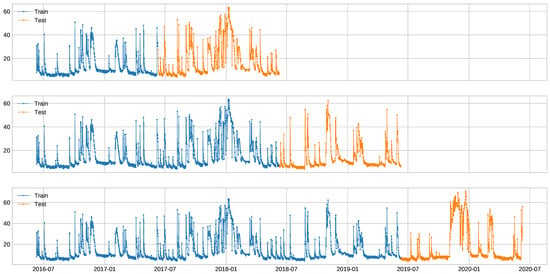
Figure 4.
Example of the chosen procedure to generate training/test splits on one of the 12 signals that composes the facade dataset.
For the facade dataset, our goal was to determine which detection methods worked better when signals were modified with different types and combinations of artificial anomalies. Because of that, we designed the following set of experiments, in which, as mentioned, we applied the same modification to all the test sets of the three different training/test setups:
- EF1
- Random mask product with variable multiplication factor: We ran several experiments in which we increased the multiplication factor of the mask product, but with fixed anomalous segments. With these experiments, we wanted to explore how the magnitude of the factor by which the signal was multiplied affects the detection results.
- EF2
- Random mask product with variable anomalous sequence length: We ran several experiments in which we increased the length of the artificial anomalies for the mask product, but with a fixed multiplication factor. With these experiments, we aimed to determine how the length of the modification applied to the signal affects the detection results.
- EF3
- Linear trend at the end: We generated a linear trend at the end of the test signal with different contamination values (i.e., always until the end of the test signal, but starting at different points). The trend was applied by multiplying it with the original signal. This would emulate, to some extent, the real anomaly found in the windows dataset caused by the A/C failure.
- EF4
- Random mask product and fixed linear trend at the end: In this last set of experiments, we randomized both the multiplication factor and length for the multiplicative mask and also included a linear trend at the end of the signal, similar to experiment EF3, but with a fixed length. With these experiments, we intended to evaluate the detection methods in a less controlled environment, in which the two types of anomalies can even be overlapped.
In all the experiments, out of the 12 signals that composed the facade dataset, the artificial anomalies could be applied to only one of them, all of them, or some. From our point of view, this is a key aspect: if the anomalies were real and not artificial, it would give us information about the kind of event that took place and caused the anomalies. For instance, if all signals were modified in the same way, it could emulate an external event that affected all the measurements, like the A/C failure in the windows dataset. However, if just one or a few signals showed abnormal segments, this might be due to failures in the recording hardware or to localized external causes (e.g., accumulated snow) that affect only a subset of the samples because of their spatial disposition. In our experiments, we would like to emulate several different situations to be able to generalize as much as possible. Therefore, each of the set of experiments described above was repeated by applying the modifications to 2 of the 12 signals, to all the signals, and to all but 2 signals.
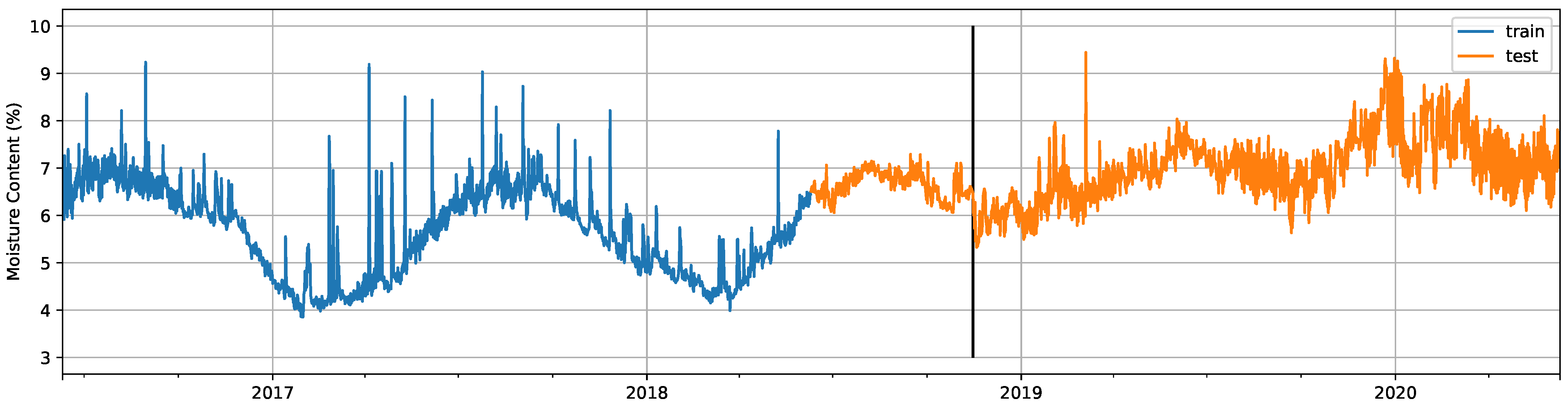
3.5.2. Windows Dataset
As mentioned, the windows dataset already included a real anomalous sequence, since the failure of the A/C system was unintended. The failure was not repaired afterward, so we labeled the whole portion of the signal after the failure date as anomalous. We decided to use a 50% training/test split, thus having the first two years of data as the training set and the last two as the test set.
The start date for the test set was 10 June 2018; the end date was 9 June 2020; and the A/C failure occurred on 15 November 2018. Therefore, the test set for the windows dataset had a contamination level of 78.39%. This value could be considered very high for other environments in which failures are promptly repaired. It is reasonable to assume that contamination levels would be much lower in more critical infrastructure. An example illustrating the data divisions for one of the signals in the windows dataset is included in Figure 5.
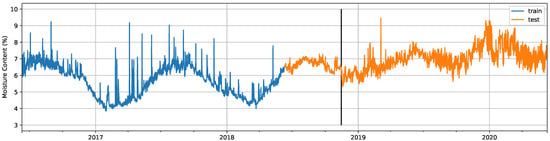
Figure 5.
Training and test splits of one of the 4 signals that composes the windows dataset, with the date on which the failure occurred marked with a vertical black line.
In this case, we ran a single set of experiments, in which we compared the results when thresholding the obtained anomaly score with different contamination values and also when using either original or seasonally-decomposed signals.
4. Results and Discussion
4.1. Data Preprocessing
4.1.1. Moisture Content
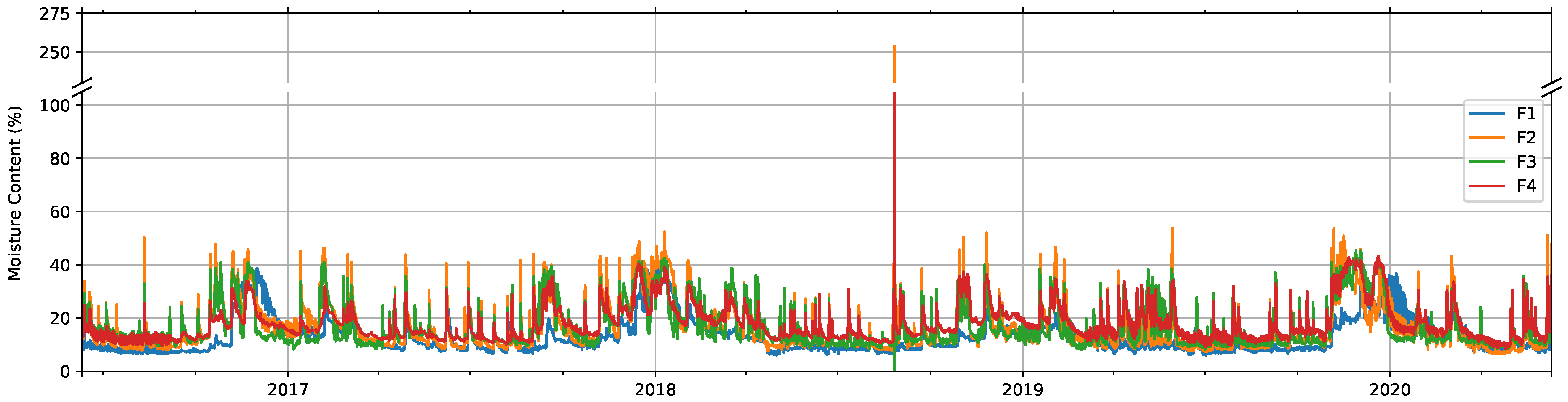
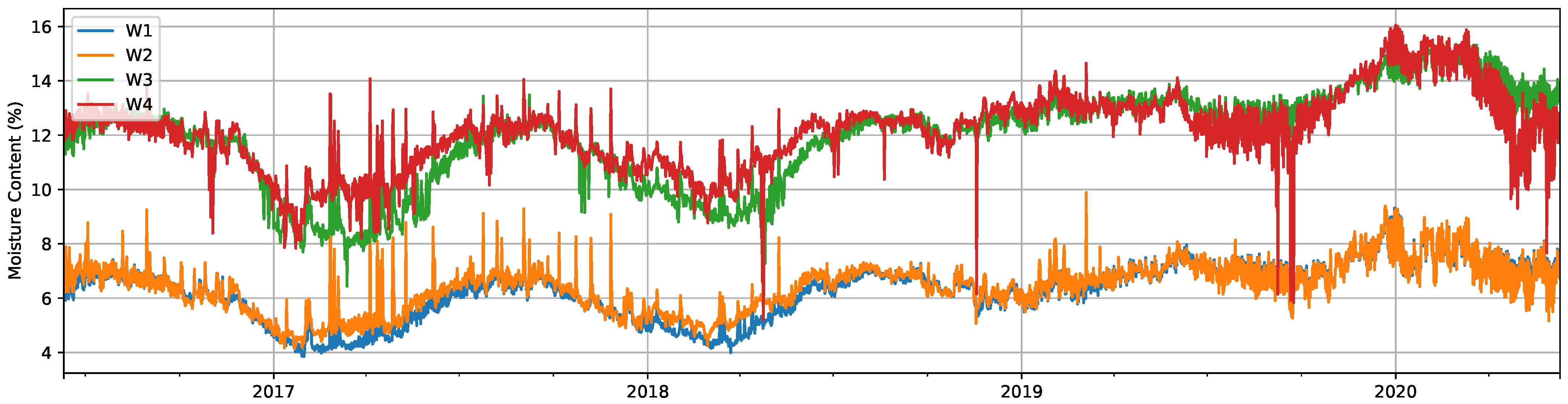
The results of the MC computation process for facade and windows data can be seen in Figure 6 and Figure 7, respectively. For clarity, Figure 6 includes only four out of the twelve total signals measured on the facade, but the rest of them (F5 to F12) present a similar evolution. While for facade signals, it is harder to notice any seasonal pattern, those for windows show a clear seasonal variation along the year, with low MC values in the months around February and high values around August. This seasonal evolution clearly changes after the failure event on 15 November 2018. It is also worth mentioning the larger range and rapidly changing behavior of facade signals, since wood samples are exposed to the outdoor climate, in contrast with the smoother appearance of those of windows. Facade values show an abnormally high measurement over 100% on 26 August 2018, at 12 h, which was most likely caused by the extremely high precipitation levels on that day and especially on the previous day in Žiri. This could have made the sensors come in direct contact with water, provoking not only extreme, but also erroneous electrical resistance measurements.
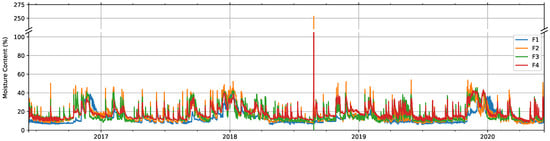
Figure 6.
Computed moisture content (%) for four of the signals measured on the facade.
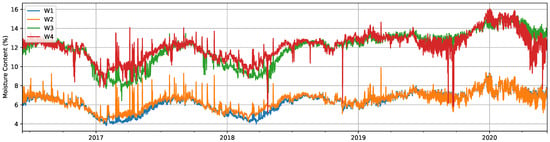
Figure 7.
Computed moisture content (%) for measurements from the windows.
4.1.2. Seasonal Decomposition
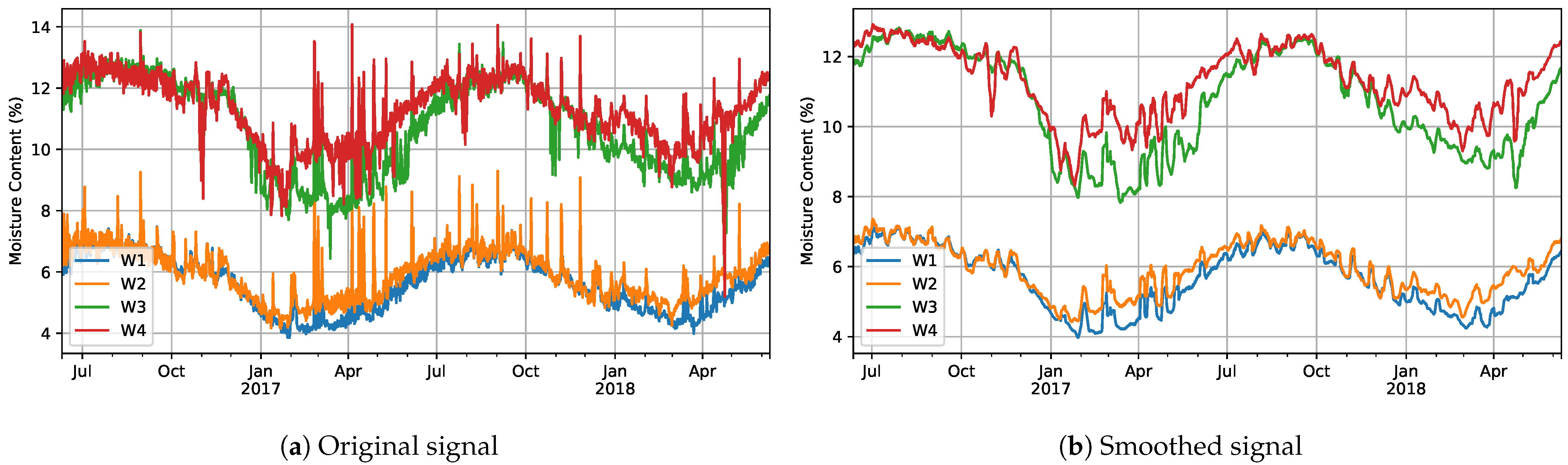
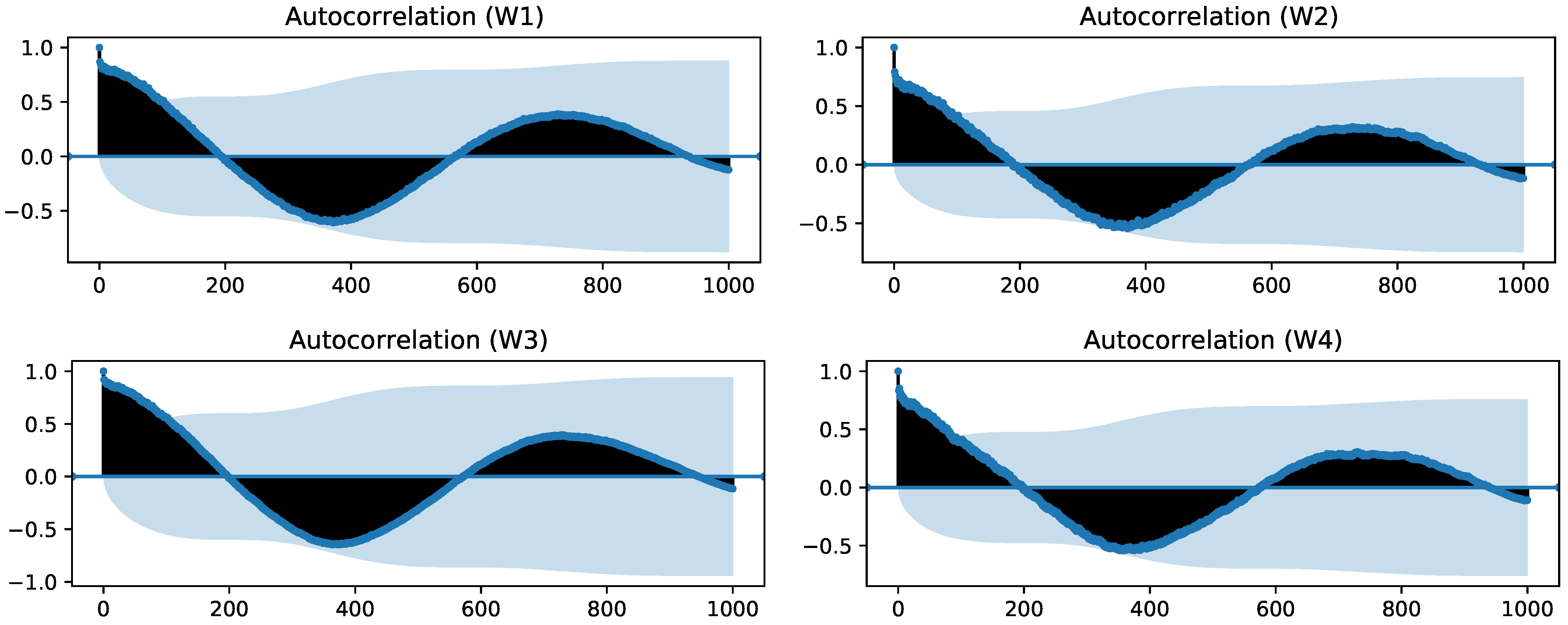
Given the simple visual observations that we previously made about our data, we assumed that seasonal decomposition would be suitable just for signals in the windows dataset. In order to check this, we wanted to confirm first that there was an underlying periodic (i.e., seasonal) component in our data. For that purpose, we carried out an autocorrelation analysis employing only data corresponding to the first two years, in order to avoid including the period after the malfunctioning. A moving average filter was applied for noise reduction to carry out this autocorrelation study. The original and smoothed signals are presented in Figure 8, while the autocorrelation function for the four signals (W1 to W4) is presented in Figure 9.
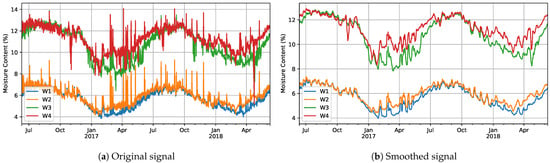
Figure 8.
Comparison of original and smoothed signals from windows after applying a moving average filter.
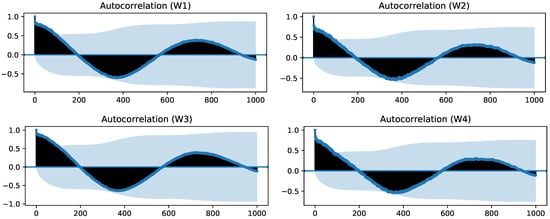
Figure 9.
Autocorrelation function for the four smoothed MC signals from windows.
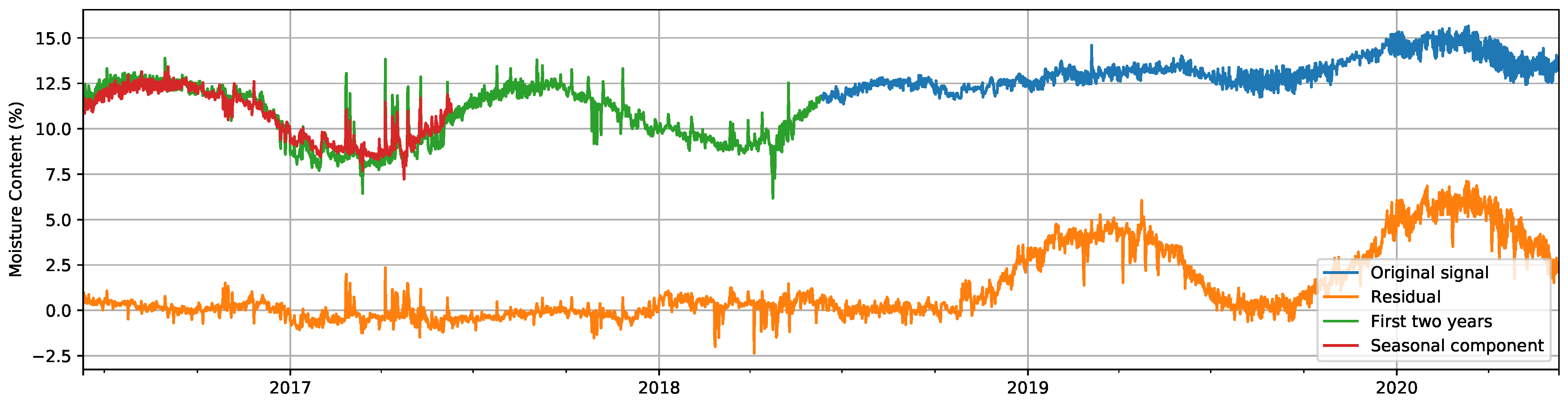
All four autocorrelation functions present a local maximum when using 730 lags (i.e., 365 days, given that the sampling period is 12 h). Even though in none of the signals, the value exceeds the confidence interval, it confirms the existence of the underlying seasonal component that we were seeking. Furthermore, we find it logical to assume that the variation of MC in these wood samples has a cyclic component with a yearly period. Consequently, in our experimental setup, we compared the results for the windows dataset when applying seasonal decomposition and when using the original computed MC signals. An example of a seasonally-decomposed signal from the dataset can be seen in Figure 10. We can observe the effect that seasonal decomposition has: after the failure, the original signal ceases to follow the seasonal variation, which makes the seasonally-decomposed signal present higher values after that point and may help detectors identify this period as abnormal.
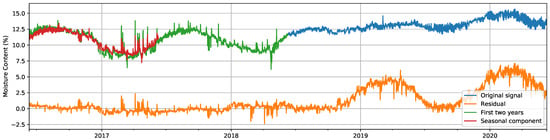
Figure 10.
Comparison of the original signal (green and blue) and its seasonally-decomposed version (orange). The section of the original signal that was used to compute the seasonal component is presented in green, while the computed seasonal component is presented in red.
4.2. Unsupervised Anomaly Detection
Finally, we include in this section the results of our experimentation when applying UAD techniques. For each one of the individual experiments, five repetitions were carried out, and all the evaluation metrics reported here are computed as their average. In all cases, the reported metric is the score, which weighs higher precision than recall and thus attenuates the influence of false negatives. The reasoning behind this was already presented in Section 3.4, but it is worth pointing it out: even when a portion of a signal is labeled as anomalous—because of added artificial anomalies for the facade dataset or the A/C failure for the windows dataset—when compared to the rest of the signal, that same portion of the signal will not necessarily look anomalous.
Another important remark to consider when interpreting the results presented here is the fact that extensive hyperparameter tuning was not carried out for any of the detection algorithms. We are aware that, if done, it could make the detection results vary to some extent. Nevertheless, the main goal of this study is to demonstrate that the application of UAD techniques to detect anomalies in wood constructions is valuable and feasible. The comparisons between algorithms that we make here should be interpreted taking all this into account.
4.2.1. Facade Dataset
As mentioned, in this case, we modify the test set by applying some specific artificial transformations, with our goal being to analyze how different characteristics of the generated anomalies affect the detection results. All the experiments included here were repeated by applying the artificial anomalies to all twelve signals, only to two signals, and to all but two signals. The average of these results is reported.
EF1. Random Mask Product with Variable Multiplication Factor
The parameters used for the random generation of the mask that is multiplied with the test portion of the signals are the following:
- Mask multiplication factor: variable between 1.25 and 3
- Minimum anomalous sequence length: 14 samples (equivalent to one week)
- Maximum anomalous sequence length: 28 samples (equivalent to two weeks)
- Number of anomalous sequences: 5
- Minimum separation between anomalous sequences: 14 samples
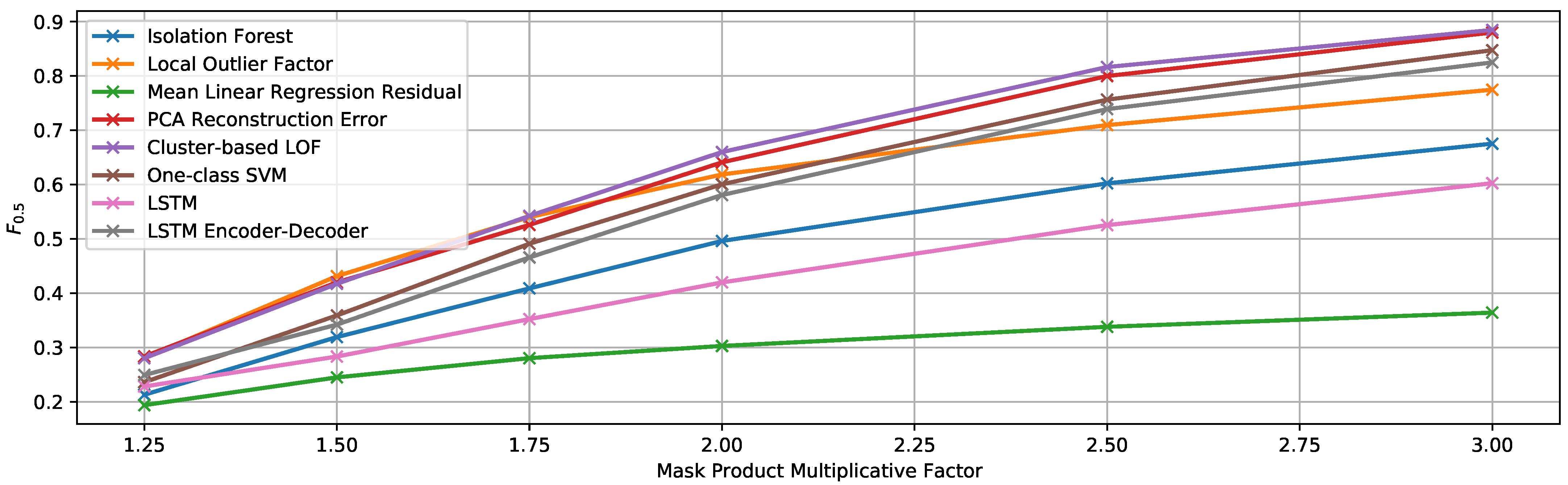
The resulting average contamination (i.e., portion of anomalous samples to the total number of samples) of the test set is 14%, the minimum and maximum values being 12% and 16%, respectively. For consistency, when setting different values for the multiplication factor, the anomalous segments in the applied mask are the same; they only vary within the five repetitions of the same experiment (and thus, the different contamination values). In other words, five masks are generated, each with different portions marked as anomalous, and each of them is applied to all the signals several times, using one multiplication factor at a time. The true contamination value in each case is used for thresholding the anomaly score. For instance, in the experiment with a 12% contamination value, twelve percent of the samples (those with higher anomaly score) will be detected as anomalous. Results for this set of experiments are illustrated in Figure 11.
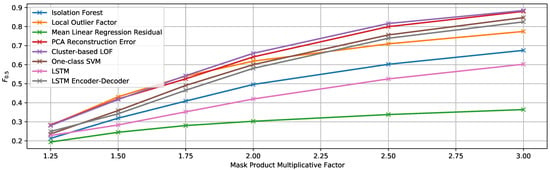
Figure 11.
score of the multivariate detection methods using the true contamination value for experiment EF1.
As we could expect, better results are obtained when the factor by which the signal is multiplied is higher. However, detecting anomalies that produce only slight modifications in the signal is more challenging, and it is probably not realistic to assume that real anomalies will change the MC signal by very high factors, so more attention should be given to lower factor values.
While the best results are achieved by the algorithm based on PCA reconstruction error when increasing the value of the signal just by 25% for the contaminated segments, the cluster-based LOFmethod [38] slightly outperforms it by a factor of 1.75 and above. This algorithm achieves a maximum -score of 0.8847 when the contaminated segments have a triplicated value. It is also worth mentioning that the mean linear regression residual, even though it performs worse than the rest overall, shows the best results for all the multiplicative factors when injecting the anomalies only into two of the 12 facade signals.
EF2. Random Mask Product with Variable Anomalous Sequence Length
The parameters used for the random generation of the mask that is multiplied with the test portion of the signals are the following:
- Mask multiplication factor: 1.5
- Anomalous sequence length: variable between 7 and 56 samples
- Number of anomalous sequences: 5
- Minimum separation between anomalous sequences: 14 samples
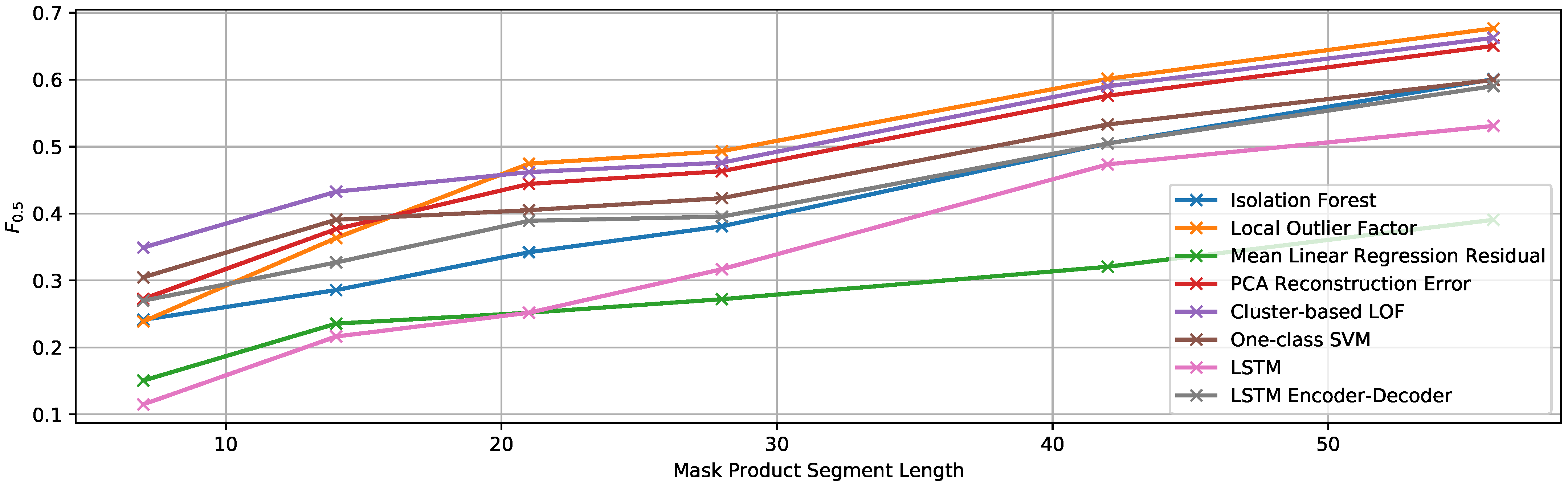
The resulting contamination (i.e., portion of anomalous samples to the total number of samples) of the test set varies between 5 and 38%. Again, the true contamination value in each case is used for thresholding the anomaly score. In Figure 12, we include the detection results for this set of experiments.
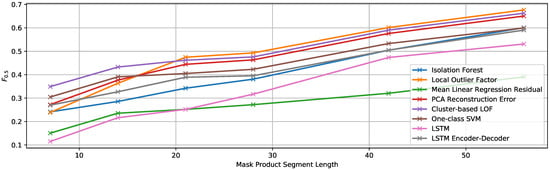
Figure 12.
score of the multivariate detection methods using the true contamination value for experiment EF2.
Similar to the results for EF1, all the curves here show an increasing trend with the length of the anomalous sequences. Thus, it is clear that having longer anomalous sequences makes it easier for the detectors to identify their samples as anomalous. The cluster-based LOF algorithm [38] achieves the best results for shorter sequences, but it is slightly outperformed in this case by the LOF [37] for longer ones. Nevertheless, both of them, as well as the PCA reconstruction error show very similar results. The best value achieved is an score of 0.6766 when the anomalies are 56 samples long. The comparison of this value with the best result obtained for the same multiplication factor (1.5) in EF1 ( = 0.4314) also proves the influence of the length of the anomalies on the detection results.
Once again, the mean linear regression algorithm shows the worst average performance, but achieves the best results when the anomalies are inserted only into two of the 12 signals in the dataset.
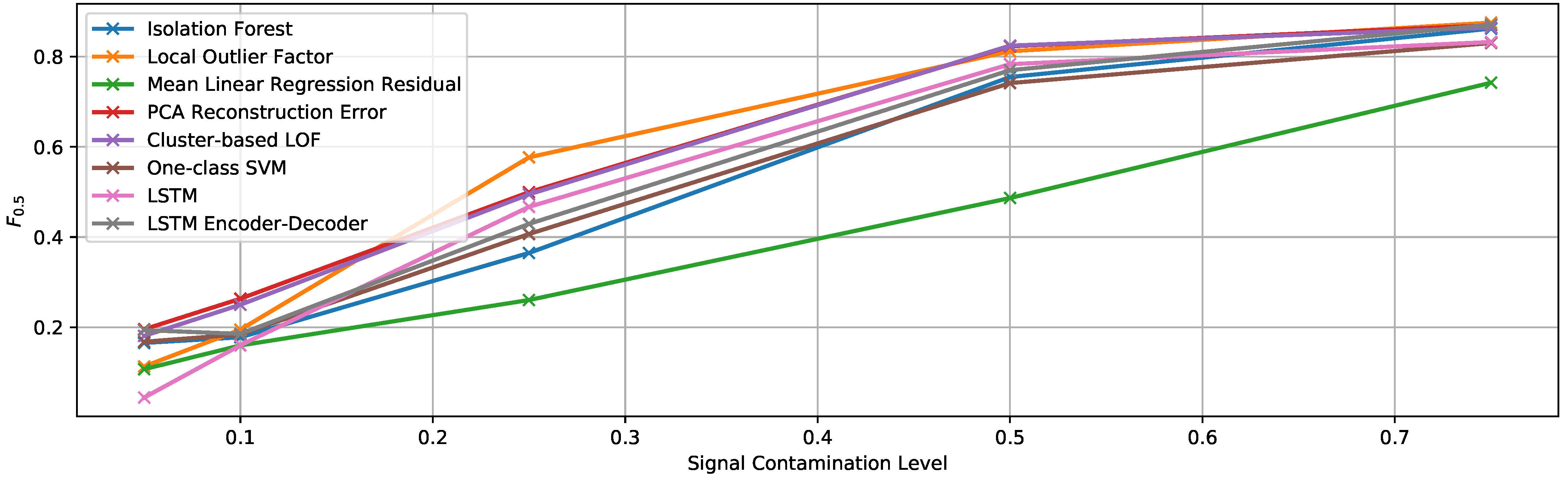
EF3. Linear Trend at the End
A linear trend component is multiplied at the end of the test set with different contamination values (i.e., different lengths), thus generating a single anomalous sequence. The parameters that characterize the anomaly generation are:
- Contamination level: variable between 0.05 and 0.75
- Function type: linear
- Maximum multiplicative factor (that of the final sample): 2
Like in the previous experiments, the true contamination value in each case is used for thresholding the anomaly score. The results for this set of experiments can be seen in Figure 13. Initial experiments when using a logarithmic function instead of a linear one show almost identical results, so we decided not to include them here to avoid repetitiveness.
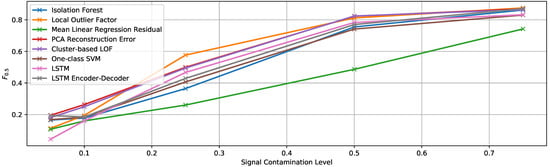
Figure 13.
score of the multivariate detection methods using the true contamination value for experiment EF3.
In this case, we could expect and we indeed observed similar results to those of the previous experiment (EF2), since we are basically increasing the length of the generated anomaly as well. Generally, LOF [37], cluster-based LOF [38], and PCA reconstruction error are the algorithms that provide the best detection results again. However, the differences to the rest of the algorithms for high contamination values are considerably small.
The mean regression residual is again the worst detector in general, but the best one when the modification is only applied to two signals. However, in this case, this applies only for lower contamination values, while for a 50% contamination and above LOF [37], it shows a higher score also when contaminating only two of the signals.
EF4. Random Mask Product and Fixed Linear Trend at the End
For the final experiment for the facade set, we combine both types of artificial anomalies to try to obtain an overview of the performance of the different algorithms. The parameters that characterize these experiments are:
- Mask multiplication factor: random between 1 and 1.5
- Minimum anomalous sequence length: 14 samples (equivalent to 1 week)
- Maximum anomalous sequence length: 56 samples (equivalent to 4 weeks)
- Number of anomalous sequences in the mask: 3
- Minimum separation between anomalous sequences in the mask: 14 samples
- Linear trend contamination level: 0.1
- Linear trend function type: linear
- Maximum multiplicative factor (that of the final sample): 1.5
Since two modifications are now applied to the test signal and the anomalous sequences are randomly chosen, it may occur that some samples get multiplied both by a random factor from the mask and by a factor from the linear trend. Thus, the maximum multiplication factor that could be applied to a sample is . However, for most of the samples labeled as anomalous, the value will be quite lower, making the detection problem especially hard. The true contamination value ranges from 5 to 38%, with an average value of 19%.
Contrary to all the previous experiments, we additionally included results when thresholding the computed anomaly score with contamination values different from the true one. The true contamination value would be unknown in a real environment, so this way, we provide a more complete evaluation of the algorithms’ performance. Furthermore, we detail the results for the three different cases depending on how many signals are contaminated. Results for this set of experiments are summarized in Table 2.

Table 2.
Results from experiment EF4 showing the score for the facade dataset when thresholding using different contamination values and injecting artificial anomalies into different sets of signals.
These results confirm that the best-performing methods to detect anomalies for the facade dataset are LOF [37], PCA reconstruction error, and Cluster-based LOF [38], all of them obtaining a very similar average score of around 31%. Furthermore, we can observe how once again, the best performing method when generating anomalies only in two of the signals is the mean linear regression residual. This shows that this method is really good at distinguishing anomalies when only a few of the signals deviate from the normal operating conditions. However, when most of them do, it is not able to identify these deviations as anomalies. On the contrary, all the other algorithms show their worst results when only two of the signals are contaminated, no matter which thresholding value we chose.
Special attention should be given when thresholding with a low contamination value and all the signals are affected by the anomalies (or all but two signals). In both cases, the LSTM encoder-decoder algorithm [40,42] shows the best results, which are not far from the overall best results (obtained when thresholding with the true contamination value). This is especially meaningful since it shows that in a real environment in which anomalies are usually rare (i.e., the contamination value can be assumed to be low, yet unknown), this algorithm may be the preferred option. Nevertheless, as we increase the thresholding value, better results are shown by other simpler algorithms.
4.2.2. Windows Dataset
The set of experiments carried out for the windows dataset does not involve artificial anomaly generation. Thus, we simply applied different thresholding contamination values to the anomaly score of the test signal, and we also compared the results when using the original or seasonally-decomposed signals. Results for all the different detection methods when thresholding with contamination values of 10%, 78.4% (true value), and 90% are summarized in Table 3.

Table 3.
Results for the windows dataset when thresholding using different contamination values. The use of the Seasonally-Decomposed signal instead of the original one is indicated with the letters SD.
The best results for the lower contamination value are achieved by most of the proposed detection methods, obtaining in all these cases a precision equal to one. This is a promising result since it indicates that all these methods succeeded in identifying only true anomalous samples when the selected thresholding value was lower than the actual contamination of the data. As we said, it is worth pointing out that, even if we decided to label as anomalous all the samples after the A/C failure occurred, that does not imply that all the samples actually show abnormal behavior. In fact, it would be reasonable to assume that not all of them actually do. Moreover, intuitively, lower contamination values such as this one, or even way lower, could be seen as more realistic in real-world scenarios in which anomalies are rare and dealt with as soon as they are detected.
When thresholding with the true contamination value, the three metrics take the same values, since the number of false positives is equal to the number of false negatives. In this case, the cluster-based LOF method [38] achieves a maximum score of 0.9581.
Surprisingly, when marking as anomalous a higher portion of anomalies than there actually are, the best results are shown by the LSTM network [40,41] using the seasonally decomposed version of the signal, and it is the only one that successfully annotates all the true anomalies as such. Nevertheless, several other algorithms achieve quite similar detection results.
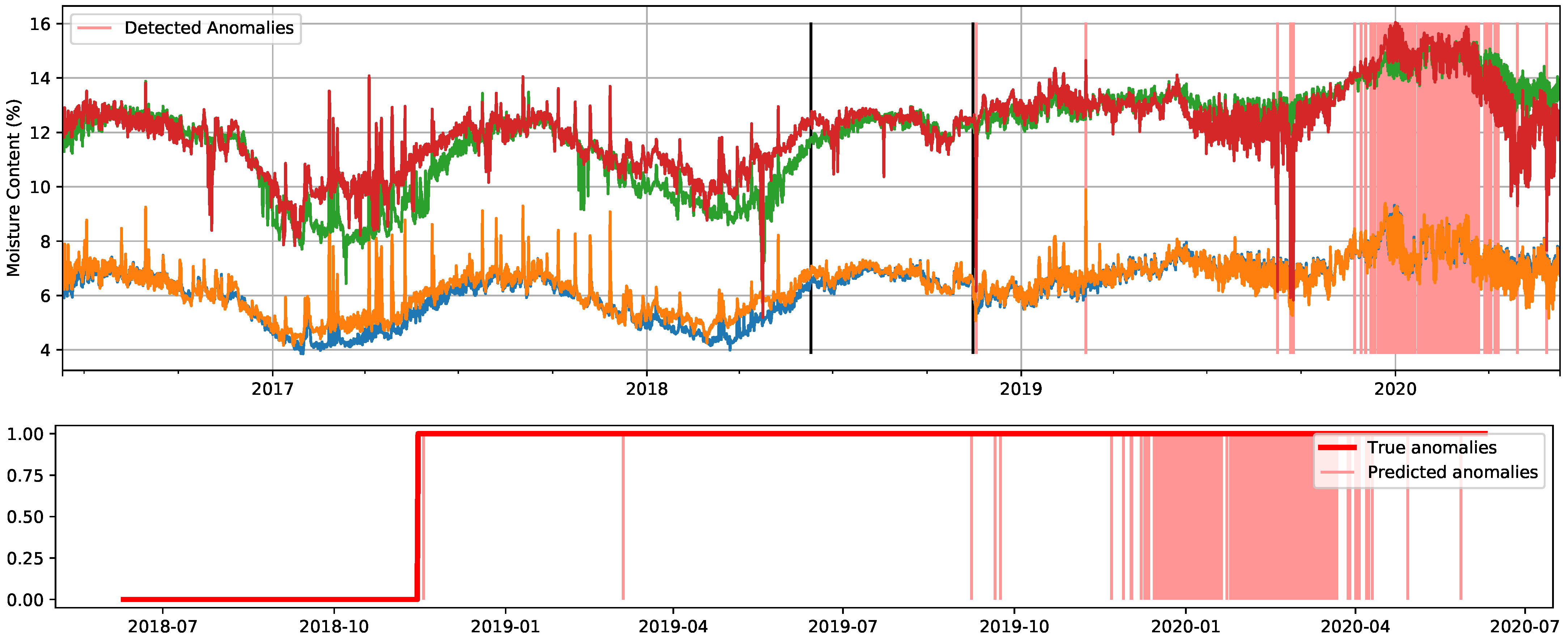
For illustrative purposes, we include in Figure 14 and Figure 15 representations of the best detection results for a thresholding contamination value of 10% and the true contamination value, respectively. In Figure 14, for which the chosen contamination value is considerably lower than the true one, we can observe how within the true anomalous segment, the method gives a higher anomaly score to spikes in the signal, as well as segments for which it is easy to visually identify deviations from the expected evolution.
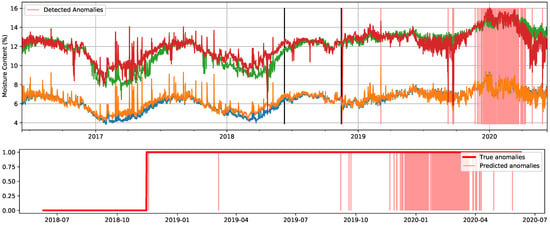
Figure 14.
Detected anomalies when using the cluster-based LOF method with the original signals and a thresholding contamination value of 10%. Predicted anomalies are marked in light red. In the top figure, two black lines determine the start of the test set and, afterwards, the moment when the A/C failed. In the bottom figure, corresponding only to the test set, true anomalies are delimited by the red line.
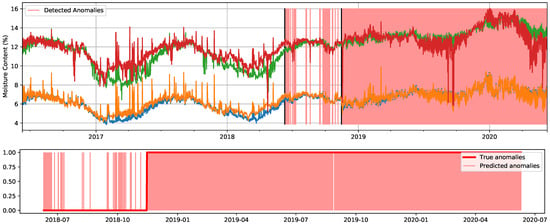
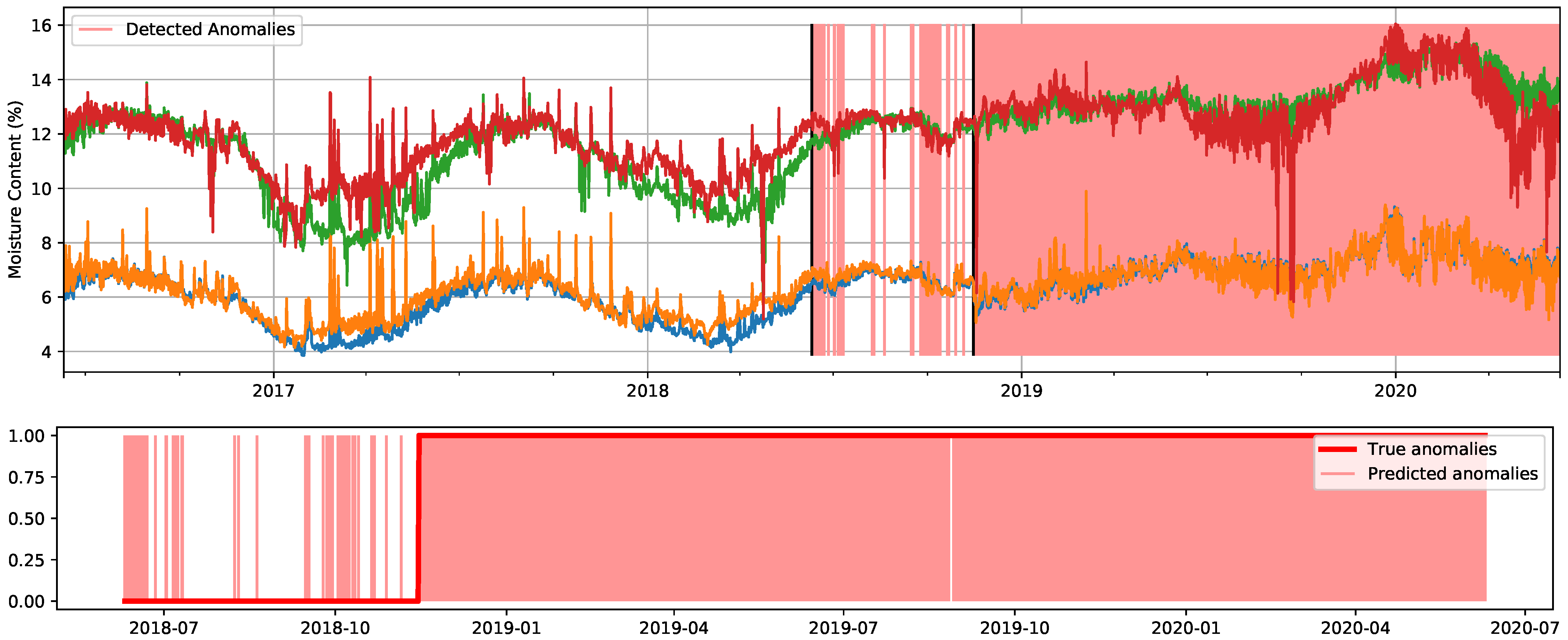
Figure 15.
Detected anomalies when using the cluster-based LOF method with the original signals and the true contamination value (78.4%). Predicted anomalies are marked in light red. In the top figure, two black lines determine the start of the test set and, afterwards, the moment when the A/C failed. In the bottom figure, corresponding only to the test set, true anomalies are delimited by the red line.
It can be seen in Figure 15 that when thresholding with the true contamination value, just a few points within the anomalous segment are not marked as anomalous. Again, this may be a consequence of these measurements being actually less anomalous than the ones that were given a high anomaly score, but were recorded before the failure, even though we labeled them as anomalies, thus counting as a missed detection. The fact that the cluster-based LOF algorithm [38] does not take into account the temporal dimension of the data makes it intuitive to think that other algorithms that do capture this dimension, such as the LSTM-based ones [40,41,42], might achieve better results. However, let us remind that extensive hyperparameter tuning was not carried out for our experiments, and still, the differences in the score for most of the algorithms are not substantial.
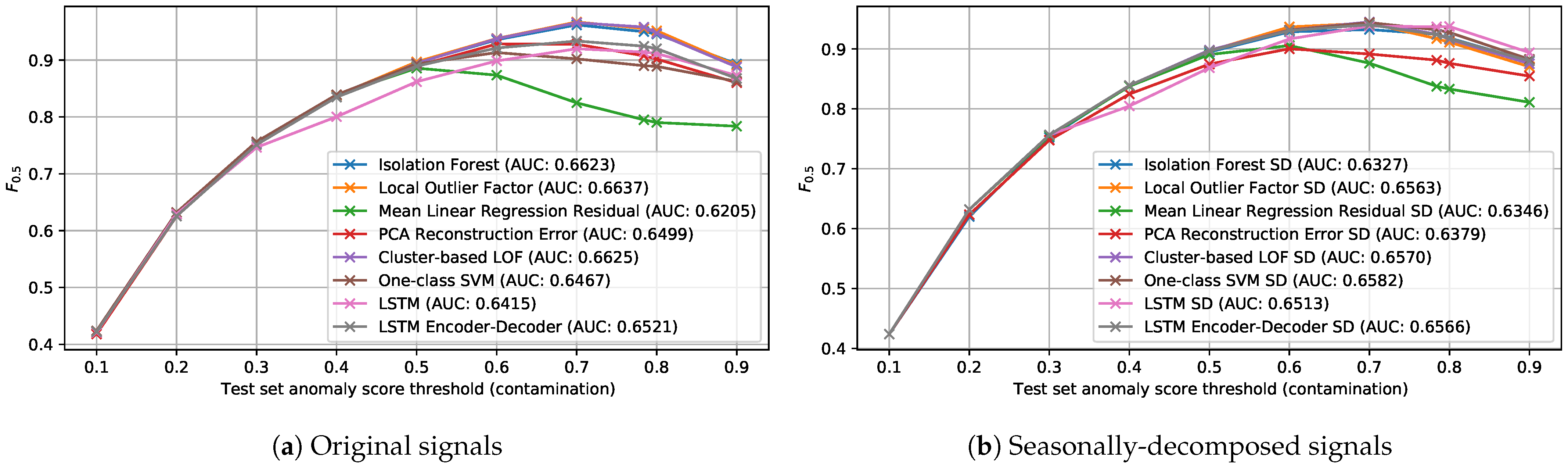
In order to compare the usefulness of applying the seasonal decomposition procedure in this case, we plot the score for different contamination values when using the original and seasonally-decomposed signals in Figure 16a,b, respectively. Additionally, we include the Area Under the Curve (AUC) for each of the detectors.
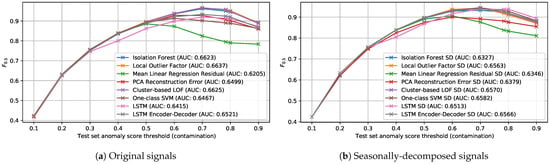
Figure 16.
F0.5 of the detection methods for different thresholding contamination values.
In all cases, the results when using one or the other version of the signal are quite similar. The fact that the yearly seasonal component that was later subtracted from the signal to obtain the seasonally-decomposed version was computed using only data for two years may explain these results. The use of more advanced decomposition techniques such as STL [43], was explored, but was unfruitful because it would require more historical data. Nevertheless, given that the application of this procedure did not result in a significant decrease for any of the detectors, we can expect that with more historical data available, a better decomposition could be achieved, which could further improve the detection results.
5. Conclusions
In this work, we explored the application of Unsupervised Anomaly Detection (UAD) techniques to Moisture Content (MC) signals recorded from different types of wood samples. Experiments were carried out on two different datasets, one corresponding to wood samples installed on the facade of a test cube and thus exposed to outdoor conditions and another one containing signals from samples installed indoors, serving as window frames.
For the facade dataset, we artificially generated different types of anomalies to evaluate our detection methods, while the measurements from the windows already included an event that we considered anomalous. Even though the fact that the evaluation was carried out with simulated anomalies should account for the interpretation of the results for the facade dataset, our experimental results show that UAD can be applied to successfully detect anomalies in both cases. When thresholding the obtained anomaly score with the true contamination value, we achieved a maximum score of 0.9581 for the detection of the real anomaly that affected the windows. Moreover, we got a precision of 1 when using a considerably lower threshold, meaning that all the detected samples were true anomalies.
In future work, we plan to make use of historical weather data to further improve the detection. Besides, work is already being done to further extend the datasets used in this work with real anomalies that could help us improve the evaluation and comparison of the anomaly detection methods.
Author Contributions
Conceptualization, Á.G.F., D.Š., and M.C.; methodology, Á.G.F.; software, Á.G.F.; validation, Á.G.F.; investigation, Á.G.F.; resources, M.C. and M.H.; data curation, Á.G.F.; writing—original draft preparation, Á.G.F.; writing—review and editing, Á.G.F., D.Š., M.C., and M.H.; visualization, Á.G.F.; supervision, D.Š. and M.C.; project administration, M.C.; funding acquisition, M.C. All authors read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Education, Science, and Sport of the Republic of Slovenia and by the European Regional Development Fund, European Commission (project WOOLF, Grant Number 5441-2/2017/241).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We would like to acknowledge the support of M. Sora, trgovina in proizvodnja, d.d., coordinator of the EU Horizon 2020 WINTHERWAX project (Grant Number 666206), for the provision of the data used in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zabel, R.A.; Morrell, J.J. Wood Microbiology: Decay and Its Prevention; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Reinprecht, L. Wood Deterioration, Protection and Maintenance; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Ribera, J.; Schubert, M.; Fink, S.; Cartabia, M.; Schwarze, F.W. Premature failure of utility poles in Switzerland and Germany related to wood decay basidiomycetes. Holzforschung 2017, 71, 241–247. [Google Scholar] [CrossRef][Green Version]
- Kutnik, M.; Suttie, E.; Brischke, C. European standards on durability and performance of wood and wood-based products—Trends and challenges. Wood Mater. Sci. Eng. 2014, 9, 122–133. [Google Scholar] [CrossRef]
- Schmidt, O. Wood and Tree Fungi; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Carll, C.G.; Highley, T.L. Decay of wood and wood-based products above ground in buildings. J. Test. Eval. 1999, 27, 150–158. [Google Scholar]
- Meyer, L.; Brischke, C. Fungal decay at different moisture levels of selected European-grown wood species. Int. Biodeterior. Biodegrad. 2015, 103, 23–29. [Google Scholar] [CrossRef]
- Zelinka, S.L.; Kirker, G.T.; Bishell, A.B.; Glass, S.V. Effects of wood moisture content and the level of acetylation on brown rot decay. Forests 2020, 11, 299. [Google Scholar] [CrossRef]
- Shigo, A.L. Detection of Discoloration and Decay in Living Trees and Utility Poles; Forest Service, US Department of Agriculture, Northeastern Forest Experiment Station: Morgantown, VA, USA, 1974; Volume 294. [Google Scholar]
- Goasduff, L. Internet of Things Market. Available online: https://www.gartner.com/en/newsroom/press-releases/2019-08-29-gartner-says-5-8-billion-enterprise-and-automotive-io (accessed on 28 July 2020).
- Jin, Z.; Zhang, Z.; Gu, G.X. Automated real-time detection and prediction of interlayer imperfections in additive manufacturing processes using artificial intelligence. Adv. Intell. Syst. 2020, 2, 1900130. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Seyedzadeh, S.; Rahimian, F.P.; Glesk, I.; Roper, M. Machine learning for estimation of building energy consumption and performance: A review. Vis. Eng. 2018, 6, 1–20. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier analysis. In Data Mining; Springer: Berlin/Heidelberg, Germany, 2015; pp. 237–263. [Google Scholar]
- Lin, J.; Yu, W.; Zhang, N.; Yang, X.; Zhang, H.; Zhao, W. A survey on internet of things: Architecture, enabling technologies, security and privacy, and applications. IEEE Internet Things J. 2017, 4, 1125–1142. [Google Scholar] [CrossRef]
- Lu, Y. Industry 4.0: A survey on technologies, applications and open research issues. J. Ind. Inf. Integr. 2017, 6, 1–10. [Google Scholar] [CrossRef]
- Cook, A.; Mısırlı, G.; Fan, Z. Anomaly detection for IoT time series data: A survey. IEEE Internet Things J. 2019, 7, 6481–6494. [Google Scholar] [CrossRef]
- Gonzaga, J.; Meleiro, L.A.C.; Kiang, C.; Maciel Filho, R. ANN-based soft-sensor for real-time process monitoring and control of an industrial polymerization process. Comput. Chem. Eng. 2009, 33, 43–49. [Google Scholar] [CrossRef]
- Cho, S.; Asfour, S.; Onar, A.; Kaundinya, N. Tool breakage detection using support vector machine learning in a milling process. Int. J. Mach. Tools Manuf. 2005, 45, 241–249. [Google Scholar] [CrossRef]
- Chen, P.Y.; Yang, S.; McCann, J.A. Distributed real-time anomaly detection in networked industrial sensing systems. IEEE Trans. Ind. Electron. 2014, 62, 3832–3842. [Google Scholar] [CrossRef]
- Feng, C.; Li, T.; Chana, D. Multi-level anomaly detection in industrial control systems via package signatures and LSTM networks. In Proceedings of the 2017 47th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Denver, CO, USA, 26–29 June 2017; pp. 261–272. [Google Scholar]
- Akouemo, H.N.; Povinelli, R.J. Probabilistic anomaly detection in natural gas time series data. Int. J. Forecast. 2016, 32, 948–956. [Google Scholar] [CrossRef]
- Araya, D.B.; Grolinger, K.; ElYamany, H.F.; Capretz, M.A.; Bitsuamlak, G. An ensemble learning framework for anomaly detection in building energy consumption. Energy Build. 2017, 144, 191–206. [Google Scholar] [CrossRef]
- Inoue, J.; Yamagata, Y.; Chen, Y.; Poskitt, C.M.; Sun, J. Anomaly detection for a water treatment system using unsupervised machine learning. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 1058–1065. [Google Scholar]
- Laptev, N.; Amizadeh, S.; Flint, I. Generic and scalable framework for automated time series anomaly detection. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; pp. 1939–1947. [Google Scholar]
- Buda, T.S.; Caglayan, B.; Assem, H. Deepad: A generic framework based on deep learning for time series anomaly detection. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2018; pp. 577–588. [Google Scholar]
- Bao, Y.; Tang, Z.; Li, H.; Zhang, Y. Computer vision and deep learning–based data anomaly detection method for structural health monitoring. Struct. Health Monit. 2019, 18, 401–421. [Google Scholar] [CrossRef]
- Rotilio, M.; Pantoli, L.; Muttillo, M.; Annibaldi, V. Performance Monitoring of Wood Construction Materials by Means of Integrated Sensors. In Key Engineering Materials; Trans. Tech. Publ.: Zurich, Switzerland, 2018; Volume 792, pp. 195–199. [Google Scholar]
- Kržišnik, D.; Brischke, C.; Lesar, B.; Thaler, N.; Humar, M. Performance of wood in the Franja partisan hospital. Wood Mater. Sci. Eng. 2019, 14, 24–32. [Google Scholar] [CrossRef]
- Humar, M.; Kržišnik, D.; Lesar, B.; Brischke, C. The performance of wood decking after five years of exposure: Verification of the combined effect of wetting ability and durability. Forests 2019, 10, 903. [Google Scholar] [CrossRef]
- Humar, M.; Lesar, B.; Kržišnik, D. Moisture Performance of Façade Elements Made of Thermally Modified Norway Spruce Wood. Forests 2020, 11, 348. [Google Scholar] [CrossRef]
- Zupanc, M.Ž.; Pogorelčnik, A.; Kržišnik, D.; Lesar, B.; Thaler, N.; Humar, M. Model za določanje življenjske dobe lesa listavcev. Les/Wood 2017, 66, 53–59. [Google Scholar] [CrossRef][Green Version]
- Otten, K.A.; Brischke, C.; Meyer, C. Material moisture content of wood and cement mortars–electrical resistance-based measurements in the high ohmic range. Constr. Build. Mater. 2017, 153, 640–646. [Google Scholar] [CrossRef]
- Brischke, C.; Lampen, S.C. Resistance based moisture content measurements on native, modified and preservative treated wood. Eur. J. Wood Wood Prod. 2014, 72, 289–292. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; pp. 93–104. [Google Scholar]
- He, Z.; Xu, X.; Deng, S. Discovering cluster-based local outliers. Pattern Recognit. Lett. 2003, 24, 1641–1650. [Google Scholar] [CrossRef]
- Schölkopf, B.; Williamson, R.C.; Smola, A.J.; Shawe-Taylor, J.; Platt, J.C. Support vector method for novelty detection. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 582–588. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long short term memory networks for anomaly detection in time series. In Proceedings; Presses Universitaires de Louvain: Ottignies-Louvain-la-Neuve, Belgium, 2015; Volume 89, pp. 89–94. [Google Scholar]
- Malhotra, P.; Ramakrishnan, A.; Anand, G.; Vig, L.; Agarwal, P.; Shroff, G. LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv 2016, arXiv:1607.00148. [Google Scholar]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).