Abstract
A variable-exponent taper equation was developed for Chinese fir (Cunninghamia lanceolate (Lamb.) Hook.) trees grown in southern China. Thirty taper equations from different groups of models (single, segmented, or variable-exponent taper equation) were compared to find the excellent basic model with S-plus software. The lowest Akaike information criteria (AIC), Bayesian information criteria (BIC), and -2loglikelihood (-2LL) was chosen to determine the best combination of random parameters. Single taper models were found having the lowest precision, and the variable-exponent taper equations had higher precision than the segmented taper equations. Four variable-exponent taper models that developed by Zeng and Liao, Bi, Kozak, Sharma, and Zhang respectively, were selected as basic model and had no difference in fit statistics between them. Compared with the model without seldom parameter, the nonlinear mixed-effects (NLME) model improves the fitting performance. The plot-level NLME model was found not to remove the residual autocorrelation. The tree-level and two-level NLME model had better simulation accuracy than the plot-level NLME model, and there were no significant differences between the tree-level and two-level NLME model. Variable-exponent taper model developed by Kozak showed the best performance while considering two-level or tree-level NLME model, and produced better predictions for medium stems compared to lower and upper stems.
1. Introduction
Stem profile equations, commonly known as taper equations, which refer to the general decrease in the regular outline of a solid body from its base to its tip. The taper equation is important mainly because it can predict the follows: (1) diameter at any height of the tree stem or height at any diameter; (2) volume at any height of the tree stem or total volume of the tree stem and total peeling volume; and (3) merchantable timber volume and dry timber height with any diameter restriction or relative height restriction [1]. The taper equation can be generally divided into three categories in the history of development. A single taper equation [2,3,4,5] is composed of simple mathematical equations, and it has disadvantage that the significantly swollen part at the bottom of the tree stem is inconsistent with the model fitting. The segmented taper equation [6,7,8,9] refers that several polynomials representing different parts of the tree stem are connected through the inflection point, and the tree stem is assumed as concave, paraboloid and conical respectively from bottom to top. However, more complex iterative operation as well as more fitting data and experience are required for the estimation of segmented taper equation inflection point. The variable-exponent taper equation [10,11,12,13] refers that the tree stem shape can be better estimated through the change of the independent variable exponent in the continuous function, which can be applied for theoretically describing the tree stem of any shape. Variable-exponent taper equation shows better imitative effect and application prospect [10,13,14,15] than other two taper equations.
Taper equation fitting data are often based on repeated measurements of diameters in the same tree at different heights. A hierarchical structure is available. There is a correlation between measured data for many times. The following assumption of error term independent identical distribution of least square method is violated, thereby possibly leading to deviation in variable parameter estimation [16]. Mixed effect model has been applied in the research of the taper equation in recent years [17,18]. Nonlinear mixed effect model is an effective way of processing stratified data and repeated measurement data, including fixed parameters and random parameters, which can meet the assumption of error term independent identical distribution. Randomness and elasticity due to known or unknown factors can be explained [19]. A nonlinear mixed model method has been utilized for fitting Max and Burkhart segmented taper equation, and the results shows that mixed effect model can improve the fitting precision of the model [20].Chinese fir is a native coniferous timber tree species in China with a long cultivation history, which is widely distributed in 18 provinces and regions in southern China. Chinese fir is favored by people because of its rapid growth, excellent material, and straight and full stem forms [21]. The result of the national continuous forest inventory shows that [22] the area of Chinese fir man-made forest has reached 9.90 million hectares, the standing volume has reached 755 million cubic meters, and they respectively account for 27.23% and 32.57% of the main dominant tree species of artificial forest in China. Chinese fir has become the most important timber plantation tree species in China. It is lack of systematic comparative analysis among many basic models while building Chinese fir taper equation. Mixed effect model is rarely used for constructing variable-exponent taper equation particularly, while the autocorrelation of the fitting data is not deeply considered.
The objective of the present study was to evaluate the performance of some well-known taper functions and develop a mixed-effects variable-exponent taper equation for Chinese fir trees in southern China.
2. Materials and Methods
2.1. Data
A total of 183 trees sampled from even-aged Chinese fir stands were used in the present study. The trees were taken from stands located in Jiangxi province of southern China, and included the typical range of diameters and heights of Chinese fir stands. The total tree height (H: m) and diameter at breast height (DBH: 1.3 m above ground level) were measured. Diameter outside bark (cm) was also measured at heights of 0.2, 1, 1.3, and 2 m and then at intervals of 1 m along the remainder of the stem. A total of 123 trees selected randomly were used as fit data, and the rest of the 60 trees were used as validation data. The tree height and DBH data statistics were shown in Table 1. Figure 1 shows the trend of the relative diameter along every tree stem with the relative height. The relative height is the ratio of the height of the off-ground tree stem and total tree height. The relative diameter is the ratio of the diameter at the height of the off-ground tree stem to DBH.

Table 1.
Summary statistics for fit data and validation data of density test stand of Chinese fir.
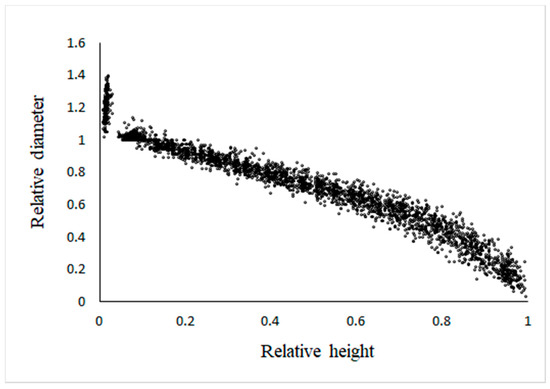
Figure 1.
Relative height plotted against relative diameter of Chinese fir.
2.2. Basic Model Selection
Thirty commonly used models with goodness of fit (Table 2) were selected as candidate models in the study based on the analysis of Rojo [15], including 18 single taper equations [2,23,24,25,26,27,28,29,30,31,32,33,34,35], 2 segmented taper equations [6,36], and 10 variable--exponent taper equations [1,12,13,14,37,38,39,40,41]. Common nonlinear least square method (NLS) was applied for regression fit on the candidate models by using S-PLUS software, and optimal basis model was selected by comparing fit statistics.

Table 2.
Thirty stem taper equation selected as candidate models.
2.3. Establishment of Mixed Effect Model
Mixed effect model contained both fixed parameters and random parameters. Random parameters were fixed parameters added to nonlinear model, which varied with changes of different blocks. A mixed effect model was established according to plot-level effect, tree-level effect and two-level effect respectively in the study. The model expression is as follows:
where refers to the kth observed value of diameter d at the height h of the jth tree in the ith plot. refers to differentiable function containing parameter vector and concomitant variable vector , refers to a error term obeying normal distribution, it is assumed that the expected value is zero with positive variance covariance structure Rij, wherein can be expressed as follows:
where β refers to n × 1-dimension fixed parameters vector, ui and uij, respectively, refer to random parameter vectors of plot level and tree level, which obey independent normal distribution, and expected value is zero with variance covariance structures ψ1 and ψ2. Aijk, Bi,jk and Cijk refer to design matrix.
2.3.1. Determination of Random Parameters
One key for establishing a mixed effect model lies in determination of fixed parameters and random parameters in the model. Too many random parameters may lead to excessive parameterization or convergence [42], The possibility of 1–2 random parameter combinations in the selected basic model was fitted. The optimal combination of fixed parameters and random parameters was determined by comparing the minimum values of statistics AIC (Akaike information criteria), BIC (Bayesian information criteria), and -2LL(-2loglikelihood).
2.3.2. Variance-Covariance Structure of Stochastic Effect
Variance covariance structure can reflect the changes among plots and among trees. Two random parameters are adopted as examples according to the study of Calama [43], variance covariance structure can be set as a positive definite structure matrix, and the structure is shown as follows:
where (i = 1, 2) refers to the variance of random parameters, (i, j = 1, 2, i ≠ j) refers to the covariance of random parameters 1, 2.
2.3.3. Intra-Group Variance-Covariance Structure
The intra-group variance-covariance structure should be determined to eliminate the correlation of intra-group error. The previous studies show that the mixed effect model with an unstructured covariance-variance matrix can be applied for explaining the autocorrelation among most observed values [16,44]. The unstructured variance–covariance matrix of random effects was used in this study. For the random error term, constant variance and independence of observations was assumed because the emphasis is on prediction rather than hypothesis testing.
2.4. Model Evaluation
The prediction of random-effects parameters was accomplished by an approximate Bayes estimator [41]. Statistical indicators for evaluating the model include adjusted determination coefficient (), mean variation (Bias) and root-mean-square error (RMSE). These expressions are shown as follows:
where yi refers to the observed value, refers to the predicted value, refers to the average value of the observed value, n refers to the number of observed values, and p refers to the model parameter number.
3. Results and Analysis
3.1. Selection of Basic Model
After estimating the fit statistics of each one of 30 models fitted, six models were selected for further analysis. In general, the variable-exponent taper models showed the best results; therefore, the four best variable-exponent taper models (Zeng and Liao [37]; Bi [12]; Kozak [1] and Sharma and Zhang [13]), the best single taper function (Cervera [26]) and the best segmented model (Max and Burkhart [6]) were selected. The parameter estimates and fit statistics of each model are shown in Table 3.

Table 3.
Fit parameters and statistics of six selected models.
It can be seen from Table 3 that Bi [12] model has the highest adjustment coefficient (: 0.9835) and the smallest root-mean-square error RMSE (0.4540) among the six models. The second model is Zeng and Liao [37] model (: 0.9830; RMSE: 0.4613). The single taper model Cervera [26] (: 0.9794; RMSE: 0.5075) is the worst. The goodness of fit of single taper equation and segmented taper equation is slightly inferior to that of variable-exponent taper equation. The goodness of fit among variable-exponent taper equations has no evident difference. The four variable-exponent taper models are selected to build a mixed effect model to compare model fitting performance.
3.2. Construction of Mixed Effect Model
A mixed effect model was built on the basis of four selected variable-exponent taper models in the study. The possibility of 1–2 random parameter combinations in the selected basic model was fitted. Wherein, Zeng and Liao [37] had 10 pairs of combinations. Bi [12] had 28 pairs of combinations. Sharma and Zhang [13] had 10 pairs of combinations. Kozak [1] had 45 pairs of combinations. The parameter combination of AIC, BIC, and -2LL with the minimum statistical indicators was selected as the optimal mixed effect model. The fitting results are shown in Table 4. It can be seen from Table 4 that the AIC value based on the plot-level effect mixed model is decreased by 3.3–5.8% compared with the basic model aiming at four variable-exponent taper equations. The AIC value based on tree-level effect mixed model is reduced by 40.7–46.6% compared with the basic model, and the AIC value nested with two level effect mixed models is decreased by 40.6–46.5% compared with the basic model. BIC and -2LL values had similar decrease rate. Wherein, AIC, BIC and -2LL values of the model Bi [12] in the basic model and the mixed model with plot-level effect were the minimum. The AIC, BIC, and 2LL values of model Kozak [1] in the mixed model with tree-level effect and two-level effects were the lowest.

Table 4.
Statistics of the Akaike information criteria (AIC), Bayesian information criteria (BIC), and -2loglikelihood (-2LL) for variable exponent taper models with different effects.
Figure 2 is the lag residual diagram of the mixed effect model added with intra-group variance- covariance structure of Kozak [1] model after determination of mixed parameters. A, B, C, and D are model lagged residual diagrams based on common nonlinear least square method, plot-level effect, tree-level effect, and nested two-level effect mixed effect respectively in the figure. It can be seen that the common least square method and mixed models based on plot-level effect had obvious positive correlation. The residual diagrams of mixed model based on tree-level effect and nested two-level effect had no prominent trend. It is obvious that the structure-free intra-group variance–covariance matrix mixed effect model can effectively eliminate autocorrelation.
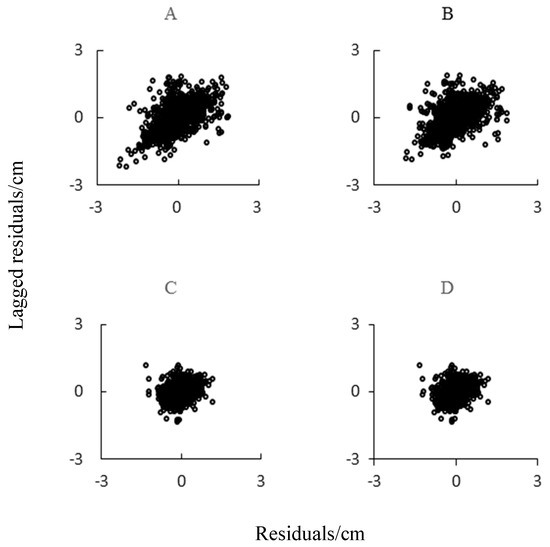
Figure 2.
Diameter residuals plotted against Lag1—residuals for Kozak [1] fitted. (A): Ordinary nonlinear least squares; (B): Plot-level effects; (C): Tree-level effects; (D): Nested effects of plot and tree.
Table 5 respectively shows fixed parameter and random parameter estimated values of four variable-exponent taper equations based on tree-level effect mixed model. It can be found that all parameters are statistically significant. Table 6 shows the fit statistics comparison of four variable-exponent taper equations in the traditional least square method and those based on plot-level effect, tree-level effect, and nested two-level effect. The simulation precision in mixed mode based on plot, tree-level effect, or nested two-level effect is higher than that of the traditional least square method. The simulation precision based on tree-level effect and nested two-level effect is higher than that based on plot-level effect mixed model. The determination coefficient of mixed effect model based on plot-level effect is higher than that of the basic model by 0.0016–0.0020. The determination coefficient of mixed model based on tree-level effect and nested two-level is higher than that of the mixed model based on plot-level effect by 0.0104–0.0117. The simulation precision of the mixed model based on the tree-level effect and nested two-level had no prominent difference. Bi [12] model has the highest precision in the least square method basic model and the mixed model of nested two-level. Kozak [1] model has the highest determination coefficient and the lowest root-mean-square error in the mixed model based on tree-level effect and nested two-level effect. It is consistent with the goodness of fit indicators AIC, BIC, and -2LL.

Table 5.
Parameter estimates and variance components of the tree levels nonlinear mixed-effects (NLME) (standard errors in parentheses).

Table 6.
Model fitting statistics of variable exponent taper models with different effects.
3.3. Predicted Diameters and Model Calibration
The established Kozak [1] mixed effect model based on tree-level effect was used for fitting the validation data to test the model’s prediction ability. The relative height of each tree in validation data was divided into 10 parts, and the prediction mean variation and SD of the diameter in each part was segmented for statistics. The result was shown in Table 7. It can be seen from Table 7 that the mean variation of the Kozak [1] mixed effect model based on the tree-level effect was smaller in the 10 segmented parts. The mean variation was slightly larger in the stem base (0.0 < h/H ≤ 0.1) and at the top of the stem (0.7 < h/H ≤ 1.0), both variations were larger than 0.8cm. However, the mean variation at the relative height of 0.3 < h/H ≤ 0.4 was the smallest, namely, reaching 0.0448 cm. The prediction accuracy of the Kozak [1] mixed effect model based on the tree-level effect is higher in the middle part of the trunk than that in the base and at the top of the stem, and SD also has the same trend. Figure 3 shows different DBH sample trees with similar total height (H = 15.7 m; D1 = 14.6 cm, D2 = 15.5 cm, D3 = 17.2 cm) and different total height with similar DBH (D = 17.2 cm; H1 = 15.7 m, H2 = 17.0 m, H3 = 17.7 m). The tree-level effect mixed model based on Kozak [1] variable-exponent equation can exactly reflect the difference of trees’ taper with different total height or DBH.

Table 7.
Examined statistics of Kozak [1] mixed model with tree-level effects.
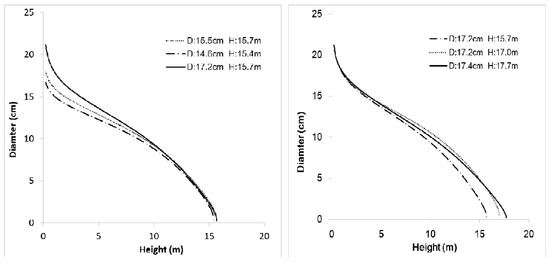
Figure 3.
Taper profiles for three different diameter at breast height (DBH) and the similar height tree, three different height and the similar DBH tree in Kozak [1] with tree-level effects NLME model.
4. Discussion
Single taper equations have been found to describe stem shape quite accurately [2,45], although more flexible equations were developed to provide a better description of the stem profile [6,10]. It was found that the model of Cervera [26] was optimal in single taper equations and only slightly lower than the other two types of stem form equations. However, the single taper equations often fail to characterize the entire stem profile and produce bias, especially for the area near the butt and at the very top sections of tree [6,8]. The model of Max and Burkhart showed the same excellent accuracy as previous studies [6]. A variable-exponent taper equation describes the bole shape with a changing exponent or variable from ground to top to represent the neiloid, paraboloid, conic, and several intermediate forms [10]. This approach is based on the assumption that the stem form varies continuously along the length of a tree [39]. In comparison with single and segmented taper models, this approach provides the lowest bias and highest precision in taper prediction [10,11,14]. In this study, the fitting precision of the variable-exponent taper equation is higher than other two groups of taper equations, which is consistent with the conclusions of previous studies [10,13]. The four optimal variable-exponent taper equations including Zeng and Liao [37], Bi [12], Kozak [1], Sharma and Zhang [13] almost provide similar results in terms of the goodness of fit statistics.
Mixed models have also been used successfully in the development of taper equations for several species throughout the world [46,47,48,49,50], showing that estimates of the mean response (fixed-effects model) can be significantly improved by including random effects parameters. This was confirmed in the present study. Further, the fitting precision of the mixed model based on tree-level effect and nested two-level effect were proved to be higher than the mixed model based on plot-level effect. The mixed models based on nested two-level effect and plot-level effect had no significant difference. Kozak [1] model had the highest adjusted determination coefficient among the four optimal variable-exponent taper equations while considering tree-level effect and nested two-level effect. The inclusion of an intra-group variance-covariance matrix in the mixed effect model can eliminate the autocorrelation, which is consistent with the results of previous studies [16,44,51,52]. It can be found that the fitting residual scatterplot of taper model based on common least square method and plot-level effect shows significant positive correlation, while the residual diagram of mixed model based on tree-level effect and nested two-level effect both have removed this trend in a large part. Although the mixed model accounting for autocorrelation does not improve the prediction performance, it improves interpretation of the statistical properties [53].
In addition to this model and its simulation methods selection, some tree or stand factors (e.g., crown height, ratio, and planting density) that have deep relationship with tree form and quality [13,54] have been introduced into taper equations to improve modeling performance [8,13,55]. Additionally, for a taper equation, its aim is to develop a volume equation and calculate stand merchantable timber volume. The stem taper model should be integrable. Unfortunately, the model of Kozak [1] is not analytically integrable. Therefore, numerical integration methods and iterative procedures to estimate height at aspecific end diameter should be used.
5. Conclusions
The variable-exponent taper equations were developed for Chinese fir, the most important commercial tree species in southern China. Through the comparison of thirty taper equations, single taper models were found having the lowest precision, and the variable-exponent taper equations had higher precision than segmented taper equations. Variable-exponent taper models developed by Zeng and Liao [37], Bi [12], Kozak [1], Sharma and Zhang [13] almost provide similar results in terms of the goodness of fit statistics, and can be selected as taper models of Chinese fir trees. The fitting precision of the mixed model based on tree-level effect and nested two-level effect proved to be higher than the mixed model based on plot-level effect. Variable-exponent taper model developed by Kozak [1] produced better predictions for medium stems compared to lower and upper stems.
Author Contributions
Conceptualization: A.D.; Methodology: S.Z. and A.D.; Investigation: A.D. and J.S.; Data Curation: A.D. and J.S.; Writing: S.Z., A.D.; Supervision: A.D.; Funding Acquisition: A.D. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Scientific and Technological Task in China (No. 2016YFD0600302), and the special science and technology innovation in Jiangxi Province (No. 201702).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We thank Z.F. Deng, S.H. Lai, and S.Z. Tong for their assistance with the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kozak, A. My last words on taper equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef]
- Kozak, A.; Munro, D.; Smith, J. Taper functions and their application in forest inventory. For. Chron. 1969, 45, 278–283. [Google Scholar] [CrossRef]
- Ormerod, D. A simple bole model. For. Chron. 1973, 49, 136–138. [Google Scholar] [CrossRef]
- Reed, D.D.; Byrne, J.C. A simple, variable form volume estimation system. For. Chron. 1985, 61, 87–90. [Google Scholar] [CrossRef]
- Sharma, M.; Oderwald, R.G. Dimensionally compatible volume and taper equations. Can. J. For. Res. 2001, 31, 797–803. [Google Scholar] [CrossRef]
- Max, T.A.; Burkhart, H.E. Segmented polynomial regression applied to taper equations. For. Sci. 1976, 22, 283–289. [Google Scholar]
- Demaerschalk, J.; Kozak, A. The whole-bole system: A conditioned dual-equation system for precise prediction of tree profiles. Can. J. For. Res. 1977, 7, 488–497. [Google Scholar] [CrossRef]
- Cao, Q.V.; Burkhart, H.E.; Max, T.A. Evaluation of two methods for cubic-volume prediction of loblolly pine to any merchantable limit. For. Sci. 1980, 26, 71–80. [Google Scholar]
- Borders, E.; Bailey, L. Compatible volume-taper models for loblolly and slash pine based on a system with segmented-stem form factors. For. Sci. 2000, 46, 1–12. [Google Scholar]
- Kozak, A. A variable-exponent taper equation. Can. J. For. Res. 1988, 18, 1363–1368. [Google Scholar] [CrossRef]
- Newnham, R. Variable-form taper functions for four alberta tree species. Can. J. For. Res. 1992, 22, 210–223. [Google Scholar] [CrossRef]
- Bi, H. Trigonometric variable-form taper equations for australian eucalypts. For. Sci. 2000, 46, 397–409. [Google Scholar]
- Sharma, M.; Zhang, S.Y. Variable-exponent taper equations for jack pine, black spruce, and balsam fir in eastern Canada. For. Ecol. Manag. 2004, 198, 39–53. [Google Scholar] [CrossRef]
- Muhairwe, C.K. Taper equations for eucalyptus pilularis and eucalyptus grandis for the north coast in new south wales, Australia. For. Ecol. Manag. 1999, 113, 251–269. [Google Scholar] [CrossRef]
- Rojo, A.; Perales, X.; Sánchez-Rodríguez, F.; Álvarez-González, J.G.; Von Gadow, K. Stem taper functions for maritime pine (Pinus pinaster ait.) in galicia (northwestern spain). Eur. J. For. Res. 2005, 124, 177–186. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, S.; Trincado, G.; Meng, S.X. Nonlinear mixed-effects modeling of variable-exponent taper equations for lodgepole pine in Alberta, Canada. Eur. J. For. Res. 2009, 128, 415–429. [Google Scholar] [CrossRef]
- Cao, Q.V.; Wang, J. Evaluation of methods for calibrating a tree taper equation. For. Sci. 2015, 61, 213–219. [Google Scholar] [CrossRef]
- Guangyi, M.; Yujun, S.; Hao, X.; de-Miguel, S. A mixed-effects model with different strategies for modeling volume in Cunninghamia lanceolata plantations. PLoS ONE 2015, 10, e0140095. [Google Scholar] [CrossRef]
- Gómez-García, E.; Crecente-Campo, F.; Diéguez-Aranda, U. Selection of mixed-effects parameters in a variable–exponent taper equation for birch trees in northwestern Spain. Ann. For. Sci. 2013, 70, 707–715. [Google Scholar] [CrossRef]
- Jiang, L.C.; Liu, R.L. A stem taper model with nonlinear mixed effects for dahurian larch. Sci. Silvae Sin. 2011, 47, 101–106. (In Chinese) [Google Scholar]
- Wu, Z.L. Chinese Fir (in Chinese); China Forestry Press: Beijing, China, 1984; Volume 10, pp. 463–470. (In Chinese) [Google Scholar]
- Li, X.Y.; Duan, A.G.; Zhang, J.G.; Zhao, S.R.; Feng, S.Q. Effects of improved varieties and densities on stand basal area growth of young Chinese fir (Cunninghamia lanceolata) plantation. For. Res. 2021, 34, 65–70. (In Chinese) [Google Scholar]
- Munro, D. The Distribution of Log Size and Volume within Trees: A Preliminary Investigation; University of British Columbia: Vancouver, BC, Canada, 1966. [Google Scholar]
- Bennett, F.A.; Swindel, B.F. Taper Curves for Planted Slash Pine. USDA Forest Service Research Note; Southeastern Forest Experiment Station (SE-179): Asheville, NC, USA, 1972; p. 4. [Google Scholar]
- Demaerschalk, J. Converting volume equations to compatible taper equations. For. Sci. 1972, 18, 241–245. [Google Scholar] [CrossRef]
- Cervera, J. El área basimétrica reducida, el volumen reducido y el perfil. Montes 1973, 174, 415–418. [Google Scholar]
- Demaerschalk, J.P. Integrated systems for the estimation of tree taper and volume. Can. J. For. Res. 1973, 3, 90–94. [Google Scholar] [CrossRef]
- Coffre, M. Modelos Fustales. Ph.D. Thesis, Universidad Austral de Chile, Valdivia, Chile, 1982; p. 44. [Google Scholar]
- Biging, G.S. Taper equations for second-growth mixed conifers of northern california. For. Sci. 1984, 30, 1103–1117. [Google Scholar]
- Reed, D.D.; Green, E.J. Compatible stem taper and volume ratio equations. For. Sci. 1984, 30, 977–990. [Google Scholar]
- Newberry, J.D.; Burkhart, H.E. Variable-form stem profile models for loblolly pine. Can. J. For. Res. 1986, 16, 109–114. [Google Scholar] [CrossRef]
- Real, P.; Moore, J. An Individual Tree System for Douglas-Fir in the Inland North-West. USDA Forestry Service General Technical Report NC-120; Dept. of Agriculture, Forest Service, North Central Forest Experiment Station: St. Paul, MN, USA, 1986; pp. 1037–1044.
- Forslund, R. The power function as a simple stem profile examination tool. Can. J. For. Res. 1991, 21, 193–198. [Google Scholar] [CrossRef]
- Thomas, C.E.; Parresol, B.R. Simple flexible trigonometric taper equations. Can. J. For. Res. 1991, 21, 1132–1137. [Google Scholar] [CrossRef]
- Jiménez, J.; Aguirre, O.; Niembro, M.; Navar, J.; Domínguez, A. Determinación de la forma externa de Pinus hartwegii lindl. En el noreste de méxico. For. Syst. 1994, 3, 175–182. [Google Scholar]
- Valenti, M.A.; Cao, Q.V. Use of crown ratio to improve loblolly pine taper equations. Can. J. For. Res. 1986, 16, 1141–1145. [Google Scholar] [CrossRef]
- Zeng, W.S.; Liao, Z.Y. A study on taper equation. Sci. Silvae Sin. 1997, 33, 127–132. (In Chinese) [Google Scholar]
- Riemer, T.; Gadow, K.V.; Sloboda, B. Ein modell zur beschreibung von baumschäften. Allg. Forst Und Jagdztg. 1995, 166, 144–147. [Google Scholar]
- Lee, W.K.; Seo, J.H.; Son, Y.M.; Lee, K.H.; Von Gadow, K. Modeling stem profiles for Pinus densiflora in Korea. For. Ecol. Manag. 2003, 172, 69–77. [Google Scholar] [CrossRef]
- Berhe, L.; Arnoldsson, G. Tree taper models forcupressus lusitanicaplantations in Ethiopia. South. For. J. For. Sci. 2008, 70, 193–203. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Modeling stand density effects on taper for jack pine and black spruce plantations using dimensional analysis. For. Sci. 2009, 55, 268–282. [Google Scholar]
- Schröder, T.; Costa, E.A.; Valério, A.F.; dos Santos Lisboa, G. Taper equations for Pinus elliottii engelm. In Southern Paraná, Brazil. For. Sci. 2015, 61, 311–319. [Google Scholar] [CrossRef]
- Calama, R.; Montero, G. Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): A calibrating approach. Silva Fenn 2005, 39, 37–54. [Google Scholar] [CrossRef]
- VanderSchaaf, C.L.; Burkhart, H.E. Comparison of methods to estimate reineke’s maximum size-density relationship species boundary line slope. For. Sci. 2007, 53, 435–442. [Google Scholar]
- Bruce, D.; Curtis, R.O.; Vancoevering, C. Development of a system of taper and volume tables for red alder. For. Sci. 1968, 14, 339–350. [Google Scholar]
- Garber, S.M.; Maguire, D.A. Modeling stem taper of three central Oregon species using nonlinear mixed effects models and autoregressive error structures. For Ecol. Manag. 2003, 179, 507–522. [Google Scholar] [CrossRef]
- Leites, L.P.; Robinson, A.P. Improving taper equations of loblolly pine with crown dimensions in a mixed-effects modeling framework. For. Sci. 2004, 50, 204–212. [Google Scholar]
- Özçelik, R.; Cao, Q. Evaluation of fitting and adjustment methods for taper and volume prediction of black pine in Turkey. For. Sci. 2017, 63, 349–355. [Google Scholar] [CrossRef]
- Özçelik, R.; Yiğit, E. Toros göknarında gövde çapı modelinin doğrusal olmayan karışık etkili modelleme yaklaşımı ile geliştirilmesi. Turk. J. For. 2018, 19, 138–148. [Google Scholar] [CrossRef][Green Version]
- Adamec, Z.; Adolt, R.; Drápela, K.; Závodský, J. Evaluation of different calibration approaches for merchantable volume predictions of Norway Spruce using nonlinear mixed effects model. Forests 2019, 10, 1104. [Google Scholar] [CrossRef]
- Lanssanova, L.R.; Machado, S.D.A.; Garrett, A.T.D.A.; Bonete, I.P.; Pelissari, A.L.; Filho, A.F.; da Silva, F.A.; Ciarnoschi, L.D. Mixed-effect non-linear modelling for diameter estimation along the stem of Tectona grandis in mid-western Brazil. South. For. 2019, 81, 167–173. [Google Scholar] [CrossRef]
- Çakir, C.Y.; Kahriman, A. Modeling stem profile of caucasian fir and oriental spruce mixed stands in Turkey using nonlinear mixed-effects models. Appl. Ecol. Environ. Res. 2018, 16, 6815–6833. [Google Scholar]
- Wang, W.; Chen, X.; Zeng, W.; Wang, J.; Meng, J. Development of a mixed-effects individual-tree basal area increment model for oaks (Quercus spp.) considering forest structural diversity. Forests 2019, 10, 474. [Google Scholar] [CrossRef]
- Salekl, L.; Sivacioglu, A.; Topacoglu, O.; Zahradnile, D.; Jerabkoval, L.; Machar, I. Crowns of Old Remnant Oak Standards. Fresenius Environ. Bull. 2017, 26, 4023–4032. [Google Scholar]
- Duan, A.G.; Zhang, S.S.; Zhang, X.Q.; Zhang, J. Development of a stem taper equation and modelling the effect of stand density on taper for Chinese fir plantations in Southern China. PeerJ 2016, 4, e1929. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).