Model-Based Growth Comparisons between Loblolly and Slash Pine and between Silvicultural Intensities in East Texas

Abstract

Growth differences between key commercial species and between silvicultural intensities (phases) within a species in a region are of great interest to foresters. This study used modeling methods to investigate these differences in east Texas. Datasets collected from loblolly and slash pine plots installed in extensively managed plantations (Phase I) and loblolly pine plots installed in intensively managed plantations (Phase II) were used. Species and silvicultural phase growth differences were determined by comparing their height–age, diameter–age, and height–diameter relationships. Slash and loblolly pine had significantly different parameter estimates for the Chapman and Richards function-based height– and diameter–age models. Slash pine grew faster than loblolly pine, with the superiority in height increasing while that of diameter growth decreased slightly with age. Slash and loblolly pine differed also in all parameter estimates of the exponential function-based height-diameter model. Loblolly pine was taller than the slash for small size (DBH ≤ 18 cm) trees, but thereafter, slash pine outperformed loblolly. While these results may encourage planting slash pine in the region, more studies are needed before definitive conclusions can be made. The differences in the height–age models for loblolly pine Phase I and II plots suggest that intensive management significantly enhanced tree height growth. However, this enhancement did not substantially change the maximum height; instead, trees reached the maximum height younger, thus effectively shortening the rotation age.

1. Introduction

Are there differences in growth between loblolly (P. taeda L.) and slash (P. elliottii Engelm.) pine when they are planted in east Texas? To date, few studies have sought to answer this question. Reference [1] compared young pine plantations in east Texas and found that slash pine outperformed loblolly pine in general. However, in another study based on data for 3-year-old stands, the opposite was true [2]. The observed results from outside Texas varied, too, and a faster growth of slash pine over loblolly pine was observed in neighboring Louisiana [3], but converse results were reported further east in Georgia and Florida [4,5,6]. Other than [1], these studies were well-designed experiments and were purposely established on sites of different soil or drainage types, with a goal of comparing the species performance under those specific conditions.

Operationally, landowners jointly apply all feasible silvicultural treatments to improve pine plantation productivity, and the intensity of pine silviculture has increased in southern United States (US), including Texas, over the past 80 years [7]. Prior to 1960, planting pine generally was limited to old fields and cutover sites; little site preparation was practiced due to the high cost. Starting in the 1970s, the importance of competition control on plantation success was recognized and site preparation using various mechanical means such as anchor chaining, chopping, burning, root raking, shearing, and disking began to be employed. The planting of the first-generation genetically improved seed sources also became prevalent. These plantations are conventionally referred to as extensively managed plantations, hereafter. Around the 1990s, the application of chemical site preparation, fertilization, midrotation thinning, and planting more advanced genetically improved seedlings became common. These plantations are referred to as intensively managed plantations. Because of the popularity, yet costly nature, there has been much interest in knowing the growth differences resulting from the intensive silvicultural practices. Reference [8] argued that southern pine in US provides the best example in improving forest productivity via silviculture including genetics, which, based on an estimation by Fox et al. [7], has enhanced pine plantation productivity greatly with average volumes per acre, increasing from 3000 ft³/acre for plantations established in the 1970s to 5000 ft³/acre for those established in the 1990s.

Nonetheless, studies are generally lacking in comparing growth performance between loblolly and slash pine and among silviculture intensities (phases), particularly at a regional level. This comparison is important as it may aid in determining species choice and management options. Conventionally, to achieve these research goals, establishing well-designed, large-scale paired studies is required, which, however, is expensive, and, therefore, often involves limited treatments and/or is installed at a limited number of sites, making it difficult to generalize comparisons across a region. Empirical forest tree growth modeling provides an alternative toward this end. Empirical forest tree growth modeling often is based on data collected from long-term permanent plots, which are typically not paired but instead installed across a region. If the plots representing different populations are well installed throughout the region, then the population differences can be sufficiently described by comparing their empirical models.

Both loblolly and slash pine are widely planted in east Texas. To provide quantitative information supporting pine plantation management, Stephen F. Austin State University in collaboration with forest companies initiated the East Texas Pine Plantation Research Project (ETPPRP) in 1982 [9]. Over the years, the ETPPRP has established studies in two phases in east Texas; in the Phase I study, plots were installed in extensively managed loblolly and slash pine plantations, and in the Phase II study, plots were installed in intensively managed loblolly pine plantations. Do the often-used growth models such as height–age, diameter–age, and height–diameter models remain parallel to each other between loblolly pine and slash pine and between Phase I and Phase II of loblolly pine in the region? The ETPPRP datasets provide a unique opportunity to compare growth differences between the two pines and between silvicultural phases via comparing these models. The results of these comparisons may provide important information to forest landowners and managers in the region for establishing and managing pine plantations.

2. Data and Methods

2.1. Data

ETPPRP Phase 1 (loblolly and slash pine) and Phase II (loblolly pine only) data were used. All plots were located within east Texas, which is located in 22 contiguous counties across east Texas, generally between 30–35° north latitude and 93–95° west longitude.

2.1.1. Phase I: Extensively Managed Plantations (EMP) of Loblolly and Slash Pine

Between 1982 and 1984, the ETPPRP installed 269 (185 for loblolly and 84 for slash pine) Phase I plots (approximately 0.1 ha per plot) in the respective EMP across east Texas (Lenhart et al. 1985) to best represent the growing conditions unique to the region. Plots were protected from operational treatments of the plantations, with no other silvicultural treatments being applied after the plots were established.

Trees were measured when a plot was installed and every three years (cycle) thereafter, for diameter at breast height (D, nearest 0.1 inch) and total height (H; nearest 1.0 foot), among others. Original values in imperial English units were converted to metric values prior to analysis. Plantation age was determined as the time between the measurement date and the plantation establishment date derived from stand records. Data were cleaned, and abnormal observations removed. Since growth modeling typically requires at least three repeated measures per individual, any plots which had ≤2 measurement cycles were excluded. After cleaning, data of 171 and 74 plots for loblolly (123,913 observations) and slash pine (42,064 observations), respectively, were used. At plot establishment, plantations averaged 10 years old with an average stocking of 1178 (loblolly) and 980 (slash pine) trees ha⁻¹. Base age 25 years site index ranged from 10 to 28 m for loblolly and from 11 to 25 m for slash pine plots. On average, each plot was measured for 7–8 cycles, with ages ranging from 2 to 45 years for loblolly and from 2 to 40 years for slash.

Table 1. Summary of the ETPPRP plots which were used in this study, by silvicultural phase and species. Note that Age is the average age of plots, H is the average total tree height, and D represents the average diameter at breast height.

Phase	Species	Number of Plot	Cycle (Time) (Range)	Observations	Age (Year) (Range)	H (m) (Std) *	D (cm) (Std)
I	Loblolly	171	7.51 (3–12)	123,913	17 (2–45)	12.72 (6.02)	15.13 (7.27)
I	Slash	74	7.32 (3–11)	42,064	16 (2–40)	11.53 (5.83)	13.96 (6.92)
II	Loblolly	128	5.30 (3–6)	71,131	17 (5–26)	11.02 (4.77)	13.97 (6.05)

* std: standard deviation.

provides detailed summary statistics for datasets. Scatter plots of tree growth against stand age are shown in Figure 1.

2.1.2. Phase II: Intensively Managed Plantations (IMP) of Loblolly Pine

The ETPPRP Phase II began in 2004 with the installation of plots in IMP of loblolly pine across the region [10]. By 2019, 133 plots were established. While the plot size, establishment, and measurement were the same as the Phase I plots, there was no surrounding buffer, as the plots were operational in nature. Plots were to receive the same treatment as the entire stand, unlike the Phase I plots, which were insulated from all subsequent management activities. Most of the Phase II plots have been thinned at least once by 2020.

Data were cleaned, and any plots which had ≤ 2 measurement cycles were removed, resulting in a total of 128 plots (71,131 individual observations) being used. At establishment, stand stocking ranged from 807 to 2118 trees ha⁻¹, and site index ranged from 16 to 28 m. Each plot was measured on average of 5.3 measurement cycles (range: 3–6), with stand age ranging from 5 to 26 years (Table 1). Scatter plots of tree height growth against stand age can be found in Figure 1.

2.2. Data Analysis

Data of the loblolly and slash pine of the Phase I plots were used to compare growth performance between species, and data of loblolly Phases I and II were used to compare the two silvicultural intensities (phases).

The Chapman–Richards (CR) equation has been commonly applied for fitting tree height and age (H-A) and diameter and age (D-A) relationships [11]:

$$Y_{ijk}=a_0\times {\left(1-exp\left(-a_{1}A\right)\right)}^{a_2}+{\epsilon }_{ijk}$$

(1)

where $Y_{ijk}$ is the H or D of the kth tree, growing at the jth plot of the ith species in the Phase I plots or the ith phase of loblolly pine at a given age, A, for comparison of phases; $a_0$ is the asymptotic parameter, defining the maximum value of the function; $a_1$ is the rate parameter, controlling how quickly the function approaches the asymptote; $a_2$ is the shape parameter, defining the inflection point of the curve; and ${\epsilon }_{ijk}$ is the within-tree random error, defined as $N\left(0, {\sigma }^2\right).$ The differences of species or silvicultural phase on the parameters were modeled using:

$$a_0=a_{00}+a_{01}{T}_i+u_{0j}+u_{0k\left(j\right)}$$

(2)

$$a_1=a_{10}+a_{11}{T}_i+u_{1j}+u_{1k\left(j\right)}$$

(3)

$$a_2=a_{20}+a_{21}{T}_i+u_{2j}+u_{2k\left(j\right)}$$

(4)

where $a_{00}$, $a_{10}$, and $a_{20}$ are the fixed-effect parameters for the reference species (loblolly pine) or phase (Phase I); $T_i$ is the effect of the ith species or phase and, therefore $a_{01}$, $a_{11}$, and $a_{21}$ represent the differences of slash pine or Phase II with the reference; $u_{0j}$, $u_{1j}$, and $u_{2j}$ were the random-effect parameters of $a_0$, $a_1$, and $a_2$, respectively, for the jth plot within a species with $u_{0j}$~$N\left(0, {\sigma }_{u_{0j}}^2\right), u_{1j}$~$N\left(0, {\sigma }_{u_{1j}}^2\right)$, and $u_{2j}$~$N\left(0, {\sigma }_{u_{2j}}^2\right)$; $u_{0k\left(j\right)}$, $u_{1k\left(j\right)}$, and $u_{2k\left(j\right)}$ were the random-effect parameters of $a_0$, $a_1$, and $a_2$, respectively, for the kth tree within a plot, with $u_{0k\left(j\right)}$~$N\left(0, {\sigma }_{u_{0k\left(j\right)}}^2\right), u_{1k\left(j\right)}$~$N\left(0, {\sigma }_{u_{1k\left(j\right)}}^2\right)$, and $u_{2k\left(j\right)}$~$N\left(0, {\sigma }_{u_{2k\left(j\right)}}^2\right)$. Due to the issue of convergence, no correlations among the random-effect parameters at each level were assumed. Equations (2)–(4) were inserted into the Equation (1) to form the full H-A and D-A models.

The height–diameter (H-D) relationship was modeled using an exponential equation:

$$H_{ijk}=b_0\times exp\left(b_1{D}_{ijk}^{-1}\right)+{\epsilon }_{ijk}$$

(5)

where $H_{ijk}$ and $D_{ijk}$ are the kth tree H and D of the jth plot of the ith species; $b_0$ and $b_1$ are fixed-effect parameters, with $b_0$ controlling the rate of increase and $b_1$ adjusting the shape of the curve, and were modeled using the following equations:

$$b_0=b_{00}+b_{01}{T}_i+u_{0j}+u_{0k\left(j\right)}$$

(6)

$$b_1=b_{10}+b_{11}{T}_i+u_{{0j}_{1j}}+u_{1k\left(j\right)}$$

(7)

$b_{00}$ and $b_{10}$ are fixed-effect parameters for the reference species (loblolly pine), and $b_{01}$ and $b_{11}$ are the estimate differences of slash pine with loblolly. All other variables are the same as previously described. Equations (6) and (7) were inserted back into Equation (5) to form the full H-D model.

Note that comparisons between slash and loblolly pine were made using H-A, D-A, and H-D models, while comparison between Phases I and II of loblolly pine was made using only H-A model. Phase II data were not suitable for modeling D-A and H-D relationships since most Phase II plots were thinned by 2020, which could substantially change diameter growth but had negligible impact on height growth [12]. In addition, due to confounding between species and phases, comparison in growth between slash pine Phase I and loblolly pine Phase II was not made.

Models were selected using a top-down strategy [13]. The full models were fitted to the data first, and the nonsignificant random effects were removed one by one based on likelihood ratio test (models were fitted using restricted maximum likelihood method). After determining the random effects, species or silvicultural phase effect were checked using likelihood ratio test (models were fitted using maximum likelihood method), and only those showing significant differences were kept in the model. To meet model assumptions (normality, independence, and equal variances), whenever needed, heteroscedasticity was modeled as a power function of the fitted values, while correlations due to the longitudinal nature of the data were modeled using an autoregressive model of order 1. Residual plots were developed to check model assumptions. Model performance was evaluated using RMSE (=$\sqrt{MSE}$) and pseudo-R² [14]. No data split was applied in model evaluation since the main objective of the study was to compare species and silvicultural phases, not specifically to develop models for prediction or projection. Average tree dimensions (H and D) were calculated using a mean response (using fixed-factor parameter estimates only) and plotted to exhibit population differences. The R nlme package [15] was used for model development and performance evaluation.

3. Results

3.1. Comparing Extensively Managed Loblolly and Slash Pine Plantations

The CR function fitted the H-A Phase I data which combine loblolly and slash pine plots well, resulting in an overall RMSE of 0.38 m and a pseudo R² of 0.92 (

Table 2. Model parameter estimates, their standard errors (SE) and significance level (Pr) of the final model for comparing loblolly and slash pine based on the Phase I plots data.

Model Parameter		H-A Model			D-A Model
		Estimate	SE	Pr	Estimate	SE	Pr
Fixed a	$a_{00}$	19.8449	0.7622	<0.001	20.4019	0.7262	<0.001
	$a_{01}$	4.2345	0.5696	<0.001	1.0138	0.5319	0.024
	$a_{10}$	0.1112	0.0013	<0.001	0.2352	0.0026	<0.001
	$a_{11}$	−0.0242	0.0010	<0.001	−0.0426	0.0020	<0.001
	$a_{20}$	2.1366	0.0600	<0.001	4.8346	0.0394	<0.001
	$a_{21}$	−0.2794	0.0433	<0.001	−1.1313	0.0257	<0.001
Random b	$V_{{\alpha }_0-p}$	13.7404			11.7354
	$V_{{\alpha }_2-p}$	0.0877			1.2582
	$V_{{\alpha }_0-T}$	0.5495			1.1073
	$V_e$	0.3841			0.3914
	Power	0.60			0.67
	Phi	0.17			0.25
Goodness-of-fit	RMSE	0.38			0.63
	R2	0.92			0.85

^a See explanations of Equation (1) in text. $a_{00}$, $a_{10}$, and $a_{20}$ were estimates for loblolly pine, and $a_{01}$, $a_{11}$, and $a_{21}$ were differences of slash pine from loblolly pine. ^b $V_{{\alpha }_0-p}$, $V_{{\alpha }_2-p}$, $V_{{\alpha }_0-T}$, $V_e$, Power, and Phi were estimated among plot variances in $a_0$, $a_2$, within-plot variance in $a_0$, error variance, power of the weighted function, and first-order correlation, respectively. Including each effect significantly improved model performance compared to the model without it, based on loglikelihood test at alpha = 0.05.

). All model parameter estimates for loblolly pine ($a_{00}$, $a_{10}$, and $a_{20}$) were significantly different from zero, as were their differences with slash pine ($a_{01}$, $a_{11}$, and $a_{21}$), with the latter having a significantly larger a₀ but smaller a₁ and a₂. Model predictions in average tree H showed that slash pine was consistently taller than loblolly pine at a given age, with this advantage increasing with age (Figure 2a). In absolute terms, slash was 1.7 m taller than loblolly at age 5, but this value increased to 4.1 m at age 25 years. The model predicted maximum H of approximately around 19 and 23 m for loblolly and slash pine, respectively.

The developed D-A model achieved an RMSE of 0.63 cm and an R² of 0.85 (Table 2). Similar to the H-A model, slash pine had a significantly larger a₀ but smaller a₁ and a₂. Slash pine had a larger D than loblolly pine at a given age, but the difference narrowed slightly with age (Figure 2b). At age 5, slash pine was 2.4 cm larger than loblolly pine, but this value reduced to only 1.3 cm at age 25 years. An asymptotic D of 21 and 23 cm for loblolly pine and slash pine, respectively, was predicted.

The exponential function modeled the H-D relationship well, with an RMSE of 1.07 m and an R² of 0.84 (

Table 3. H-D model parameter estimates, their standard errors (SE), and significance level (Pr) for H-D model comparing slash and loblolly pine based on the Phase I plots data.

Model Parameter		Estimate	SE	Pr
Fixed a	$b_{00}$	26.0146	1.4075	<0.001
	$b_{01}$	2.1673	1.0205	0.034
	$b_{10}$	−9.7877	0.6334	<0.001
	$b_{11}$	−1.4726	0.4593	0.001
Random b	$V_{b_0-p}$	53.1107
	$V_{b_1-p}$	10.6804
	$V_e$	3.1329
	Power	0.1255
Goodness-of-fit	RMSE	1.07
	R2	0.84

^a See explanations of Equation (5) in text. $b_{00}$ and $b_{10}$ were estimates for loblolly pine, and $b_{01}$ and $b_{11}$ were differences of slash pine from loblolly pine. ^b $V_{b-p}$, $V_{b_1-p}$, $V_e$, and Power were estimated among plot variances in $b_0$, $b_1$, random error variance, and power of the weighted function, respectively. Including each effect significantly improved model performance compared to the model without it, based on loglikelihood test at alpha = 0.05.

). The species differences in b₀ and b₁ estimates were statistically significant, with slash pine having a larger b₀ but a smaller b₁. The two curves were not parallel and crossed over with increasing tree size; loblolly had a larger H when D was approximately 18 cm or less, and thereafter, the order reversed (Figure 2c).

Substantial variation existed among plots in a₀ and a₂ and within-plot (tree to tree) in a₀ for both the H-A and D-A models (Table 2). For the exponential H-D model, among plot variation was substantial in both b₀ and b₁, while their within-plot variation was not important (Table 3). For all the models, incorporating the weights of the fitted values and the first-order correlation significantly improved model performance (Table 2 and Table 3). Model assumptions of all three models were met based on residual plots.

3.2. Comparing Extensively and Intensively Managed Loblolly Pine

The CR function fitted the H-A relationship to the dataset combining loblolly Phase I and II plots well, resulting in an overall RMSE of 0.31 m and R² of 0.88 (

Table 4. H-A model parameter estimates, their standard errors (SE), and significance level (Pr) for comparing loblolly pine of extensively (Phase I) and intensively (Phase II) managed plantations.

Model Parameter		Estimate	SE	Pr
Fixed a	$a_{00}$	21.5316	0.2120	<0.001
	$a_{10}$	0.0905	0.0005	<0.001
	$a_{11}$	0.0152	0.0011	<0.001
	$a_{20}$	1.8729	0.0231	<0.001
	$a_{21}$	−0.4686	0.0344	<0.001
Random b	Va0-P	12.5521
	Va2-P	0.0846
	Va0-T	1.8556
	Verr	0.0956
	Power	0.64
	Phi	0.23
Goodness-of-fit	RMSE	0.31
	R2	0.88

^a$a_{00}$ was a global estimate for both phases. $a_{10}$ and $a_{20}$ were estimates for Phase I, and $a_{11}$ and $a_{21}$ were differences of Phase II from Phase I. ^b See Table 2.

). All model parameters for the Phase I were significantly different from zero. Relative to the Phase I, the trees in Phase II had a comparable a₀, a significantly larger a₁, but a smaller a₂. Consequently, trees in the Phase II plots were consistently taller than those in the Phase I plots, but the superiority varied with age, increasing with age until approximately age 10 and, thereafter, declining. Average H was 3.3 and 6.2 m for Phases I and II, respectively, at age 5, a difference of 2.9 m; this value maximized at age 11 (3.6 m) but reduced to 1.9 m at age 25 (Figure 3).

The random effects of the model were similar to that of models comparing species (Table 4). Between-plot variance in a₀ and a₂ and within-plot variance in a₁ were statistically larger than 0. Using weights of fitted values and the correlated covariance of the first-order correlation significantly improved model performance. Model assumptions of all three models were met based on residual plots.

4. Discussion

The ETPPRP data collection efforts were not originally designed to compare populations (species or phases), with none of the plots being installed side by side. To answer the research questions, the ETPPRP data were used to determine whether the growth curves from two datasets (or populations) estimated the same population function. The method is not universal, requiring two assumptions [16]: (1) the datasets are sampled within a target region, representing a wide range of stand conditions and management options, and (2) a mathematical function is suitable for both datasets. The ETPPRP plots were carefully selected to represent the respective plantations in east Texas [9,10], and mathematical functions used to describe H-A or H-D relationships of slash and loblolly pine or different phases have often been the same [10,17]. The quality of the fitted Chapman–Richards function to the combined datasets of species or phases in this study (Table 2, Table 3 and Table 4) confirmed the effectiveness of the method. A mixed-effects modeling approach was adopted to account for plot to plot and within-plot variation, making the inclusion of additional predictor variables unnecessary. Thus, the between species or phase differences revealed in this study reflect an overall trend in the environment sampled and may not be applicable to a specific site within the environment or outside the environment. A similar procedure has often been used to compare growth models between regions, spacings, or species [10,18,19,20,21].

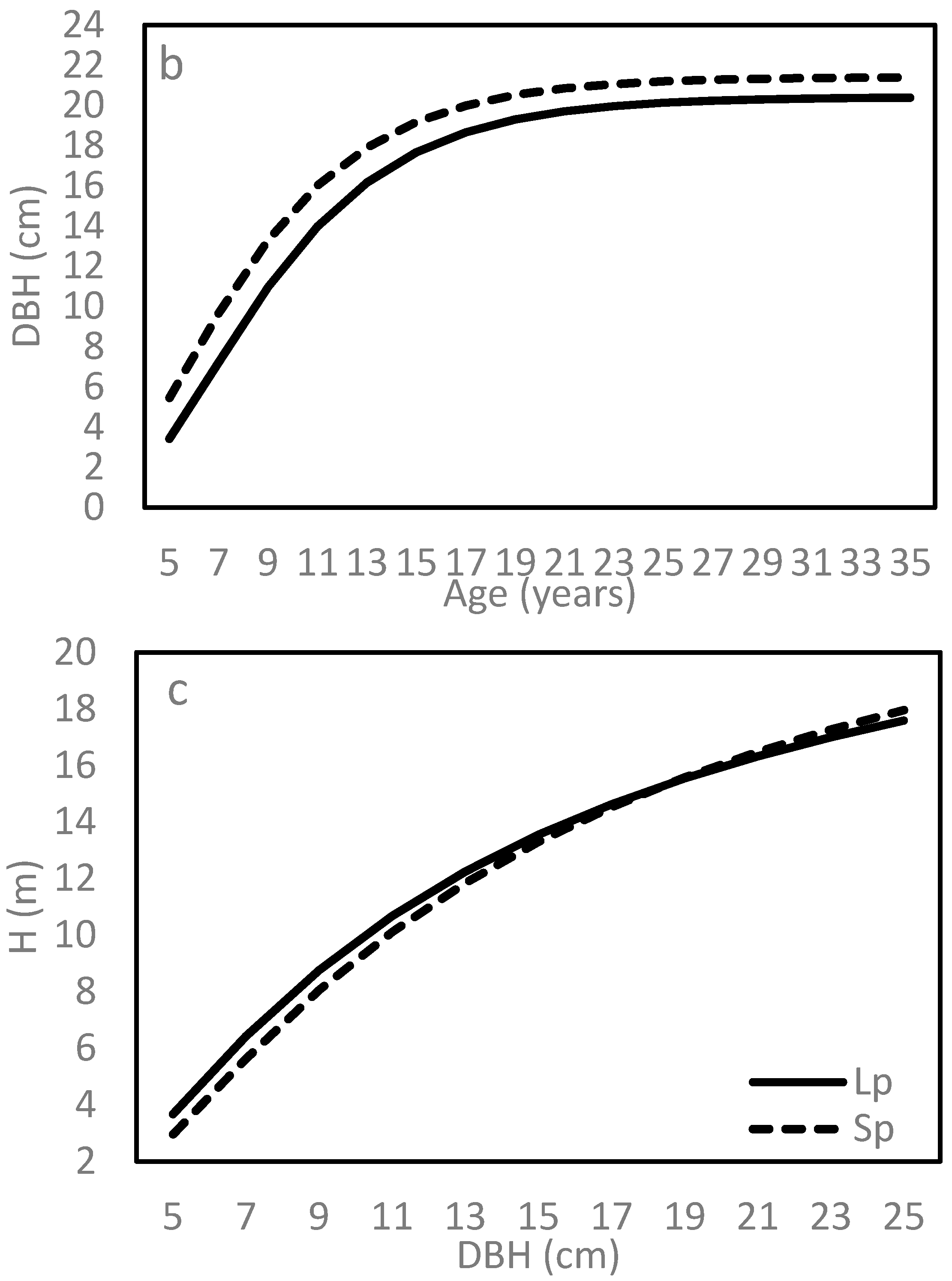
By using part of the ETPPRP Phase I plot data (the first 3 measurement cycles), Reference [1] calculated descriptive statistics and found that slash pine grew faster than loblolly pine, both in height and diameter in east Texas. This study extended that of [1] with additional data that extended to age 40–45 years and used modeling techniques. Our results show that slash pine outperformed loblolly pine in growth during the period, although the superiority of slash varied with age and trait (Figure 2a,b). The superiority in H increased while that in D decreased with age. At rotation age (assumed 25 years), slash pine was about 4 m (23.5%) taller and only about 1 cm (5.3%) larger than loblolly pine. Overall, relative to loblolly pine, in east Texas, planting slash pine is likely accompanied with growth gains, most of which being contributed by its faster height growth. Slash pine had a larger maximum H and D than loblolly pine (Table 2), and slash pine approximated the maximum H later than loblolly pine but approximated a maximum D at the similar age (Figure 2a,b). In support our finding, a faster growth of slash pine over loblolly pine at midrotation age was observed in the designed studies in Louisiana [3,22]. This finding, however, may not be true in other regions such as in Georgia and Florida, where loblolly pine often outperformed slash pine in growth [4,23]. Most recently, Reference [6] reported that loblolly pine was taller than, but comparable in diameter to, slash pine at age 21 when both were planted in the lower coastal plain.

The age-based H-D curve reflects the dynamic growth differences in H and D of a species. The H-D curves of two pines crossed over (Figure 2c); loblolly pine trees were taller at a given D when trees were small in size, yet slash pine became taller as trees increased in size. While statistical significance was found between species in the relationship, the actual differences in H at a given D, however, were small: less than 0.8 m when D ranged from 5 to 25 cm. Thus, for this relationship, the practical differences may be much less than what the statistical significance indicates. While H-D models often are used in forest inventory to predict H using D to save time and effort, in terms of forest management, the H-D curve describes tree H/D ratio, an indicator of stand stability. Trees with an H/D ratio of 80:1 or less are considered stable [24], reducing tree susceptibility to storm or wind damage. Based on our models, both species had an H/D ratio larger than 80 when tree D ranged from 7 to 19 cm (a corresponding age from 6 to 15 years based on the D-A models). Thus, there is a high risk of damage from storm and wind for midrotation plantations for both pines in the region. Tree H/D ratios are strongly related with spacing; silvicultural measures such as thinning can substantially change the ratio. In east Texas, early responses of loblolly pine diameter growth to thinning have recently been reported [12]; this information is lacking in slash pine. Given the potential damage from storm or wind, more studies are needed to optimize tree H/D ratio via silvicultural measures.

Since their establishment, no human intervention was applied to the Phase I plots, and thus, the results in this study provide a description of postinstallation growth under natural conditions. While different growth rates were observed between the species, their growth patterns were similar. For both pines, height growth appeared to cease gradually, while diameter growth appeared more suddenly around age 18 (Figure 2a,b). This is likely an adaptative strategy to competition; with increasing competition, both species allocate more carbohydrates to H than D growth to capture more of the available light. The phenomenon differs from the self-thinning rule, which assumes that average tree D continually increases with a sacrifice in survival under intensive competition. Clearly, more studies are needed to further understand the mechanism of plantation responses to competition, in particular photosynthate allocation, for both pines.

In the last three decades, forest landowners and managers in Texas have changed their preference from slash to loblolly pine [1]. Nonetheless, in terms of growth, the results in this study support planting slash pine over loblolly pine. Many managers may be hesitant to change species for several reasons. Previous experience with extensive slash pine fusiform rust infection is a discouraging aspect of planting slash pine. Reference [25] analyzed fusiform rust infection using the Phase I plot data of this study and found that the occurrence in slash pine (31% for the first six cycles but reduced to 12% at the 11th cycle) was much higher than in loblolly pine (8% for the first six cycles but reduced to 3–4% at the 11th cycle) plantations. The typical location of stem galls on trees in young slash pine is within 1 m of the ground, reducing the utilization for high value products. Partly, due to fusiform infection, the loblolly pine plantations had higher (i.e., about 4% higher at age 25 for SI = 24 m) survival than slash pine plantations in the Phase I plot data [26,27], resulting in less volume per unit area for the latter. However, most of the Phase I plantations were established using unimproved seed sources, and rust-resistant slash pine families are now available for planting from several seedling suppliers, which should greatly reduce fusiform rust incidence and potentially improve survival [8]. Some silvicultural measures may be used to mitigate the issues, reducing the site preparation necessary for stand establishment and postponing fertilizing after the pine trees are large enough (i.e., 8 years old), thus reducing the probability of fusiform rust occurrence on main-stem [25]. Ice damage can also be an issue [1]. Even though ice storms are infrequent in east Texas, damage due to ice loads can be severe in slash pine plantations. Overall, sufficient information in Texas is not available to determine if the faster tree growth of slash pine observed in this study can be transferred into higher stand-level productivity. Further investigation, in particular on fusiform rust resistance performance of genetically improved slash pine seedlots, is needed before an operational recommendation can be made. That average height gains from more intensive management were greater in loblolly pine than in slash pine in southeastern US [23], which, however, is not confirmed in east Texas.

The faster growth of loblolly pine observed in Phase II over Phase I (Figure 3) is, as expected, a result of the combined effects of advanced silviculture and tree breeding. Though, on average, Phase II plots are younger than Phase I (Table 1), and most Phase II plots have reached rotation age. Based on predicted average heights, trees in Phase II were 3.7 m (40.1%) taller than those in the Phase I at age 11, although the value decreased to 1.9 m (10.7%) at age 25 (Figure 3). Reference [23] compared the loblolly pine growth from ages 2 to 15 years under operational (an intensity between Phases I and II) and intensive (an intensity similar to the Phase II) cultural intensities and found the gain in height from intensive silviculture increased with age and maximized at age 10 (about 2 m taller), which is in parallel to our result. Based on the ETPPRP G&Y models [10], the 3.7 m increase in 11 year height, with other predictors constant, would result in an increase in volume per hectare by 38%. The results further confirmed that applying silvicultural measures did not substantially increase the maximum H; instead, the maximum H was achieved at an earlier age (Figure 3) and therefore effectively shortens rotation ages (e.g., to reach an H of 20 m, the Phase II plots took 25 years while the Phase I plots needed 35 years). This is in parallel with the effect of tree breeding on stand productivity that the greatest gain from tree improvement is due to a significant reduction in rotation age when improved seed sources are used in reforestation [28]. The dataset combining Phases I and II cannot be used to compare diameter growth between the phases, since Phase I plots were not but most Phase II plots were thinned. However, in 18 unthinned plots of an ETPPRP thinning study installed also in intensively managed (Phase II) plantations of loblolly pine across east Texas [12], the average D reached 20.1 cm (17.4–22.4 cm from ages 11–15 years) at an average age of 12.8 years, compared to the average D of the Phase I plots, 15.1 cm (13.5–16.0 cm from ages 11–15 years) at an age of 13.1 years—an increase of 33.1% from the intensive silviculture. This is inconsistent with a study in southeastern US where loblolly pine diameter growth was not impacted by silvicultural intensity [23]. In the literature, few papers have covered joint effects of silvicultural measures on forest productivity. Reference [7] estimated that rotation age for southern pine decreased from 50 to under 20 years from 1940 to 2010 due to intensive silviculture including tree breeding.

In this study, sample data were clustered due to the use of multilevel cluster samples (plots and trees with a plot), and thus observations within the same level were correlated. In the ETPPRP plot establishment, an effort was made to cover various conditions across the region but to minimize within-plot variation, thus minimizing within-plot variance while maximizing between plot variance. Our results showed that more variation was found at the plot level than at the within-plot level for each model parameter, and this was particularly true for the H-D model, where the within-plot variation was negligible for all the parameters. Supporting our results, Reference [29] argued that only the between-plot variation was important in modeling H-D relationships for both pine species in east Texas. However, for the H- and D-A models, within-plot variation in the asymptote parameter was also important (Table 2 and Table 3). Biologically, the high variances of the random effects indicate that much of the variation was not explained by the fixed effects of the model. Incorporating stand and tree characteristics into the models can reduce plot-to-plot or within-plot variation, which is out of the scope of the study. The nonlinear mixed models in this study could be used to predict H or D, with or without using random effects. When the model with the estimated random effects is used, a subject-specific or localized H growth can be predicted [29]. Since the goal was to compare populations, random effects were not used in prediction, which may bias the prediction precision but would not change the conclusions.

The results of this study have significant scientific and practical significance for pine management in the western Gulf region. Growth potential is often a key determinant in species choice in reforestation. Unlike previous studies [1,2,3,4,5,6], this study used empirical modeling paired with mixed-modeling approaches, which allowed us not only to discern growth differences between the two pines and silvicultural phases but also showed the temporal patterns in the differences over stand development. The comparison in growth between silvicultural phases is new and is becoming an important topic with more advanced silviculture being practiced; to our knowledge, only one study [23] has investigated the topic. The results also have important implications on developing G&Y models. The results (Table 2, Table 3 and Table 4) indicate that a global model for both pines or for different silvicultural phases in the region may be inappropriate. Reference [10] developed a joint whole stand model system for both extensively and intensively managed loblolly pine plantations by using the combined data of the Phase I and II plots. The system included a global H-A model, without accounting for the potential differences between the phases. Based on our results, incorporating the differences in the H-A model between the phases into the system can further improve the model precision. Since 2010, more advanced silviculture measures, in particular the use of advanced genetics such as the deployment of elite families and clones [8], have been widely practiced in establishing and managing pine plantations, which will enhance the plantation productivity greatly. The ETPPRP is considering establishing its Phase III research plots in plantations established using more advanced silviculture and genetics. When data are available, it is important to test model differences among Phase I, II, and III plots, which, in addition to deepen understanding of their effects on growth, will provide important information in incorporating silviculture and genetics into G&Y modeling.

5. Conclusions

H-A, DBH-A, and H-DBH models for loblolly and slash pine in east Texas were successfully developed with model parameters specific for each species being provided (Table 2, Table 3 and Table 4). These models can be used as interim tools for growth and yield prediction in the region. Modeling results confirmed that planted slash pine grew faster, in particular in height growth, than loblolly pine. We recommend considering planting of slash pine in areas where fusiform rust and ice damage are not a high risk and/or when fusiform rust-resistant genotypes are available. For loblolly pine, intensive management greatly enhanced height growth relative to extensive management and thus shortened the rotation. Overall, comparisons between species or silvicultural measures are complicated and operational recommendations can only be made after a complete analysis involving survival, wood quality, and others factors, in addition to tree growth, is performed.