Abstract
The degree of mechanical reinforcement provided by plants depends upon its roots distribution in the soil and mechanical properties of the roots. The mechanical properties and distribution of root traits (root diameter and number) in the soil of the standing forest depends on the tree stem diameter. This variation of root traits with tree stem diameter is rarely investigated. Therefore, this research presents the effect of tree stem diameter on the distribution of roots within the standing forest of Cunninghamia in the Longchi forest area, Sichuan province, China. In this area, shallow landslides take place frequently. We investigated the root traits distribution for trees with different stem diameters, i.e., 220 mm, 320 mm, 450 mm, and 468 mm, to show the variation of roots distribution in the soil with stem diameter. The root architecture of the selected trees was studied by step excavation method of the root zone accompanied by measurement of roots physical parameters (roots number and roots diameter) and indices (roots area ratio (RAR), roots biomass (RB), and roots distribution (RD)). We measured the root’s maximum tensile strength by performing root tensile tests in the laboratory. The field and laboratory-measured data were used to estimate the root cohesion by both the commonly used model Wu and Waldron Model (WWM) and Fiber Bundle Model (FBM). The results indicate that the tree stem diameter correlates with both the root distribution and the tensile strength. The roots indices and root cohesion increase with an increase in the diameter of the tree. Further, RAR decreases with depth and lateral distance from the tree stem, while the maximum values were observed in 10 cm depth. The relationship between roots diameter and roots tensile strength is established through power function. The average root cohesion estimated for a tree with stem diameter 220 mm is 23 kPa, 29 kPa for 320 mm, 54 kPa for 450 mm, and 63 kPa for 460 mm. This effect of stem diameter on the increase of soil shear resistance should be considered while evaluating the stability of slopes in standing forests. The comparison between WWM and FBM for investigated species suggests that WWM estimates the cohesion values greater than FBM by 65%.
1. Introduction
The control of geological hazards, particularly soil erosion and slope instability, always remained challenging in hilly slopes. The 2620 globally recorded non-seismic landslides resulted in 32,322 deaths [1]. Petley [1] shows a substantial geological landslide disaster risk in mountainous regions. In 2015, global leadership restated the need for increased resilience to disaster risk as an integral part of a sustainable built environment through UN Sendai Framework for Disaster Risk Reduction and the Sustainable Development Goals (SDGs) [2,3]. The prevention of these geological disasters through conventional structures, which are steel, or concrete made, are mostly uneconomical and have an adverse effect on the environment. Because of these reasons, the soil bio-engineering measures, which are economically sustainable, are gaining popularity as a remedial measure for control of soil erosion and landslides preventions. The study on the role of plants as bioengineering measures has revealed that roots can enhance soil mechanical properties [4,5,6,7]. This enhancement of soil mechanical properties by roots depends on roots tensile strength, soil–roots interaction, roots spatial distribution, and soil cover [8,9,10]. Therefore, it is necessary to study the bio-engineering traits such as the spatial distribution of roots, roots length, and variation of roots indices (roots area ratio, roots distribution, roots biomass) with stem diameter to evaluate the bio-remedial measure performance of a species to control soil erosion and slope stability related hazards [6,11].
The fine and lateral roots provide mechanical reinforcement to the soil by intertwining and exerting traction on the soil mass, while in the case of thick and vertical roots, it is by acting like a soil nail [12]. It has been demonstrated in the literature that root architecture-related factors such as roots distribution (RD), root area ratio (RAR), roots number (RN), branching pattern, and also the maximum depth of the roots are having a significant impact on the improvement of soil shear strength properties [13,14,15,16]. These indices of the root system depend on the plant species, environmental conditions, and soil factors. The environmental factors and root physical properties (diameter, length, decay rate, orientation, and topology) significantly affect root tensile resistance [7].
Many researchers have investigated the role of forest plant roots in increasing soil shear resistance. Genet et al. [17] studied the role of tree age and spatial distribution of Cryptomeria japonica D. Don forest stands in the stability of slopes. The authors [17] reported that the root numbers are high for younger trees as compared to the older ones. However, the tensile strength of the younger tree roots is less than the root tensile strength of older trees. Genet et al. [17] also reported that trees’ stand structure has a significant effect on the stability of slopes. Fu et al. [18] studied the effect of roots architectural properties on the stability of the loess hill slope of Northeast Qinghai, China, and reported that the root architectural indices have a great impact on the shear strength of the loess. This study also concluded that with an increase in root indices (roots number, roots biomass, and roots area ratio), the shear strength of the soil increases. Wang et al. [19] studied the effect of the roots system biomechanical properties on the strength of soil with depth on the slope scale in the Bailong River Basin (Gansu Province, China) and concluded that the shear strength and stability of slope in geohazard prone areas could be improved with plant roots. Bischetti et al. [20] investigated the root cohesion of forest trees in the Italian Alpines region by performing field investigations and tensile tests on roots. It was concluded that there is great variability of root cohesion with site conditions (slope steepness, soil depth, fertility, etc.). Similarly, Moresi et al. [7] investigated the variability of roots biomechanical traits and root cohesion with soil depth and trees diversity in a Montane Mediterranean forest watershed. It was shown that roots cohesion and mechanical properties change both with tree species and depth. The conclusion of these studies is that roots mechanical reinforcement magnitude depends on the roots indices (RAR, RB, and RN), plant species, depth below the ground surface, and mechanical properties of the roots (roots tensile strength). The cited studies explained the role plant roots, tree age, and different species in enhancing the soil mechanical properties. However, the role of tree stem diameter for a standing forest is rarely investigated. Further, in slope stability of vegetated slope it is important to measure the roots diameter and number for RAR calculations and roots additional cohesion. For such estimation of roots number and roots diameter, the tree stem diameter can be an indicator to correlate the tree stem diameter with roots number/diameter distribution in the soil. Therefore, the variation of roots architectural indices and root cohesion with tree stem diameter should be studied.
In this study, the root distribution of stands of Cunninghamia is investigated, which plays a role in soil fixation in the Longchi forest area, Sichuan, China. This area has a history of a number of geological hazards, including shallow landslides and debris flows, due to which it is also referred to as a geological hazards museum [21,22]. This research examined four different stem diameters of standing Cunninghamia on the slope. The root’s physical parameters (roots diameters, roots numbers, and roots biomass) were measured in lateral and vertical directions. The investigation of the roots cohesion value of different stem diameter trees could improve our knowledge about the estimation of root reinforcement and design of the bio-geotechnical application in an effective way. Plant trees and site conditions have a significant impact on the biomechanical properties of root traits [23], while the site conditions represent the important property to be considered for modeling slope stability and landslide initializing process. The root cohesion value of the selected trees calculated from field and laboratory study can be used for estimation of root cohesion in similar areas and environments. The output of this research can be used for stability evaluation of forest trees vegetated slopes by adding the results in already available models such as an infinite slope SLIP4X [24]; the analytical 2D models [25,26], the infinite slope 3D model PRIMULA [27], and 3D limit equilibrium based model (3DTLE) [28]. This research will contribute to the stability analysis of vegetated slopes for standing forests. The standing forest trees have trees with different stem diameters. Therefore, while evaluating the stability of slopes having standing forests, the variation of root cohesion with tree diameter should be considered. Further, this research will help to design root reinforced soil samples for laboratory testing, i.e., RD, RB, and RAR can be used to decide the number of roots, biomass, or root area per fraction of the soil. Additionally, the output of this research will further push the idea of varying cohesion along with the lateral distance from the tree stem.
2. Materials and Methods
2.1. Study Area
The Longchi national forest (1829 m mean altitude, 31°8′29″ N, 103°34′30″ E), an ecosystem conservation region with a dense forest of subtropical alpines, is located at a 10 km distance from Dujiangyan city. It lies on the western border mountains of Sichuan Basin, the transition belt from Qingzang Plateau to Chengdu plain. This area’s climatic attributes belong to the semitropical moist region, with a mild climate and distinguishable 4 seasons [29]. This area faces abundant rainfall with an average annual rainfall of 1134.8 mm. The frequency of rainstorms in summers is high, with intense rainfall events for a short duration, and precipitation is mostly concentrated in the months from May to September [29]. The area also faces high incidences of geological hazards, while landslides with shallow failure are the most common geological hazards [17]. The study area has a thin soil layer over the bedrock. The thin soil layer is classified as dark brown clayey soil, whereas the bedrock mostly comprises of granites and diorites and Triassic rocks, which are constituted of mudstone and sandstone [30]. The observed depth of the rock at the location of tree diameter with 220 mm and 320 mm was 40 cm below the ground level, while the depth of bedrock at the location of tree diameter with 450 mm and 468 mm diameter was 50 cm below the ground level. Such shallow depth of bedrock was also consistent with the study of Genet et al. [17]. The field investigations were carried out during the month of August. Four different locations were selected for studying the distribution of the roots in the field (Figure 1).
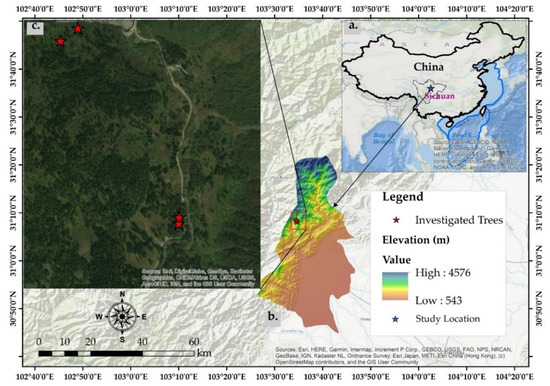
Figure 1.
Location details of the study area.
2.2. Selection of Trees and Roots Sampling
Cunninghamia is the major tree type for ecological restoration in southwest china [17] and is the dominant vegetation type in the current study area. Therefore, the distribution of the roots of Cunninghamia was investigated in the current study. Four (04) trees with different stem diameters were selected for roots zone excavation. The location and diameter at breast height (DBH, referred to as tree stem diameter in the manuscript) of each tree are given in Table 1. The main factors involved in the selection of trees were to be the same species, its distance from nearby trees, slope angle, and depth to bedrock/thickness of the clay layer. The selected 4 trees were qualifying at relatively far apart. The trees were selected such that their distance from nearby trees should be at least 3.0 m to reduce the effect of tree competition on the root system [31]. The distance of the nearest tree from the 220 mm diameter tree was 5.30 m, for 320 mm tree diameter this distance was 5.90 m, for the tree with diameter 450 mm it was 6.50 m, and for the tree with diameter 468 m it was 6.30 m. Prior to recording, the root geospatial distribution of the selected trees, 1 Cunninghamia tree root, was exposed by the excavation method to assess the roots distribution and roots distance from the tree stem. After the assessment of the roots, the geospatial distribution of the selected 4 trees was recorded. The roots were also collected for conducting roots tensile tests from the excavated zone with care to avoid any damage or stressing of roots. The roots selected were, where possible, straight with less tortuosity and having fewer numbers of branching points. The collected samples were sealed in bags, transported to the laboratory, and to maintain roots freshness, and all collected roots were stored in the refrigerator at 4 °C [32]. Soil samples from each tree locations were collected, ignoring the humus layer.

Table 1.
Description of investigated trees.
2.3. Soil Properties
The collected loess was 1st oven-dried for 24 h, and then sieved analysis was performed. After that, the physical properties, including density and Atterberg’s limits, were measured for the sieved sample. The Atterberg’s limit was determined by using the fall cone test method as per the procedure of GB/T50123 [33], which explains the plastic and the liquid limit for 2 mm and 17 mm penetration, respectively. The fall cone test apparatus consists of a cone penetrometer with a cone angle of 30o and a cone mass of 76 g. The soil density at field moisture content was determined by performing a modified Proctor’s test [34]. Further, the sieved sample’s grain size fraction was evaluated using a laser particle size analyzer. The gradation curve for soil samples is shown in Figure 2. The physical properties of the collected soil at the selected trees are given in Table 2. The average depth of the humus layer was 5 cm at the selected tree locations.
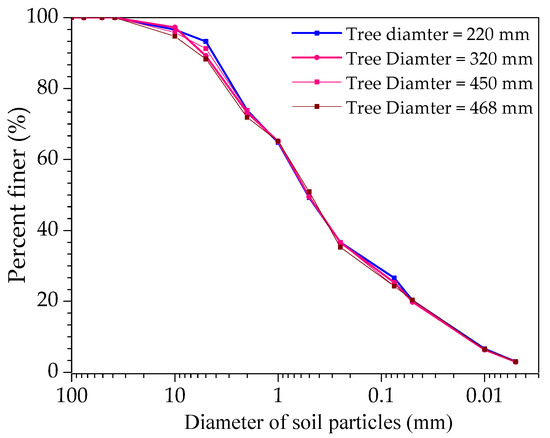
Figure 2.
Gradation curves for the collected loess samples.

Table 2.
Description of soil at the investigated tree locations.
2.4. Excavation Methodology and Measurement of Root Traits
The step-by-step excavation method was adopted in this research work, as recommended by Fu et al. [18]. The following steps were adopted in excavation and recording the roots architectural indices of the selected trees.
- The area under the crown of the candidate’s trees for excavation was properly cleaned. All the shrubs and other loose materials were removed.
- An excavation zone for each tree was established with a different diameter ranging between 2.70 m to 3.0 m (boundary marked with red color, Figure 3a).
 Figure 3. (a) Excavation zone marked on the ground with white chalk powder, (b) incremental excavation (depth of each increment (h) was 10 cm for each zone).
Figure 3. (a) Excavation zone marked on the ground with white chalk powder, (b) incremental excavation (depth of each increment (h) was 10 cm for each zone). - In each established zone, the space was divided into sub-zones in horizontal direction composed of various geometrical shapes, as proposed by Zhang et al. [35] and shown in Figure 3a (one subzone boundary is marked with green color).
- The sub-zones dimension was decided by ground slope conditions, tree stem diameter, and distribution of roots. On average, the length of one subzone in the horizontal direction was 20 cm. The excavation zones were carefully marked on the ground with white chalk powder.
- After marking the excavation area, incremental step by step excavation of the sub-zones was done both lateral and in the vertical direction. During excavation, the roots of the shrubs were removed with the excavated soil as the stem of all the shrubs were cut down during the surface cleaning process. Further, the texture of the roots facilitated us whether it belonged to the shrubs or selected tree.
- For each vertical excavation, 10 cm increments were selected below the ground surface until the roots maximum growth depth was reached. In each excavated zone, the roots, which were protruding from the vertical profile (a × h Figure 3b), were counted, and the diameter of each counted root was measured using a digital Vernier caliper. Only those roots were considered, which were in the cross-sectional area (a × h (Figure 3b)), assuming all these roots play a role in providing additional root cohesion. If a root was branched inside the excavated area, the branched roots were not counted, as only the roots crossing the cross-sectional area (a × h) will play a role in root cohesion at that profile [36]. From these roots counting and roots diameter, the roots area ( was calculated. This was used in equation −1 to calculate the roots area ratio (RAR). This calculation of RAR is consistent with the study of [7,18].
- Once the excavation for the vertical increment of 10 cm was completed, all the roots in this trench were cut down and properly bagged in plastic bags for roots biomass calculations before starting excavation for the next 10 cm in the same subzone.
- After excavation of the topsoil layer to a depth of 10 cm (Figure 3b), the next excavation was carried out 10 cm deeper with excavation in the lateral direction unchanged.
- For all the tree excavations, they were carried out in the upslope direction. The orientation of the tree roots was generally upslope and increased soil stability [37]. However, the trees developed different root architecture systems on different sides [38]; therefore, excavation was performed on the same side for all the trees for consistency in result comparison.
2.5. Developing Indices for Root Architectural System
This section introduces the indices that will be used to describe the architecture of the root. Root architecture can be described as the spatial distribution of the root indices [39]. Many variables can be used for defining the root architecture system, and these variables can be computed at different levels, such as root system level, individual root level, or root segment level. Reubens et al. [14] have given a detailed review of the roots structural characteristics that play a promising role in the stability of different slopes and reducing erosion process.
The different characteristics of the root system defined by Reubens et al. [14], some of these have been identified as having an important role in soil fixation, while others are considered rarely, but they are nevertheless promising. The relationship of root structure and soil mechanical reinforcement is currently based on root bulk characteristics such as RAR, RD, and RB. RAR is expressed as the portion of the effective soil cross-sectional area occupied by total roots cross-section [40] and given by the following equation.
where represents the diameter of the “i-th” root among the total number of n roots, dimensions a and h are shown in Figure 3b, where, for each trench excavation, is 10 cm While the roots area () is calculated using the number of roots counted and roots diameter measured, as discussed in Section 2.3. is represented in %. Further, we have counted all the roots but considered only the roots having a diameter smaller than 10 mm in the calculation of RAR [7,17].
RD can be defined as the total identified number of roots available in a volume fraction of the soil [17]. It can be estimated as:
where a, h, and b can be calculated, as shown in Figure 3b. RD can be expressed in roots/cm3.
RB is expressed as the fresh weight of the roots available in unit volume of the soil [17] and can be calculated as:
RB can be expressed in g/cm3.
2.6. Root Tensile Strength
The mechanical properties of roots have been evaluated by conducting root tensile tests. Before conducting tensile tests on the roots, synthetic resign reinforcement was applied to both ends of all the root samples, as proposed by Nilaweera and Nutalaya [41]. After the application of resin, roots were placed in a refrigerator for 48 h at 4 °C for resin hardening. This reinforcement of resin enabled the clamping device force to transfer in a better way for roots tensile strength testing without slipping and damaging the roots segment ends. Before the test performance, the diameter was measured at both ends and mid of the root using an electronic Vernier caliper with an accuracy of 1/50 mm. A total of 100 samples per tree diameter were used for tensile testing. The number of samples was selected in such a way that it should include each diameter of the root. Only straight roots and with no apparent defects were tested.
The roots tensile strength was determined using MTS Bionix® Servohydraulic Test Systems (MTS Systems Corporation, Eden Prairie, MN, USA) at Southwest Jiaotong University, Chengdu, China (Figure 4). The machine used 3 main systems to perform the test (1) generation of traction force by the hydraulic system, (2) displacement and load measurement, and (3) acquisition of data. All the roots were tested at a strain rate of 10 mm/min. During testing, some roots samples failed by pulling out from the resin reinforcement, and some failed near the clamps. Such results were discarded, and only those tests in which the sample break near the middle was accepted and used for data analysis. The average rate of success for tensile tests was 53%. The reason for such a low rate of success was the pull out of roots from the resin during tests, in addition to the breakage of the root near the clamp. As in some samples, the bond between the root and resin was not developed properly. Further, in some root samples, the resin was broken by the clamping system of the machine. Similar issues in root tensile testing were also reported by Nilaweera and Nutalaya [41] and Bischati et al. [20]. The maximum tensile force to break the root () was obtained from the test, while the tensile strength () was calculated as proposed by Bischetti et al. [20].
where is the root mean diameter.
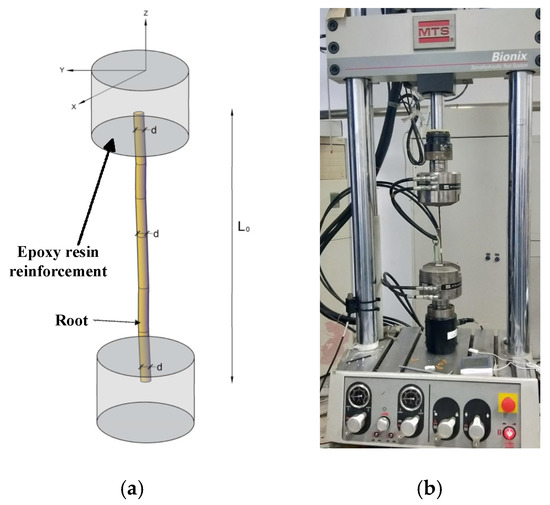
Figure 4.
Root sample and performance of the tensile test. (a) Casting of root terminals in synthetic resins. The tensile force of the root was measured in z-direction, d = root diameter measurement, L0 is the root initial length (b) MTS Bionix® Servohydraulic Test System used for performing the tensile test.
The power regression analysis was employed to develop the best-fitted relation between the diameter of roots and root tensile strength as given in Equation (5), and the same has been reported by many researchers [42,43]
where, and are the empirical constants, which vary from plant trees to trees, the constant represents a scaling factor while counts for the rate of decrease in strength. These constant plays a significant role in comparing the tensile strength among different plant trees.
2.7. Root Additional Cohesion
The increase in cohesion contributed by roots to the soil was estimated using both the FBM [16] and WWM [44]. These models were the most widely used models to estimate additional root cohesion. Both of these models were based on the assumption of roots breakage. WWM model assumed that the roots grew vertically and acted as cables such that during shearing of the soil, the load was transferred to roots [15]. Another assumption of this model was that the tensile strength of the root was fully mobilized to contributes to the shear strength of the soil by providing additional cohesion. The roots cohesion can be expressed as an additional cohesion to soil shear strength [44].
where, is the shear strength of the soil, is the shear strength of soil root composite (kPa). The shearing force results in deformation and stretching of the roots provided that sufficient interface friction, effective (anchorage) length, and confining stresses are available to prevent slipping or pull out of the roots [15]. The tensile forces that develop in the roots during shearing of the soil are calculated with the tangential component, which is resisting the shearing and normal components. This enhancement in shear strength of the soil results due to the full mobilization of the roots tensile strength can be expressed by [44]:
where is the shearing distortion angle of the shearing zone for root breakage, is the root tensile strength and is the angle of internal friction. The bracketed term can be replaced by the term k′ [15]. The value of k′ ranges from 1.1 to 1.3, while many authors have proposed a common value of 1.2 [44,45,46]. Therefore, the value for term k′ was also adopted as 1.2 for this study. Thus, the simplified form of Equation (7) can be expressed as,
The FBM is extensively recommended for calculating the root mechanical reinforcement. This model assumes apportioning of the load base on the root diameters. When the load exceeds a particular root diameter tensile strength, the model assumes redistribution of the load from the failed roots to the remaining intact roots. The model can be expressed as [16]:
where the index represents the root number arranged in the order of weakest to strongest , is the root, which will fail first and will be removed from the calculations. Where is the total stress, which will cause the failure of root j in the bundle of roots and represent the tensile strength of the weakest intact roots. This model assumes the equal distribution of load among the roots regardless of its dimensions.
2.8. Statistical Analysis
The statistical analysis of the data was carried out using SPSS software 18.0 (SPSS Inc., Chicago, IL, USA). The power-law regression analysis was carried out to find the correlation between root diameter and tensile strength. The values of adjusted R2 and p-value were calculated to show the goodness of fit, considering a significance level of 0.05. The Kolmogorov–Smirnov’s (K.-S.) test was applied to confirm the homogeneity and normality of the variance using a significance level of 0.05. The data of roots distribution, roots area ratio, roots biomass, and roots cohesion were analyzed using analysis of variance (ANOVA) tests with pairwise Tukey’s Studentized test to determine the variation between the selected trees according to distance from the tree and depth. To evaluate the differences in tensile strength of roots and the number of roots between the investigated trees, analysis of covariance (ANCOVA) with HSD (honestly significant difference) was applied. The values were presented as mean value ± standard error.
3. Results
3.1. Roots System and Spatial Distribution of Roots
The investigated species root system was VH (vertical and horizontal) as per the root classification system introduced by Yen [47]. The root system was classified based on field investigations. The observed depth of bedrock at the selected tree location was 0.4–0.5 m below the ground level in the study area. Such shallow depth of bedrock in the study area was also reported by Genet et al. [17]. Therefore, the roots of the investigated trees were concentrated in shallow depth. The results also showed that large variability exists in the distribution of the roots with the tree stem diameter.
The maximum observed penetration depth of roots for the tree with stem diameter 220 mm and 320 mm was 40 cm below the ground level and for trees with stem diameter 450 and 468 mm, it was 50 cm below the ground level. The observed lateral root length roots varied from 270 cm to 300 cm. The identified roots were classified on the bases of their diameters into different classes as (a) d ≤ 1 mm (b) 1 < d≤ 2 mm (c) 2 < d ≤ 5 mm (d) 5 < d ≤ 10 mm (e) 10 < d ≤ 20 mm (f) 20 mm ≤ d [48]. The variation of roots number and diameter, both with depth and distance from the tree stem, is shown in Figure 5 and Figure 6. The tree with a 468 mm stem diameter had a greater number of fine to medium roots (roots diameter <10 mm) (F = 7.62, p = 0.001, ANCOVA) than the other investigated trees with smaller stem diameters. Further, the ANOVA (Table 3) results suggested that the mean number of fine to medium roots varied significantly among the investigated trees, both with depth and with horizontal distance from the tree stem.
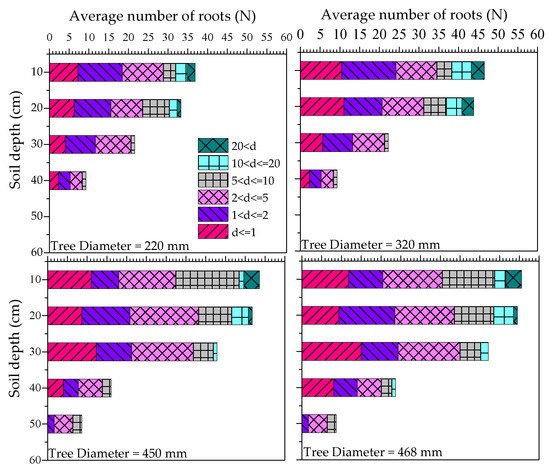
Figure 5.
Root distribution with depth (d = root diameter in mm).
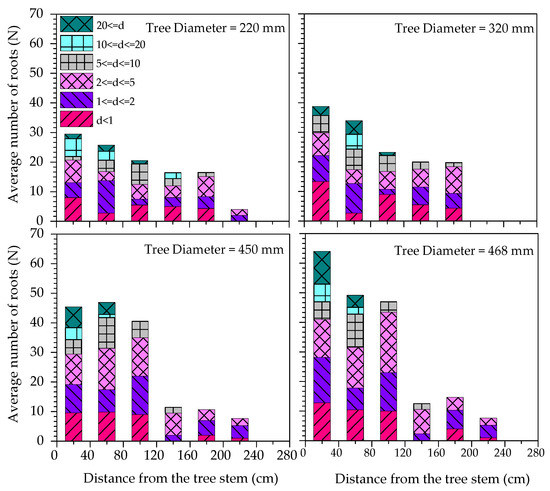
Figure 6.
Root distribution along with the horizontal distance from the tree stem (d = root diameter in mm).

Table 3.
ANOVA test results for roots diameter variation between investigated trees.
3.2. Distribution of Root Indices with Depth
In the established zones for excavation, root area ratio (RAR), roots density (RD), and root biomass (RB) were calculated with depth increments of 10 cm. Indices at particular depths intervals were calculated by taking an average of recorded roots in that interval for the entire lateral direction. The spatial distribution of roots indices and RB with depth is shown in Figure 7. These indices showed variation with stem diameter and were concentrated in the top 20 cm and then decreased rapidly after this depth. The mean RAR varied significantly among the investigated trees (F = 2.373, p = 0.118, ANOVA) and with regard to depth (F = 34.042, p < 0.001, ANOVA). The mean RD also showed significant variation (F = 25.536, p < 0.001, ANOVA) with tree diameter and with depth (F = 34.298, p < 0.001, ANOVA). Similar variation for RB (F = 15.074, p < 0.001, ANOVA) with tree stem diameter and depth was (F = 64.087, p < 0.001, ANOVA) observed.
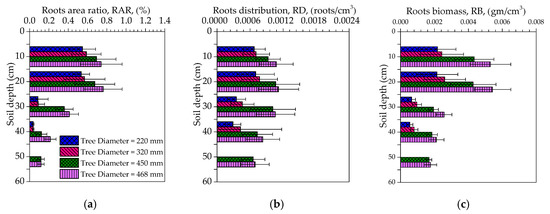
Figure 7.
Variation of roots indices with depth (a) roots area ratio (RAR) (b) roots distribution (RD), and (c) roots biomass (RB).
RAR value in the first layer (0–10 cm) ranged from 0.74% (tree stem diameter = 468 mm) to 0.55% (tree stem diameter = 220 mm), in the second layer (10–20 cm) this value ranged from 0.76% (tree stem diameter = 468 mm) to 0.53% (tree stem diameter = 220 mm), in the third layer (20–30 cm) this ranged from 0.41% (tree stem diameter = 468 mm) to 0.09% (tree stem diameter = 220 mm), in the fourth layer (30–40 cm) this ranged from 0.21% (tree stem diameter = 468 mm) to 0.12% (stem diameter = 220 mm) tree, while in the deepest layer (40–50 cm), this value was 0.12% (tree stem diameter = 450 mm). The variability of roots distribution (RD) with stem diameter was also prominent; the root system was more concentrated in the top 10 cm. In this context the range of roots distribution in the first layer (0–10 cm) was 0.00108 roots/cm3 (tree stem diameter = 468 mm) to 0.00068 roots/cm3 (tree stem diameter = 220 mm), in the second layer (20–30 cm) this value ranged from 0.0012 roots/cm3 (tree stem diameter = 468 mm) to 0.0007 roots/cm3 (tree stem diameter = 220 mm); in the third layer (20–30 cm) this value was from 0.0011 roots/cm3 (tree stem diameter = 468 mm) to 0.0004 roots/cm3 (tree stem diameter = 220 mm), in the fourth layer (30–40 cm) this value ranged from 0.00083 roots/cm3 (tree stem diameter = 468 mm) to 0.0005 roots/cm3 (tree stem diameter = 450 mm), while in the deepest layer (40–50 mm) this value was 0.0007 roots/cm3 (tree stem diameter = 450 mm). Similarly, the variability of roots biomass along with depth was also quite large. The RB was more in the top 10 cm, and after that, the decrease of biomass for all investigated trees was significant. The value of maximum biomass was observed as 0.0049 g/cm3 (tree stem diameter = 468 mm).
3.3. Distribution of Root Indices with Horizontal Distance from the Tree Stem
The roots architectural indices with horizontal distance from the stem of the tree were investigated, and equivalent plots are shown in Figure 8. Indices at a certain horizontal distance from the tree stem were calculated by taking an average of recorded roots in that distance for the entire depth. The roots architectural indices and biomass for all investigated trees, with approximately 80% and 70%, existed in the lateral distance of 0–60 cm; first, it increased with distance and decreased with variations.
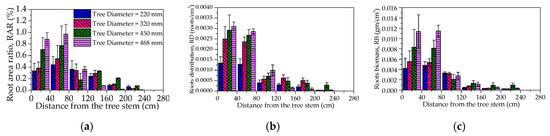
Figure 8.
Variation of roots indices with lateral distance from the tree stem (a) RAR (b) RD, and (c) RB.
RD of all investigated trees showed a mild decrease in the first 50 cm from the tree stem. After that, it decreased systemically with distance from the tree. The maximum percentage of root biomass for all investigated trees was concentrated in the first 50 cm; after that, root biomass decreased rapidly to 100 cm, and then it showed a systemic pattern in the decrease of roots biomass.
3.4. Root Tensile Strength
The tensile tests were carried out on roots samples having a diameter range between 0.76 mm to 9.8 mm for the 320 mm diameter tree, 0.50 mm to 9.81 for 320 mm diameter tree, 0.60 mm to 9.98 mm for 450 mm tree diameter, and 0.67 mm to 8.53 mm for 468 mm tree diameter. The root tensile strength was different among the investigated trees (F = 104.86, p < 0.001, ANCOVA) (root diameter as a covariate). The relation between tensile strength (tr) and root diameter is shown in Figure 9. The mean root tensile strength for 220 mm diameter tree was 11.8 ± 2.1 MPa, for 320 mm diameter tree was 14.1 ± 2.4 MPa, for 450 mm diameter tree was 15.9 ± 2 MPa, and for 468 mm diameter tree was 19.9 ± 2.2 MPa. A significant decrease was observed in the tensile strength of the roots with an increasing root diameter (Table 4), such as from 40 MPa (0.76 mm diameter root) to 3 MPa (9.98 mm diameter root) for 220 mm tree diameter, 107 MPa (0.5 mm diameter root) to 3 MPa (9.81 mm diameter root) for 320 mm tree diameter, 77 MPa (0.6 mm root diameter) to 5 MPa (9.98 mm root diameter) for 450 mm diameter tree, 70 MPa (0.67 mm root diameter) to 6 MPa (8.53 mm root diameter) for 468 mm diameter tree. The observed relationship attributes to the variation in the structure of the roots because coarse roots have relatively less cellulose content per unit mass compared to fine roots [49].
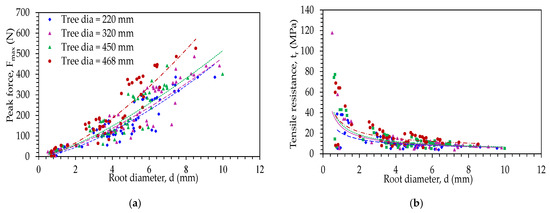
Figure 9.
Roots tensile test results with power fit functions (a) Fmax and d (b) tr and d.

Table 4.
Statistical values of the roots tested and roots tensile strength.
The coefficient of correlations developed for the investigate trees given in Equation (5) are shown in Table 5. The developed correlation was tr = 20.369d−0.522 (R2 = 0.37, p < 0.001) for 220 mm diameter tree, tr = 26.47d−0.636 (R2 = 0.47, p < 0.001) for 320 mm diameter tree, tr = 28.933d−0.644 (R2 = 0.52, p < 0.001) for 450 mm diameter tree and tr = 30.639d−0.522 (R2 = 0.36, p < 0.001) for 468 mm diameter tree. The maximum tensile force (Fmax) obtained from the tensile test showed the trend of increase with increasing root diameter. The power-law regression method was used for fitting the positive correlation between Fmax and root diameter (d), which gives Fmax = 18.89d1.3644 (R2 = 0.80, p < 0.001) for 220 mm diameter tree, Fmax = 15.98d1.4776 (R2 = 0.82, p <0.001) for 320 mm diameter tree, Fmax = 22.71d1.3588 (R2 = 0.83, p < 0.001) for 450 mm diameter tree and Fmax = 24.05d1.4775 (R2 = 0.81, p < 0.001) for 468 mm diameter tree. The roots tensile data and correlation developed showed that increase in tree stem diameter from 220 mm to 468 mm resulted in an average increase in root tensile resistance of 33%.

Table 5.
The power-law functions coefficients for tensile strength and tensile for with co-efficient of correlation.
3.5. Variation of Root Cohesion with Depth
In this study, the root cohesion was calculated using WWM and FBM, which has been used by many authors [15,48,49,50,51,52]. The results exhibited high variability in root cohesion for the investigated trees (Figure 10). The root cohesion varied significantly with tree diameter (F = 9.80, p < 0.001, ANOVA) and also with depth (F = 105.722, p < 0.001, ANOVA). The maximum value of cr was observed in the top 20 cm layer. Below this depth, the cr value decreased with the depth significantly. This decline in cr with depth and stem diameter was also reported by other studies [4,20,23,53,54].
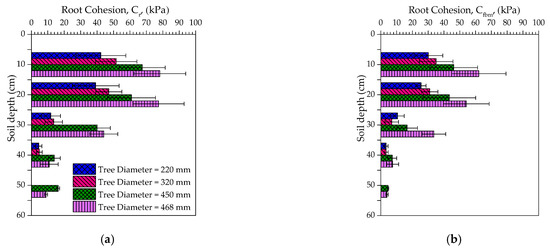
Figure 10.
Variation of the root cohesion with depth (a) Wu and Waldron Model (WWM) (cr) (b) Fiber Bundle Model (FBM)(cfbm).
The range for maximum roots cohesion (cr) value in the first layer (0–10 cm) for the selected trees was observed as 78 KPa (tree stem diameter = 468 mm) to 42 kPa (tree stem diameter = 220 mm), while this value in the second layer (10–20 cm) ranged from 77 kPa (tree stem diameter = 468 mm) to 39 kPa (tree stem diameter = 220 mm), in the third layer (20–30 cm) this ranged from 44 kPa (tree stem diameter = 468 mm) to 12 kPa (tree stem diameter = 220 mm), in the fourth layer (30–40 cm) it was 14 kPa (tree stem diameter = 468 mm) to 5 kPa (tree stem diameter = 220 mm), while in the deepest layer (40–50 cm) it was from 16 kPa (tree stem diameter = 468 mm) to 9 kPa (tree stem diameter = 450 mm).
The ratio between root cohesion calculated using WWM and FBM is given in Table 6. This suggests that WWM overestimated the root cohesion by 65%.

Table 6.
Roots cohesion values for investigated species and ratio between WWM and FBM.
3.6. Variation of Root Cohesion with Horizontal Distance from the Tree Stem
The root cohesion estimated by both WWM (cr) and FBM (cfbm), showed a decrease significantly with the distance from the tree stem (Figure 11). The value of the root cohesion was high in the lateral distance of 60 cm from the tree stem, and after that, this value decreased significantly. The average maximum value of root cohesion for the tree with a stem diameter of 468 cm was 155 kPa at a distance of 20 cm, for the tree with a stem diameter of 450 mm, this value was 118 kPa at a distance of 60 cm, while for the tree with a stem diameter of 320 mm this value was 61 kPa at a distance of 20 cm, for a tree with a stem diameter of 220 mm was 42 kPa, and after that, it decreased systemically for all investigated trees.
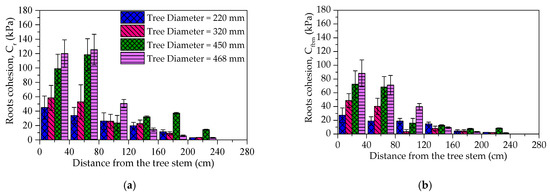
Figure 11.
Distribution of root cohesion with horizontal distance from stem of the tree (a) WWM (b) FBM.
4. Discussion
4.1. Roots Traits and Architectural Indices
The study through the field investigation reveals that the root architecture of the investigated species is the VH type. Many studies recommend the trees with such root architecture for slope stabilization [55,56]. In this study, the spatial distribution of roots architectural indices (RAR. RD, and RB) for the selected trees were investigated, and assessment was done both in the horizontal and vertical. This study investigated the distribution of the roots in the upslope direction because the roots mostly grow in the upslope direction to provide stability to the soil [37]. The upslope grown roots also provide good anchorage to the slope compared to roots on the downslope direction [57]. Wang et al. [36] also showed that the additional cohesion provided by the roots was almost the same on different slope directions of the tree. Further, Genet et al. [17] reported that a significant difference was not observed in RD measured in a different direction around the same tree. However, the different active mechanical forces on the slope may cause the tree to develop an asymmetrical root architectural system [58]. Additionally, studies have revealed that root architecture indices differ with slope steepness and specific to species [59]. Therefore, this study is specific to the investigated species, climatic condition, and roots investigation in the upslope direction. Our field investigation indicates that the selected tree’s root zone was located in a vertical direction ranging between 40 cm to 50 cm depth, while in the lateral distance from the tree stem, it ranged between 270 cm and 300 cm. This range of root zone was consistent to that reported by Genet et al. [17] for the same environmental conditions. The possible reason for such a shallow root zone may be due to shallow bedrock in the study area. The maximum depth of the roots depends on the interaction among structures of the soil, soil zone saturation, precipitation, and tree competition [60]. A natural obstacle like stone bedrock can also dramatically affect the root’s architectural characteristics [61]. Stability to trees with such root architecture is provided by the lateral spread of roots, which resists the uprooting of the tree [62].
The investigated tree showed significant variability in diameter classes of roots. In addition, a tree with a large diameter has more fine roots than a tree with a smaller diameter. Additionally, Figure 4 shows that the upper layer (0–10 cm) has more fine roots than the relatively deeper layer. This greater number of fine roots in the top 10 cm layer may attribute to better moisture content, aeration, and nutrient level [63]. The physical properties of the soil at the locations of investigated trees are comparable. However, the nutrient level plays a significant role in the distribution of the roots [64]. We have not evaluated the role of nutrients at the location of the selected trees; therefore, this may result in different results for different locations.
The study of the spatial distribution of roots architectural indices (RAR, RD, and RB) is important to scale the mechanical reinforcement of roots. This study reveals that significant variability in roots indices occurred between the investigated trees. The average values of the indices for the investigated trees are shown in Figure 12. The presented results are for the selected species in the standing forest of Longchi forest with shallow bedrock. We found that roots indices increase with an increase in tree diameter. The results also show that this increase in average roots indices is more prominent when the tree diameter increases from 220 mm to 320 mm. We also observed that most of the biomass for all the investigated trees were located in the top 20 cm. After this depth, the roots indices decrease. While in the lateral direction, most of the biomass is concentrated in the 100 cm length. After that, the roots biomass decrease. The decrease in roots biomass with depth is reported by many studies. This decrease of RAR with depth could be attributed to decreased nutrients and other biological status, coupled with soil impedance increase [62]. The RAR values calculated in this research are higher than those published by Genet et al. [17], who studied comparable species. The difference in RAR could attribute to the difference in soil and environmental growth condition of the tree [65]. Further, sampling methodology also plays a significant role in the calculation of RAR.
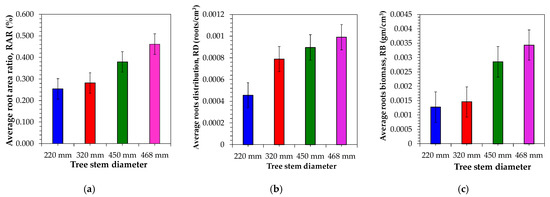
Figure 12.
Variation of roots indices with tree stem diameter (a) RAR (b) RD (c) RB.
4.2. Roots Tensile Strength
In total, we tested 100 representative roots per diameter class for tensile strength. In general, the increase in the root diameter results in a decrease in root tensile strength. However, the roots of the same diameter collected from different tree stem diameters have different tensile strength. For the same diameter root, an increase in tree diameter results in an increase of tensile strength. This variability of tensile strength can arise from many factors, including soil, root age, root structure, or root bark [66]. However, further study is suggested on roots cross-section/cellulose contents at the microscopic level to investigate this increase of roots tensile strength with tree diameter. The tensile test results confirmed that a power relationship exists between the roots tensile strength and root diameter. This relationship has been validated by many authors [13,20], while from the chemical perspective, the influence of root diameter on the tensile strength of roots has been evaluated by Baets et al. [15]. The values of tensile strength calculated for the selected trees lie in the ranges reported by other researchers for trees [20,67,68,69,70]. However, in the reported literature, there is significant variability in the root tensile strength for most of the investigated trees [71]. This variability can arise from different environmental conditions for growing [72], which includes the moisture contents of the soil and other physical characteristics, and factors like roots preservation methods prior to conducting the tests, the time passed before testing, and differences in machines used to conduct tensile strength tests [20]. This further highlights the importance of research on the native species at local environment.
4.3. Roots Cohesion
The root cohesion is calculated using the model suggested by Wu et al. [44] and the Fiber Bundle Model proposed by [16]. In the Wu and Waldron model, the values of coefficients k″ and k′ as given in equation 7 play a crucial role in the calculation of root cohesion. Many researchers have suggested assuming the value for k″ much smaller than 1.0, significantly affecting the root reinforcement value [13,73]. Moreover, the spatial distribution of RAR plays a significant role in the estimation of root cohesion, although some differences can be related to the dependency on the tensile strength of root and distribution of root diameter [50]. In general, the estimated values of root cohesion are higher in the topsoil layer and near the tress stem. Considerable variability is observed in the estimated roots cohesion with the tree stem diameter (Figure 13). The estimated average cr values in this study are consistent with those reported by Genet et al. [17] and Moresi et al. [7], but higher than the mean values reported by other authors, estimated by using the same methodology [5,74,75]. Nevertheless, Schmidt et al. [23] observed that the mean cr could be high as 100 kPa due to lateral roots for natural forests having a RAR value between 0.001 to 0.1%. Overestimation is also involved in RAR estimation since all the roots were considered orientated perpendicularly to the soil shearing zone. However, it does not represent the realistic conditions of the field. It is very important to take orientation into account. Moreover, this influence is against safety and, therefore, of primordial importance. Since laboratory investigations have revealed that reinforcement provided by perpendicularly orientated fibers to the shearing zone can be compared to that provided by fiber randomly orientated [76]. The range of roots diameter plays an important role in the calculation of RAR, which differs from study to study. More explanation regarding the higher value of cr is the assumption of the WWM model that during shearing of the soil, the tensile strength of the roots is fully mobilized, and roots failure occurs at breaking at once. In actual conditions, during shearing of soil root composite, roots break progressively because of having different tensile strength [16,75].
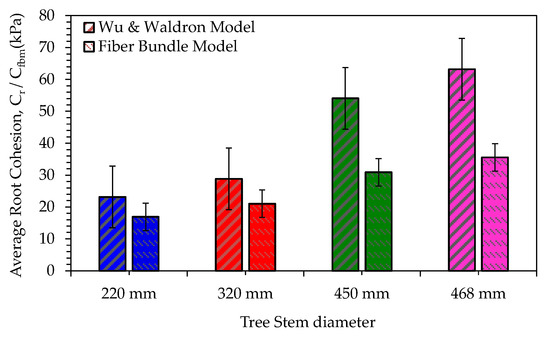
Figure 13.
Variation of average root cohesion with tree diameter.
The comparison of root cohesion values estimated in our research by FBM and WWM indicates that WWM gives higher root cohesion values than FBM. Similar observations are also reported by other studies [20,52]. The ratio between cfbm and cr range between 0.28 to 0.75.
5. Conclusions
In this study, we have demonstrated the role of stem diameter in providing root cohesion to the soil through field investigations, laboratory testing, and performing statistical analysis. Information about the variation of bio-engineering roots traits with a stem diameter of stand forest is important to understand the efficiency of stand forests in providing resistance against erosion and slope stability related failures. We have investigated the root system of Cunninghamia and the variation of roots indices with tree diameter. The following conclusions are drawn from the current study;
- The tree stem diameter is having a significant impact on the roots indices and root cohesion. The roots indices and root cohesion increase with an increase in tree diameter.
- The tree diameter governs the average root cohesion estimated for the investigated trees. The variation of stem diameter from 220 mm to 460 mm results in increased cohesion from 23 kPa to 63 kPa.
- The maximum depth and lateral distance of the root system for the investigated tree are 50 cm and 300 cm, respectively.
- The values of roots architectural indices are significantly higher in the topsoil depth range (0–20 cm) of the root zone and near to the tree stem in the lateral distance range (0–100 cm).
- Root cohesion estimated by FBM shows the same trend of decrease as that of WWM. However, FBM estimated that cohesion values were less than that of WWM values by the reduction factor of 0.55–0.79.
- The tree with a large stem diameter has more number of fine to medium roots (roots diameter <10 mm) than a tree with smaller stem diameter.
- The same diameter roots class of trees with large stem diameter is having more tensile strength as compared to trees with a smaller diameter. The increase in tree diameter from 220 mm to 468 mm diameter results in the increase of roots tensile strength by 33%.
The results could significantly improve the understanding of the implementation of ecological measures for natural hazards prevention. Further studies are warranted to elucidate the impact of tree position with different stem diameters on the slope and hydrological root reinforcement to the soil. Also, in this study, it is not possible to evaluate the direction of the roots, which is a key parameter regarding soil reinforcement in slope stability. Therefore, future research is warranted to develop the root orientation architectural model. Additionally, the conclusion of this research is drawn based on root zone excavation in the upslope direction. Moreover, the output of this research can be incorporated in slope stability models, provides new areas for research, especially by incorporating the root cohesion combined with the root’s architectural indices and variation of indices with tree stem diameter, in modeling stability of vegetated mountain slopes.
Author Contributions
Conceptualization, A.M. and Y.-J.J.; methodology A.M. and J.-J.L.; software, A.M. and S.S.; investigation A.M., Y.-J.J., and J.-J.L.; formal analysis, A.M., Y.-J.J., and R.M.; data curation, S.S. and L.-J.S.; writing—original draft preparation, A.M., Y.-J.J., and S.S.; writing—review and editing, Y.-J.J. and L.-J.S.; R.M., supervision, Y.-J.J.; project administration, Y.-J.J.; funding acquisition, Y.-J.J. and L.-J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 41761144077) and the Strategic Priority Research Program of the Chinese Academy of Science (grant number XDA 23090202).
Acknowledgments
The authors acknowledge the CAS Pioneer Hundred Talents Program and Southwest Jiaotong University. We used the device of Southwest Jiaotong University for roots tensile test. We are also thankful to Sofia Das for her critical review of the first paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- UN. Sendai Framework for Disaster Risk Reduction 2015–2030; UN: New York, NY, USA, 2015; Available online: http://www.preventionweb.net/files/43291_sendaiframeworkfordrren.pdf (accessed on 5 August 2020).
- UN. Transforming Our World: The 2030 Agenda for Sustainable Development; UN A/RES/70/1; UN: New York, NY, USA, 2015; Available online: https://sustainabledevelopment.un.org/post2015/transformingourworld/publication (accessed on 5 August 2020).
- Wu, T. Slope stabilization. In Slope Stabilization and Erosion Control: A Bioengineering Approach; Morgan, R.P.C., Rickson, R.J., Eds.; E&FN Spon: London, UK, 1995; pp. 233–281. [Google Scholar]
- Van Beek, L.P.H.; Wint, J.; Cammeraat, E.L.H.; Edwards, J.P. Observation and Simulation of Root Reinforcement on Abandoned Mediterranean Slopes. Plant Soil 2005, 278, 55–74. [Google Scholar] [CrossRef]
- Stokes, A.; Atger, C.; Bengough, A.G.; Fourcaud, T.; Sidle, R.C. Desirable plant root traits for protecting natural and engineered slopes against landslides. Plant Soil 2009, 324, 1–30. [Google Scholar] [CrossRef]
- Moresi, F.V.; Maesano, M.; Matteucci, G.; Romagnoli, M.; Sidle, R.C.; Mugnozza, G.S. Root Biomechanical Traits in a Montane Mediterranean Forest Watershed: Variations with Species Diversity and Soil Depth. Forests 2019, 10, 341. [Google Scholar] [CrossRef]
- Stokes, A.; Douglas, G.B.; Fourcaud, T.; Giadrossich, F.; Gillies, C.; Hubble, T.; Kim, J.H.; Loades, K.W.; Mao, Z.; McIvor, I.R.; et al. Ecological mitigation of hillslope instability: Ten key issues facing researchers and practitioners. Plant Soil 2014, 377, 1–23. [Google Scholar] [CrossRef]
- Giadrossich, F.; Cohen, D.; Schwarz, M.; Seddaiu, G.; Contran, N.; Lubino, M.; Valdés-Rodríguez, O.A.; Niedda, M.; Valdés-Rodrŕguez, O.A. Modeling bio-engineering traits of Jatropha curcas L. Ecol. Eng. 2016, 89, 40–48. [Google Scholar] [CrossRef]
- Graf, F.; Frei, M. Soil aggregate stability related to soil density, root length, and mycorrhiza using site-specific Alnus incana and Melanogaster variegatus s.l. Ecol. Eng. 2013, 57, 314–323. [Google Scholar] [CrossRef]
- Lozanova, L.; Zhiyanski, M.; Vanguelova, E.; Bratanova-Doncheva, S.; Marinov, M.; Lazarova, S. Dynamics and Vertical Distribution of Roots in European Beech Forests and Douglas Fir Plantations in Bulgaria. Forests 2019, 10, 1123. [Google Scholar] [CrossRef]
- Świtała, B.M.; Wu, W. Numerical modelling of rainfall-induced instability of vegetated slopes. Géotechnique 2018, 68, 481–491. [Google Scholar] [CrossRef]
- Waldron, L.; Dakessian, S. Soil reinforcement by roots: Calculation of increased soil shear resistance from root properties. Soil Sci. 1981, 132, 427–435. [Google Scholar] [CrossRef]
- Reubens, B.; Poesen, J.; Danjon, F.; Geudens, G.; Muys, B. The role of fine and coarse roots in shallow slope stability and soil erosion control with a focus on root system architecture: A review. Trees 2007, 21, 385–402. [Google Scholar] [CrossRef]
- De Baets, S.; Poesen, J.; Reubens, B.; Wemans, K.; De Baerdemaeker, J.; Muys, B. Root tensile strength and root distribution of typical Mediterranean plant species and their contribution to soil shear strength. Plant Soil 2008, 305, 207–226. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Genet, M.; Kokutse, N.; Stokes, A.; Fourcaud, T.; Cai, X.; Ji, J.; Mickovski, S. Root reinforcement in plantations of Cryptomeria japonica D. Don: Effect of tree age and stand structure on slope stability. For. Ecol. Manag. 2008, 256, 1517–1526. [Google Scholar] [CrossRef]
- Fu, J.-T.; Hu, X.-S.; Brierley, G.; Qiao, N.; Yu, Q.-Q.; Lu, H.-J.; Li, G.-R.; Zhu, H.-L. The influence of plant root system architectural properties upon the stability of loess hillslopes, Northeast Qinghai, China. J. Mt. Sci. 2016, 13, 785–801. [Google Scholar] [CrossRef]
- Wang, X.; Hong, M.-M.; Huang, Z.; Zhao, Y.-F.; Ou, Y.-S.; Jia, H.-X.; Li, J. Biomechanical properties of plant root systems and their ability to stabilize slopes in geohazard-prone regions. Soil Tillage Res. 2019, 189, 148–157. [Google Scholar] [CrossRef]
- Bischetti, G.B.; Chiaradia, E.A.; Epis, T.; Morlotti, E. Root cohesion of forest species in the Italian Alps. Plant Soil 2009, 324, 71–89. [Google Scholar] [CrossRef]
- Wang, G.-X. Key technique in landslide control and its handling measures. Yanshilixue Yu Gongcheng Xuebao Chin. J. Rock Mech. Eng. 2005, 24, 3818–3827. [Google Scholar]
- Zhang, B.; Zhang, S.; Zhou, W. Investigation and assessment of landslides and debris flows in Sichuan province of China by remote sensing technique. Chin. Geogr. Sci. 2006, 16, 223–228. [Google Scholar] [CrossRef]
- Schmidt, K.; Roering, J.; Stock, J.; Dietrich, W.; Montgomery, D.; Schaub, T. The variability of root cohesion as an influence on shallow landslide susceptibility in the Oregon Coast Range. Can. Geotech. J. 2001, 38, 995–1024. [Google Scholar] [CrossRef]
- Greenwood, J.R. SLIP4EX—A Program for Routine Slope Stability Analysis to Include the Effects of Vegetation, Reinforcement and Hydrological Changes. Geotech. Geol. Eng. 2006, 24, 449–465. [Google Scholar] [CrossRef]
- Chiaradia, E.A.; Vergani, C.; Bischetti, G.B. Evaluation of the effects of three European forest types on slope stability by field and probabilistic analyses and their implications for forest management. For. Ecol. Manag. 2016, 370, 114–129. [Google Scholar] [CrossRef]
- Dietrich, W.; McKean, J.; Bellugi, D.; Perron, T. The prediction of shallow landslide location and size using a multidimensional landslide analysis in a digital terrain model. In Proceedings of the Fourth International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment (DFHM-4), Chengdu, China, 10–13 September 2007; Chen, C.L., Major, J.J., Eds.; IOS Press: Amsterdam, The Netherlands, 2007. 12p. [Google Scholar]
- Hess, D.M.; Leshchinsky, B.A.; Bunn, M.; Mason, H.B.; Olsen, M.J. A simplified three-dimensional shallow landslide susceptibility framework considering topography and seismicity. Landslides 2017, 14, 1677–1697. [Google Scholar] [CrossRef]
- Milledge, D.; Bellugi, D.; Mckean, J.A.; Densmore, A.L.; Dietrich, W.E. A multidimensional stability model for predicting shallow landslide size and shape across landscapes. J. Geophys. Res. Earth Surf. 2014, 119, 2481–2504. [Google Scholar] [CrossRef]
- Ma, Y.; Li, C. Research on the Debris Flow Hazards after the Wenchuan Earthquake in Bayi Gully, Longchi, Dujiangyan, Sichuan Province, China. In Proceedings of the 2017 International Conference on Advanced Materials Science and Civil Engineering (AMSCE 2017), Phuket, Thailand, 21–22 April 2017. [Google Scholar]
- Chang, M.; Tang, C.; Zhang, D.-D.; Ma, G.-C. Debris flow susceptibility assessment using a probabilistic approach: A case study in the Longchi area, Sichuan province, China. J. Mt. Sci. 2014, 11, 1001–1014. [Google Scholar] [CrossRef]
- Coomes, D.A.; Grubb, P.J. Impacts of root competition in forests and woodlands: A theoretical framework and review of experiments. Ecol. Monogr. 2000, 70, 171–207. [Google Scholar] [CrossRef]
- Zhang, C.-B.; Chen, L.-H.; Liu, Y.-P.; Ji, X.; Liu, X.-P. Triaxial compression test of soil–root composites to evaluate influence of roots on soil shear strength. Ecol. Eng. 2010, 36, 19–26. [Google Scholar] [CrossRef]
- GB/T50123 Standard for Soil Test Method; Ministry of Construction, P.R. China: Beijing, China, 2019. (In Chinese)
- Method C. In ASTM D1557; ASTM: West Conshohocken, PA, USA, 1991.
- Zhang, D.; Cheng, J.; Liu, Y.; Zhang, H.; Ma, L.; Mei, X.; Sun, Y. Spatio-Temporal Dynamic Architecture of Living Brush Mattress: Root System and Soil Shear Strength in Riverbanks. Forests 2018, 9, 493. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, M.; Meng, X.; Chen, G.; Zeng, R.; Yang, Q.; Liu, Y.; Wang, B. Evaluation of the Effects of Forest on Slope Stability and Its Implications for Forest Management: A Case Study of Bailong River Basin, China. Sustainability 2020, 12, 6655. [Google Scholar] [CrossRef]
- Yamadera, Y. Shizen Kankyou wo Saisei Suru Midori no Gizyutsu; Nougyoudoboku Jigyou Kyoukai: Tokyo, Japan, 1993; Volume 85. [Google Scholar]
- Nicoll, B.; Berthier, S.; Achim, A.; Gouskou, K.; Danjon, F.; Van Beek, L.P.H. The architecture of Picea sitchensis structural root systems on horizontal and sloping terrain. Trees 2006, 20, 701–712. [Google Scholar] [CrossRef]
- Gregory, P. Roots: Growth, Activity and Interactions with Soils; Wiley-Blackwell Press: Hoboken, NJ, USA, 2006. [Google Scholar]
- Gray, D.H.; Leiser, A.T. Biotechnical Slope Protection and Erosion Control; Van Nostrand Reinhold Company Inc.: New York, NY, USA, 1982. [Google Scholar]
- Nilaweera, N.S.; Nutalaya, P. Role of tree roots in slope stabilisation. Bull. Eng. Geol. Environ. 1999, 57, 337–342. [Google Scholar] [CrossRef]
- Bischetti, G.; Bonfanti, F.; Greppi, M. Misura della resistenza alla trazione delle radici: Apparato sperimentale e metodologia d’analisi. Quad. Idronomia Mont. 2003, 21, 349–360. [Google Scholar]
- Operstein, V.; Frydman, S. The influence of vegetation on soil strength. Proc. Inst. Civ. Eng. Ground Improv. 2000, 4, 81–89. [Google Scholar] [CrossRef]
- Wu, T.H.; McKinnell III, W.P.; Swanston, D.N. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Waldron, L.J. The Shear Resistance of Root-Permeated Homogeneous and Stratified Soil. Soil Sci. Soc. Am. J. 1977, 41, 843–849. [Google Scholar] [CrossRef]
- Burylo, M.; Hudek, C.; Rey, F. Soil reinforcement by the roots of six dominant species on eroded mountainous marly slopes (Southern Alps, France). Catena 2011, 84, 70–78. [Google Scholar] [CrossRef]
- Yen, C. Tree root patterns and erosion control. In Proceedings of the International Workshop on Soil Erosion and Its Countermeasures, Chiang Mai, Thailand, 11–19 November 1984; Soil and Water Conservation Society of Thailand: Bangkok, Thailand, 1987; pp. 92–111. [Google Scholar]
- Böhm, W. Root parameters and their measurement. In Methods of Studying Root Systems; Springer: Berlin/Heidelberg, Germany, 1979; pp. 125–138. [Google Scholar]
- Genet, M.; Stokes, A.; Fourcaud, T.; Norris, J.E. The influence of plant diversity on slope stability in a moist evergreen deciduous forest. Ecol. Eng. 2010, 36, 265–275. [Google Scholar] [CrossRef]
- Simon, A.; Collison, A.J.C. Quantifying the mechanical and hydrologic effects of riparian vegetation on streambank stability. Earth Surf. Process. Landf. 2002, 27, 527–546. [Google Scholar] [CrossRef]
- Pollen-Bankhead, N.; Simon, A. Hydrologic and hydraulic effects of riparian root networks on streambank stability: Is mechanical root-reinforcement the whole story? Geomorphology 2010, 116, 353–362. [Google Scholar] [CrossRef]
- Comino, E.; Druetta, A. The effect of Poaceae roots on the shear strength of soils in the Italian alpine environment. Soil Tillage Res. 2010, 106, 194–201. [Google Scholar] [CrossRef]
- Norris, J.E.; Stokes, A.; Mickovski, S.B.; Cammeraat, E.; van Beek, R.; Nicoll, B.C.; Achim, A. Slope Stability and Erosion Control: Ecotechnological Solutions; Springer: Dordrecht, Netherlands, 2008. [Google Scholar]
- Wu, T.H.; Beal, P.E.; Lan, C. In-situ shear test of soil-root systems. J. Geotech. Eng. 1988, 114, 1376–1394. [Google Scholar] [CrossRef]
- Danjon, F.; Reubens, B. Assessing and analyzing 3D architecture of woody root systems, a review of methods and applications in tree and soil stability, resource acquisition and allocation. Plant Soil 2008, 303, 1–34. [Google Scholar] [CrossRef]
- Ghestem, M.; Veylon, G.; Bernard, A.; Vanel, Q.; Stokes, A. Influence of plant root system morphology and architectural traits on soil shear resistance. Plant Soil 2014, 377, 43–61. [Google Scholar] [CrossRef]
- Sun, H.-L.; Li, S.-C.; Xiong, W.-L.; Yang, Z.-R.; Cui, B.-S.; Yang, T. Influence of slope on root system anchorage of Pinus yunnanensis. Ecol. Eng. 2008, 32, 60–67. [Google Scholar] [CrossRef]
- Chiatante, D.; Scippa, S.G.; Di Iorio, A.; Sarnataro, M. The Influence of Steep Slopes on Root System Development. J. Plant Growth Regul. 2003, 21, 247–260. [Google Scholar] [CrossRef]
- Stokes, A. The Supporting Roots of Trees and Woody Plants: Form, Function and Physiology; Springer: Dordrecht, Netherlands, 2013; Volume 87. [Google Scholar]
- Sudmeyer, R.A.; Speijers, J.; Nicholas, B.D. Root distribution of Pinus pinaster, P. radiata, Eucalyptus globulus and E. kochii and associated soil chemistry in agricultural land adjacent to tree lines. Tree Physiol. 2004, 24, 1333–1346. [Google Scholar] [CrossRef]
- Quine, C.P.; Burnand, A.C.; Coutts, M.P.; Reynard, B.R. Effects of Mounds and Stumps on the Root Architecture of Sitka Spruce on a Peaty Gley Restocking Site. For. Int. J. For. Res. 1991, 64, 385–401. [Google Scholar] [CrossRef]
- Coutts, M.; Nielsen, C.; Nicoll, B. The development of symmetry, rigidity and anchorage in the structural root system of conifers. Plant Soil 1999, 217, 1–15. [Google Scholar] [CrossRef]
- John, B.; Pandey, H.N.; Tripathi, R.S. Vertical distribution and seasonal changes of fine and coarse root mass in Pinus kesiya Royle Ex.Gordon forest of three different ages. Acta Oecol. 2001, 22, 293–300. [Google Scholar] [CrossRef]
- Goss, M.; Miller, M.; Bailey, L.; Grant, C. Root growth and distribution in relation to nutrient availability and uptake. Eur. J. Agron. 1993, 2, 57–67. [Google Scholar] [CrossRef]
- Rundel, P.; Nobel, P. Structure and Function in Desert Root Systems; Blackwell Scientific Publications: Oxford, UK, 1991; pp. 349–378. ISBN 0632027576. [Google Scholar]
- Genet, M.; Stokes, A.; Salin, F.; Mickovski, S.B.; Fourcaud, T.; Dumail, J.-F.; Van Beek, R. The Influence of Cellulose Content on Tensile Strength in Tree Roots. Plant Soil 2005, 278, 1–9. [Google Scholar] [CrossRef]
- Zhang, C.-B.; Chen, L.-H.; Jiang, J. Why fine tree roots are stronger than thicker roots: The role of cellulose and lignin in relation to slope stability. Geomorphology 2014, 206, 196–202. [Google Scholar] [CrossRef]
- Vergani, C.; Schwarz, M.; Cohen, D.; Thormann, J.; Bischetti, G.B. Effects of root tensile force and diameter distribution variability on root reinforcement in the Swiss and Italian Alps. Can. J. For. Res. 2014, 44, 1426–1440. [Google Scholar] [CrossRef]
- Vergani, C.; Chiaradia, E.; Bischetti, G. Variability in the tensile resistance of roots in Alpine forest tree species. Ecol. Eng. 2012, 46, 43–56. [Google Scholar] [CrossRef]
- Hales, T.C.; Cole-Hawthorne, C.; Lovell, L.; Evans, S.L. Assessing the accuracy of simple field based root strength measurements. Plant Soil 2013, 372, 553–565. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Wang, Y.; Ma, C. Effects of root spatial distribution on the elastic-plastic properties of soil-root blocks. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Tosi, M. Root tensile strength relationships and their slope stability implications of three shrub species in the Northern Apennines (Italy). Geomorphology 2007, 87, 268–283. [Google Scholar] [CrossRef]
- Docker, B.B.; Hubble, T.C.T. Quantifying root-reinforcement of river bank soils by four Australian tree species. Geomorphology 2008, 100, 401–418. [Google Scholar] [CrossRef]
- O’loughlin, C.; Ziemer, R.R. The importance of root strength and deterioration rates upon edaphic stability in steepland forests. In Proceedings of the IUFRO Workshop P. 1.07-00 Ecology of Subalpine Ecosystems as a Key to Management, Corvallis, OR, USA, 2–3 August 1982; Oregon State University: Corvallis, OR, USA, 1982; pp. 70–78. [Google Scholar]
- Mickovski, S.B.; Van Beek, L.P.H. Root morphology and effects on soil reinforcement and slope stability of young vetiver (Vetiveria zizanioides) plants grown in semi-arid climate. Plant Soil 2009, 324, 43–56. [Google Scholar] [CrossRef]
- Gray, D.H.; Ohashi, H. Mechanics of Fiber Reinforcement in Sand. J. Geotech. Eng. 1983, 109, 335–353. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).