Impacts of Global Climate Change on Duration of Logging Season in Siberian Boreal Forests
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
- three-hourly meteorological observations (SROK8C);
- daily soil temperature at depths down to 320 cm (TPG);
- daily air temperature and precipitation (TTTR).
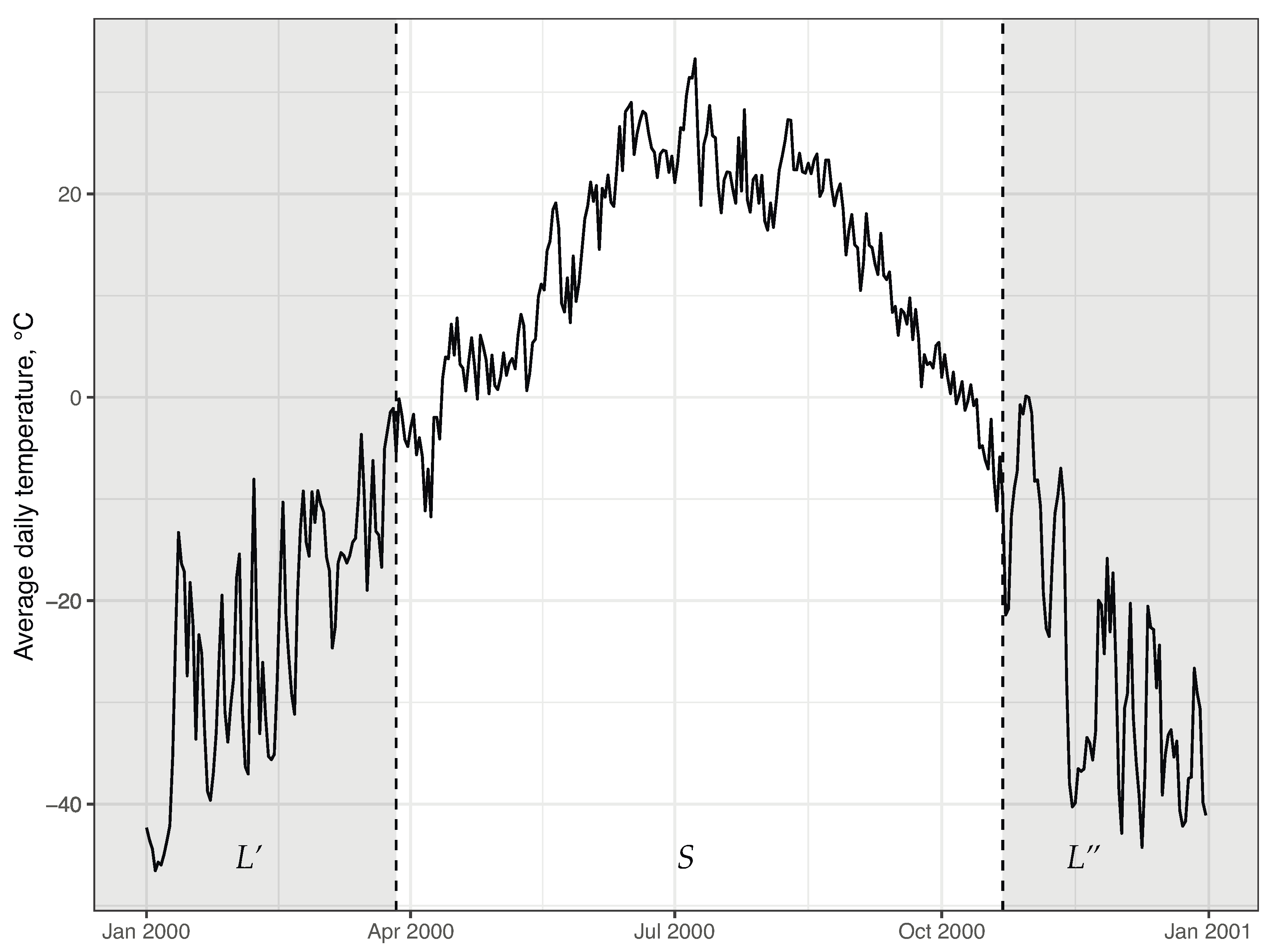
2.2. Calculation of Logging Season Duration
2.3. Trend Presence Testing
2.4. Modeling and Forecasting of Logging Season Duration
- Box–Cox transformation (if needed). If the variance of a time series is not constant, the Box–Cox transformation makes the data approximate to a normal distribution according to the following rule:To select the value of parameter, we used the technique proposed by V. M. Guerrero [61].
- Selection of the differencing degree. The most common tests for stationarity/non-stationarity are Augmented Dickey–Fuller (ADF) [62] and Kwiatkowski–Phillips–Schmidt–Shin (KPSS) [63]. For our research, we used the KPSS-test, which assumes a more easy-to-operate hypothesis of stationarity. When at some step the KPSS null-hypothesis of stationarity is not rejected, the d parameter of ARIMA model should be set to the current order of differencing.
- Fitting of p and q parameters. As there is no finite algorithm to calculate the numbers of AR and MA model components, the straightforward evaluation of all possible combinations was used. The maximum values of p and q were usually set to five. We used the Akaike information criterion (AIC) to select the best-fitted model. In our study, we employed Corrected Akaike information criterion (AICc), a modified AIC criterion for small samples. Its formula is given as:where k—flag of constant term presence ( if , and , otherwise) and is the maximum value of the likelihood function. A model with the lowest value of AICc should be selected as the best fit.
- Checking that residuals look like white noise. The Ljung–Box test was used to test whether there is no serial correlation in the residuals of the fitted model. If it is not the case, another model should be selected.
3. Results and Discussion
3.1. Logging Season Duration Shortening
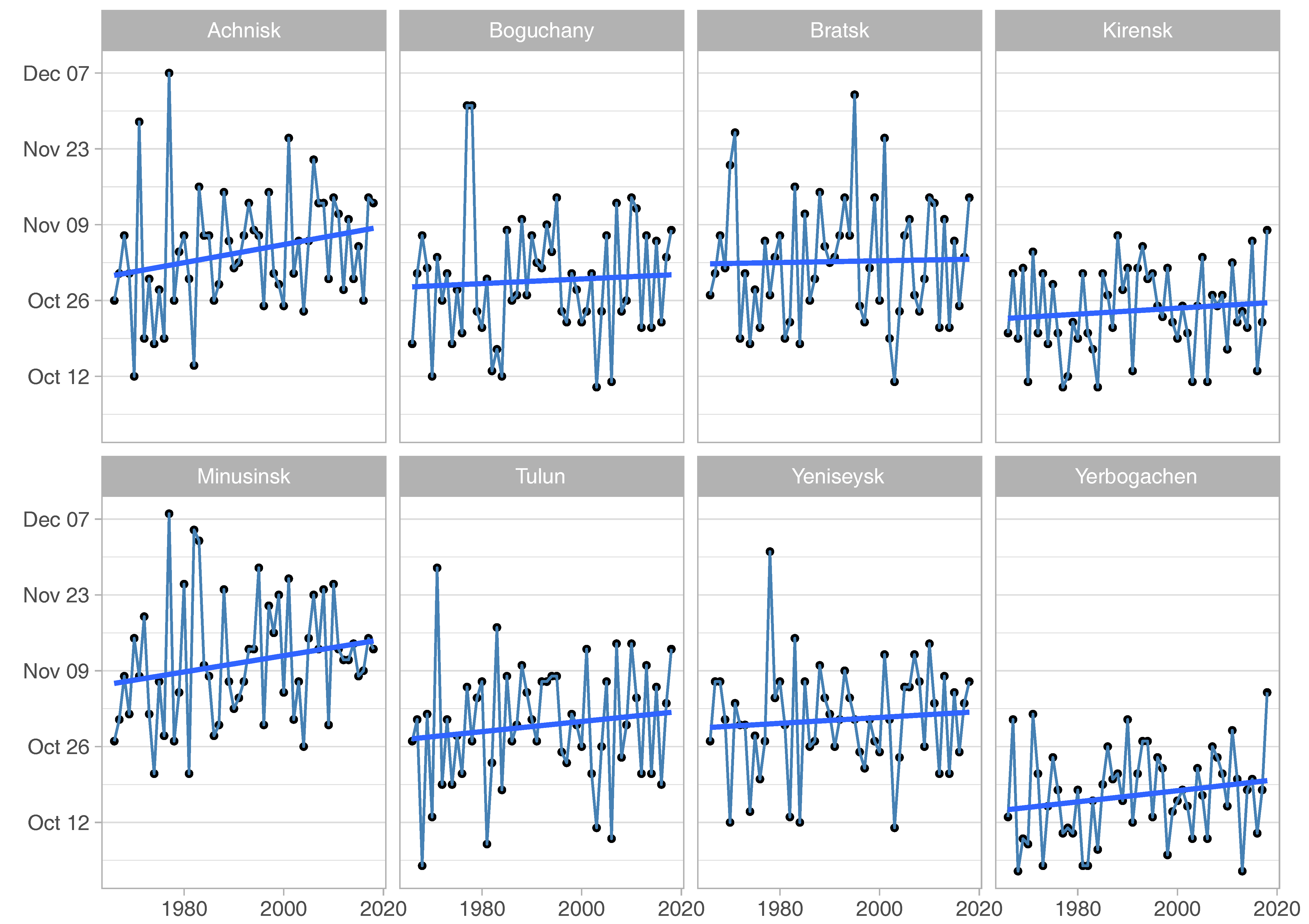
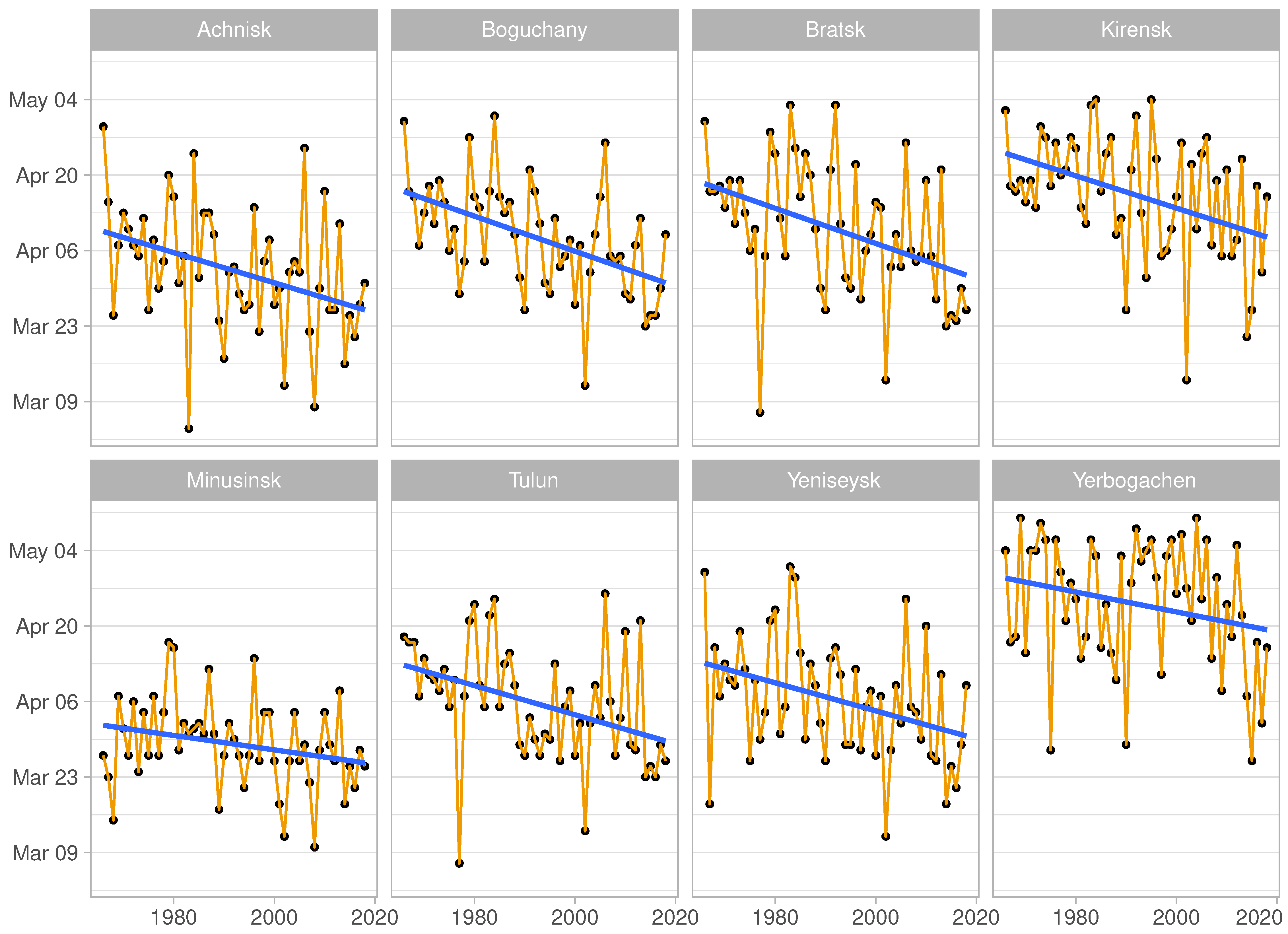
3.2. Tendencies of Expectable Season Start/End Boundaries
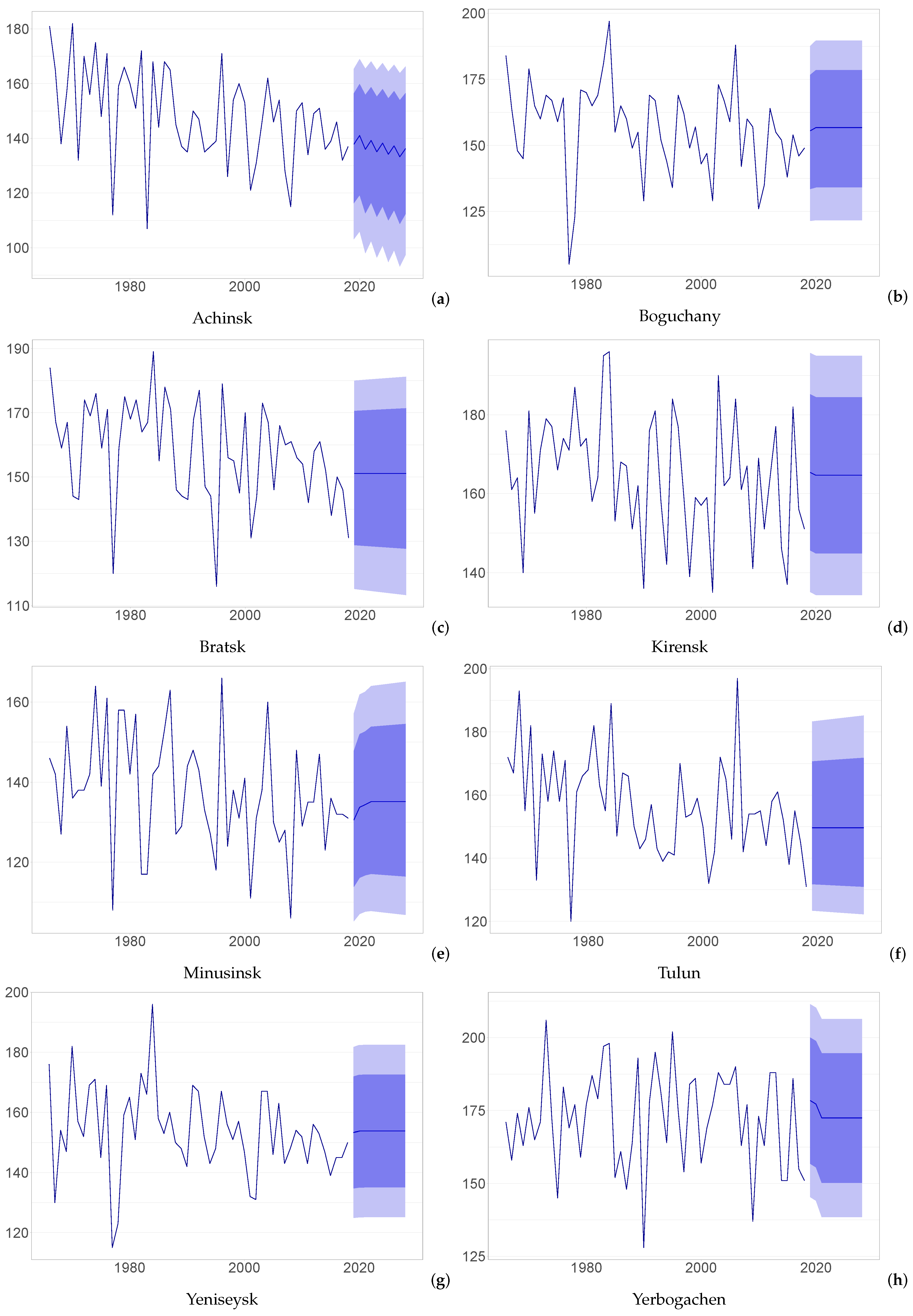
3.3. Logging Season Duration Modeling and Forecasting
4. Conclusions
- There is strong evidence of logging season duration shortening during the retrospective period of 1966–2018 for almost all considered stations. Although the considered stations are located in similar natural conditions, the local climate varies significantly and affects the economic potential of logging activity.
- The gradual reduction of logging season durations has an uneven effect on the start and end boundaries of the season. Climate warming has almost no effect on the start date of the season in winter, but it significantly shifts the boundaries of the season end in spring.
- Despite some limitations of ARIMA modeling framework forecasting performance caused by the lack of prolonged-time series of temperature and wind speed available for calculating the logging season durations, a set of ARIMA models of acceptable quality was elaborated. These forecasting models show that in the nearest future, the trends of gradual shortening of logging season duration will hold for the most part of stations. The most pronounced effect is observed for Achinsk station, where, according to our calculations the logging season will decrease from days during the historical sample (1966–2018) to days in 2028.
- In our opinion, the identified downward trends in the duration of the potential logging season in the largest Siberian logging regions are a direct consequence of the global climate change observed during the period on which the database used was based.
- From an economic perspective, shorter duration of logging season means fewer wood stocks available for cutting that would make companies unable to comply with their logging plans and lead them to suffer losses in the future. In this regard, logging companies will have to adapt to these changes by redefining their economic strategies in terms of intensifying timber harvesting operations.
- The approach we used in this study might be applied to the prediction of establishment and then the loss of ice roads to access remote mines and communities in circumpolar areas.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bukvareva, E.N.; Grunewald, K.; Bobylev, S.N.; Zamolodchikov, D.G.; Zimenko, A.V.; Bastian, O. The current state of knowledge of ecosystems and ecosystem services in Russia: A status report. Ambio 2015, 44, 491–507. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Tol, R.S.J. The Economic Effects of Climate Change. J. Econ. Perspect. 2009, 23, 29–51. [Google Scholar] [CrossRef]
- Bosello, F.; Roson, R.; Tol, R.S. Economy-wide estimates of the implications of climate change: Human health. Ecol. Econ. 2006, 58, 579–591. [Google Scholar] [CrossRef]
- Dell, M.; Jones, B.F.; Olken, B.A. Climate Change and Economic Growth: Evidence from the Last Half Century; Working Paper 14132; National Bureau of Economic Research: Cambridge, MA, USA, 2008. [Google Scholar]
- Maddison, D. The amenity value of the climate: The household production function approach. Resour. Energy Econ. 2003, 25, 155–175. [Google Scholar] [CrossRef]
- Labriet, M.; Joshi, S.R.; Vielle, M.; Holden, P.B.; Edwards, N.R.; Kanudia, A.; Loulou, R.; Babonneau, F. Worldwide impacts of climate change on energy for heating and cooling. Mitig. Adapt. Strateg. Glob. Chang. 2015, 7, 1111–1136. [Google Scholar] [CrossRef]
- Rehdanz, K.; Maddison, D. Climate and happiness. Ecol. Econ. 2005, 52, 111–125. [Google Scholar] [CrossRef]
- Boisvenue, C.; Running, S.W. Impacts of climate change on natural forest productivity–evidence since the middle of the 20th century. Glob. Chang. Biol. 2006, 12, 862–882. [Google Scholar] [CrossRef]
- Lutz, D.A.; Shugart, H.H.; White, M.A. Sensitivity of Russian forest timber harvest and carbon storage to temperature increase. Forestry 2013, 86, 283–293. [Google Scholar] [CrossRef]
- Garcia-Gonzalo, J.; Peltola, H.; Briceño-Elizondo, E.; Kellomäki, S. Effects of climate change and management on timber yield in boreal forests, with economic implications: A case study. Ecol. Modell. 2007, 209, 220–234. [Google Scholar] [CrossRef]
- Kirilenko, A.P.; Sedjo, R.A. Climate change impacts on forestry. Proc. Natl. Acad. Sci. USA 2007, 104, 19697–19702. [Google Scholar] [CrossRef]
- Tian, X.; Sohngen, B.; Kim, J.B.; Ohrel, S.; Cole, J. Global climate change impacts on forests and markets. Environ. Res. Lett. 2016, 11, 035011. [Google Scholar] [CrossRef]
- Brecka, A.F.J.; Shahi, C.; Chen, H.Y.H. Climate change impacts on boreal forest timber supply. For. Policy Econ. 2018, 11–21. [Google Scholar] [CrossRef]
- Goltsev, V.; Lopatin, E. The impact of climate change on the technical accessibility of forests in the Tikhvin District of the Leningrad Region of Russia. Int. J. For. Eng. 2013, 24, 148–160. [Google Scholar] [CrossRef]
- Saad, C.; Boulanger, Y.; Beaudet, M.; Gachon, P.; Ruel, J.C.; Gauthier, S. Potential impact of climate change on the risk of windthrow in eastern Canada’s forests. Clim. Chang. 2017, 487–501. [Google Scholar] [CrossRef]
- Ivantsova, E.D.; Pyzhev, A.I.; Zander, E.V. Economic Consequences of Insect Pests Outbreaks in Boreal Forests: A Literature Review. J. Sib. Fed. Univ. Humanit. Soc. Sci. 2019, 627–642. [Google Scholar] [CrossRef]
- Shvidenko, A.Z.; Schepaschenko, D.G. Climate change and wildfires in Russia. Contemp. Probl. Ecol. 2013, 7, 683–692. [Google Scholar] [CrossRef]
- Kharuk, V.I.; Im, S.T.; Petrov, I.A.; Golyukov, A.S.; Ranson, K.J.; Yagunov, M.N. Climate-induced mortality of Siberian pine and fir in the Lake Baikal Watershed, Siberia. For. Ecol. Manag. 2017, 384, 191–199. [Google Scholar] [CrossRef]
- Tchebakova, N.M.; Parfenova, E.I.; Korets, M.A.; Conard, S.G. Potential change in forest types and stand heights in central Siberia in a warming climate. Environ. Res. Lett. 2000, 11, 035016. [Google Scholar] [CrossRef]
- Hanewinkel, M.; Cullmann, D.A.; Schelhaas, M.J.; Nabuurs, G.J.; Zimmermann, N.E. Climate change may cause severe loss in the economic value of European forest land. Nat. Clim. Chang. 2000, 203–207. [Google Scholar] [CrossRef]
- Fei, S.; Desprez, J.M.; Potter, K.M.; Jo, I.; Knott, J.A.; Oswalt, C.M. Divergence of species responses to climate change. Sci. Adv. 2017, 3, e1603055. [Google Scholar] [CrossRef]
- Drobyshev, I.; Gewehr, S.; Berninger, F.; Bergeron, Y. Species specific growth responses of black spruce and trembling aspen may enhance resilience of boreal forest to climate change. J. Ecol. 2013, 1, 231–242. [Google Scholar] [CrossRef]
- Johnstone, J.F.; Hollingsworth, T.N.; Chapin, F.S.; Mack, M.C. Changes in fire regime break the legacy lock on successional trajectories in Alaskan boreal forest. Glob. Chang. Biol. 2013, 4, 1281–1295. [Google Scholar] [CrossRef]
- Rittenhouse, C.D.; Rissman, A.R. Changes in winter conditions impact forest management in north temperate forests. J. Environ. Manag. 2015, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Hellmann, L.; Tegel, W.; Kirdyanov, A.V.; Eggertsson, Ó.; Esper, J.; Agafonov, L.; Nikolaev, A.N.; Knorre, A.A.; Myglan, V.S.; Sidorova, O.C.; et al. Timber Logging in Central Siberia is the Main Source for Recent Arctic Driftwood. Arct. Antarct. Alp. Res. 2015, 47, 449–460. [Google Scholar] [CrossRef]
- Kuloglu, T.Z.; Lieffers, V.J.; Anderson, A.E. Impact of Shortened Winter Road Access on Costs of Forest Operations. Forests 2019, 10, 447. [Google Scholar] [CrossRef]
- FAO. Global Forest Resources Assessment 2015. Country Report. Russian Federation. Available online: http://www.fao.org/3/a-az316e.pdf (accessed on 27 April 2020).
- Rosstat. Unified Interdepartmental Information and Statistical System (EMISS). Harvested Wood Volume. Available online: https://fedstat.ru/indicator/37848 (accessed on 27 August 2019).
- LUKE. Finnish Forest Statistics. Available online: https://stat.luke.fi/sites/default/files/suomen_metsatilastot_2019_verkko2.pdf (accessed on 27 April 2020).
- Mokhirev, A.P.; Medvedev, S.O.; Smolina, O.N. Factors influencing the accessibility of timber transport roads. For. Eng. J. 2019, 103–113. [Google Scholar] [CrossRef]
- Pyzhev, A.I. Global climate change and logging volumes in Siberian regions from 1946 to 1992. Terra Econ. 2020, 18, 140–153. [Google Scholar] [CrossRef]
- Gordeev, R.V.; Pyzhev, A.I. Analysis of the Global Competitiveness of the Russian Timber Industry. ECO 2015, 109–130. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 7 August 2019).
- Pebesma, E. Simple Features for R: Standardized Support for Spatial Vector Data. R J. 2018, 10, 439–446. [Google Scholar] [CrossRef]
- Tennekes, M. Tmap: Thematic Maps in R. J. Stat. Softw. 2018, 84, 1–39. [Google Scholar] [CrossRef]
- South, A. Rnaturalearth: World Map Data from Natural Earth. R Package Version 0.1.0. Available online: https://CRAN.R-project.org/package=rnaturalearth (accessed on 8 December 2019).
- Bulygina, O.; Veselov, V.; Razuvaev, V.; Aleksandrova, T. Description of Hourly Data Set of Meteorological Parameters Obtained at Russian Stations. Available online: http://meteo.ru/english/climate/descrip12.htm (accessed on 5 December 2019).
- Veselov, V.; Pribylskaya, I. AISORI Specialized Technology. Available online: http://aisori.meteo.ru/ClimateR (accessed on 5 December 2019).
- Administration of Krasnoyarsk Krai. The Decree Dated November 12, 2001 under no. 786-P on Operating Conditions during the Cold Season; Administration of Krasnoyarsk Krai: Krasnoyarsk Krai, Russia, 2001; Available online: http://docs.cntd.ru/document/985003848 (accessed on 12 May 2019).
- Administration of Irkutsk Oblast. The Decree Dated September 26, 2001 under no. 33/201-pg on the Temperature Limits When Operating Outdoors and in Enclosed Unheated Rooms during the Cold Season; Administration of Irkutsk Oblast: Irkutsk, Russia, 2001; Available online: http://docs.cntd.ru/document/469412568 (accessed on 12 May 2019).
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 26, 1–22. [Google Scholar] [CrossRef]
- Hyndman, R.; Athanasopoulos, G.; Bergmeir, C.; Caceres, G.; Chhay, L.; O’Hara-Wild, M.; Petropoulos, F.; Razbash, S.; Wang, E.; Yasmeen, F. Forecast: Forecasting Functions for Time Series and Linear Models. R Package Version 8.12. Available online: http://pkg.robjhyndman.com/forecast (accessed on 4 May 2020).
- Pohlert, T. Trend: Non-Parametric Trend Tests and Change-Point Detection. R Package Version 1.1.2. Available online: https://CRAN.R-project.org/package=trend (accessed on 8 May 2020).
- Moritz, S.; Bartz-Beielstein, T. imputeTS: Time Series Missing Value Imputation in R. R J. 2017, 9, 207–218. [Google Scholar] [CrossRef]
- Trapletti, A.; Hornik, K. Tseries: Time Series Analysis and Computational Finance. R Package Version 0.10-47. Available online: https://CRAN.R-project.org/package=tseries (accessed on 8 May 2020).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Wei, T.; Simko, V. R Package “Corrplot”: Visualization of a Correlation Matrix. (Version 0.84). Available online: https://github.com/taiyun/corrplot (accessed on 8 May 2020).
- Dahl, D.B.; Scott, D.; Roosen, C.; Magnusson, A.; Swinton, J. Xtable: Export Tables to LaTeX or HTML, R package version 1.8-4; 2019. Available online: https://CRAN.R-project.org/package=xtable (accessed on 12 May 2020).
- Mann, H.B. Nonparametric Tests Against Trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Multivariate Analysis; Griffin: London, UK, 1975. [Google Scholar]
- Chen, W.J. Is the Green Solow Model Valid for CO2 Emissions in the European Union? Environ. Resour. Econ. 2017, 67, 23–45. [Google Scholar] [CrossRef]
- Hamed, K.H.; Ramachandra Rao, A. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Škvareninová, J.; Tuhárska, M.; Škvarenina, J.; Babálová, D.; Slobodníková, L.; Slobodník, B.; Středová, H.; Minďaš, J. Effects of light pollution on tree phenology in the urban environment. Morav. Geogr. Rep. 2017, 25, 282–290. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The Mann-Kendall Test Modified by Effective Sample Size to Detect Trend in Serially Correlated Hydrological Series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Vido, J.; Tadesse, T.; Šustek, Z.; Kandrík, R.; Hanzelová, M.; Jaroslav, S.; Škvareninová, J.; Hayes, M. Drought Occurrence in Central European Mountainous Region (Tatra National Park, Slovakia) within the Period 1961–2010. Adv. Meteorol. 2015, 2015. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970; p. 553. [Google Scholar]
- Lin, M.; Zhang, Z.; Cao, Y. Forecasting Supply and Demand of the Wooden Furniture Industry in China. For. Prod. J. 2019, 69, 228–238. [Google Scholar] [CrossRef]
- Michinaka, T.; Kuboyama, H.; Tamura, K.; Oka, H.; Yamamoto, N. Forecasting Monthly Prices of Japanese Logs. Forests 2016, 7, 94. [Google Scholar] [CrossRef]
- Buratto, D.; Junior, R.T.; Silva, J.; Frega, J.; Wiecheteck, M.; Silva, C. Use of Artificial Neural Networks and ARIMA to Forecasting Consumption Sawnwood of Pinus sp. in Brazil. Int. For. Rev. 2019, 21, 51–61. [Google Scholar] [CrossRef]
- Guerrero, V.M. Time-series analysis supported by power transformations. J. Forecast. 1993, 12, 37–48. [Google Scholar] [CrossRef]
- Said, S.E.; Dickey, D.A. Testing for unit roots in autoregressive-moving average models of unknown order. Biometrika 1984, 71, 599–607. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Sukhova, M.G. Climate and Recreational-Climatic Resources of Altai-Sayan Mountainous Region Landscapes. Probl. Contemp. Sci. Pract. Vernadsky Univ. 2009, 2, 82–84. [Google Scholar]
| Station Name | WMO Index | Latitude (N) | Longitude (E) | Altitude, m a.s.l. | Onset of Observations | Relocation Note |
|---|---|---|---|---|---|---|
| Yeniseysk (ENI) | 29,263 | 77 | 1853 | 15 times until 1915 without coordinates change | ||
| Boguchany (BOG) | 29,282 | 131 | 1930 | 2 km NW in 1960 | ||
| Achinsk (ACH) | 29,467 | 265 | 1940 | 1 km S in 1956 | ||
| Minusinsk (MIN) | 29,866 | 254 | 1885 | 800 m NW in 1990 | ||
| Bratsk (BRT) | 30,309 | 410 | 1901 | 4 km NW in 1956 | ||
| Kirensk (KIR) | 30,230 | 256 | 1892 | 1.5 E in 1909, to the waterfront of the Lena river in 1931, to the right bank of the Lena river in 1933 and 1.5 km S—SW in 1942 | ||
| Tulun (TUL) | 30,504 | 523 | 1940 | 1.3 km W in 1951 | ||
| Yerbogachen (YER) | 24,817 | 284 | 1936 | No relocations |
| Krasnoyarsk | Irkutsk | ||
|---|---|---|---|
| NA | 40 | NA | |
| NA | 22 | ||
| 5 | 3 | ||
| 10 | |||
| 15 | |||
| 20 | |||
| Station Name | Mean | S.D. | z | p-Value | Trend Characteristics | ||
|---|---|---|---|---|---|---|---|
| 1 | Acninsk | 148.42 | 17.27 | 0.00 | Decreasing trend | ||
| 2 | Boguchany | 156.40 | 17.19 | 0.01 | Decreasing trend | ||
| 3 | Bratsk | 157.72 | 15.72 | 0.01 | Decreasing trend | ||
| 4 | Kirensk | 164.64 | 15.32 | 0.08 | Decreasing trend | ||
| 5 | Minusinsk | 137.58 | 14.37 | 0.04 | Decreasing trend | ||
| 6 | Tulun | 156.79 | 15.96 | 0.00 | Decreasing trend | ||
| 7 | Yeniseysk | 153.75 | 14.48 | 0.02 | Decreasing trend | ||
| 8 | Yerbogachen | 172.15 | 16.89 | 0.99 | No trend |
| Station Name | Mean/Drift | AICc | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | Achinsk | ||||||||
| 2 | Boguchany | ||||||||
| 3 | Bratsk | ||||||||
| 4 | Kirensk | ||||||||
| 5 | Minusinsk | ||||||||
| 6 | Tulun | ||||||||
| 7 | Yeniseysk | ||||||||
| 8 | Yerbogachen | ||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chugunkova, A.V.; Pyzhev, A.I. Impacts of Global Climate Change on Duration of Logging Season in Siberian Boreal Forests. Forests 2020, 11, 756. https://doi.org/10.3390/f11070756
Chugunkova AV, Pyzhev AI. Impacts of Global Climate Change on Duration of Logging Season in Siberian Boreal Forests. Forests. 2020; 11(7):756. https://doi.org/10.3390/f11070756
Chicago/Turabian StyleChugunkova, Anna V., and Anton I. Pyzhev. 2020. "Impacts of Global Climate Change on Duration of Logging Season in Siberian Boreal Forests" Forests 11, no. 7: 756. https://doi.org/10.3390/f11070756
APA StyleChugunkova, A. V., & Pyzhev, A. I. (2020). Impacts of Global Climate Change on Duration of Logging Season in Siberian Boreal Forests. Forests, 11(7), 756. https://doi.org/10.3390/f11070756





