1. Introduction
For better conservation of biological diversity, ecologists have explored the spatial distribution patterns of rare species. A variety of ecological mechanisms can contribute to species rarity; for example, habitat heterogeneity, dispersal limitation, and pest-pressure hypothesis [
1,
2,
3]. However, the general relationship between species rarity and non-independence of species distribution remains to be explored [
3,
4,
5].
The definition of distributional non-independence or non-randomness can be multifaceted, some tangible forms of which can be aggregated distribution [
6,
7], regular distribution or correlated distribution [
8]. For the multivariate framework that will be employed here, we interpret the term distributional non-independence as a correlated multivariate distribution. That is, distribution of individuals of different species across different quadrats presents some degree of correlation [
8]. Therefore, if some species present aggregate (random or regular) distributions, because of the multivariate correlation effect, it is also expected that other species in the assemblage also present aggregate (random or regular) distribution. This positive correlation cannot be predicted by totally independent and random distribution models (i.e., the Poisson model) [
6,
7,
8]. For the tropical and subtropical forest plots investigated below, a positive correlated distribution was confirmed. Moreover, it has been observed that the multi-species correlated distribution should present a mixed pattern of aggregate and random distributions of different species [
8]. However, as mentioned above, the relationship between the correlated distribution of the entire ecological assemblage and rare species distribution is totally unclear, even though the relationship between the abundance variability and distributional aggregation, as one form of distributional non-independence, has been well explored at the species level [
9,
10]. Finally, the scale dependency effect using quadrat sampling further obscures the general relationship between the two quantities.
Empirically, at a species level, rare species show more spatially aggregated distribution compared with common tree species in both temperate and tropical forests [
4,
5,
9,
11]. However, the relationship may be more complex than previously thought as the definition of rare species is relative, somewhat arbitrary, and related to some abundance thresholds [
12,
13,
14,
15,
16]. For example, a variety of rarity threshold rules are employed to classify rare species in the studied assemblages [
12,
13,
14].
Other than the species abundance threshold, it is also important to recognize that the spatial extent of studied areas also influences the definition of rare species in community ecology [
16]. This is particularly true when conducting local sampling or surveys of ecological assemblages in a large region or habitat. How should we define a rare species? If a limited local sampling can survey only 10% of the whole region at the local scale, we may argue that species A is rare when its individuals have a number of 5 based on the surveyed area, in comparison to a reference species B that has 100 individuals in the surveyed area. However, if species A has a much more aggregated distribution and has 10,000 individuals in the remaining 90% unsampled part of the region, while the distribution of species B is fully random with 900 individuals in the remaining area, then species B (total population size = 1000), at the regional scale, is definitely much rarer than species A (total population size = 10,005). Therefore, when studying scale-related species rarity patterns, it is necessary to clearly define the corresponding sampling spatial extent and the population threshold [
16].
Moreover, if the studied assemblage has more rare species, then the corresponding species abundance distribution should become more right skewed in the curve shape (i.e., abundances of most species tend to concentrate at small values while the other species are highly abundant, which results in the abundance distribution displaying a long right-tailed pattern), which would result in a large variation of species abundance. As such, if a positive relationship is observed between population rarity and non-random distribution of a species, then a systematic association should be expected between the abundance variability and distributional non-independence of the entire assemblage.
An important factor that can hinder the progress of earlier work in evaluating the relationships between non-independence, variability, and rarity is related to the statistical methods used in these studies. The independent negative binomial distribution (NBD) statistical model was widely used for describing aggregated distribution of a single species [
6,
17,
18,
19,
20,
21]. However, the species-specific NBD model does not consider that the distribution of individuals of a species in different sampling quadrats may be non-random and spatially dependent.
In summary, in our present study, a multivariate statistical model negative multinomial model (NMM) is used to describe assemblage-level correlated distribution patterns to evaluate the relationship between species rarity, non-independent distribution, and abundance variability (quantified by the coefficient of variation, CV) patterns. Based on the NMM-induced assemblage-level correlated distribution and the context of the sampling theorem, we derived the theoretical sampling theory for two forms of rarity, locally rare species and regionally rare species, with respect to the changing sampling area fraction.
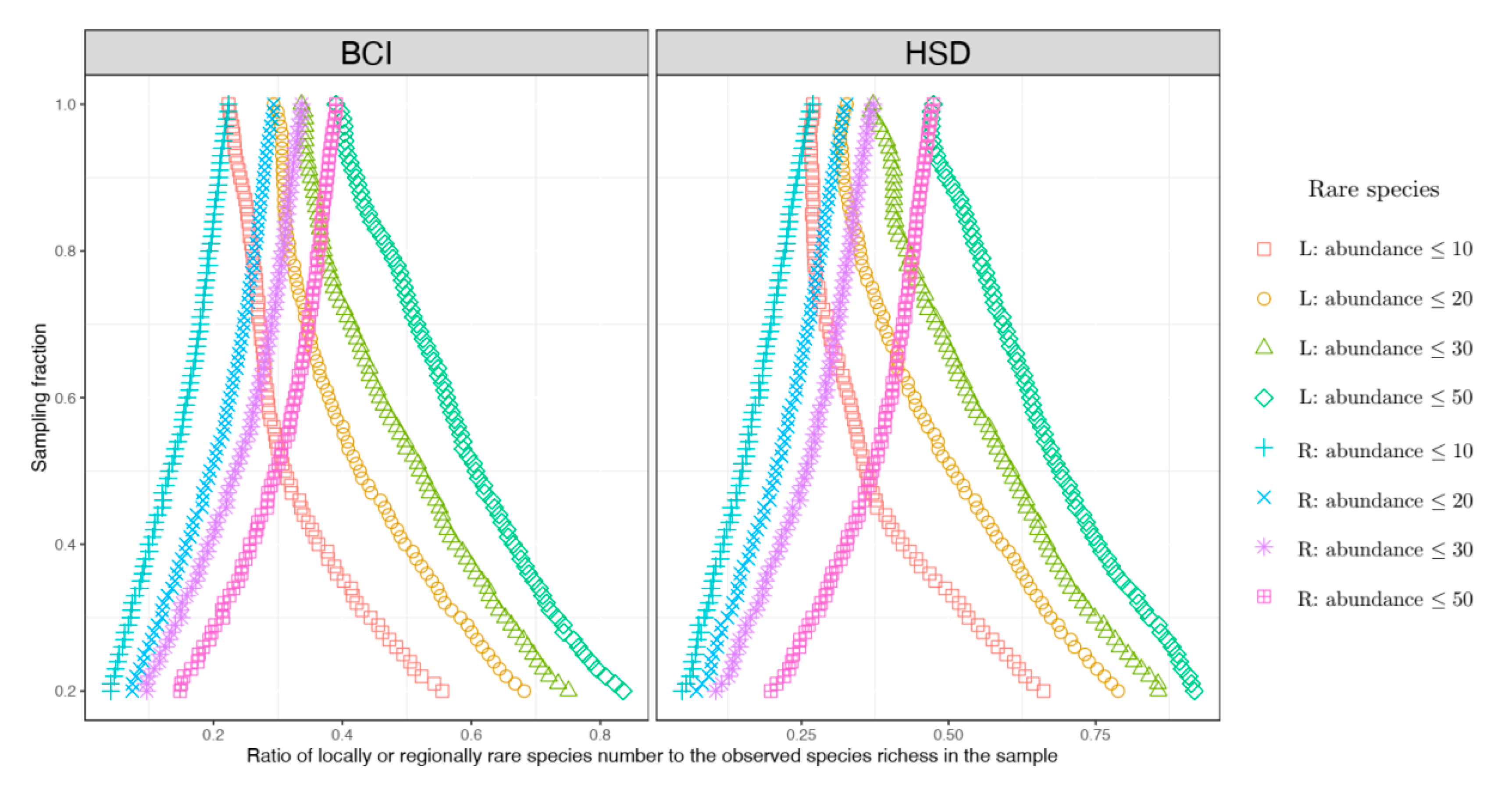
In our study, we define locally rare species are those with an abundance not greater than a rarity threshold in the local sample, while regionally rare species are defined by their abundances (the total number of individuals spread over the entire forest plot) being not greater than the same rarity threshold. Two permanent tropical forest plots were analysed for testing the empirical deviation from the theoretical expectation. We confirmed that locally rare species and regionally rare species presented nearly opposite mirror-like curve patterns when the sampling size of the local quadrat increased. Finally, we also showed that neighbouring unseen species can have impacts on the estimation of the assemblage-level correlated distribution.
Our central goal of conducting such analyses is to better characterize multi-species distributional non-randomness patterns using a multivariate model for theoretically deriving and empirically verifying two different forms of rare species–area relationships. The findings at the forest-plot scales provided in the study can be used to extrapolate rare species diversity at larger spatial scales to better inform global and regional biodiversity conservation and to interpolate rare species diversity at smaller spatial scales.
2. Materials and Methods
In the following section, we built an NMM to capture the correlated multivariate distribution patterns of the individuals of species across different sampling quadrats. For modelling simplicity, we will assume different species in an assemblage sharing the same statistical parameters in the modelling. Throughout the paper, we define unseen species as those species with zero abundance in the locally sampled area but which could be observed elsewhere when the studied region is expanded to cover more neighbouring areas. Even though we did not explicitly study endemic species that are important and essential for biodiversity conservation [
22,
23], those regionally rare species investigated here are very likely to be endemic when sampling grain sizes are sufficiently large to cover all individuals of these species.
2.1. The Negative Multinomial Model
A region with an area size
A (e.g., the area size of the entire forest plot in our empirical tests) has
S species. The abundances of these
S species are denoted by
, each of which is assumed to follow an NBD whose probability function is as follows [
8,
20,
21]:
where
k represents a shape parameter measuring non-independence of the spatial distribution of individuals of a species (
k > 0). In a single-species setting, a large
k indicates a reduced aggregation of organisms (i.e., their distribution tends to be more random) and vice versa. Under the multivariate setting that will be discussed below, this shape parameter
k was used to model the strength of positively correlated distributions of different species across different sampling quadrats. A large (or small)
k indicates that the positive correlation strength of multiple species’ distributions becomes weak (or strong), implying that the degree of assemblage-level distributional non-independence or non-randomness is weak (or strong). Finally, the parameter
u is reciprocally related to the mean population abundance of the NBD model for fixed values of both
k and area size
A, which is
, and it is also related to the variance of the model as follows:
. A low
u implies a high density of species populations per unit of sampling area.
Based on Equation (1), the
CV of species abundance at the spatial scale of the entire region
A is a function of both
k and
u and can be explicitly expressed as follows:
This relationship implies that species in ecological communities with a high variability of species abundance tend to have a strong level of multi-species correlated distribution based on the reciprocal relationship between CV and k (if other parameters A and u are fixed in Equation (2)).
For sampling convenience, the region is divided into
q quadrats, with areas
and
. Note that the sizes of
could be different. Let
denote the corresponding numbers of individuals of species
i scattered over these
q quadrats. When the total abundance of species
i (
) is determined, a natural assumption for
is to enforce a multinomial distribution as follows:
Because
follows NBD as in Equation (1), the unconditional joint distribution of
is a negative multinomial distribution (NMD) as follows [
21]:
The model derived from Equation (4) (which is NMM) describes the multi-species spatial distributional patterns over different quadrats of the studied region at the assemblage level. When the shape parameter k value is very small (or very large), the positive correlated distributions of individual species tend to be strong (or weak) and accordingly, the abundance variability (measured by CV in Equation (2)) will be high (or low).
However, if
(at the whole assemblage level) follows a random distribution (i.e., Poisson model with intensity
and probability function
), then the unconditional distribution of
(species level) is expressed as follows:
which indicates the abundances of species
i scattered over
q quadrats, following independent and random Poisson distributions. The detailed derivation of Equation (5) is shown in the Additional Methods of the Supporting Information.
When a local area
a is surveyed within region
A, then the model in Equation (4) can be refined as a negative trinomial distribution (NTD):
where
is the number of individuals of species
i in the local area
a;
x and
y are two nonnegative integers with
. Note that all species share the same parameters
k and
u because they are distributed in the same region and are affected by similar environmental factors. The marginal distribution of
Ni,a is derived from the model in Equation (6) as follows:
For the derivation of Equation (7) from the NTD in detail above, please refer to the Additional Methods of the Supporting Information. After a simple transformation, this form is identical to the conventional negative binomial probability model used in previous studies [
6,
17,
24]. At the spatial scale when the sampling quadrat has a size of
a, the corresponding population mean is
, variance
, and
CV .
2.2. Parameter Estimation
Let
denote the number of species with
m individuals in the sampled assemblage; thus, (
f1,
f2, ...,
fτ) follows a multinomial distribution with a total number of species
S over the entire region
A and cell probabilities
, where
for a local sample
and
; therefore, the likelihood function is expressed as follows:
which is viewed as a conditional likelihood function based on the observed number of species,
, in the local sample. Analogous applications can be found in previous studies [
21,
25,
26,
27].
The maximum likelihood estimators
and
of
and
can be solved by maximizing the likelihood function in Equation (8). We place all species in the likelihood model, and only a pair of
and
is obtained. The variances of the parameters are calculated using the observed information matrix, and the details are presented in the Supporting Information (
Equation (S1)). Additionally, for computing convenience, the R code for calculating the maximum likelihood estimates of
and
, their estimated standard errors, and corresponding 95% confidence intervals is provided in the Supporting Information.
In this likelihood function, we controlled the potential effect of unseen species
by normalizing
with the sum as one. As a comparison, we also presented an alternative likelihood function without accounting for the influence of unseen species
(Supporting Information
Equation (S2)) and fitted the corresponding parameter values. Our results show that the strength of distributional non-independence is weaker when the effect of unseen species
exists.
To unravel the general relationships between locally rare species, regionally rare species, and sampling fractions of local area sizes, based on the formulae of NMD or NTD (Equation (4) or (6)), the expected ratio of locally rare species to the observed species numbers can be approximately expressed as follows:
where
represents the abundance threshold for rare species (which is 10, 20, 30 or 50 as mentioned above).
As a comparison, the expected ratio of regionally rare species to the observed species numbers can be approximately expressed as follows:
By comparing Equations (9) and (10), one can see that because obviously holds for , across different sampling fractions is always true. The equality becomes true only when (i.e., the sampling fraction ).
2.3. Empirical Tests
Two forest-plot datasets from tropical areas were employed as sampling populations to evaluate the assemblage-level relationships among the species abundance rarity, and variability and distributional non-independence across various spatial sampling scales. The Barro Colorado Island (BCI) plot is located in Panama, Central America, and has a size of 50 ha (1000 × 500 m) [
28,
29,
30,
31,
32]. The BCI plot has been canvassed eight times, and the data used here were collected in 2005, which showed that it contained 208,383 trees (diameter at breast height ≥1 cm) and 300 species. The Heishiding (HSD; 50 ha; 2011 census) plot located within the Heishiding Provincial Reserve in Guangdong Province of China [
33] contains 156 species identified from 37,858 individuals (diameter at breast height ≥10 cm).
To evaluate the multiscale relationships among species rarity, abundance variability, and non-independence at the assemblage level, we conducted a multiscale sampling scheme to randomly sample local communities from small to large until the entire forest plot was accounted for. To be specific, at each given spatial grain scale (or quadrat size), 100 local communities were randomly sampled. This was done by randomly placing 100 quadrats with the same grain size inside the forest plot. These quadrats may or may not have overlapped, depending on the size of sampling quadrat placed inside the forest plot. Note that, in this random sampling process, it was ensured that the entire region of each of the 100 quadrats was fully covered by the forest plot to avoid edge effects.
For each of these 100 randomly sampled local communities (i.e., the composition of species at each spatial sampling scale less than the size of the entire plot), we calculated or measured the following quantities: (1) degree of assemblage non-independence, which is reflected by the estimated shape parameter
k for each local assemblage; (2) the size of the local assemblage, which is the number of individuals of all species found in the local assemblage; (3) percent of locally rare species, which is the percent of species with abundances of less than 10, 20, 30 or 50 found in the local assemblage relative to the total number of species found in the local assemblage; (4) percent of regionally rare species, which is the percent of species with abundances of less than 10, 20, 30 or 50 found at the entire forest plot level (e.g., BCI as a whole) relative to the total number of species found in the local assemblage; and (5) abundance variability, which is represented by the estimated
CVa for the species abundance distribution in the local assemblage. It is worth noting that the above definition of locally and regionally rare species was not ad hoc, as each was studied separately in the previous empirical literature [
34,
35,
36,
37,
38].
The averages of these quantities for 100 randomly sampled assemblages were taken to represent the overall non-randomness degree and abundance variability at that scale. Our analyses were multiscale, since we analysed many spatial scales (or quadrat sizes) from small to large for each forest plot to show crossing-scale patterns, i.e., the range of sampling spatial scales for both plots was from 20,000 m2 to 500,000 m2.
3. Results
Our empirical applications (
Table 1) showed that the interspecific distribution of tree species in the HSD forest plot was less positively correlated (
k = 0.16445), while the tree distributions were more correlated in the BCI plot in Panama, which had a corresponding
k value of 0.1003. By contrast, regarding the comparison of the two
CVs, the BCI forest plot had a higher value than the HSD plot. Finally, the estimated
u in the BCI plot was lower (implying a high density of species populations per unit of sampling area) than that in the HSD plot (
Table 1). Across the different sampling scales, the fitted
k and
u values were positively correlated at the assemblage level (
Figure S1).
Theoretically, when parameter
u is fixed, a higher
k would result in a lower probability of being rare (i.e., having a small population size ≤10, 20, or 30) for a single species (
Figure 1). By contrast, when parameter
k is fixed, a lower mean abundance of a species (higher
u) will result in a higher probability of being rare (i.e., having a small population size ≤10, 20, or 30) for a single species (
Figure S2). This is expected given that
u is inversely related to the mean population density of a species; a higher
u implies that the sampled assemblage is small and frequently filled with rare species.
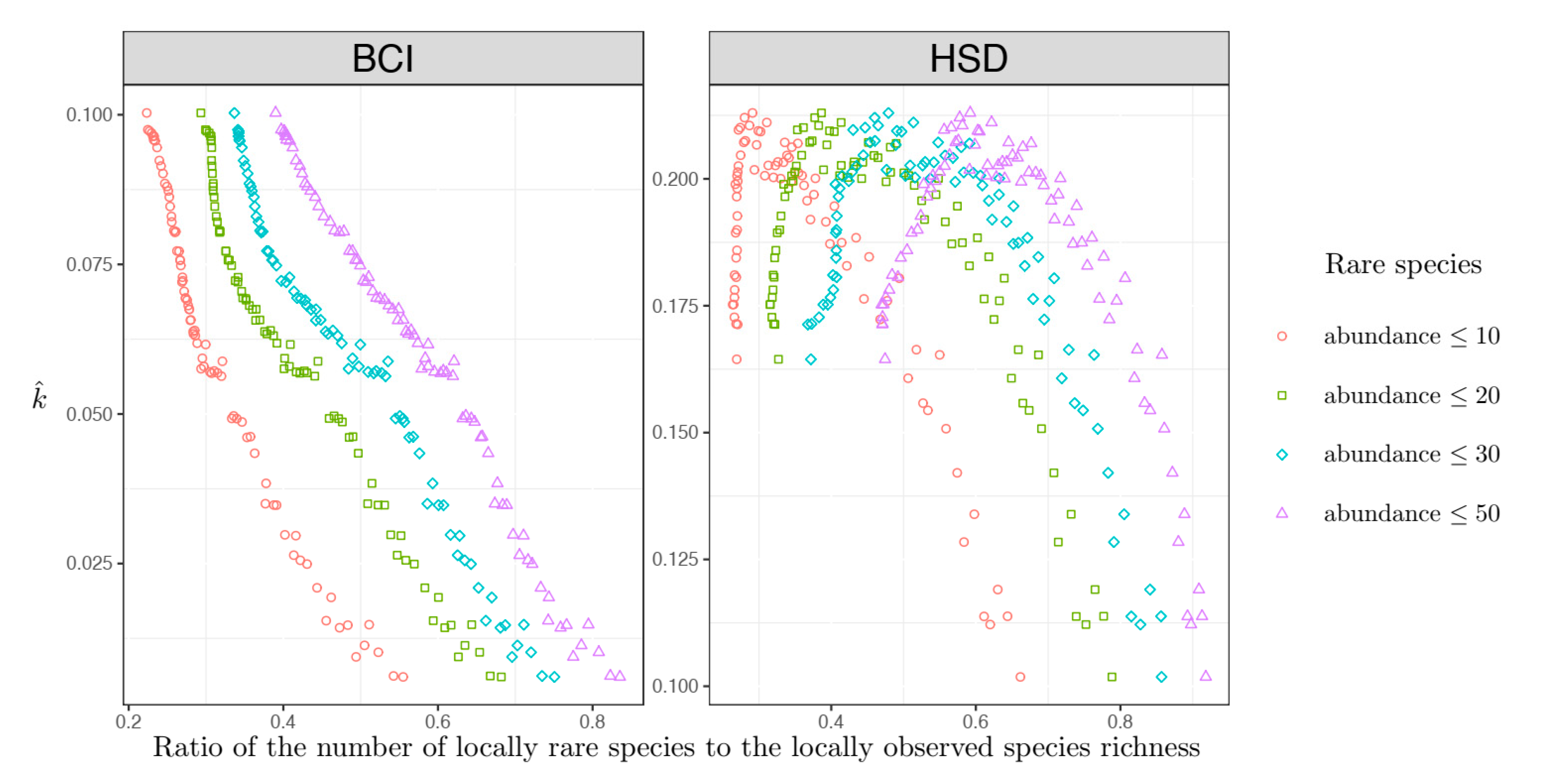
Locally sampled communities with a high amount of locally rare species always had a higher assemblage non-independence level, regardless of the plots investigated (
Figure 2). However, when the percent of locally rare species was not so high, in the HSD plot, there was a negative association between assemblage non-independence level and the percent of locally rare species (
Figure 2). The opposite pattern (
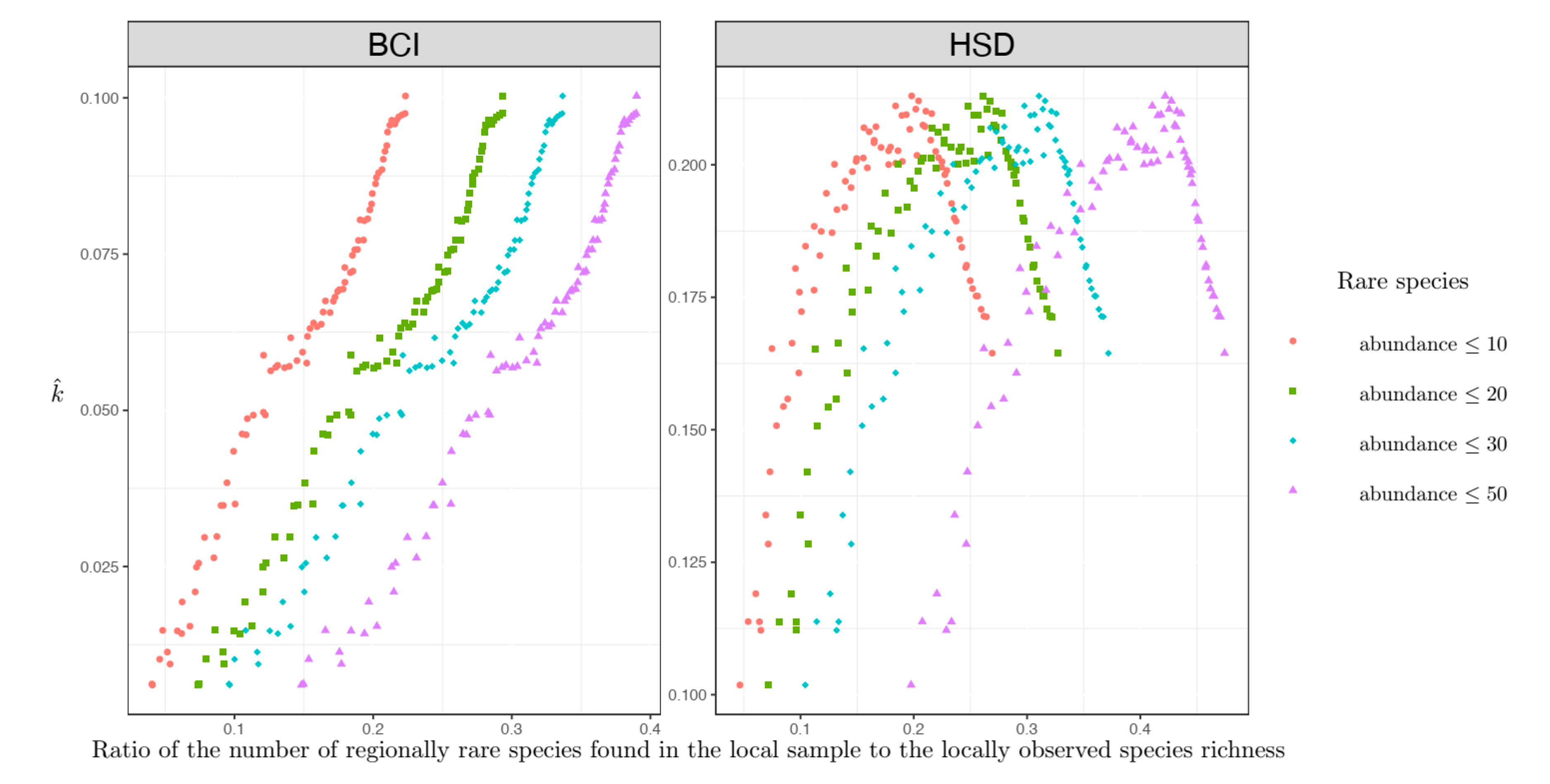
Figure 3) was observed when only the regionally rare species were considered.
In the multiscale setting, when the shape parameter was estimated to have small values, the percent of regionally rare species was low, and the assemblage-level non-independence was always high (
Figure 3). However, when the shape parameter was estimated to have large values, there were more regionally rare species, and the assemblage non-independence degree usually decreased (
Figure 3) except that a positive relationship existed between the non-independence level and the percent of regionally rare species for the HSD plot (
Figure 3).
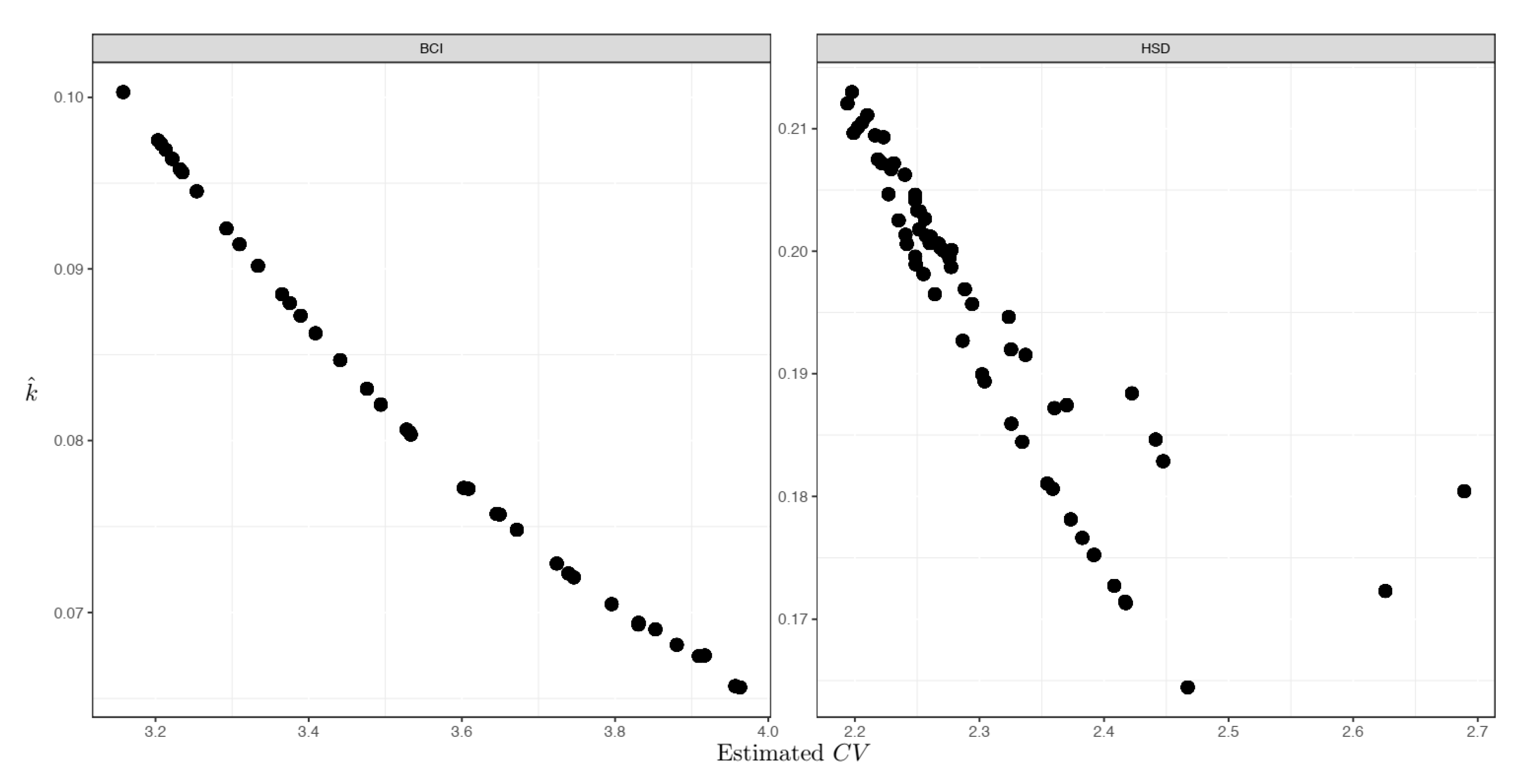
Empirical tests from the two forest plots verified the theoretical relationship (Equation (2)) between the
CV and the non-independence parameter (
Figure 4). When the
CV tended to be large, the corresponding assemblage non-independence degree was high (therefore a low
k). By contrast, when the
CV was small, the non-independence status tended to be low (a high
k accordingly) (
Figure 4).