Tree Ring-Based Estimation of Landslide Areal Reactivation as a Fundament of Magnitude–Frequency Assessment
Abstract
1. Introduction
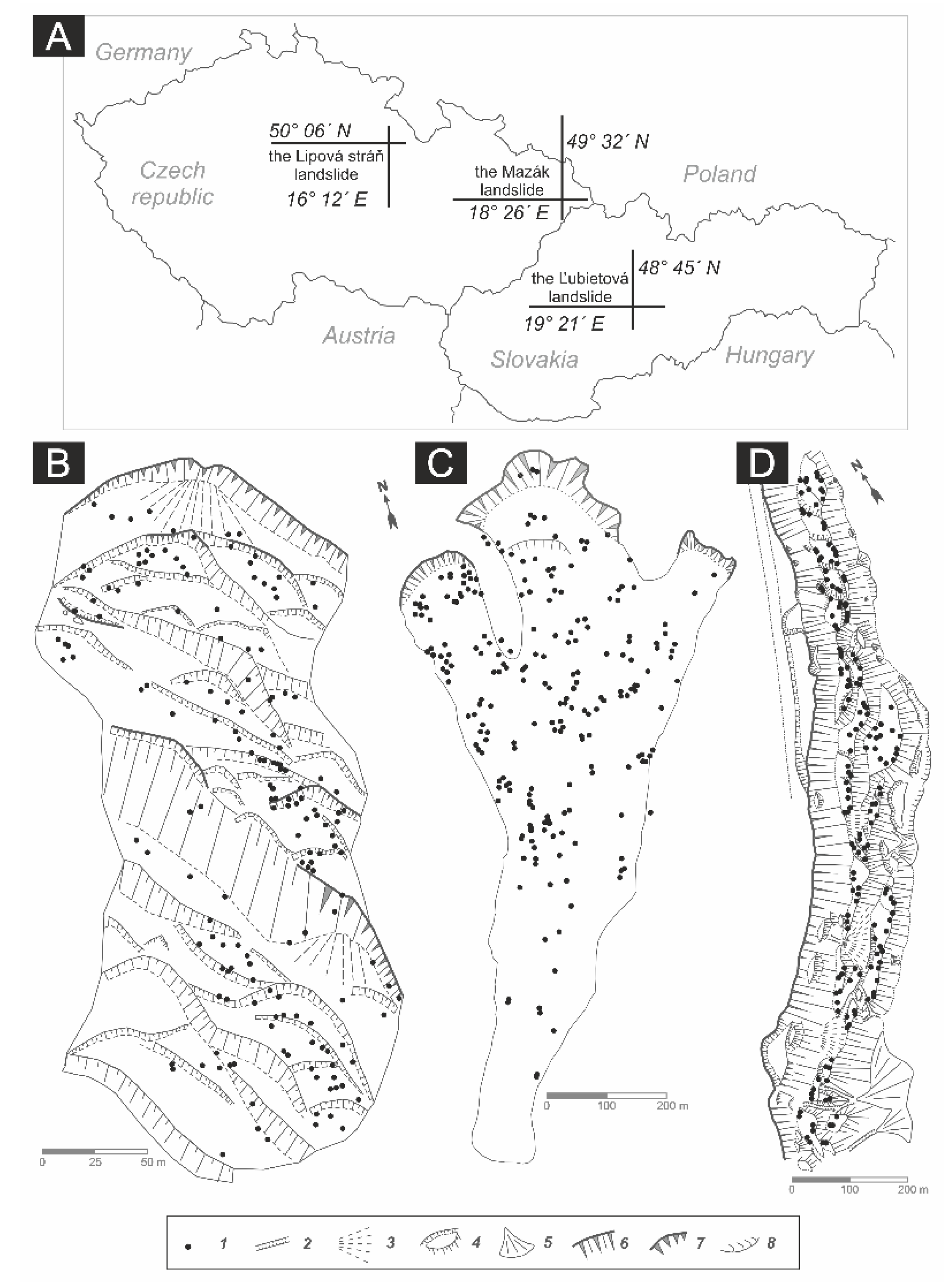
2. Study Area
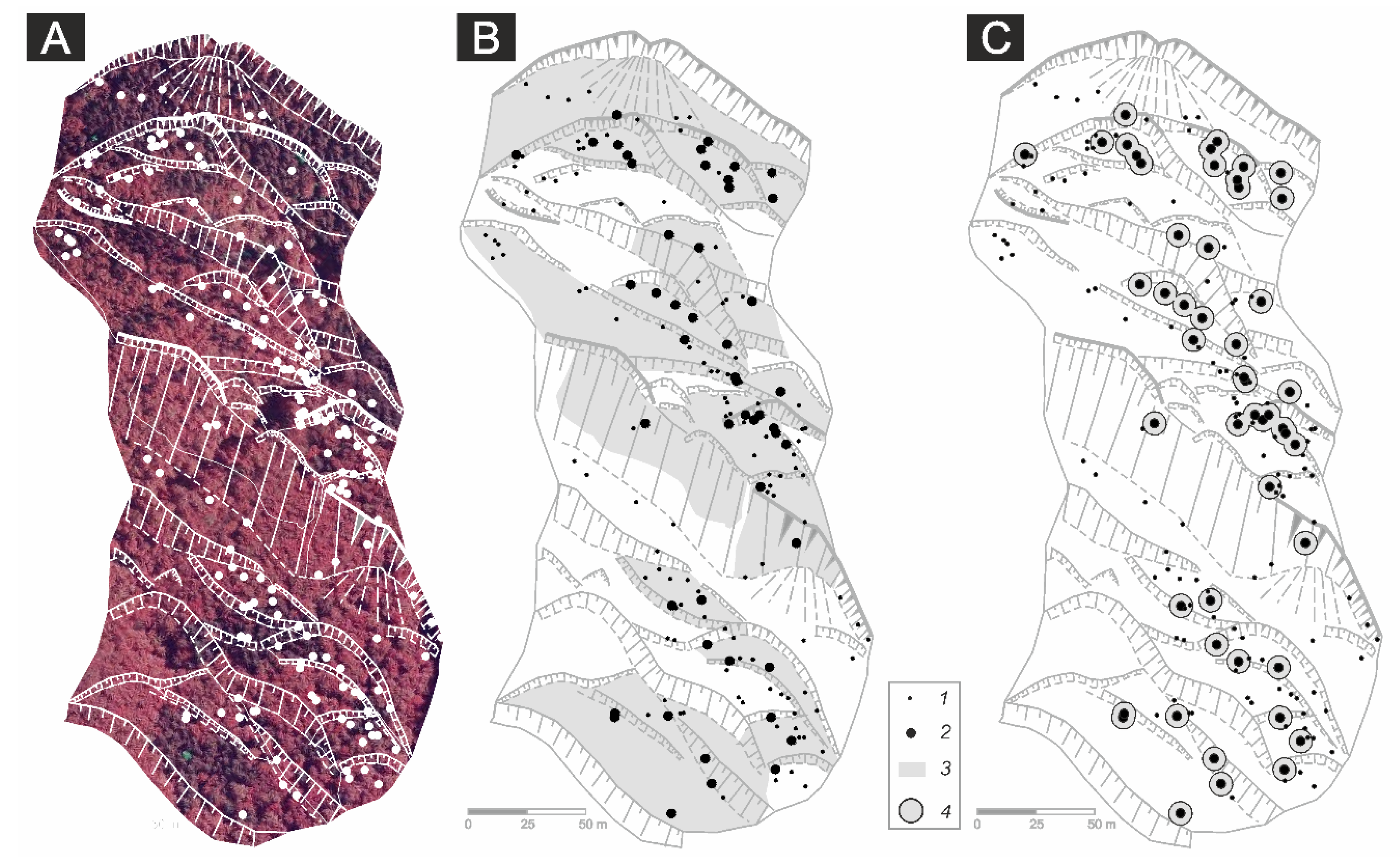
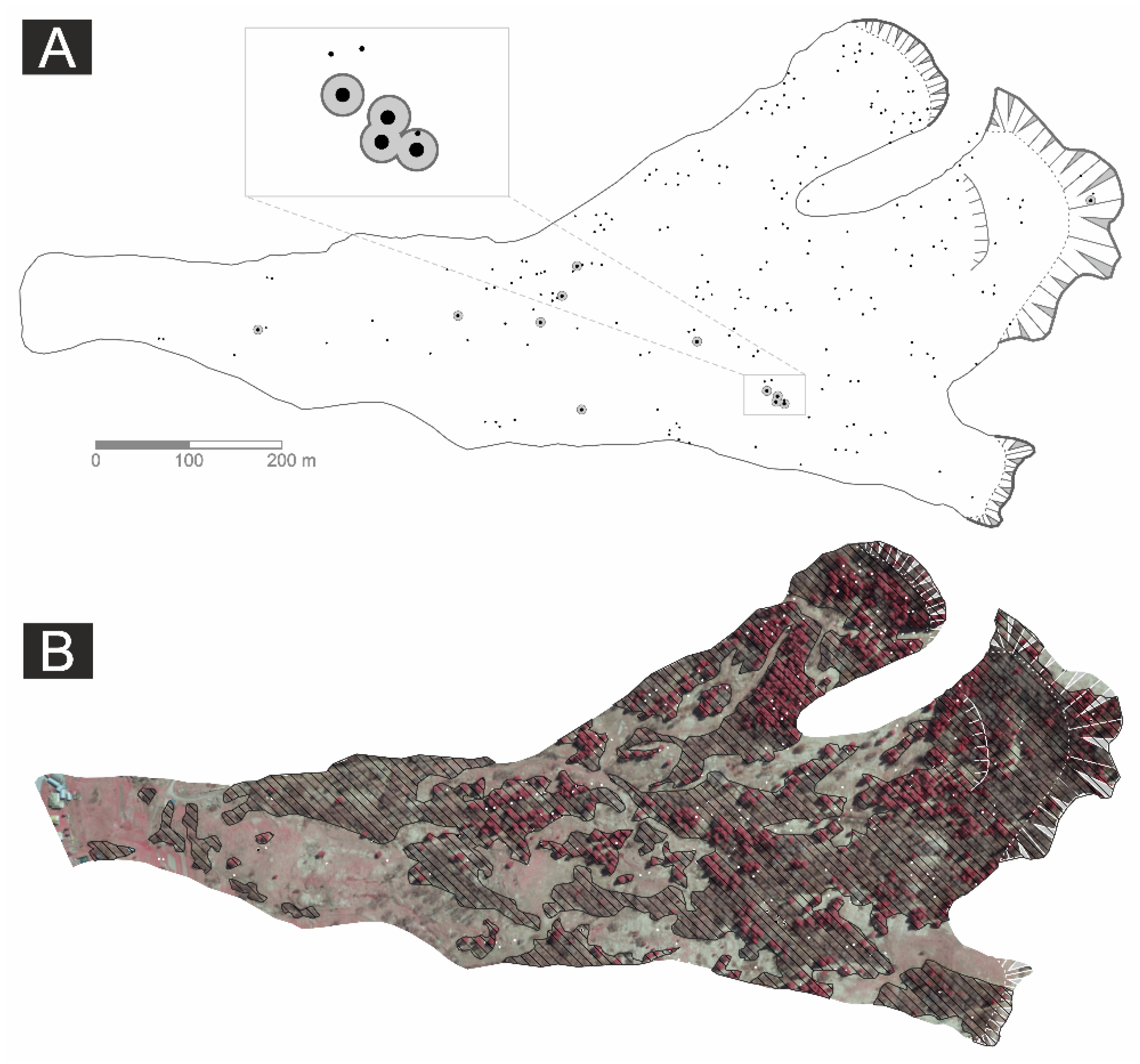
3. Materials and Methods
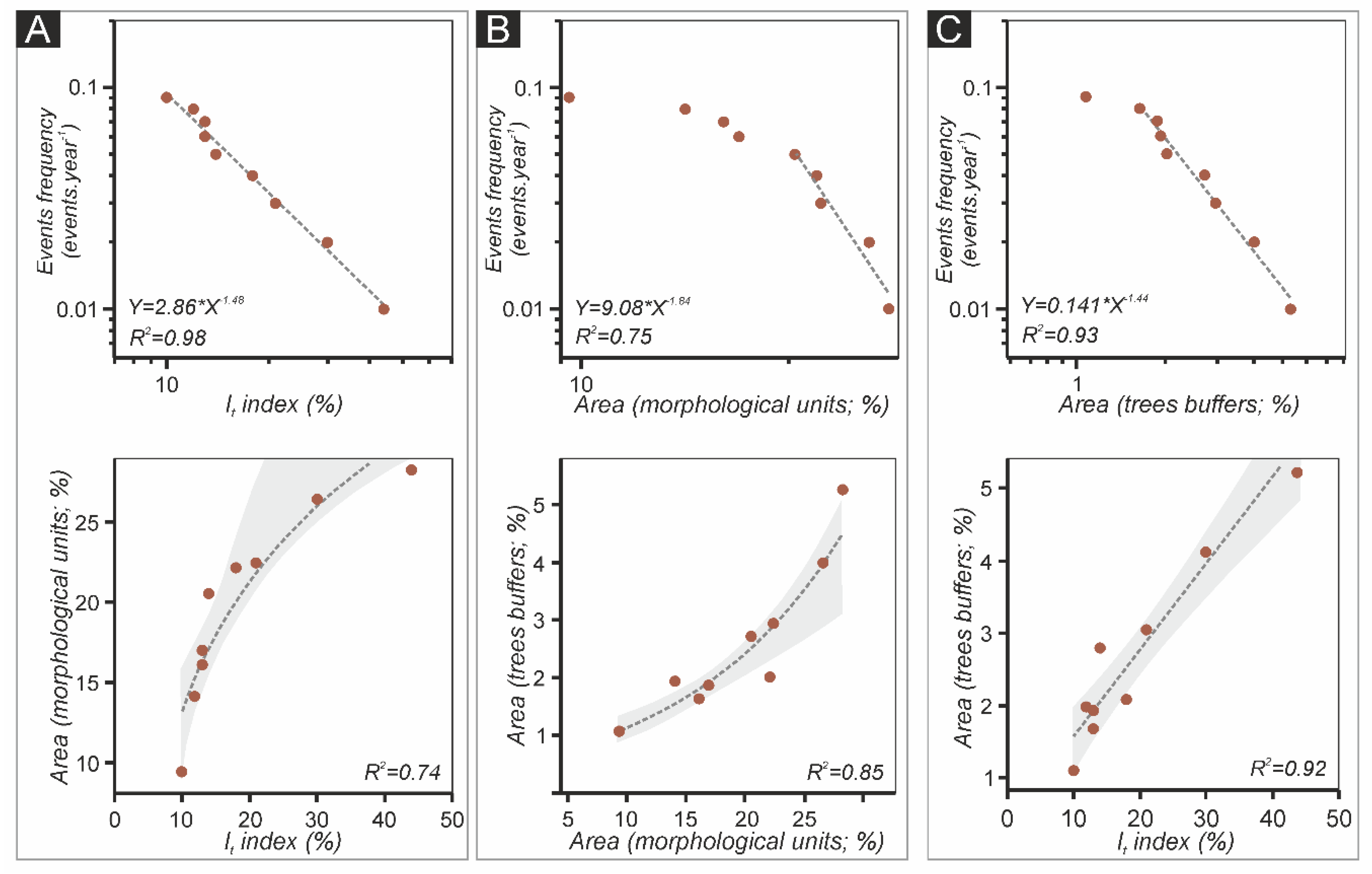
4. Results
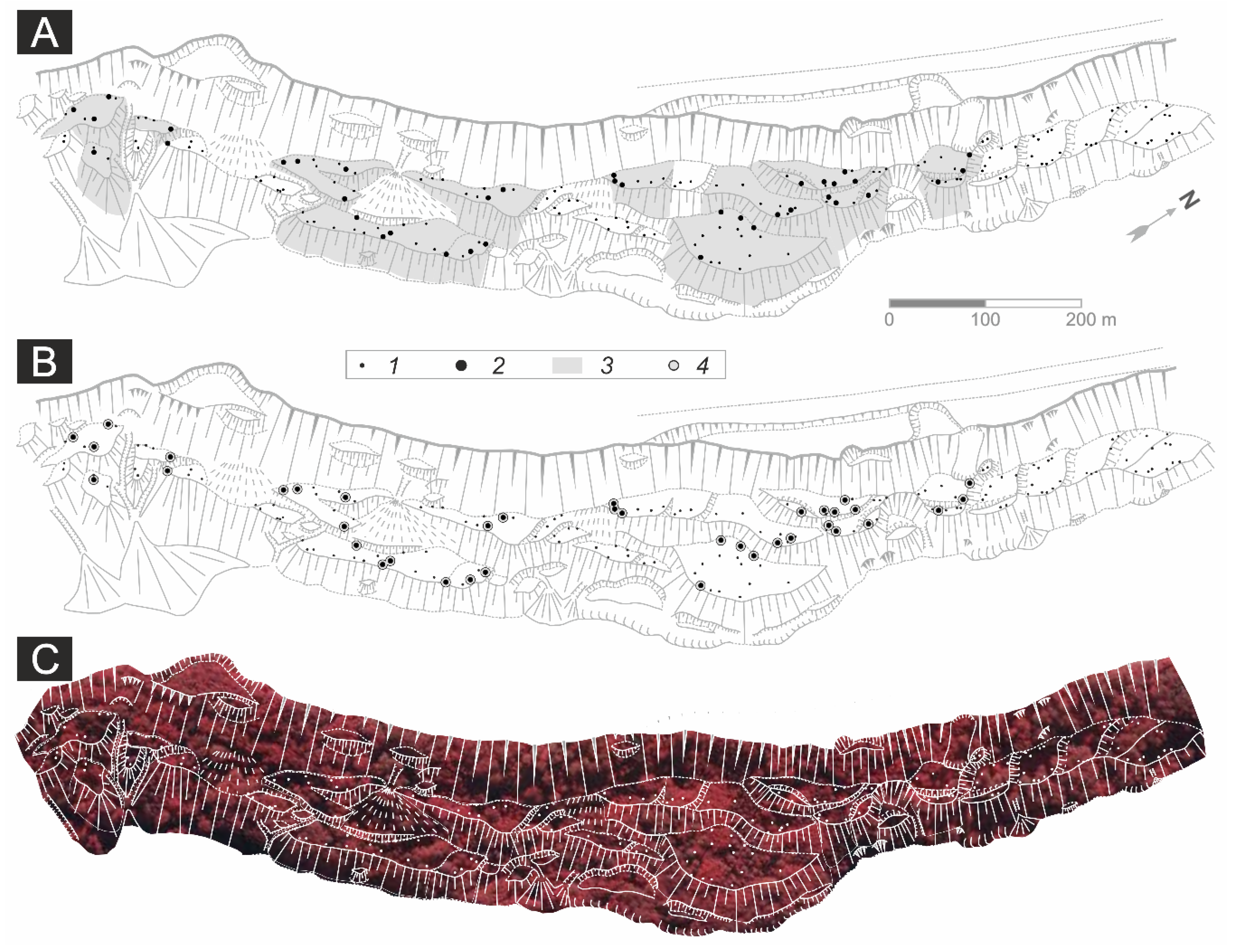
4.1. Number of Sampled Trees, Dated Growth Disturbances and Reconstructed Mass Movement Events
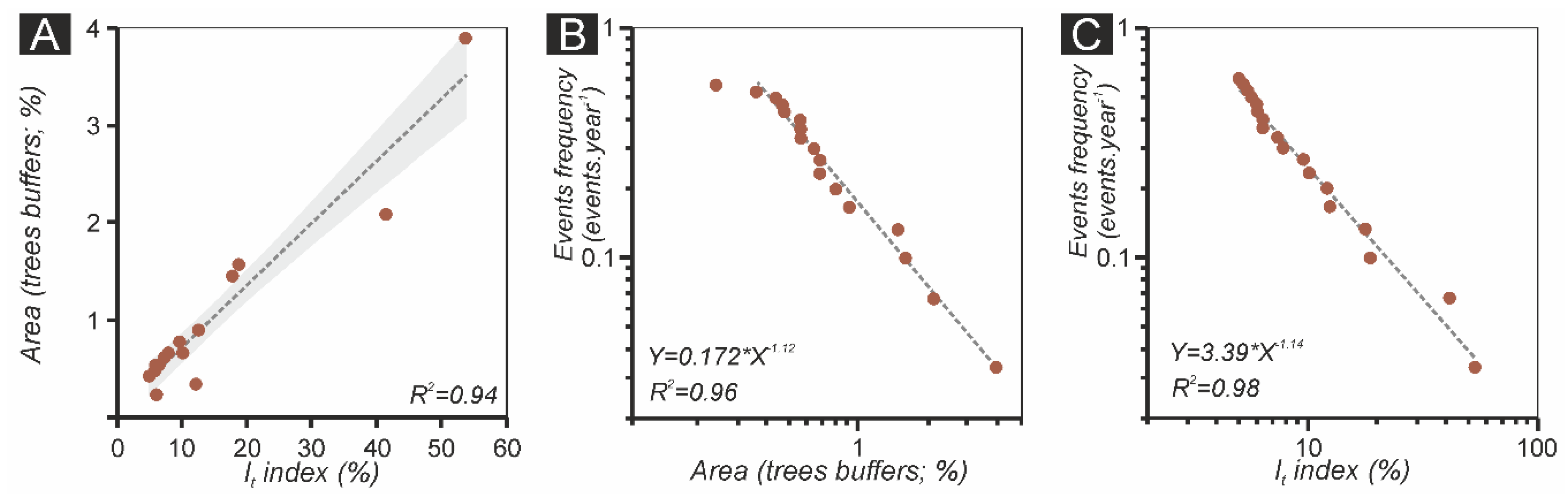
4.2. Magnitude–Frequency Relationships of Mass Movement Events
5. Discussion
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Rickenmann, D. Empirical relationships for debris flows. Nat. Hazards 1999, 19, 47–77. [Google Scholar] [CrossRef]
- Hungr, O.; Evans, S.G.; Hazzard, J. Magnitude and frequency of rock falls and rock slides along the main transportation corridors of south-western British Columbia. Can. Geotech. J. 1999, 36, 224–238. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Wieczorek, G.F. Rockfall hazard and risk assessment in the Yosemite Valley, California, USA. Nat. Hazards Earth Syst. Sci. 2003, 3, 491–503. [Google Scholar] [CrossRef]
- Van Steijn, H. Debris-flow magnitude–frequency relationships for mountainous regions of Central and Northwest Europe. Geomorphology 1996, 15, 259–273. [Google Scholar] [CrossRef]
- Jakob, M.; Bovis, M.; Oden, M. The significance of channel recharge rates for estimating debris-flow magnitude and frequency. Earth Surf. Process. Landf. 2005, 30, 755–766. [Google Scholar] [CrossRef]
- Hungr, O.; McDougall, S.; Wise, M.; Cullen, M. Magnitude–frequency relationships of debris flows and debris avalanches in relation to slope relief. Geomorphology 2008, 96, 355–365. [Google Scholar] [CrossRef]
- Mao, L.; Cavalli, M.; Comiti, F.; Marchi, L.; Lenzi, M.A.; Arattano, M. Sediment transfer processes in two Alpine catchments of contrasting morphological settings. J. Hydrol. 2009, 364, 88–98. [Google Scholar] [CrossRef]
- Mediero, L.; Santillán, D.; Garrote, L.; Granados, A. Detection and attribution of trends in magnitude, frequency and timing of floods in Spain. J. Hydrology 2017, 517, 1072–1088. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.; Singh, V.P.; Sun, P.; Chen, X.; Kong, D. Magnitude, frequency and timing of floods in the Tarim River basin, China: Changes, causes and implications. Glob. Planet. Chang. 2016, 139, 44–55. [Google Scholar] [CrossRef]
- Hovius, N.; Stark, C.P.; Allen, P.A. Sediment flux from a mountain belt derived by landslide mapping. Geology 1997, 25, 231–234. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L.; Guzzetti, F.; Reichenbach, P. Landslide inventories and their statistical properties. Earth Surf. Process. Landf. 2004, 29, 687–711. [Google Scholar] [CrossRef]
- Van Den Eeckhaut, M.; Poesen, J.; Govers, G.; Verstraeten, G.; Demoulin, A. Characteristics of the size distribution of recent and historical landslides in a populated hilly region. Earth Planet. Sci. Let. 2007, 256, 588–603. [Google Scholar] [CrossRef]
- Pelletier, J.D.; Malamud, B.D.; Blodgett, T.; Turcotte, D.L. Scale-invariance of soil moisture variability and its implications for the frequency–size distribution of landslides. Eng. Geol. 1997, 48, 255–268. [Google Scholar] [CrossRef]
- Yanosky, T.M.; Jarrett, R.D. Dendrochronologic evidence for the frequency and magnitude of paleofloods. In: House, P.K.; Webb, R.H.; Baker, V.R.; Levish, D.R. (Eds) Ancient floods, modern hazards: Principles and Applications of Paleoflood Hydrology. Water Sci. Appl. 2002, 5, 77–89. [Google Scholar]
- Guzzetti, F.; Malamud, B.D.; Turcotte, D.L.; Reichenbach, P. Power-lawcorrelations of landslide areas in central Italy. Earth Planet. Sci. Lett. 2002, 195, 169–183. [Google Scholar] [CrossRef]
- Tanyas, H.; van Westen, C.J.; Allstadt, K.E.; Jibson, R.W. Factors controlling landslide frequency-area distribution. Earth Surf. Proc. Landforms 2019, 30, 900–917. [Google Scholar] [CrossRef]
- Dai, F.C.; Lee, C.F. Frequency–volume relation and prediction of rainfall induced landslides. Eng. Geol. 2001, 59, 253–266. [Google Scholar] [CrossRef]
- Lang, A.; Moya, J.; Corominas, J.; Schrott, L.; Dikau, R. Classic and new dating methods for assessing the temporal occurrence of mass movements. Geomorphology 1999, 30, 33–52. [Google Scholar] [CrossRef]
- Raška, P.; Klimeš, J.; Dubišar, J. Using local archive sources to reconstruct historical landslide occurrence in selected urban regions of the Czech Republic: Examples from regions with different historical development. Land Degrad. Dev. 2015, 2, 142–157. [Google Scholar] [CrossRef]
- Pánek, T. Recent progress in landslide dating: A global overview. Progress Phys. Geogr. 2015, 39, 168–198. [Google Scholar] [CrossRef]
- Alestalo, J. Dendrochronological interpretation of geomorphic processes. Fennia 1971, 105, 1–139. [Google Scholar]
- Stoffel, M.; Butler, D.R.; Corona, C. Mass movements and tree rings: A guide to dendrogeomorphic field sampling and dating. Geomorphology 2013, 200, 106–120. [Google Scholar] [CrossRef]
- Corona, C.; Lopez-Saez, J.; Stoffel, M. Defining optimal sample size, sampling design and thresholds for dendrogeomophic landslide sampling. Quat. Geochronol. 2014, 22, 72–84. [Google Scholar] [CrossRef]
- Strunk, H. Dating of geomorphological processes using dendrogeomorphological methods. Catena 1997, 31, 137–151. [Google Scholar] [CrossRef]
- Stoffel, M.; Bollschweiler, M. Tree-ring reconstruction of past debris flows based on a small number of samples–possibilities and limitations. Landslides 2009, 6, 225–230. [Google Scholar] [CrossRef][Green Version]
- Šilhán, K.; Pánek, T.; Hradecký, J.; Stoffel, M. Tree-age control on reconstructed debris-flow frequencies: Examples from a regional dendrogeomorphic reconstruction in the Crimean Mountains. Earth Surf. Process. Landf. 2015, 40, 243–251. [Google Scholar] [CrossRef]
- Corona, C.; Rovéra, G.; Lopez-Saez, J.; Stoffel, M.; Perfettini, P. Spatio-temporal reconstruction of snow avalanche activity using tree rings: Jean Jeanne avalanche talus, Massif de l’Oisans, France. Catena 2010, 83, 107–118. [Google Scholar]
- Voiculescu, M.; Onaca, A. Snow avalanche assessment in the Sinaia ski area (Bucegi Mountains, Southern Carpathians) using the dendrogeomorphology method. Area 2013, 45, 109–122. [Google Scholar] [CrossRef]
- Stoffel, M.; Schneuwly, D.; Bollschweiler, M.; Lièvre, I.; Delaloye, R.; Myint, M.; Monbaron, M. Analyzing rockfall activity (1600–2002) in a protection forest–a case study using dendrogeomorphology. Geomorphology 2005, 68, 224–241. [Google Scholar] [CrossRef]
- Šilhán, K.; Pánek, T.; Hradecký, J. Implications of spatial distribution of rockfall reconstructed by dendrogeomorphological methods. Nat. Hazards Earth Syst. Sci. 2013, 13, 1817–1826. [Google Scholar] [CrossRef]
- Trappmann, D.; Corona, C.; Stoffel, M. Rolling stones and tree rings: A state of research on dendrogeomorphic reconstructions of rockfall. Prog. Phys. Geogr. 2013, 37, 701–716. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Diez-Herrero, A.; Stoffel, M.; Bollschweiler, M.; Bodoque, J.M.; Ballesteros, J.A. Dendrogeomorphic analysis of flash floods in a small ungauged mountain catchment (Central Spain). Geomorphology 2010, 118, 383–392. [Google Scholar] [CrossRef]
- Ballesteros-Cánovas, J.A.; Czajka, B.; Janecka, K.; Lempa, M.; Kaczka, R.J.; Stoffel, M. Flash floods in Tatra Mountain streams: Frequency and triggers. Sci. Tot. Environ. 2015, 511, 639–648. [Google Scholar] [CrossRef] [PubMed]
- Šilhán, K. Frequency, predisposition and triggers of floods in Flysch Carpathians: Regional study using dendrogeomorphic methods. Geomorphology 2015, 234, 243–253. [Google Scholar] [CrossRef]
- Fantucci, R.; Sorriso-Valvo, M. Dendrogeomorphological analysis of a slope near Lago, Calabria (Italy). Geomorphology 1999, 30, 165–174. [Google Scholar] [CrossRef]
- Lopez-Saez, J.; Corona, C.; Stoffel, M.; Astrade, L.; Berger, F.; Malet, J.P. Dendrogeomorphic reconstruction of past landslide reactivation with seasonal precision: Bois Noir landslide, southern French Alps. Landslides 2012, 9, 189–203. [Google Scholar] [CrossRef]
- Šilhán, K.; Pánek, T.; Dušek, R.; Havlů, D.; Brázdil, R.; Kašičková, L.; Hradecký, J. The dating of bedrock landslide reactivations using dendrogeomorphic techniques: The Mazák landslide, Outer Western Carpathians (Czech Republic). Catena 2013, 104, 1–13. [Google Scholar] [CrossRef]
- Moya, J.; Corominas, J. Determination of the spatial and temporal activity of landslides based on tree-ring analysis. In Proceedings of the Seventh International Symposium of Landslides, Balkema, Rotterdam, 17–21 June 1996; pp. 321–326. [Google Scholar]
- Stoffel, M. Magnitude-frequency relationships of debris flows–a case study based on field surveys and tree-ring records. Geomorphology 2010, 116, 67–76. [Google Scholar] [CrossRef]
- Jakob, M.; Friele, P. Frequency and magnitude of debris flows on Cheekye River, British Columbia. Geomorphology 2010, 114, 382–395. [Google Scholar] [CrossRef]
- Corominas, J.; Moya, J. Contribution of dendrochronology to the determination of magnitude–frequency relationships for landslides. Geomorphology 2010, 124, 137–149. [Google Scholar] [CrossRef]
- Stefanini, M.C. Spatio-temporal analysis of a complex landslide in the Northern Apennines (Italy) by means of dendrochronology. Geomorphology 2004, 63, 191–202. [Google Scholar] [CrossRef]
- Šilhán, K. Dendrogeomorphological analysis of the evolution of slope processes on flysch rocks (Vsetínské vrchy Mts; Czech Republic). Carpath. J. Earth Environ. Sci. 2012, 7, 39–49. [Google Scholar]
- Wistuba, M.; Malik, I.; Wójcicki, K.; Michałowicz, P. Coupling between landslides and eroding stream channels reconstructed from spruce tree rings (examples from the Carpathians and Sudetes–Central Europe). Earth Surf. Process. Landf. 2015, 40, 293–312. [Google Scholar] [CrossRef]
- Šilhán, K. Can tree tilting indicate mechanisms of slope movement? Eng. Geol. 2015, 199, 157–164. [Google Scholar] [CrossRef]
- Šilhán, K. How different are the results acquired from mathematical and subjective methods in dendrogeomorphology? Insights from landslide movements. Geomorphology 2016, 253, 189–198. [Google Scholar] [CrossRef]
- Prokešová, R.; Kardoš, M.; Tábořík, P.; Medveďová, A.; Stacke, V.; Chudý, F. Kinematic behaviour of a large earthflow defined by surface displacement monitoring, DEM differencing, and ERT imaging. Geomorphology 2014, 224, 86–101. [Google Scholar] [CrossRef]
- Šilhán, K.; Prokešová, R.; Medveďová, A.; Tichavský, R. The effectiveness of dendrogeomorphic methods for reconstruction of past spatio-temporal landslide behaviour. Catena 2016, 147, 325–333. [Google Scholar] [CrossRef]
- Čech, S. Geological map 1:50 000 Rychnov nad Kněžnou; Czech Geological Survey: Brno, Czechia, 2001. [Google Scholar]
- Fussgänger, F.; Jadroň, D.; Banský, M.; Tyleček, B. Ľubietová—Translational Slide, Final Report from Geological Surveying; Geofond: Bratislava, Slovakia, 1978; p. 78. (In Slovak) [Google Scholar]
- Stoffel, M.; Bollschweiler, M. Tree-ring analysis in natural hazards research–an overview. Nat. Hazards Earth Syst. Sci. 2008, 8, 187–202. [Google Scholar] [CrossRef]
- VIAS Vienna Institute of Archaeological Science, Time Table. Installation and Instruction Manual, Ver. 2.1; VIAS: Wien, Austria, 2005. [Google Scholar]
- Westing, A.H. Formation and function of compression wood in gymnosperms II. Bot. Rev. 1965, 34, 51–78. [Google Scholar] [CrossRef]
- Carrara, P.; O’Neill, J.M. Tree-ring dated landslide movements and their relationship to seismic events in southwestern Montana, USA. Quat. Res. 2003, 59, 25–35. [Google Scholar] [CrossRef]
- Braam, R.R.; Weiss, E.E.J.; Burrough, P.A. Spatial and temporal analysis of mass movement using dendrochronology. Catena 1987, 14, 573–584. [Google Scholar] [CrossRef]
- Shroder, J.F. Dendrogeomorphological analysis of mass movement on Table Cliffs Plateau, Utah. Quat. Res. 1978, 9, 168–185. [Google Scholar] [CrossRef]
- Reardon, B.A.; Pederson, G.T.; Caruso, C.J.; Fagre, D.B. Spatial reconstructions and comparisons of historic snow avalanche frequency and extent using tree rings in Glacier National Park, Montana, U.S.A. Arct. Antarct. Alp. Res. 2008, 40, 148–160. [Google Scholar] [CrossRef]
- ESRI. ArcGIS 10.1; ESRI: Redlands, CA, USA, 2011. [Google Scholar]
- Šilhán, K.; Pánek, T.; Hradecký, J. Tree-ring analysis in the reconstruction of slope instabilities associated with earthquakes and precipitation (the Crimean Mountains, Ukraine). Geomorphology 2012, 173–174, 174–184. [Google Scholar] [CrossRef]
- Lopez-Saez, J.; Corona, C.; Stoffel, M.; Schoeneich, P.; Berger, F. Probability maps of landslide reactivation derived from tree-ring records: Pra Bellon landslide, southern French Alps. Geomorphology 2012, 138, 189–202. [Google Scholar] [CrossRef]
- Zhang, Y.; Stoffel, M.; Liang, E.; Guillet, S.; Shao, X. Centennial-scale process activity in a complex landslide body in the Qilian Mountains, northeast Tibetan Plateau, China. Catena 2019, 179, 29–38. [Google Scholar] [CrossRef]
- Šilhán, K. Tree ring eccentricity in the dendrogeomorphic analysis of landslides—A comparative study. Catena 2019, 174, 1–10. [Google Scholar] [CrossRef]
- Šilhán, K.; Stoffel, M. Impacts of age-dependent tree sensitivity and dating approaches on dendrogeomorphic time series of landslides. Geomorphology 2015, 236, 34–43. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Guzzetti, F.; Rossi, M. Probability distributions of landslide volumes. Nonlinear Process. Geophys. 2009, 16, 179–188. [Google Scholar]


© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šilhán, K. Tree Ring-Based Estimation of Landslide Areal Reactivation as a Fundament of Magnitude–Frequency Assessment. Forests 2020, 11, 400. https://doi.org/10.3390/f11040400
Šilhán K. Tree Ring-Based Estimation of Landslide Areal Reactivation as a Fundament of Magnitude–Frequency Assessment. Forests. 2020; 11(4):400. https://doi.org/10.3390/f11040400
Chicago/Turabian StyleŠilhán, Karel. 2020. "Tree Ring-Based Estimation of Landslide Areal Reactivation as a Fundament of Magnitude–Frequency Assessment" Forests 11, no. 4: 400. https://doi.org/10.3390/f11040400
APA StyleŠilhán, K. (2020). Tree Ring-Based Estimation of Landslide Areal Reactivation as a Fundament of Magnitude–Frequency Assessment. Forests, 11(4), 400. https://doi.org/10.3390/f11040400




