A Novel GIS-Based Random Forest Machine Algorithm for the Spatial Prediction of Shallow Landslide Susceptibility

Abstract

This study developed and verified a new hybrid machine learning model, named random forest machine (RFM), for the spatial prediction of shallow landslides. RFM is a hybridization of two state-of-the-art machine learning algorithms, random forest classifier (RFC) and support vector machine (SVM), in which RFC is used to generate subsets from training data and SVM is used to build decision functions for these subsets. To construct and verify the hybrid RFM model, a shallow landslide database of the Lang Son area (northern Vietnam) was prepared. The database consisted of 101 shallow landslide polygons and 14 conditioning factors. The relevance of these factors for shallow landslide susceptibility modeling was assessed using the ReliefF method. Experimental results pointed out that the proposed RFM can help to achieve the desired prediction with an F1 score of roughly 0.96. The performance of the RFM was better than those of benchmark approaches, including the SVM, RFC, and logistic regression. Thus, the newly developed RFM is a promising tool to help local authorities in shallow landslide hazard mitigations.

1. Introduction

A landslide, which is defined as the slope movement of soil, mud, debris, or rock, is the most common geological hazard in the world [1]. This hazard happens as a consequence of other events or actions, such as torrential rain, earthquake, deforestation, or mineral exploitation. Globally, landslides have substantial social and economic impacts. Globally, during the 1995–2014 period, more than 3876 landslides occurred causing 163,658 deaths and 11,689 injuries [2].

Vietnam is one of the countries profoundly affected by landslides in Asia. According to the Institute of Geosciences and Mineral Resources in Vietnam, there are more than 10,200 locations that have a high risk of landslides in the northern mountainous provinces [3]. From 2000 to 2015, there were 250 flash floods and landslides, with 779 people killed or going missing and 426 others injured. Therefore, being able to predict future landslides can assist with policy-making and development-planning and, as a result, can save lives and reduce economic damages through prevention and mitigation measures.

Landslide prediction can be built in the form of susceptibility maps where the likelihood of a future landslide occurring is given based on a set of local terrain conditions and geo-environmental factors [4]. Literature review shows that five main approaches are used for constructing landslide susceptibility, namely: (a) geomorphological mapping, (b) heuristic or index-based approaches, (c) analysis of landslide inventories, (d) physics-based methods, and (e) statistically-based methods. The first two approaches are qualitative methods [4]. In other words, they are subjective and present susceptibility levels in descriptive terms. They rely heavily on the researcher in charge. In geomorphological mapping, a direct method, the susceptibility map is built through evaluating and mapping the actual and potential slope failure [5,6,7,8]. In the heuristic approach, the researcher ranks and weights all the known instability factors based on their expert experience [9]. The last three approaches are indirect and quantitative. Analyses of landslide inventories use present and past landslides to predict the occurrence of future ones [10,11]. Physics-based methods, on the other hand, use simplified physical models to simulate and predict slope instability [12,13,14]. Lastly, statistically-based methods attempt to build the functional relationship between past landslides, present landslides, and some inferred conditioning factors [15,16,17,18,19,20].

Among these approaches, statistically-based methods are by far the most popular ones. According to [4], from January 1983 to June 2016, there were 565 peer-reviewed articles on statistically-based landslide susceptibility models. The popularity of these techniques include both classical ones, such as discriminant analysis, logistic regression [21,22,23,24,25], data overlay, multi-criteria decision evaluation, and machine-learning-based ones, such as artificial neural networks [26], neuro-fuzzy models [27], support vector machine [28], decision trees [29], and sophisticated hybrid or ensemble learning approaches [16,30,31,32].

Multiple factors determine the popularity of statistically-based methods. First, it is their use of natural characteristics that allow them to be used in many scenarios for different regions of interest [4]. Second, these methods have demonstrated their effectiveness for a wide range of applications, as reported in various previous works [33,34]. Third, with the introduction of GIS, spatial-temporal landslide data can be seamlessly integrated with data of multiple conditioning factors. This provides a perfect setting for statistically-based methods to be built.

With GIS, greater inferred instability factors, including the relationship between past and present landslides, are considered and these factors become more and more nonlinear. Consequently, traditional linear methods, such as linear discriminant analysis and linear/logistics regression, are not satisfactory. Since 2000, machine learning and artificial intelligence (MLAI) have become increasingly popular due to their ability to handle multiple governing factors and nonlinearity. Thus, MLAIs have proven their efficiency in the spatial prediction of various geoscience fields, such as atmospheric particulate matter [35], earth fissure [36], snow avalanche [37,38], multi-hazard exposure [39], groundwater [40], and flash flood [41,42]. In landslide studies, the most vital issue for the successful application of MLAI is the ability to generate probabilistic inferences, which are widely used for susceptibility indices. Following this success trend, new and advanced MLAI algorithms for landslide modeling have received much interest. This is because, despite their versatility, there is still no single algorithm that is the best for all study areas [43,44]. The effectiveness of MLAI algorithms can significantly depend not only on the characteristics of the considered study region but also on the data available.

In this work, we developed and proposed, for the first time, a novel hybridization of random forest classifier (RFC) and support vector machine (SVM), named random forest machine (RFM), for shallow landslide susceptibility prediction. The RFC model, also called a random decision forest classifier, was introduced initially by Ho [45] and, then, further developed by Breiman [46]. Whereas, the SVM model, developed by Vapnik and collaborators [47,48], is widely recognized as a powerful and robust model in environmental modeling. It is noted that the application of individual RFC or SVM for landslide susceptibility studies has been widely carried out [25,49,50,51].

The critical advantage of RFC is to build a forest of tree predictors, where each predictor operates on a random subset of data. The final classification is developed to take into account the results of all the predictors. The SVM classifier, on the other hand, is a maximum-margin classifier, where hyper-planes are constructed to separate classes. To the best of our knowledge, no research on a combination of the two algorithms has been conducted. Thus, the novelty of our proposed hybrid method is that SVM builds decision functions by using sub-datasets generated by RFC. Then, support vectors are determined to maximize the margins between the training data and the classifying borders.

Consequently, smoother final borders were derived with lows for both the number of trees and the depth level of each tree. Furthermore, the proposed hybrid method also avoided the limitations of SVM when working with large training datasets. Herein, the model only fed their subsets and facilitated parallel model training. The rest of the paper is organized as follows: the second section provides a general description and inventory of the study area. The third section reviews the RFC and SVM algorithms. The combination of these two algorithms to build landslide susceptibility maps is explained in the fourth section, followed by the reported experimental results. The last section is devoted to the discussion of experimental results.

2. The Study Area and the Landslide Inventory

2.1. General Description of the Study Area

The city chosen was the capital city of Lang Son province in northern Vietnam. It is located between the longitudes of 106°41′34′′ E and 106°48′32′′ E, and between the latitudes of 21°49′43′′ N and 21°57′13′′ N. The study area was roughly 101.3 km², slightly larger than the official area of Lang Son city (see Figure 1). The elevation of the area ranges from 214 to 800 m, with an average of 325.6 m above standard sea level.

The area has a strong northeastern-monsoon-influenced climate with high humidity (between 80% and 85%) and a high amount of rainfall (annually average from 1200 to 1600 mm). The rainy season is usually from May to September, but might last longer, up to 10 months. The area is relatively far from the sea and rarely on the direct path of tropical cyclones or tropical depressions. However, these extreme weather events can affect the weather of the region, causing prolonged torrential rains, which are the leading cause of landslides in the region, according to historical records.

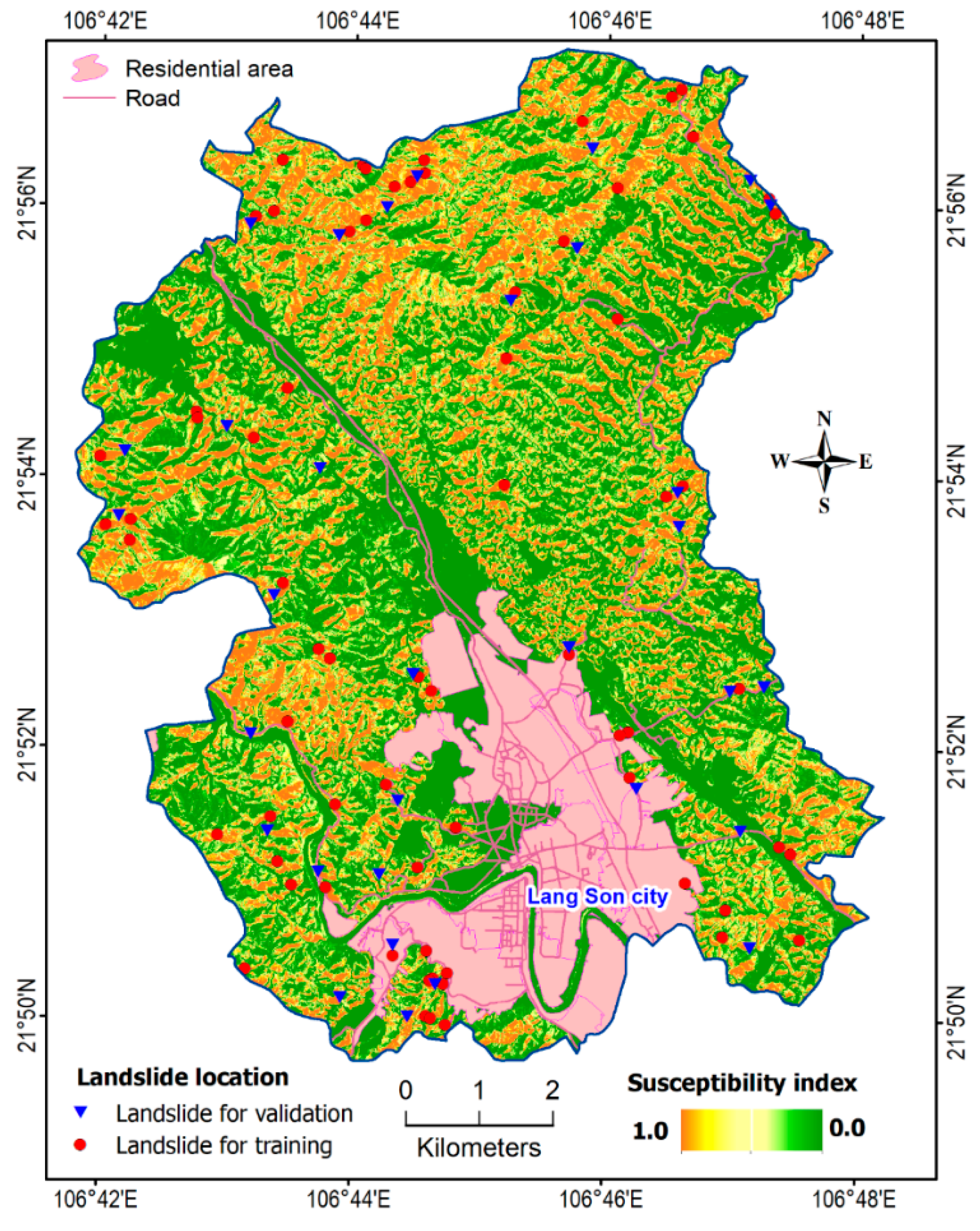
2.2. Landslide Inventory Map

Information on past landslides in the area were collected to build the inventory map. We used different ways to obtain the necessary data. For landslides occurring before 2003, the locations were extracted from (1) field survey data with handheld GPSs and (2) one-meter resolution aerial photographs provided by the Vietnam Aerial Photography and Photogrammetry company [52]. For landslides that occurred in the period from 2003 to 2009, we got the locations from previous projects [53]. Lastly, for recent landslides, the locations were obtained from the field works of [32]. The inventory map contained only the information of rainfall-induced landslides, as there has never been a documented earthquake-induced landslide in the region. Few rockfall events were eliminated from the inventory as we were only interested in soil slides and debris flows.

In the final version of the inventory map (refer to Figure 1), there were 101 landslide polygons, which were split into two separate groups. Group 1 with 69 polygons was devoted to model training and group 2, consisting of 32 polygons, was employed for model validation. The total number of pixels of both groups was 3455, where 2410 pixels belonged to group 1 and 1045 pixels belonged to group 2. In order to have a complete data set, the GIS database was used to sample non-landslide locations.

2.3. Landslide Conditioning Factors

One of the few widely accepted principles in landslide prediction is that the conditioning factors that caused past and recent landslides will likely be the ones triggering future landslides [4]. Also, according to previous studies [54,55,56], a good selection of landslide conditioning factors is one of the vital requirements to have accurate landslide susceptibility maps. Based on an analysis performed by [32], other previous works [24,52], and the availability of data in the study region, 14 conditioning factors were chosen for this study. They included 10 geomorphometrical factors, namely, slope angle (SA), slope length (SL), slope aspect (SA), curvature (Curv.), elevation (Elev.), topographic wetness index (TWI), stream power index (SPI), sediment transport index (STI), valley depth (VD), toposhade (Topo.), and 4 geo-environmental factors, namely lithology (Lith.), land use (LU), soil type (ST), and distance to faults (DTF).

The geomorphometrical factors were derived from topographic maps at 1:5000 scale for the Lang Son city and 1:10,000 scale for the other study areas. These maps were derived from 1:20,000 scale aerial photos using the Imagestation Stereo Softcopy Kit software Version 2.3 (Intergraph Corporation, Huntsville, AL, USA). The intervals of contour lines were from 0.5 m for flat areas to 5 m for mountainous areas. First, a 5 m × 5 m digital elevation map (DEM) was generated from topographic maps. Then, ArcGIS 10.7.1 (ESRI Inc., Redlands, CA, USA) was utilized to obtain all the geomorphometrical factors using a raster resolution of 5 m. Jenks Natural Break optimization method [57] in ArcGIS 10.2 was employed to classify continuous-values factors (except slope aspect) into classes, as proposed by [58].

Regarding the four geo-environmental factors, lithology was obtained from four tiles of the Geological and Mineral Resources Map (GMRM) of Vietnam at a scale of 1:50,000. Soil type, on the other hand, was extracted from National Pedology Maps (NPM) at a scale of 1:100,000. Land use was obtained from a land use status map at scale 1:50,000 provided by the local authority. Lastly, distance to faults was constructed from the fault lines of the lithological data using ArcGIS 10.2. In summary, all 14 selected conditioning factors and their classes are summarized in Figure 2.

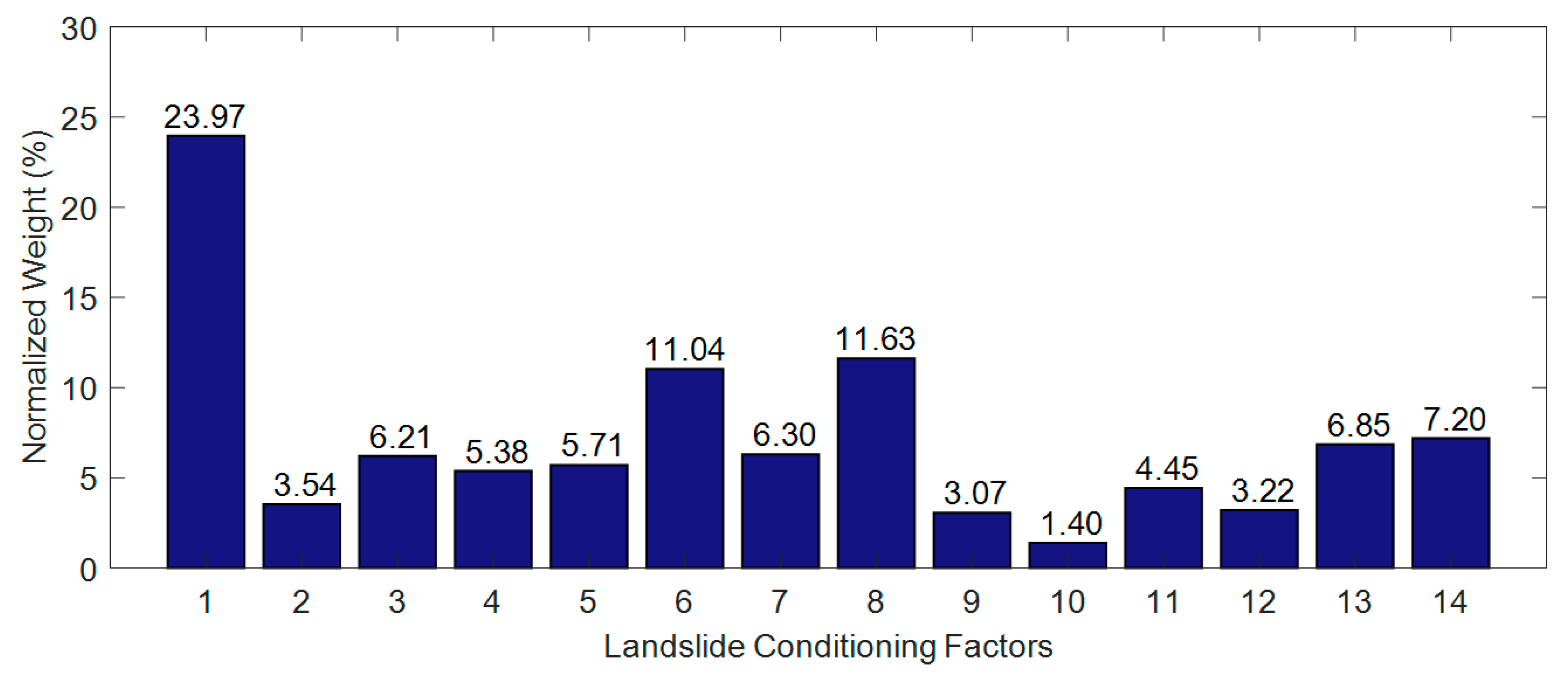
2.4. Investigation on the Importance of the Landslide Conditioning Factors

Before the RFM model training phase commenced, it was necessary to inspect the relevancy of the collected variables used for landslide susceptibility mapping. In this study, the relevance of the influencing factors was preliminarily evaluated by the ReliefF method [59]. The ReliefF method is a probabilistic method used to inspect the conditional dependencies between variables and is capable of expressing the discriminative power of each variable used for data classification purposes. This method calculates a weight value for each variable to quantify its relevancy. A large weight is typically associated with an essential factor. The ReliefF analysis results are depicted in Figure 3. As can be seen from this figure, the slope was the most relevant factor for spatial mapping of landslide susceptibility in the study area, followed by SPI and elevation. Moreover, since all of the variable weights were not null, there was no redundant variable and all of them could be used for spatial mapping of landslide susceptibility.

3. Research Methodology

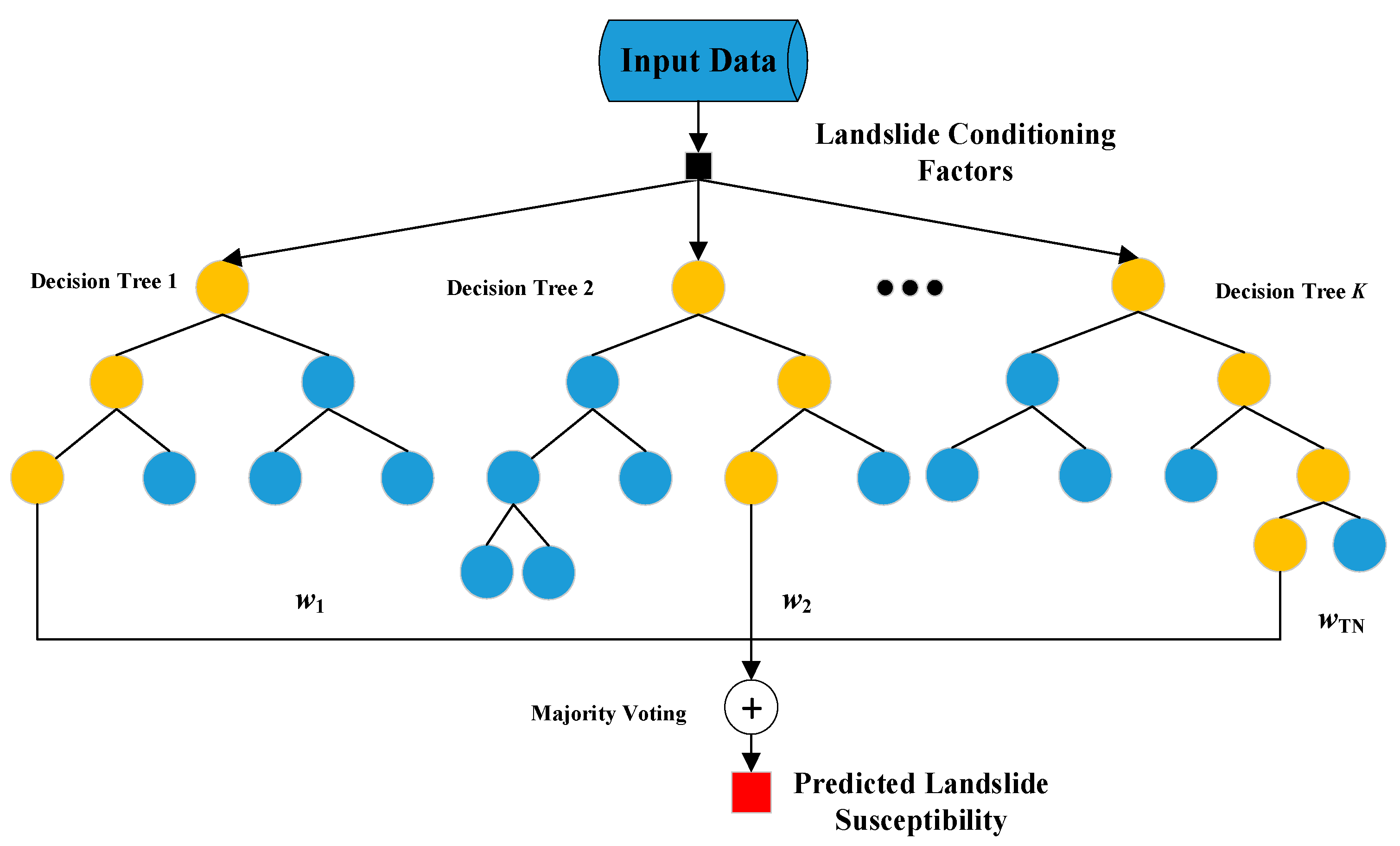
3.1. Random Forest Classifier

RFC is an effective decision tree ensemble used for large-scale and multivariate pattern recognition [60]. This ensemble learning is established based on the concept of the random subspace method [45] and the stochastic discrimination method of classification [61]. The RFC was then further extended by Breiman [46] who introduced the concept of bagging and random feature selection. Equipped with these features, a random forest model becomes a powerful tool to construct an ensemble of classification trees. Successfully applications of RFC have been reported in various studies [25,35,49,62,63,64], including landslide modeling [25,65,66]

Given a labeled data set (D) for training D = (X, Y), in which $x_i\in X$ (i = 1,2, …, N, where N is the number of training samples) is a data sample and $y_i\in Y$ is its class label, the RFC method aims at constructing a model, which is capable of separating the input space into different disjoint regions. Each of the regions is characterized by one class label. To achieve this goal, the method trains k individual decision trees, where each tree is associated with a random Θ_k vector, which represents a subspace of the original input space. Subsequently, a single tree k is constructed by sampling with replacement n < N data samples from the original training set. An individual tree ($h_k$) is therefore expressed as:

$$h_k\left(X,{\mathsf{\Theta }}_k\right)=Y$$

(1)

During the training phase of a decision tree, a node can be expanded with two children to enhance the data classification performance (see Figure 4). This process is characterized by a split cut at the corresponding dth dimension of the input data. The decision tree algorithm selects the most suitable node using the Gini impurity index ($G$) product ($P$) [49]; this product is computed as follows:

$$P=G_1{G}_2$$

(2)

where a Gini impurity index ($G$) of set $k$ is defined as follows [67]:

$$G_k=1-{\displaystyle \sum }_{i=1}^{n_{kc}}{p}_{ki}^2$$

(3)

where $n_{kc}$ represents the number of classes in the considered set and $p_{ki}$ denotes the ratio of the present class $i$ in this set.

When a new input query is presented to the model, the RFC determines its output class through the majority vote standard [68]. Thus, the class label ($y)$ of an input data x is computed from the established ensemble in the following manner:

$$y=H\left(x\right)\underset{z}{=argmax}\left({\displaystyle \sum }_{k}I\left(h_k\left(x,{\mathsf{\Theta }}_k\right)=z\right)\right)$$

(4)

where $I\left(t\right)$ denotes an indicator function defined as follows:

$$I\left(t\right)=\{\begin{array}{cc}1,& t \mathrm{is}\mathrm{true}\\ 0,& t \mathrm{is}\mathrm{false}\end{array}$$

(5)

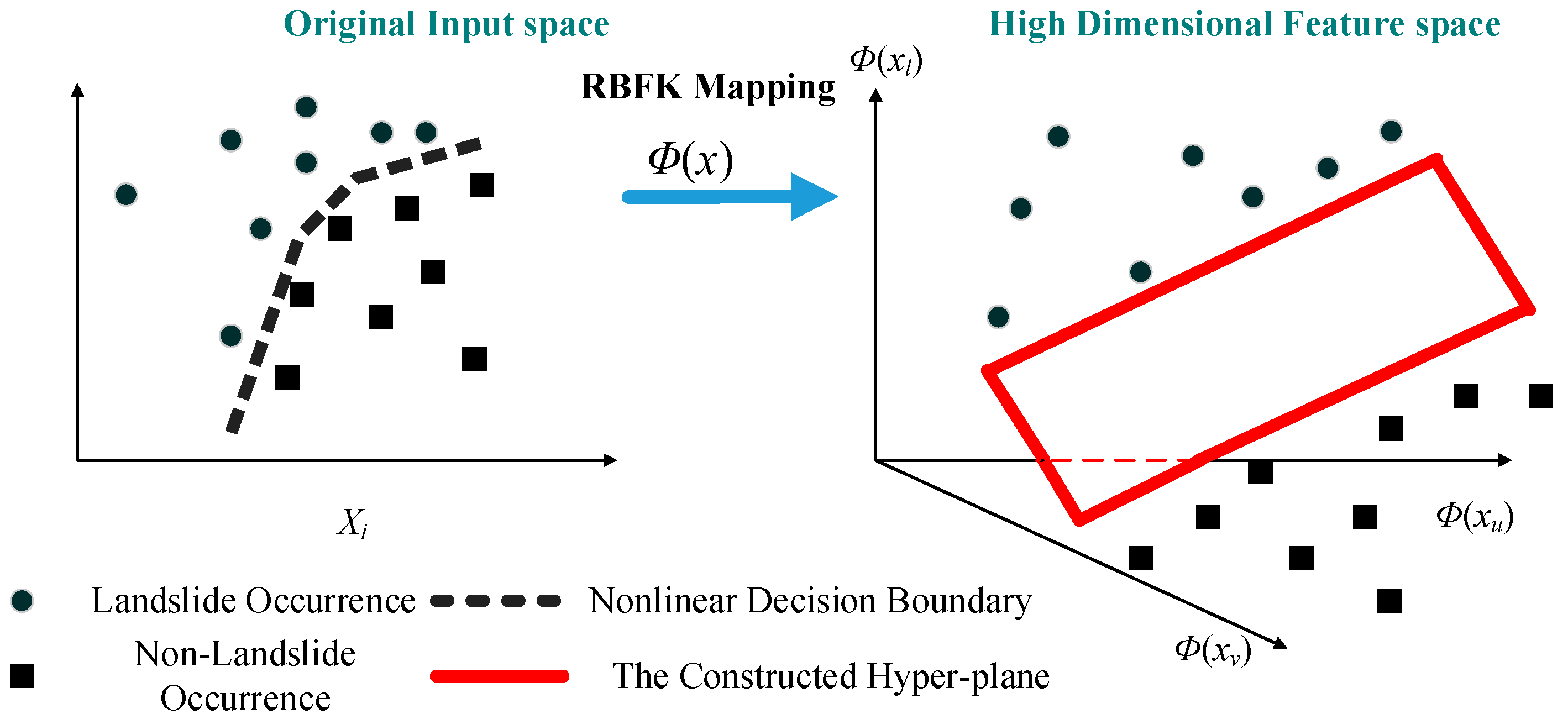
3.2. Support Vector Machine (SVM)

Support vector machine (SVM), proposed by Vapnik [47], is a powerful method for data classification, which is formulated on the basis of statistical learning theory. The main advantages of the SVM are the capability to deal with nonlinearly separable data, the ability to cope with multivariate data, resilience to noise, and the ability to avoid overfitting. The SVM deals with nonlinear datasets via the employment of kernel tricks. This machine learning method first maps the data from the original input space to a high-dimensional feature space within which a hyper-plane can be used to perform data classification (see Figure 5). An SVM-based model is also built on the concept of the maximum margin classifier, which is less sensitive to noise. Moreover, this machine learning is based on the concept of structural risk minimization, which can be resistant to overfitting. Due to such reasons, the SVM has been successfully employed for pattern recognition tasks in natural hazard mapping [37,69,70,71,72]. In landslide modeling, the SVM has been considered to be a standard method in susceptibility mapping and prediction [23,50,51,73,74].

Given a training dataset ${(x_k,y_k)}_{k=1}^N$ with input data $x_k\in R^n$ and corresponding class labels $y_k\in \left(-1,+1\right),$ the SVM model constructs a classification boundary from the training set so that the margin between the two classes is as wide as possible. Herein, the class output of −1 denoted a non-landslide occurrence and +1 represented a landslide occurrence.

The training phase of the SVM-based classification model boils down to solving the following constrained nonlinear programming [75]:

$$\mathrm{Minimize}{J}_p\left(w,e\right)=\frac{1}{2}{w}^{T}w+c\frac{1}{2}{\sum }_{k=1}^N{e}_k^2,$$

(6)

$$\mathrm{subjected}\mathrm{to} y_k\left(w^T\phi \left(x_k\right)+b\right)\ge 1-e_k,k=1,\dots ,N,e_k\ge 0,$$

(7)

where $w \in$Rⁿ denotes a normal vector to the classification hyper-plane; $w^T$ is the transpose matrix of w; b $\in$R denotes the model bias; $e_k>0$ denotes slack variables; c denotes a penalty constant; $\phi \left(x\right)$ is the aforementioned nonlinear data mapping; and $J_p\left(w,e\right)$ is the constrained nonlinear programming.

Another advantage of the SVM is that its training and prediction phase do not require the explicit expression of $\phi \left(x\right)$. Alternatively, the algorithm only requires computing the product of $\phi \left(x\right)$ in the input space, which is essentially a kernel function ($K\left(x_k,x_l\right)$) given by:

$$K\left(x_k,x_l\right)=\phi {(x_k)}^T\phi \left(x_l\right).$$

(8)

where $x_l$ is the RBF center.

Moreover, the radial basis function kernel (RBFK) is often used in the SVM’s training and prediction phases. The formulation of the RBFK is given by:

$$K\left(x_k,x_l\right)=\exp (-\frac{\Vert x_k-x_l\Vert {}^2}{2{\sigma }^2}),$$

(9)

where $\sigma$ denotes a tuning parameter, which can be determined via a grid search process [76].

Accordingly, the SVM model used for landslide susceptibility mapping can be presented as follows:

$$y\left(x_l\right)=sign\left({\sum }_{k=1}^{SV}{\alpha }_k{y}_{k}K\left(x_k,x_l\right)+b\right),$$

(10)

where ${\alpha }_k$ is the solution of the dual form of the aforementioned nonlinear programming and SV denotes the number of support vectors (the number of ${\alpha }_k>0$).

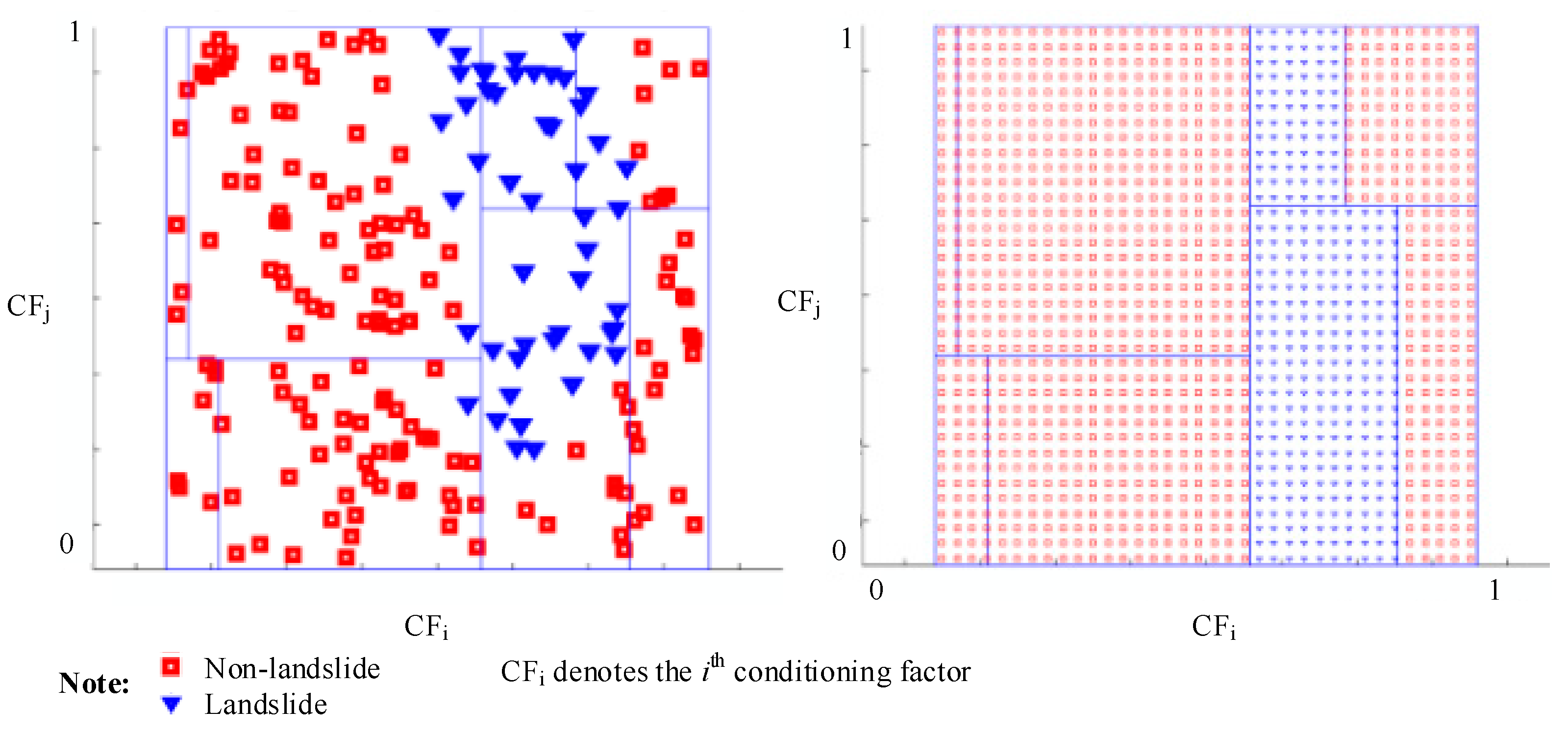
4. The Proposed Random Forest Machine (RFM) for GIS-Based Landslide Susceptibility Prediction

The overall structure of the proposed RFM model, which is a combination of the GIS database, RFC (random forest classifier) and SVM (support vector machine) algorithms is demonstrated in Figure 6. In order to construct the newly developed machine learning model for predicting a landslide, the GIS database of the studied region is first established. Accordingly, digital topographic maps, land use maps at a scale of 1:50,000, Landsat-8 Operational Land Imager (OLI) images with a resolution of 30 m, and geological data (e.g., lithology, soil type, and distance to fault) were utilized. In total, 101 landslide locations were identified and processed to formulate the GIS database for the study area. It was noted that all landslide conditioning variables were converted into a raster format with 5 m resolution utilizing a geospatial tool developed by the authors and opened in the ArcGIS software package.

Since the landslide susceptibility mapping was formulated as a supervised learning task, it was necessary to divide the whole collected data into training and testing datasets. The first set was used to construct the machine learning model, whereas the second set was reserved to verify the model’s predictive performance. Thus, the whole dataset, consisting of 6910 samples (3455 landslide pixels and 3455 non-landslide points), was separated into the two subsets above within which the testing samples accounted for 30% of the data. The label of the dataset was encoded −1 for the negative class and +1 for the positive class. Moreover, the employed landslide conditioning factors were converted from categorical classes into continuous values within the range of 0.01 and 0.99 using a method described in Tien Bui et al. [77]. The purpose of this data conversion was to facilitate the subsequent pattern classification process.

Based on the collected GIS database, the RFM developed in this study was utilized as an intelligent data classification method to categorize the pixels into the positive class of landslide and the negative class of non-landslide. In the standard procedure of a decision tree, a model performs splitting operations at thresholds that are orthogonal to the axes of the input space (refer to Figure 7). The splitting regions were characterized by hyper-rectangles and the final decision borders had the form of linear functions parallel to the coordinate axes. The linear-decision borders undoubtedly limit the flexibility of the classifier and also necessitate a large number of individual trees to capture a complex decision surface. Therefore, this study proposed to combine SVM and RFC by adding SVM directly into the structure of individual trees.

Specifically, for each hyper rectangle, the SVM model was trained and its support vectors were identified. These support vectors helped to define the decision surface that maximizes the margins between the training data and the classifying borders. The direct outcome of this RFC-SVM integration was smooth final borders with a low number of trees and low levels on each tree (refer to Figure 8). Notably, another advantage of the proposed combined method was that it helps to overcome the limitations of SVM used for a large-scale training dataset where a vast kernel matrix must be computed because the whole dataset is divided into subsets by the RFC algorithm; thus, this helped to reduce the number of elements in the kernel matrices of the SVM models. The rules used to construct the RFM model were as follows (refer to Figure 6):

(i)

If all the training data points in a node belong to the same class, then the node label is assigned as the data label;

(ii)

If there are different labels in a node, the SVM structure is used to classify the data stored in this node.

Furthermore, to evaluate the RFM performance, the true positive rate (TPR; the percentage of positive instances correctly classified), the false positive rate (FPR; the percentage of negative instances misclassified), the false negative rate (FNR; the percentage of positive instances misclassified), and the true negative rate (TNR; the percentage of negative instances correctly classified) can be used [52,65,78,79,80]. These indices are given by:

$$\mathrm{TPR}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}},$$

(11)

$$\mathrm{FPR}=\frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TN}},$$

(12)

$$\mathrm{FNR}=\frac{\mathrm{FN}}{\mathrm{TP}+\mathrm{FN}},$$

(13)

$$\mathrm{TNR}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}},$$

(14)

where TP, TN, FP, and FN are the true positive, true negative, false positive, and false negative, respectively.

Based on the aforementioned indices, the classification rate (CAR), precision, recall, and F1 score [81] can be calculated as follows:

$$\mathrm{CAR}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}},$$

(15)

$$\mathrm{Precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}},$$

(16)

$$\mathrm{Recall}= \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} ,$$

(17)

$$\mathrm{F}1\mathrm{Score}=\frac{2\mathrm{TP}}{2\mathrm{TP}+\mathrm{FP}+\mathrm{FN}}.$$

(18)

It was noted that the goal of this study was to construct a landslide prediction model with good precision (low false positive outcomes) and recall (low false-negative outcomes) results. Therefore, this study assigned equal weighting values for precision and recall indices.

5. Experimental Results

This section presents the experimental results of the RFM model used for spatial landslide susceptibility mapping. As stated earlier, to train and test the model predictive capability, the original dataset was randomly divided into training (70%) and testing (30%) sets. Accordingly, the numbers of data samples (or pixels within the map of the study area) in the whole dataset, training, and testing sets were 3455, 2410, and 1045, respectively.

It was also noted that all 14 conditioning factors were used for spatial landslide modeling. Besides, to diminish the bias caused by randomness in the data sampling process, repeated sampling with 20 runs were performed. In each run, the training and testing datasets were extracted randomly from the collected dataset. The experimental outcomes of the proposed RFM model are reported in

Table 1. Training performance of the RFM model.

Run No.	CAR	TPR	FPR	FNR	TNR	Precision	Recall	F1 Score
1	0.965	0.945	0.013	0.055	0.987	0.988	0.945	0.966
2	0.969	0.949	0.009	0.051	0.991	0.991	0.949	0.970
3	0.969	0.951	0.012	0.049	0.988	0.989	0.951	0.970
4	0.965	0.944	0.012	0.056	0.988	0.989	0.944	0.966
5	0.967	0.948	0.013	0.052	0.987	0.988	0.948	0.968
6	0.966	0.945	0.012	0.055	0.988	0.988	0.945	0.966
7	0.967	0.949	0.012	0.051	0.988	0.989	0.949	0.969
8	0.965	0.946	0.014	0.054	0.986	0.986	0.946	0.966
9	0.969	0.950	0.011	0.050	0.989	0.990	0.950	0.970
10	0.963	0.941	0.013	0.059	0.987	0.988	0.941	0.964
11	0.969	0.949	0.010	0.051	0.990	0.990	0.949	0.969
12	0.967	0.947	0.012	0.053	0.988	0.988	0.947	0.967
13	0.966	0.945	0.010	0.055	0.990	0.990	0.945	0.967
14	0.967	0.948	0.011	0.052	0.989	0.990	0.948	0.969
15	0.966	0.945	0.011	0.055	0.989	0.990	0.945	0.967
16	0.969	0.952	0.012	0.048	0.988	0.988	0.952	0.970
17	0.968	0.948	0.010	0.052	0.990	0.991	0.948	0.969
18	0.965	0.946	0.015	0.054	0.985	0.986	0.946	0.966
19	0.967	0.946	0.012	0.054	0.988	0.988	0.946	0.967
20	0.968	0.949	0.012	0.051	0.988	0.989	0.949	0.969
Mean	0.967	0.947	0.012	0.053	0.988	0.989	0.947	0.968
SD	0.002	0.003	0.001	0.003	0.001	0.001	0.003	0.002

and

Table 2. Testing performance of the RFM model.

	CAR	TPR	FPR	FNR	TNR	Precision	Recall	F1 Score
1	0.954	0.934	0.024	0.066	0.976	0.978	0.934	0.956
2	0.960	0.939	0.017	0.061	0.983	0.984	0.939	0.961
3	0.962	0.941	0.016	0.059	0.984	0.985	0.941	0.963
4	0.950	0.920	0.015	0.080	0.985	0.986	0.920	0.952
5	0.957	0.932	0.014	0.068	0.986	0.987	0.932	0.959
6	0.953	0.929	0.019	0.071	0.981	0.982	0.929	0.955
7	0.955	0.930	0.017	0.070	0.983	0.984	0.930	0.956
8	0.959	0.937	0.019	0.063	0.981	0.982	0.937	0.959
9	0.951	0.923	0.020	0.077	0.980	0.980	0.923	0.951
10	0.960	0.936	0.015	0.064	0.985	0.986	0.936	0.960
11	0.958	0.939	0.020	0.061	0.980	0.981	0.939	0.960
12	0.949	0.927	0.027	0.073	0.973	0.974	0.927	0.950
13	0.949	0.921	0.019	0.079	0.981	0.982	0.921	0.950
14	0.959	0.937	0.017	0.063	0.983	0.984	0.937	0.960
15	0.955	0.929	0.018	0.071	0.982	0.983	0.929	0.955
16	0.957	0.931	0.016	0.069	0.984	0.985	0.931	0.957
17	0.966	0.948	0.014	0.052	0.986	0.987	0.948	0.967
18	0.955	0.929	0.016	0.071	0.984	0.985	0.929	0.956
19	0.957	0.930	0.015	0.070	0.985	0.985	0.930	0.956
20	0.955	0.931	0.016	0.069	0.981	0.982	0.931	0.956
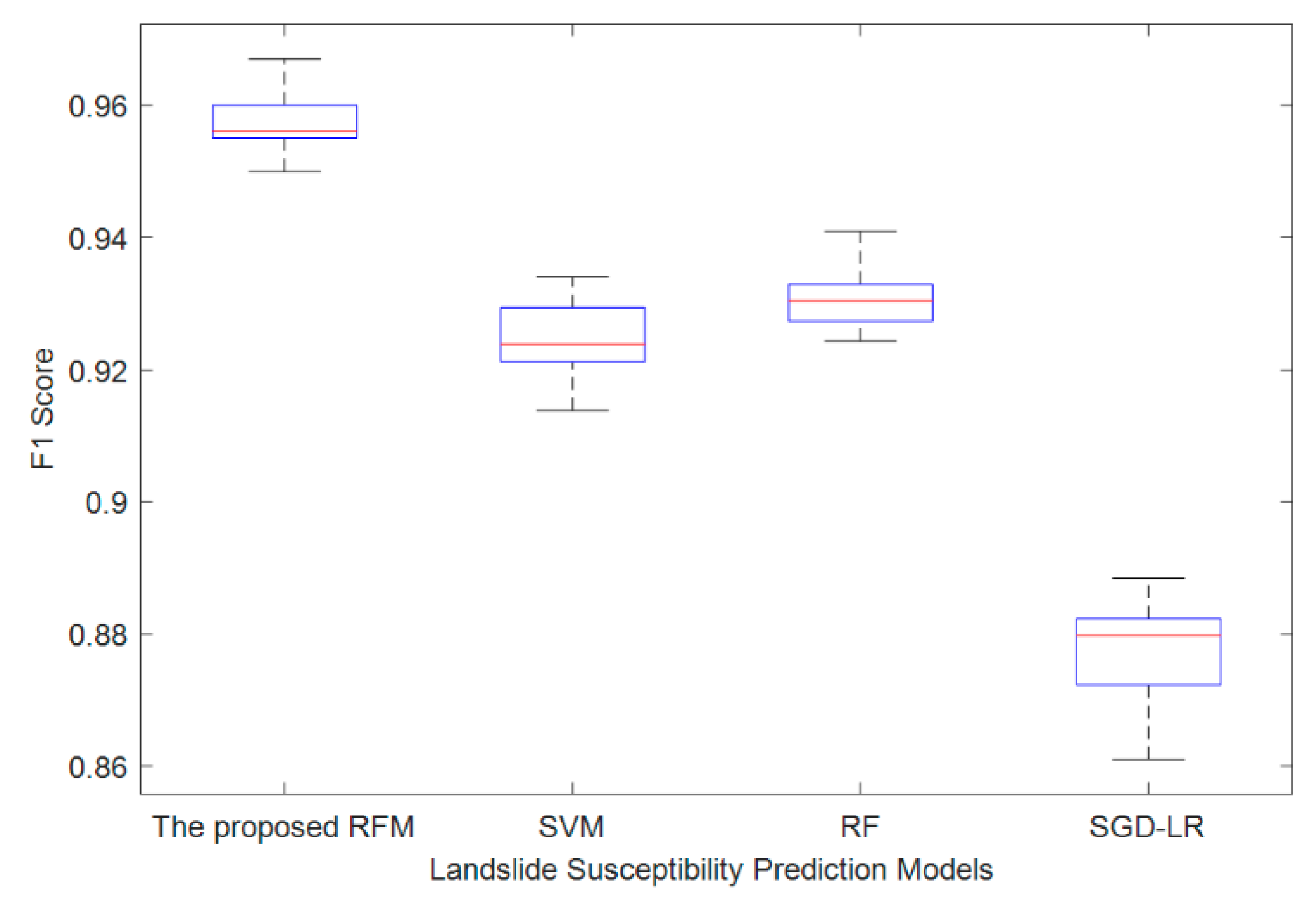
Mean	0.956	0.932	0.017	0.068	0.982	0.983	0.932	0.957
SD	0.004	0.007	0.003	0.007	0.003	0.003	0.007	0.004

, including the mean and standard deviation (SD) of the performance measurement indices.

Moreover, to confirm the predictive performance of the proposed RFM used for spatial mapping of landslide susceptibility in the study region, its predictive result was compared to those of the SVM, RFC, and stochastic gradient descent logistic regression (SGD-LR). All of the selected benchmark models have been employed for spatial prediction of landslide with good predictive performances [21,23,25,49,50,51,64,82]. The SVM and RFC models were implemented with the help of the MATLAB machine learning toolbox (Natick, MA, USA) [83]. The RFC was constructed with 100 individual decision trees. Besides, the SGD-LR was developed in the MATLAB environment by the authors. The prediction results of the proposed RFM, as well as other benchmark models, are summarized in

Table 3. Prediction result comparison.

Phase	Indices	The Proposed RFM		SVM		RFC		SGD-LR
		Mean	Std	Mean	Std	Mean	Std	Mean	Std
Training	CAR (%)	96.685	0.170	93.042	0.247	94.172	0.276	87.461	0.290
	TPR	0.947	0.003	0.972	0.003	0.983	0.002	0.913	0.005
	FNR	0.053	0.003	0.111	0.004	0.100	0.005	0.164	0.004
	FPR	0.012	0.001	0.028	0.003	0.017	0.002	0.087	0.005
	TNR	0.988	0.001	0.889	0.004	0.901	0.005	0.836	0.004
	Precision	0.989	0.001	0.897	0.004	0.908	0.005	0.848	0.003
	Recall	0.947	0.003	0.972	0.003	0.983	0.002	0.913	0.005
	F1 score	0.968	0.002	0.933	0.002	0.944	0.003	0.879	0.003
Testing	CAR (%)	95.578	0.438	92.144	0.575	92.714	0.495	87.342	0.776
	TPR	0.932	0.007	0.965	0.006	0.978	0.004	0.911	0.011
	FNR	0.068	0.007	0.122	0.010	0.124	0.010	0.164	0.009
	FPR	0.018	0.003	0.035	0.006	0.022	0.004	0.089	0.011
	TNR	0.982	0.003	0.878	0.010	0.876	0.010	0.836	0.009
	Precision	0.983	0.003	0.888	0.008	0.888	0.008	0.848	0.007
	Recall	0.932	0.007	0.965	0.006	0.978	0.004	0.911	0.011
	F1 score	0.957	0.004	0.925	0.005	0.931	0.005	0.878	0.008

and Figure 9. As can be seen from this table, the average performance of the RFM (F1 score = 0.957) was better than those of the SVM (F1 score = 0.925), RFC (F1 score = 0.931), and SGD-LR (F1 score = 00.878). Also, the consuming time for runing the RFM, SVM, RFC, and SGD-LR models were 2.72, 2.66, 6.45, and 3.51, respectively. This fact indicates that the proposed RFM, which was an integration of the RFC and SVM, is more computationally efficient than the RFC model. Besides, there was only a minor difference in computing time between the RFM and the individual SVM model.

Also, the non-parametric Wilcoxon signed-rank test [84] was used to better demonstrate the statistical significance of the difference in model results. A detailed explanation of this test for landslide susceptibility mapping can be found in [43]. In this research, the significant level (p-value) of the employed hypothesis test was set to be 0.05. The results of the Wilcoxon signed-rank test performed on the models’ F1 score outcomes are reported in

Table 4. The Wilcoxon signed-rank test results.

Pairwise Model Comparison	p-Value	Test Outcome
The proposed RFM vs. SVM	0.0001	Significant
The proposed RFM vs. RF	0.0001	Significant
The proposed RFM vs. SGD-LR	0.0001	Significant

. As shown in this table, with p-values <0.05, the null hypothesis of equal means could be confidently rejected and it is possible conclude that that the predictive performances of the landslide prediction models were statistically different. These facts confirmed that the newly developed RFM is highly suited for the spatial prediction of a landslide in the study region.

Since the proposed RFM achieved the most desired predictive result with the GIS database collected from the study area, this innovative prediction model was then employed to construct a landslide susceptibility map. The landslide susceptibility map for the study area established by the RFM is demonstrated in Figure 10. To validate the accuracy and helpfulness of the newly created susceptibility map, the landslide inventory map, which showed the locations of the past landslide occurrences, was overlaid with the new map. The graphic curve [85] was then plotted with the percentage of the landslide pixels on the y-axis and the percentage of pixels of susceptible classes arranged from high to low susceptible indexes. As can be seen from the graphic curve, most of the actual landslide pixels were located in high and very high classes, whereas very few actual landslide pixels were found to be in low and very low classes. These facts confirm the correctness and applicability of the susceptibility map created by the newly developed RFM model. The MATLAB codes and data of the proposed model in this study are in a github repository, that can be found at https://github.com/NhatDucHoang/RFC_SVC_LandslidePredictionModel.

6. Conclusions

For land use planning and hazard mitigation, landslide susceptibility evaluation is a crucial task performed by the local authority in mountainous and remote areas in northern Vietnam. These areas have been devastated by natural hazards, including landslides, in recent years due to the combined effects of climate change and human activities (e.g., deforestation). Thus, establishing an updated landslide susceptibility map with better accuracy and reliability is a practical need. To achieve this goal, this study proposed a novel hybrid machine learning framework that employed the RFC and SVM models. The SVM model was integrated into the RFC structure to improve its performance by constructing smooth and flexible class boundaries instead of linear boundaries used by the standard RFC model.

To train and test the capability of the proposed hybrid framework, named as RFM, a GIS database containing information of 101 historical landslide occurrences was used. Experimental results demonstrated that the RFM with an F1 score of roughly 0.96 is superior to other benchmark models of the SVM, RFC, and SGD-LR. Hence, the newly developed ensemble data-driven model can be a helpful tool to assist local authorities in identifying landslide-prone areas so that the task of land use planning can be carried out more effectively. Since the RFM has achieved superior prediction performance for Lang Son city (Vietnam), the proposed hybrid machine learning model has the potential to be applied in other areas outside the study region. Nevertheless, one shortcoming of the current study is that the feature selection method has not been integrated into the model. Therefore, the future extension of this study may include the utilization of more advanced feature selection strategies. Furthermore, the integration of other sophisticated machine learning methods (e.g., the least-squares SVM) with the RFC can be worth investigating.