Size Effect on the Elastic Mechanical Properties of Beech and Its Application in Finite Element Analysis of Wood Structures
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Equipment
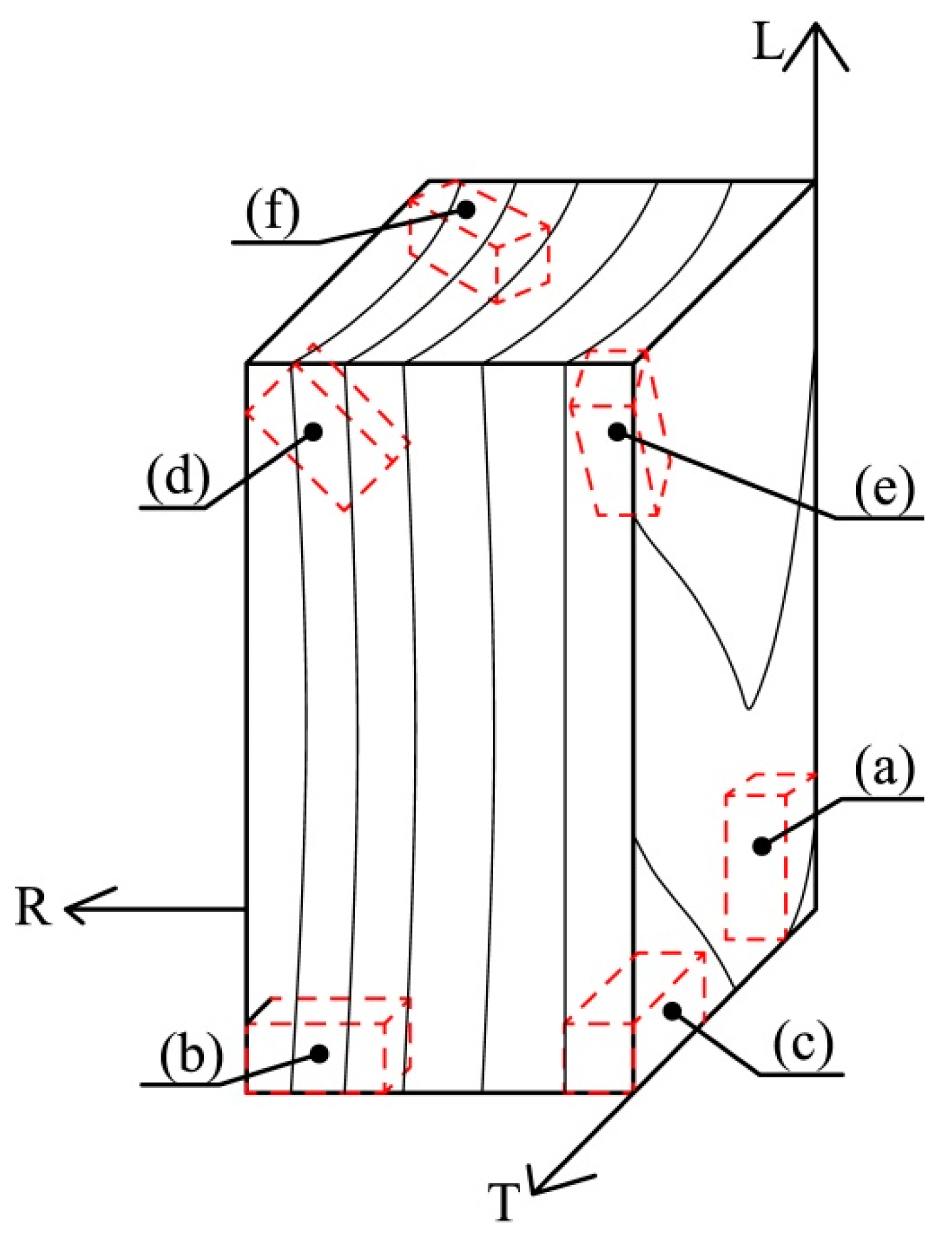
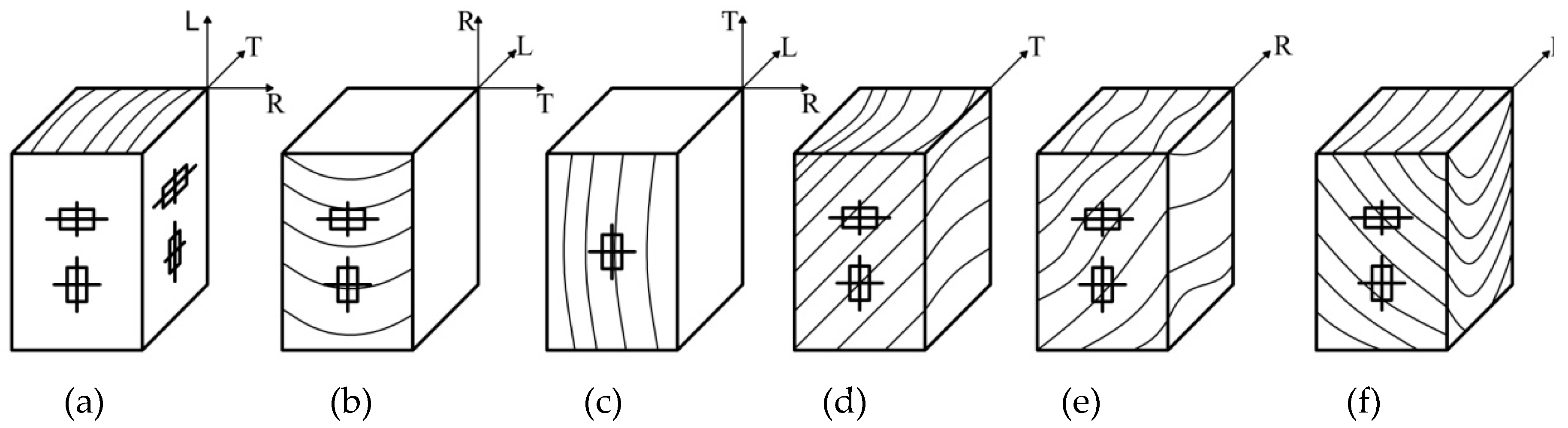
2.2. Specimens Preparation
2.3. Testing Methods
2.3.1. Physical Properties of European Beech Wood
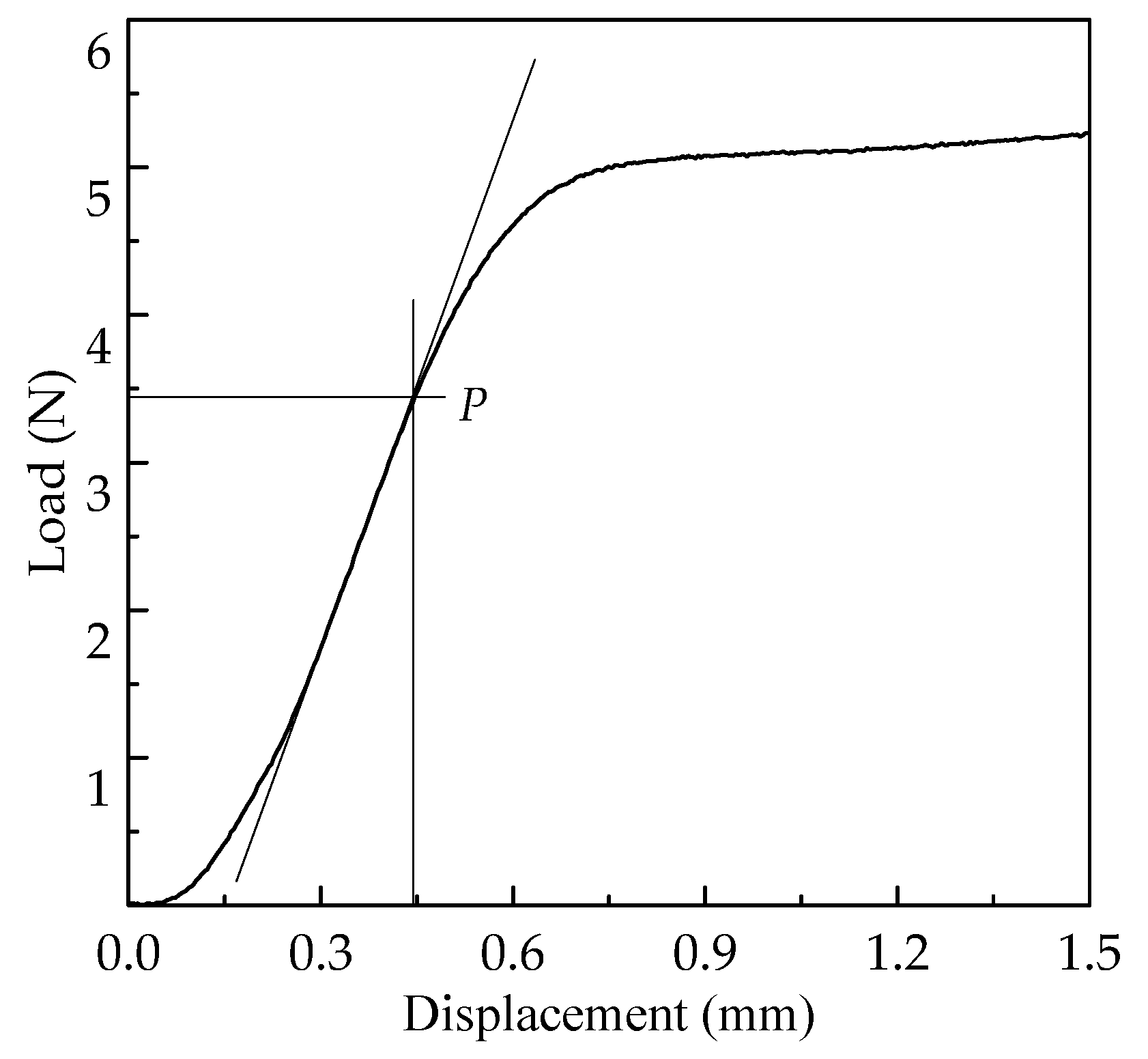
2.3.2. Proportional Limit Stress and Elastic Constants
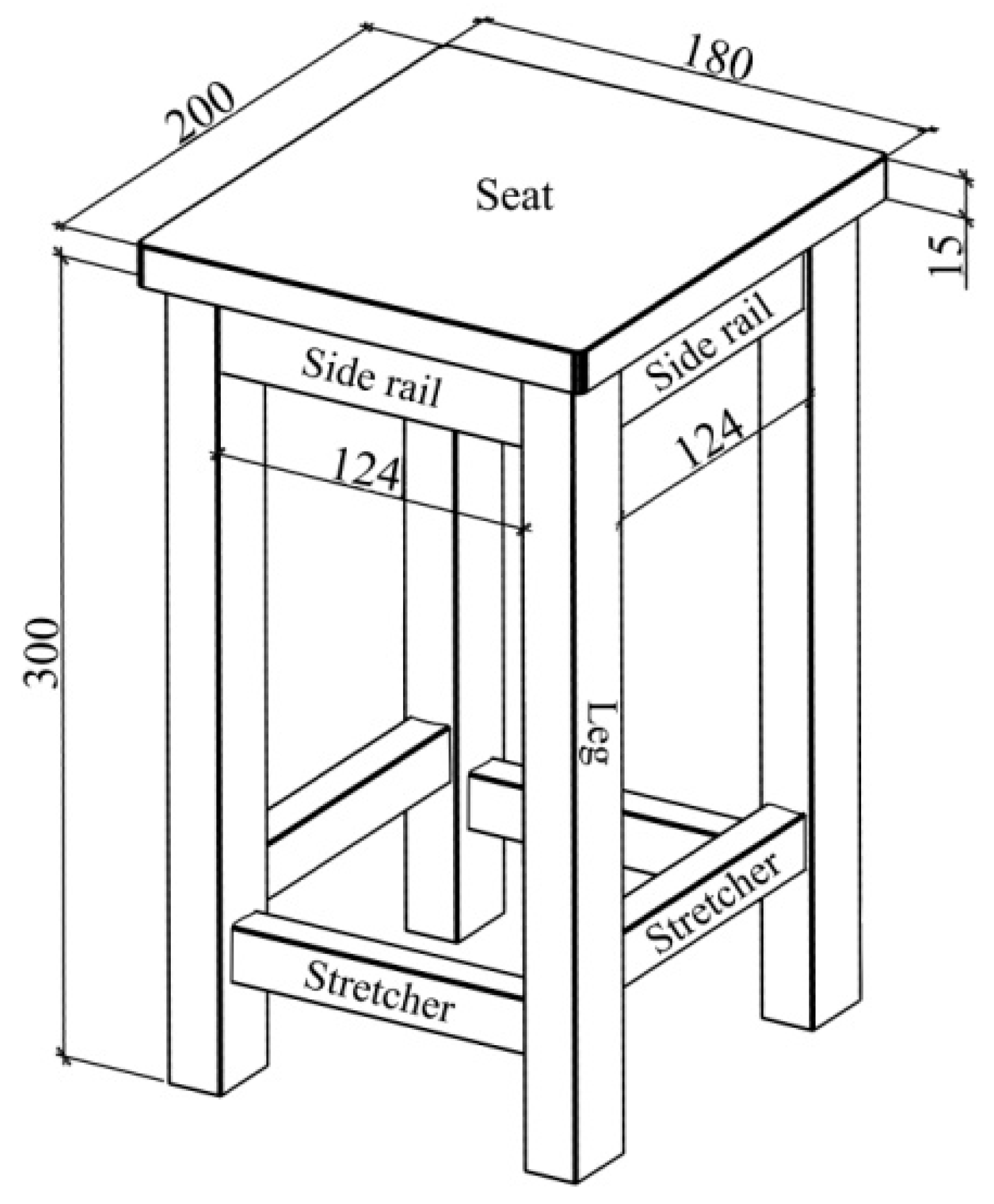
2.3.3. Load Capacity of Chair
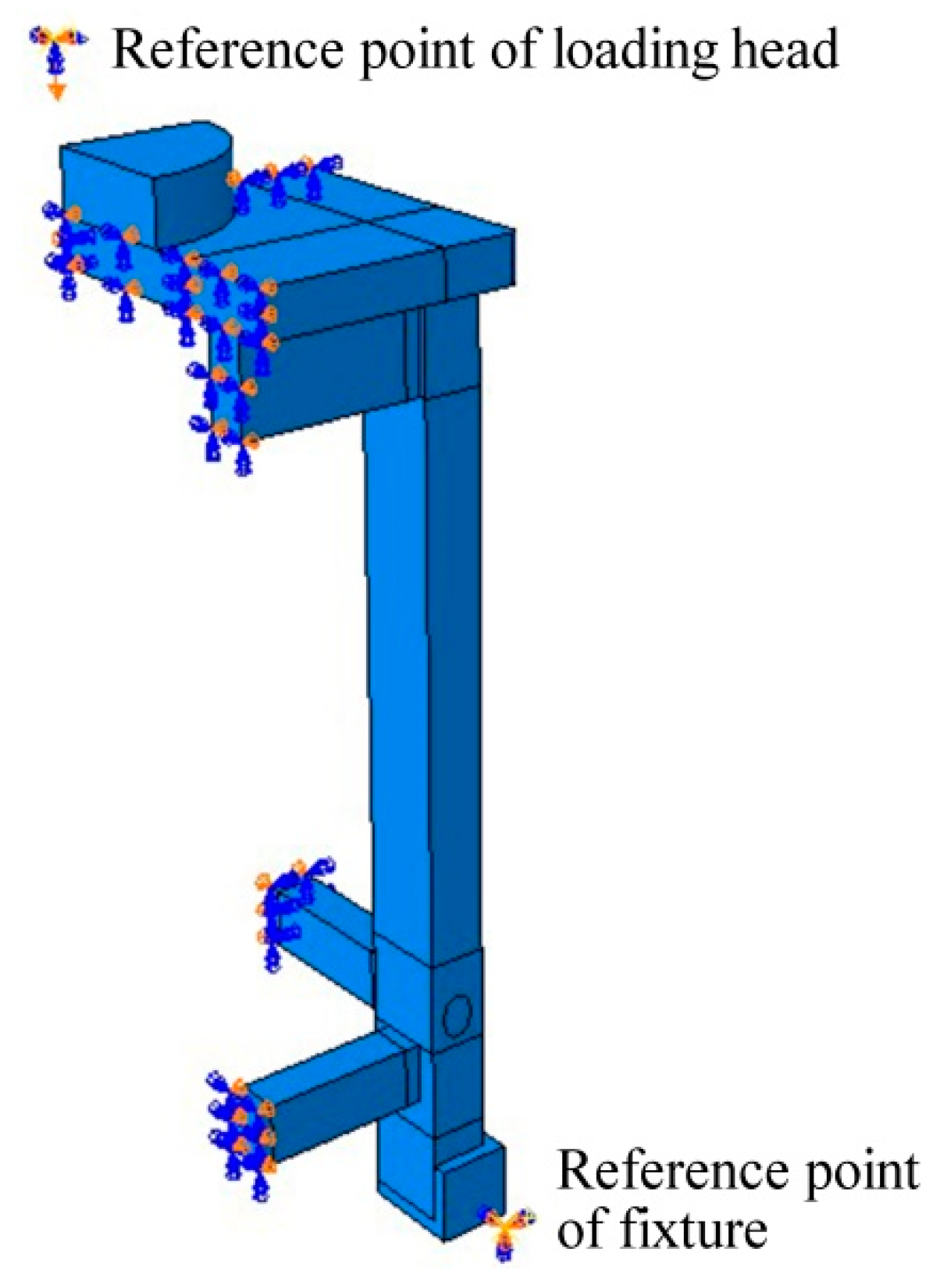
2.4. Modeling
3. Results and Discussion
3.1. Physical Properties of European Beech Wood
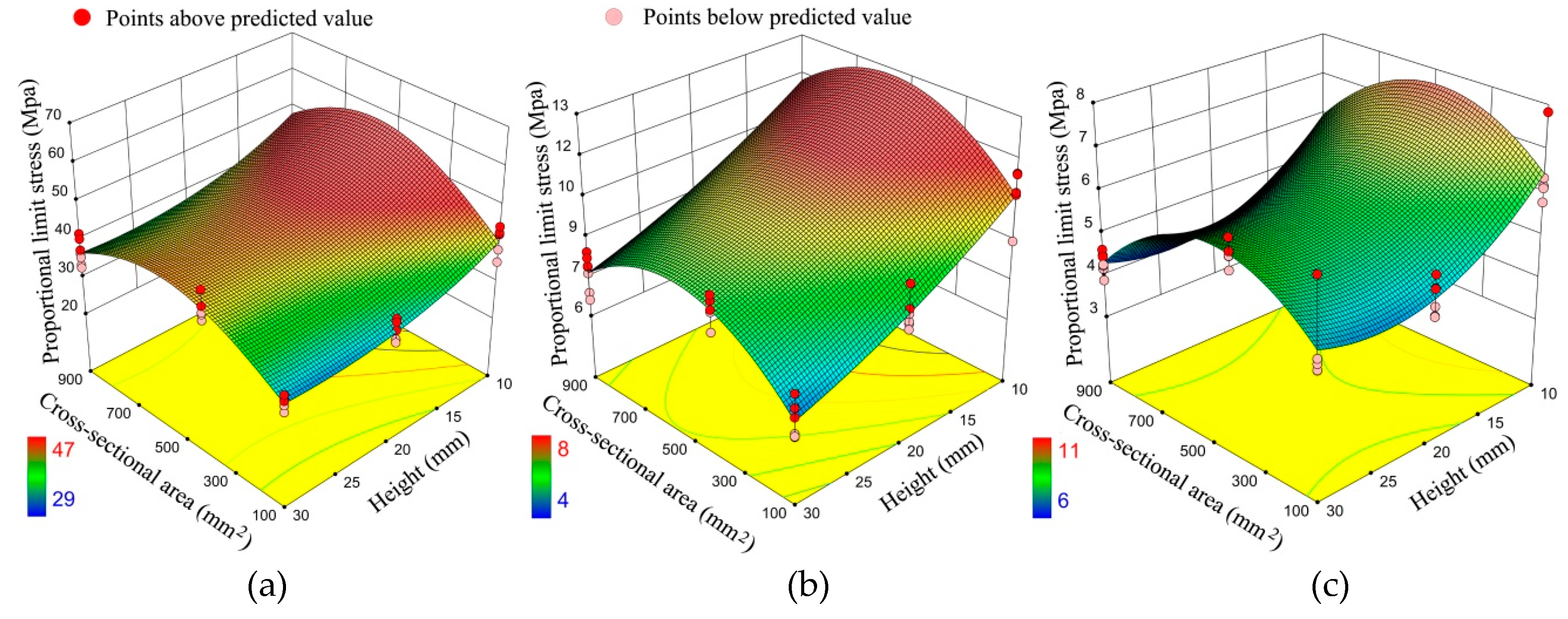
3.2. Size Effect on Proportional Limit Stresses of European Beech
3.3. Size Effect on Elastic Constants of Beech
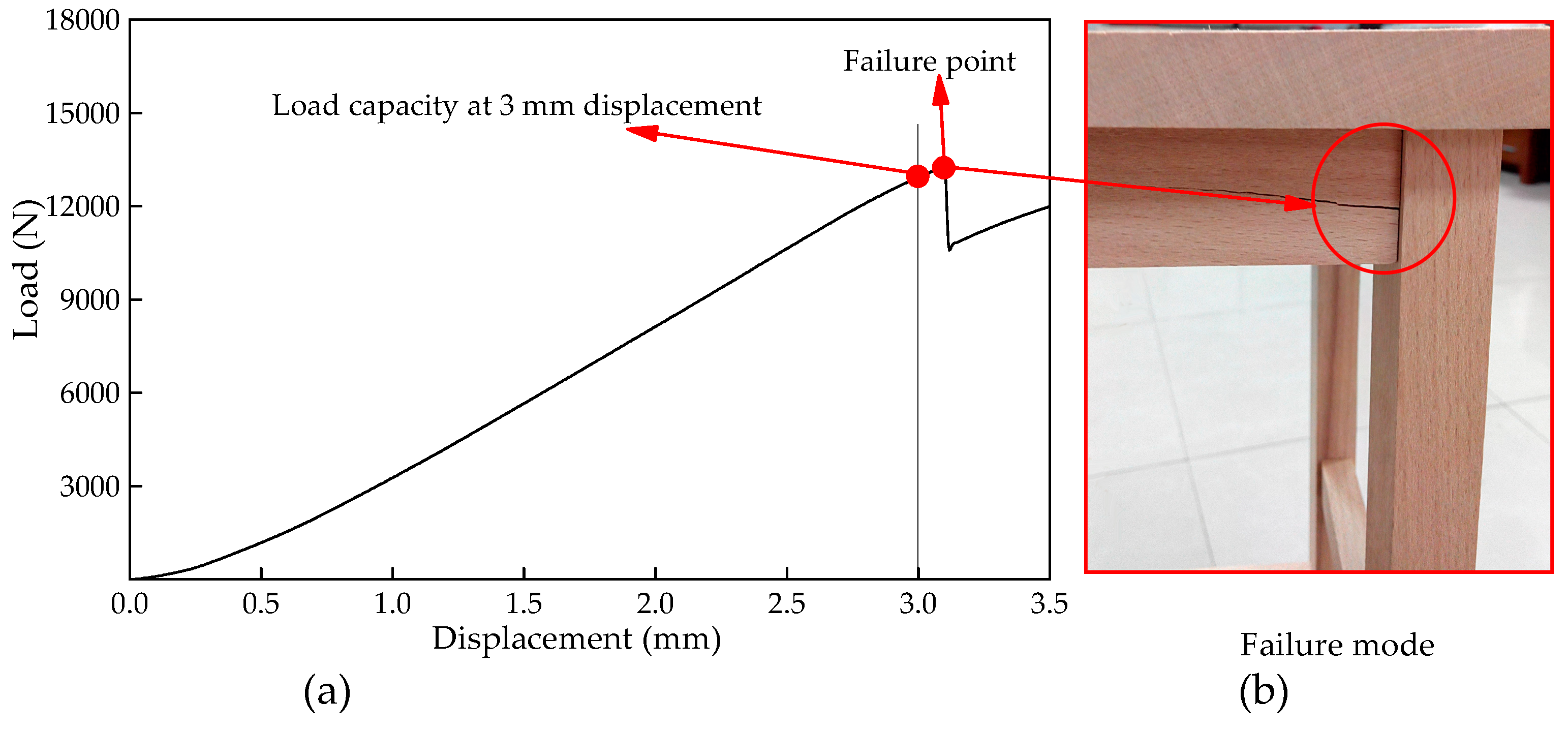
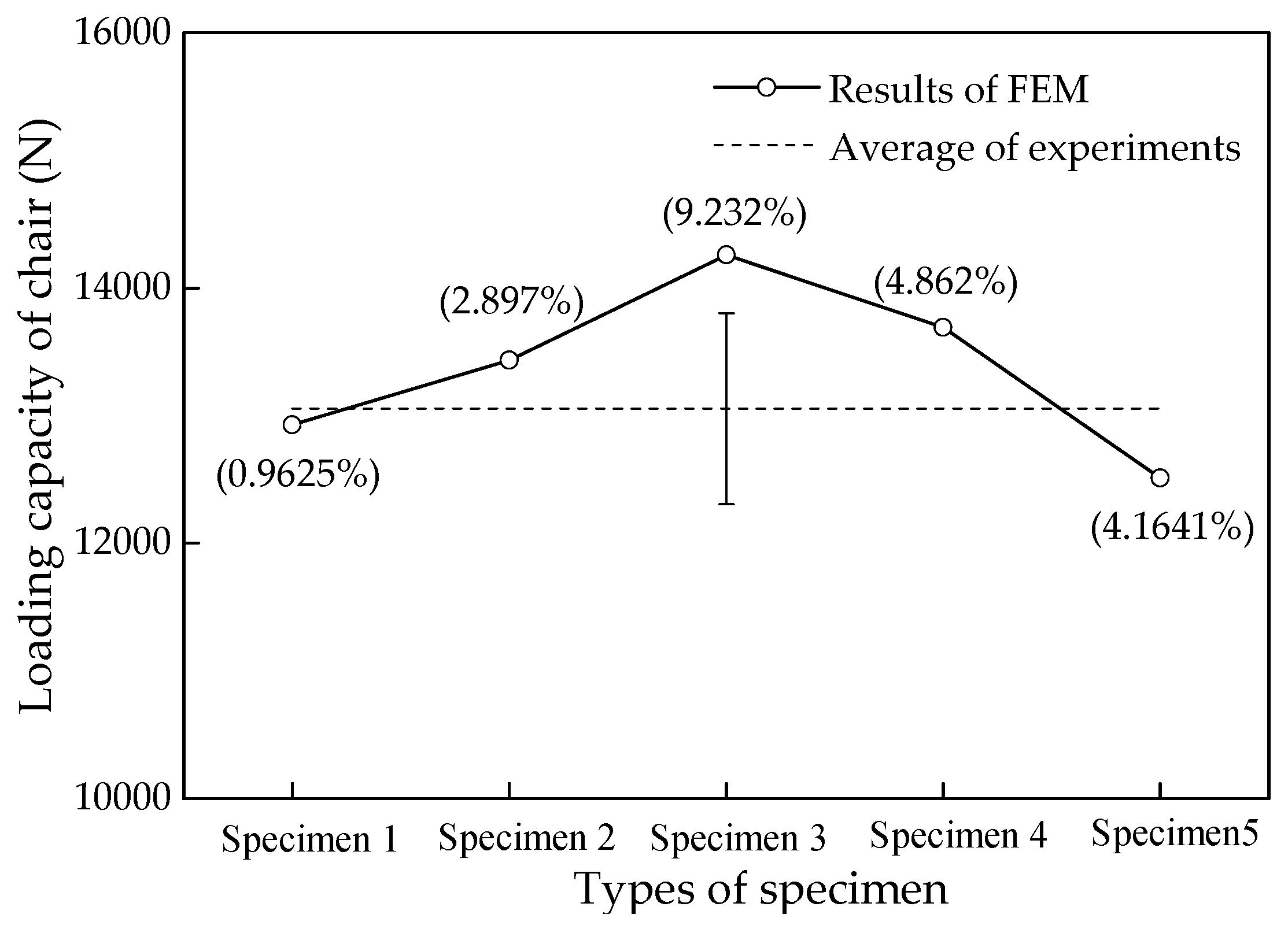
3.4. Load Capacity of Chair and Failure Mode
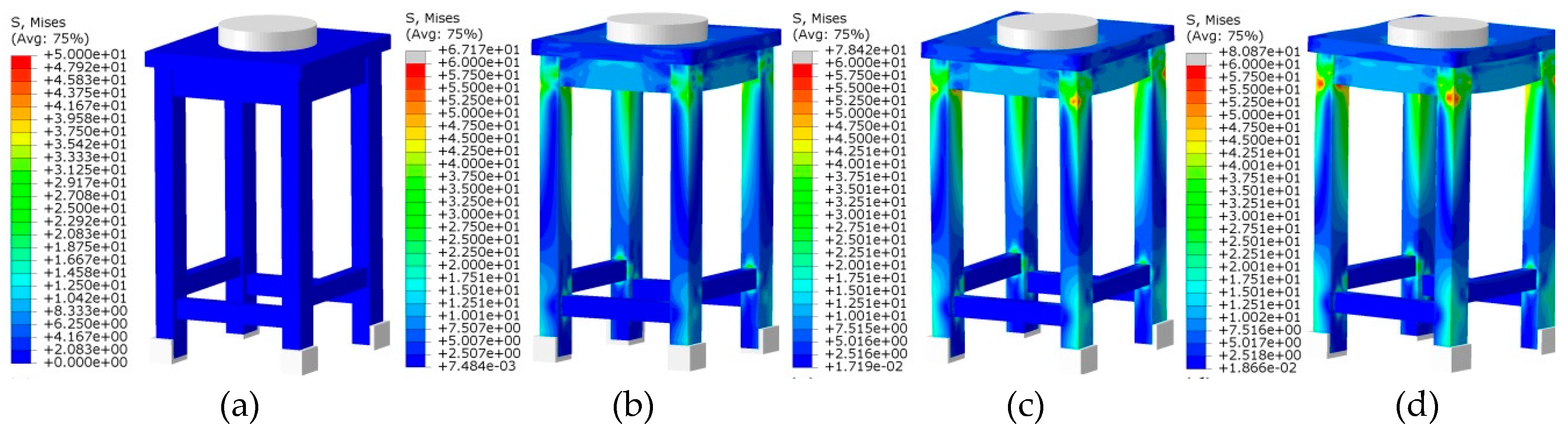
3.5. Comparison and Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zauner, M.; Niemz, P. Uniaxial compression of rotationally symmetric Norway spruce samples: Surface deformation and size effect. Wood Sci. Technol. 2014, 48, 1019–1032. [Google Scholar] [CrossRef]
- Zhang, F.; Li, L.; Zhang, L.; Xu, Z. Study of the determination of the elastic constants and mechanical property parameters of five kinds of wood commonly used in furniture. For. Mach. Woodwork. Equip. 2012, 40, 16–19. [Google Scholar]
- Wang, L.Y.; Lu, Z.Y.; Shen, S.J. Study on twelve elastic constant values of Betula platyphylla Suk. wood. J. Beijing For. Univ. 2003, 25, 64–67, (In Chinese with English Summary). [Google Scholar]
- CNS GB/T 1935. Method of Testing in Compressive Strength Parallel to Grain of Wood; Chinese National Standard: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Hu, W.G.; Guan, H.Y. Study on elastic constants of beech in different stress states. J. For. Eng. 2017, 2, 31–36, (In Chinese with English Summary). [Google Scholar]
- Aira, J.R.; Arriaga, F.; González, G.L. Determination of the elastic constants of scots pine (Pinus sylvestris L.) wood by means of compression tests. Biosyst. Eng. 2014, 126, 12–22. [Google Scholar] [CrossRef]
- Aydin, Y.; Aydin, M. Comparison of temperature dependent Young’s modulus of oriental beech (Fagus orientalis L.) that determined by ultrasonic wave propagation and compression test. Turk. J. For. 2018, 19, 185–191. [Google Scholar] [CrossRef]
- Shao, Z.P.; Zhou, S. Study on determining the elastic constants of wood of Cunninghamia lanceolata by means of electric resistance-strain gauges. J. Anhui Agri. Univ. 2001, 28, 32–35, (In Chinese with English Summary). [Google Scholar]
- Murata, K.; Tanahashi, H. Measurement of Young’s modulus and Poisson’s ratio of wood specimens in compression test. J. Soc. Mater. Sci. Jpn. 2010, 59, 285–290. [Google Scholar] [CrossRef]
- Liu, F.L.; Jiang, F.; Zhang, J.Z.; Zhang, H.J.; Wang, X.P.; Yang, Z.H. Twelve elastic constants values of larch forest. J. North. For. Univ. 2015, 30, 227–231, (In Chinese with English Summary). [Google Scholar]
- ASTM D143-94. Standard Test Methods for Small Clear Specimens of Timber; ASTM International: West Conshohocken, PA, USA, 2010. [Google Scholar]
- Straže, A.; Gorišek, Z. Analysis of size effect on determination of mechanical properties of Norway spruce wood. In Proceedings of the 22nd International Scientific Conference on Wood is Good-EU Preaccession Challenges of the Sector, Zagreb, Croatia, 21 October 2011; pp. 183–190. [Google Scholar]
- Madsen, B.; Tomoi, M. Size effects occurring in defect-free spruce-pine-fir bending specimens. Can. J. Civil Eng. 2011, 18, 637–643. [Google Scholar] [CrossRef]
- Zhou, H.B.; Ren, H.Q.; Lu, J.X. Size effect of length on flexural strength of Chinese fir dimension lumber used in wood structure. J. Build. Mater. 2009, 12, 501–504, (In Chinese with English Summary). [Google Scholar]
- Madsen, B.; Buchanan, A.H. Size effect in timber explained by a modified weakest link theory. Can. J. Civil Eng. 1986, 13, 218–2232. [Google Scholar] [CrossRef]
- Madsen, B.; Nielsen, P.C. In-Grade Testing: Size Investigation on Lumber Subjected to Bending; Structural Research Series, Report No. 15; Department of Civil Engineering; University of British Columbia: Vancouver, BC, Canada, 1976; p. 10. [Google Scholar]
- ASTM D1990-07. Standard Practice for Establishing Allowable Properties for Visually-Grade Dimension Lumber from in Grade Tests of Full-Size Specimens; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- Fotsing, J.A.; Foudjet, A. Size effect of two Cameroonian hardwoods in compression and bending parallel to the Grain. Holzforsch.-Int. J. Biol. Chem. Phys. Technol. Wood 1995, 49, 376–378. [Google Scholar] [CrossRef]
- Zhou, H.B.; Han, L.Y.; Ren, H.Q.; Lu, J.X. Size effect on strength properties of Chinese larch dimension lumber. BioResources 2015, 10, 3790–3797. [Google Scholar] [CrossRef]
- Yu, Y.; Jiang, Z.H.; Tian, G.L. Size effect on longitudinal MOE of microtomed wood sections and relevant theoretical explanation. For. Stud. China 2009, 11, 243–248. [Google Scholar] [CrossRef]
- Karakoc, A.; Freund, J. Effect of size and measurement domain on the in-plane elasticity of wood-like cellular materials. J. Mater. Sci. 2016, 51, 1490–1495. [Google Scholar] [CrossRef]
- Buyuksari, U.; As, N.; Dundar, T.; Sayan, E. Micro-tensile and compression strength of scots pine wood and comparison with standard-size test results. Drvna. Ind. 2017, 68, 129–136. [Google Scholar] [CrossRef]
- ASTM D4442-92. Standard Test Methods for Direct Moisture Content Measurements of Wood and Wood-Based Materials; ASTM International: West Conshohocken, PA, USA, 2010. [Google Scholar]
- ASTM D 2395-93. Standard Test Methods for Specific Gravity of Wood and Wood-Based Materials; ASTM International: West Conshohocken, PA, USA, 2010. [Google Scholar]
- Hu, W.G.; Guan, H.Y. Experimental and numerical study on optimization design of stretcher positions. Wood Res. 2017, 62, 575–586. [Google Scholar]
- Hu, W.G.; Guan, H.Y. Investigation on withdrawal force of mortise and tenon joint based on friction properties. J. For. Eng. 2017, 02, 158–162, (In Chinese with English Summary). [Google Scholar]
- Hu, W.G.; Guan, H.Y.; Zhang, J.L. Finite element analysis of tensile load resistance of mortise-and-tenon joints considering tenon fit effects. Wood Fiber Sci. 2018, 50, 121–131. [Google Scholar] [CrossRef]
- Kasal, A.; Smardzewski, J.; Kuskun, T.; Erdil, Y.Z. Numerical analysis of various sizes of mortise and tenon furniture joints. BioResources 2016, 11, 6836–6853. [Google Scholar] [CrossRef]
- Chin, W.W. Commentary: Issues and opinion on structural equation modeling. MIS Quart. 1988, 22, 7–16. [Google Scholar]
- Hearmon, R.F.S.; Barkas, W.W. The effect of grain direction on the Young’s moduli and rigidity moduli of beech and sitka spruce. Proc. Phys. Soc. 1941, 53, 674–680. [Google Scholar] [CrossRef]
- Madsen, B. Structural Behaviour of Timber; Timber Engineering LTD: Vancouver, BC, Canada, 1992. [Google Scholar]
- Hering, S.; Keunecke, D.; Niemz, P. Moisture-dependent orthotropic elasticity of beech wood. Wood Sci. Technol. 2011, 46, 927–938. [Google Scholar] [CrossRef]
- Xavier, J.; De Jesus, A.M.P.; Morais, J.J.L.; Pinto, J.M.T. Stereovision measurements on evaluating the modulus of elasticity of wood by compression tests parallel to the grain. Constr. Build. Mater. 2012, 26, 207–215. [Google Scholar] [CrossRef]
- Ghavidel, A.; Mousavi, S.R.; Rashki, M. The effect of FEM mesh density on the failure probability analysis of structures. KSCE. J. Civil Eng. 2017, 00, 1–13. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech-T. ASME. 1951, 18, 293–297. [Google Scholar]



| Specimen Types | Dimensions | Number | ||||
|---|---|---|---|---|---|---|
| Cross-Sectional Area (mm2) | Height (mm) | Elastic Constants | Proportional Limit Stress | Total | ||
| Width (mm) | Length (mm) | |||||
| 1 | 10 | 10 | 10 | 30 | 30 | 60 |
| 2 | 10 | 10 | 20 | 30 | 30 | 60 |
| 3 | 10 | 10 | 30 | 30 | 30 | 60 |
| 4 | 20 | 20 | 30 | 30 | 30 | 60 |
| 5 | 30 | 30 | 30 | 30 | 30 | 60 |
| Monitor Factor | Sum of Squares | Degree of Freedom | Mean Squares | Fisher’s F-Test | Significance |
|---|---|---|---|---|---|
| Intercept | 17,851.842 | 1 | 17,851.842 | 6394.165 | p < 0.01 |
| Height (a) | 219.444 | 2 | 109.722 | 39.300 | p < 0.01 |
| Cross-sectional Area (b) | 181.119 | 2 | 90.559 | 32.437 | p < 0.01 |
| a × b | 0 | 0 | |||
| Error | 167.514 | 60 | 2.792 |
| Specimen Type | EL (MPa) | ER (MPa) | ET (MPa) | μLR | μLT | μRT | GL (MPa) | GR (MPa) | GT (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 13449 | 1027 | 764 | 0.697 | 0.720 | 0.444 | 527 | 399 | 173 |
| COV (%) | 4.8 | 5.8 | 4.5 | 1.0 | 9.4 | 0.8 | 6.4 | 2.7 | 10.3 |
| 2 | 15284 | 1161 | 863 | 0.643 | 0.549 | 0.644 | 729 | 462 | 265 |
| COV (%) | 0.3 | 2.7 | 0.7 | 3.0 | 1.3 | 3.5 | 1.0 | 5.5 | 13.1 |
| 3 | 17980 | 1537 | 1041 | 0.398 | 0.625 | 0.515 | 945 | 499 | 373 |
| COV (%) | 2.4 | 6.8 | 2.0 | 1.9 | 0.5 | 2.8 | 1.5 | 14.4 | 4.5 |
| 4 | 14075 | 1482 | 707 | 0.710 | 0.338 | 0.465 | 832 | 444 | 259 |
| COV (%) | 1.1 | 2.8 | 4.7 | 7.7 | 14.1 | 2.8 | 3.0 | 7.8 | 1.3 |
| 5 | 12617 | 1337 | 642 | 0.408 | 0.368 | 0.588 | 828 | 398 | 169 |
| COV (%) | 1.9 | 3.1 | 6.8 | 0.9 | 10.1 | 0.3 | 10.4 | 3.8 | 18.6 |
| Monitored Factor | Dependent Variable | Sum of Squares | Degree of Freedom | Mean Squares | Fisher’s F-Test | Significance |
|---|---|---|---|---|---|---|
| Cross-sectional Area × Height | EL | 176,983,729.639 | 4 | 44,245,932.410 | 237.704 | p < 0.01 |
| ER | 899,669.479 | 4 | 224,917.370 | 39.344 | p < 0.01 | |
| ET | 195,869.174 | 4 | 48,967.294 | 30.436 | p < 0.01 | |
| νLR | 0.293 | 4 | 0.073 | 51.594 | p < 0.01 | |
| νLT | 0.318 | 4 | 0.079 | 24.222 | p < 0.01 | |
| νRT | 0.082 | 4 | 0.021 | 65.324 | p < 0.01 | |
| GLR | 293,182.023 | 4 | 73,295.506 | 19.698 | p < 0.01 | |
| GLT | 21,512.839 | 4 | 5378.210 | 6.430 | p < 0.01 | |
| GRT | 84,329.602 | 4 | 21,082.400 | 19.736 | p < 0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, W.; Wan, H.; Guan, H. Size Effect on the Elastic Mechanical Properties of Beech and Its Application in Finite Element Analysis of Wood Structures. Forests 2019, 10, 783. https://doi.org/10.3390/f10090783
Hu W, Wan H, Guan H. Size Effect on the Elastic Mechanical Properties of Beech and Its Application in Finite Element Analysis of Wood Structures. Forests. 2019; 10(9):783. https://doi.org/10.3390/f10090783
Chicago/Turabian StyleHu, Wengang, Hui Wan, and Huiyuan Guan. 2019. "Size Effect on the Elastic Mechanical Properties of Beech and Its Application in Finite Element Analysis of Wood Structures" Forests 10, no. 9: 783. https://doi.org/10.3390/f10090783
APA StyleHu, W., Wan, H., & Guan, H. (2019). Size Effect on the Elastic Mechanical Properties of Beech and Its Application in Finite Element Analysis of Wood Structures. Forests, 10(9), 783. https://doi.org/10.3390/f10090783






