Local Adaptation and Response of Platycladus orientalis (L.) Franco Populations to Climate Change
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Materials
2.2. 7-Year Tree Height Estimation Method
2.3. Climate and Geographic Variables
2.4. Universal Response Function (URF)
2.5. Applications of URF
3. Results
3.1. Estimated 7-Year Tree Height
3.2. Universal Response Function
3.3. Spatial Variation in Growth Performances
3.4. Projections for Future Climates
4. Discussion
4.1. Model Performance
4.2. Spatial Variation in Height Growth
4.3. Regional Variation in Adaptation to Future Climates
4.4. The Risk to Local Populations Suffering from Maladaptation in Future Climates
4.5. Forest Management Practices to Promote Climate Change Adaptation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Summary for policymakers. In Climate Change 2014: Impacts, Adaptation and Vulnerability. Contribution of Working Group ii to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; pp. 1–32. [Google Scholar]
- Rahmstorf, S. A semi-empirical approach to projecting future sea-level rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Sodhi, N.S.; Brook, B.W.; Bradshaw, C.J. Causes and consequences of species extinctions. Princet. Guide Ecol. 2009, 1, 514–520. [Google Scholar]
- Alberto, F.J.; Aitken, S.N.; Alía, R.; González-Martínez, S.C.; Hänninen, H.; Kremer, A.; Lefèvre, F.; Lenormand, T.; Yeaman, S.; Whetten, R. Potential for evolutionary responses to climate change-evidence from tree populations. Glob. Chang. Biol. 2013, 19, 1645–1661. [Google Scholar] [CrossRef] [PubMed]
- Frank, A.; Howe, G.T.; Sperisen, C.; Brang, P.; Clair, J.B.S.; Schmatz, D.R.; Heiri, C. Risk of genetic maladaptation due to climate change in three major European tree species. Glob. Chang. Biol. 2017, 23, 5358–5371. [Google Scholar] [CrossRef] [PubMed]
- Kremer, A.; Ronce, O.; Robledo-Arnuncio, J.J.; Guillaume, F.; Bohrer, G.; Nathan, R.; Bridle, J.R.; Gomulkiewicz, R.; Klein, E.K.; Ritland, K. Long-distance gene flow and adaptation of forest trees to rapid climate change. Ecol. Lett. 2012, 15, 378–392. [Google Scholar] [CrossRef] [PubMed]
- Montwé, D.; Isaac-Renton, M.; Hamann, A.; Spiecker, H. Cold adaptation recorded in tree rings highlights risks associated with climate change and assisted migration. Nat. Commun. 2018, 9, 1574. [Google Scholar] [CrossRef]
- Price, T.D.; Qvarnström, A.; Irwin, D.E. The role of phenotypic plasticity in driving genetic evolution. Proc. R. Soc. B Biol. Sci. 2003, 270, 1433–1440. [Google Scholar] [CrossRef]
- Ash, J.D.; Givnish, T.J.; Waller, D.M. Tracking lags in historical plant species’ shifts in relation to regional climate change. Glob. Chang. Biol. 2017, 23, 1305–1315. [Google Scholar] [CrossRef]
- Bertrand, R.; Lenoir, J.; Piedallu, C.; Riofrío-Dillon, G.; De Ruffray, P.; Vidal, C.; Pierrat, J.-C.; Gégout, J.-C. Changes in plant community composition lag behind climate warming in lowland forests. Nature 2011, 479, 517–520. [Google Scholar] [CrossRef]
- Isaac-Renton, M.G.; Roberts, D.R.; Hamann, A.; Spiecker, H. Douglas-fir plantations in Europe: A retrospective test of assisted migration to address climate change. Glob. Chang. Biol. 2014, 20, 2607–2617. [Google Scholar] [CrossRef]
- Visser, M.E. Keeping up with a warming world; assessing the rate of adaptation to climate change. Proc. R. Soc. Lond. B Biol. Sci. 2008, 275, 649–659. [Google Scholar] [CrossRef] [PubMed]
- Harsch, M.A.; Phillips, A.; Zhou, Y.; Leung, M.R.; Rinnan, D.S.; Kot, M. Moving forward: Insights and applications of moving-habitat models for climate change ecology. J. Ecol. 2017, 105, 1169–1181. [Google Scholar] [CrossRef]
- Booth, T.H.; Nix, H.A.; Hutchinson, M.F.; Jovanic, T. Niche analysis and tree species introduction. For. Ecol. Manag. 1988, 23, 47–59. [Google Scholar] [CrossRef]
- Kohlmann, B.; Nix, H.; Shaw, D. Environmental predictions and distributional limits of chromosomal taxa in the Australian Grasshoppercaledia captiva (F.). Oecologia 1988, 75, 483–493. [Google Scholar] [CrossRef] [PubMed]
- Dyderski, M.K.; Paź, S.; Frelich, L.E.; Jagodziński, A.M. How much does climate change threaten European forest tree species distributions? Glob. Chang. Biol. 2018, 24, 1150–1163. [Google Scholar] [CrossRef] [PubMed]
- Booth, T.H. Why understanding the pioneering and continuing contributions of bioclim to species distribution modelling is important. Austral Ecol. 2018, 43, 852–860. [Google Scholar] [CrossRef]
- Hu, X.-G.; Wang, T.; Liu, S.-S.; Jiao, S.-Q.; Jia, K.-H.; Zhou, S.-S.; Jin, Y.; Li, Y.; El-Kassaby, Y.A.; Mao, J.-F. Predicting future seed sourcing of Platycladus orientalis (L.) for future climates using climate niche models. Forests 2017, 8, 471. [Google Scholar] [CrossRef]
- Hu, X.-G.; Jin, Y.; Wang, X.-R.; Mao, J.-F.; Li, Y. Predicting impacts of future climate change on the distribution of the widespread conifer Platycladus orientalis. PLoS ONE 2015, 10, e0132326. [Google Scholar] [CrossRef]
- Andalo, C.; Beaulieu, J.; Bousquet, J. The impact of climate change on growth of local White spruce populations in Quebec, Canada. For. Ecol. Manag. 2005, 205, 169–182. [Google Scholar] [CrossRef]
- Ikeda, D.H.; Max, T.L.; Allan, G.J.; Lau, M.K.; Shuster, S.M.; Whitham, T.G. Genetically informed ecological niche models improve climate change predictions. Glob. Chang. Biol. 2017, 23, 164–176. [Google Scholar] [CrossRef]
- Mátyás, C. Modeling climate change effects with provenance test data. Tree Physiol. 1994, 14, 797–804. [Google Scholar] [CrossRef] [PubMed]
- Rehfeldt, G.E.; Ying, C.C.; Spittlehouse, D.L.; Hamilton, D.A. Genetic responses to climate in Pinus contorta: Niche breadth, climate change, and reforestation. Ecol. Monogr. 1999, 69, 375–407. [Google Scholar] [CrossRef]
- Schmidtling, R. Use of provenance tests to predict response to climate change: Loblolly pine and Norway spruce. Tree Physiol. 1994, 14, 805–817. [Google Scholar] [CrossRef] [PubMed]
- Rehfeldt, G.E.; Wykoff, W.R.; Ying, C.C. Physiologic plasticity, evolution, and impacts of a changing climate on Pinus contorta. Clim. Chang. 2001, 50, 355–376. [Google Scholar] [CrossRef]
- Wang, T.; Hamann, A.; Yanchuk, A.; O’neill, G.; Aitken, S. Use of response functions in selecting lodgepole pine populations for future climates. Glob. Chang. Biol. 2006, 12, 2404–2416. [Google Scholar] [CrossRef]
- Yang, J.; Pedlar, J.H.; McKenney, D.W.; Weersink, A. The development of universal response functions to facilitate climate-smart regeneration of black spruce and white pine in Ontario, Canada. For. Ecol. Manag. 2015, 339, 34–43. [Google Scholar] [CrossRef]
- Chakraborty, D.; Schueler, S.; Lexer, M.J.; Wang, T. Genetic trials improve the transfer of douglas-fir distribution models across continents. Ecography 2018, 41, 88–101. [Google Scholar] [CrossRef]
- Chakraborty, D.; Wang, T.; Andre, K.; Konnert, M.; Lexer, M.J.; Matulla, C.; Weißenbacher, L.; Schueler, S. Adapting douglas-fir forestry in central europe: Evaluation, application, and uncertainty analysis of a genetically based model. Eur. J. For. Res. 2016, 135, 919–936. [Google Scholar] [CrossRef]
- Wang, T.; O’Neill, G.A.; Aitken, S.N. Integrating environmental and genetic effects to predict responses of tree populations to climate. Ecol. Appl. 2010, 20, 153–163. [Google Scholar] [CrossRef]
- Chen, C. Studies on provenance trial of Platycladus orientalis. J. Beijing For. Univ. 2001, 23, 60–62. (In Chinese) [Google Scholar]
- Chen, X.; Shen, X. Provenance studies on the survival rates and growth of the juvenile plantations of Platycladus orientalis. J. Beijing For. Univ. 1994, 18, 20–27. (In Chinese) [Google Scholar]
- Chen, X.; Shen, X.; Shi, W. Overwintering and growth performance of different provenances of Platycladus orientalis in Beijing. J. Beijing Univ. Agric. 1990, 5, 19–27. (In Chinese) [Google Scholar]
- Dong, T.; Chen, X.; Zhang, X.; Li, Z.; Kong, W. Platycladus Orientalis, 1st ed.; Henan Science and Technology Press: Zhengzhou, China, 1990. [Google Scholar]
- Ma, F.; Jia, L.; Duan, J.; Zhou, X. Compilation of site index table for plantations of Platycladus orientalis in Beijing mountainous area. J. Beijing For. Univ. 2008, 30, 78–82. (In Chinese) [Google Scholar]
- Tang, G.; Ding, Y.; Wang, S.; Ren, G.; Liu, H.; Zhang, L. Comparative analysis of china surface air temperature series for the past 100 years. Adv. Clim. Chang. Res. 2010, 1, 11–19. [Google Scholar] [CrossRef]
- Fu, Y.-H.; Lu, R.-Y.; Guo, D. Changes in surface air temperature over china under the 1.5 and 2.0 °C global warming targets. Adv. Clim. Chang. Res. 2018, 9, 112–119. [Google Scholar] [CrossRef]
- Du, L.; Yu, H. Preliminary reports on provenance test of Platycladus orientalis in Guizhou. Guizhou For. Sci. Technol. 1994, 22, 20–22. (In Chinese) [Google Scholar]
- Chen, X.; Shen, X. Studies on genotype-environment interactions of seedling height in provenances trials of Platycladus orientalis. J. Beijing For. Univ. 1987, 9, 232–240. (In Chinese) [Google Scholar]
- Deng, C.; Ma, J.; Dong, S. Preliminary study on the variation of seedling provenance traits of Platycladus orientalis. Sichuan For. Sci. Technol. 1986, 7, 27–34. (In Chinese) [Google Scholar]
- Cao, F. Study on the introduced seedling of Platycladus orientalis. J. Jiangsu For. Sci. Technol. 1992, 2, 13–15. (In Chinese) [Google Scholar]
- Li, J.; Xu, W.; Sun, W.; Sun, C.; Fu, J. Study on characteristic variation of Platycladus orientalis provenance test during seedling period. Liaoning For. Sci. Technol. 1986, 6, 14–18. (In Chinese) [Google Scholar]
- Zhao, B. Variation of growing characteristics in the seedling stage of Platycladus orientalis provenance trial. Shanxi For. Sci. Technol. 1990, 4, 1–6. (In Chinese) [Google Scholar]
- Mao, A.; Li, J.; Zhang, C.; Li, Q.; Wang, S.; Chen, X.; Li, Y. Geographic variation and provenance selection of Platycladus orientalis in a 19-year-old testing plantation. J. Beijing For. Univ. 2010, 32, 63–68. (In Chinese) [Google Scholar]
- Dong, T.; Zhang, X.; Kong, W.; Zhai, B.; Qi, M. Study on the geographical variation of seedling characters of Platycladus orientalis. Henan For. Sci. Technol. 1990, 4, 13–18. (In Chinese) [Google Scholar]
- Sun, Z.; Qu, X. Seedling provenance test reports of Platycladus orientalis. Shandong For. Sci. Technol. 1989, 2, 60–64. (In Chinese) [Google Scholar]
- Yang, X.; Zhang, D.; Li, B.; Zhang, Y.; Zheng, J. Provenance test and superior provenance selection of Platycladus orientalis. Shanxi For. Sci. Technol. 1993, 4, 1–4. (In Chinese) [Google Scholar]
- Luo, W.; He, Z.; Zhou, J. Preliminary seedling provenance test of Platycladus orientalis. Shanxi For. Sci. Technol. 1988, 2, 1–6. (In Chinese) [Google Scholar]
- Qu, X.; Shi, X.; Xia, J. Preliminary report on young plantation of Platycladus orientalis. For. Sci. Technol. 1990, 2, 12–15. (In Chinese) [Google Scholar]
- Li, S.; Zhou, J.; Hu, M.; Li, W. Study on geographical variation Platycladus orientalis among different provenances. Gansu For. Sci. Technol. 1986, 1, 74–83. (In Chinese) [Google Scholar]
- Wu, H.; Tang, H.; Xing, S. The appraisal and selection of good fast growing provenances of Platycladus orientalis (linn.) franco. Chin. Agric. Sci. Bull. 2010, 26, 104–109. (In Chinese) [Google Scholar]
- Zhang, D.; Liu, S. Preliminary study on the growth of geographical variation of Platycladus orientalis. Shanxi For. Sci. Technol. 1995, 1, 38–40. (In Chinese) [Google Scholar]
- Shi, X.; Qu, X. Seedling provenance test of Platycladus orientalis. For. Sci. Technol. 1987, 7, 60–64. (In Chinese) [Google Scholar]
- Shi, W. A preliminary report on provenance test of one year seedling of Platycladus orientalis (L.) Franco. J. Beijing For. Univ. 1986, 1, 74–83. (In Chinese) [Google Scholar]
- Wang, R.; Wang, M. Preliminary report on provenance test of Platycladus orientalis. J. Hebei For. Technol. 1990, 1, 30–34. (In Chinese) [Google Scholar]
- Ji, H.; Li, W. Study on seedling height growth and geographical variation of Platycladus orientalis. Inn. Mong. For. Sci. Technol. 1991, 2, 18–24. (In Chinese) [Google Scholar]
- Shi, X.; Yang, X.; Shi, Z.; Ding, M. Study on introduction and provenance test of Platycladus orientalis in yanbei at shanxi provence. For. Sci. Technol. 1995, 11, 13–16. (In Chinese) [Google Scholar]
- Mihai, G.; Mirancea, I.; Duta, C. Variation of the quantitative traits in a progeny test of Abies alba (mill.) at the nursery stage. Silvae Genet. 2014, 63, 275–284. [Google Scholar] [CrossRef]
- O’Brien, S.T.; Hubbell, S.P.; Spiro, P.; Condit, R.; Foster, R.B. Diameter, height, crown, and age relationship in eight neotropical tree species. Ecology 1995, 76, 1926–1939. [Google Scholar] [CrossRef]
- Wang, T.; Wang, G.; Innes, J.L.; Seely, B.; Chen, B. ClimateAP: An application for dynamic local downscaling of historical and future climate data in asia pacific. Front. Agric. Sci. Eng. 2017, 4, 448–458. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous united states. Int. J. Climatol. A J. R. Meteorol. Soc. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Judd, C.M.; Westfall, J.; Kenny, D.A. Treating stimuli as a random factor in social psychology: A new and comprehensive solution to a pervasive but largely ignored problem. J. Personal. Soc. Psychol. 2012, 103, 54–69. [Google Scholar] [CrossRef] [PubMed]
- Bates, D.; Maechler, M.; Bolker, B.; Walker, S. Lme4: Linear mixed-effects models using Eigen and S4. R package version 1.1–7. 2013. Available online: http://lme4.r-forge.r-project.org/ (accessed on 25 July 2019).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Li, S.; He, H.; Peng, W.; Zhou, J.; Wang, F. A study on geographic provenance selection of platycladus orientalis. J. Gansu For. Sci. Technol. 1998, 1, 2–11. (In Chinese) [Google Scholar]
- Qu, X.; Shi, X.; Xia, J.; Fu, Y. A preliminary report on young provenances test of platycladus orientalis. For. Sci. Technol. 1992, 2, 12–15. (In Chinese) [Google Scholar]
- Clark, P.C., Jr. The Effects of Multicollinearity in Multilevel Models. Ph.D. Thesis, Wright State University, Dayton, OH, USA, 2013. [Google Scholar]
- Carter, K. Provenance tests as indicators of growth response to climate change in 10 north temperate tree species. Can. J. For. Res. 1996, 26, 1089–1095. [Google Scholar] [CrossRef]
- O’Neill, G.A.; Nigh, G.; Wang, T.; Ott, P.K. Growth response functions improved by accounting for nonclimatic site effects. Can. J. For. Res. 2007, 37, 2724–2730. [Google Scholar] [CrossRef]
- Johnson, R.; Stritch, L.; Olwell, P.; Lambert, S.; Horning, M.E.; Cronn, R. What are the best seed sources for ecosystem restoration on blm and usfs lands? Nativ. Plants J. 2010, 11, 117–131. [Google Scholar] [CrossRef]
- Kawecki, T.J.; Ebert, D. Conceptual issues in local adaptation. Ecol. Lett. 2004, 7, 1225–1241. [Google Scholar] [CrossRef]
- Aitken, S.N.; Yeaman, S.; Holliday, J.A.; Wang, T.; Curti-McLane, S. Adaptation, migration or extirpation: Climate change outcomes for tree populations. Evol. Appl. 2008, 1, 95–111. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Shi, X. Seed Zones of Chinese Forest Trees—Seed Zones of Platycladus Orientalis (Linn.) Franco. Available online: http://www.spsp.gov.cn/page/P393/71.shtml (accessed on 19 June 2019).
- Mátyás, C. Adaptational Lag: A General Feature of Natural Populations. In Proceedings of the Joint Meeting of Western Forest Genetics Association and IUFRO Working Parties, Douglas-fir, Contorta Pine, Sitka Spruce, and Abies Breeding and Genetic Resources, Olympia, WA, USA, 11 August 1990; pp. 20–24. [Google Scholar]
- Hoffmann, A.A.; Sgrò, C.M. Climate change and evolutionary adaptation. Nature 2011, 470, 479. [Google Scholar] [CrossRef]
- Hutchinson, G.E. Concluding remarks. Cold Spring Harb. Symp. Quant. Biol. 1957, 22, 415–427. [Google Scholar] [CrossRef]
- Hu, X.-G.; Liu, H.; Jin, Y.; Sun, Y.-Q.; Li, Y.; Zhao, W.; El-Kassaby, Y.A.; Wang, X.-R.; Mao, J.-F. De novo transcriptome assembly and characterization for the widespread and stress-tolerant conifer Platycladus orientalis. PLoS ONE 2016, 11, e0148985. [Google Scholar] [CrossRef] [PubMed]
- Leech, S.M.; Almuedo, P.L.; O’Neill, G. Assisted migration: Adapting forest management to a changing climate. J. Ecosyst. Manag. 2011, 12, 18–34. [Google Scholar]
- Meier, E.S.; Lischke, H.; Schmatz, D.R.; Zimmermann, N.E. Climate, competition and connectivity affect future migration and ranges of European trees. Glob. Ecol. Biogeogr. 2012, 21, 164–178. [Google Scholar] [CrossRef]
- Vilà-Cabrera, A.; Coll, L.; Martinez-Vilalta, J.; Retana, J. Forest management for adaptation to climate change in the mediterranean basin: A synthesis of evidence. For. Ecol. Manag. 2018, 407, 16–22. [Google Scholar] [CrossRef]
- Kramer, K.; Buiteveld, J.; Forstreuter, M.; Geburek, T.; Leonardi, S.; Menozzi, P.; Povillon, F.; Schelhaas, M.; du Cros, E.T.; Vendramin, G. Bridging the gap between ecophysiological and genetic knowledge to assess the adaptive potential of European beech. Ecol. Model. 2008, 216, 333–353. [Google Scholar] [CrossRef]
- Lefèvre, F.; Boivin, T.; Bontemps, A.; Courbet, F.; Davi, H.; Durand-Gillmann, M.; Fady, B.; Gauzere, J.; Gidoin, C.; Karam, M.-J. Considering evolutionary processes in adaptive forestry. Ann. For. Sci. 2014, 71, 723–739. [Google Scholar] [CrossRef]
- Mueller, J.M.; Hellmann, J.J. An assessment of invasion risk from assisted migration. Conserv. Biol. 2008, 22, 562–567. [Google Scholar] [CrossRef]
- Graham, R.L.; Turner, M.G.; Dale, V.H. How increasing CO2 and climate change affect forests. BioScience 1990, 40, 575–587. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; Heuvelink, G.B.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B. Soilgrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- Bussotti, F.; Pollastrini, M.; Holland, V.; Brueggemann, W. Functional traits and adaptive capacity of European forests to climate change. Environ. Exp. Bot. 2015, 111, 91–113. [Google Scholar] [CrossRef]
- Schelhaas, M.-J.; Nabuurs, G.-J.; Hengeveld, G.; Reyer, C.; Hanewinkel, M.; Zimmermann, N.E.; Cullmann, D. Alternative forest management strategies to account for climate change-induced productivity and species suitability changes in Europe. Reg. Environ. Chang. 2015, 15, 1581–1594. [Google Scholar] [CrossRef]
- Temperli, C.; Bugmann, H.; Elkin, C. Adaptive management for competing forest goods and services under climate change. Ecol. Appl. 2012, 22, 2065–2077. [Google Scholar] [CrossRef] [PubMed]
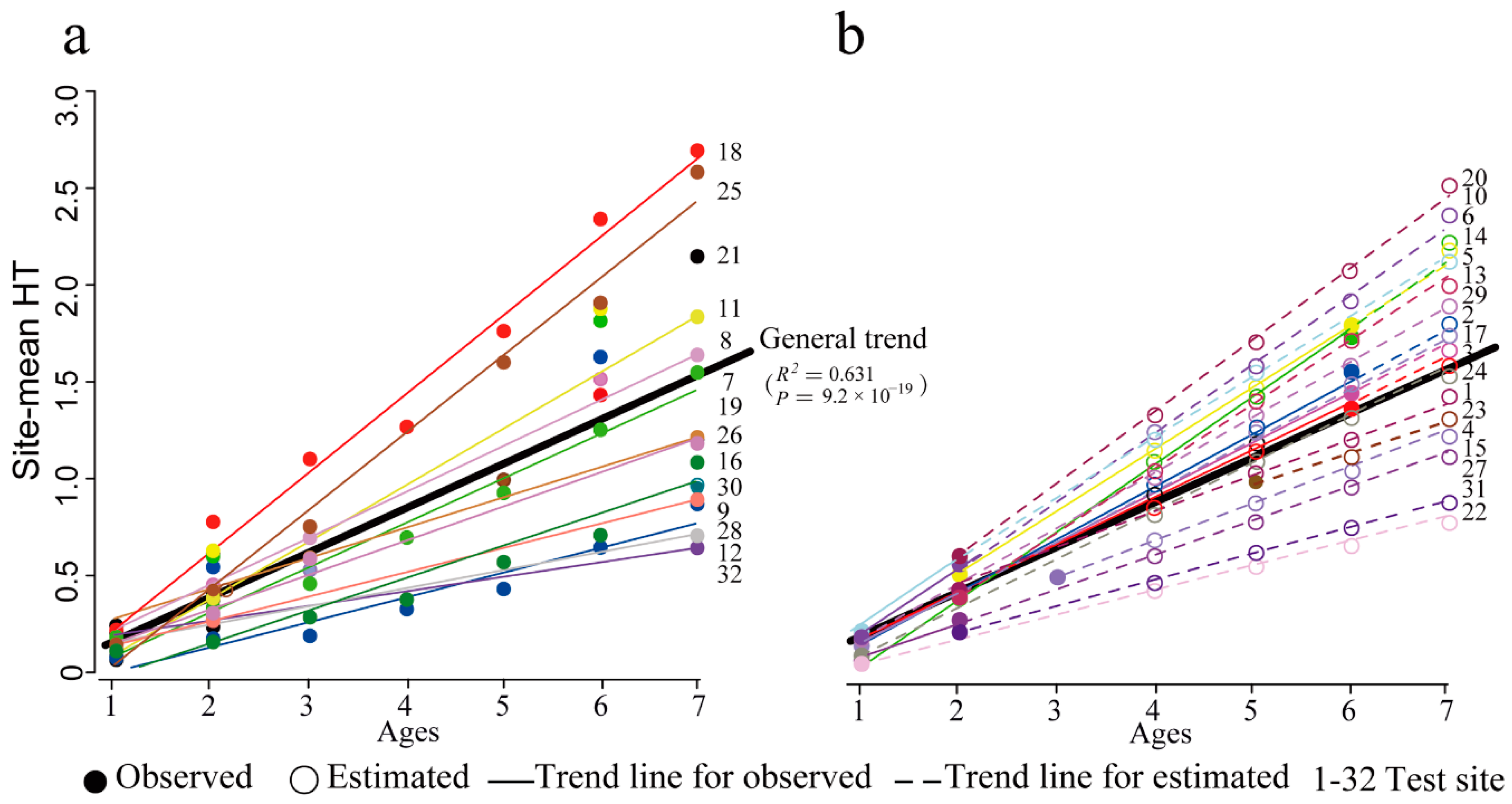
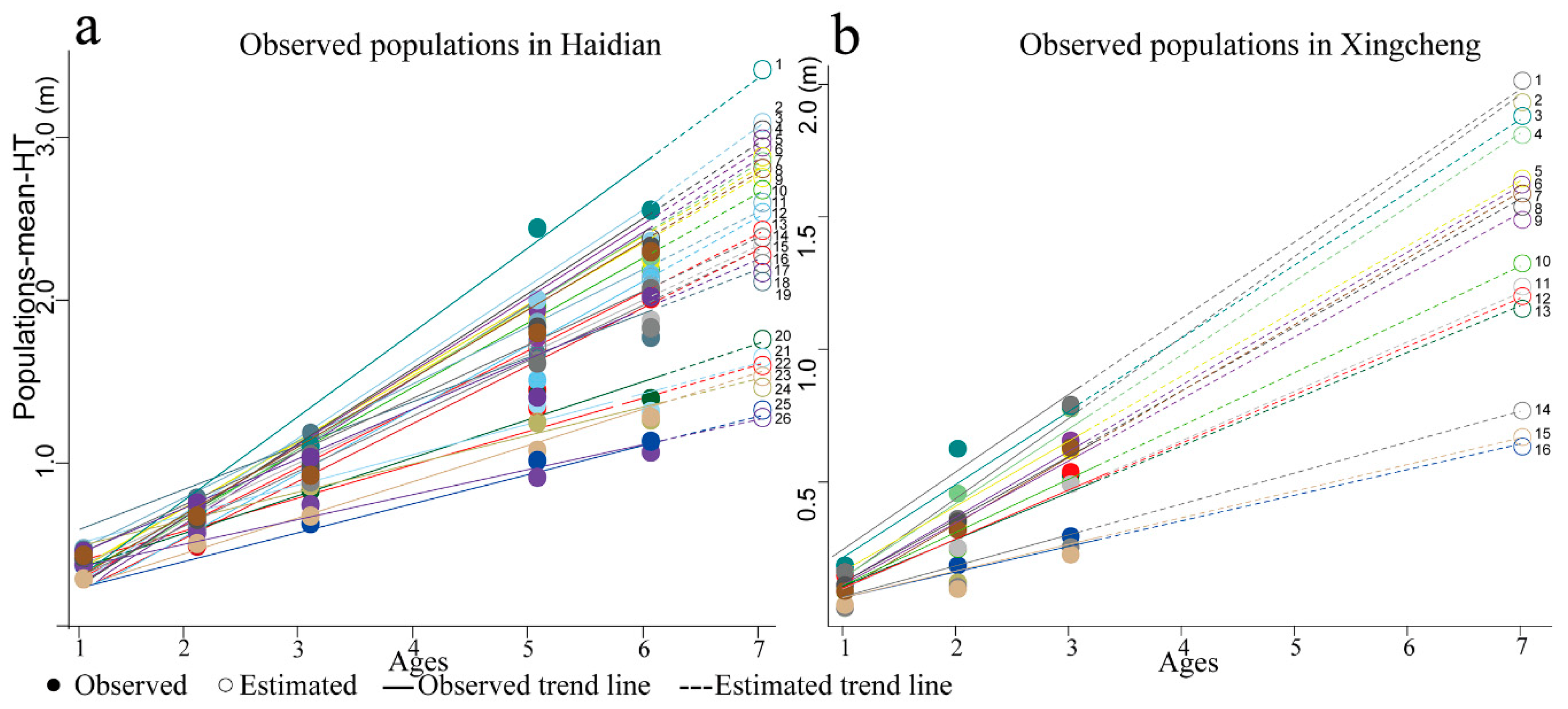
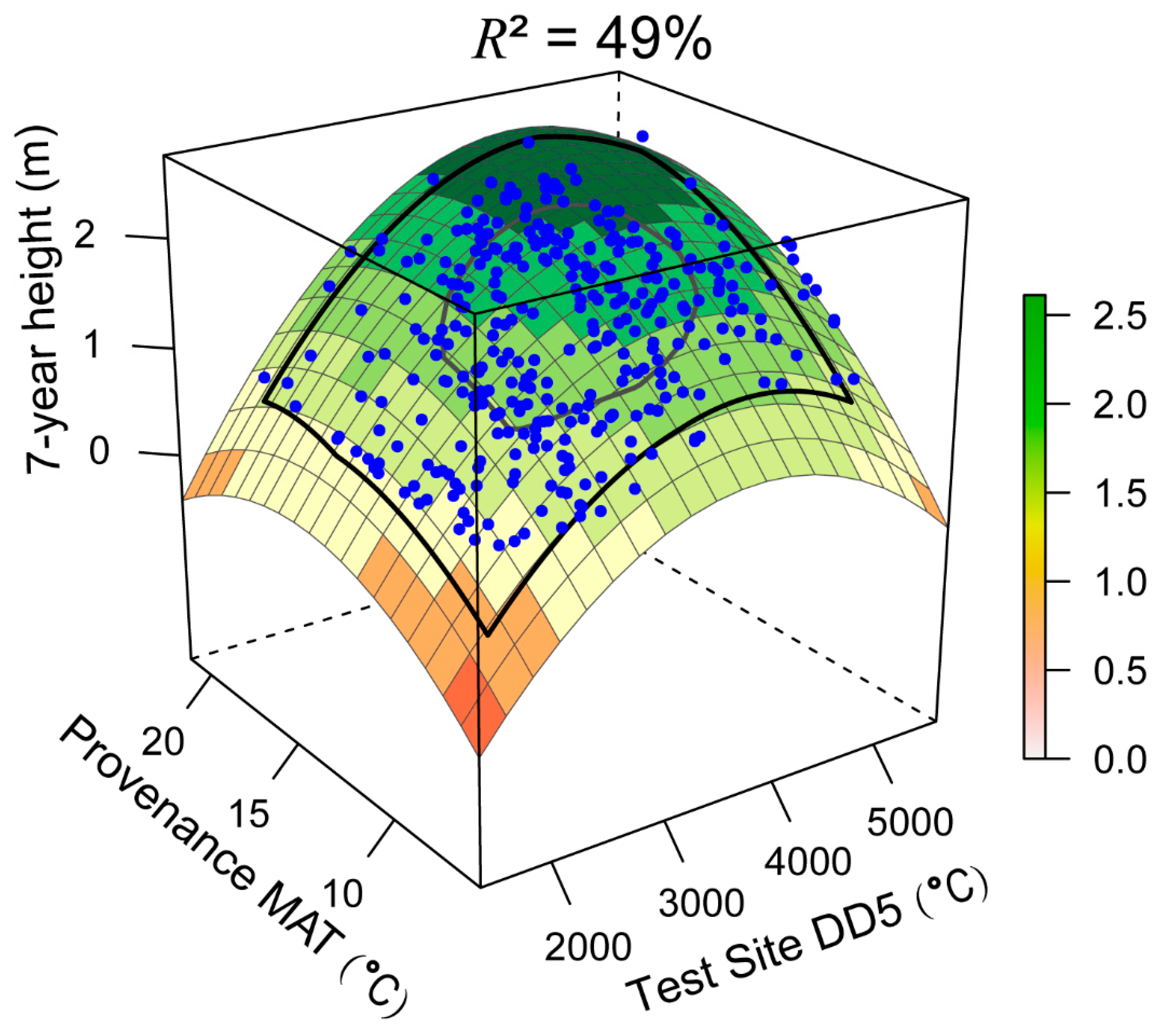
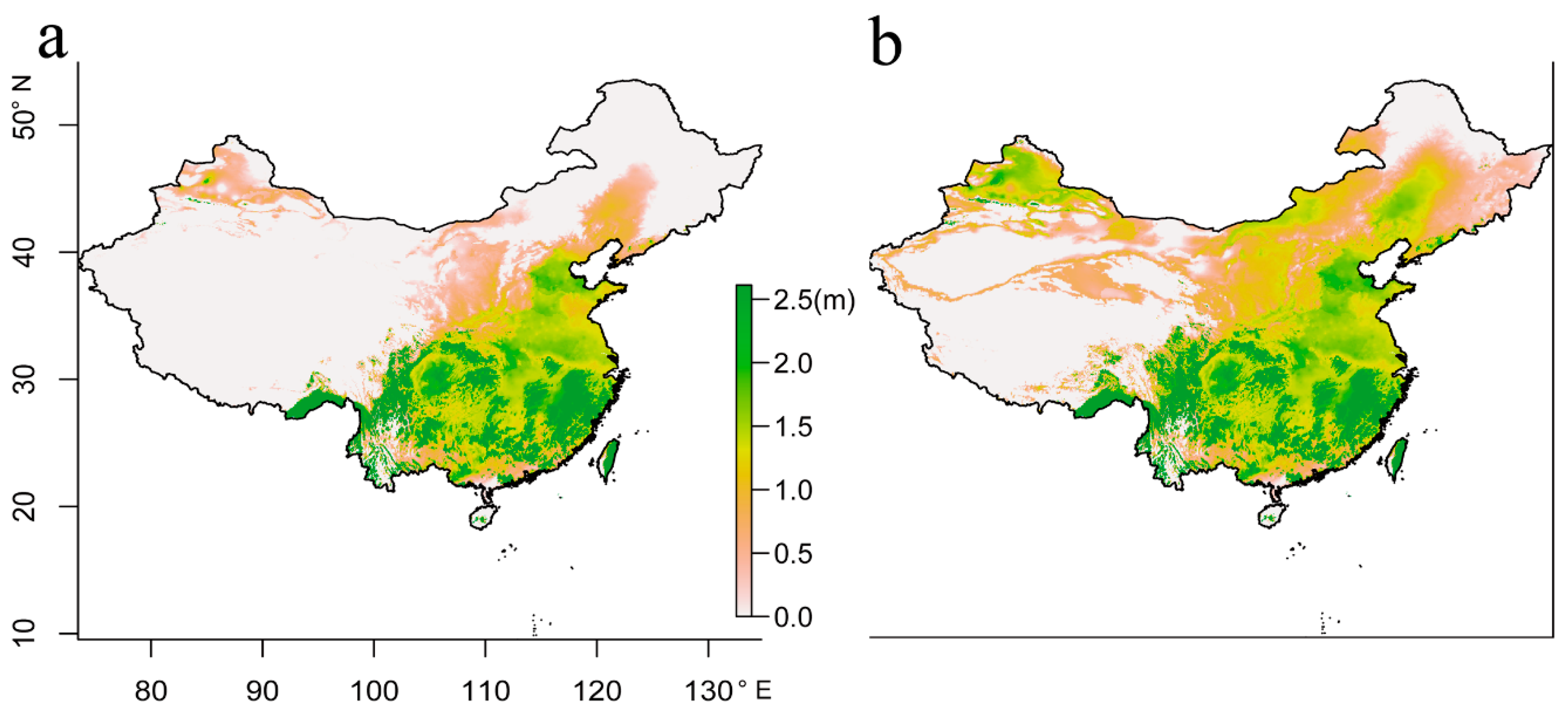
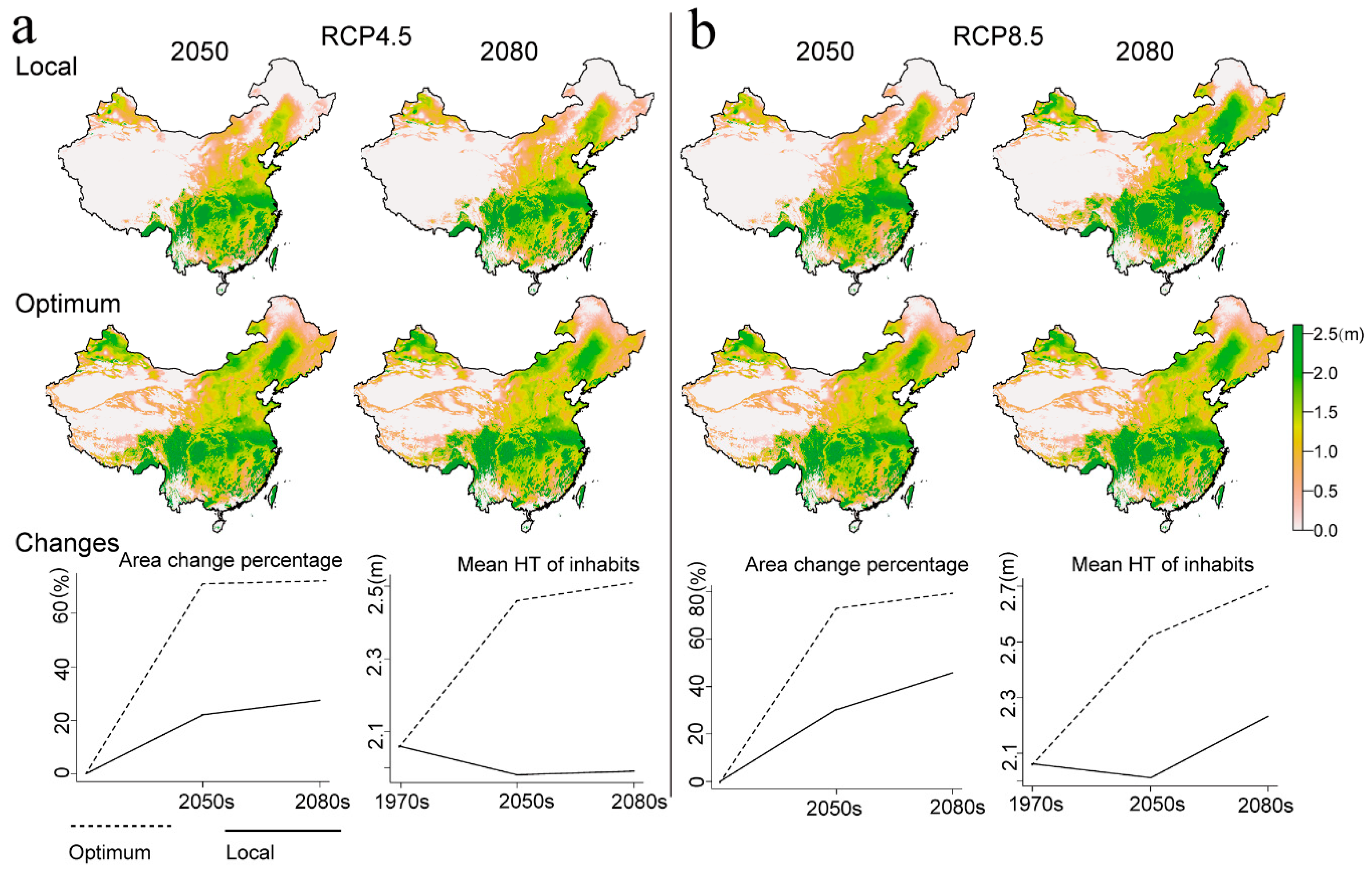
| No. | Test Site | Latitude | Longitude | Elevation | No. of pop 1 | Ages of obs 2 | Used in URF | Source | |
|---|---|---|---|---|---|---|---|---|---|
| Provenance | Trial Mean | ||||||||
| 1 | Guiyang | 25.93 | 106.55 | 957 | 33 | 1 | [38] | ||
| 2 | Nanping | 26.66 | 118.12 | 739 | 23 | 2 | 6 | Yes | [32,39] |
| 3 | Cili | 29.47 | 111.05 | 761 | 23 | 2 | 6 | Yes | [32,39] |
| 4 | Chongqing | 30 | 107.04 | 808 | 27 | 5 | [31] | ||
| 5 | Deyang | 31.68 | 104.5 | 988 | 16 | 1–2 | [40] | ||
| 6 | Queshan | 32.79 | 114.01 | 155 | 23 | 2 | 6 | Yes | [32,39] |
| 7 | Xuzhou | 33.73 | 117.78 | 23 | 20 | 1–7 | 7 | Yes | [41] |
| 8 | Liangdang | 33.99 | 106.25 | 1193 | 21 | 3 | 7 | Yes | [32,42] |
| 9 | Luonan | 34 | 110.35 | 1296 | 7 | 1–2 | 7 | Yes | [32,43] |
| 10 | Jiaxian | 34.1 | 113.18 | 642 | 70 | 1–2, 19 | [33,44] | ||
| 11 | Dengfeng | 34.35 | 113.07 | 334 | 14 | 2 | 7 | Yes | [32,39] |
| 12 | Chunhua | 34.79 | 108.54 | 1025 | 15 | 1–2 | 7 | Yes | [33,43] |
| 13 | Jiyuan | 34.88 | 112.95 | 110 | 25 | 1–2 | [45] | ||
| 14 | Zaozhuang | 34.99 | 117.71 | 366 | 18 | 2 | 6 | Yes | [32,46] |
| 15 | Zhengning | 35.39 | 108.49 | 1260 | 21 | 3 | [42] | ||
| 16 | Jishan | 35.77 | 110.99 | 1597 | 23 | 7 | 7 | Yes | [47] |
| 17 | Yanan | 36.06 | 109.26 | 971 | 28 | 1–2 | [48] | ||
| 18 | Pingyin | 36.08 | 116.33 | 297 | 21 | 1–7 | 7 | Yes | [49] |
| 19 | Lanzhou | 36.12 | 103.71 | 1551 | 21 | 3 | 7 | Yes | [32,50] |
| 20 | Yidu | 36.41 | 118.27 | 575 | 19 | 2 | [46] | ||
| 21 | Yuanshan | 36.49 | 117.86 | 250 | 37 | 23 | 7 | Yes | [32,51] |
| 22 | Taiyuan | 37.76 | 112.3 | 1799 | 51 | 1 | [52] | ||
| 23 | Yulin | 39.03 | 111.08 | 868 | 14 | 1 | [53] | ||
| 24 | Mentougou | 39.98 | 116.05 | 157 | 29 | 1 | 6 | Yes | [54] |
| 25 | Haidian | 40.01 | 116.34 | 51 | 26 | 1–3, 5–6 | 7 | Yes | [32,33] |
| 26 | Zunhua | 40.19 | 117.63 | 260 | 20 | 1–6 | 7 | Yes | [32,55] |
| 27 | Helin | 40.26 | 112.06 | 1262 | 27 | 1–2 | [56] | ||
| 28 | Datong | 40.35 | 113.58 | 1392 | 8 | 1–7 | 7 | [57] | |
| 29 | Miyun | 40.4 | 117.06 | 206 | 24 | 1 | [32,53] | ||
| 30 | Xingcheng | 40.64 | 120.77 | 43 | 16 | 1–3 | 7 | Yes | [32,50] |
| 31 | Zhuozi | 40.97 | 112.15 | 1437 | 3 | 1–2 | [56] | ||
| 32 | Lingyuan | 41.19 | 118.98 | 1209 | 10 | 2 | 7 | Yes | [32,39] |
| Code | Variable Name |
|---|---|
| MAT (°C) | Mean annual temperature |
| MWMT (°C) | Mean warmest month temperature |
| MCMT (°C) | Mean coldest month temperature |
| TD | Continentally, temperature difference between MWMT and MCMT |
| MAP (mm) | Mean annual precipitation |
| AHM | Annual heat-moisture index (MAT + 10)/(MAP/1000)) |
| DD < 0 (°C) | Degree-days below 0 °C |
| DD > 5 (°C) | Degree-days above 5 °C |
| NFFD (day) | Number of frost-free days |
| EMT (°C) | Extreme minimum temperature over a 30-year period |
| EXT (°C) | Extreme maximum temperature over a 30-year period |
| PAS (mm) | Precipitation as snow |
| Eref | Hargreaves reference evaporation |
| CMD | Climatic moisture deficit |
| Source of Variation | Degree of Freedom | Sum of Squares | Mean Squares | F Value | Pr (>F) Value |
|---|---|---|---|---|---|
| Site | 18 | 121.6 | 6.756 | 64.989 | <2 × 10−16 |
| Population | 68 | 29.45 | 0.433 | 4.167 | <2 × 10−17 |
| Residuals | 283 | 29.42 | 1.104 |
| Estimate | Std. Error | T Value | Pr (>|t|) | Significance | |
|---|---|---|---|---|---|
| (Intercept) | −8.31 | 1.40 | −5.95 | 6.33 × 10−9 | *** |
| MAP_s | −6.71 × 10−3 | 2.11 × 10−3 | −3.18 | 1.59 × 10−3 | ** |
| DD5_s | 5.11 × 10−3 | 8.14 × 10−4 | 6.27 | 9.87 × 10−10 | *** |
| CMD_s | 9.25 × 10−3 | 3.73 × 10−3 | 2.48 | 1.35 × 10−2 | * |
| MAT_p | 4.31 × 10−1 | 6.95 × 10−2 | 6.20 | 1.54 × 10−9 | *** |
| MAP_s2 | 1.99 × 10−5 | 4.06 × 10−6 | 4.90 | 1.41 × 10−6 | *** |
| DD5_s2 | 1.18 × 10−6 | 3.86 × 10−7 | 3.04 | 2.47 × 10−3 | ** |
| MAT_p2 | −1.29 × 10−2 | 2.63 × 10−3 | −4.9 | 1.45 × 10−6 | *** |
| MAP_s × DD5_s | −1.11 × 10−5 | 2.55 × 10−6 | −4.33 | 1.87 × 10−5 | *** |
| MAP_s × CMD_s | 2.59 × 10−5 | 4.82 × 10−6 | 5.36 | 1.43 × 10−7 | *** |
| DD5_s × CMD_s | −1.02 × 10−5 | 2.24 × 10−6 | −4.54 | 7.68 × 10−6 | *** |
| Climate Change Scenario | Area (× 106 km2) | Change in Area (%) 1 | ||
|---|---|---|---|---|
| Local | Optimal | Local | Optimal | |
| Current | 3.74 | 6.26 | 67.40 | |
| RCP4.5-2050 | 4.56 | 6.40 | 22.01 | 71.28 |
| RCP4.5-2080 | 4.77 | 6.43 | 27.50 | 71.95 |
| RCP8.5-2050 | 4.88 | 6.47 | 30.44 | 72.95 |
| RCP8.5-2080 | 5.45 | 6.70 | 45.83 | 79.32 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.-G.; Mao, J.-F.; El-Kassaby, Y.A.; Jia, K.-H.; Jiao, S.-Q.; Zhou, S.-S.; Li, Y.; Coops, N.C.; Wang, T. Local Adaptation and Response of Platycladus orientalis (L.) Franco Populations to Climate Change. Forests 2019, 10, 622. https://doi.org/10.3390/f10080622
Hu X-G, Mao J-F, El-Kassaby YA, Jia K-H, Jiao S-Q, Zhou S-S, Li Y, Coops NC, Wang T. Local Adaptation and Response of Platycladus orientalis (L.) Franco Populations to Climate Change. Forests. 2019; 10(8):622. https://doi.org/10.3390/f10080622
Chicago/Turabian StyleHu, Xian-Ge, Jian-Feng Mao, Yousry A. El-Kassaby, Kai-Hua Jia, Si-Qian Jiao, Shan-Shan Zhou, Yue Li, Nicholas C. Coops, and Tongli Wang. 2019. "Local Adaptation and Response of Platycladus orientalis (L.) Franco Populations to Climate Change" Forests 10, no. 8: 622. https://doi.org/10.3390/f10080622
APA StyleHu, X.-G., Mao, J.-F., El-Kassaby, Y. A., Jia, K.-H., Jiao, S.-Q., Zhou, S.-S., Li, Y., Coops, N. C., & Wang, T. (2019). Local Adaptation and Response of Platycladus orientalis (L.) Franco Populations to Climate Change. Forests, 10(8), 622. https://doi.org/10.3390/f10080622







