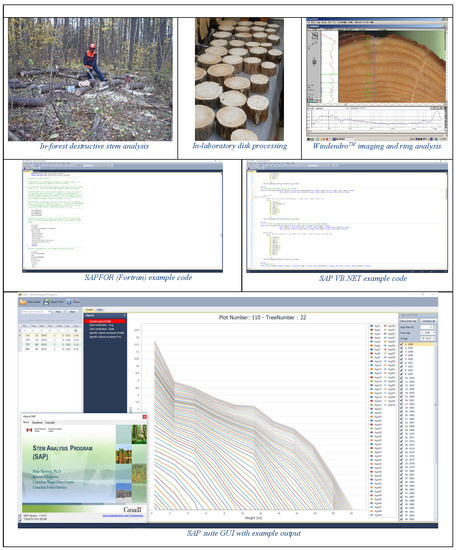
Examining Naturogenic Processes and Anthropogenic Influences on Tree Growth and Development via Stem Analysis: Data Processing and Computational Analytics
Abstract
1. Introduction
2. Materials and Methods
2.1. Stem Analysis Computational Algorithm: Structure and Development
2.2. Exemplification of the Utility of the Resultant SAP Suite
3. Results
3.1. Overview of the Resultant SAP Suite
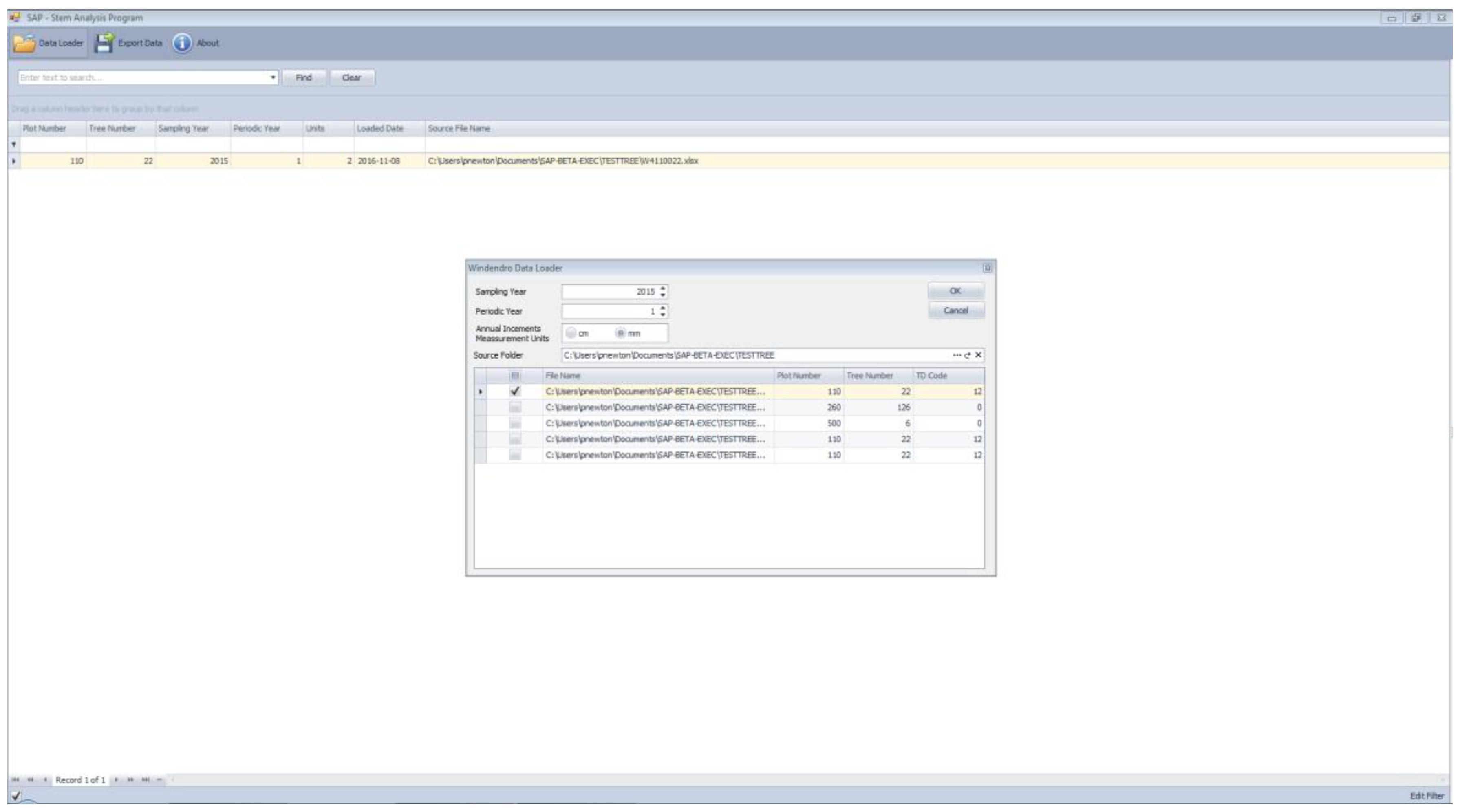
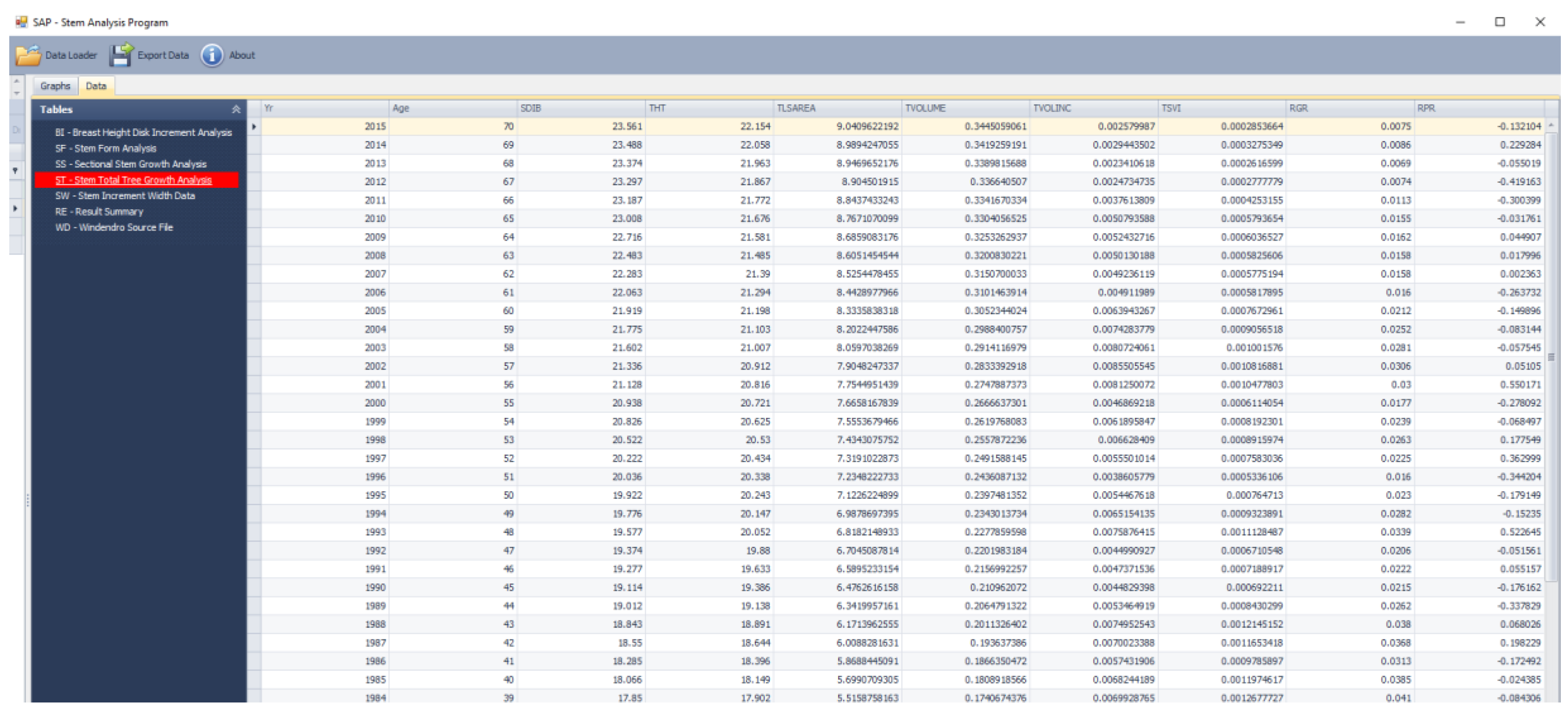
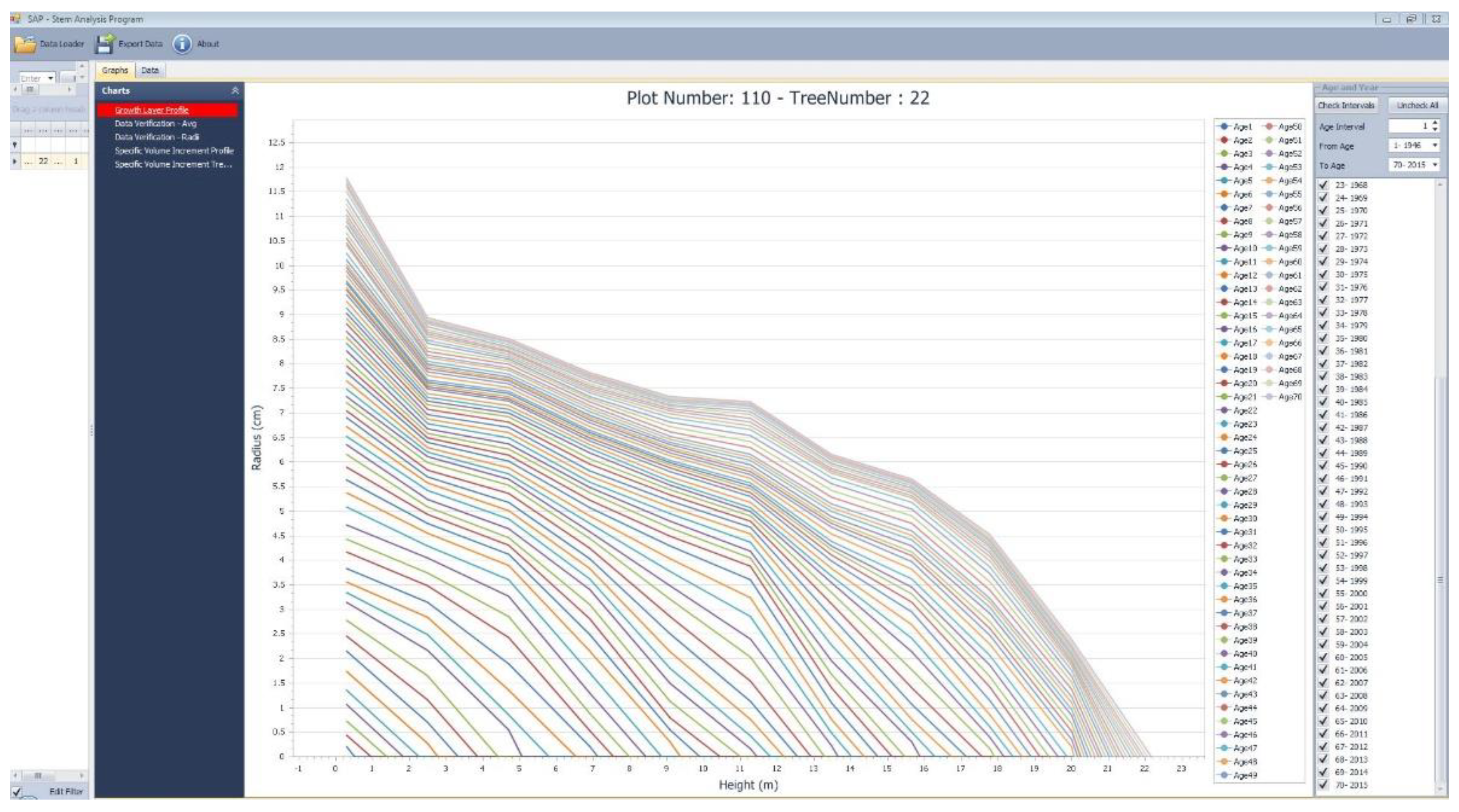
3.2. Input File Format and Structure, Program Execution, and Generated Output
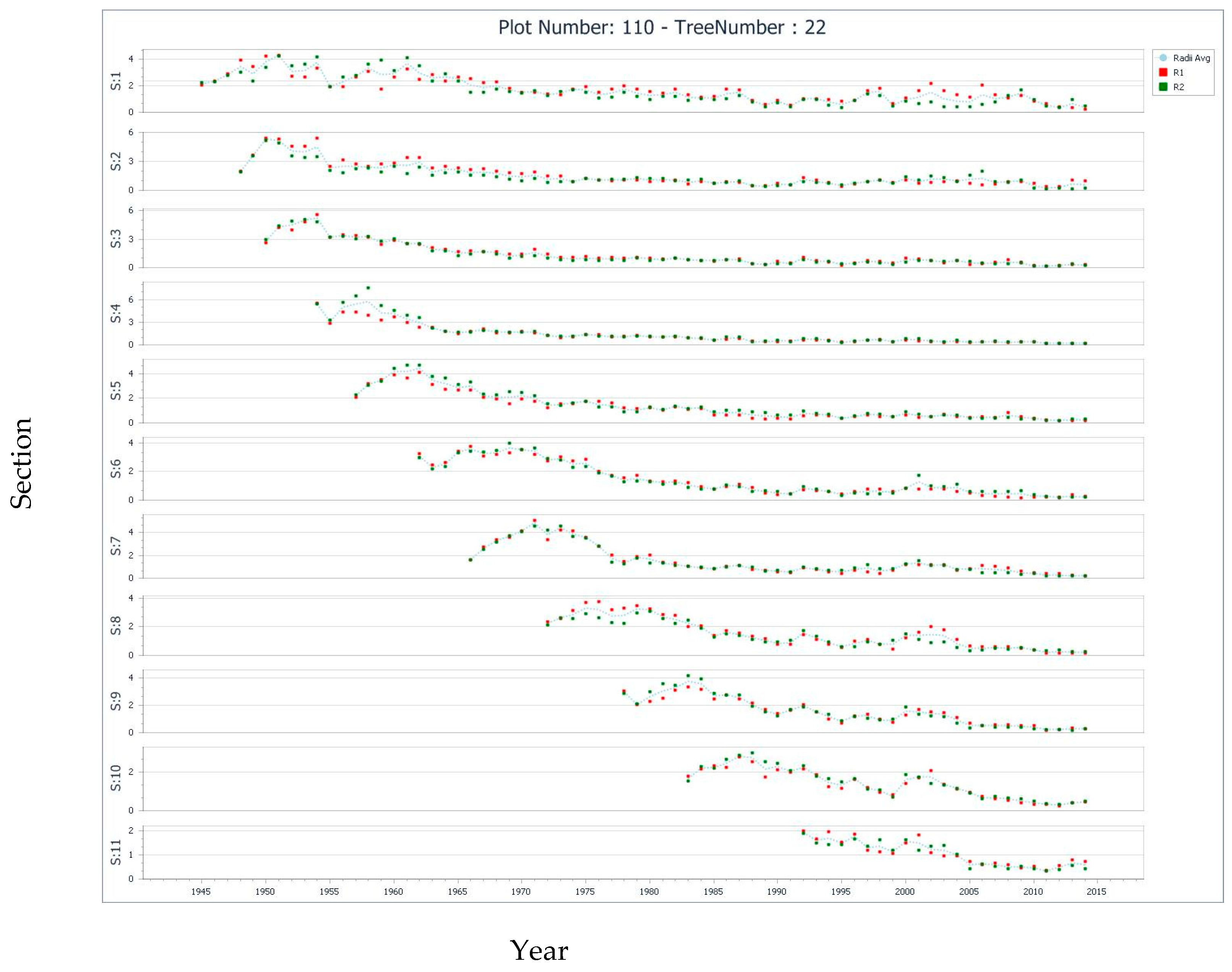
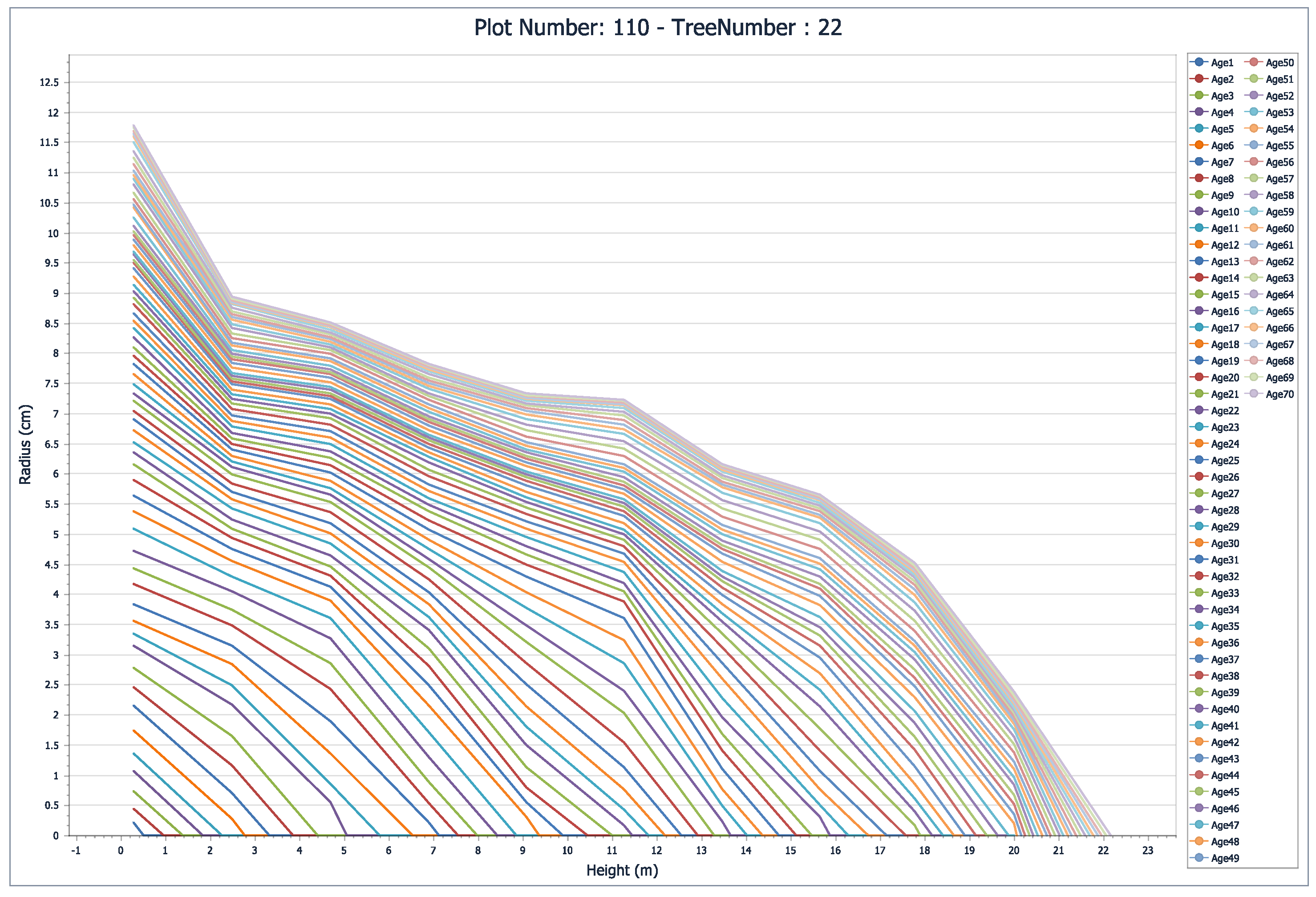
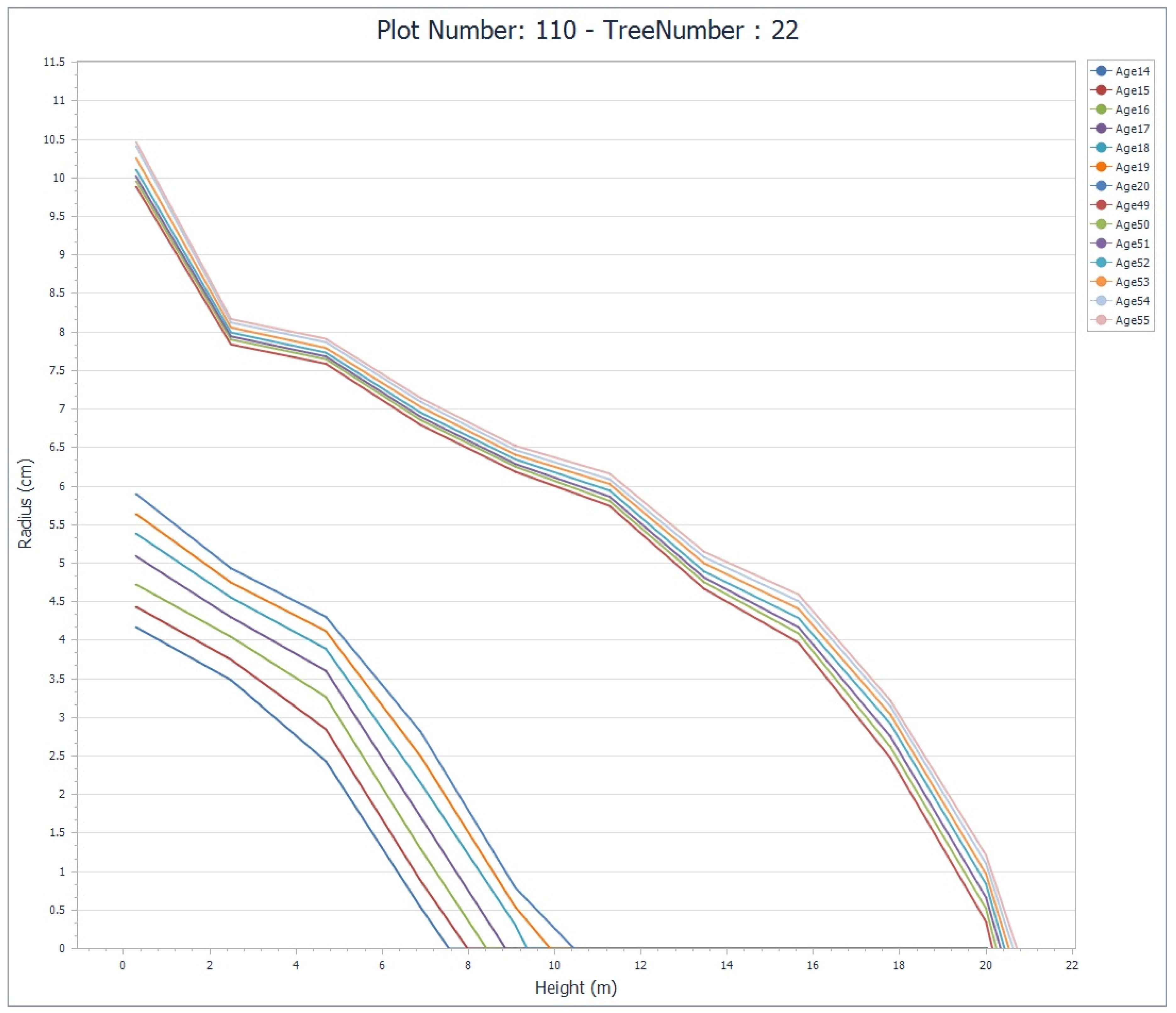
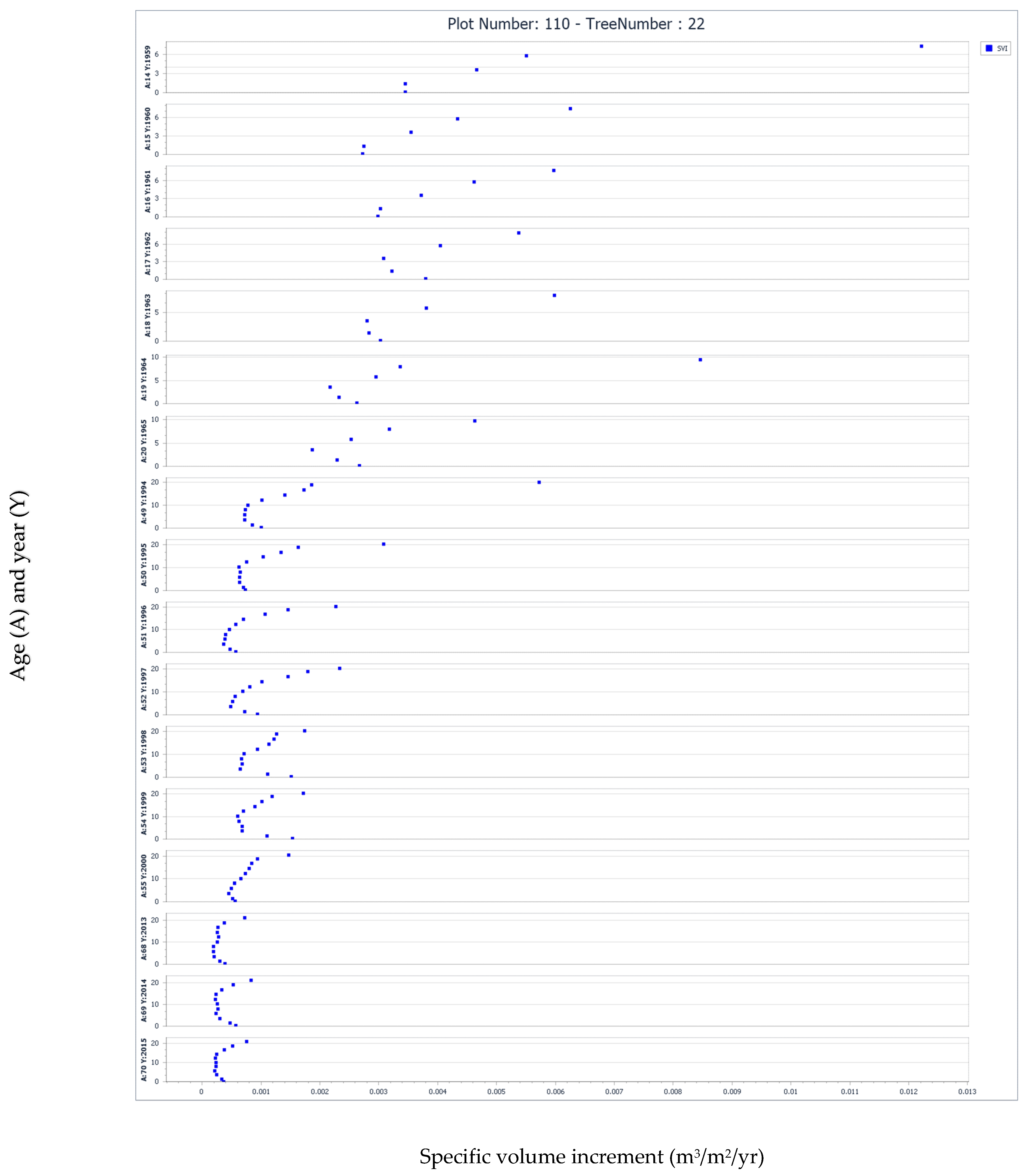
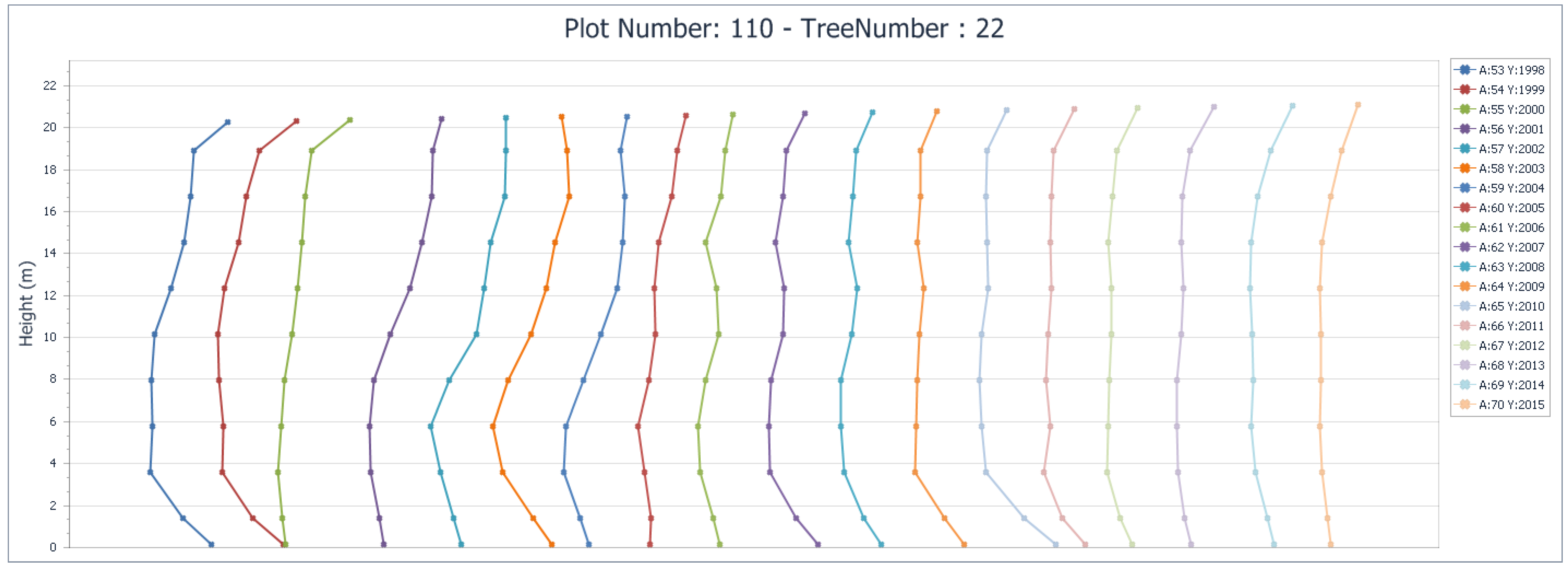
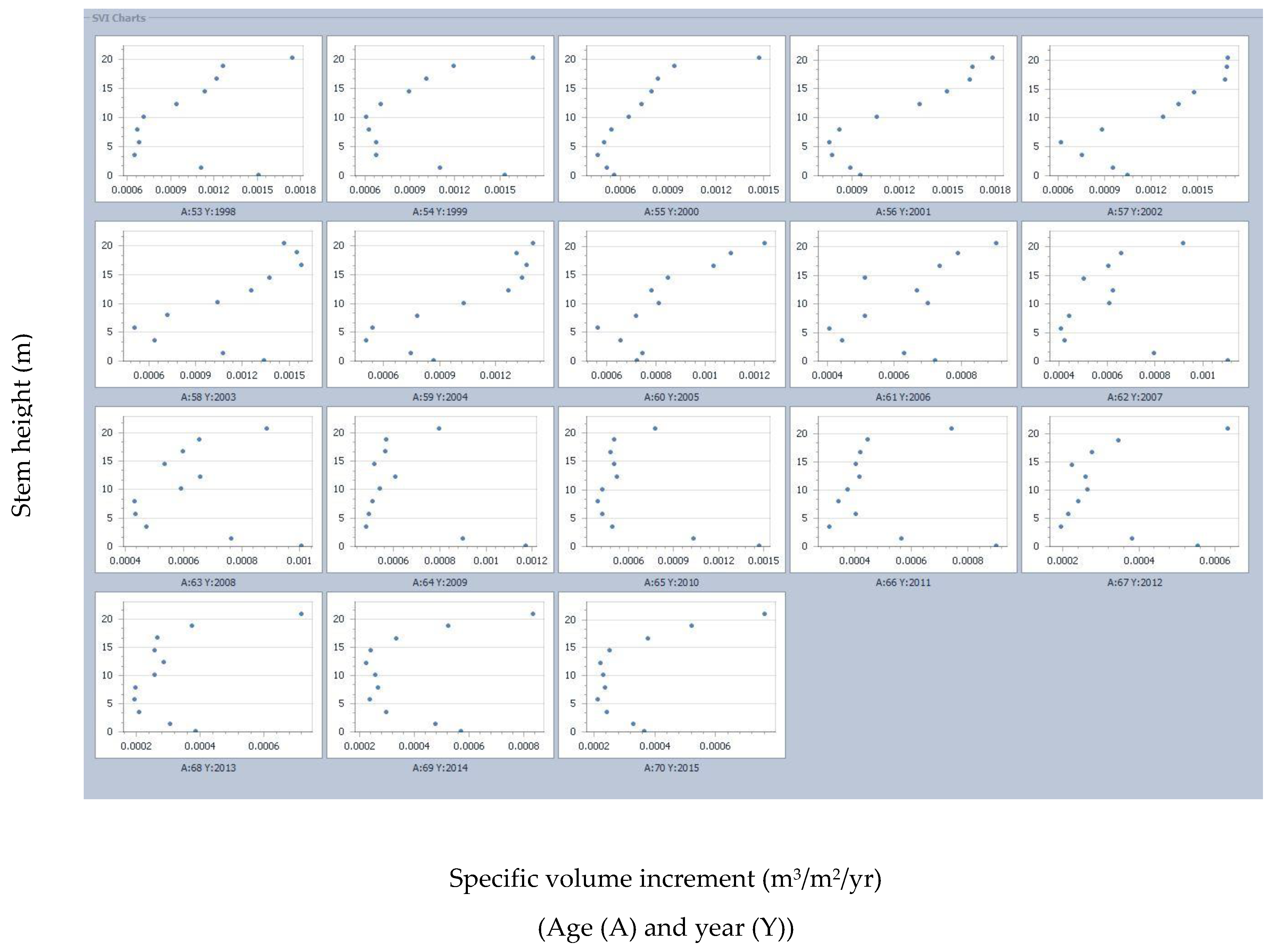
3.3. Interpretation Guidance and Related Inferences Derived
4. Discussion
4.1. The SAP Suite
4.2. Analytics of Whole Tree Stem Analysis
5. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Analytical Structure, Computation Formulae and Underlying Geometric Assumptions Deployed in the SAPFOR Algorithm
Appendix A.1. Growth Diameter and Basal Area Analysis Subroutine (GDB)
Appendix A.2. Growth Volume and Allometric Analysis Subroutine (GVA)
Appendix A.2.1. Sectional Computations
Appendix A.2.2. Cumulative Computations
References
- Shea, S.R.; Armson, K.A. Stem analysis of jack pine (Pinus banksiana Lamb.): Techniques and concepts. Can. J. For. Res. 1972, 2, 392–406. [Google Scholar] [CrossRef]
- Newton, P.F.; Jolliffe, P.A. Assessing processes of intraspecific competition within spatially heterogeneous black spruce stands. Can. J. For. Res. 1998, 28, 259–275. [Google Scholar] [CrossRef]
- Mitchell, S.J. Stem growth responses in Douglas-fir and Sitka spruce following thinning: Implications for assessing wind-firmness. For. Ecol. Manag. 2000, 135, 105–114. [Google Scholar] [CrossRef]
- Thomson, A.J.; van Sickle, G.A. Estimation of tree growth losses caused by pest activity. Can. J. For. Res. 1980, 10, 176–182. [Google Scholar] [CrossRef]
- Mette, T.; Falk, W.; Uhl, E.; Biber, P.; Pretzsch, H. Increment allocation along the stem axis of dominant and suppressed trees in reaction to drought—Results from 123 stem analyses of Norway spruce, Scot pine and European beech. Austrian J. For. Sci. 2015, 132, 223–238. [Google Scholar]
- Lee, E.H.; Beedlow, P.A.; Waschmann, R.S.; Burdick, C.A.; Shaw, D.C. Tree-ring analysis of the fungal disease Swiss needle cast in western Oregon coastal forest. Can. J. For. Res. 2013, 43, 677–690. [Google Scholar] [CrossRef]
- Wang, X.; Stenströmc, E.; Bobergc, J.; Olsd, C.; Drobyshev, I. Outbreaks of Gremmeniella abietina cause considerable decline in stem growth of surviving Scots pine trees. Dendrochronologia 2017, 44, 39–47. [Google Scholar] [CrossRef]
- Piene, H. Early Growth Responses to Operational Spacing in Young Balsam Fir Stands on the Cape Breton Highlands, Nova Scotia; Information Report M-X-125; Environment Canada, Canadian Forestry Service, Maritimes Forest Research Centre: Fredericton, NB, Canada, 1981. [Google Scholar]
- Goudiaby, V.; Brais, S.; Berninger, F.; Schneider, R. Vertical patterns in specific volume increment along stems of dominant jack pine (Pinus banksiana) and black spruce (Picea mariana) after thinning. Can. J. For. Res. 2012, 42, 733–748. [Google Scholar] [CrossRef]
- LeBlanc, D.C.; Raynal, D.J.; White, E.H. Acidic deposition and tree growth: I. The use of stem analysis to study historical growth patterns. J. Environ. Qual. 1987, 16, 325–333. [Google Scholar] [CrossRef]
- Wood, L.J.; Smith, D.J.; Hartley, I.D. Predicting softwood quality attributes from climate data in interior British Columbia, Canada. For. Ecol. Manag. 2016, 361, 81–89. [Google Scholar] [CrossRef]
- Côté, D.; Lupi, C.; Gagnon, R.; Lord, D.; Morin, H. Growth dynamics of successive post-fire cohorts of black spruce: Is site potential reduced? For. Chron. 2014, 90, 96–104. [Google Scholar] [CrossRef]
- Girardin, M.P.; Guo, X.J.; De Jong, R.; Kinnard, C.; Bernier, P.; Raulier, F. Unusual forest growth decline in boreal North America covaries with the retreat of Arctic sea ice. Glob. Chang. Biol. 2014, 20, 851–866. [Google Scholar] [CrossRef] [PubMed]
- Holeksa, J.; Zielonka, T.; Zywiec, M.; Fleischer, P. Identifying the disturbance history over a large area of larch–spruce mountain forest in Central Europe. For. Ecol. Manag. 2016, 361, 318–327. [Google Scholar] [CrossRef]
- Esper, J.; Cook, E.R.; Fritz, H.; Schweingruber, F.H. Low-frequency signals in long tree-ring chronologies for reconstructing past temperature variability. Science 2002, 295, 2250–2253. [Google Scholar] [CrossRef]
- Wilson, R.; Anchukaitis, K.; Briffa, K.R.; Büntgen, U.; Cook, E.; D’Arrigo, R.; Davi, N.; Esper, J.; Frank, D.; Gunnarson, B.; et al. Last millennium northern hemisphere summer temperatures from tree rings: Part I: The long term context. Quat. Sci. Rev. 2016, 134, 1–18. [Google Scholar] [CrossRef]
- PAGES 2k Consortium. Continental-scale temperature variability during the past two millennia. Nat. Geosci. 2013, 6, 339–346. [Google Scholar] [CrossRef]
- Marvel, K.; Cook, B.I.; Bonfils, C.J.W.; Durack, P.J.; Smerdon, J.E.; Williams, A.P. Twentieth-century hydroclimatic changes consistent with human influence. Nature 2019, 569, 59–65. [Google Scholar] [CrossRef]
- Fritts, H.C.; Swetnam, T.W. Dendroecology: A tool for evaluating variations in past and present forest environments. Adv. Ecol. Res. 1989, 19, 111–188. [Google Scholar]
- Cook, E.R.; Kairiukstis, L.A. Methods of Dendrochronology: Applications in the Environmental Sciences; Springer Science & Business Media B.V.: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Zhao, S.; Pederson, N.; D’Orangeville, L.; HilleRisLambers, J.; Boose, E.; Penone, C.; Bauer, B.; Jiang, Y.; Manzanedo, R.D. The International Tree Ring Data Bank (ITRDB) revisited: Data availability and global ecological representativity. J. Biogeogr. 2019, 46, 355–368. [Google Scholar] [CrossRef]
- Babst, F.; Bouriaud, O.; Poulter, B.; Trouet, V.; Girardin, M.P.; Frank, D.C. Twentieth century redistribution in climatic drivers of global tree growth. Sci. Adv. 2019, 5, eaat4313. [Google Scholar] [CrossRef]
- Heger, L. A method of constructing site-index curves from stem analysis. For. Chron. 1968, 44, 11–15. [Google Scholar] [CrossRef][Green Version]
- B.C. Forest Productivity Council. Minimum Standards and Stem Analysis Procedures for Site Index Research. 2000. Available online: https://www.for.gov.bc.ca › hre › pubs › docs › stem_analysis (accessed on 5 September 2019).
- Newton, P.F.; Sharma, M. Evaluation of sampling design on taper equation performance in plantation-grown Pinus banksiana. Scand. J. For. Res. 2008, 23, 358–370. [Google Scholar] [CrossRef]
- Subedi, N.; Sharma, M. Evaluating height-age determination methods for jack pine and black spruce plantations using stem analysis data. North. J. Appl. For. 2010, 27, 50–55. [Google Scholar] [CrossRef]
- Duff, G.H.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species. I. The controls of cambial and apical activity in Pinus resinosa Ait. Can. J. Bot. 1953, 31, 471–513. [Google Scholar] [CrossRef]
- Duff, G.H.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species. II. Specific increments and their relation to the quantity and activity of growth in Pinus resinosa Ait. Can. J. Bot. 1957, 35, 527–572. [Google Scholar] [CrossRef]
- Duff, G.H.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species. III. The time scale of morphogenesis at the stem apex of Pinus resinosa Ait. Can. J. Bot. 1958, 36, 687–706. [Google Scholar] [CrossRef]
- Forward, D.F.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species. IV. Radial growth in branches and main axis of Pinus resinosa Ait. Under conditions of open growth, suppression and release. Can. J. Bot. 1961, 39, 385–409. [Google Scholar] [CrossRef]
- Forward, D.F.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species. V. Further studies of wood growth in branches and main axis of Pinus resinosa Ait. Under conditions of open growth, suppression and release. Can. J. Bot. 1961, 39, 411–436. [Google Scholar] [CrossRef]
- Forward, D.F.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species. VI. The significance of specific increment of cambial area in Pinus resinosa Ait. Can. J. Bot. 1962, 40, 95–111. [Google Scholar] [CrossRef]
- Forward, D.F.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species. VII. Progress and control of longitudinal growth of branches in Pinus resinosa Ait. Can. J. Bot. 1964, 42, 923–950. [Google Scholar] [CrossRef]
- Newton, P.F. Stem analysis program for coniferous forest tree species. Comput. Electron. Agric. 2003, 39, 61–66. [Google Scholar] [CrossRef]
- Newton, P.F. A stem analysis computational algorithm for estimating volume growth and its empirical evaluation under various sampling strategies. Comput. Electron. Agric. 2004, 44, 21–31. [Google Scholar] [CrossRef]
- Evans, G.C. The Quantitative Analysis of Plant Growth; University of California Press: Berkeley, CA, USA, 1972. [Google Scholar]
- Husch, B.; Miller, C.I.; Beers, T.W. Forest Mensuration, 3rd ed.; Ronald Press Co.: New York, NY, USA, 1982. [Google Scholar]
- Brand, D.G.; Weetman, G.F.; Rehsler, P.R. Growth analysis of perennial plants: The relative production rate and its yield components. Ann. Bot. 1987, 59, 45–53. [Google Scholar] [CrossRef]
- Rowe, J.S. Forest Regions of Canada; Publication No. 1300; Government of Canada, Department of Environment, Canadian Forestry Service: Ottawa, ON, Canada, 1972.
- Chambers, B.A.; Naylor, B.J.; Nieppola, J.; Merchant, B.; Uhlig, P. Field Guide to Forest Ecosystems of Central Ontario; SCSS Field Guide FG-01; Ontario Ministry of Natural Resources, Southcentral Science Section, Science Development and Transfer Branch: North Bay, ON, Canada, 1997.
- Carmean, W.H.; Hazenberg, G.; Niznowski, G.P. Polymorphic site index curves for jack pine in Northern Ontario. For. Chron. 2001, 77, 141–150. [Google Scholar] [CrossRef]
- Kershaw, J.A., Jr.; Ducey, M.J.; Beers, T.W.; Husch, B. Forest Mensuration, 5th ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2017. [Google Scholar]
- Farrar, J.L. Longitudinal variation in the thickness of the annual ring. For. Chron. 1961, 37, 323–330. [Google Scholar] [CrossRef][Green Version]
- Muhairwe, C.K. Tree form and taper variation over time for interior lodgepole pine. Can. J. For. Res. 1994, 24, 1904–1913. [Google Scholar] [CrossRef]
- Matérn, B. On the geometry of cross-section of a stem. Medd. Från Statens Skogsforskningsinstitut Band 1956, 46, 1–28. [Google Scholar]
- Carmean, W.H. Site index curves for upland oaks in the central states. For. Sci. 1972, 1, 109–120. [Google Scholar]
- Newberry, J.D. A note on Carmean’s estimate of height from stem analysis data. For. Sci. 1991, 37, 368–369. [Google Scholar]
- Dyer, M.E.; Bailey, R.L. A test of six methods for estimating true heights from stem analysis data. For. Sci. 1987, 33, 3–13. [Google Scholar]
- Fabbio, G.; Frattegiani, M.; Manetti, M.C. Height estimation in stem analysis using second differences. For. Sci. 1994, 40, 329–340. [Google Scholar]
- Franceschini, T.; Martin-Ducup, O.; Schneider, R. Allometric exponents as a tool to study the influence of climate on the trade-off between primary and secondary growth in major north-eastern American tree species. Ann. Bot. 2016, 117, 551–563. [Google Scholar] [CrossRef] [PubMed]
- Causton, D.R.; Venus, J.C. The Biometry of Plant Growth; Edward Arnold: London, UK, 1981. [Google Scholar]
- Johann, K. Eine neue Jahrringmessanlage für Bohrkerne und Stammscheiben. Forstarchiv 1977, 10, 204–206. [Google Scholar]
- Graham, R.T. Measuring Annual Growth Rings Using an Electronic Measurement Machine; Research Note 289; USDA Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1980.
- Jordon, G.A.; Ballance, R.H. A microcomputer-based annual ring measurement system. For. Chron. 1983, 59, 21–25. [Google Scholar] [CrossRef][Green Version]
- Clarke, R.F.; Murchison, G.H. 1987. Evaluation of Holman-Digimicrometer. For. Chron. 1987, 63, 80–83. [Google Scholar] [CrossRef]
- Liu, C.J. Tree ring scanner: An automatic tree-ring-measuring machine. In Proceedings of the Mensuration, Growth and Yield Instruments and Methods in Forest Mensuration Workshop; Solomon, D., Brann, T.B., Eds.; Miscellaneous Publication 69; Maine Agricultural Experiment Station, University of Maine: Orono, MA, USA, 1986; pp. 129–132. [Google Scholar]
- Clyde, M.A.; Titus, S.J. A new computerized system for tree ring measurement and analysis. For. Chron. 1987, 63, 23–27. [Google Scholar] [CrossRef][Green Version]
- Fayle, D.C.F.; Maclver, D.; Bentley, C.V. Computer-graphing of annual ring widths during measurement. For. Chron. 1983, 59, 291–293. [Google Scholar] [CrossRef][Green Version]
- MacIvor, D.C.; Raymond, F.; Dallans, H. TRIM Sampling Design Manual; Forest Resources Group, Ontario Ministry of Natural Resources, Queen’s Park: Toronto, ON, Canada, 1985. [Google Scholar]
- Varem-Sanders, T.M.L.; Cambell, I.D. DendroScan: A Tree-Ring Width and Density Measurement System; UBC Press: Vancouver, BC, Canada, 1996. [Google Scholar]
- Guay, R.; Gagnon, R.; Morin, H. A new automatic and interactive tree ring measurement system based on a line scan camera. For. Chron. 1992, 68, 138–141. [Google Scholar] [CrossRef]
- Regent Instruments Inc. WinDENDROTM Tree Rings and Wood Density. Available online: http://regent.qc.ca/assets/windendro_software.html (accessed on 5 September 2019).
- Levanič, T. ATRICS-A new system for image acquisition in dendrochronology. Tree Ring Res. 2007, 63, 117–122. [Google Scholar] [CrossRef]
- Pluth, D.J.; Cameron, D.R. Announcing Fortran IV program for computing and graphing tree growth parameters from stem analysis. For. Sci. 1971, 17, 102. [Google Scholar]
- Kavanagh, J. Stem analysis: Sampling Techniques and Data Processing. Master’s Thesis, School of Forestry, Lakehead University, Thunder Bay, ON, Canada, 1983. Available online: http://knowledgecommons.lakeheadu.ca/bitstream/handle/2453/2322/KavanaghJ1983m-1b.pdf?sequence=1&isAllowed=y (accessed on 4 September 2019).
- Timmer, V.R.; Verch, B.R. SAPP: A computer program for plotting stem analysis. For. Chron. 1983, 59, 298–303. [Google Scholar] [CrossRef][Green Version]
- Rinn, F. TSAP-Win. Rinntech®; Heidelberg, Germany. 2003. Available online: http://www.rinntech.de/content/view/17/48/lang,english/index.html (accessed on 5 September 2016).
- Özdemir, G.A.; Özdemir, E. Stem analysis program (GOAP) for evaluating of increment and growth data at individual tree. J. Fac. For. Istanb. Univ. 2016, 66, 659–673. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Newton, P.F. Examining Naturogenic Processes and Anthropogenic Influences on Tree Growth and Development via Stem Analysis: Data Processing and Computational Analytics. Forests 2019, 10, 1058. https://doi.org/10.3390/f10121058
Newton PF. Examining Naturogenic Processes and Anthropogenic Influences on Tree Growth and Development via Stem Analysis: Data Processing and Computational Analytics. Forests. 2019; 10(12):1058. https://doi.org/10.3390/f10121058
Chicago/Turabian StyleNewton, Peter F. 2019. "Examining Naturogenic Processes and Anthropogenic Influences on Tree Growth and Development via Stem Analysis: Data Processing and Computational Analytics" Forests 10, no. 12: 1058. https://doi.org/10.3390/f10121058
APA StyleNewton, P. F. (2019). Examining Naturogenic Processes and Anthropogenic Influences on Tree Growth and Development via Stem Analysis: Data Processing and Computational Analytics. Forests, 10(12), 1058. https://doi.org/10.3390/f10121058