Effect of Seed Transfer on Selected Wood Quality Attributes of Jack Pine (Pinus banksiana Lamb.) †
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Collection
2.2. Sample Preparation and Wood Quality Attribute Measurements
2.3. Statistical Analyses
2.3.1. Transition Age and Juvenile Wood Proportion
2.3.2. Variation and Ranking among Provenances
3. Results
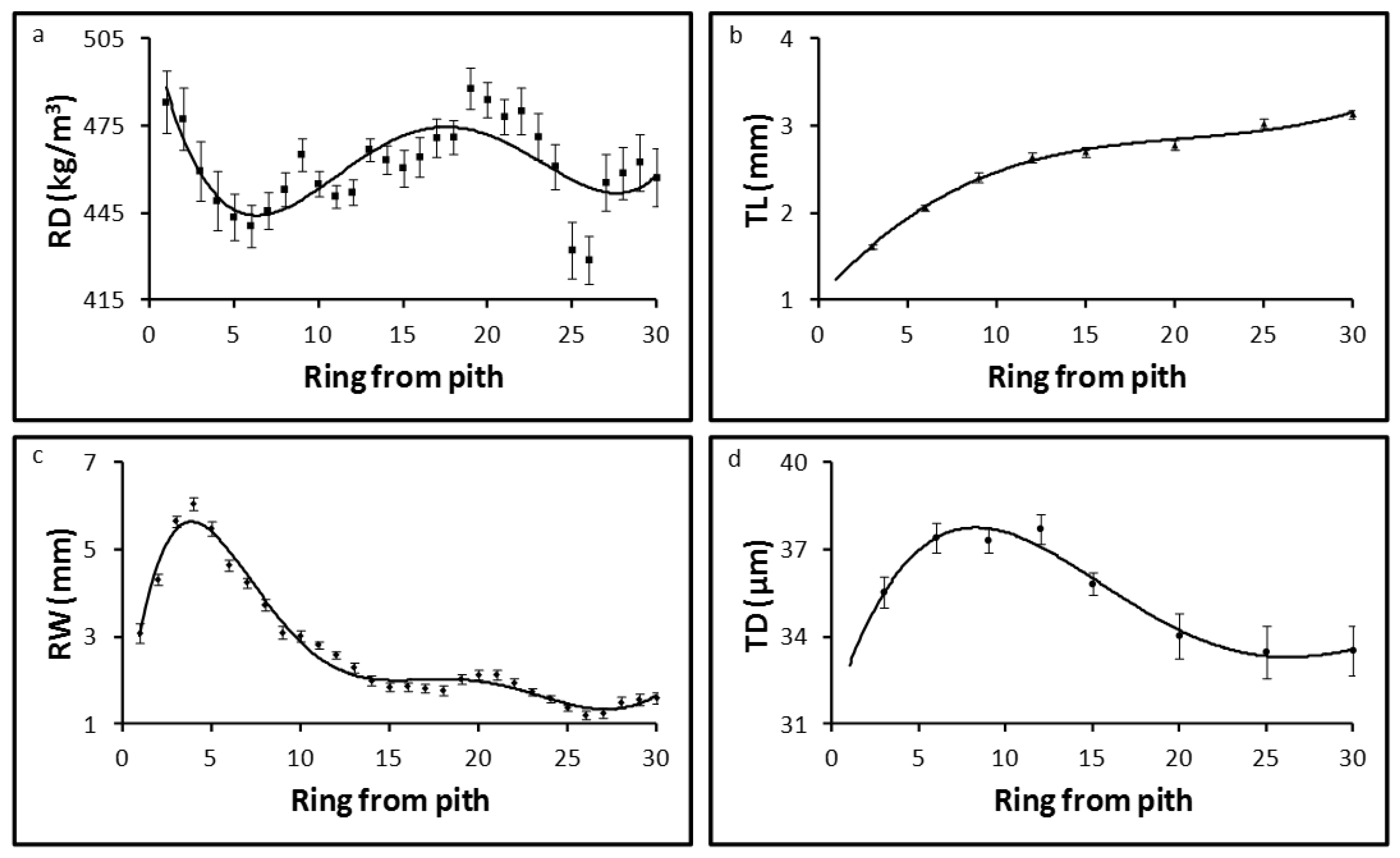
3.1. Radial Pattern of Wood Quality Attributes
3.2. Overall Wood Quality of the Provenances
3.3. Variation among Provenances
3.4. Ranking of Provenances
4. Discussion
4.1. Radial Patterns and Mean Values of the Selected Wood Quality Attributes
4.2. Overall Wood Quality of the Provenances
4.3. Variation among Provenances
4.4. Ranking of Provenances
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rudolph, T.D.; Laidly, P.R. Jack pine. In Sylvics—Volume 1: Conifers; Burns, R.M., Honkala, B.H., Eds.; Agriculture Handbook; USDA, Forest Service: Washington, DC, USA, 1990; p. 654. [Google Scholar]
- MRNF. Ressources et Industries Forestières: Portrait Statistique 2017; Ministère des Forêts, de la Faune et des Parcs. Direction du Développement de L’industrie des Produits du Bois: Québec, QC, Canada, 2017; p. 133.
- Matyas, C. Modeling climate change effects with provenance test data. Tree Physiol. 1994, 14, 797–804. [Google Scholar] [CrossRef] [PubMed]
- Zobel, B.J.; Van Buijtenen, J.P. (Eds.) Wood Variation: Its Causes and Control; Springer Series in Wood Science; Springer: Berlin, Germany, 1989; p. 363. [Google Scholar]
- Pedlar, J.H.; McKenney, D.W. Assessing the anticipated growth response of northern conifer populations to a warming climate. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Savva, Y.; Koubaa, A.; Tremblay, F.; Bergeron, Y. Effects of radial growth, tree age, climate, and seed origin on wood density of diverse jack pine populations. Trees Struct. Funct. 2010, 24, 53–65. [Google Scholar] [CrossRef]
- Savva, Y.; Denneler, B.; Koubaa, A.; Tremblay, F.; Bergeron, Y.; Tjoelker, M.G. Seed transfer and climate change effects on radial growth of jack pine populations in a common garden in Petawawa, Ontario, Canada. For. Ecol. Manag. 2007, 242, 636–647. [Google Scholar] [CrossRef]
- Beaulieu, J. Genetic variation in tracheid length and relationships with growth and wood traits in eastern white spruce (Picea glauca). Wood Fiber Sci. 2003, 35, 609–616. [Google Scholar]
- Bendtsen, B.A.; Senft, J. Mechanical and anatomical properties in individual growth rings of plantation-grown eastern cottonwood and loblolly pine. Wood Fiber Sci. 1986, 18, 23–38. [Google Scholar]
- Fujiwara, S.; Yang, K.C. The relationship between cell length and ring width and circumferential growth rate in five canadian species. IAWA J. 2000, 21, 335–345. [Google Scholar] [CrossRef]
- Mvolo, C.S.; Koubaa, A.; Beaulieu, J.; Cloutier, A.; Mazerolle, M.J. Variation in Wood Quality in White Spruce (Picea Glauca (Moench) Voss). Part I. Defining the juvenile–mature wood transition based on tracheid length. Forests 2015, 6, 183–202. [Google Scholar] [CrossRef]
- Zobel, B.J.; Sprague, J.R. (Eds.) Juvenile Wood in Forest Trees; Springer: Berlin, Germany, 1998; p. 300. [Google Scholar]
- Anfodillo, T.; Deslauriers, A.; Menardi, R.; Tedoldi, L.; Petit, G.; Rossi, S. Widening of xylem conduits in a conifer tree depends on the longer time of cell expansion downwards along the stem. J. Exp. Bot. 2012, 63, 837–845. [Google Scholar] [CrossRef]
- Larson, P.R.; Kretschmann, D.E.; Clark, A., III; Isebrands, J.G. Formation and Properties of Juvenile Wood in Southern Pines: A Synopsis; General Technical Report, FPL-GTR-129; United States Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2001; p. 42.
- Savidge, R. Intrinsic regulation of cambial growth. J. Plant Growth Regul. 2001, 20, 52–77. [Google Scholar] [CrossRef]
- Larson, P.R. A biological approach to wood quality. Tappi 1962, 45, 443–448. [Google Scholar]
- Clark, A., III; Saucier, J.R. Influence of initial planting density, geographic location, and species on juvenile wood formation in southern pine. For. Prod. J. 1989, 39, 42–48. [Google Scholar]
- Saucier, J.R. Forest Management and wood quality. In Proceedings of the Southern Plantation Wood Quality Workshop, Athens, Greece, 6–7 June 1989; p. 104. [Google Scholar]
- Szymanski, M.B.; Tauer, C.G. Loblolly pine provenance variation in age of transition from juvenile to mature wood specific gravity. For. Sci. 1991, 37, 160–174. [Google Scholar]
- Loo, J.A.; Tauer, C.G.; McNew, R.W. Genetic variation in the time of transition from juvenile to mature wood in loblolly pine (Pinus taeda L.). Silvae Genet. 1985, 34, 14–19. [Google Scholar]
- Holst, M.J. All-Range Jack Pine Provenance Experiment; Internal Report Pet-ps-6; Petawawa Forest Experiment Station: Chalk River, ON, Canada, 1967. [Google Scholar]
- Parker, W.H.; Thomson, A.M.; Lesser, M.R. Identification of Jack Pine Seed Sources to Compensate for Loss of Growth Resulting from Climate Change: Part 2; Living Legacy Research Program-Lakehead University: Lakehead, ON, Canada, 2006; p. 169. [Google Scholar]
- Savva, Y.; Bergeron, Y.; Denneler, B.; Koubaa, A.; Tremblay, F. Effect of interannual climate variations on radial growth of jack pine provenances in Petawawa, Ontario. Can. J. For. Res. 2008, 38, 619–630. [Google Scholar] [CrossRef]
- Koubaa, A.; Zhang, S.Y.; Makni, S. Defining the transition from earlywood to latewood in black spruce based on intra-ring wood density profiles from X-ray densitometry. Ann. For. Sci. 2002, 59, 511–518. [Google Scholar] [CrossRef]
- Franklin, G.L. Preparation of thin sections of synthetic resins and wood-resin composites, and a new macerating method for wood. Nature 1945, 155, 51. [Google Scholar] [CrossRef]
- Fries, A.; Ericsson, T.; Morling, T. Measuring relative fibre length in Scots pine by non-destructive wood sampling. Holzforschung 2003, 57, 400–406. [Google Scholar] [CrossRef]
- SAS Institute Inc. SAS® 9.4 Statements; SAS Institute Inc.: Cary, NC, USA, 2013. [Google Scholar]
- Yang, K.C. Impact of spacing on width and basal area of juvenile and mature wood in Picea mariana and Picea glauca. Wood Fiber Sci. 1994, 26, 479–488. [Google Scholar]
- Wang, M.; Stewart, J.D. Determining the transition from juvenile to mature wood microfibril angle in lodgepole pine: A comparison of six different two-segment models. Ann. For. Sci. 2012, 69, 927–937. [Google Scholar] [CrossRef]
- Alteyrac, J.; Cloutier, A.; Zhang, S.Y. Characterization of juvenile wood to mature wood transition age in black spruce (Picea mariana (Mill.) B.S.P.) at different stand densities and sampling heights. Wood Sci. Technol. 2006, 40, 124–138. [Google Scholar] [CrossRef]
- Singer, J.D. Using SAS PROC MIXED to fit multilevel models, hierarchical models, and individual growth models. J. Educ. Behav. Stat. 1998, 24, 323–355. [Google Scholar] [CrossRef]
- Falconer, D.S.; Mackay, T.F.C. (Eds.) Introduction to Quantitative Genetics, 4th ed.; Pearson Education Limited: Harlow, UK, 1996; p. 464. [Google Scholar]
- Reich, P.B.; Sendall, K.M.; Rice, K.; Rich, R.L.; Stefanski, A. Geographic range predicts photosynthetic and growth response to warming in co-occurring tree species. Nat. Clim. Chang. 2015, 5. [Google Scholar] [CrossRef]
- Beaulieu, J.; Corriveau, A. Variabilité de la densité du bois et de la production des provenances d’épinette blanche, 20 ans après plantation. Can. J. For. Res. 1985, 15, 833–838. [Google Scholar] [CrossRef]
- Magnussen, S.; Yeatman, C.W. Height growth components in inter- and intra-provenance jack pine families. Can. J. For. Res. 1989, 19, 962–972. [Google Scholar] [CrossRef]
- Magnussen, S.; Smith, V.G.; Yeatman, C.W. Tree size, biomass, and volume growth of twelve 34-year-old Ontario jack pine provenances. Can. J. For. Res. 1985, 15, 1129–1136. [Google Scholar] [CrossRef]
- Sanio, K. Über die Grösse der Holzzellen bei der gemeinen Kiefer (Pinus sylvestris). Jahrb. Wiss. Bot. 1872, 8, 401–420. [Google Scholar]
- Cown, D.J. Variation in tracheid dimensions in the stem of a 26-year-old radiata pine tree. Appita 1975, 28, 237–245. [Google Scholar]
- Brändström, J. Micro and ultrastructural aspects of Norway spruce tracheids: A review. IAWA J. 2001, 22, 333–353. [Google Scholar] [CrossRef]
- Kučera, B. A hypothesis relating current annual height increment to juvenile wood formation in Norway spruce. Wood Fiber Sci. 1994, 26, 152–167. [Google Scholar]
- Bouslimi, B.; Koubaa, A.; Bergeron, P.Y. Anatomical properties in Thuja occidentalis: Variation and relationship to biological processes. IAWA J. 2014, 35, 363–384. [Google Scholar] [CrossRef]
- Bannan, M.W. The length, tangential diameter, and length/width ratio of conifer tracheids. Can. J. Bot. 1965, 43, 967–984. [Google Scholar] [CrossRef]
- Mvolo, C.S.; Koubaa, A.; Beaulieu, J.; Cloutier, A.; Defo, M.; Yemele, M.-C. Phenotypic correlations among growth and selected wood properties in white spruce (Picea glauca (Moench) Voss). Forests 2019, 10, 589. [Google Scholar] [CrossRef]
- Mvolo, C.S.; Koubaa, A.; Defo, M.; Beaulieu, J.; Yemele, M.-C.; Cloutier, A. Prediction of tracheid length and diameter in white spruce (Picea glauca (Moench) Voss). IAWA J. 2015, 36, 186–207. [Google Scholar] [CrossRef]
- Olson, M.E. Xylem hydraulic evolution, I.W. Bailey, and Nardini & Jansen (2013): Pattern and process. New Phytol. 2014, 203, 7–11. [Google Scholar] [PubMed]
- Zhang, S.Y.; Koubaa, A. Les Résineux de L’est du Canada: Écologie Forestière, Caractéristiques, Transformation et Usages; Publication Spéciale SP-526F; FPInnovations: Québec, QC, Canada, 2009; p. 400. [Google Scholar]
- Jessome, A.P. Résistance et Propriétés Connexes des Bois Indigènes; Forintek Canada Corp: Sainte-Foy, QC, Canada, 2000; p. 37. [Google Scholar]
- Goudiaby, V.; Brais, S.; Grenier, Y.; Berninger, F. Thinning effects on jack pine and black spruce photosynthesis in eastern boreal forests of Canada. Silva Fenn. 2011, 45, 595–609. [Google Scholar] [CrossRef]
- Morris, D.M.; Bowling, C.; Hills, S.C. Growth and form responses to pre-commercial thinning regimes in aerially seeded jack pine stands: 5th year results. For. Chron. 1994, 70, 780–787. [Google Scholar] [CrossRef][Green Version]
- Isenberg, I.H.; Harder, M.L.; Louden, L. Pulpwoods of the United States and Canada, Volume I: Conifers; Institute of Paper Chemistry: Appleton, WI, USA, 1980; p. 219. [Google Scholar]
- Panshin, A.J.; de Zeuuw, C. Textbook of Wood Technology: Structure, Identification, Properties, and Uses of the Commercial Woods of the United States and Canada, 4th ed.; McGraw-Hill Book Co.: New York, NY, USA, 1980; p. 722. [Google Scholar]
- Larson, P.R. (Ed.) The Vascular Cambium: Development and Structure; Springer: Berlin, Germany, 1994; p. 725. [Google Scholar]
- Anfodillo, T.; Petit, G.; Crivellaro, A. Axial conduit widening in woody species: A still neglected anatomical pattern. IAWA J. 2013, 34, 352–364. [Google Scholar] [CrossRef]
- Rosner, S. Hydraulic and biomechanical optimization in Norway spruce trunkwood—A review. IAWA J. 2013, 34, 365–390. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the structure and allometry of plant vascular systems. Nature 1999, 400, 664–667. [Google Scholar] [CrossRef]
- Olson, M.E.; Anfodillo, T.; Rosell, J.A.; Petit, G.; Crivellaro, A.; Isnard, S.; León-Gómez, C.; Alvarado-Cárdenas, L.O.; Castorena, M. Universal hydraulics of the flowering plants: Vessel diameter scales with stem length across angiosperm lineages, habits and climates. Ecol. Lett. 2014, 17, 988–997. [Google Scholar] [CrossRef] [PubMed]
- Bannan, M.W. Anticlinal divisions and cell length in conifer cambium. For. Prod. J. 1967, 17, 63–69. [Google Scholar]
- King, J.P. Seed Source Variation in Tracheid Length and Specific Gravity of Five-Year-Old Jack Pine Seedlings. In Proceedings of the Eighth Lake States Forest Tree Improvement Conference, Madison, WI, USA, 12–13 September 1967; pp. 5–9. [Google Scholar]
- Savidge, R.A. Tree growth and wood quality. In Wood Quality and Its Biological Basis; Barnett, J.R.J., Ed.; Blackwell: Boca Raton, FL, USA, 2003; pp. 1–29. [Google Scholar]
- Carlquist, S. (Ed.) Ecological Strategies of Xylem Evolution; University of California Press: Berkeley, CA, USA, 1975; p. 259. [Google Scholar]
- Aubin, I.; Garbe, C.M.; Colombo, S.; Drever, C.R.; McKenney, D.W.; Messier, C.; Pedlar, J.; Saner, M.A.; Venier, L.; Wellstead, A.M.; et al. Why we disagree about assisted migration: Ethical implications of a key debate regarding the future of Canada’s forests. For. Chron. 2011, 87, 755–765. [Google Scholar] [CrossRef]
- Pedlar, J.H.; McKenney, D.W.; Beaulieu, J.; Colombo, S.J.; McLachlan, J.S.; O’Neill, G.A. The implementation of assisted migration in Canadian forests. For. Chron. 2011, 87, 766–770. [Google Scholar] [CrossRef]
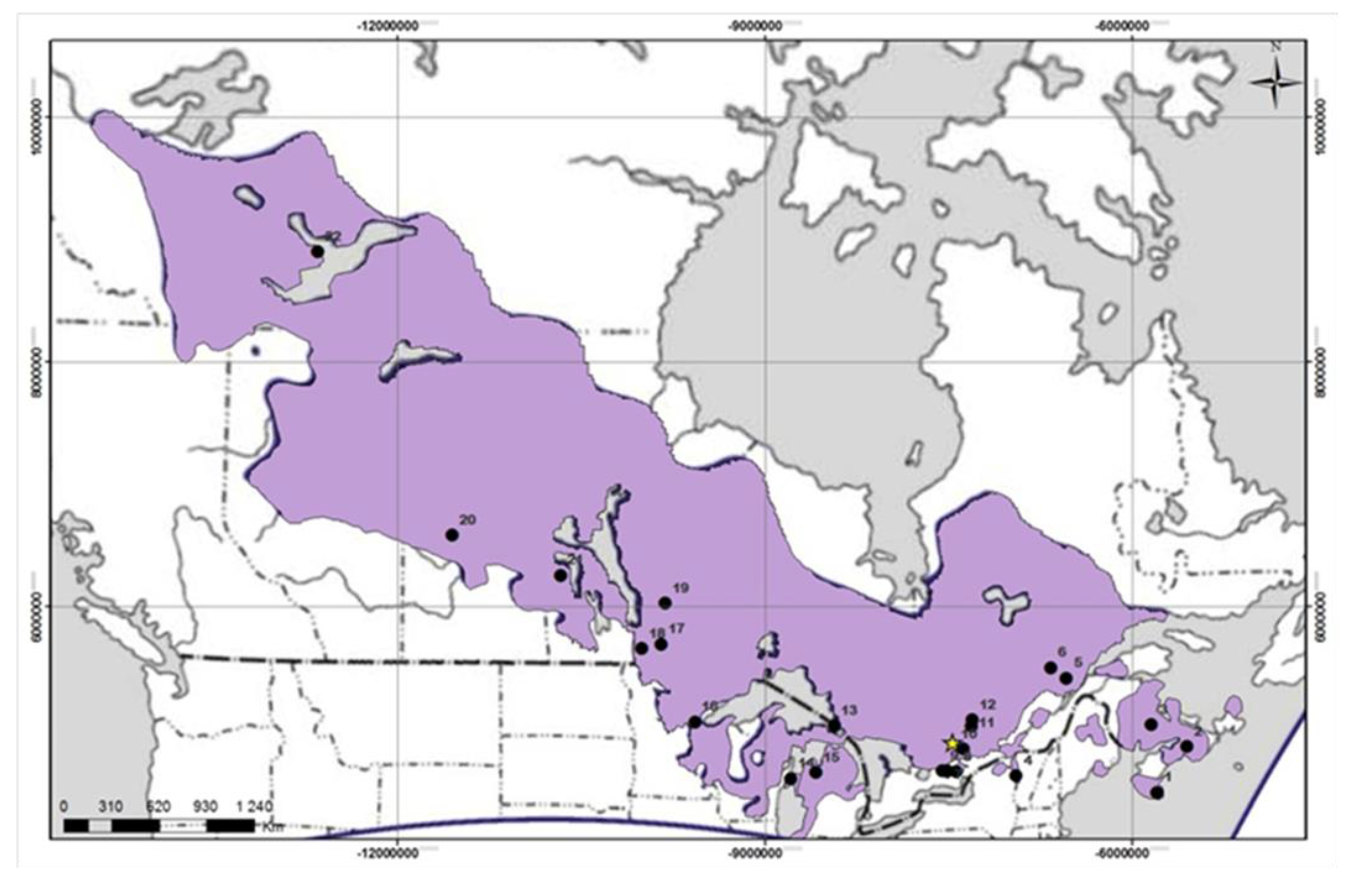
| ID | Origin, Province, or State | Seedlot | Lat. | Long. | Temp. | Prec. |
|---|---|---|---|---|---|---|
| 14 | Freesoil, Michigan | 3271 | 44.1 | 86.1 | 8.3 | 747 |
| 1 | Birchtown Brook, Nova Scotia | 3202 | 43.5 | 65.2 | 6.7 | 1463 |
| 15 | Fite Lake, Michigan | 3272 | 44.3 | 85.2 | 6.7 | 795 |
| 8 | Clare River, Ontario | 3240 | 44.4 | 77 | 6.1 | 877 |
| 4 | Upper Jay, New York | 3223 | 44.2 | 73.5 | 5.6 | 984 |
| 7 | Twin Lakes, Ontario | 3239 | 44.4 | 77.5 | 5.6 | 721 |
| 2 | Thomson Station, Nova Scotia | 3206 | 45.4 | 63.5 | 5 | 1075 |
| 9 | Kaladar, Ontario | 3241 | 44.4 | 77.1 | 5 | 721 |
| 10 | Douglas, Ontario | 3242 | 45.3 | 76.6 | 5 | 755 |
| 3 | Cains River, New Brunswick | 3211 | 46.3 | 65.5 | 4.4 | 1180 |
| 11 | Horry Lake, Québec | 3247 | 46.2 | 76.1 | 4.4 | 768 |
| * | Petawawa Research Forest | − | 45.6 | 77.3 | 4.3 | 853 |
| 16 | Cloquet, Minnesota | 3279 | 46.4 | 92.3 | 3.9 | 758 |
| 12 | Baskatong Lake, Québec | 3248 | 46.5 | 76.1 | 3.3 | 865 |
| 13 | Dunbar Forest, Michigan | 3259 | 46.3 | 84.2 | 3.3 | 760 |
| 5 | Port Alfred, Québec | 3230 | 48.2 | 70.5 | 2.2 | 984 |
| 17 | Kenora, Ontario | 3282 | 49.5 | 94.3 | 2.2 | 655 |
| 18 | Hadashville, Manitoba | 3283 | 49.3 | 95.5 | 1.7 | 548 |
| 6 | Alex River, Québec | 3232 | 48.6 | 71.5 | 1.1 | 809 |
| 19 | Red Lake, Ontario | 3286 | 51 | 94.1 | 0.6 | 518 |
| 20 | Big River, Saskatchewan | 3288 | 53.5 | 107 | 0.6 | 410 |
| 21 | Cowan, Manitoba | 3290 | 52 | 100 | 0 | 455 |
| 22 | Yellowknife, Northwest Territories | 3297 | 62.3 | 114 | −5.6 | 215 |
| ID | Origin, Province or State | Seedlot | RW | RD | TL | TD | TH | DBH | TA | JWP |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Birchtown Brook, Nova Scotia | 3202 | 2.03 | 454 | 2.7 | 37.2 | 15.4 | 14.8 | 10 | 43 |
| 2 | Thomson Station, Nova Scotia | 3206 | 2.63 | 475 | 2.5 | 33.7 | 16.5 | 20.0 | 14 | 42 |
| 3 | Cains River, New Brunswick | 3211 | 2.71 | 461 | 1.9 | 31.4 | 18.0 | 20.4 | 12 | 36 |
| 4 | Upper Jay, New York | 3223 | 3.56 | 456 | 2.5 | 37.3 | 17.5 | 27.7 | 13 | 28 |
| 5 | Port Alfred, Quebec | 3230 | 2.36 | 458 | 2.5 | 35.0 | 18.9 | 17.8 | 12 | 30 |
| 6 | Alex River, Quebec | 3232 | 2.66 | 469 | 2.7 | 36.3 | 18.0 | 21.7 | 11 | 28 |
| 7 | Twin Lakes, Ontario | 3239 | 2.81 | 485 | 2.5 | 37.2 | 17.3 | 21.4 | 13 | 37 |
| 8 | Clare River, Ontario | 3240 | 2.45 | 457 | 2.6 | 35.0 | 18.4 | 19.4 | 8 | 20 |
| 9 | Kaladar, Ontario | 3241 | 2.77 | 448 | 2.7 | 37.7 | 17.9 | 20.6 | 11 | 29 |
| 10 | Douglas, Ontario | 3242 | 3.18 | 468 | 2.5 | 37.8 | 18.1 | 25.0 | 8 | 17 |
| 11 | Horry Lake, Quebec | 3247 | 2.51 | 457 | 2.5 | 35.4 | 19.2 | 18.9 | 11 | 33 |
| 12 | Baskatong Lake, Quebec | 3248 | 2.79 | 458 | 2.7 | 37.2 | 18.1 | 21.7 | 9 | 22 |
| 13 | Dunbar Forest, Michigan | 3259 | 2.66 | 469 | 2.5 | 33.6 | 18.2 | 21.1 | 10 | 22 |
| 14 | Freesoil, Michigan | 3271 | 3.11 | 466 | 2.7 | 37.4 | 19.7 | 25.2 | 13 | 29 |
| 15 | Fite Lake, Michigan | 3272 | 2.96 | 466 | 2.9 | 30.0 | 19.3 | 22.6 | 11 | 27 |
| 16 | Cloquet, Minnesota | 3279 | 2.60 | 465 | 2.6 | 36.5 | 18.8 | 20.8 | 11 | 22 |
| 17 | Kenora, Ontario | 3282 | 2.68 | 450 | 2.7 | 36.6 | 19.1 | 21.9 | 11 | 23 |
| 18 | Hadashville, Manitoba | 3283 | 2.63 | 435 | 2.4 | 36.0 | 18.3 | 19.4 | 13 | 48 |
| 19 | Red Lake, Ontario | 3286 | 2.19 | 473 | 2.5 | 35.8 | 16.6 | 18.2 | 8 | 24 |
| 20 | Big River, Saskatchewan | 3288 | 2.45 | 456 | 2.6 | 35.3 | 18.2 | 18.4 | 10 | 28 |
| 21 | Cowan, Manitoba | 3290 | 2.17 | 458 | 2.4 | 36.1 | 15.9 | 16.1 | 8 | 17 |
| 22 | Yellowknife, Northwest Territories | 3297 | 2.95 | 457 | 2.6 | 34.9 | 17.4 | 22.6 | 11 | 28 |
| WQA | Sources of Variation | ||||||
|---|---|---|---|---|---|---|---|
| Random Effects | ICC | ||||||
| Provenances | Residuals (Trees) | ||||||
| Estimate | Z Value | Pr > Z | Estimate | Z Value | Pr > Z | ||
| Juvenile Wood | |||||||
| RW | 0.09 | 1.54 | 0.0619 | 0.25 | 4.47 | <0.0001 | 0.26 |
| RD | 768.9 | 2.76 | 0.0029 | 356.5 | 4.42 | <0.0001 | 0.68 |
| TL | 0.01 | 1.27 | 0.1020 | 0.04 | 4.41 | <0.0001 | 0.21 |
| TD | 0.30 | 0.27 | 0.3939 | 7.98 | 4.50 | <0.0001 | 0.04 |
| Mature Wood | |||||||
| RW | 0.07 | 1.85 | 0.0319 | 0.13 | 4.47 | <0.0001 | 0.34 |
| RD | 559.6 | 2.17 | 0.0151 | 724.1 | 4.44 | <0.0001 | 0.44 |
| TL | 0.02 | 1.65 | 0.0498 | 0.06 | 4.47 | <0.0001 | 0.30 |
| TD | 1.54 | 0.64 | 0.2602 | 15.0 | 4.47 | <0.0001 | 0.09 |
| Whole Pith-to-Bark Section | |||||||
| DBH | 5.82 | 2.08 | 0.0187 | 8.4 | 4.44 | <0.0001 | 0.41 |
| RW | 0.08 | 2.01 | 0.0224 | 0.13 | 4.46 | <0.0001 | 0.38 |
| RD | 63.2 | 1.73 | 0.0420 | 142.9 | 4.46 | <0.0001 | 0.31 |
| TL | 0.02 | 1.95 | 0.0253 | 0.04 | 4.48 | <0.0001 | 0.08 |
| TD | 1.08 | 0.48 | 0.3158 | 15.3 | 4.51 | <0.0001 | 0.07 |
| TH | 0.37 | 0.89 | 0.1871 | 2.4 | 4.49 | <0.0001 | 0.13 |
| TA | 0.08 | 0.06 | 0.4745 | 9.3 | 4.26 | <0.0001 | 0.01 |
| JWP | 16.6 | 0.64 | 0.2621 | 155.9 | 4.20 | <0.0001 | 0.10 |
| ID | Origin, Province or State | RW Rank | RD Rank | TL Rank | TH Rank | SI | Final Rank | Temp. | Lat. |
|---|---|---|---|---|---|---|---|---|---|
| 15 | Fite Lake, Michigan | 19 | 15.5 | 22 | 21 | 18.7 | 1 | 6.7 | 44.3 |
| 14 | Freesoil, Michigan | 20 | 15.5 | 18.5 | 22 | 18.6 | 2 | 8.3 | 44.1 |
| 10 | Douglas, Ontario | 21 | 17 | 7.5 | 11.5 | 15.8 | 3 | 5 | 45.3 |
| 7 | Twin Lakes, Ontario | 17 | 22 | 7.5 | 5 | 15.1 | 4 | 5.6 | 44.4 |
| 6 | Alex River, Quebec | 11.5 | 18.5 | 18.5 | 9.5 | 14.7 | 5 | 1.1 | 48.6 |
| 12 | Baskatong Lake, Quebec | 16 | 11 | 18.5 | 11.5 | 14.0 | 6 | 3.3 | 46.5 |
| 13 | Dunbar Forest, Michigan | 11.5 | 18.5 | 7.5 | 13.5 | 13.5 | 7 | 3.3 | 46.3 |
| * | Petawawa Research Forest | − | − | − | − | − | − | 4.3 | 45.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mvolo, C.S.; Koubaa, A.; Beaulieu, J.; Cloutier, A. Effect of Seed Transfer on Selected Wood Quality Attributes of Jack Pine (Pinus banksiana Lamb.). Forests 2019, 10, 985. https://doi.org/10.3390/f10110985
Mvolo CS, Koubaa A, Beaulieu J, Cloutier A. Effect of Seed Transfer on Selected Wood Quality Attributes of Jack Pine (Pinus banksiana Lamb.). Forests. 2019; 10(11):985. https://doi.org/10.3390/f10110985
Chicago/Turabian StyleMvolo, Cyriac S., Ahmed Koubaa, Jean Beaulieu, and Alain Cloutier. 2019. "Effect of Seed Transfer on Selected Wood Quality Attributes of Jack Pine (Pinus banksiana Lamb.)" Forests 10, no. 11: 985. https://doi.org/10.3390/f10110985
APA StyleMvolo, C. S., Koubaa, A., Beaulieu, J., & Cloutier, A. (2019). Effect of Seed Transfer on Selected Wood Quality Attributes of Jack Pine (Pinus banksiana Lamb.). Forests, 10(11), 985. https://doi.org/10.3390/f10110985







