Comparison of Fixed- and Mixed-Effects Approaches to Taper Modeling for Scots Pine in West Poland
Abstract
1. Introduction
2. Materials and Methods
2.1. Taper Function
2.2. Volume Prediction
3. Results
Volume Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kidombo, S.D.; Dean, T.J. Growth of tree diameter and stem taper as affected by reduced leaf area on selected branch whorls. Can. J. For. Res. 2018, 48, 317–323. [Google Scholar] [CrossRef]
- Brooks, J.R.; Jiang, L.; Clark, A. Compatible Stem Taper, Volume, and Weight Equations for Young Longleaf Pine Plantations in Southwest Georgia. South. J. Appl. For. 2007, 31, 187–191. [Google Scholar] [CrossRef]
- Dudzińska, M. Model of the percentage share of the stem sections in the total stem volume for the mountain and lowland beech. Sylwan 2003, 147, 28–37. (In Polish) [Google Scholar]
- Socha, J. A taper model for Norway spruce (Picea abies (L.) Karst.). Forestry 2002, 5, 3. [Google Scholar]
- Socha, J.; Kubik, I. A taper model for mountain spruce stands in medium age classes. Sylwan 2005, 149, 42–52. (In Polish) [Google Scholar]
- Bruchwald, A. The use of research on stem fullness for Scots pine taper model development. Folia For. Pol. For. 1980, 24, 101–109. (In Polish) [Google Scholar]
- Kozak, A. Effects of multicollinearity and autocorrelation on the variable-exponent taper functions. Can. J. For. Res. 1997, 27, 619–629. [Google Scholar] [CrossRef]
- Kozak, A.; Munro, D.D.; Smith, J.H.G. Taper Functions and their Application in Forest Inventory. For. Chron. 1969, 45, 278–283. [Google Scholar] [CrossRef]
- Demaerschalk, J.P. Converting Volume Equations to Compatible Taper Equations. For. Sci. 1972, 18, 241–245. [Google Scholar] [CrossRef]
- Biging, G.S. Taper Equations for Second-Growth Mixed Conifers of Northern California. For. Sci. 1984, 30, 1103–1117. [Google Scholar]
- Arias-Rodil, M.; Castedo-Dorado, F.; Cámara-Obregón, A.; Diéguez-Aranda, U. Fitting and Calibrating a Multilevel Mixed-Effects Stem Taper Model for Maritime Pine in NW Spain. PLoS ONE 2015, 10, e0143521. [Google Scholar] [CrossRef]
- Bruchwald, A. Dendrometry, 3rd ed.; SGGW Press: Warsaw, Poland, 1999; p. 262. (In Polish) [Google Scholar]
- Lee, W.-K.; Seo, J.-H.; Son, Y.-M.; Lee, K.-H.; von Gadow, K. Modeling stem profiles for Pinus. densiflora. in Korea. For. Ecol. Manag. 2003, 172, 69–77. [Google Scholar] [CrossRef]
- Kershaw, J.A.; Ducey, M.J.; Beers, T.W.; Husch, B. Forest Mensuration, 5th ed.; Wiley-Blackwell: Oxford, UK, 2016; p. 630. [Google Scholar]
- Max, T.A.; Burkhart, H.E. Segmented Polynomial Regression Applied to Taper Equations. For. Sci. 1976, 22, 283–289. [Google Scholar]
- Kublin, E.; Breidenbach, J.; Kändler, G. A flexible stem taper and volume prediction method based on mixed-effects B-spline regression. Eur. J. For. Res. 2013, 132, 983–997. [Google Scholar] [CrossRef]
- Burkhart, H.E.; Avery, T.E.; Bullock, B.P. Forest Measurements, 6th ed.; Waveland Press Inc.: Long Grove, IL, USA, 2018; p. 434. [Google Scholar]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS, 1st ed.; Springer: New York, NY, USA, 2000; p. 537. [Google Scholar]
- Mehtätalo, L.; Lappi, J. Biometrics for forestry and environmental data with examples in R. 2019; Unpublished work. [Google Scholar]
- Trincado, G.; Burkhart, H.E. A generalized approach for modeling and localizing stem profile curves. For. Sci. 2006, 52, 670–682. [Google Scholar]
- Lappi, J. Mixed linear models for analyzing and predicting stem form variation of Scots pine. Comm. Inst. For. Fenn. 1986, 134, 1–69. [Google Scholar]
- Lappi, J. A multivariate, nonparametric stem-curve prediction method. Can. J. For. Res. 2006, 36, 1017–1027. [Google Scholar] [CrossRef]
- Özçelik, R.; Brooks, J.R.; Jiang, L. Modeling stem profile of Lebanon cedar, Brutian pine, and Cilicica fir in Southern Turkey using nonlinear mixed-effects models. Eur. J. For. Res. 2011, 130, 613–621. [Google Scholar] [CrossRef]
- Diéguez-Aranda, U.; Castedo-Dorado, F.; Álvarez-González, J.G.; Rojo, A. Compatible taper function for Scots pine plantations in northwestern Spain. Can. J. For. Res. 2006, 36, 1269–1279. [Google Scholar] [CrossRef]
- Mehtätalo, L.; de-Miguel, S.; Gregoire, T.G. Modelling height-diameter curves for prediction. Can. J. For. Res. 2015, 45, 826–837. [Google Scholar] [CrossRef]
- De-Miguel, S.; Mehtätalo, L.; Shater, Z.; Kraid, B.; Pukkala, T. Evaluating marginal and conditional predictions of taper models in the absence of calibration data. Can. J. For. Res. 2012, 42, 1383–1394. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, S.; Trincado, G.; Meng, S.X. Nonlinear mixed-effects modelling of variable-exponent taper equations for lodgepole pine in Alberta, Canada. Eur. J. For. Res. 2009, 128, 415–429. [Google Scholar] [CrossRef]
- Bańkowski, J.; Cieśla, A.; Czerepko, J.; Czępińska-Kamińska, D.; Kliczkowska, A.; Kowalkowski, A.; Krzyżanowski, A.; Mąkosa, K.; Sikorska, E.; Zielony, R. Siedliskowe Podstawy Hodowli Lasu; Soil Science Society of Poland: Warsaw, Poland, 2003. (In Polish) [Google Scholar]
- Bureau for Forest Management and Geodesy. The National Forest Inventory Results for 2014–2018; Bureau for Forest Management and Geodesy: Sękocin Stary, Poland, 2019. (In Polish) [Google Scholar]
- Bruchwald, A.; Rymer-Dudzińska, T. Empirical equations for determining timber volume of stem on stump for pine. Ann. Wars. Agric. Univ. For. Wood Technol. 1988, 36, 51–55. [Google Scholar]
- Bruchwald, A. New Empirical Formulae for Determination of Volume of Scots Pine Stands. Folia For. Pol. For. 1996, 38, 5–10. [Google Scholar]
- Bruchwald, A.; Rymer-Dudzińska, T.; Dudek, A.; Michalak, K.; Wróblewski, L.; Zasada, M.; Tomusiak, R. Merchantable volume tables based on the stump diameter. Sylwan 2002, 146, 5–16. (In Polish) [Google Scholar]
- Bruchwald, A. An indirect method of building a taper model construction for pine stem inside bark. Sylwan 2004, 148, 3–7. (In Polish) [Google Scholar]
- Siekierski, K. Taper model for Scots pine. Sylwan 1992, 136, 43–51. (In Polish) [Google Scholar]
- Socha, J.; Grabczyński, S.; Ochał, W. Relationship between the accuracy of a taper model and a taken sample size. Acta Agrar. Silvestria 2012, 50, 83–92. [Google Scholar]
- Özçelik, R.; Wiant, H.V.; Brooks, J.R. Accuracy using xylometry of log volume estimates for two tree species in Turkey. Scand. J. For. Res. 2008, 23, 272–277. [Google Scholar] [CrossRef]
- Tiurin, A.W. Forest Mensuration; Goslestexizdat: Moscow, Russia, 1945. (In Russian) [Google Scholar]
- Gieruszyński, T. Dendrometry; Forest Research Institute: Warsaw, Poland, 1949. (In Polish) [Google Scholar]
- Grochowski, J. Dendrometry; State Agricultural and Forestry Press: Warsaw, Poland, 1973. (In Polish) [Google Scholar]
- R Core Team. R: A. Language and Environment. for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- RStudio Team. RStudio: Integrated Development for R; RStudio Inc.: Boston, MA, USA, 2015. [Google Scholar]
- Pinheiro, J.; Bates, D.; Saikat, D.; Deepayan, S. nlme: Linear and Nonlinear Mixed Effects Models. 2019, p. 325. Available online: https://cran.r-project.org/web/packages/nlme/nlme.pdf (accessed on 30 September 2019).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; p. 260. [Google Scholar]
- Höjer, A. Tallens och granens tillväxt. In Om Vara Barrskogar; Lovén, F., Ed.; Uddeholms Aktiebolag: Stockolm, Swedish, 1903; pp. 87–120. (In Swedish) [Google Scholar]
- Kozak, A. A variable-exponent taper equation. Can. J. For. Res. 1988, 18, 1363–1368. [Google Scholar] [CrossRef]
- Kozak, A. My last words on taper equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef]
- Riemer, T.; von Gadow, K.; Sloboda, B. Ein Modell zur Beschreibung von Baumschäften. Allg. For. Jagdztg. 1995, 166, 144–147. (In German) [Google Scholar]
- Arias-Rodil, M.; Diéguez-Aranda, U.; Rodríguez Puerta, F.; López-Sánchez, C.A.; Canga Líbano, E.; Cámara Obregón, A.; Castedo-Dorado, F. Modelling and localizing a stem taper function for Pinus radiata in Spain. Can. J. For. Res. 2015, 45, 647–658. [Google Scholar] [CrossRef]
- Westfall, J.A.; Scott, C.T. Taper models for commercial tree species in the northeastern United States. For. Sci. 2010, 56, 515–528. [Google Scholar]
- Cao, Q.V.; Wang, J. Calibrating fixed- and mixed-effects taper equations. For. Ecol. Manag. 2011, 262, 671–673. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, Y.; Jia, L.; Mason, E.G.; We, S.; Sun, C.; Duan, J. Compatible taper-volume models of Quercus variabilis Blume forests in north China. iForest-Biogeosci. For. 2017, 10, 567. [Google Scholar] [CrossRef]
- Fang, Z.; Borders, E.; Bailey, L. Compatible Volume-Taper Models for Loblolly and Slash Pine Based on a System with Segmented-Stem Form Factors. For. Sci. 2000, 46, 1–12. [Google Scholar]
- Bi, H. Trigonometric Variable-Form Taper Equations for Australian Eucalypts. For. Sci. 2000, 46, 397–409. [Google Scholar]
- Socha, J. The use of a trigonometric taper model for the determination of the shape of spruce stems. Sylwan 2004, 148, 3–10. (In Polish) [Google Scholar]
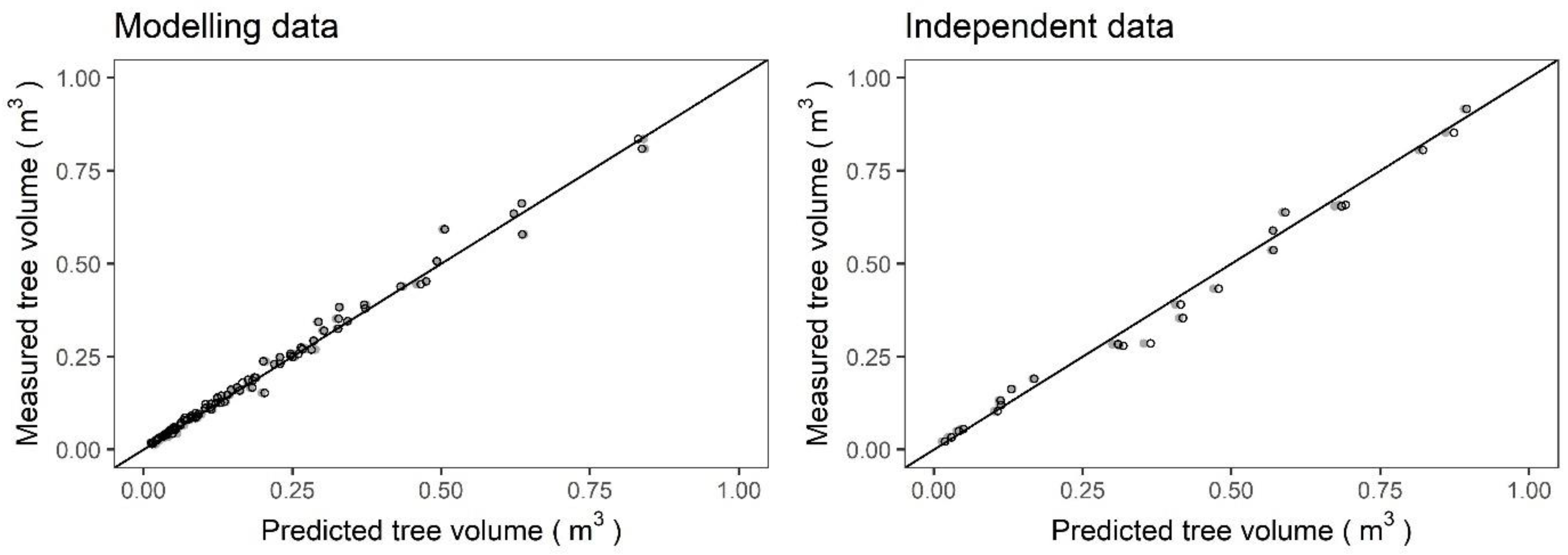
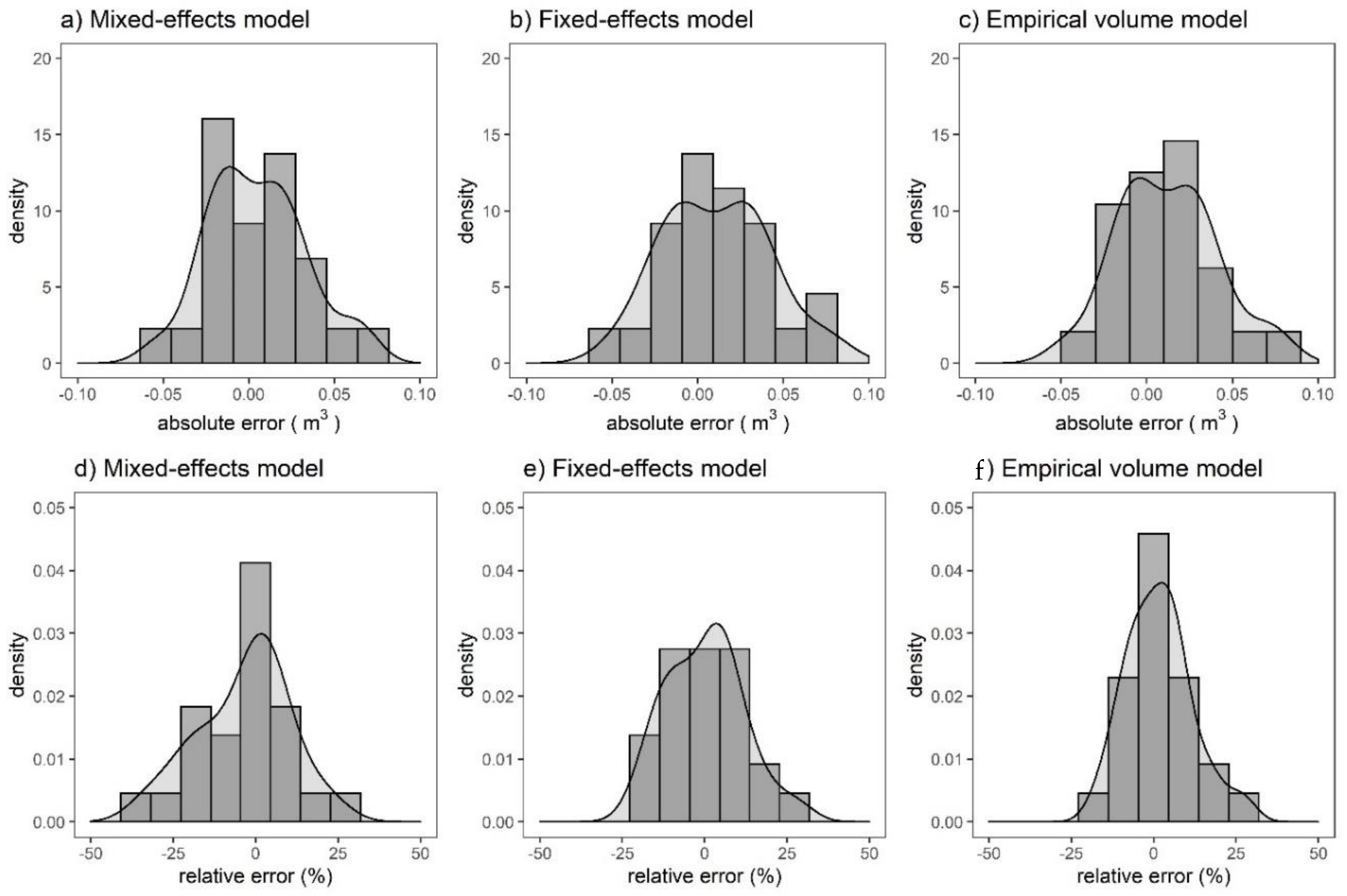
| Statistics | Modeling Data | Independent Data | ||||
|---|---|---|---|---|---|---|
| DBH | H | V | DBH | H | V | |
| Minimum | 6.7 | 6.95 | 0.0153 | 6.85 | 9.18 | 0.0214 |
| Median | 14.9 | 15.03 | 0.1272 | 21.23 | 22.37 | 0.3199 |
| Mean | 15.7 | 15.51 | 0.1923 | 20.87 | 19.84 | 0.3984 |
| Maximum | 31.5 | 25.65 | 0.8642 | 34.25 | 26.95 | 1.0229 |
| Stand. Dev. | 6.04 | 3.93 | 0.1808 | 7.94 | 5.83 | 0.307 |
| Stand. Error | 0.64 | 0.41 | 0.0191 | 1.62 | 1.19 | 0.0627 |
| Model Type | R2 | RMSE | ME |
|---|---|---|---|
| Mixed-effects | 0.9954 | 0.4522 | −0.00006 |
| Fixed-effects | 0.984 | 0.8453 | 0.00019 |
| Parameter | Mixed-Effects Model | Fixed-Effects Model |
|---|---|---|
| b1 | 1.1484 (0.1321) | 0.8159 (0.0512) |
| b2 | 0.8581 (0.0584) | 0.9516 (0.0308) |
| b3 | 0.0952 (0.0493) | 0.0971 (0.0241) |
| b4 | 0.2795 (0.0056) | 0.3169 (0.0069) |
| b5 | −3.6430 (0.2547) | −3.6172 (0.1956) |
| b6 | −2.5514 (0.4425) | −0.7535 (0.2373) |
| b7 | −1.0268 (0.6595) | 1.4009 (0.4004) |
| b8 | 0.1408 (0.0076) | 0.0867 (0.0056) |
| sd(β1) | 0.0269 | - |
| sd(β2) | 1.7571 | - |
| sd(β3) | 1.8647 | - |
| corr (β1, β2) | −0.594 | - |
| corr (β1, β3) | −0.844 | - |
| corr (β2, β3) | 0.750 | - |
| 0.49202 | - |
| Independent Data | ||||||
|---|---|---|---|---|---|---|
| Error | MEM | FEM | EVM | |||
| AE (m3) | RE (%) | AE (m3) | RE (%) | AE (m3) | RE (%) | |
| Minimum | −0.0522 | −33.72 | −0.0473 | −19.73 | −0.0464 | −16.48 |
| Maximum | 0.0666 | 23.29 | 0.0786 | 27.50 | 0.0768 | 26.87 |
| Median | 0.0032 | −0.46 | 0.0103 | 2.31 | 0.0116 | 2.02 |
| Mean | 0.0047 | −3.62 | 0.011 | 0.11 | 0.0121 | 1.67 |
| Stand. dev. | 0.0279 | 13.68 | 0.0305 | 11.34 | 0.0287 | 9.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bronisz, K.; Zasada, M. Comparison of Fixed- and Mixed-Effects Approaches to Taper Modeling for Scots Pine in West Poland. Forests 2019, 10, 975. https://doi.org/10.3390/f10110975
Bronisz K, Zasada M. Comparison of Fixed- and Mixed-Effects Approaches to Taper Modeling for Scots Pine in West Poland. Forests. 2019; 10(11):975. https://doi.org/10.3390/f10110975
Chicago/Turabian StyleBronisz, Karol, and Michał Zasada. 2019. "Comparison of Fixed- and Mixed-Effects Approaches to Taper Modeling for Scots Pine in West Poland" Forests 10, no. 11: 975. https://doi.org/10.3390/f10110975
APA StyleBronisz, K., & Zasada, M. (2019). Comparison of Fixed- and Mixed-Effects Approaches to Taper Modeling for Scots Pine in West Poland. Forests, 10(11), 975. https://doi.org/10.3390/f10110975






