Influence of Stem Taper on the Yield of Black Spruce Stands and Trees Following Commercial Thinning †
Abstract
1. Introduction
2. Material and Methods
2.1. Study Area
2.2. Stand Measurements
2.3. Selected Tree Measurements
2.3.1. Selected Tree Neighborhood
2.3.2. Growth Measurement
2.3.3. Stem Shape
2.3.4. Statistical Analysis
3. Results
3.1. Variations in Volume
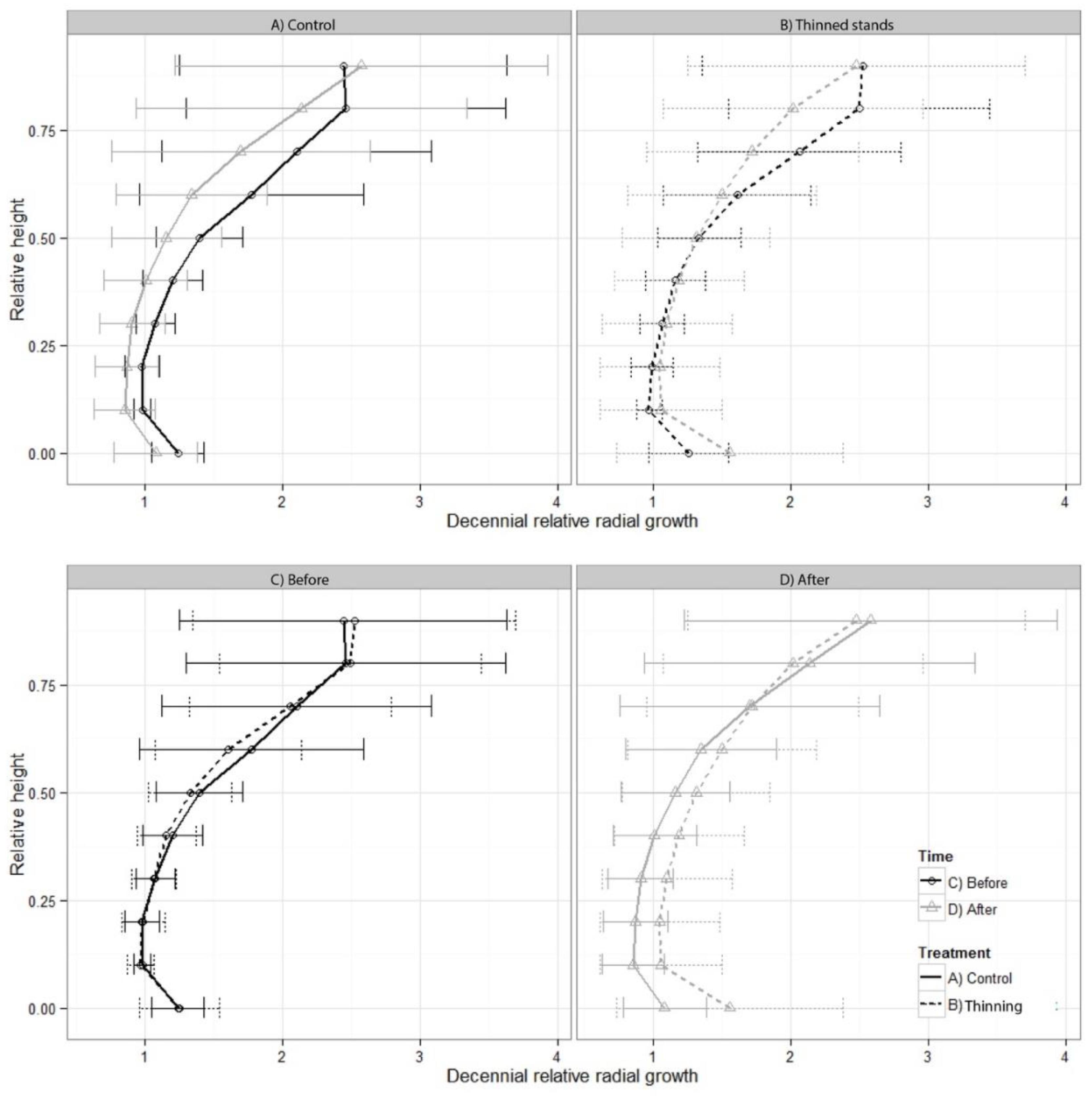
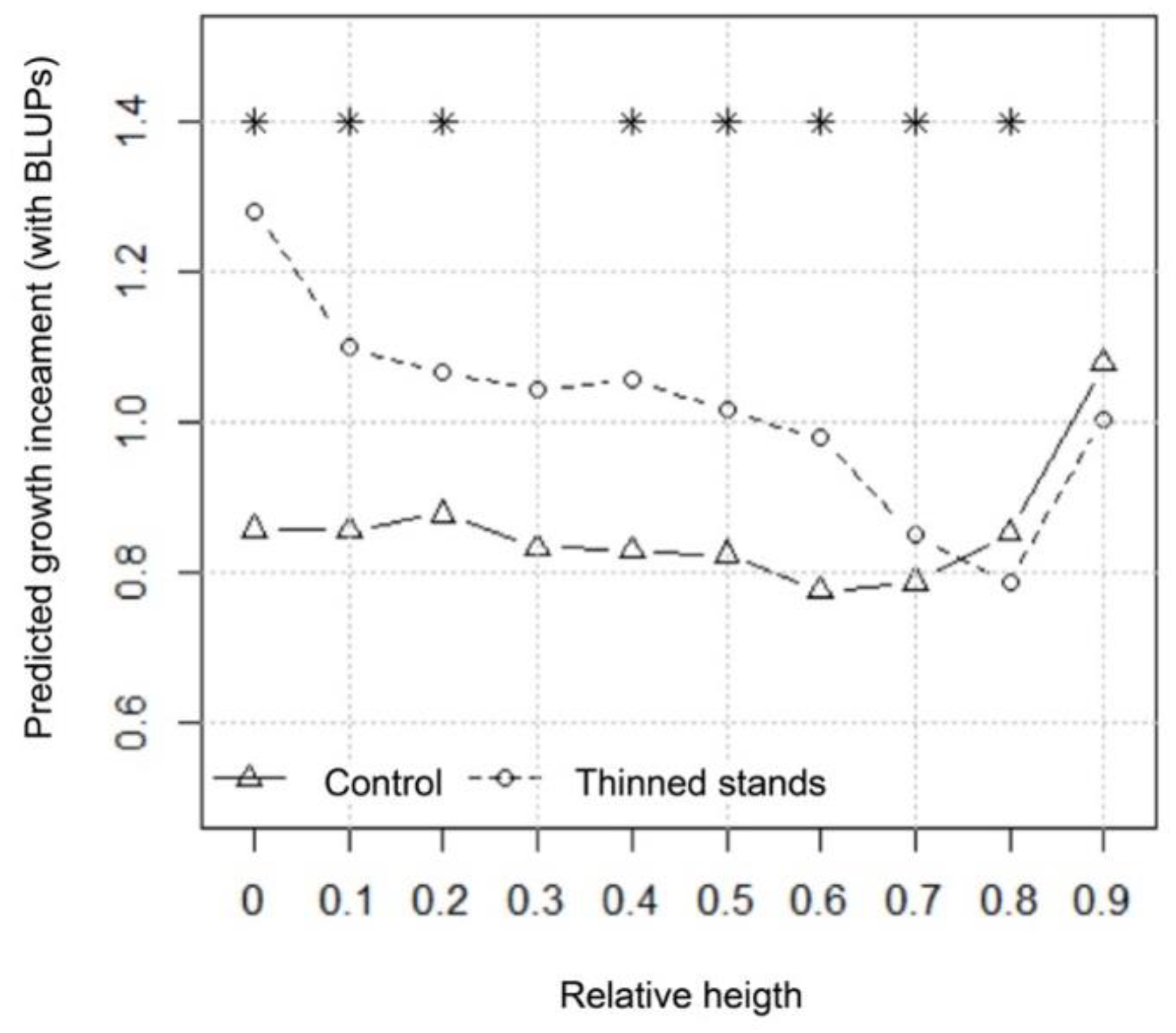
3.2. Radial Growth Response in Relation to Taper and Stem Shape
4. Discussion
4.1. Thinning Effect on Stand Attributes
4.2. Wood Allocation and Stem Shape Variations Following Treatment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Parent, B.; Fortin, C. Ressources Et Industries Forestières—Portrait Statistique Édition 2008; Gouvernement du Québec. Ministère des Ressources Naturelles et de la Faune-Direction du Développement de L’industrie des Produits Forestiers: Québec, QC, Canada, 2008; p. 513.
- Zhang, S.Y.; Koubaa, A. Les Résineux de l’est du Canada: Écologie Forestière, Caractéristiques, Transformation Et Usages; Publication spéciale SP-526F; FPInnovations: Québec, QC, Canada, 2009; p. 400. [Google Scholar]
- Bureau du forestier en chef. Bilan D’aménagement Forestier Durable Au Québec 2000–2008; Gouvernement du Québec, Roberval: Québec, QC, Canada, 2010; p. 290.
- Keyser, T.L. Thinning and site quality influence aboveground tree carbon stocks in yellow-poplar forests of the southern Appalachians. Can. J. For. Res. 2010, 40, 659–667. [Google Scholar] [CrossRef]
- Greene, D.F.; Zasada, J.C.; Sirois, L.; Kneeshaw, D.; Morin, H.; Charron, I.; Simard, M.J. A review of the regeneration dynamics of North American boreal forest tree species. Can. J. For. Res. 1999, 29, 824–839. [Google Scholar] [CrossRef]
- Lafleur, B.; Fenton, N.J.; Simard, M.; Leduc, A.; Paré, D.; Valeria, O.; Bergeron, Y. Ecosystem management in paludified boreal forests: Enhancing wood production, biodiversity, and carbon sequestration at the landscape level. For. Ecosyst. 2018, 5, 27. [Google Scholar] [CrossRef]
- Norton, M.R.; Hannon, S.J. Songbird response to partial-cut logging in the boreal mixedwood forest of Alberta. Can. J. For. Res. 1997, 27, 44–53. [Google Scholar] [CrossRef]
- Montoro Girona, M.; Rossi, S.; Lussier, J.-M.; Walsh, D.; Morin, H. Understanding tree growth responses after partial cutting: A new approach. PLoS ONE 2017, 12, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Soucy, M.; Lussier, J.M.; Lavoie, L. Long-term effects of thinning on growth and yield of an upland black spruce stand. Can. J. For. Res. 2012, 42, 1669–1677. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.Q.; Liu, S.; Oeding, J. A meta-analysis on the impacts of partial cutting on forest structure and carbon storage. Biogeosciences 2013, 10, 3691–3703. [Google Scholar] [CrossRef]
- Lemay, A.; Krause, C.; Achim, A.; Begin, J. Growth and wood quality of black spruce and balsam fir following careful logging around small merchantable stems (CLASS) in the boreal forest of Quebec, Canada. Forestry 2018, 91, 271–282. [Google Scholar] [CrossRef]
- Pamerleau-Couture, E.; Rossi, S.; Pothier, D.; Krause, C. Wood properties of black spruce (Picea mariana (Mill.) BSP) in relation to ring width and tree height in even- and uneven-aged boreal stands. Ann. For. Sci. 2019, 76, 43. [Google Scholar] [CrossRef]
- Kozak, A. A variable-exponent taper equation. Can. J. For. Res. 1988, 18, 1363–1368. [Google Scholar] [CrossRef]
- Brais, S.; Harvey, B.D.; Bose, A. Stem- and stand-level growth and mortality following partial cutting in eastern boreal poplar—White spruce stands. Can. J. For. Res. 2019, 49, 463–470. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Chauret, G.; Swift, E.; Duchesne, I. Effects of precommercial thinning on tree growth and lumber quality in a jack pine stand in New Brunswick, Canada. Can. J. For. Res. 2006, 36, 945–952. [Google Scholar] [CrossRef]
- Gardiner, B.A.; Stacey, G.R.; Belcher, R.E.; Wood, C.J. Field and wind tunnel assessments of the implications of respacing and thinning for tree stability. Forestry 1997, 70, 233–252. [Google Scholar] [CrossRef]
- Anyomi, K.A.; Ruel, J.-C. A multiscale analysis of the effects of alternative silvicultural treatments on windthrow within balsam fir dominated stands. Can. J. For. Res. 2015, 45, 1739–1747. [Google Scholar] [CrossRef]
- Perron, J.-Y.; Fortin, M.; Ung, C.-H.; Morin, P.; Blais, L.; Blais, G.; Carpentier, J.-P.; Cloutier, J.; Del Degan, B.; Demers, D.; et al. Dendrométrie Et Inventaire Forestier. In Manuel de Foresterie, 2nd ed.; OIFQ, Ed.; Éditions Multimondes: Québec, QC, Canada, 2009; pp. 567–630. [Google Scholar]
- Hillman, G.R.; Takyi, S.K. Response of black spruce to thinning and fertilization in a drained swamp. North J. Appl. For. 1998, 15, 98–105. [Google Scholar] [CrossRef]
- Viens, É. Effets de L’éclaircie Commerciale Sur La Croissance Et La Forme de La Tige du Pin Gris (Pinus banksiana Lamb.) en Abitibi, Québec. Master’s Thesis, Université du Québec à Chicoutimi, Chicoutimi, Saguenay, QC, Canada, 2001. [Google Scholar]
- Perron, J.Y. Tarif de Cubage Général, Volume Marchand; Gouvernement du Québec, Ministère de l’Énergie et des Ressources: Québec, QC, Canada, 1985; p. 53.
- Mailly, D.; Turbis, S.; Pothier, D. Predicting basal area increment in a spatially explicit, individual tree model: A test of competition measures with black spruce. Can. J. For. Res. 2003, 33, 435–443. [Google Scholar] [CrossRef]
- Vincent, M.; Krause, C.; Zhang, S. Radial growth response of black spruce roots and stems to commercial thinning in boreal forest. Forestry 2009, 82, 557–571. [Google Scholar] [CrossRef]
- Guay, R.; Gagnon, R.; Morin, H. A new automatic and interactive tree ring measurement system based on a line scan camera. For. Chron. 1992, 68, 138–141. [Google Scholar] [CrossRef]
- Stokes, M.A.; Smiley, T.L. An Introduction to Tree-ring Dating; University of Chicago Press: Chicago, IL, USA, 1968. [Google Scholar]
- Krause, C.; Gionest, F.; Morin, H.; MacLean, D.A. Temporal relations between defoliation caused by spruce budworm (Choristoneura fumiferana Clem.) and growth of balsam fir (Abies balsamea (L.) Mill.). Dendrochronologia 2003, 21, 23–31. [Google Scholar] [CrossRef]
- Holmes, R.L. Computer assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar]
- Demaerschalk, J.P.; Kozak, A. Whole-bole system—Conditioned dual-equation ystem for precise prediction of tree profiles. Can. J. For. Res. 1977, 7, 488–497. [Google Scholar] [CrossRef]
- Perez, D.-N.; Burkhart, H.-E.; Stiff, C.-T. A variable-form taper function for Pinus oocarpa Schiede in central Honduras. For. Sci. 1990, 36, 186–191. [Google Scholar]
- Morris, D.M.; Forslund, R.R. The relative importance of competition, microsite, and climate in controlling the stem taper and profile shape in jack pine. Can. J. For. Res. 1992, 22, 1999–2003. [Google Scholar] [CrossRef]
- Forslund, R.R. The power function as a simple stem profile examination tool. Can. J. For. Res. 1991, 21, 193–198. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Stinson, S.D. 50 years of low thinning in second-growth Douglas-fir. For. Chron. 1999, 75, 401–405. [Google Scholar] [CrossRef]
- Mäkinen, H.; Hynynen, J.; Isomäki, A. Intensive management of Scots pine stands in southern Finland: First empirical results and simulated further development. For. Ecol. Manag. 2005, 215, 37–50. [Google Scholar] [CrossRef]
- Skovsgaard, J.P. Analysing effects of thinning on stand volume growth in relation to site conditions: A case study for even-aged Sitka spruce (Picea sitchensis (Bong.) Carr.). Forestry 2009, 82, 87–104. [Google Scholar] [CrossRef]
- Weetman, G.F.; Roberge, M.R.; Meng, C.H. Black spruce-15-year growth and microbiological response to thinning and fertilization. Can. J. For. Res. 1980, 10, 502–509. [Google Scholar] [CrossRef]
- Lundqvist, L.; Chrimes, D.; Elfving, B.; Morling, T.; Valinger, E. Stand development after different thinnings in two uneven-aged Picea abies forests in Sweden. For. Ecol. Manag. 2007, 238, 141–146. [Google Scholar] [CrossRef]
- Bella, I.E.; De Franceschi, J.P. Commercial Thinning Improves Growth of Jack; Information Report NOR-X-112; Northern Forest Research Centre: Edmonton, AB, Canada, 1974. [Google Scholar]
- Curtis, R.O.; Marshall, D.D. Levels-of-growing-stock Cooperative Study in Douglas-fir: Report No. 14-Stampede Creek: 30-year Results; Research paper PNW-RP-543; Pacific Northwest Research Station, USDA-Forest-Service: Washington, DC, USA, 2002; p. 77.
- Pape, R. Effects of thinning regime on the wood properties and stem quality of Picea abies. Scand. J. For. Res. 1999, 14, 38–50. [Google Scholar] [CrossRef]
- Mäkinen, H.; Isomäki, A. Thinning intensity and growth of Norway spruce stands in Finland. Forestry 2004, 77, 349–364. [Google Scholar] [CrossRef]
- Lähde, E.; Laiho, O.; Norokorpi, Y. Structure transformation and volume increment in Norway spruce-dominated forests following contrasting silvicultural treatments. For. Ecol. Manag. 2001, 151, 133–138. [Google Scholar] [CrossRef]
- Goudiaby, V.; Brais, S.; Berninger, F.; Schneider, R. Vertical patterns in specific volume increment along stems of dominant jack pine (Pinus banksiana) and black spruce (Picea mariana) after thinning. Can. J. For. Res. 2012, 42, 733–748. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Modeling stand density effects on taper for jack pine and black spruce plantations using dimensional analysis. For. Sci. 2009, 55, 268–282. [Google Scholar]
- Larson, P.R. Stem form development of forest trees. For. Sci. 1963, 9, 1–42. [Google Scholar] [CrossRef]
- Tasissa, G.; Burkhart, H.E. An application of mixed effects analysis to modeling thinning effects on stem profile of loblolly pine. For. Ecol. Manag. 1998, 103, 87–101. [Google Scholar] [CrossRef]
- Sharma, M.; Zhang, S.Y. Variable-exponent taper equations for jack pine, black spruce, and balsam fir in eastern Canada. For. Ecol. Manag. 2004, 198, 39–53. [Google Scholar] [CrossRef]
- Hébert, F.; Krause, C.; Plourde, P.-Y.; Achim, A.; Prégent, G.; Ménétrier, J. Effect of tree spacing on tree level volume growth, morphology, and wood properties in a 25-year-old Pinus banksiana plantation in the boreal forest of Quebec. Forests 2016, 7, 276. [Google Scholar] [CrossRef]
- Lemay, A.; Krause, C.; Achim, A. Primary and secondary branch growth in black spruce and balsam fir after careful logging around small merchantable stems (CLASS). Forests 2019, 10, 500. [Google Scholar] [CrossRef]
| Site | Location | Annual Precipitation (mm) | Temperature (Min/Max, °C) | Year of Thinning | Ageinit | DBHinit (cm) | Ginit (Residuals and Harvested, m2 ha−1) | Gharvested (%) |
|---|---|---|---|---|---|---|---|---|
| HEB95 | N47.887 W71.464 | 992.9 | −12.1/17.9 | 1995 | 48.4 (10) | 13.0 (3.7) | 29.16 | 19.6 |
| HEB96-1 | N48.315 W71.679 | 992.9 | −12.1/17.9 | 1996 | 58.7 (9) | 15.4 (4.1) | 23.76 | 9.7 |
| HEB96-2 | N48.279 W71.683 | 992.9 | −12.1/17.9 | 1996 | 53.2 (8) | 16.6 (4) | 41.05 | 31.8 |
| HEB C | N48.145 W71.589 | 992.9 | −12.1/17.9 | 51.3 (9) | 15.8 (5.2) | 48.27 | ||
| LB95 | N48.033 W72.33 | 1012.7 | −16.8/17.3 | 1995 | 81.9 (27) | 14.7 (3.2) | 33.08 | 13.1 |
| LB C | N48.032 W72.334 | 1012.7 | −16.8/17.3 | 67.1 (23) | 14.6 (4.4) | 17.15 | ||
| LC96 | N48.143 W71.879 | 1036.7 | −11.7/19.3 | 1996 | 56.3 (6) | 15.1 (1.8) | 44.85 | 39.6 |
| LC C | N48.143 W71.878 | 1036.7 | −11.7/19.3 | 54.9 (13) | 20.7 (4.8) | 35.24 | ||
| LJ96 | N48.983 W72.738 | 919.8 | −18.4/17.6 | 1996 | 46.8 (6) | 13.6 (2.5) | 42.30 | 52.5 |
| LJ C | N48.983 W72.741 | 919.8 | −18.4/17.6 | 53.1 (7) | 12.3 (2.5) | 48.87 | ||
| MV95 | N48.794 W70.544 | 1187.3 | −16.1/17.5 | 1995 | 60.9 (11) | 14.1 (3.1) | 40.04 | 39.7 |
| MV96 | N48.76 W70.551 | 1187.3 | −16.1/17.5 | 1996 | 59.5 (8) | 12.9 (2.4) | 32.98 | 30.8 |
| MV C | N48.764 W70.55 | 1187.3 | −16.1/17.5 | 52.8 (12) | 14.6 (3.8) | 49.82 | ||
| SL97 | N48.874 W71.747 | 1061.4 | −11.7/18.2 | 1997 | 57.1 (7) | 17.1 (2.4) | 40.10 | 37.4 |
| SL C | N48.874 W71.475 | 1061.4 | −11.7/18.2 | 50.2 (7) | 15.5 (5.6) | 33.99 | ||
| Mean for harvested stands | 58 | 14.7 | 38.5 | 30.5 | ||||
| Mean for controls | 55 | 15.6 | 38.9 | |||||
| Stands | Vinitit (m3 ha−1) | Vf (m3 ha−1) | Vtot (Partial and Final Harvest) | AVSinit (m3) | AVSf (m3) | Stand Volume Increment (%) (RES Stems Only) |
|---|---|---|---|---|---|---|
| HEB95 | 83.82 | 69.46 | 88.78 | 0.073 | 0.104 | 107.69 |
| HEB96-1 | 219.16 | 204.29 | 225.50 | 0.195 | 0.215 | 103.20 |
| HEB96-2 | 248.14 | 182.18 | 263.63 | 0.140 | 0.152 | 109.30 |
| HEB C | 285.64 | 306.04 | 306.04 | 0.127 | 0.136 | 107.14 |
| LB95 | 204.48 | 187.85 | 216.97 | 0.134 | 0.163 | 107.12 |
| LB C | 96.40 | 110.41 | 110.41 | 0.101 | 0.116 | 114.54 |
| LC96 | 272.16 | 180.16 | 294.35 | 0.125 | 0.185 | 114.05 |
| LC C | 229.39 | 237.41 | 237.41 | 0.255 | 0.264 | 103.50 |
| LJ96 | 239.99 | 124.97 | 259.03 | 0.084 | 0.076 | 117.97 |
| LJ C | 283.74 | 298.07 | 298.07 | 0.073 | 0.076 | 105.05 |
| MV95 | 190.80 | 124.75 | 201.48 | 0.079 | 0.111 | 109.36 |
| MV96 | 157.27 | 120.41 | 172.11 | 0.068 | 0.102 | 114.05 |
| MV C | 268.48 | 280.42 | 280.42 | 0.098 | 0.102 | 104.45 |
| SL97 | 263.55 | 183.81 | 278.52 | 0.162 | 0.223 | 108.86 |
| SL C | 218.27 | 225.40 | 225.40 | 0.140 | 0.145 | 103.27 |
| Mean | ||||||
| Harvested stands | 208.82 | 153.10 | 222.26 | 0.118 | 0.148 | 110.18 |
| Controls | 230.32 | 242.96 | 242.96 | 0.132 | 0.140 | 106.33 |
| Sites | Number of Selected Trees | Mean DBH (cm) | Mean H (m) | Number of Living Competitors | Mean DBH of Living Competitors (cm) | Number of Stumps of Competitors | Mean DBH of Stumps of Competitors (cm) |
|---|---|---|---|---|---|---|---|
| HEB95 | 6 | 17.1 (3.4) | 12.5 (1.4) | 1.5 (1.5) | 13.4 (1.8) | 1.3 (1.0) | 11.6 (3.7) |
| HEB96-1 | 6 | 17.2 (3.1) | 14.4 (2.1) | 2.2 (1.0) | 19.7 (2.7) | 0.7 (1.2) | 18.8 (2.5) |
| HEB96-2 | 6 | 19.4 (3.2) | 16.3 (2.3) | 2.7 (0.8) | 15.2 (2.1) | 0.8 (0.4) | 18.3 (6.2) |
| HEB C | 3 | 18.9 (4.5) | 16.0 (2.3) | 3.3 (1.2) | 14.4 (3.2) | N/A | N/A |
| LB95 | 6 | 16.7 (2.9) | 16.1 (2.6) | 3.0 (2.5) | 17.5 (1.1) | 1.7 (1.2) | 18 (4.6) |
| LB C | 3 | 16.9 (6.1) | 14.1 (3.6) | 2.7 (0.6) | 16.5 (0.8) | N/A | N/A |
| LC96 | 6 | 22.5 (5.6) | 18.2 (1.9) | 1.8 (0.8) | 19.2 (2.2) | 2.5 (2.2) | 11.2 (0.7) |
| LC C | 3 | 17.9 (3.4) | 16.6 (0.6) | 2.3 (1.2) | 23.4 (2.0) | N/A | N/A |
| LJ96 | 6 | 12.3(2.0) | 13.2 (0.9) | 2.2 (0.8) | 13.2 (0.8) | 1.7 (1.2) | 12.8 (2.9) |
| LJ C | 3 | 12.2 (2.4) | 14.0 (1.6) | 6.0 (1.7) | 11.1 (0.6) | N/A | N/A |
| MV95 | 6 | 15.1 (3.6) | 13.0 (1.7) | 2.5 (1.6) | 15.8 (1.0) | 0.7 (0.8) | 12.7 (1.2) |
| MV96 | 5 | 14.4 (1.6) | 12.7 (0.7) | 2.0 (1.6) | 15.0 (1.1) | 1.6 (1.8) | 9.8 (0.2) |
| MV C | 3 | 16.2 (1.6) | 12.7 (0.7) | 2.3 (2.1) | 12.1 (1.3) | N/A | N/A |
| SL97 | 6 | 17.0 (3.2) | 16.0 (1.5) | 1.8 (1.0) | 25.2 (7.3) | 0.8 (1.3) | 15 (1.7) |
| SL C | 3 | 14.4 (3.5) | 13.9 (2.7) | 3.7 (2.1) | 11.5 (2.4) | N/A | N/A |
| Mean | |||||||
| Harvested stands | 6 | 16.9 (1.2) | 14.7 (0.5) | 2.2 (0.6) | 17.2 (2.0) | 1.3 (0.5) | 14.2 (1.9) |
| Controls | 3 | 16.1 (3.6) | 14.5 (1.9) | 3.4 (1.5) | 14.8 (1.7) | N/A | N/A |
| Variable | Effect | Num DF | Den DF | F Value | p Value |
|---|---|---|---|---|---|
| (a) Stand volume increment | Intercept Treatment Ginit | 1 1 1 | 7 7 7 | 19.655 1.583 −0.057 | <0.0001 0.139 0.956 |
| (b) Vtot harvested | Intercept Treatment Vinit | 1 1 1 | 7 7 7 | 0.593 0.670 50.815 | 0.564 0.516 <0.0001 |
| (c) Stem volume increment | Intercept Treatment Ginit | 1 1 1 | 928 928 928 | 0.659 −0.182 0.561 | 0.510 0.856 0.575 |
| Variable | Effect | Num DF | Den DF | F Value | p Value |
|---|---|---|---|---|---|
| (a) lnGrowthInc 1 | Intercept | 1 | 621 | 433.040 | <0.0001 |
| Treatment | 1 | 63 | 12.762 | 0.0007 | |
| Relative height (RH) | 9 | 621 | 23.516 | <0.0001 | |
| CIs | 1 | 63 | 16.948 | 0.0001 | |
| Treatment × RH | 9 | 621 | 7.810 | <0.0001 | |
| (b) ASEC 2 | Intercept | 1 | 70 | 286.119 | <0.0001 |
| Treatment | 1 | 63 | 8.55034 | 0.0048 | |
| Time | 1 | 70 | 211.583 | <0.0001 | |
| CIs | 1 | 63 | 4.3794 | 0.0404 | |
| (c) lnTaper 3 | Intercept | 1 | 70 | 367.546 | <0.0001 |
| Treatment | 1 | 63 | 4.665 | 0.0346 | |
| Time | 1 | 70 | 35.913 | <0.0001 | |
| Slenderness | 1 | 63 | 23.072 | <0.0001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vincent, M.; Krause, C.; Koubaa, A. Influence of Stem Taper on the Yield of Black Spruce Stands and Trees Following Commercial Thinning. Forests 2019, 10, 1024. https://doi.org/10.3390/f10111024
Vincent M, Krause C, Koubaa A. Influence of Stem Taper on the Yield of Black Spruce Stands and Trees Following Commercial Thinning. Forests. 2019; 10(11):1024. https://doi.org/10.3390/f10111024
Chicago/Turabian StyleVincent, Manon, Cornelia Krause, and Ahmed Koubaa. 2019. "Influence of Stem Taper on the Yield of Black Spruce Stands and Trees Following Commercial Thinning" Forests 10, no. 11: 1024. https://doi.org/10.3390/f10111024
APA StyleVincent, M., Krause, C., & Koubaa, A. (2019). Influence of Stem Taper on the Yield of Black Spruce Stands and Trees Following Commercial Thinning. Forests, 10(11), 1024. https://doi.org/10.3390/f10111024






