A Nonlinear Mixed-Effects Height-to-Diameter Ratio Model for Several Tree Species Based on Czech National Forest Inventory Data
Abstract
1. Introduction
2. Materials and Methods
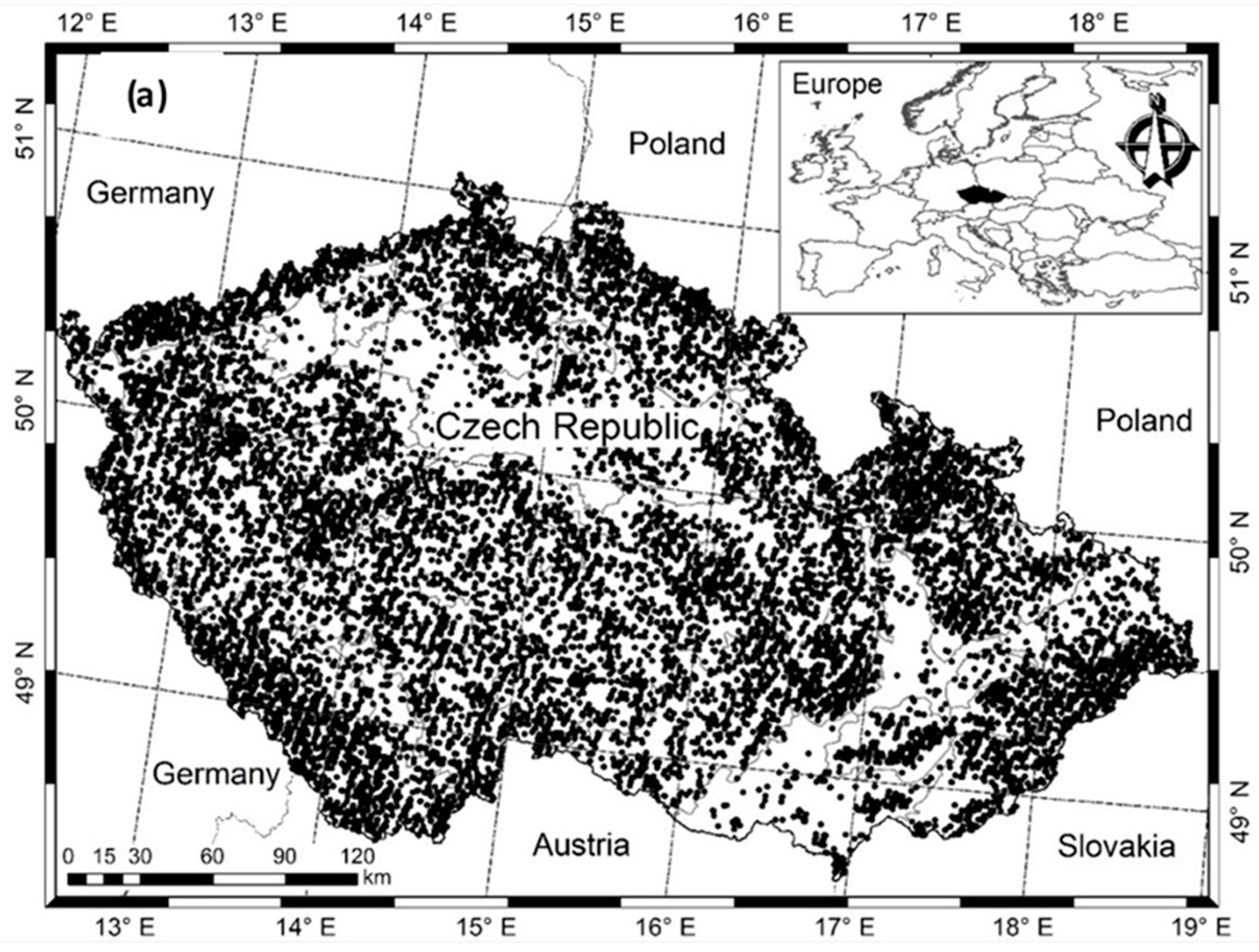
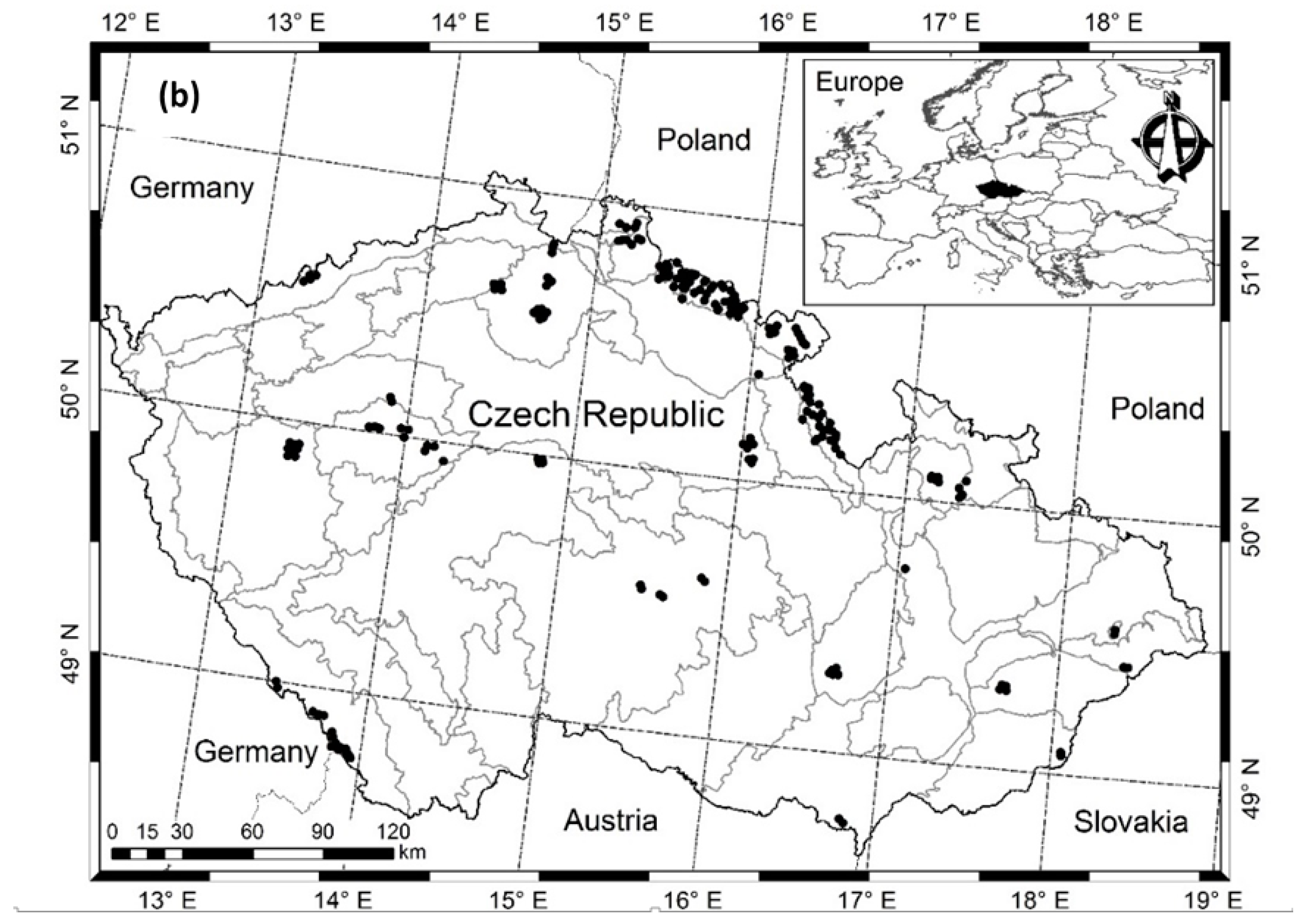
2.1. Data Materials
2.2. Training Dataset
2.3. Validation Dataset
2.4. Data Analysis
2.4.1. Deriving Stand-Level Variables
2.4.2. Model Construction
| Canopy Height Class | CC1 | CC2 |
| CHC1 | 0 | 0 |
| CHC2 | 1 | 0 |
| CHC3 | 0 | 1 |
| Tree Species | TS1 | TS2 | TS3 | TS4 | TS5 | TS6 |
| Norway spruce | 0 | 0 | 0 | 0 | 0 | 0 |
| Scots pine | 1 | 0 | 0 | 0 | 0 | 0 |
| European larch | 0 | 1 | 0 | 0 | 0 | 0 |
| Fir species | 0 | 0 | 1 | 0 | 0 | 0 |
| European beech | 0 | 0 | 0 | 1 | 0 | 0 |
| Oak species | 0 | 0 | 0 | 0 | 1 | 0 |
| Birch and alder speices | 0 | 0 | 0 | 0 | 0 | 1 |
2.4.3. Estimating Model Parameters and Evaluation
2.4.4. Calibrating Mixed-Effects Model and Predicting Sample Plot-Specific HDR
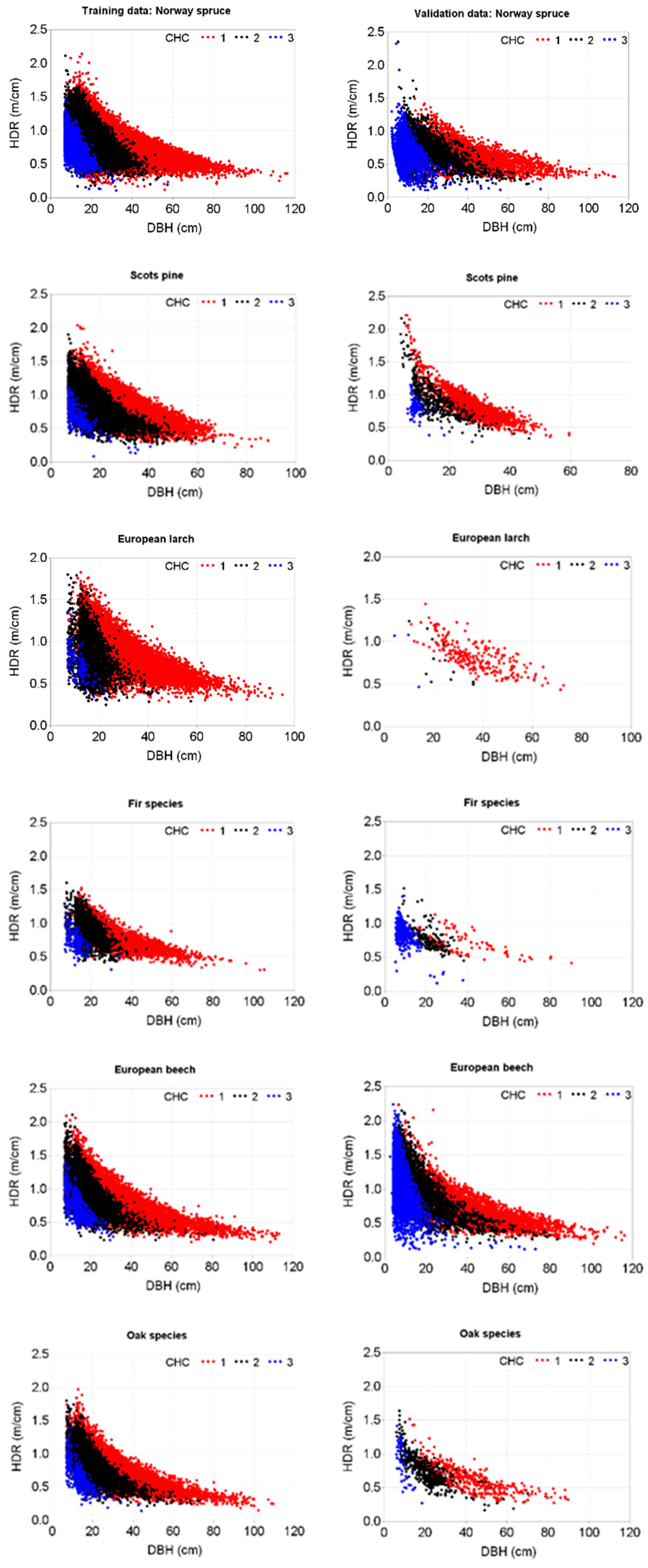
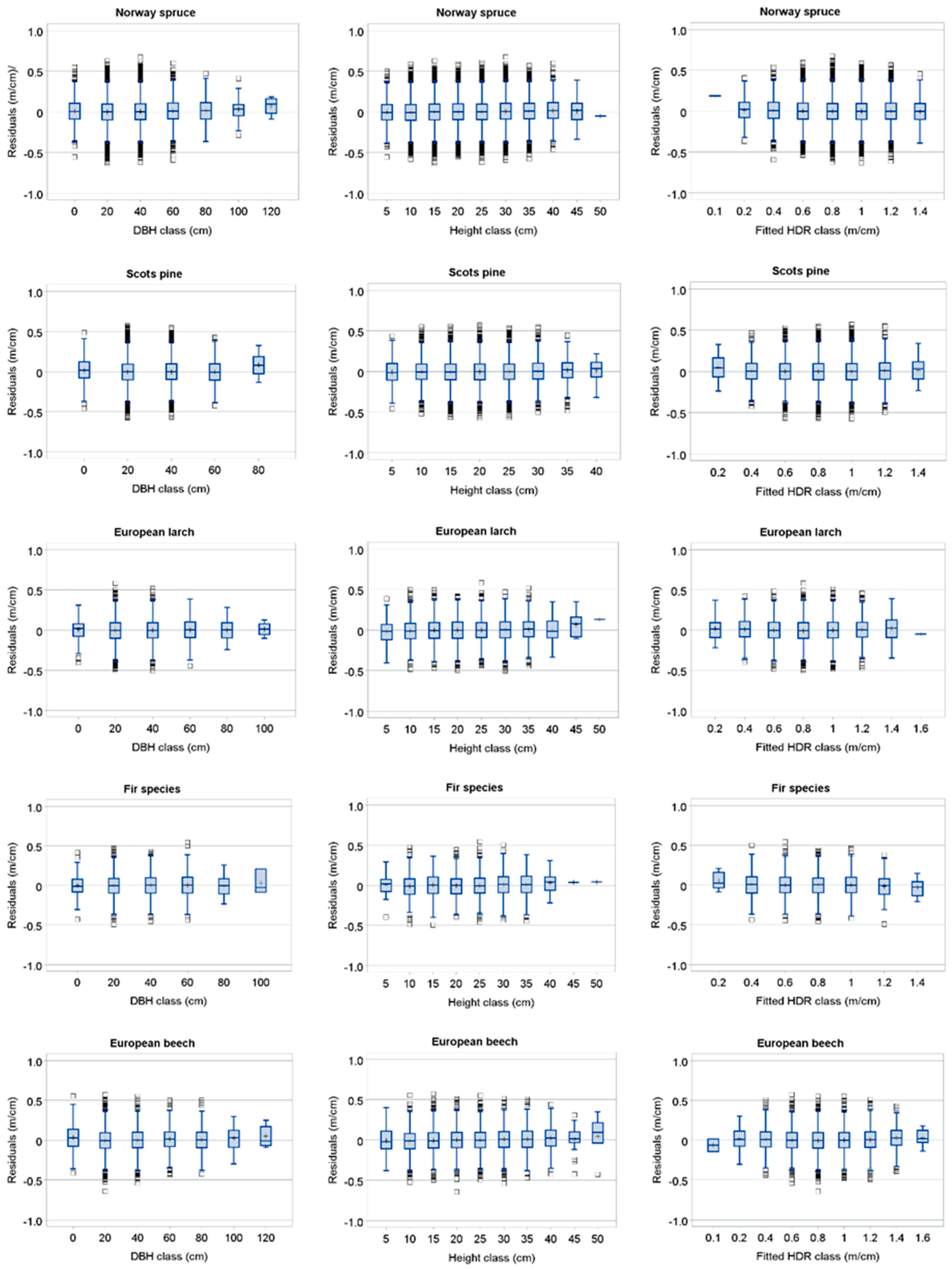
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wonn, H.T.; O’Hara, K.L. Height: Diameter ratios and stability relationships for four northern rocky mountain tree species. West. J. Appl. For. 2001, 16, 87–94. [Google Scholar]
- Vospernik, S.; Monserud, R.A.; Sterba, H. Do individual-tree growth models correctly represent height:diameter ratios of Norway spruce and Scots pine? For. Ecol. Manag. 2010, 260, 1735–1753. [Google Scholar] [CrossRef]
- Valinger, E.; Fridman, J. Modelling probability of snow and wind damage in Scots pine stands using tree characteristics. For. Ecol. Manag. 1997, 97, 215–222. [Google Scholar] [CrossRef]
- Valinger, E.; Fridman, J. Factors affecting the probability of windthrow at stand level as a result of Gudrun winter storm in southern Sweden. For. Ecol. Manag. 2011, 262, 398–403. [Google Scholar] [CrossRef]
- Cremer, K.W.; Borough, C.J.; McKinnell, F.H.; Carter, P.R. Effects of stocking and thinning on wind damage in plantation. N. Z. J. For. Sci. 1982, 12, 244–268. [Google Scholar]
- Castedo-Dorado, F.; Crecente-Campo, F.; Álvarez-Álvarez, P.; Barrio-Anta, M. Development of a stand density management diagram for radiata pine stands including assessment of stand stability. Forestry 2009, 82, 1–16. [Google Scholar] [CrossRef]
- Wallentin, C.; Nilsson, U. Storm and snow damage in a Norway spruce thinning experiment in southern Sweden. Forestry 2014, 87, 229–238. [Google Scholar] [CrossRef]
- Jiao-jun, Z.; Feng-qin, L.; Yutaka, G.; Matsuzaki, T.; Yamamoto, M. Effects of thinning on wind damage in Pinus thunbergii plantation. J. For. Res. 2003, 14, 1–8. [Google Scholar] [CrossRef]
- Nykänen, M.L.; Peltola, H.; Quine, C.; Kellomäki, S.; Broadgate, M. Factors affecting snow damage of trees with reference to European conditions. Silva Fenn. 1997, 31, 193–213. [Google Scholar] [CrossRef]
- Schütz, J.-P.; Götz, M.; Schmid, W.; Mandallaz, D. Vulnerability of spruce (Picea abies) and beech (Fagus sylvatica) forest stands to storms and consequences for silviculture. Eur. J. For. Res. 2006, 125, 291–302. [Google Scholar] [CrossRef]
- Urata, T.; Shibuya, M.; Koizumi, A.; Torita, H.; Cha, J. Both stem and crown mass affect tree resistance to uprooting. J. For. Res. 2011, 17, 65–71. [Google Scholar] [CrossRef]
- Schmidt, M.; Hanewinkel, M.; Kändler, G.; Kublin, E.; Kohnle, U. An inventory-based approach for modeling single-tree storm damage—An experience with the winter storm of 1999 in southwestern Germany. Can. J. For. Res. 2010, 40, 1636–1652. [Google Scholar] [CrossRef]
- Albrecht, A.; Hanewinkel, M.; Bauhus, J.; Kohnle, U. How does silviculture affect storm damage in forests of south-western Germany? Results from empirical modeling based on long-term observations. Eur. J. For. Res. 2012, 131, 229–247. [Google Scholar] [CrossRef]
- Bošeľa, M.; Konôpka, B.; Šebeň, V.; Vladovič, J.; Tobin, B. Modelling height to diameter ratio—An opportunity to increase Norway spruce stand stability in the Western Carpathians. Lesnicky Casopis For. J. 2014, 60, 71–80. [Google Scholar] [CrossRef]
- Moore, J.R. Differences in maximum resistive bending moments of Pinus radiata trees grown on a range of soil types. For. Ecol. Manag. 2000, 135, 63–71. [Google Scholar] [CrossRef]
- Peltola, H.; Kellomäki, S.; Hassinen, A.; Granander, M. Mechanical stability of Scots pine, Norway spruce and birch: An analysis of tree-pulling experiments in Finland. For. Ecol. Manag. 2000, 135, 143–153. [Google Scholar] [CrossRef]
- Peltola, H.; Kellomäki, S.; Väisänen, H.; Ikonen, V.P. A mechanistic model for assessing the risk of wind and snow damage to single trees and stands of Scots pine, Norway spruce, and birch. Can. J. For. Res. 1999, 29, 647–661. [Google Scholar] [CrossRef]
- Peltola, H.M. Mechanical stability of trees under static loads. Am. J. Bot. 2006, 93, 1501–1511. [Google Scholar] [CrossRef]
- Opio, C.; Jacob, N.; Coopersmith, D. Height to diameter ratio as a competition index for young conifer plantations in northern British Columbia, Canada. For. Ecol. Manag. 2000, 137, 245–252. [Google Scholar] [CrossRef]
- Opio, C.; van Diest, K.; Jacob, N. Intra-seasonal changes in height to diameter ratios for lodgepole pine in the central interior of British Columbia. West. J. Appl. For. 2003, 18, 52–59. [Google Scholar]
- Yang, Y.; Huang, S. Effects of competition and climate variables on modelling height to live crown for three boreal tree species in Alberta, Canada. Eur. J. For. Res. 2018, 137, 153–167. [Google Scholar] [CrossRef]
- MacDonald, B.; Morris, D.M.; Marshall, P.L. Assessing components of competition indices for young boreal plantations. Can. J. For. Res. 1990, 20, 1060–1068. [Google Scholar] [CrossRef]
- Morris, D.M.; MacDonald, G.B. Development of a competition index for young conifer plantations established on boreal mixed wood sites. For. Chron. 1991, 67, 403–410. [Google Scholar] [CrossRef][Green Version]
- Temesgen, H.; LeMay, V.; Mitchell, S.J. Tree crown ratio models for multi-species and multi-layered stands of southeastern British Columbia. For. Chron. 2005, 81, 133–141. [Google Scholar] [CrossRef]
- Hasenauer, H.; Monserud, R.A. A crown ratio model for Austrian forests. For. Ecol. Manag. 1996, 84, 49–60. [Google Scholar] [CrossRef]
- Wykoff, W.R.; Crookston, N.L.; Stage, A.R. User’s Guide to the Stand Prognosis Model; Gen. Tech. Rep. INT-133; USDA, Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1982; p. 112.
- Mustard, J.; Harper, G. A Summary of the Available Information on Height to Diameter Ratio; BC Ministry of Forests: Victoria, BC, Canada, 1998; p. 120.
- Nilsson, U. Competition in Young Stands of Norway Spruce and Scots Pine. Ph.D. Thesis, Swedish University of Agricultural Sciences, Uppsala, Sweden, 1993; p. 173. [Google Scholar]
- Hasenauer, H.; Monserud, R.A.; Gregoire, T.G. Using simultaneous regression techniques with individual-tree growth models. For. Sci. 1998, 44, 87–95. [Google Scholar]
- Zimmerman, M.H.; Brown, C.L. Trees: Structure and Function; Springer: New York, NY, USA, 1971; p. 336. [Google Scholar]
- Burton, P.J. Some limitations inherent to static indices of plant competition. Can. J. For. Res. 1993, 23, 2141–2152. [Google Scholar] [CrossRef]
- Kamimura, K.; Shiraishi, N. A review of strategies for wind damage assessment in Japanese forests. J. For. Res. 2007, 12, 162–176. [Google Scholar] [CrossRef]
- Maclsaac, D.A.; Navratil, S. Competition dynamics in juvenile boreal hardwood-conifer mixes. In Silviculture of Temperate and Broadleaf Conifer Mixers; Comeau, P., Thomas, K.D., Eds.; BC Ministry of Forests: Victoria, BC, Canada, 1996; pp. 23–34. [Google Scholar]
- Henry, H.A.L.; Aarssen, L.W. The interpretation of stem diameter-height allometry in trees: Biomechanical constraints, neighbour effects, or biased regressions? Ecol. Lett. 1999, 2, 89–97. [Google Scholar] [CrossRef]
- Ruel, J.-C.; Messier, C.; Claveau, Y.; Doucet, R.; Comeau, P. Morphological indicators of growth response of coniferous advance regeneration to overstorey removal in the boreal forest. For. Chron. 2000, 76, 633–642. [Google Scholar] [CrossRef]
- Tilman, D. Plant Strategies and the Dynamics and the Structure of Plant Communities; Princeton University Press: Princeton, NJ, USA, 1988; p. 360. [Google Scholar]
- Wiklund, K.; Konôpka, B.; Nilsson, L.-O. Stem form and growth in Picea abies (L.) karst, in response to water and mineral nutrient availability. Scand. J. For. Res. 1995, 10, 326–332. [Google Scholar] [CrossRef]
- Homeier, J.; Breckle, S.-W.; Günter, S.; Rollenbeck, R.T.; Leuschner, C. Tree diversity, forest structure and productivity along altitudinal and topographical gradients in a species-rich ecuadorian montane rain forest. Biotropica 2010, 42, 140–148. [Google Scholar] [CrossRef]
- Martín-Alcón, S.; González-Olabarría, J.R.; Coll, L. Wind and snow damage in the Pyrenees pine forests: Effect of stand attributes and location. Silva Fenn. 2010, 44, 399–410. [Google Scholar] [CrossRef]
- Lohmander, P.; Helles, F. Windthrow probability as a function of stand characteristics and shelter. Scand. J. For. Res. 1987, 2, 227–238. [Google Scholar] [CrossRef]
- Schelhaas, M.J.; Kramer, K.; Peltola, H.; van der Werf, D.C.; Wijdeven, S.M.J. Introducing tree interactions in wind damage simulation. Ecol. Model. 2007, 207, 197–209. [Google Scholar] [CrossRef]
- Mitchell, S.J. Wind as a natural disturbance agent in forests: A synthesis. Forestry 2013, 86, 147–157. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S. Modeling individual tree height to diameter ratio for Norway spruce and European beech in Czech Republic. Trees 2016, 30, 1969–1982. [Google Scholar] [CrossRef]
- Slodicak, M.; Novak, J. Silvicultural measures to increase the mechanical stability of pure secondary Norway spruce stands before conversion. For. Ecol. Manag. 2006, 224, 252–257. [Google Scholar] [CrossRef]
- Slodičák, M. Thinning regime in stands of Norway spruce subjected to snow and wind damage. In Wind and Trees; Coutts, M.P., Grace, J., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 436–447. [Google Scholar]
- Mäkinen, H.; Nöjd, P.; Isomäki, A. Radial, height and volume increment variation in Picea abies (L.) Karst. Stands with varying thinning intensities. Scand. J. For. Res. 2002, 17, 304–316. [Google Scholar] [CrossRef]
- Harrington, T.B.; Harrington, C.A.; DeBell, D.S. Effects of planting spacing and site quality on 25-year growth and mortality relationships of Douglas-fir (Pseudotsuga menziesii var. menziesii). For. Ecol. Manag. 2009, 258, 18–25. [Google Scholar] [CrossRef]
- Pinheiro, J.C.; Bates, D.M. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000. [Google Scholar]
- West, P.W.; Ratkowsky, D.A.; Davis, A.W. Problems of hypothesis testing of regressions with multiple measurements from individual sampling units. For. Ecol. Manag. 1984, 7, 207–224. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Schabenberger, O.; Barrett, J.P. Linear modelling of irregularly spaced, unbalanced, longitudinal data from permanent-plot measurements. Can. J. For. Res. 1995, 25, 137–156. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, H.; Sharma, R.P.; Pang, L.; Wang, G. A generalized nonlinear mixed-effects height to crown base model for Mongolian oak in northeast China. For. Ecol. Manag. 2017, 384, 34–43. [Google Scholar] [CrossRef]
- Fu, L.; Sun, H.; Sharma, R.P.; Lei, Y.; Zhang, H.; Tang, S. Nonlinear mixed-effects crown width models for individual trees of Chinese fir (Cunninghamia lanceolata) in south-central China. For. Ecol. Manag. 2013, 302, 210–220. [Google Scholar] [CrossRef]
- Sharma, R.P.; Breidenbach, J. Modeling height-diameter relationships for Norway spruce, Scots pine, and downy birch using Norwegian national forest inventory data. For. Sci. Technol. 2015, 11, 44–53. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S.; Podrázský, V.; Jansa, V. Modelling individual tree height to crown base of Norway spruce (Picea abies (L.) Karst.) and European beech (Fagus sylvatica L.). PLoS ONE 2017, 12, e0186394. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.P.; Bílek, L.; Vacek, Z.; Vacek, S. Modelling crown width-diameter relationship for Scots pine in the central Europe. Trees 2017, 31, 1875–1889. [Google Scholar] [CrossRef]
- Adame, P.; Hynynen, J.; Cañellas, I.; del Río, M. Individual-tree diameter growth model for rebollo oak (Quercus pyrenaica Willd.) coppices. For. Ecol. Manag. 2008, 255, 1011–1022. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Næsset, E. Weibull models for single-tree increment of Norway spruce, Scots pine, birch and other broadleaves in Norway. Scand. J. For. Res. 2009, 24, 54–66. [Google Scholar] [CrossRef]
- Crecente-Campo, F.; Tomé, M.; Soares, P.; Dieguez-Aranda, U. A generalized nonlinear mixed-effects height-diameter model for Eucalyptus globulus L. in northwestern Spain. For. Ecol. Manag. 2010, 259, 943–952. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S.; Kučera, M. Modelling individual tree height-diameter relationships for multi-layered and multi-species forests in central Europe. Trees 2018. [Google Scholar] [CrossRef]
- Monserud, R.A.; Sterba, H. A basal area increment model for individual trees growing in even- and uneven-aged forest stands in Austria. For. Ecol. Manag. 1996, 80, 57–80. [Google Scholar] [CrossRef]
- Sharma, R.P.; Brunner, A. Modeling individual tree height growth of Norway spruce and Scots pine from national forest inventory data in Norway. Scand. J. For. Res. 2017, 32, 501–514. [Google Scholar] [CrossRef]
- Sharma, R.P.; Brunner, A.; Eid, T. Site index prediction from site and climate variables for Norway spruce and Scots pine in Norway. Scand. J. For. Res. 2012, 27, 619–636. [Google Scholar] [CrossRef]
- Sharma, R.P.; Brunner, A.; Eid, T.; Øyen, B.-H. Modelling dominant height growth from national forest inventory individual tree data with short time series and large age errors. For. Ecol. Manag. 2011, 262, 2162–2175. [Google Scholar] [CrossRef]
- Šmelko, Š.S.; Merganič, J. Some methodological aspects of the national forest inventory and monitoring in Slovakia. J. For. Sci. 2008, 54, 476–483. [Google Scholar] [CrossRef]
- FMI. Inventarizace Lesů, Metodika Venkovního Sběru Dat [Forest Inventory, Field Data Collection Methodology]; FMI: Brandýs nad Labem, Czech Republic, 2003; p. 136.
- Kučera, M. Výstupy NIL2-Zastoupení dřevin a věková struktura Lesa [Outputs of NIL2-Representation of tree species and the age structure of forest]. In XIX. Sněm Lesníků; Vašíček, J., Skála, V., Eds.; Ministry of Environment: Hradec Králové, Czech Republic, 2016; pp. 37–53. [Google Scholar]
- FMI. National Forest Inventory in the Czech Republic 2001–2004: Introduction, Methods, Results; FMI: Brandýs nad Labem, Czech Republic, 2007; p. 224.
- Sharma, R.P.; Vacek, Z.; Vacek, S.; Jansa, V. Modelling individual tree diameter growth for Norway spruce in Czech Republic using generalized algebraic difference approach. J. For. Sci. 2017, 63, 227–238. [Google Scholar]
- Vacek, S.; Vacek, Z.; Bílek, L.; Simon, J.; Remeš, J.; Hůnová, I.; Král, J.; Putalova, T.; Mikeska, M. Structure, regeneration and growth of Scots pine (Pinus sylvestris L.) stands with respect to changing climate and environmental pollution. Silva Fenn. 2016, 50, 1564. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S. Individual tree crown width models for Norway spruce and European beech in Czech Republic. For. Ecol. Manag. 2016, 366, 208–220. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S. Modelling tree crown-to-bole diameter ratio for Norway spruce and European beech. Silva Fenn. 2017, 51, 1740. [Google Scholar] [CrossRef]
- Vacek, Z.; Vacek, S.; Bílek, L.; Král, J.; Remeš, J.; Bulušek, D.; Králíček, I. Ungulate impact on natural regeneration in spruce-beech-fir stands in Černý důl Nature Reserve in the Orlické Hory mountains, case study from central Sudetes. Forests 2014, 5, 2929–2946. [Google Scholar] [CrossRef]
- Vacek, Z.; Vacek, S.; Bílek, L.; Remeš, J.; Štefančík, I. Changes in horizontal structure of natural beech forests on an altitudinal gradient in the Sudetes. Dendrobiology 2015, 73, 33–45. [Google Scholar] [CrossRef]
- Vacek, S.; Vacek, Z.; Kalousková, I.; Cukor, J.; Bílek, L.; Moser, W.K.; Bulušek, D.; Podrázský, V.; Řeháček, D. Sycamore maple (Acer pseudoplatanus L.) stands on former agricultural land in the Sudetes—Evaluation of ecological value and production potential. Dendrobiology 2018, 79, 61–76. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Hao, K.; Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. For. Ecol. Manag. 2017, 389, 364–373. [Google Scholar] [CrossRef]
- Schroder, J.; von Gadow, K. Testing a new competition index for Maritime pine in northwestern Spain. Can. J. For. Res. 1999, 29, 280–283. [Google Scholar] [CrossRef]
- Zhao, D.; Kane, M.; Borders, B.E. Crown ratio and relative spacing relationships for loblolly pine plantations. Open J. For. 2012, 2, 101–115. [Google Scholar] [CrossRef]
- Ferguson, I.S.; Leech, J.W. Generalized least squares estimation of yield functions. For. Sci. 1978, 24, 27–42. [Google Scholar]
- Staudhammer, C.; LeMay, V. Height prediction equations using diameter and stand density measures. For. Chron. 2000, 76, 303–309. [Google Scholar] [CrossRef]
- Mehtatalo, L. Height-diameter models for Scots pine and birch in Finland. Silva Fenn. 2005, 39, 55–66. [Google Scholar] [CrossRef]
- Adame, P.; del Rio, M.; Canellas, I. A mixed nonlinear height-diameter model for pyrenean oak (Quercus pyrenaica Willd.). For. Ecol. Manag. 2008, 256, 88–98. [Google Scholar] [CrossRef]
- Bates, D.M.; Watts, D.G. Nonlinear Regression Analysis and Its Applications; John Wiley and Sons: New York, NY, USA, 1988. [Google Scholar]
- Vonesh, E.F.; Chinchilli, V.M. Linear and Nonlinear Models for the Analysis of Repeated Measurements; Marcel Dekker: New York, NY, USA, 1997; p. XII. [Google Scholar]
- SAS Institute Inc. SAS/ETS1 9.4 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2013. [Google Scholar]
- Littell, R.C.; Milliken, G.A.; Stroup, W.W.; Wolfinger, R.D.; Schabenberger, O. SAS for Mixed Models, 2nd ed.; SAS Institute Inc.: Cary, NC, USA, 2006; 814p. [Google Scholar]
- Sheiner, L.B.; Beal, S.L. Evaluation of methods for estimating population pharmacokinetic parameters. I. Michaelis-menten model: Routine clinical pharmacokinetic data. J. Pharmacokinet. Biopharm. 1980, 8, 553–571. [Google Scholar] [CrossRef]
- Akaike, H. A new look at statistical model identification. IEEE Trans. Autom. Control 1972, 19, 716–723. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 3rd ed.; Wiley: New York, NY, USA, 2001; p. 641. [Google Scholar]
- Hall, D.B.; Bailey, R.L. Modeling and prediction of forest growth variables based on multilevel nonlinear mixed models. For. Sci. 2001, 47, 311–321. [Google Scholar]
- Calama, R.; Montero, G. Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain. Can. J. For. Res. 2004, 34, 150–163. [Google Scholar] [CrossRef]
- Vanclay, J.K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Oxon, UK, 1994; p. 312. [Google Scholar]
- Hasenauer, H. Concepts within tree growth modeling. In Sustainable Forest Management: Growth Models for Europe; Hasenauer, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; p. 398. [Google Scholar]
- Short III, E.A.; Burkhart, H. Prediction crown-height increment for thinned and unthinned loblolly pine plantations. For. Sci. 1992, 38, 594–610. [Google Scholar]
- Eerikainen, K. Predicting the height-diameter pattern of planted Pinus kesiya stands in Zambia and Zimbabwe. For. Ecol. Manag. 2003, 175, 355–366. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. For. Ecol. Manag. 2007, 249, 187–198. [Google Scholar] [CrossRef]
- Vargas-Larreta, B.; Castedo-Dorado, F.; Alvarez-Gonzalez, J.G.; Barrio-Anta, M.; Cruz-Cobos, F. A generalized height-diameter model with random coefficients for uneven-aged stands in El Salto, Durango (Mexico). Forestry 2009, 82, 445–462. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Wang, G.; Tang, S. Modelling a system of nonlinear additive crown width models applying seemingly unrelated regression for Prince Rupprecht larch in northern China. For. Ecol. Manag. 2017, 386, 71–80. [Google Scholar] [CrossRef]
- Soares, P.; Tomé, M. A tree crown ratio prediction equation for eucalypt plantations. Ann. For. Sci. 2001, 58, 193–202. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P.; Uhl, E.; Dahlhausen, J.; Rötzer, T.; Caldentey, J.; Koike, T.; van Con, T.; Chavanne, A.; Seifert, T.; et al. Crown size and growing space requirement of common tree species in urban centres, parks, and forests. Urban For. Urban Green. 2015, 14, 466–479. [Google Scholar] [CrossRef]
- Corral-Rivas, J.J.; Gonzalez, J.G.A.; Aguirre, O.; Hernandez, F. The effect of competition on individual tree basal area growth in mature stands of Pinus cooperi Blanco in Durango (Mexico). Eur. J. For. Res. 2005, 124, 133–142. [Google Scholar] [CrossRef]
- Fonseca, T.F.; Duarte, J.C. A silvicultural stand density model to control understory in maritime pine stands. iForest-Biogeosci. For. 2017, 10, 829–836. [Google Scholar] [CrossRef]
- Robinson, A.P.; Wykoff, W.R. Imputing missing height measures using a mixed-effects modeling strategy. Can. J. For. Res. 2004, 34, 2492–2500. [Google Scholar] [CrossRef]
- Trincado, G.; VanderSchaaf, C.L.; Burkhart, H.E. Regional mixed-effects height-diameter models for loblolly pine (Pinus taeda L.) plantations. Eur. J. For. Res. 2007, 126, 253–262. [Google Scholar] [CrossRef]
- Sharma, R.P.; Vacek, Z.; Vacek, S. Nonlinear mixed effect height-diameter model for mixed species forests in the central part of the Czech Republic. J. For. Sci. 2016, 62, 470–484. [Google Scholar]
- Özçelik, R.; Cao, Q.V.; Trincado, G.; Göçer, N. Predicting tree height from tree diameter and dominant height using mixed-effects and quantile regression models for two species in Turkey. For. Ecol. Manag. 2018, 419, 240–248. [Google Scholar] [CrossRef]
- Ruel, J.-C. Understanding windthrow: Silvicultural implications. For. Chron. 1995, 71, 434–445. [Google Scholar] [CrossRef]
- Rijal, B.; Weiskittel, A.R.; Kershaw, J.A. Development of height to crown base models for thirteen tree species of the North American Acadian Region. For. Chron. 2012, 88, 60–73. [Google Scholar] [CrossRef]

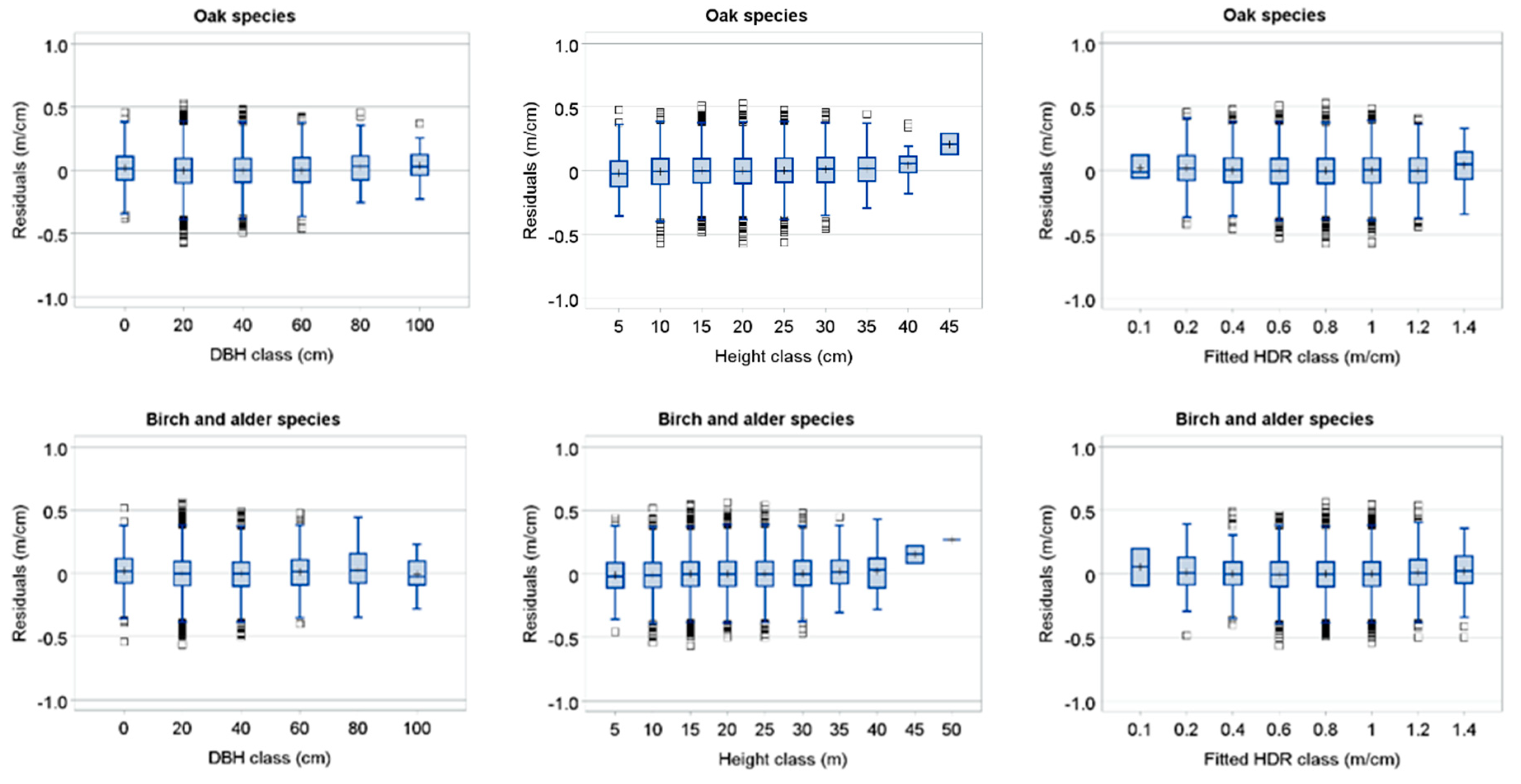



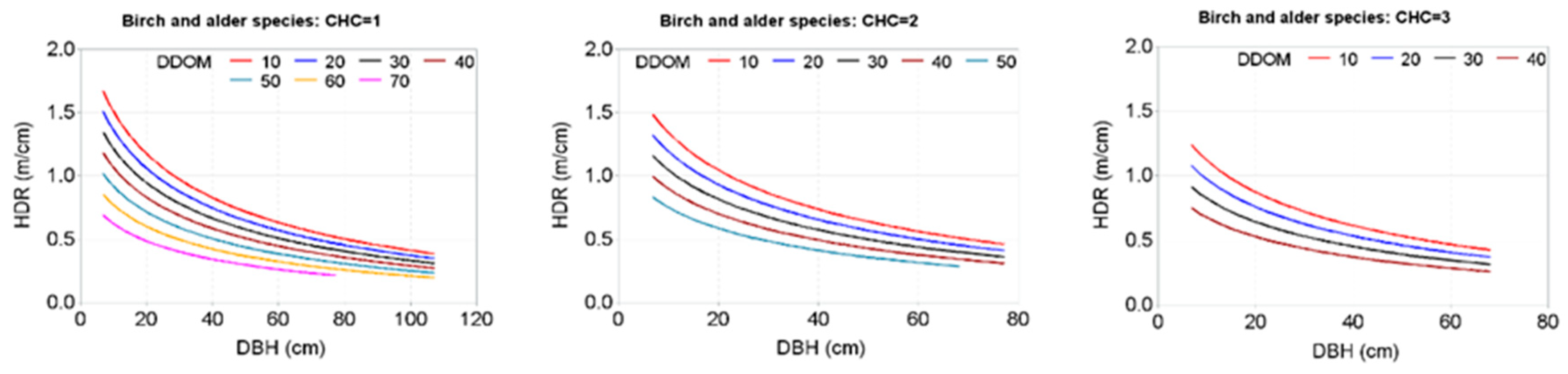

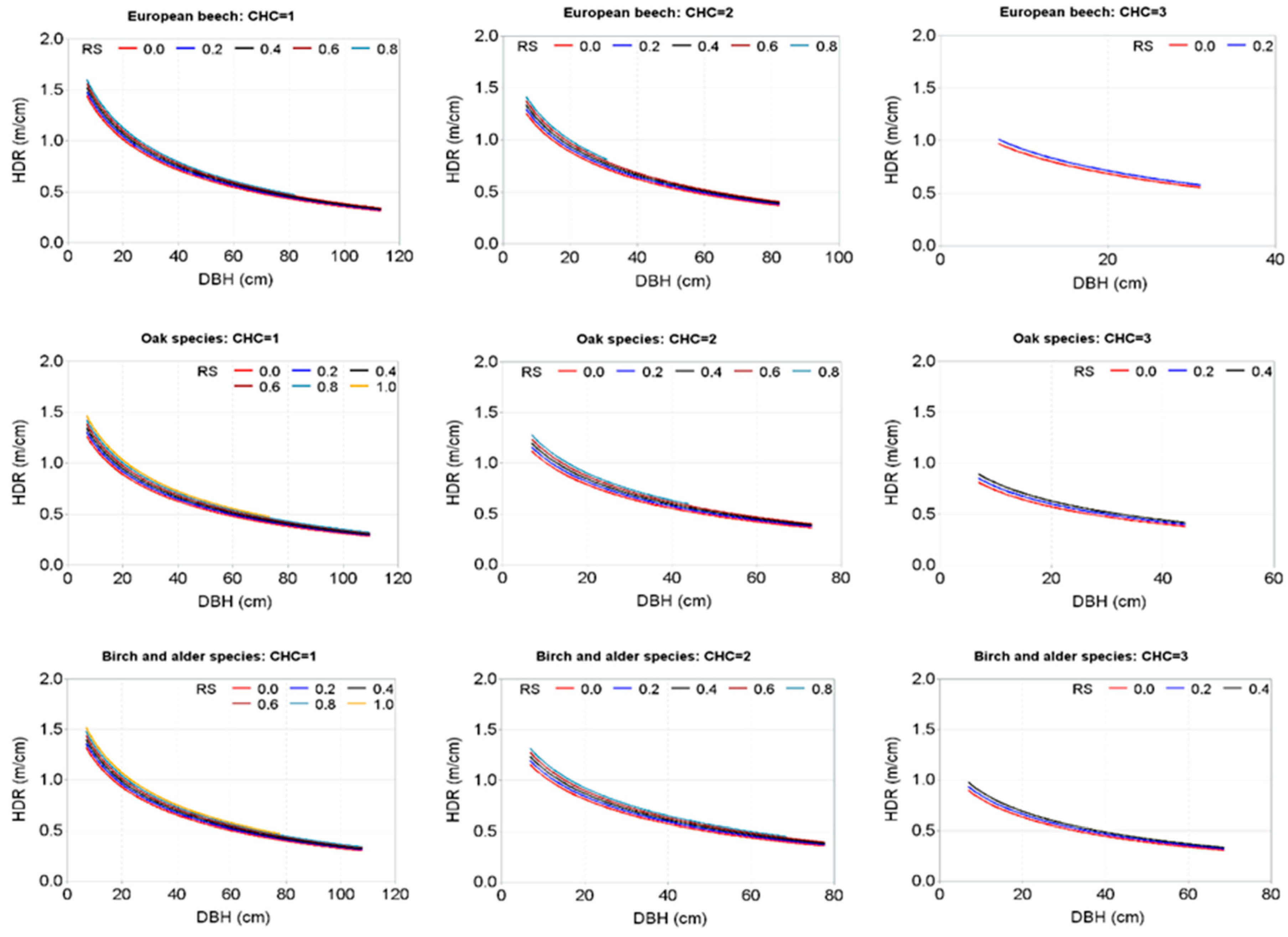
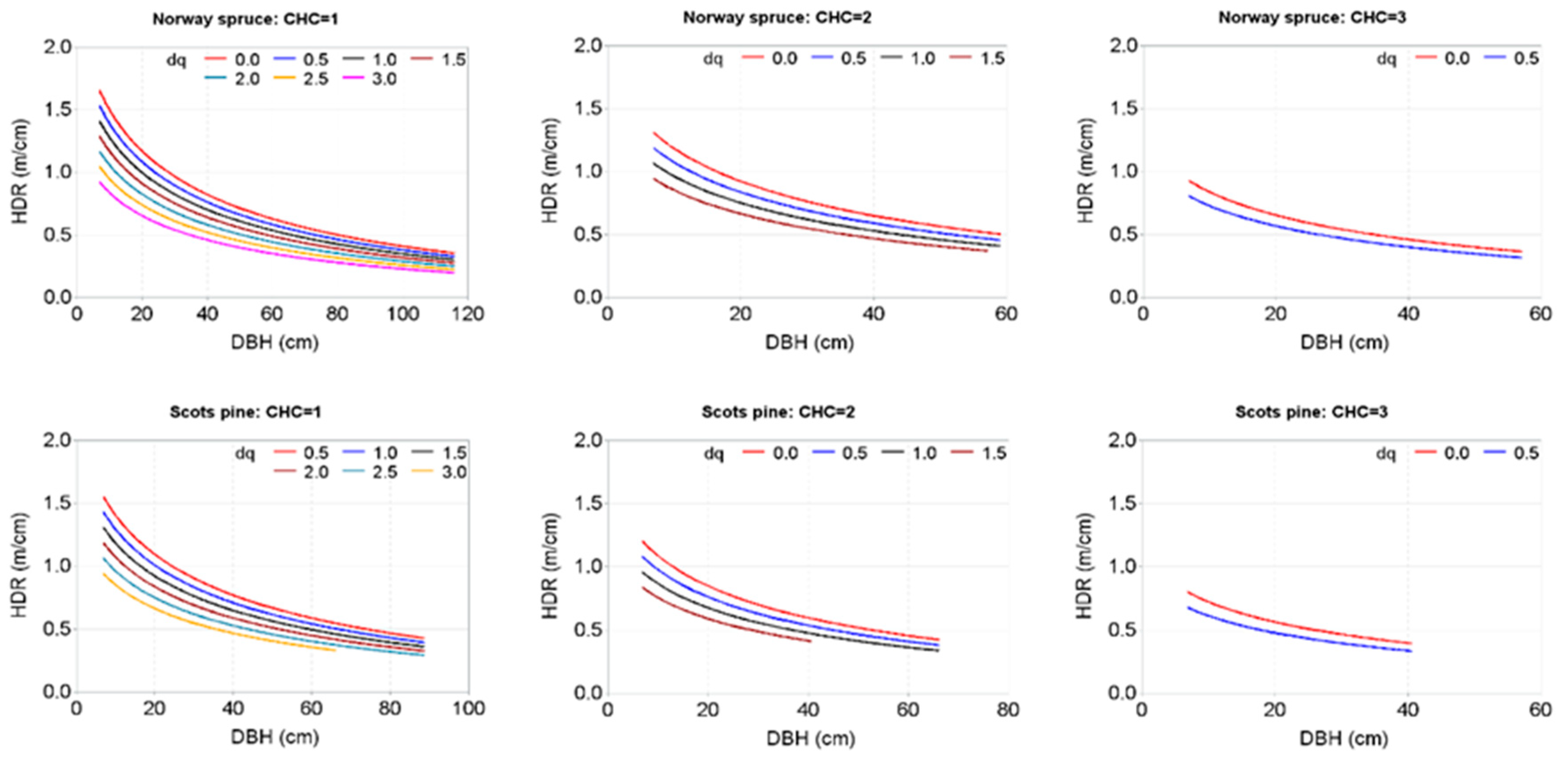
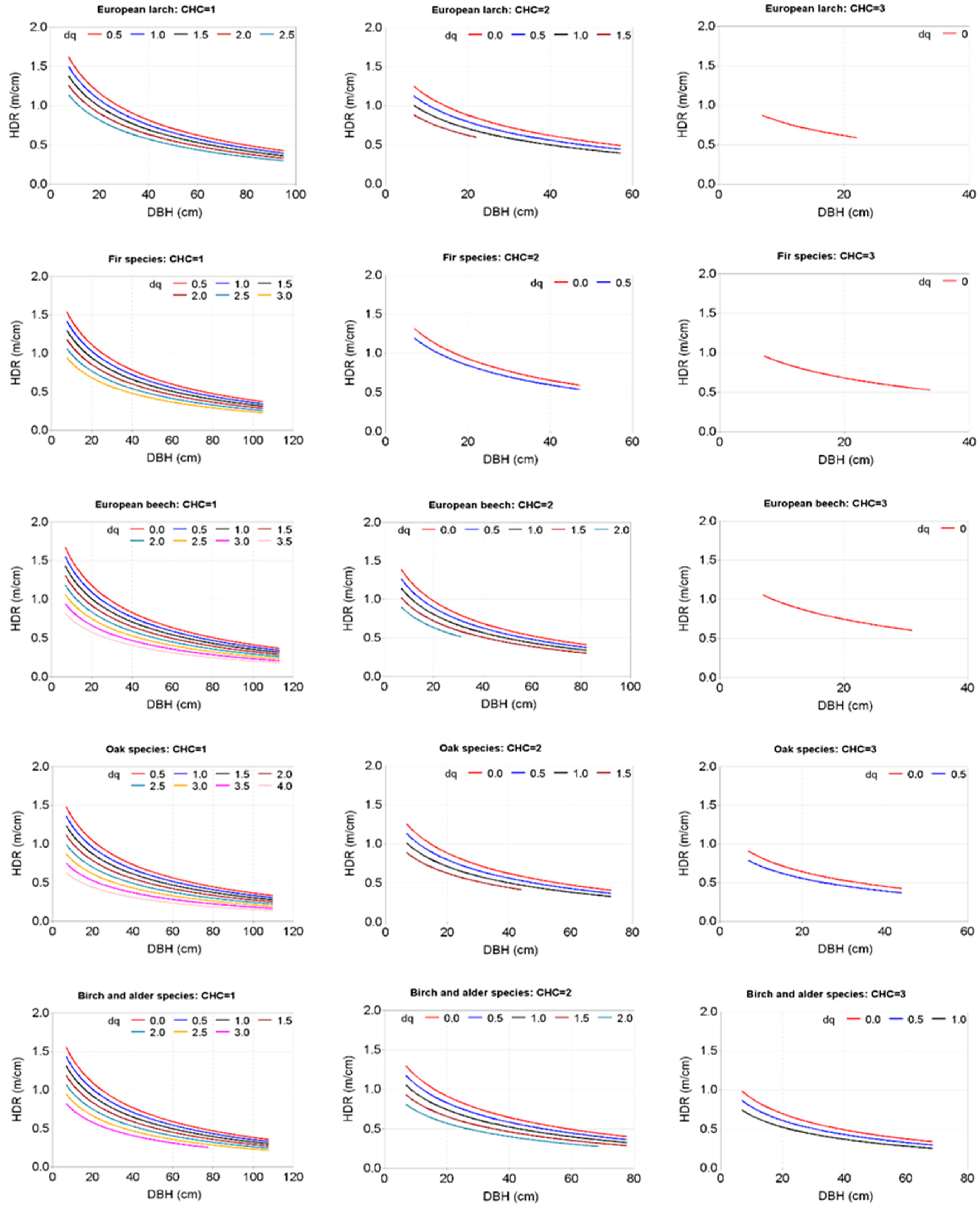
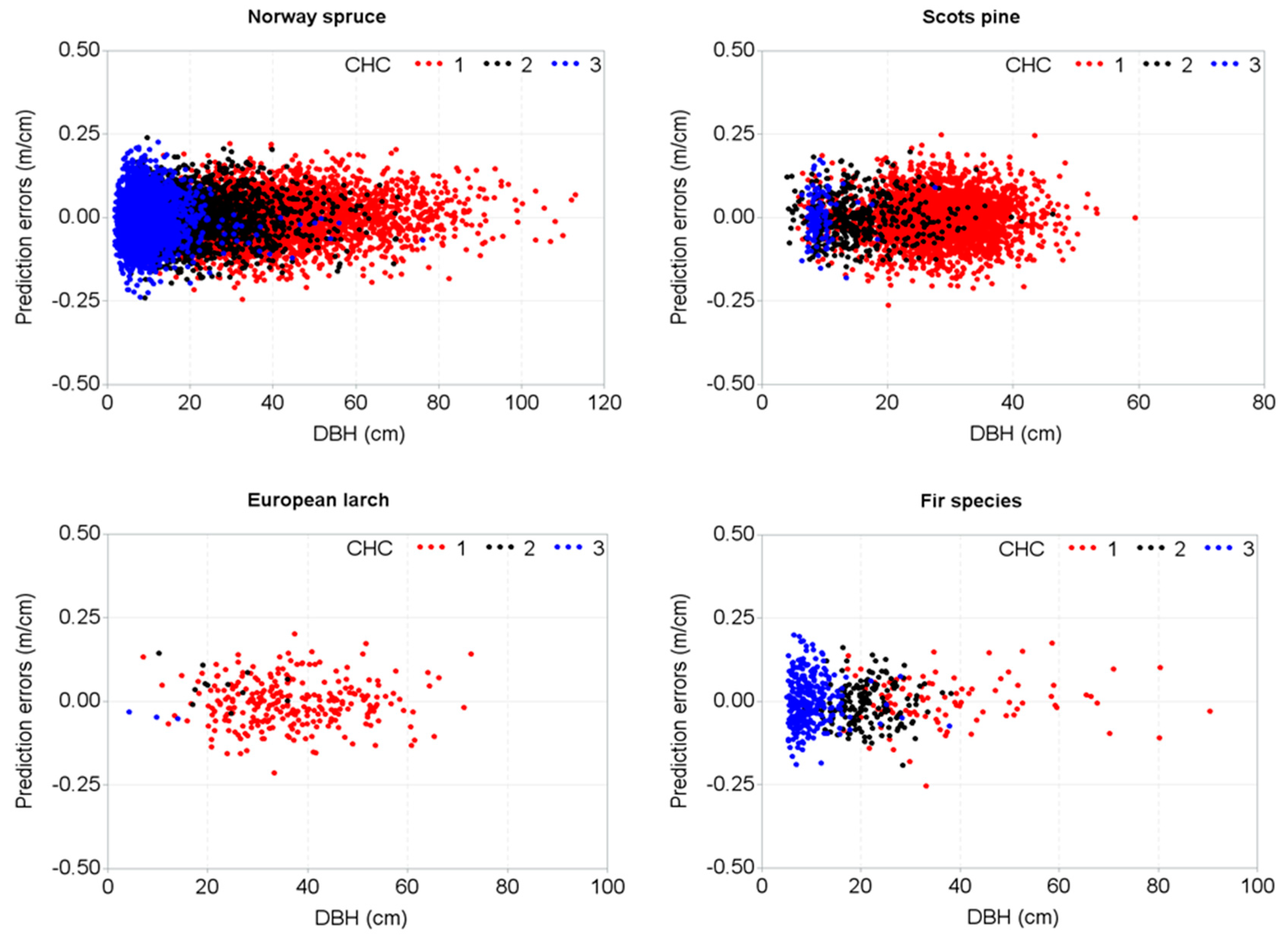
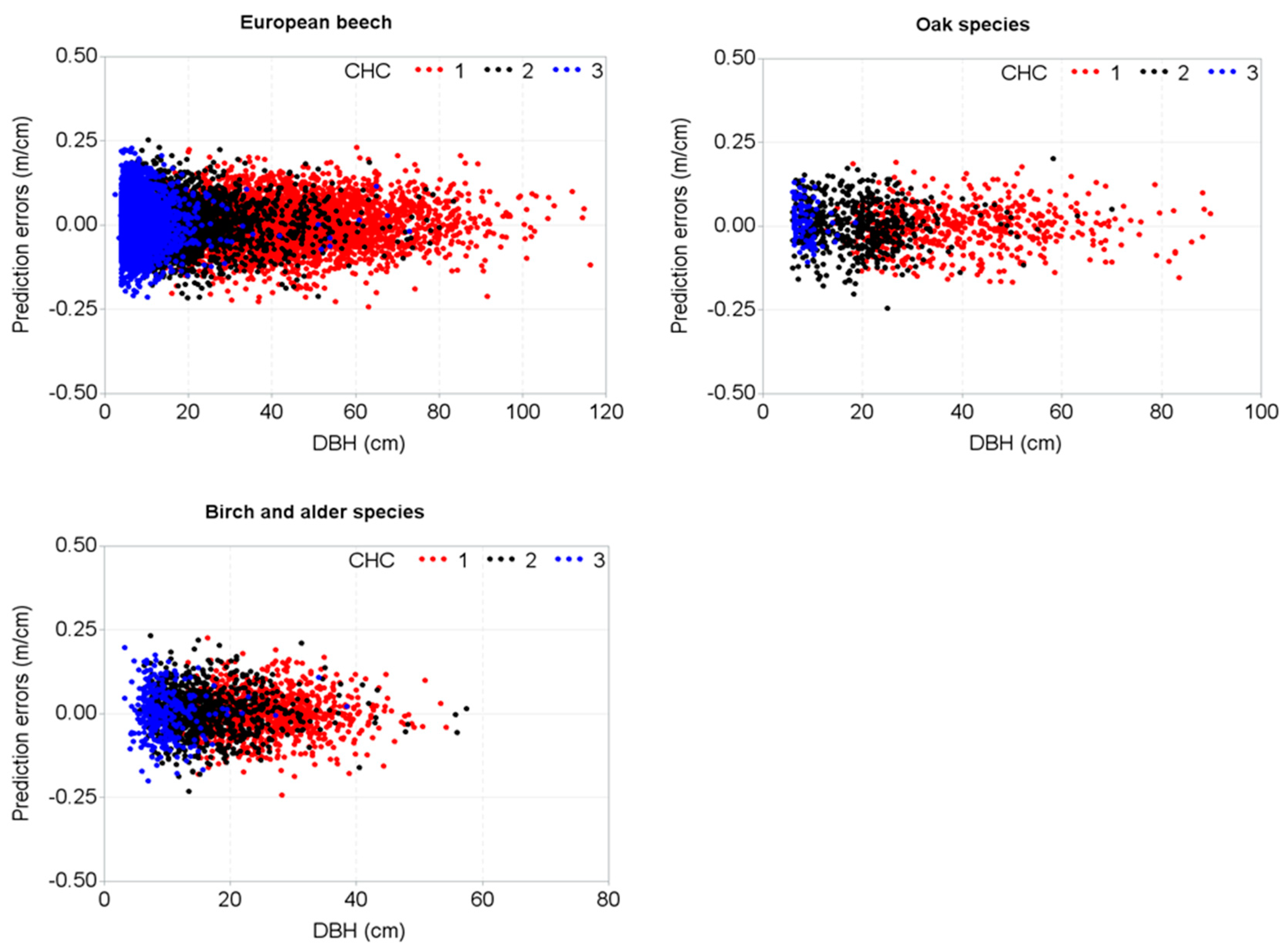
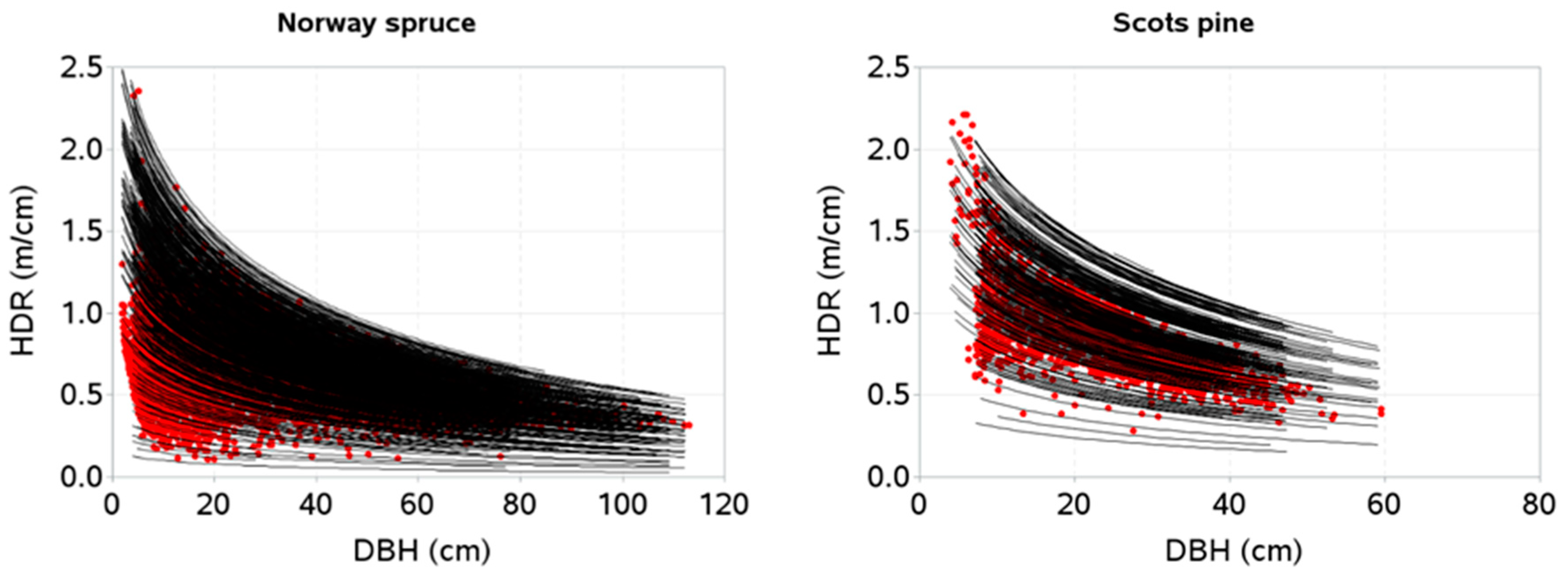

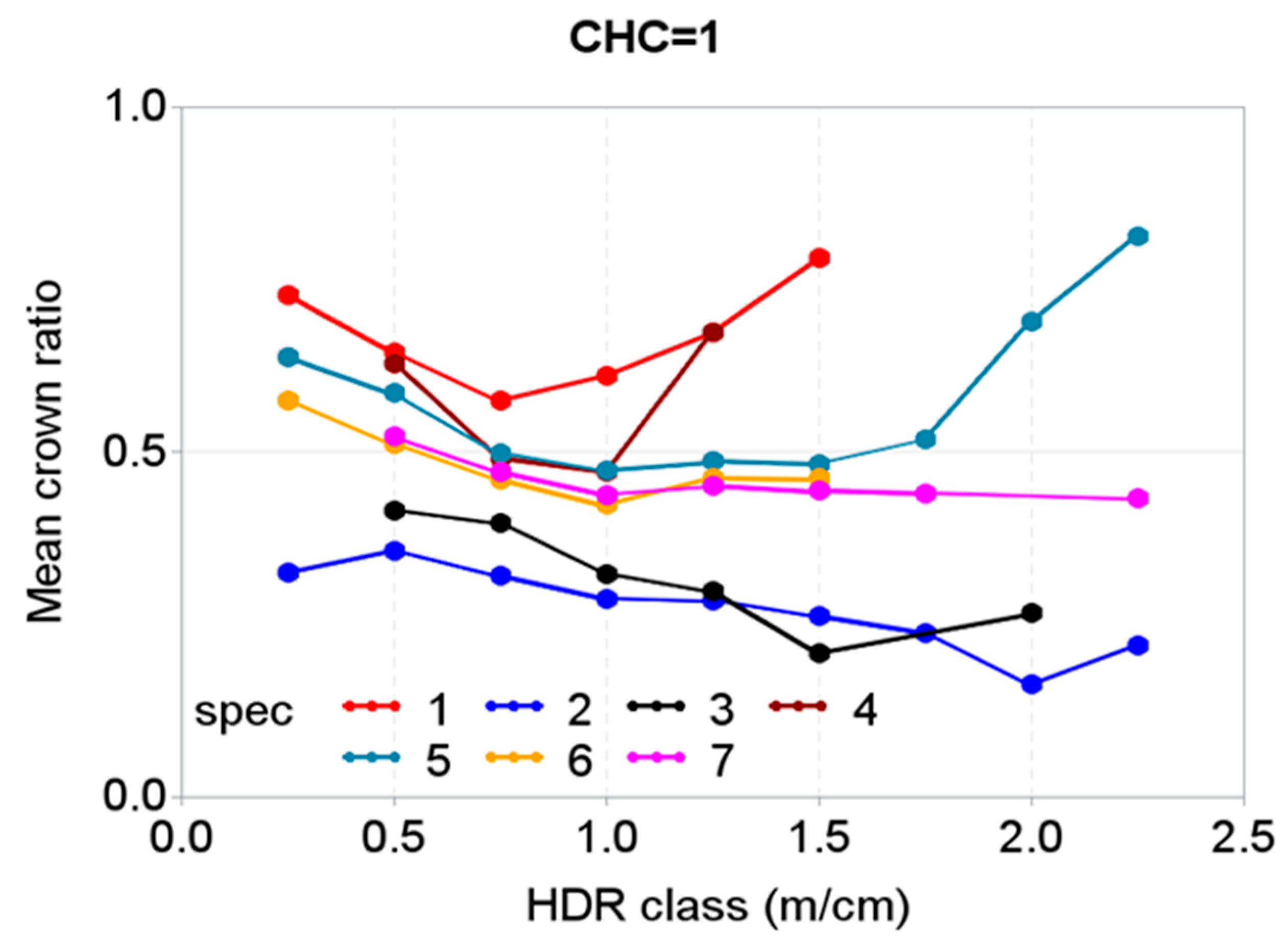
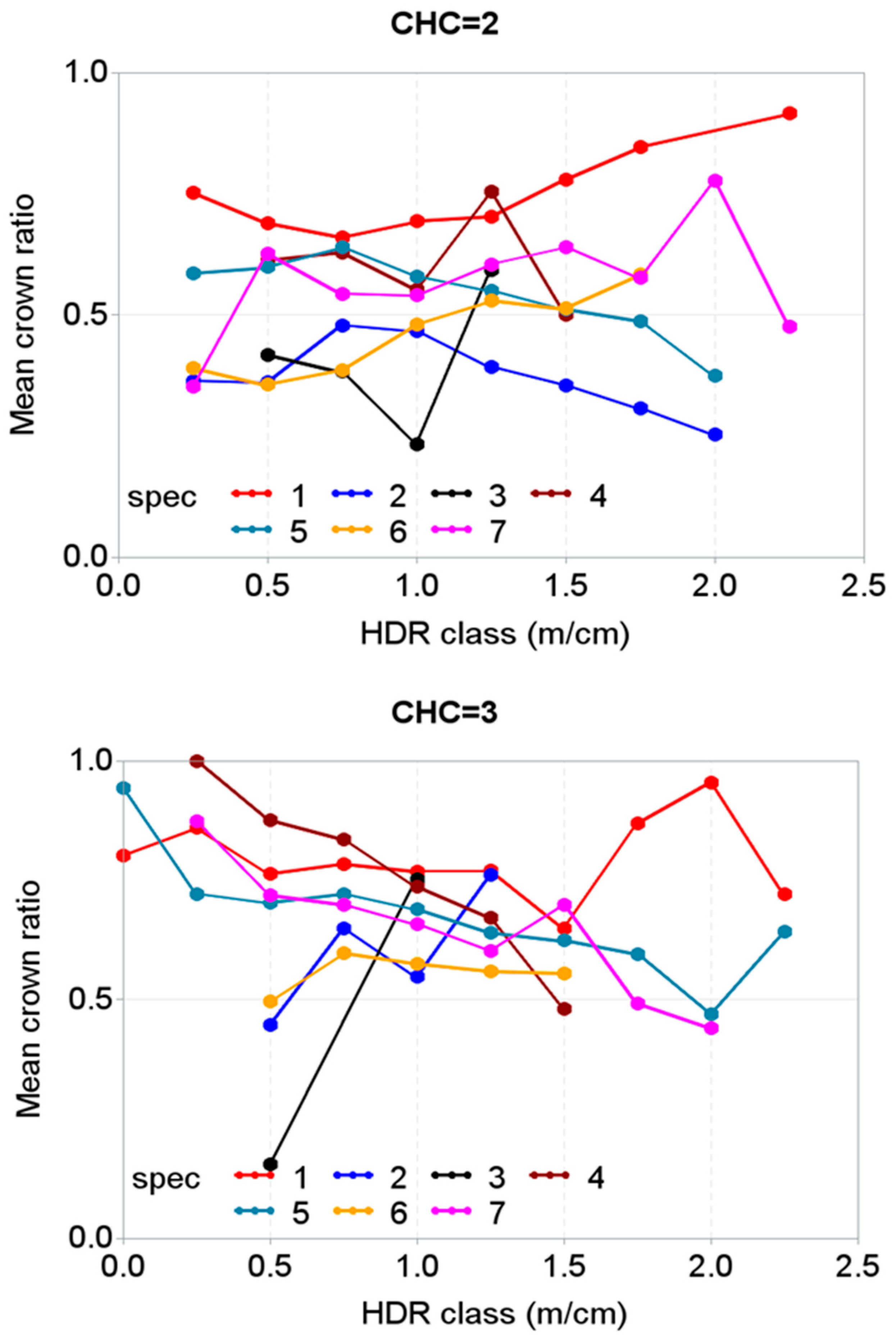
| Variables | Statistics (Mean ± Standard Deviation (Range)) | |
|---|---|---|
| Training Data | Validation Data | |
| Number of sample plots | 13,875 | 220 |
| Number of HDR sample trees | 348,980 | 25,146 |
| Number of HDR sample trees per sample plot | 36.5 ± 15.9 (4–90) | 232.3 ± 167.8 (8–664) |
| Number of stems (N ha−1) | 1514 ± 671 (40–5460) | 940 ± 711 (32–4700) |
| Stand basal area (BA, m2 ha−1) | 38.3 ± 13.5 (0.07–85.4) | 41.3 ± 14.4 (0.1–81.1) |
| BA of trees lager than a subject tree (BAL, m2 ha−1) | 28.5 ± 14.4 (0–83.3) | 32.2 ± 17.6 (0–79.5) |
| Quadratic mean DBH per sample plot (QMD, cm) | 27.3 ± 6.9 (8.7–84.2) | 28.6 ± 10.3 (9.6–87.3) |
| DBH-to-QMD ratio (dq) | 0.95 ± 0.31 (0.13–4.5) | 0.86 ± 0.52 (0.04–7) |
| Arithmetic mean DBH per sample plot (AMD, cm) | 25.8 ± 6.6 (8.5–78.4) | 24.9 ± 10.6 (9.1–84.4) |
| Dominant height per sample plot (HDOM, m) | 23.2 ± 6.2 (4.4–42.4) | 27.5 ± 6.9 (8–42.8) |
| Dominant diameter (DDOM, cm) | 31.5 ± 8.1 (8.6–78.4) | 49.7 ± 14.2 (13.3–84.4) |
| Total height (H, m) | 21.1 ± 7.1 (1.5–54.3) | 17.2 ± 9.3 (1.4–50.6) |
| Diameter at breast height (DBH, cm) | 26.4 ± 11.6 (7–117.3) | 25.2 ± 17.4 (2–118.1) |
| Height-to-DBH ratio (HDR, m cm−1) | 0.85 ± 0.19 (0.08–2.15) | 0.81 ± 0.28 (0.11–2.3) |
| Estimate | Standard Error | t-Value | Pr > |t| | |
|---|---|---|---|---|
| Fixed | ||||
| α1 | −0.4005 | 0.001765 | −226.98 | <0.0001 |
| α2 | −1.0526 | 0.004407 | −238.81 | <0.0001 |
| α3 | 0.7998 | 0.004939 | 161.95 | <0.0001 |
| α4 | 0.4568 | 0.002249 | 203.06 | <0.0001 |
| α5 | −0.02188 | 0.000223 | −97.98 | <0.0001 |
| α6 | 0.1236 | 0.01565 | 7.90 | <0.0001 |
| α7 | −0.4599 | 0.002771 | −165.97 | <0.0001 |
| α8 | 0.01049 | 0.001457 | 7.20 | <0.0001 |
| α9 | 0.07762 | 0.002047 | 37.91 | <0.0001 |
| α10 | −0.04291 | 0.003544 | −12.11 | <0.0001 |
| α11 | 0.01252 | 0.002087 | 6.00 | <0.0001 |
| α12 | −0.04845 | 0.002019 | −23.99 | <0.0001 |
| α13 | 0.04806 | 0.001804 | 26.65 | <0.0001 |
| b2 | 0.1823 | 0.000747 | 244.09 | <0.0001 |
| Variance | ||||
| σ2ui | 0.01109 | |||
| σ2 | 0.006923 | |||
| Fit statistics | ||||
| RMSE | 0.0923 | |||
| R2adj | 0.7863 | |||
| AIC | −729778 |
| Species | RMSE | R2 |
|---|---|---|
| Norway spruce | 0.0673 | 0.8922 |
| Scots pine | 0.0657 | 0.9039 |
| European larch | 0.0667 | 0.8821 |
| Fir species | 0.0654 | 0.8574 |
| European beech | 0.0676 | 0.9605 |
| Oak species | 0.0681 | 0.9176 |
| Birch and alder species | 0.0668 | 0.9328 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, R.P.; Vacek, Z.; Vacek, S.; Kučera, M. A Nonlinear Mixed-Effects Height-to-Diameter Ratio Model for Several Tree Species Based on Czech National Forest Inventory Data. Forests 2019, 10, 70. https://doi.org/10.3390/f10010070
Sharma RP, Vacek Z, Vacek S, Kučera M. A Nonlinear Mixed-Effects Height-to-Diameter Ratio Model for Several Tree Species Based on Czech National Forest Inventory Data. Forests. 2019; 10(1):70. https://doi.org/10.3390/f10010070
Chicago/Turabian StyleSharma, Ram P., Zdeněk Vacek, Stanislav Vacek, and Miloš Kučera. 2019. "A Nonlinear Mixed-Effects Height-to-Diameter Ratio Model for Several Tree Species Based on Czech National Forest Inventory Data" Forests 10, no. 1: 70. https://doi.org/10.3390/f10010070
APA StyleSharma, R. P., Vacek, Z., Vacek, S., & Kučera, M. (2019). A Nonlinear Mixed-Effects Height-to-Diameter Ratio Model for Several Tree Species Based on Czech National Forest Inventory Data. Forests, 10(1), 70. https://doi.org/10.3390/f10010070






