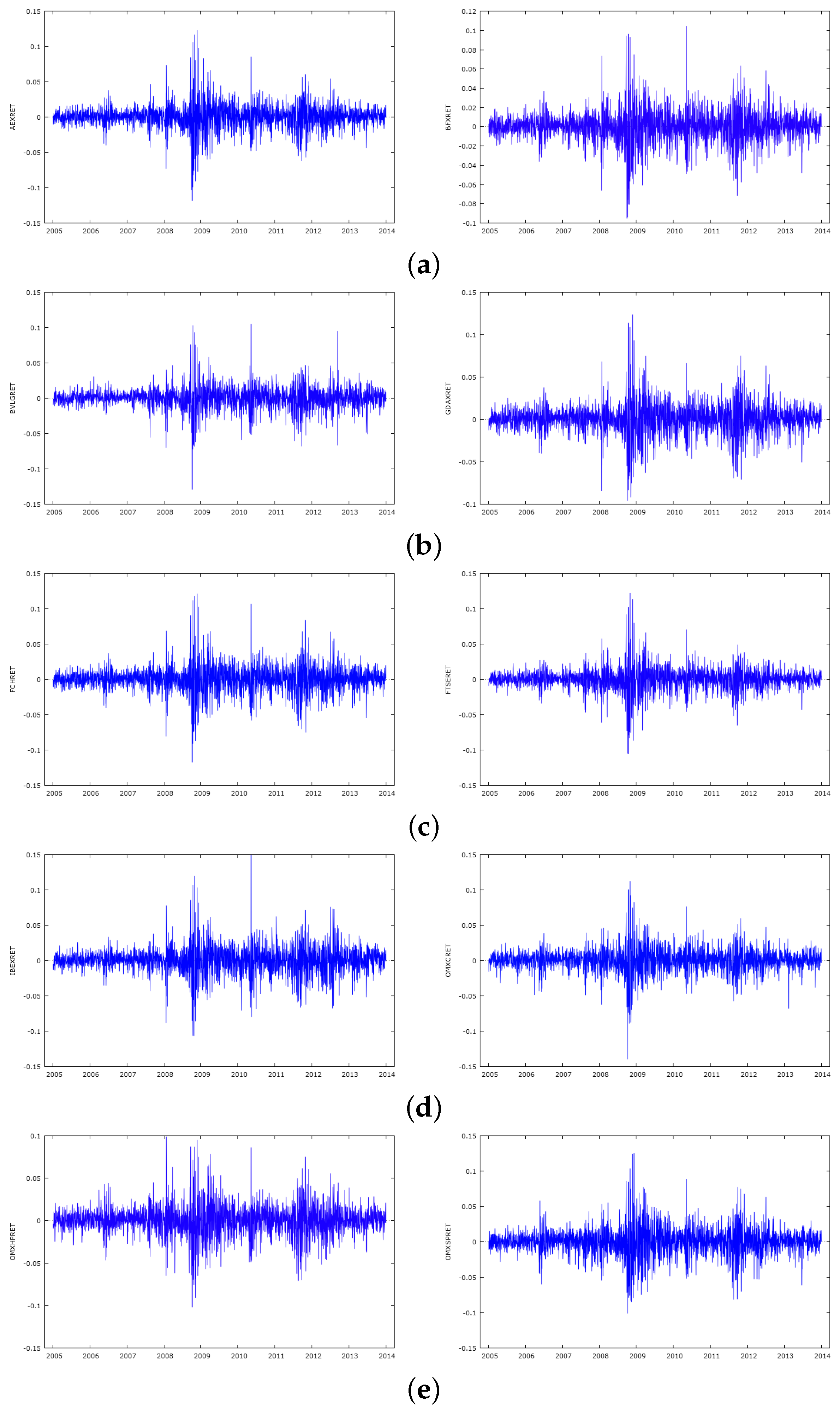
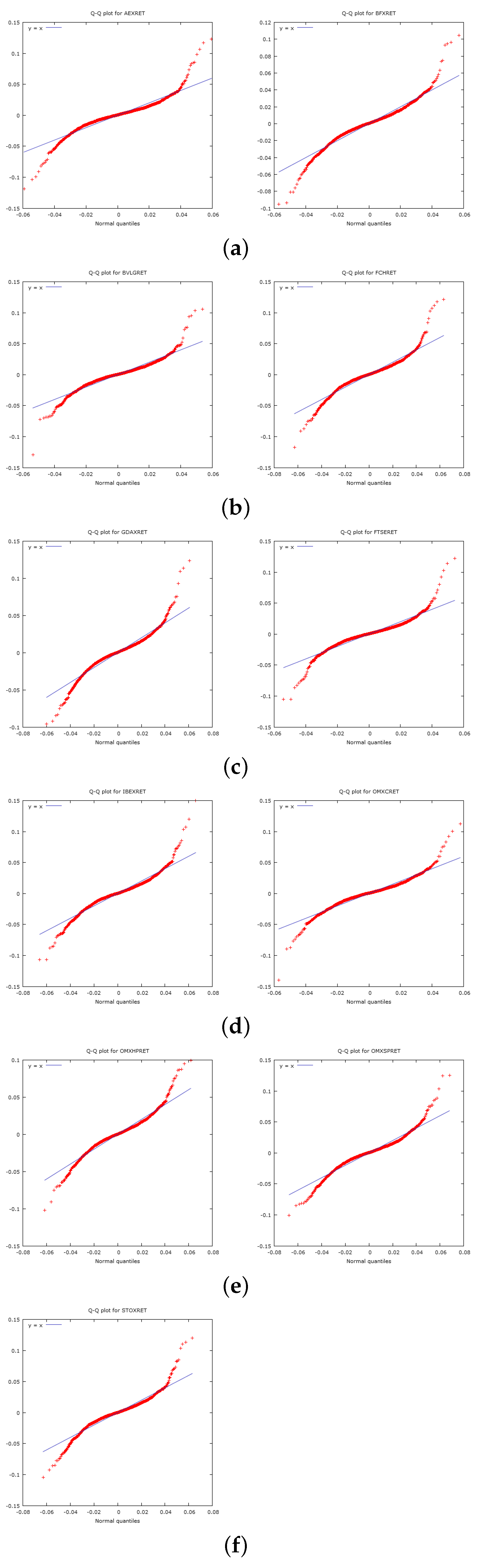
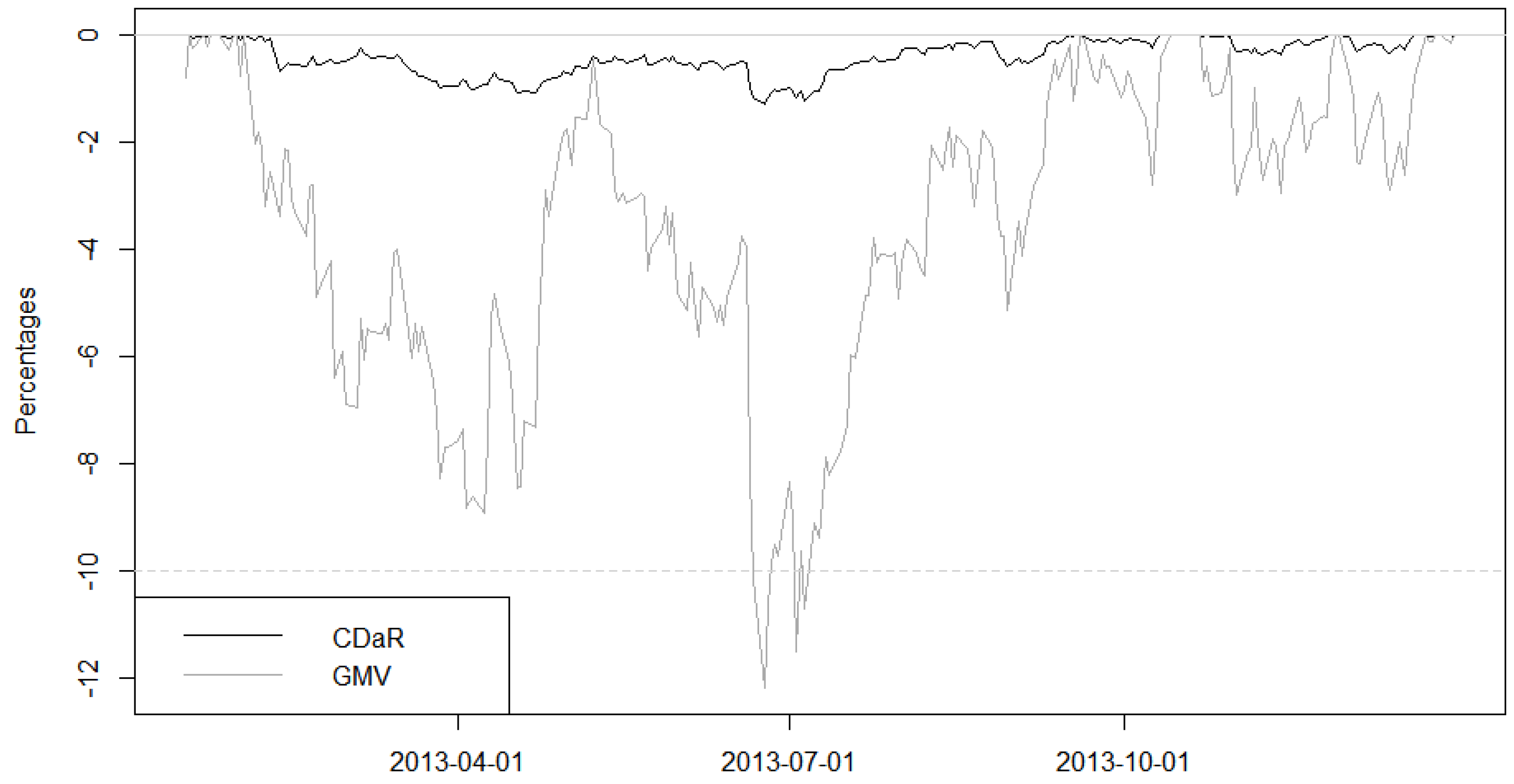
We proceed by adopting a variety of portfolio selection approaches and adopt a naive portfolio benchmark with 1/
N weights as a comparator. This approach was also used by DeMiguel
et al. [
23], in an out-of-sample analysis, of the mean-variance portfolio selection criteria, employing U.S. data sets, plus a variety of adjustments for estimation risk. They concluded that there are still “many miles to go” before the gains promised by portfolio optimisation techniques can be realised out of sample.
Our focus is broader than theirs, in that we employ a variety of portfolio optimisation techniques that go well beyond mean-variance optimisation. We contrast naive diversification, with mean-variance analysis, plus other portfolio optimisation techniques, such as the optimisation of conditional value at risk (CVaR), and other techniques, such as various draw-down strategies, and our analysis is conducted across the major European equity markets.
2.2. Markowitz Mean-Variance Analysis
Markowitz [
1] founded modern mathematical finance and ushered in formal portfolio analysis in one giant step with his introduction of the mean-variance model of the risk-return relationship. Variance is an appropriate risk-measure if either the investor’s utility set is quadratic or the return series considered are multivariate normal.
The Markowitz [
1] approach can be presented as the following non-linear-programming problem.
In the above formulation, ω are the portfolio weights for the universe of the assets available, are the number of periods considered for the returns r and for , which is the forecast return. The optimisation involves minimizing the portfolio variance subject to the portfolio forecast return being set to a level C. A full investment constraint and positive constraints on the weights are included, effectively ruling out short sales. In our subsequent analyses, we apply mean-variance optimisation with both a positive weight constraint and with an upper limit on the weight of any one security being less than 0.4% or 40% of the chosen portfolio.
Jagganathan and Ma [
24] demonstrate that the placement of a short-sale constraint on the minimum variance portfolio is equivalent to shrinking the elements of the covariance matrix. For this reason, we do not make any other adjustments for estimation risk. See, for example, the discussions in Best and Grauer [
25], Chan, Karceski and Lakonishok [
26] and Ledoit and Wolf [
27].
2.3. Optimising Conditional Value at Risk
Uryasev and Rockafellar [
28] in a series of papers have advocated CVaR as a useful risk metric. Pflug [
29] proved that CVaR is a coherent risk measure with a number of attractive properties, such as convexity and monotonicity, among other desirable characteristics. A number of papers apply CVaR to portfolio optimization problems; see, for example, Rockafeller and Uryasev [
30], Andersson
et al. [
31], Alexander, Coleman and Li [
32], Alexander and Baptista [
33] and Rockafellar
et al. [
19].
The conditional value at risk of
X at level
is defined by:
which can also be expressed as:
Pffaf ([
34] p. 223) recapitulates Uryasev [
35], noting that the following risk measures are needed in order to define CVaR:
, the α quantile of a loss distribution;
, the expected losses strictly exceeding VaR (i.e., mean excess loss or expected shortfall);
, the expected losses that are weakly exceeding VaR, i.e., losses that are equal to or exceed VaR.
The CVaR is then defined as a weighted average between VaR and
:
where the weight
is given by
and
denotes the probability that losses do not exceed or are equal to VaR for a given confidence level.
Rockafellar and Uryasev ([
36] p. 22) further elaborate on some of these issues in their discussion of the ‘fundamental risk quadrangle’, and suggest a way round the issue of the non-elicitability of CVaR by utilising quantile regression, as pioneered by Koenker and Basset [
37]. Fissler and Ziegel [
38] further concur, in a discussion of higher order elicitability and Osbond’s principle, and again mention quantile and expectile regression. They demonstrate that the pair (value at risk, expected shortfall) is elicitable, subject to mild regularity assumptions, which involve the relevant distributions consisting of absolutely continuous distributions with unique quantiles. This does not seem unreasonable in the case of financial return distributions.
In terms of portfolio selection, CVaR can be represented as a non-linear programming minimisation problem with an objective function given as:
where
υ is the
α-quantile of the distribution. In the discrete case, this was shown by Rockefellar and Uryasev [
28] to be capable of being represented by using auxiliary variables in the linear programming formulation below:
where
υ represents the VaR at the
α coverage rate and
the deviations below the VaR.
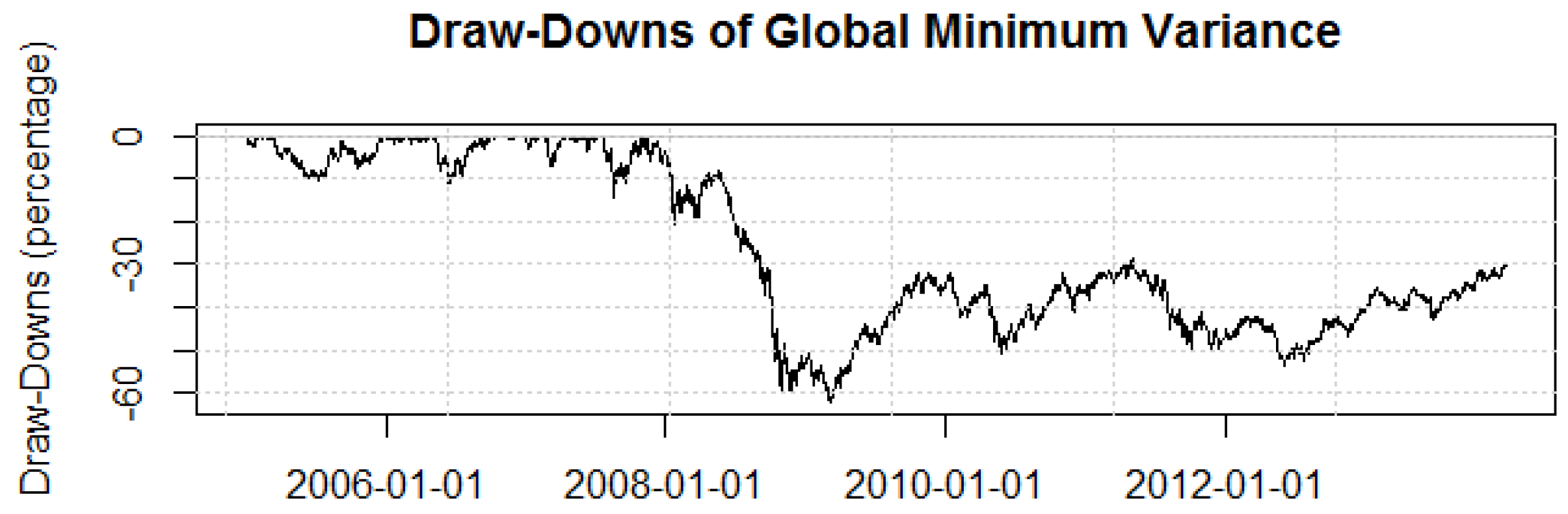
2.4. Optimal Draw-Down Portfolios
Chekhlov
et al. [
39,
40,
41] considered the optimization of portfolios with respect to the portfolio’s draw-down. The conditional draw-down (CDD) measure includes the maximum draw-down (MaxDD) and average draw-down (AvDD) as its limiting cases. The CDD family of risk functional measures is similar to CVaR. Chekhlov
et al. [
41] suggest that portfolio managers would like to avoid large draw-downs and/or extended draw-downs, as this may lead to a loss of mandate or withdrawal of business.
The analysis can be developed as follows; let a portfolio be optimised over some time interval
, and let
be the portfolio value at some moment in time
. The portfolio draw-down is defined as:
If we think in terms of the portfolio’s constituent assets and write
as the un-compounded portfolio value at time
t, with
ω the portfolio weights for the
N constituent assets and write
for the cumulated returns, the draw-down can be written as:
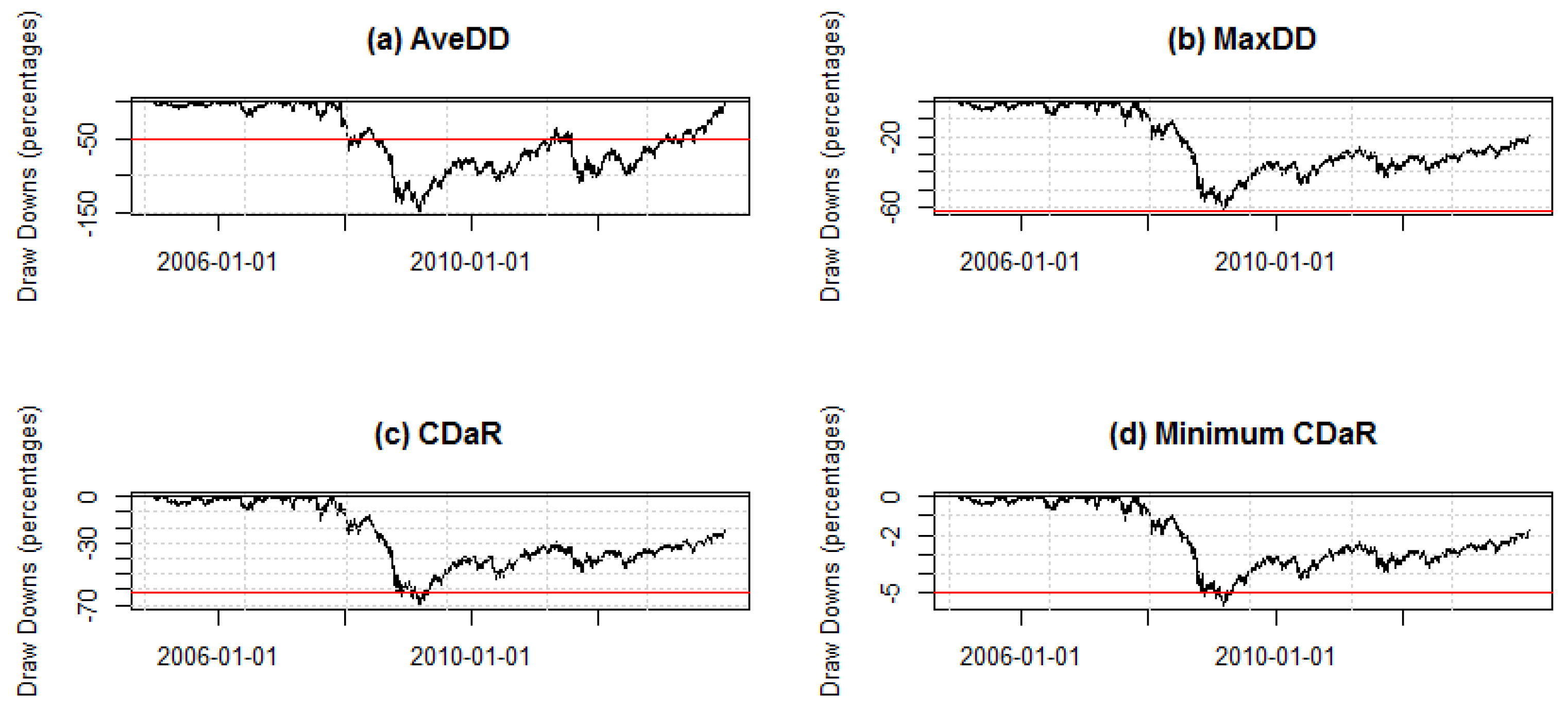
This definition can be converted into the three previously-mentioned functional risk measures; MaxDD, AvDD and conditional draw-down at risk (CDaR). CDaR is dependent on the chosen confidence level
α in the same way that CVaR is. CDaR can be defined as:
where
ς is the threshold value for draw-downs so that only
observations exceed this value. The limiting cases of this family of risk functions are MaxDD and the AvDD. In the case that
, CDaR approaches the maximum draw-down,
. The AvDD results from the case in which
. That is,
.
These risk functionals can be used in terms of the optimization of a portfolio’s draw-down and implemented as inequality constraints for a fixed share of the wealth at risk.
The goal of maximizing the average annualised portfolio return with respect to limiting the maximum draw-down can be written:
where
u denotes a
vector of slack variables in the program formulation, in effect the maximum portfolio values up to time period
k with
.
We include these three approaches to portfolio optimisation, CDaR, MaxDD and AvDD, in our portfolio analyses. We use programs from the R library to conduct our analyses, in particular, the packages fPortfolio, FRAPO and PerformanceAnalytics. We also modify R code from Pfaff [
34] to undertake the various draw-down optimisations.
The above approaches to portfolio analysis can be characterised under the general heading of operational research methods featuring applications of multi-criteria optimization methods to portfolio selection problems. Surveys of various aspects of this literature are provided by Sawik [
42,
43,
44].
The application of coherent risk measures has generated a large literature, which attempts to extend their application to a dynamic context in a variety of different ways. For applications of these approaches see the early work by Riedel [
45] or the more recent survey by Acciaio and Penner [
46]. This area of the literature is still being developed and is based on the previously-mentioned coherent risk measures of Artzner
et al. [
47]. Their original approach, based on the capital requirements framework, is the framework adopted in our paper. Delbaen [
48] and Follmer and Schied [
49] provide a comprehensive presentation of the theory of static coherent and convex risk measures. The most recent comprehensive application of this approach to portfolio selection is provided by Rujeerapaiboon
et al. [
50].
Platen and Heath [
51] embark on an initially different approach in a probabilistic Markovian framework in their benchmark approach to quantitative finance. A central component of these approaches is the use of the ‘growth optimal portfolio’ (GOP). The GOP is the portfolio that has the maximal expected growth rate over any time horizon. This strictly positive portfolio almost surely outperforms any other strictly positive portfolio over a sufficiently long time horizon, as first noted by Kelly [
52].
Although Kelly’s strategy promise of doing better than any other strategy seems compelling, some economists have argued strenuously against it, mainly because an individual’s specific investing constraints override the desire for optimal growth rate. The conventional alternative is utility theory, which says bets should be sized to maximize the expected utility of the outcome (to an individual with logarithmic utility, the Kelly bet maximizes utility, so there is no conflict in this case). The Kelly approach assumes the only important thing is long-term wealth. Most people also care about the path to get there. Kelly betting leads to highly volatile short-term outcomes, which many people find unpleasant, even if they believe they will do well in the end. Samuelson [
53,
54], in particular, was a long time critique of the Kelly criterion.