On a Discrete Interaction Risk Model with Delayed Claims
Abstract
:1. Introduction
2. The Generating Function of the Expected Discounted Penalty Function
3. Recursive Equations for
4. Ruin-Related Quantities
4.1. The Evaluation of
| (0, 1) | (0, 0) | 0.2411265 | 0.1440916 | 0.1242079 | 0.0978323 | 0.0697250 | 0.0443761 |
| (0.2, 0.3) | 0.2016123 | 0.1048111 | 0.0925975 | 0.0735956 | 0.0524333 | 0.0333685 | |
| (0.7, 0.6) | 0.1760715 | 0.0747127 | 0.0679853 | 0.0545247 | 0.0388603 | 0.0247297 | |
| (1, 1) | 0.1805556 | 0.0702160 | 0.0649220 | 0.0524670 | 0.0375076 | 0.0238703 | |
| (2, 2) | (0, 0) | 0.0172947 | 0.0217721 | 0.0258049 | 0.0181552 | 0.0127906 | 0.0081399 |
| (0.2, 0.3) | 0.0220675 | 0.0285528 | 0.0344494 | 0.0216139 | 0.0153322 | 0.0097567 | |
| (0.7, 0.6) | 0.0255570 | 0.0342691 | 0.0422659 | 0.0244623 | 0.0174832 | 0.0111258 | |
| (1, 1) | 0.0263873 | 0.0366490 | 0.0461370 | 0.0257016 | 0.0184810 | 0.0117674 | |
| (0, 5) | (0, 0) | 0.0067270 | 0.0052610 | 0.0045711 | 0.0035766 | 0.0025444 | 0.0016194 |
| (0.2, 0.3) | 0.0098012 | 0.0060842 | 0.0053607 | 0.0042411 | 0.0030194 | 0.0019216 | |
| (0.7, 0.6) | 0.0121226 | 0.0058755 | 0.0053210 | 0.0042648 | 0.0030384 | 0.0019335 | |
| (1, 1) | 0.0127322 | 0.0049514 | 0.0045781 | 0.0036998 | 0.0026449 | 0.0016832 | |
| (4, 2) | (0, 0) | 0.0025660 | 0.0032303 | 0.0038286 | 0.0048460 | 0.0032192 | 0.0020417 |
| (0.2, 0.3) | 0.0042676 | 0.0055218 | 0.0066621 | 0.0085932 | 0.0052395 | 0.0033295 | |
| (0.7, 0.6) | 0.0055996 | 0.0075085 | 0.0092606 | 0.0122356 | 0.0070499 | 0.0044883 | |
| (1, 1) | 0.0059314 | 0.0082381 | 0.0103709 | 0.0140154 | 0.0077988 | 0.0049779 | |
| (3, 5) | (0, 0) | 0.0003576 | 0.0004502 | 0.0005336 | 0.0005255 | 0.0003656 | 0.0002324 |
| (0.2, 0.3) | 0.0007714 | 0.0009981 | 0.0012042 | 0.0010776 | 0.0007582 | 0.0004823 | |
| (0.7, 0.6) | 0.0011091 | 0.0014871 | 0.0018341 | 0.0015225 | 0.0010926 | 0.0006952 | |
| (1, 1) | 0.0011517 | 0.0015995 | 0.0020136 | 0.0015696 | 0.0011413 | 0.0007273 | |
| (5, 3) | (0, 0) | 0.0003576 | 0.0004502 | 0.0005336 | 0.0006754 | 0.0005648 | 0.0003558 |
| (0.2, 0.3) | 0.0007714 | 0.0009981 | 0.0012042 | 0.0015533 | 0.0012039 | 0.0007628 | |
| (0.7, 0.6) | 0.0011091 | 0.0014871 | 0.0018341 | 0.0024234 | 0.0017872 | 0.0011391 | |
| (1, 1) | 0.0011517 | 0.0015995 | 0.0020136 | 0.0027213 | 0.0019283 | 0.0012343 | |
| (5, 5) | (0, 0) | 0.0000479 | 0.0000602 | 0.0000714 | 0.0000904 | 0.0000766 | 0.0000482 |
| (0.2, 0.3) | 0.0001319 | 0.0001707 | 0.0002060 | 0.0002657 | 0.0002090 | 0.0001323 | |
| (0.7, 0.6) | 0.0002010 | 0.0002696 | 0.0003325 | 0.0004393 | 0.0003288 | 0.0002095 | |
| (1, 1) | 0.0001973 | 0.0002740 | 0.0003449 | 0.0004661 | 0.0003303 | 0.0002114 |
4.2. The Evaluation of
- (i)
- For , it holds thatwith
- (ii)
- For , we have
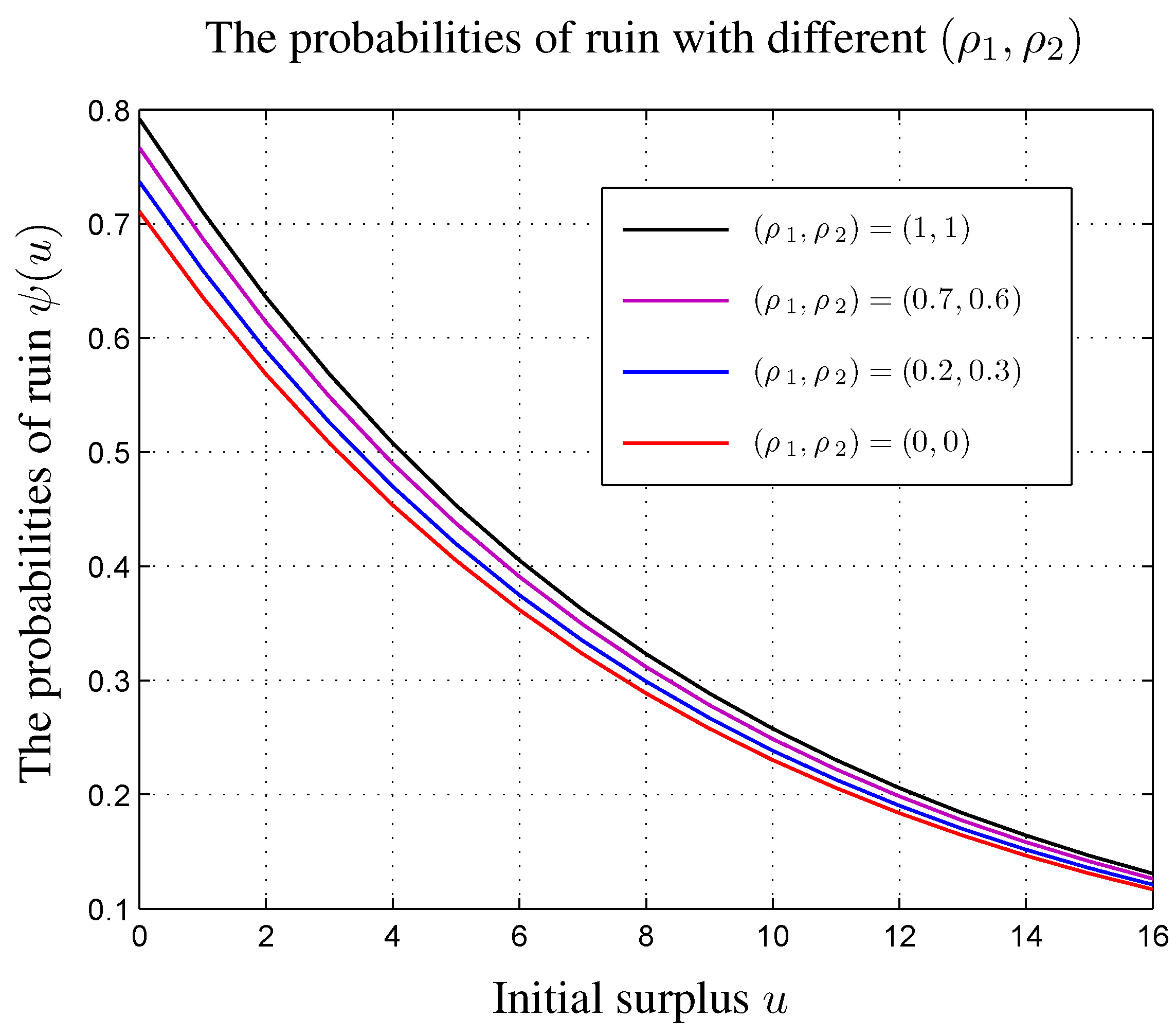
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- K.C. Yuen, and J. Guo. “Ruin probabilities for time-correlated claims in the compound binomial model.” Insur. Math. Econ. 29 (2001): 47–57. [Google Scholar] [CrossRef]
- H. Albrecher, and O. Boxma. “A ruin model with dependence between claim sizes and claim intervals.” Insur. Math. Econ. 35 (2004): 245–254. [Google Scholar] [CrossRef]
- E. Marceau. “On the discrete-time compound renewal risk model with dependence.” Insur. Math. Econ. 44 (2009): 245–259. [Google Scholar] [CrossRef]
- H. Cossette, E. Marceau, and F. Marri. “Analysis of ruin measures for the classical compound Poisson risk model with dependence.” Scand. Actuar. J. 2010 (2010): 221–245. [Google Scholar] [CrossRef]
- J.K. Woo. “A generalized penalty function for a class of discrete renewal processes.” Scand. Actuar. J. 2012 (2012): 130–152. [Google Scholar] [CrossRef]
- Z. Zhang, H. Yang, and H. Yang. “On a Sparre Andersen risk model with time-dependent claim sizes and jump-diffusion perturbation.” Methodol. Comput. Appl. Probab. 14 (2012): 973–995. [Google Scholar] [CrossRef]
- Y. Xiao, and J. Guo. “The compound binomial risk model with time-correlated claims.” Insur. Math. Econ. 41 (2007): 124–133. [Google Scholar] [CrossRef]
- Z. Bao, and H. Liu. “The compound binomial risk model with delayed claims and random income.” Math. Comput. Model. 55 (2012): 1315–1323. [Google Scholar] [CrossRef]
- X. Wu, and S. Li. “On a discrete time risk model with time-delayed claims and a constant dividend barrier.” Insur. Mark. Co. Anal. Actuar. Comput. 3 (2012): 50–57. [Google Scholar]
- R.S. Ambagaspitiya. “On the distribution of a sum of correlated aggregate claims.” Insur. Math. Econ. 23 (1998): 15–19. [Google Scholar] [CrossRef]
- R.S. Ambagaspitiya. “On the distributions of two classes of correlated aggregate claims.” Insur. Math. Econ. 24 (1999): 301–308. [Google Scholar] [CrossRef]
- H. Cossette, and E. Marceau. “The discrete-time risk model with correlated classes of business.” Insur. Math. Econ. 26 (2000): 133–149. [Google Scholar] [CrossRef]
- S. Li, and J. Garrido. “Ruin probabilities for two classes of risk processes.” Astin Bull. 35 (2005): 61–77. [Google Scholar] [CrossRef]
- S. Chadjiconstantinidis, and A.D. Papaioannou. “Analysis of the Gerber-Shiu function and dividend barrier problems for a risk process with two classes of claims.” Insur. Math. Econ. 45 (2009): 470–484. [Google Scholar] [CrossRef]
- L. Ji, and C. Zhang. “The Gerber-Shiu penalty functions for two classes of renewal risk processes.” J. Comput. Appl. Math. 233 (2010): 2575–2589. [Google Scholar] [CrossRef]
- X. Wu, and K.C. Yuen. “On an Interaction Risk Model with Delayed Claims.” In Proceedings of The 35th Astin Colloquium, Bergen, Norway, 6–9 June 2004; Volume 17.
- P. Brémaud. “An insensitivity property of Lundberg’s estimate for delayed claims.” J. Appl. Probab. 37 (2000): 914–917. [Google Scholar] [CrossRef]
- J. Trufin, H. Albrecher, and M. Denuit. “Ruin problems under IBNR dynamics.” Appl. Stoch. Models Bus. Ind. 27 (2011): 619–632. [Google Scholar] [CrossRef]
- A. Dassios, and H. Zhao. “A risk model with delayed claims.” J. Appl. Probab. 50 (2013): 686–702. [Google Scholar] [CrossRef]
- T. Rolski, H. Schmidli, V. Schmidt, and J.L. Teugels. Stochastic Processes for Insurance and Finance. Chichester, UK: Wiley, 1999, pp. 167–176. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Bao, Z. On a Discrete Interaction Risk Model with Delayed Claims. J. Risk Financial Manag. 2015, 8, 355-368. https://doi.org/10.3390/jrfm8040355
Liu H, Bao Z. On a Discrete Interaction Risk Model with Delayed Claims. Journal of Risk and Financial Management. 2015; 8(4):355-368. https://doi.org/10.3390/jrfm8040355
Chicago/Turabian StyleLiu, He, and Zhenhua Bao. 2015. "On a Discrete Interaction Risk Model with Delayed Claims" Journal of Risk and Financial Management 8, no. 4: 355-368. https://doi.org/10.3390/jrfm8040355
APA StyleLiu, H., & Bao, Z. (2015). On a Discrete Interaction Risk Model with Delayed Claims. Journal of Risk and Financial Management, 8(4), 355-368. https://doi.org/10.3390/jrfm8040355