1. Introduction
Since the beginning of the 1980s many countries all over the world have experienced financial crises with different degrees of severity. Savings and loans crises in the 1980s, the 1987 stock market crash, the Tequila crisis in 1994, the Asian crisis of 1997–1998, and finally the global financial crisis of 2008 all hit the entire world’s economies and financial markets. Among them, the recent financial crisis was agreed to be the worst financial crisis since the Great Depression, which resulted in the collapse of many large financial institutions.
Although many of these crises could be avoided, the world had to cope with these crises, which caused high inflation, rising leverage, large current account deficits, slowing global economy, and high unemployment rates, especially among the young people. It is noteworthy that the global financial system was exposed to different financial crises and financial distress repeatedly due to the fact that markets and policymakers again forgot the lessons of the past. Each time a financial crisis occurs, the financial system, which plays a critical role in the economy by channeling funds from those with surplus funds to those in need of funds, is adversely affected.
Asymmetric information is the major obstacle in front of the financial system to perform this job efficiently [
1]. The problems of moral hazard and adverse selection are inevitable if one party of a financial contract does not have the same information as the other part does. A financial crisis can be defined as a non-linear disruption to financial markets in which the asymmetric information problems of adverse selection and moral hazard become worse, so that the financial system is no longer able to channel funds to those who have productive investment opportunities [
2,
3]. This is mainly due to the reason that it would be much harder to distinguish them from potential borrowers, who do not have profitable investment opportunities. Consequently, a serious reduction in the amount of provided credits leads individuals and companies to minimize their spending, resulting in contraction of economic activity, which can be quite grievous for the society. Four factors increase asymmetric information problems which lead to financial crises: deterioration of financial sector balance sheets, increases in interest rates, increases in uncertainty, and deterioration of non-financial sector balance sheets as a result of changes in asset prices [
1].
Although asymmetric information on the recent global financial crisis is not the only factor that led to the crisis, it was effective on the spread of the crisis all over the world through the monetary policies of central banks of major developed countries and financial innovations. Thus, in order to prevent recurrence of financial crises, it is crucial to analyze the recent global crisis in terms of asymmetric information based on the following perspectives. First, the uncertainty in the level of asset prices and the asymmetric information caused the problem of liquidity in the markets. However, the initiation of the crisis could not be realized due to the problem of asymmetric information. Second, financial innovations since the beginning of the 2000s led to the problem of asymmetric information because investors purchased these instruments without having as much information as the creators of these instruments. Third, state guarantee is one of the main reasons of moral hazard due to the reason that the finance managers take excessive risks to gain high returns. They take excessive risks with other people’s money because they are aware that they will be assisted in case of a crisis by the government [
4]. Consequently, asymmetric information paved the way to the increase in the factors that led to the recent financial crisis through moral hazard and adverse selection.
While the world economy is still having a recovery period to eliminate the major damages caused by the recent financial crisis on the industrialized and the developing countries, it is crucial to learn from previous experiences provided by the past financial crises. Developing better quantitative theoretical models and creating better early warning systems to predict the potential financial crises in order to reduce the negative consequences of those crises have been a major field of interest among the researchers. However, researchers have not been quite successful at predicting the timing of crises [
5]. Additionally, many central banks used various early warning systems to observe the risks of banks. However, recurrence of crises in the last few decades such as the Asian crisis, the Russian crisis or the Brazilian bank crisis all indicate that it is not so easy to predict financial crises or bank crises prior to their occurrences [
6].
The rising interest of research activities in the field of artificial neural networks (ANNs) indicates that neural networks (NNs) have superior prediction and explanation capabilities as compared to many other statistical methods. Their ability to learn from experience is one of the major advantages of using NNs. ANNs have many areas of application in the field of finance and forecasting is one of these major fields of application. Forecasting has been generally conducted by the linear models, which are easy to develop and implement. However, linear models have several serious shortcomings that they have difficulties in capturing any non-linear relationships in the data [
7]. An important feature of NNs, different from traditional methods is their ability to classify data that are not linearly separable applications of ANNs, has increased considerably in many different fields in recent years due to their huge storage capacity and their superiority in learning and prediction [
8].
NNs have been developed from the field of artificial intelligence and brain modeling. The functioning of the NNs mimic the way human brain processes information. External and internal information, which flows through the network during the learning phase, determine the structure of the model [
6]. The most widely used NN model for economic forecasting is the multilayer perceptron (MLP) and back propagation. A MLP is a back propagation ANN model, which matches sets of input data into a set of appropriate output. To train the network, MLP uses a supervised learning technique called back propagation. A multilayer network trained with a back propagation algorithm is a commonly-preferred method by most NN aimed to solve the problem of forecasting. This is mainly because the processes are easy to understand and results are easy to interpret [
8].
NNs are learning systems which can model the relationship between the dependent and independent variables. In a neural network application, the two main subjects are the network structure and the learning algorithm. Learning is important because it minimizes the difference between the desired output and actual output [
9]. We can categorize the two main types of learning mechanisms as supervised and unsupervised learning. In supervised learning, the network learns to generalize some given examples and it is trained by providing it with input and matching output patterns. These patterns can either be provided by a teacher or by the system [
10]. On the other hand, in unsupervised learning, there is no predetermined set of categories into which the patterns are to be classified [
11].
The back propagation algorithm and the genetic algorithm are the two most important algorithms to train neural networks. The back propagation algorithm is a basic learning algorithm which is commonly used in the training of multi-layered ANNs. Researchers generally prefer to use it because it gives efficient results and is easy to prove and to comprehend. The Back-Propagation Neural Networks (BPPN) model is a multilayer neural network model, which is composed of the input layer with artificial neural networks, the hidden layer, and the output layer. While the input layer is responsible for delivering the incoming data to the hidden layer, the hidden layer processes this information and sends it to the output layer. Finally, the output layer processes this information coming from the hidden layer and produces the output to be generated and sends them to the outer world [
12]. In this respect, BPPN functions by receiving inputs from units of a lower level and transmits output to the units of the upper layer. The number of hidden layers and the artificial neurons in the hidden layers are generally obtained by the method of trial-and-error. BPPN has a higher classification and prediction performance than many other methods due to the reason that it is not subject to the classification restriction of a single-layer network [
6].
There are many studies which show that ANNs can be successfully applied to the prediction of financial crises, currency crises, financial distress or bank failures. Research on prediction of financial crises or bankruptcy through ANNs goes back to 1990s and researchers accelerated their efforts since the beginning of 2000s. Odom and Sharda [
13] were the ones who employed ANN in their analysis of bankruptcy prediction. Their results indicate that the ANN has a better performance and prediction capability as compared to the model based on multivariate diagnostic analysis. Salchenberger
et al. [
14] also observed that models based on NNs have a higher accuracy and better prediction performance than the logistic regression (Logit) analysis. Nag and Mitra [
17] used ANN to develop an early warning system (EWS) to predict currency crises in Malaysia, Thailand, and Indonesia. They compared their results with those of signal approach. They concluded that the ANN outperforms Kaminsky, Lisondo and Reinhart [
18] model especially concerning out-of-sample predictions.
Tam [
19] and Tam and Kiang [
20] used a BPPN model to predict bank failures for a sample of banks prior to their failures. They found that BPPN outperforms all other techniques in terms of their predictive accuracy. They also found that a BPPN has better classification accuracy. Bell [
21] compared Logit and BPPN models to predict bank failures. He reached the conclusion that neither Logit nor the BPPN model is superior to each other in terms of prediction performance. On the other hand, he adds that BPPN performs better for complex decision processes.
In the early 2000s, the number of studies based on ANNs has increased considerably. Some of these researchers have proven the superiority of ANNs as compared to other methods. Among these researchers, Franck and Schmied [
15] observed that a MLP has a higher predictive accuracy than a Logit model in forecasting currency crises and speculative attacks which occurred in Brazil and Russia in the late 1990s. Roy [
22] and Peltonen [
23] suggested alternative EWS for prediction of currency crisis in transition economies by using ANN. Brockett [
24] compared the statistical methods of Logit and multiple discriminant analysis and the back propagation algorithm to forecast the financial crisis. The study found that BPPN has a greater accuracy performance with regard to traditional statistical models.
Celik and Karatepe [
25] suggested that ANN models can successfully determine the rates of non-performing loans relative to total loans. Davis and Karim [
26] employed statistical and intelligence techniques to analyze the banking crises. They used the Logit and the Signal Extraction EWS methods. They found that Logit model functions better as a global EWS and Signal Extraction performs better as a country-specific EWS. Ravi and Pramodh [
27] suggested a Principal Component Neural Network (PCNN) architecture for the bankruptcy prediction in commercial banks. They used the data of Spanish and Turkish banks and found that hybrid models which combine PCNN and several other models have better performance capabilities than other methods. Wu [
28] investigated the financial crisis of Chinese companies by using ANN and multiple discriminant analysis. His study indicates that NNs can forecast a financial crisis with a much higher accuracy in the short and medium term. Jardin [
29] indicated that researchers obtained better results with NN based models by using 500 ratios from 200 previous papers after an in-depth review of financial literature.
In this study, we try to examine whether the forecast errors obtained by the ANN models have a significant effect on the breakout of financial crisis. In addition to this, we try to analyze whether asymmetric information exists in our study and since asymmetric information leads to forecast errors, we try to investigate how much the asymmetric information and forecast errors are reflected on the results of our ANN output values. In accordance with this purpose, we established two different ANN models. The aim of the first ANN is to obtain the adequate results in order to predict a potential future crisis in Turkey and to find the forecast errors of these obtained estimates. The forecast error is related to the degree of uncertainty associated with a measure of skill. Our basic idea for solving the problem of model comparison is to compare the entropies of the forecast errors. That is, we will investigate the difference in forecast errors and entropies. In this context, the present paper will also complement some of the views and the entropy of forecast errors presented in Schneider and Griffies [
40] and Delsole [
41].
On the other hand, the aim of our second ANN is to use the input variables that are supposed to be influential on the Turkish economy and that we think are effective on the outbreak of financial crisis. In our second ANN model, we try to predict the future values of Borsa Istanbul 100 Index (BIST), gold price (GP) and the US dollar to Turkish lira exchange rate, USD/TRY (USD), as output variables that may have a direct impact on the Turkish economy. In other words, while the main purpose of the first ANN is to directly estimate the potential financial crisis, the main purpose of our second ANN is to determine whether the point estimations of crisis that we obtained by the first ANN and our three output variables steering the economy coincide with each other in terms of results.
The major contribution of our study to the existing literature is the analysis of the financial crises by using the ANN models in addition to the econometric and financial approaches. This is also the main difference of our study from the other studies as an innovative contribution to the academic literature. We obtained our ANN models by using different approaches. In this regard, the number of studies that combine the ANN models with financial and econometric approaches are limited and thus, our study is one of these unique and innovative studies.
The present paper is organized as follows. In
Section 2, we review some forecast error measures. In
Section 3, we give information about research methodology. In
Section 4, we present the design of neural network ensemble and conduct our research analysis.
Section 5 is the discussion and the conclusion part of the study.
2. Forecast Error Measures
In evaluating the used methods and the size of their forecasting errors, it is critical to separate between model data fit and the post-sample used for improving the estimating model measures. Probes have indicated that post-sample accuracies are not invariably related to those of the model that best fits available observation data [
30,
31]. This means that we must judge the convenience of whichever measure we use by how effectively it ensures information about post-sample performances [
32,
42].
Measures of forecast accuracy can be divided into the two parts: those that are “scale-dependent” and those that are not [
33]. The most commonly used scale-dependent summary measures of forecast accuracy consist in the distributions of absolute errors (|E|) or squared errors (E
2), adopted the number of observations (n). These scale-dependent measures include Mean Square Error (MSE), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Median Absolute Error (MEDAE). Some methods are better when, for example, Mean Absolute Percentage Errors (MAPEs) are used, while others are better when rankings are utilized. Forecast accuracy measures were suggested in the past by many researchers and several researchers made advices about what should be used when comparing the accuracy of forecast methods applied to multivariate time series data. Our focus here is on measures of forecast accuracy which indicates that percentage errors are not scale-independent.
To understand whether the asymmetric information exists in the relationship between the predicted values and the actual values, we use the accuracy of coherence forecasts and the entropy among forecasts as proxies for asymmetric information in this study. These proxies are based on forecasts made in the month before the predicted values were calculated. We preferred to analyze forecast properties which were obtained by the ANN for the largest forecasting horizon in order to provide for the unbiased prediction and to determine the degree of the uncertainness and asymmetric information in forecasts. There is a direct link between asymmetric information and asymmetric forecast errors because, in a system where asymmetric information exists, we also see forecast errors. As the rate of the differences between actual value and predicted value increases (as the information asymmetry increases), we expect to have more forecast error measurements which lead to larger forecast errors or values.
Symmetric mean absolute percentage error (SMAPE or sMAPE) is an accuracy measure based on percentage (or relative) errors [
43]. It is usually defined as follows;
where A
t is the actual value and F
t is the forecast value [
33,
42,
43]. The mean absolute percentage error (MAPE), also known as mean absolute percentage deviation (MAPD), is a measure of accuracy of a method for constructing fitted time series values in statistics, specifically in trend estimation. It usually expresses accuracy as a percentage, and is defined by the following formula;
The main application of entropy in information theory was provided by the Shannon entropy (SE). According to the SE, higher uncertainty in the messages of the system also means higher entropy due to the reason that the entropy equals the expected information in a message, which measures the compression ratio that can be implemented without losing any information [
34]. In this study, we aimed to assess the impact of forecast errors on the asymmetric information. We prefer to use the SE as it assists us in identifying the degree of asymmetric information.
The SE is calculated by using the following formula:
for a random variable with sample space
and associated probability measure
. This represents the average information of the random variable
, or in the case that
represents an individual symbol from a sequence of symbols intended to convey information, the information per symbol [
35].
Since entropy in financial systems presents a stochastic assessment to a system’s macroeconomic and financial changefulness, higher entropy also means a greater lack of information on the exact structure of the system. Hence, it has many similarities with entropy reproduced in information theory. This definition is fundamentally based on Shannon entropy and in this regard it is a measure for the amount of randomness hidden in an information arrangement. This means that an order with redundant information or statistical regularities exhibits small values of entropy [
35]. For example white noise gives rise to the highest entropy value. Since this paper is focused on time-series analysis, the information theoretical definition of entropy will be considered.
3. Research Methodology
In this study, we use six macro-economic and financial variables to study their effects on stock future price. Monthly data between January 1990 and February 2015 have been used in this study for the detailed examination of the subject. Monthly data were obtained from the Data Distribution System of the Central Bank of Turkey.
In this research, we established two ANNs in order to predict a potential financial crisis. In our first ANN, our main objective is to predict the financial crisis directly. For this aim, we included the variable of crisis into other variables to obtain the crisis as a single variable. The most important aspect of our first ANN is to be able obtain the result of whether there is a crisis or not. That is the reason why the variables in
Figure 1 take values between 0 and 1. Our main objective in the second ANN is to obtain the variables of USD, BIST, and GP, as they are the most important variables that are affective on the Turkish economy. We realize this aim by setting the relationships between the six input variables that we employed in the second ANN. After using three output variables in the second ANN, we compare the variable of crisis in our first ANN with the aim of determining whether the results of two ANNs coincide with each other. Thus, as a last step, we try to determine whether the findings of two ANNs are related with the asymmetric information. We used forecast errors such as MAPE, SMAPE, and SE to investigate whether these results are related with the results of the first and the second ANN. Finally, we divided our forecasts into the periods as prior to crisis, during crisis, and after crisis. Consequently, we examined whether asymmetric information exists in our study and whether our results are due to the asymmetric information or not.
A total of 302 data points have been obtained in the data series. To investigate the effectiveness of NN ensembles, the total available data have been divided into three parts as training, testing and evaluation. Data from January 1990 until December 1995 with 72 observations have been used for model building. The next 230 observations that belong to the time period of January 1996 and February 2015 have been used for the validation purpose. The out-of-sample period, which was included in the future values, consists of the last 12 months.
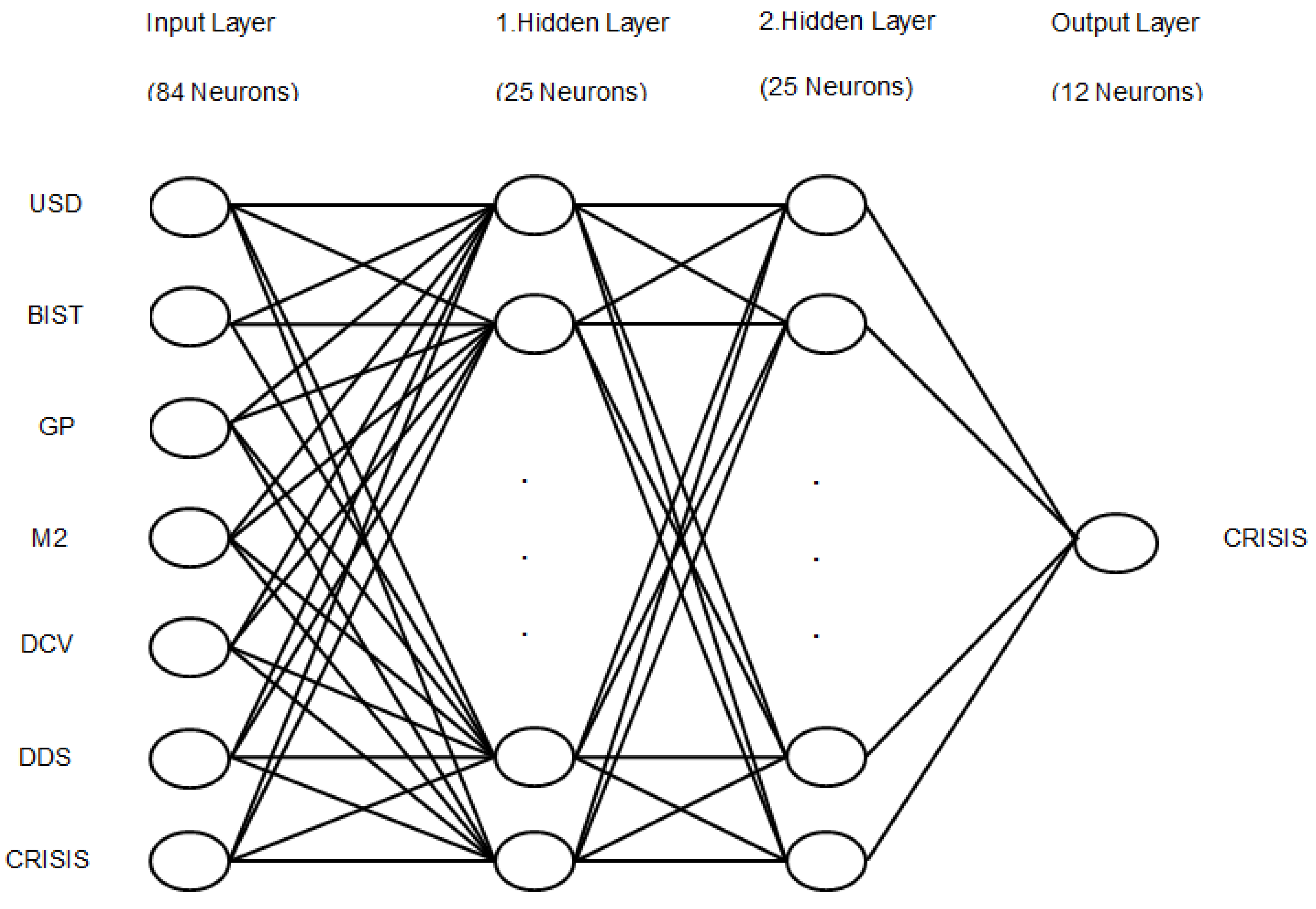
Figure 1.
The depiction of the proposed methodology for the first ANN constituted with seven inputs and one output.
Figure 1.
The depiction of the proposed methodology for the first ANN constituted with seven inputs and one output.
Briefly the methodology steps of the study are:
Identifying related factors among macro-economic and financial variables through the variables adopted in financial literature.
Constituting the financial crisis variable through the ANN.
Modeling and estimating the financial crisis through 7 and 6 variables by using multilayered neural network.
Evaluating the asymmetric information of the obtained forecasting results through symmetry measurements such as MAPE, sMAPE, and SE.
MAPE is the most commonly-used measurement to evaluate cross-sectional forecasts. In addition, MAPE has valuable statistical properties in that it makes use of all observations and has the smallest variability from sample to sample [
33,
36,
37]. To determine whether the asymmetric information is related to the financial crisis, we divide the time series into four parts as the whole results, before, during, and after the outbreak of a financial crisis. The whole data calculate their entropy, MAPE, and sMAPE, respectively. According to most econometricians, in many cases, the forecast errors are due to the absence of variables that are necessary in the model or due to bad specification. This situation is also one of the major causes of the increase in the number of forecast errors. If the wrong specification does not exist in the chosen model, the availability of asymmetric information also appears to be one of the most important reasons of forecast. We can also observe asymmetric information in high-frequency time series. Since the ANN models used in this study are obtained by 0.01% maximum margin of error, it is supposed that the calculated sMAPE, MAPE, and SE values’ forecast errors are due to asymmetric information that derives from high-frequency time series.
4. Design of Neural Network Ensemble and the Empirical Findings
Multilayer feedforward neural network (MLNN) models are the most popular network paradigm for time series forecasting applications and they are the focus of this paper. Compared to traditional statistical forecasting models, NNs have more factors to be determined. Those factors related to the NN model architecture include the number of input variables, the number of hidden layers and hidden nodes, the number of output nodes, the activation functions for hidden and output nodes, and the training algorithm. In this study, ANN models have hidden layers and the ANN models which do not have hidden layers can be used in special cases where relationships between variables are linear. In other words, if what the ANN will find out is linear, the hidden layers do not exist in NN model. Time series, generally, have high frequencies that the relationship between variables is supposed to be non-linear, as mentioned before. On the other hand, the number of hidden layers and neurons in the hidden layers has been designated by the method of trial-and-error. Furthermore, the normalization or denormalization of networks has been constituted by the built-in functions and normalization of numeric values which take part in ENCOG framework [
44].
In this paper, we have built two NN models compiled with forecast monthly financial crisis variables in Turkey that can be seen from our two figures. The first ANN model is a multivariate and fully-linked model based on past macroeconomic variables, which have a serious impact on the occurrence of the financial crisis. The purpose of this model is to determine whether another crisis will break out in the future. In accordance with this purpose, we give the value of 1 if the financial crisis existed in the past period. Otherwise, we give the value of 0. From
Figure 1, which shows our first ANN, it can be observed that a crisis variable has been obtained as our output variable. This new variable along with other six variables generate the first ANN model’s inputs. The variable of crisis as the output variable by the ANN model, covering seven variables, indicates one of the major differences of this study than other studies in the literature. Here, establishing the model process has been considered by the logic of logistic regression.
Since future financial crises depend on previous macroeconomic variables affecting the outbreak of a financial crisis, a multivariate model has been implemented. The first ANN model requires previous data such as GP, BIST, USD, money supply (M2), domestic credit volume (DCV), domestic debt stock (DBS), and crisis (CRISIS) that are accepted receiving between 0 and 1 values as data input patterns. They have the layered structure shown in
Figure 1. This model is a fully connected model since each input unit broadcasts its signal to each hidden layer unit. Rprop, short for resilient back propagation, is a learning heuristic for supervised learning in feed forward artificial neural networks. This is a first-order optimization algorithm [
38]. Rprop has several superior capabilities as compared to other ANNs that it determines the weights in the network structure by itself so that the process is much accelerated as compared to other ANNs.
Figure 1 is a fully-connected multivariate model which depends on the past macroeconomic variables. The input layer consists of 84 neurons. Two hidden layers are comprised of 25 neurons for each. The output layer is composed of 12 neurons. The predictions are made by using feed-forward neural networks, since they are able to learn non-linear ensembles between inputs and outputs. MAPE, sMAPE, and SE in which the error signal associated with the output layer is directly commeasurable with the difference between the predicted and actual output values. We prefer to provide overall network performance through SE function and the other forecast error measurements.
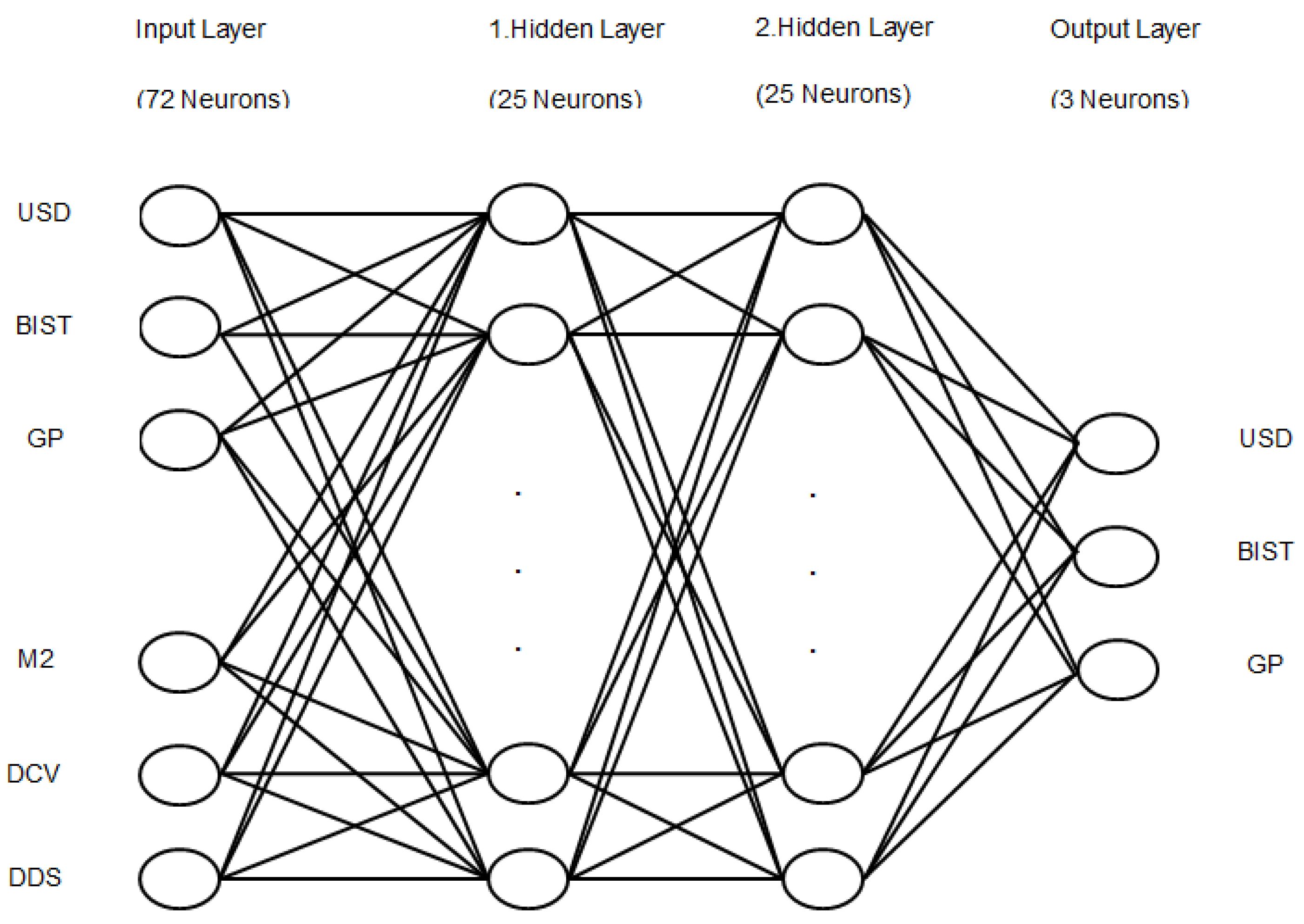
The second ANN model is a multivariate fully linked model and has the exchange rate of USD, BIST, GP, money supply (M2, DCV, DDS as input units. Here, the input layer consists of 72 neurons. There are 25 neurons in each hidden layers and the output layer has three neurons (see
Figure 2). To build the models, the network is processed in three stages: the training stage, the testing stage, and the evaluation stage. The resilient back propagation algorithm is used in the training stage to accelerate the back propagation algorithm and to reduce stagnation periods. The first and the second ANN models are trained, tested, and evaluated by using the period extending from January 1990 until February 2015.
The crisis data has been estimated from February 2015 to February 2016. According the results of this model in
Figure 1, the outbreak of crisis in Turkey seems to be in the time period of February 2015 and July 2015.
Due to the ease of its application, time series, which take part in ENCOG framework, have been given preference in the Temporal Neural Dataset class of software that are constituted for the data sets. This study was prepared for the study of multilayer supervised learning algorithms. Additionally, we have benefited from several strategies in order to assist coding in the framework such as “If certain number of iterations has been passed in the training of the network, restart to learning” or “If the error value does not progress a significant proportion, restart to learning”.
The normalization and the denormalization of data have been done with the help of built-in functions found in the framework. In the predicting of the first ANN, while the crisis is forecasted, the training has been done with the first 217 data. Afterwards, with the constituted network, the data set of 302, ranging from 218, has been used as a validation set. We observed that we estimated one of the networks trained with 100 per cent accuracy. With this network, twelve-month forecasting has been done beginning from the 303rd data. During the process of forecasting the crisis, it has been trained by different networks and the network that predicts the best of validation set has been chosen as the direct network.
In forecasting of the second ANN, while the network is being trained the variables of the first 72 months have been used as training data. In the same manner, we tried to estimate each month starting from the 73rd month that are in the data set. For each month to be predicted, the ANN has been trained iteratively with its previous three-year data. For the 303rd and the following months, again its previous 72-month data has been given to the ANN as a training set and the missing months have been filled by the prediction values obtained in previous iterations.
Figure 2.
The depiction of the second ANN model constituted with six input layers and three output layers.
Figure 2.
The depiction of the second ANN model constituted with six input layers and three output layers.
The exchange rate of USD/TRY (USD, the Borsa Istanbul 100 Index (BIST), and gold price (GP) are the output variables of the ANN model of
Figure 2. They have been deliberately selected as they are generally the most affected variables for crises in Turkey.
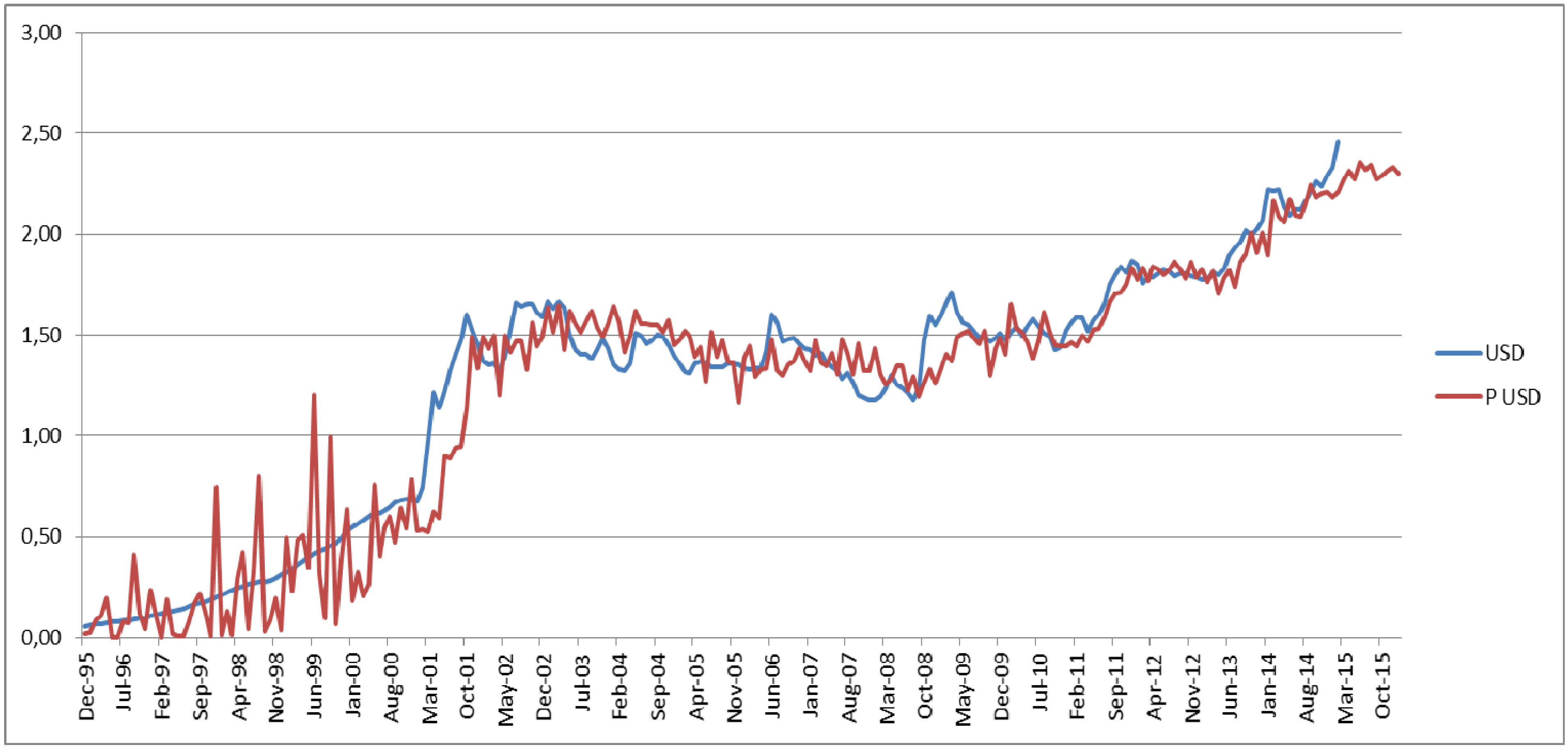
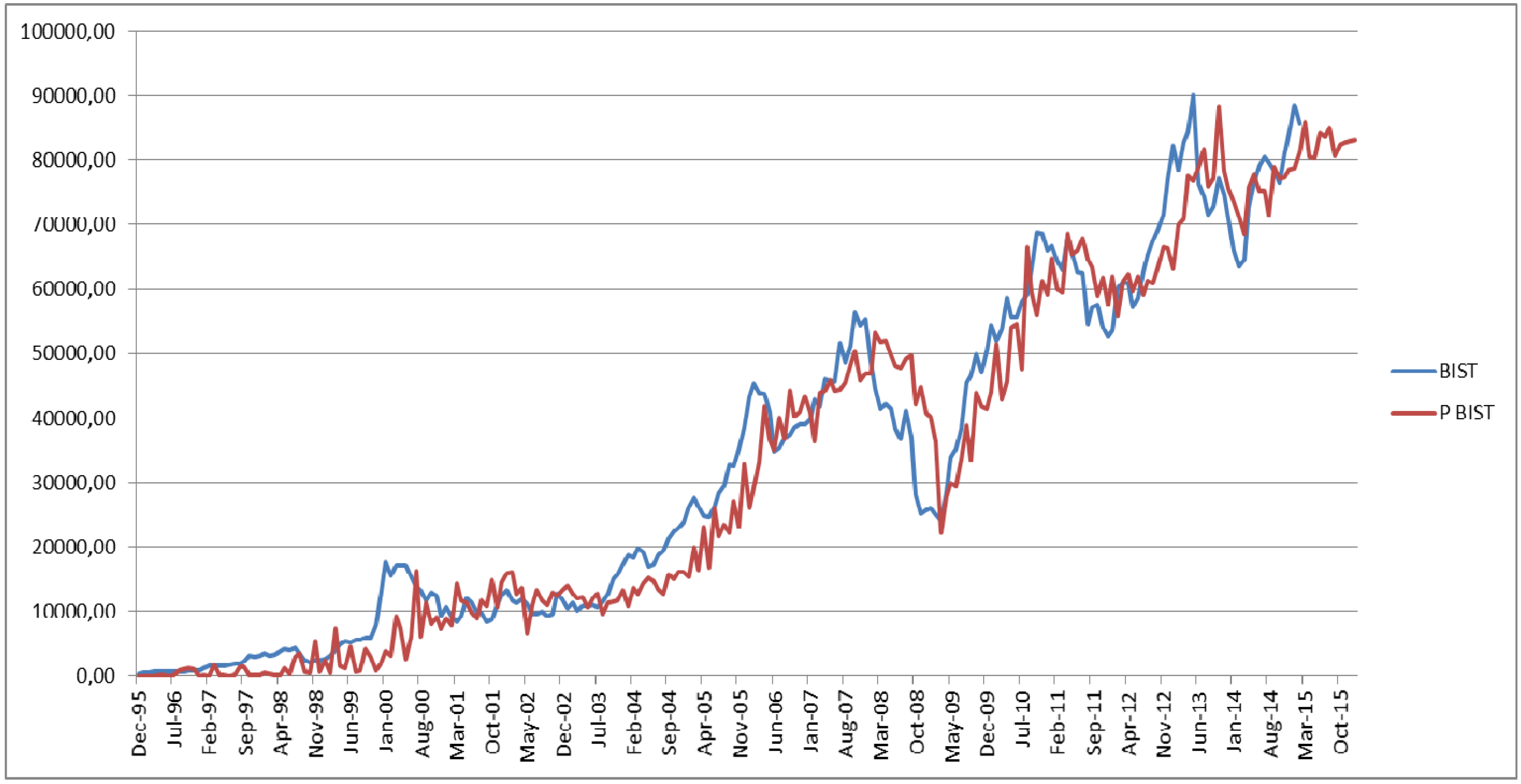
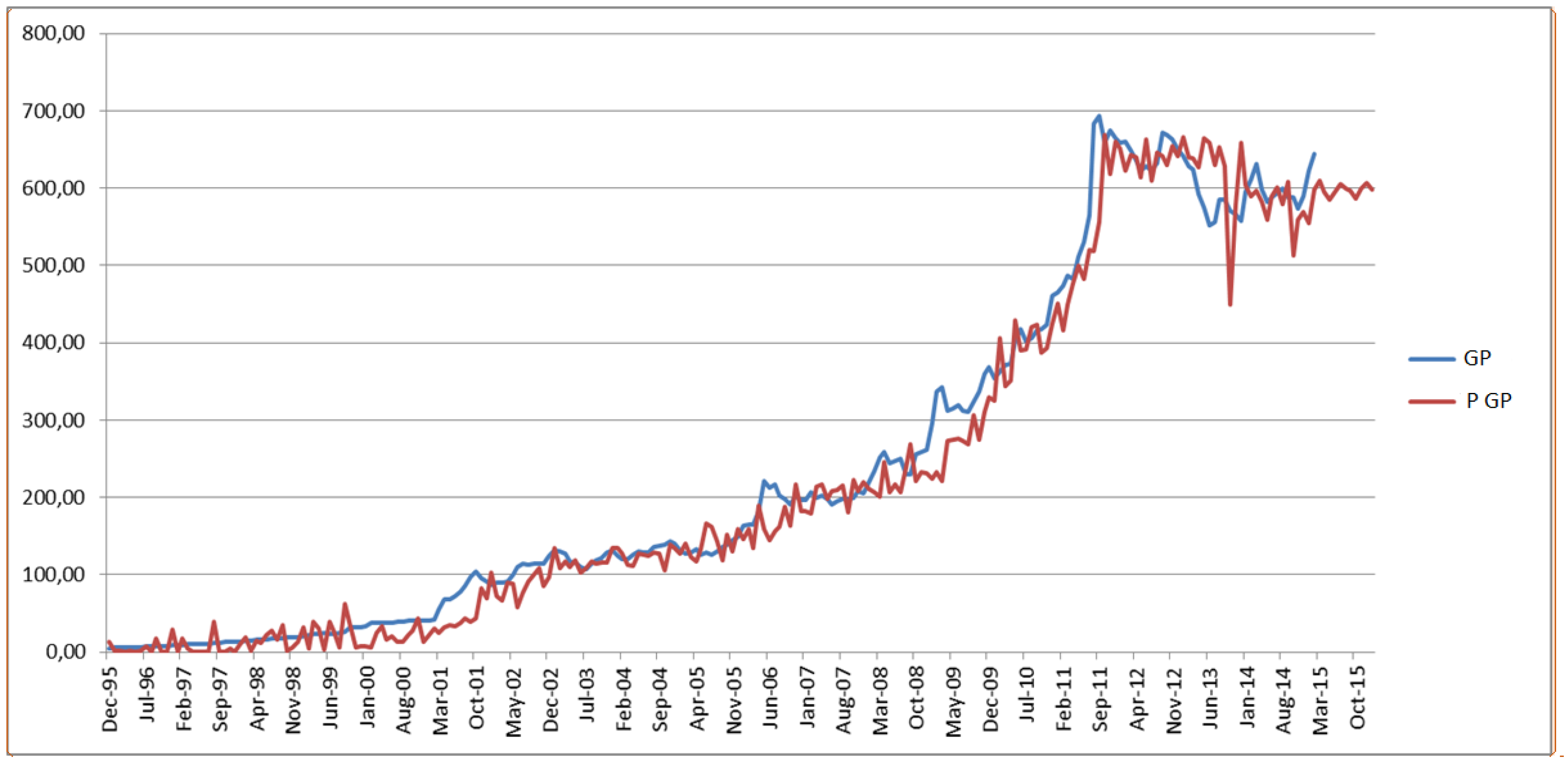
Figure 3,
Figure 4 and
Figure 5 demonstrate the comparison between the real values and the predicted values of these variables for the time period of December 1995 and October 2015. It is striking that the actual values and the predicted values are very close to each other in all these three figures. When these figures are examined in detail, it is observed that the predicted ANN model has a strong explanation ability for the 2001 and 2008 crises. When these figures are viewed in terms of the asymmetric information, the variables appear to deviate and show disturbances prior to 2001 and 2008 crises and following them.
In
Figure 3, there are some major fluctuations in the period of 1995 and 2001 due to the training of the ANN. However, particularly the period between March 2001 and March 2015 indicates how close the predicted values with actual values are for the variable of USD. In
Figure 4, the variable of the Borsa Istanbul 100 Index (BIST) obviously indicates the rapid economic growth beginning from 2002 until 2008. The period between March 2008 and May 2009 is one the major falls in the value of BIST. The period starting after this fall until March 2015 also indicates the significant parallelism between predicted values and actual values of BIST. The predictive power of
Figure 5, which shows the real and predicted values of gold prices (GP), is quite striking since prediction of different variables in a complex and dynamic economic and business environment is indeed a very difficult task. This precision is provided by using an advanced and sophisticated technique such as ANN, which indicates the superior performance of it in the prediction of different variables.
Figure 3.
The Comparison between the actual values (USD) and the predicted values (P USD) obtained by the second ANN model.
Figure 3.
The Comparison between the actual values (USD) and the predicted values (P USD) obtained by the second ANN model.
Figure 4.
The comparison between the actual values (BIST) and the predicted values (PBIST) obtained by the second ANN model.
Figure 4.
The comparison between the actual values (BIST) and the predicted values (PBIST) obtained by the second ANN model.
Figure 5.
The comparison between the actual values (GP) and the predicted values (P GP) obtained by the second ANN model.
Figure 5.
The comparison between the actual values (GP) and the predicted values (P GP) obtained by the second ANN model.
The answer to the question of whether these disturbances that occur in the tackled macroeconomic variables lead to forecast errors and asymmetric information in the financial complexity systems can be answered by evaluating the MAPE, sMAPE, and the SE values in
Table 1,
Table 2,
Table 3 and
Table 4. These tables list the results of training the ANN with each of the symmetrized measures. While the MAPE and the sMAPE values represent the symmetry measures, the value of SE give us the entropy values.
Table 1, which indicates some symmetry measurements with the whole results of the second ANN output variables, clearly reveals the success of the network organization under the direction of the symmetrized information measures.
Table 1 is also important in terms of examining the relationship between diversification and information asymmetry because it presents symmetry measures of the output variables that are obtained by the whole second ANN.
Table 2,
Table 3 and
Table 4 demonstrate some symmetry measures prior to, after, and during the financial crisis with the results of the second ANN output variables respectively. The more the values are different from 0.50, the more asymmetry we observe for our variables. By reviewing the values, we can determine how much our variables are affected from asymmetric information and their success on the prediction of financial crisis. The asymmetric information is reflected in the variables, which leads to the deterioration of the system.
Table 2 clearly indicates that our variables have been deteriorated mostly prior to the financial crisis. This is more evident especially for our variable of the BIST. This result that we obtained is particularly important since it can be guiding for the prediction of the future financial crises. This is mainly because it can function as an early warning signal before the crises.
Table 3 displays that the reflections of the asymmetric information can also be observed after the financial crisis. This is mostly evident for our variable of the exchange rate of USD.
Table 1.
Some symmetry measures with the whole results of the second ANN output variables.
Table 1.
Some symmetry measures with the whole results of the second ANN output variables.
| Variables | MAPE | sMAPE | SE |
|---|
| P-USD | 0,233795 | 0,259054 | 0,490194 |
| P-BIST | 0,2979441 | 0,409444817 | 0,520474501 |
| P-GP | 0,28199499 | 0,35654177 | 0,51499577 |
Table 2.
Some symmetry measures prior to the financial crisis with the result of the second ANN output variables.
Table 2.
Some symmetry measures prior to the financial crisis with the result of the second ANN output variables.
| Variables | MAPE | sMAPE | SE |
|---|
| P-USD | 0,693821 | 0,780014 | 0,365896 |
| P-BIST | 0,699714818 | 1,145152353 | 0,360465821 |
| P-GP | 0,75348091 | 0,99799538 | 0,30768931 |
Table 3.
Some symmetry measures after the financial crisis with the results of the second ANN output variables.
Table 3.
Some symmetry measures after the financial crisis with the results of the second ANN output variables.
| Variables | MAPE | sMAPE | SE |
|---|
| P-USD | 0,078712 | 0,077303 | 0,288659 |
| P-BIST | 0,186697824 | 0,20131717 | 0,452037062 |
| P-GP | 0,1121769 | 0,12041367 | 0,35404741 |
Table 4.
Some symmetry measures during the financial crisis with the results of the second ANN output variables.
Table 4.
Some symmetry measures during the financial crisis with the results of the second ANN output variables.
| Variables | MAPE | sMAPE | SE |
|---|
| P-USD | 0,299768 | 0,362415 | 0,521021 |
| P-BIST | 0,261079863 | 0,242397891 | 0,505825762 |
| P-GP | 0,46626279 | 0,62913661 | 0,51325499 |
5. Discussion and Conclusion
Recently, especially since the beginning of the 2008 crisis, there has been a growing interest for the prediction of the financial crises in order to prevent their adverse consequences. The concept of asymmetric information plays a vital role for both macroeconomics and finance since it is one of the major causes of the financial crisis. There is extensive evidence that in financial markets information is distributed unevenly among different financial actors. As prices reflect expectations of various market participants, the precision level of sources of information is essential. The asymmetric information approach explains the patterns in the data and many features of the crises which are otherwise hard to explain. It also suggests why financial crises have had such important consequences for the aggregate economy over the past fifty years. Fridman [
39] asserted that monetary policy may have an asymmetric effect on real economic activity. In this context, the asymmetric information approach can be viewed as complementary to the monetarist view of financial crises since it provides an important transmission mechanism concerning how macroeconomic disturbances affect aggregate economic activity.
In this study, we have tried to examine whether the forecast errors obtained by the ANN models have a significant effect on the outbreak of a financial crisis. In addition to this, we analyzed whether asymmetric information exists in our study. Since asymmetric information leads to forecast errors, we investigated how much the asymmetric information and forecast errors are reflected on the results of our ANN output values. The asymmetric information and forecast error in financial crises highlight the timing patterns in the data and many other features of these crises, which are otherwise hard to explain. They also suggest why financial crises have had such important consequences on the world economy in the last few decades.
In our study, we used USD, BIST, and GP as our output variables of the second ANN model. We observe that the predicted ANN model has a strong explanation capability for the 2001 and 2008 crises. The values of the variables appear to deviate and show disturbances prior to 2001 and 2008 crises and then follow them. In addition to this, our results obtained by the first ANN indicate that there is a higher probability that a crisis could occur in Turkey between July 2015 and February 2016. However, realization of these results could change a lot depending upon macroeconomic disturbances which are affected by the asymmetric information.
Our calculations of some symmetry measures (MAPE and sMAPE) clearly demonstrate the degree of asymmetric information and the deterioration of the financial system prior to, during, and after the financial crisis. We found that there is more asymmetric information prior to crisis as compared to the sub-sampling. In particular the sub-sampling after the crisis has played a vital role in producing the information flow during the period of financial crisis. Our result that the deterioration of the system, which has been reflected on our second ANN output values, is more obvious prior to the financial crisis is worthy of note for the conduct of future researches. The asymmetric information and the deterioration of the system can be interpreted as early warning signals before the potential crises. In our study, the reflections of the asymmetric information can also be observed during and after the financial crisis. A systematic part of the error may be estimated with a high degree of certainty which may lead to asymmetric information and disturbances. The degree of uncertainty should be related to the forecast anomalies as stated by Schneider and Griffies [
40] and Delsole [
41]; in other words, that time series have a high-frequency, which derives from asymmetric information in the financial markets.
To sum up, as a suggestion for further research this evidence, which seems to favor an asymmetric information view of financial crises, should be carefully considered by the researchers. We also suggest investigating the use of time series with respect to comparing forecast results and the empirically-based research of MAPE, sMAPE, and SE as these methods can be used in terms of determining the timing of the outbreak of a crisis and to evaluate the financial structure.