Volatility Forecast in Crises and Expansions
Abstract
:1. Introduction
2. Model
2.1. HAR-RV Model with Regime Switching
2.2. Econometric Framework for the Non-Linear Model
2.2.1. Estimation
2.2.2. Testing for Non-Linearity
- Draw residuals with replacement from the linear TAR(1) model.
- Generate a recursively “fake” dataset using initial conditions and estimates of the TAR(1) model, where p equals 22.
- Estimate the TAR(1) and TAR(2) models on the “fake” dataset.
- Compute and on the fake dataset, where b refers to specific bootstrap replication.
- Compute statistics from (15).
- Repeat Steps (1)–(5) a large number of times.
- The bootstrap p-value () equals the percentage of times that exceeds the actual statistic .
2.2.3. Testing for Remaining Non-Linearity
2.2.4. Asymptotic Distribution of the Threshold Parameter
2.2.5. Stationarity
2.3. Forecasting
2.3.1. One-Step-Ahead Forecast
2.3.2. Conditional Distribution of Returns
3. Empirical Analysis
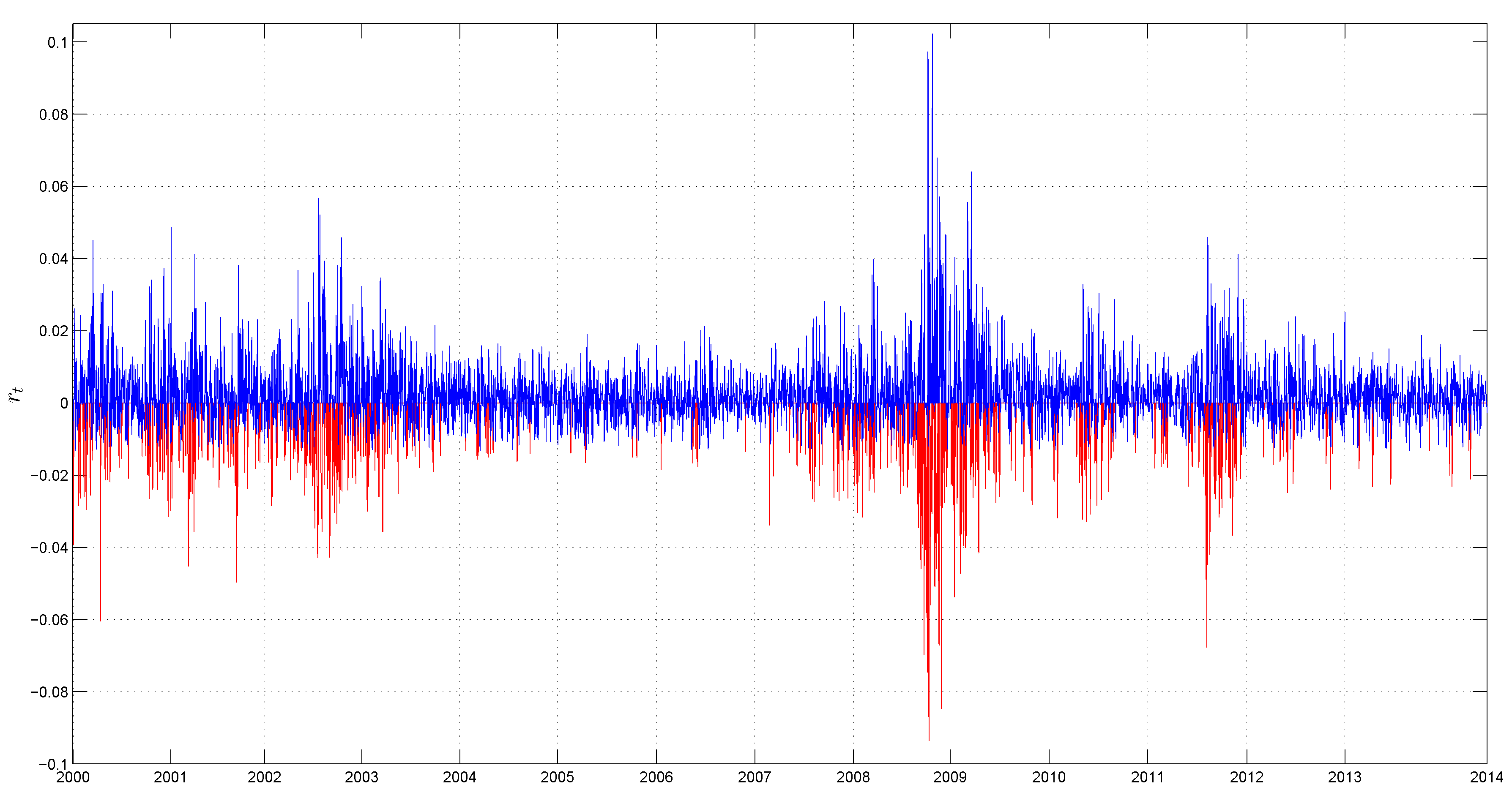
3.1. Data
3.2. Preliminary Data Analysis
| Mean | 0.08 | 8.0E-05 | 1.2E-04 | 9.3E-03 | −9.65 |
| Variance | 1.19 | 1.5E-04 | 7.5E-08 | 3.8E-05 | 1.08 |
| Skewness | −3.3E-03 | −0.15 | 14.26 | 3.32 | 0.50 |
| Kurtosis | 2.57 | 10.24 | 381.25 | 24.58 | 3.47 |
| D-F test | p = 0.00 | p = 0.00 | p = 0.00 | p = 0.00 | p = 0.06 |
| Normality test (J-Btest) | p = 0.00 | p = 0.00 | p = 0.00 | p = 0.00 | p = 0.00 |
| L-Btest 5 lags | p = 0.01 | p = 0.00 | p = 0.00 | p = 0.00 | p = 0.00 |
| L-B test 10 lags | p = 0.08 | p = 0.00 | p = 0.00 | p = 0.00 | p = 0.00 |
| L-B test 15 lags | p = 0.07 | p = 0.00 | p = 0.00 | p = 0.00 | p = 0.00 |
| ARCH effect | p = 0.00 | p = 0.00 | p = 0.00 | p = 0.00 | p = 0.00 |
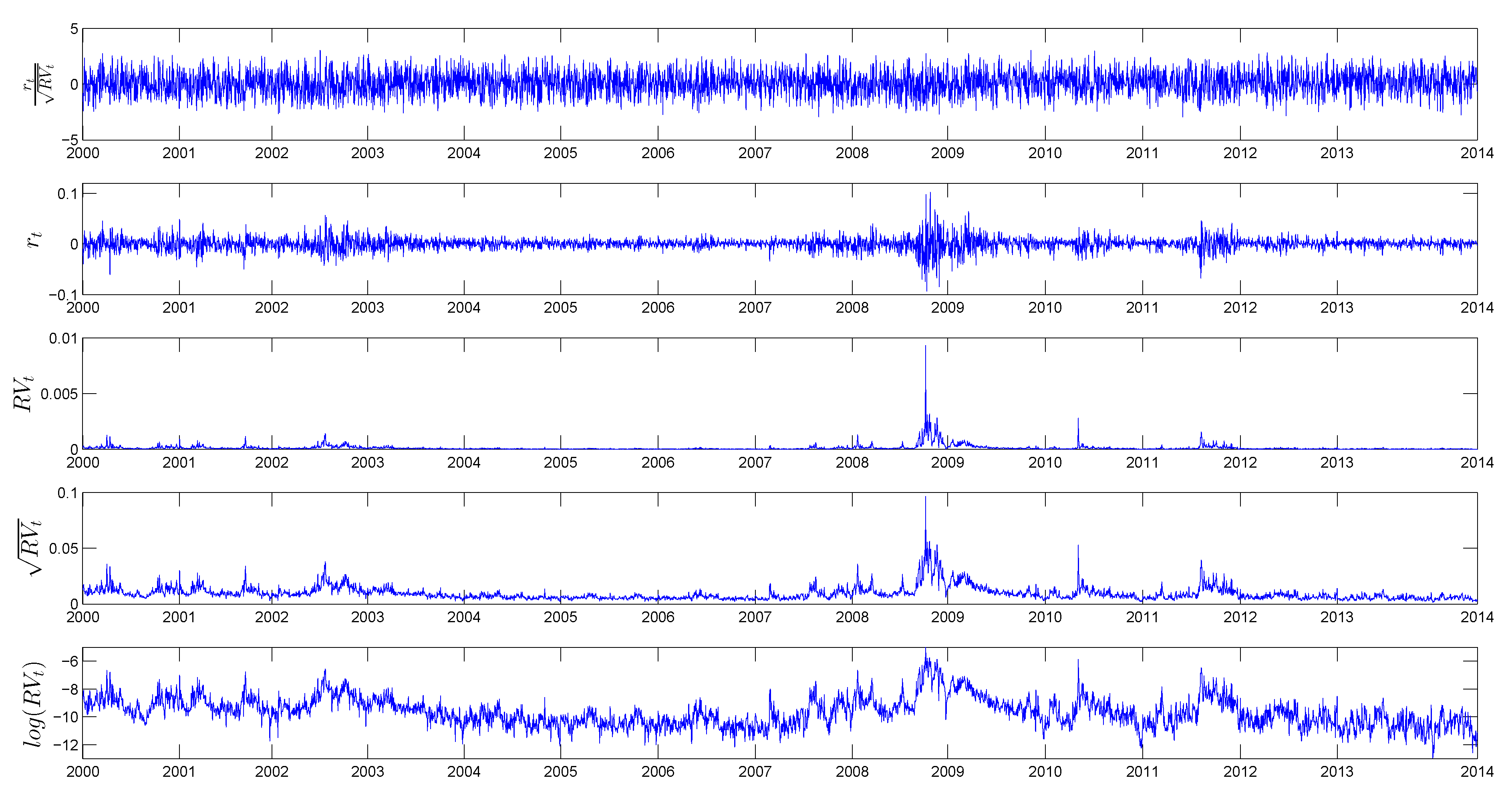
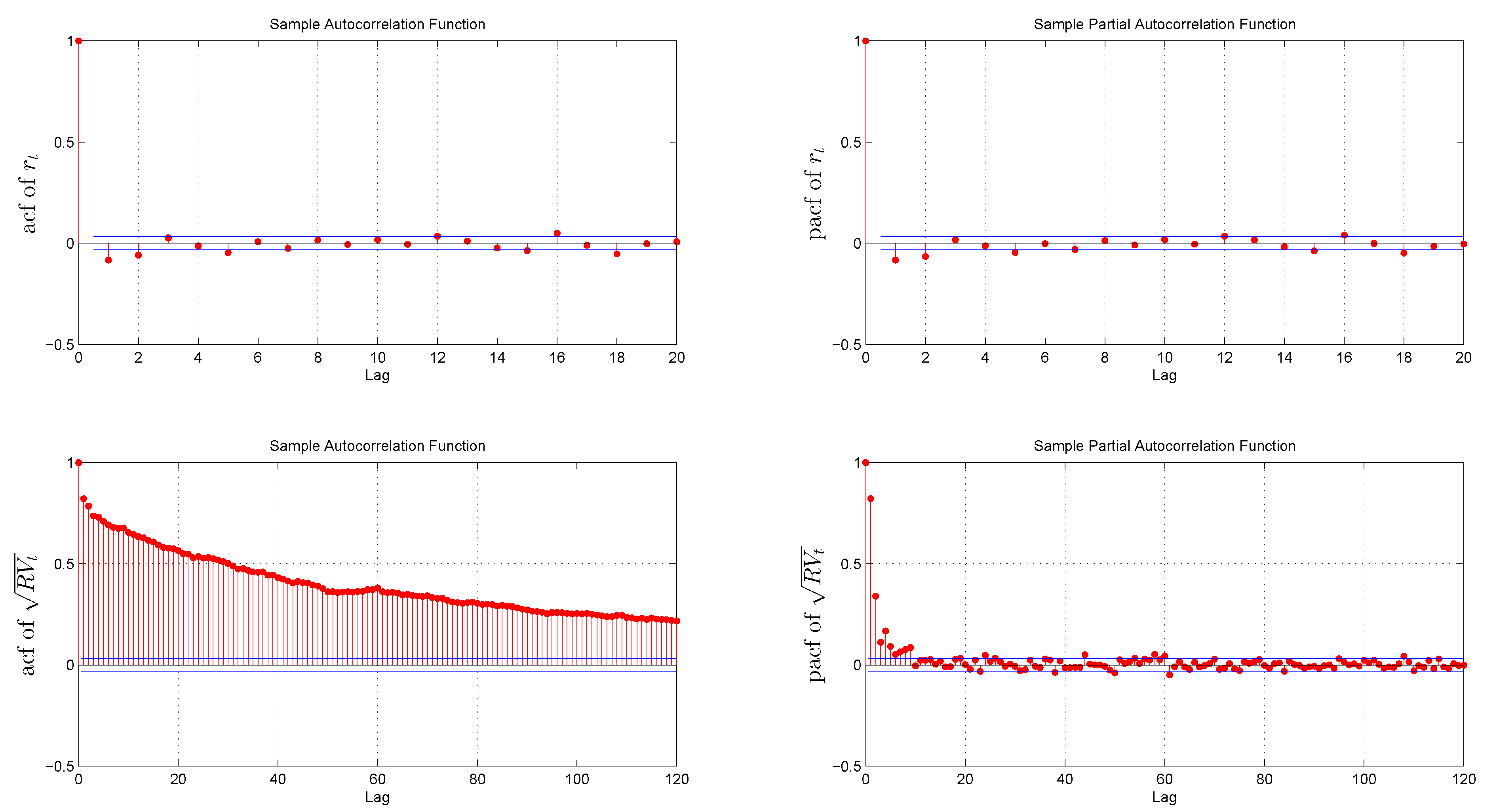
3.3. Benchmark HAR Model
| Estimate | SE | Estimate | SE | Estimate | SE | |
| c | 1.3E-05 | 4.5E-06 | 4.6E-04 | 2.0E-04 | −0.44 | 0.108 |
| 0.223 | 0.146 | 0.395 | 0.058 | 0.336 | 0.025 | |
| 0.461 | 0.165 | 0.384 | 0.081 | 0.440 | 0.036 | |
| 0.216 | 0.073 | 0.171 | 0.048 | 0.178 | 0.029 | |
| 50.4% | 72.6% | 73.2% | ||||
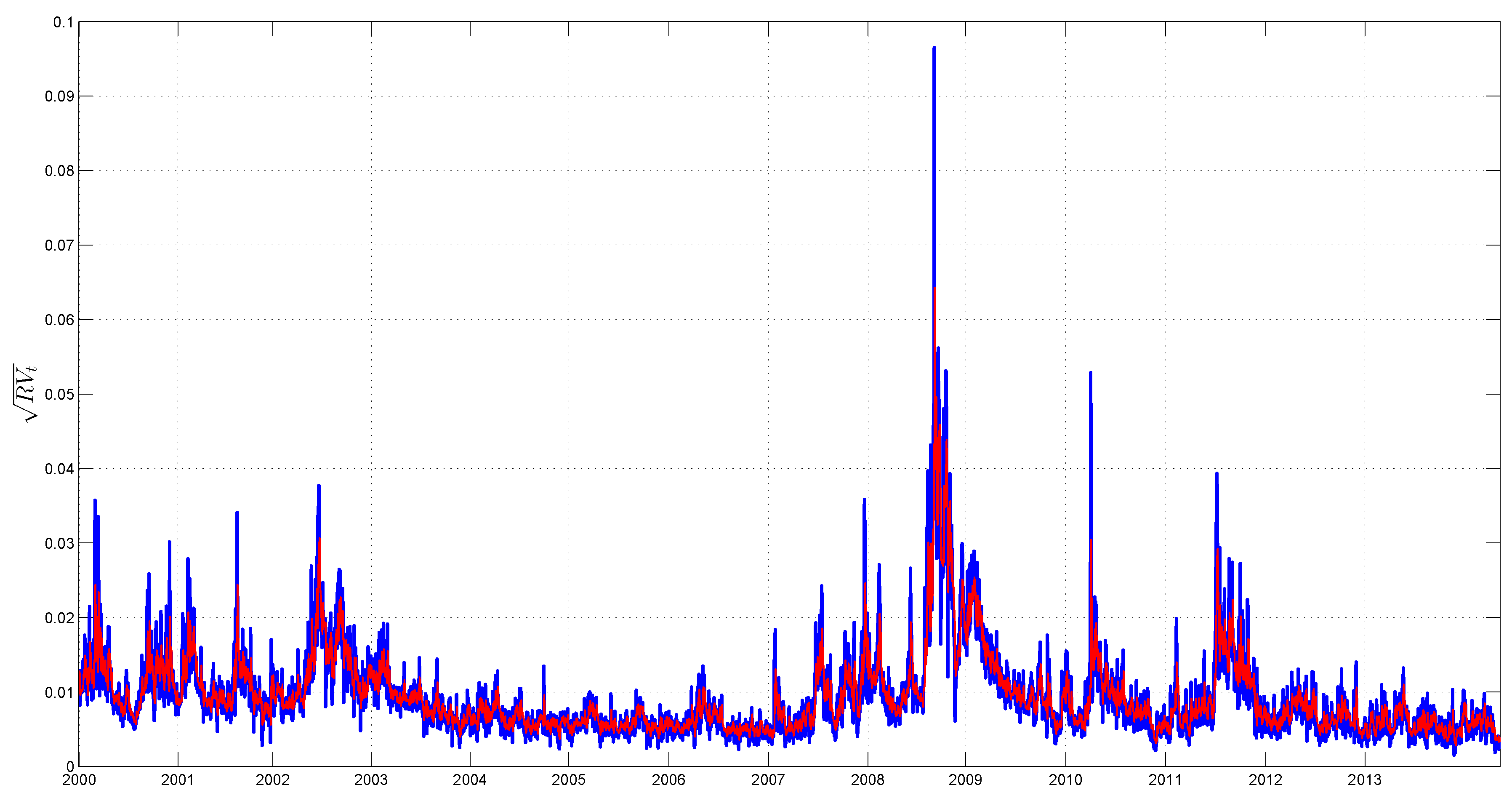
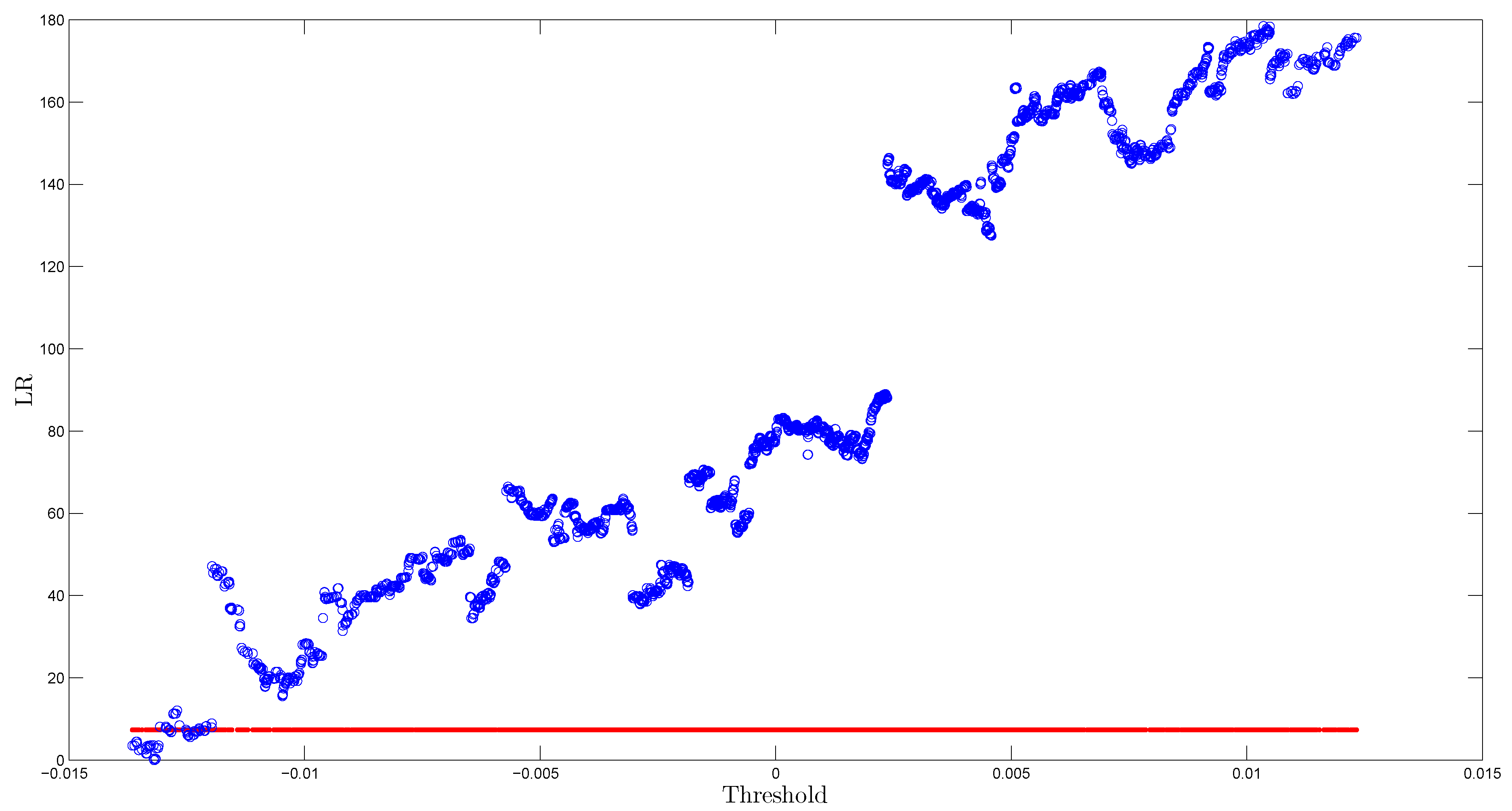
3.4. The TAR(2) Model
| of TAR(1) | 50.4% | 72.6% | 73.2% |
| of TAR(2) | 58.0% | 74.9% | 74.7% |
| τ | −0.013 | −0.013 | 0.001 |
| l | 0 | 0 | 0 |
| 649.6 | 318.3 | 214.0 | |
| 0.00 | 0.03 | 0.00 |
| Estimate | SE | Estimate | SE | Estimate | SE | |
| −2.6E-06 | 4.1E-05 | −9.3E-05 | 9.5E-04 | −0.321 | 0.138 | |
| 0.331 | 0.189 | 0.332 | 0.085 | 0.347 | 0.029 | |
| 1.091 | 0.372 | 0.811 | 0.191 | 0.475 | 0.045 | |
| −0.138 | 0.275 | −0.018 | 0.128 | 0.133 | 0.037 | |
| 2.1E-05 | 5.6E-06 | 0.001 | 1.8E-04 | -0.515 | 0.150 | |
| 0.182 | 0.156 | 0.340 | 0.067 | 0.220 | 0.038 | |
| 0.260 | 0.139 | 0.317 | 0.067 | 0.498 | 0.050 | |
| 0.268 | 0.097 | 0.204 | 0.045 | 0.243 | 0.041 | |
| τ | −0.013 | −0.013 | 0.001 | |||
| l | 0 | 0 | 0 | |||
| 58.0% | 74.9% | 74.7% | ||||
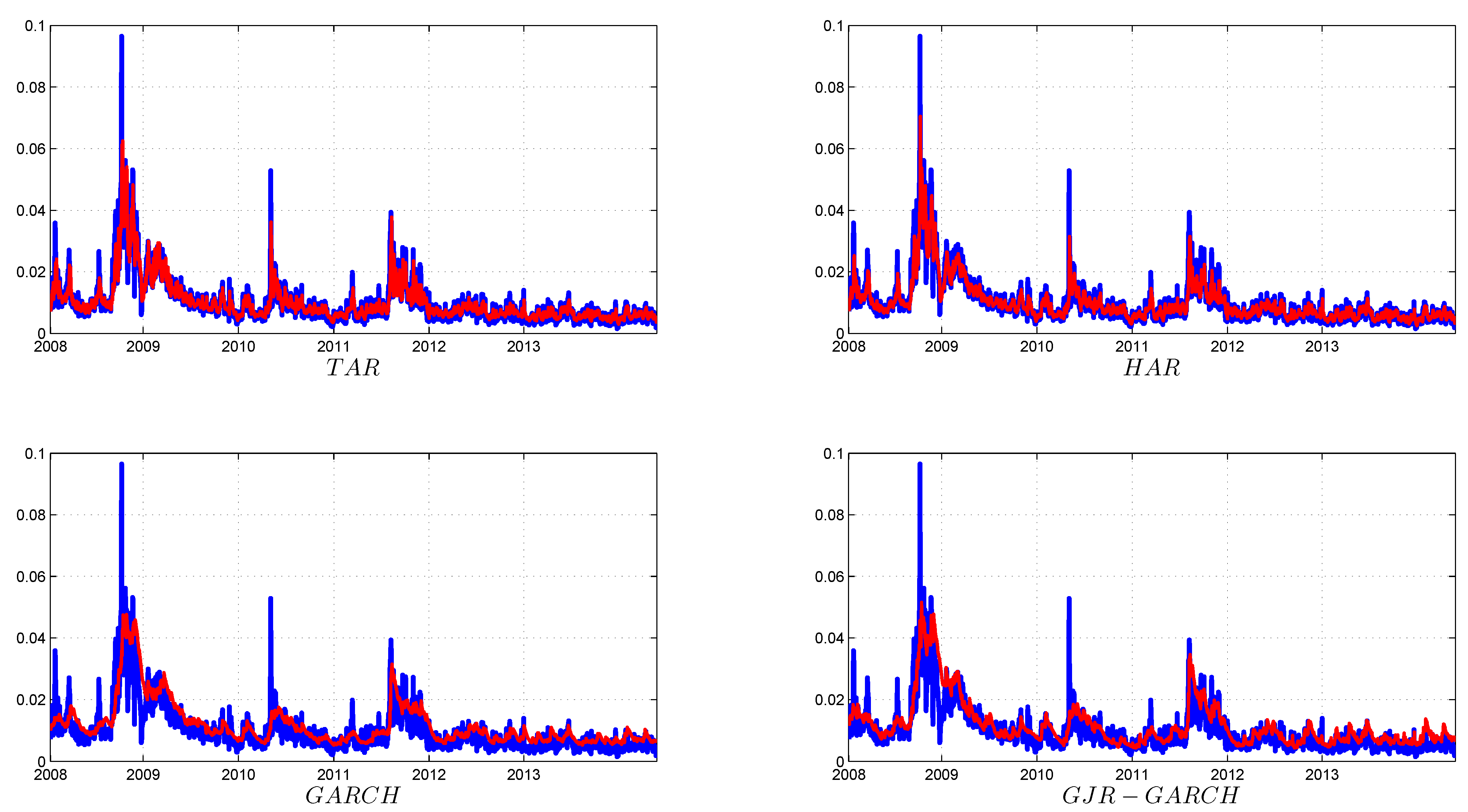
4. Forecast
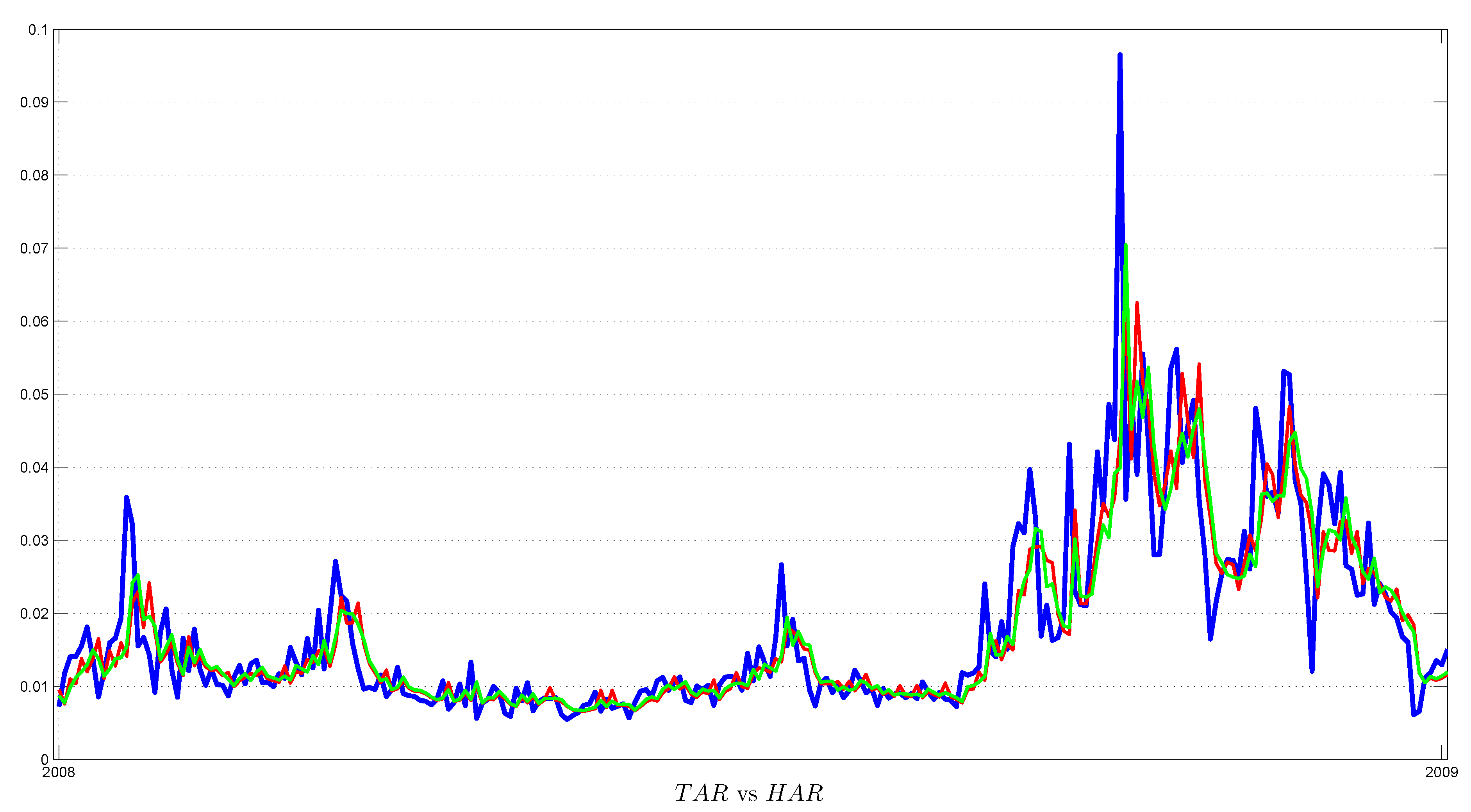
4.1. One-Day-Ahead Forecast
| TAR | HAR | GARCH | GJR | TAR | HAR | GARCH | GJR | TAR | HAR | GARCH | GJR | |
| RMSE | 7.0 | 0.96 | 0.78 | 0.85 | 4.9 | 0.96 | 0.72 | 0.73 | 3.8 | 0.98 | 0.77 | 0.82 |
| MAE | 4.1 | 0.97 | 0.67 | 0.76 | 3.6 | 0.95 | 0.63 | 0.66 | 2.3 | 0.99 | 0.67 | 0.71 |
| R2 | 0.70 | 0.68 | 0.56 | 0.64 | 0.42 | 0.38 | 0.24 | 0.39 | 0.75 | 0.74 | 0.66 | 0.70 |
| pGW | NA | 0.54 | 0.00 | 0.00 | NA | 0.12 | 0.00 | 0.00 | NA | 0.71 | 0.00 | 0.00 |
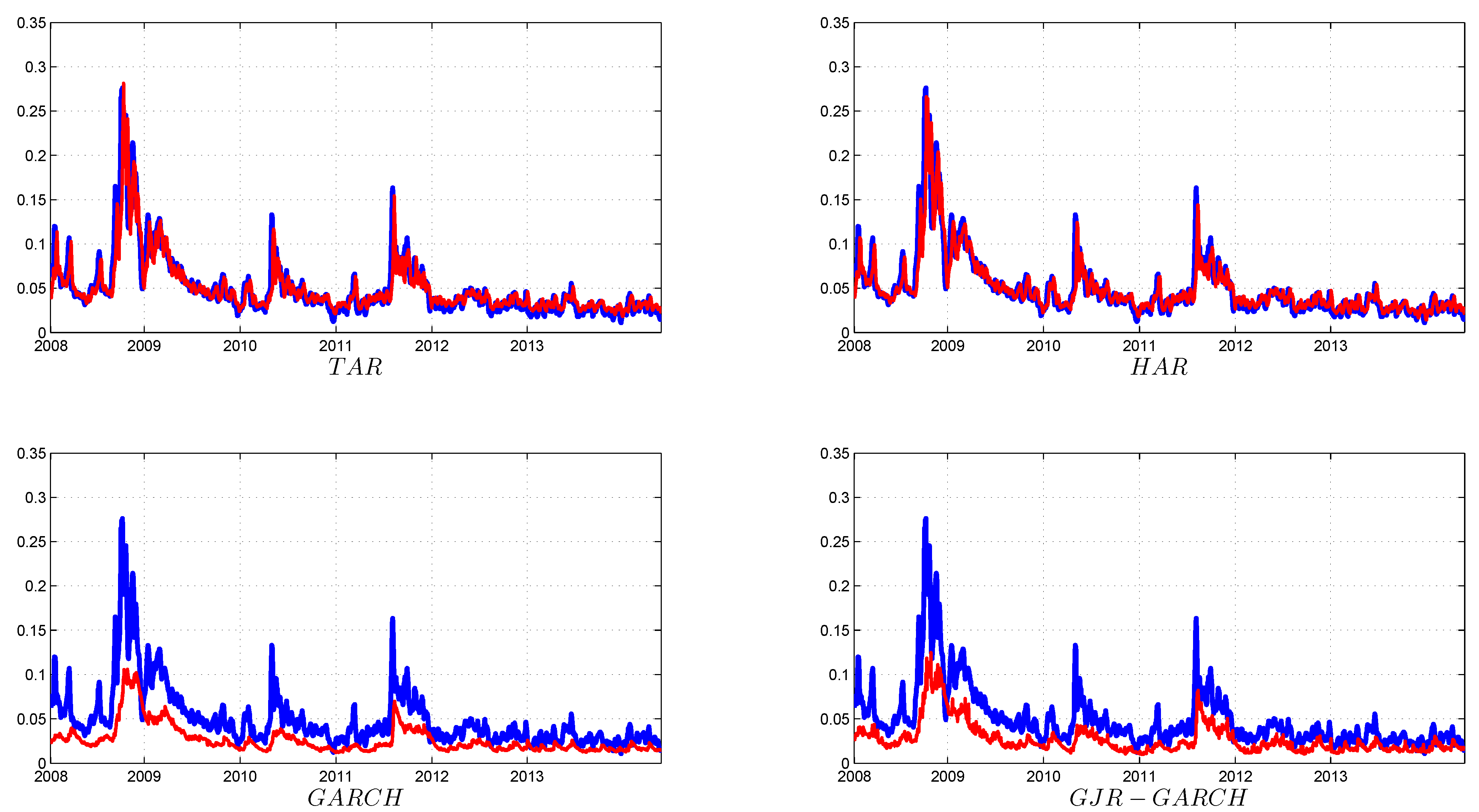
4.2. Multiple-Step-Ahead Forecast
| TAR | HAR | GARCH | GJR | TAR | HAR | GARCH | GJR | TAR | HAR | GARCH | GJR | |
| 5-days-ahead forecast | ||||||||||||
| RMSE | 33.5 | 0.98 | 0.56 | 0.55 | 23.1 | 0.99 | 0.60 | 0.59 | 17.3 | 0.99 | 0.53 | 0.55 |
| MAE | 22.2 | 0.98 | 0.49 | 0.47 | 14.5 | 0.96 | 0.46 | 0.45 | 10.1 | 0.98 | 0.43 | 0.44 |
| R2 | 0.67 | 0.67 | 0.61 | 0.64 | 0.27 | 0.26 | 0.16 | 0.20 | 0.76 | 0.75 | 0.71 | 0.75 |
| pGW | NA | 0.13 | 0.00 | 0.00 | NA | 0.06 | 0.00 | 0.00 | NA | 0.03 | 0.00 | 0.00 |
| 10-days-ahead forecast | ||||||||||||
| RMSE | 69.2 | 0.98 | 0.48 | 0.48 | 47.6 | 0.98 | 0.50 | 0.50 | 35.2 | 0.98 | 0.44 | 0.45 |
| MAE | 47.0 | 0.97 | 0.41 | 0.40 | 30.6 | 0.96 | 0.36 | 0.35 | 20.6 | 0.97 | 0.33 | 0.33 |
| R2 | 0.63 | 0.63 | 0.61 | 0.61 | 0.15 | 0.15 | 0.16 | 0.14 | 0.73 | 0.73 | 0.71 | 0.74 |
| pGW | NA | 0.21 | 0.00 | 0.00 | NA | 0.31 | 0.00 | 0.00 | NA | 0.01 | 0.00 | 0.00 |
5. Conclusions
Acknowledgements
Appendix A
Appendix B
| Parameters | All Sample | In-Sample |
|---|---|---|
| 0.0840 | 0.0488 | |
| 1.0907 | 1.0937 | |
| 0.0093 | 0.0087 | |
| 0.0296 | 0.0369 |
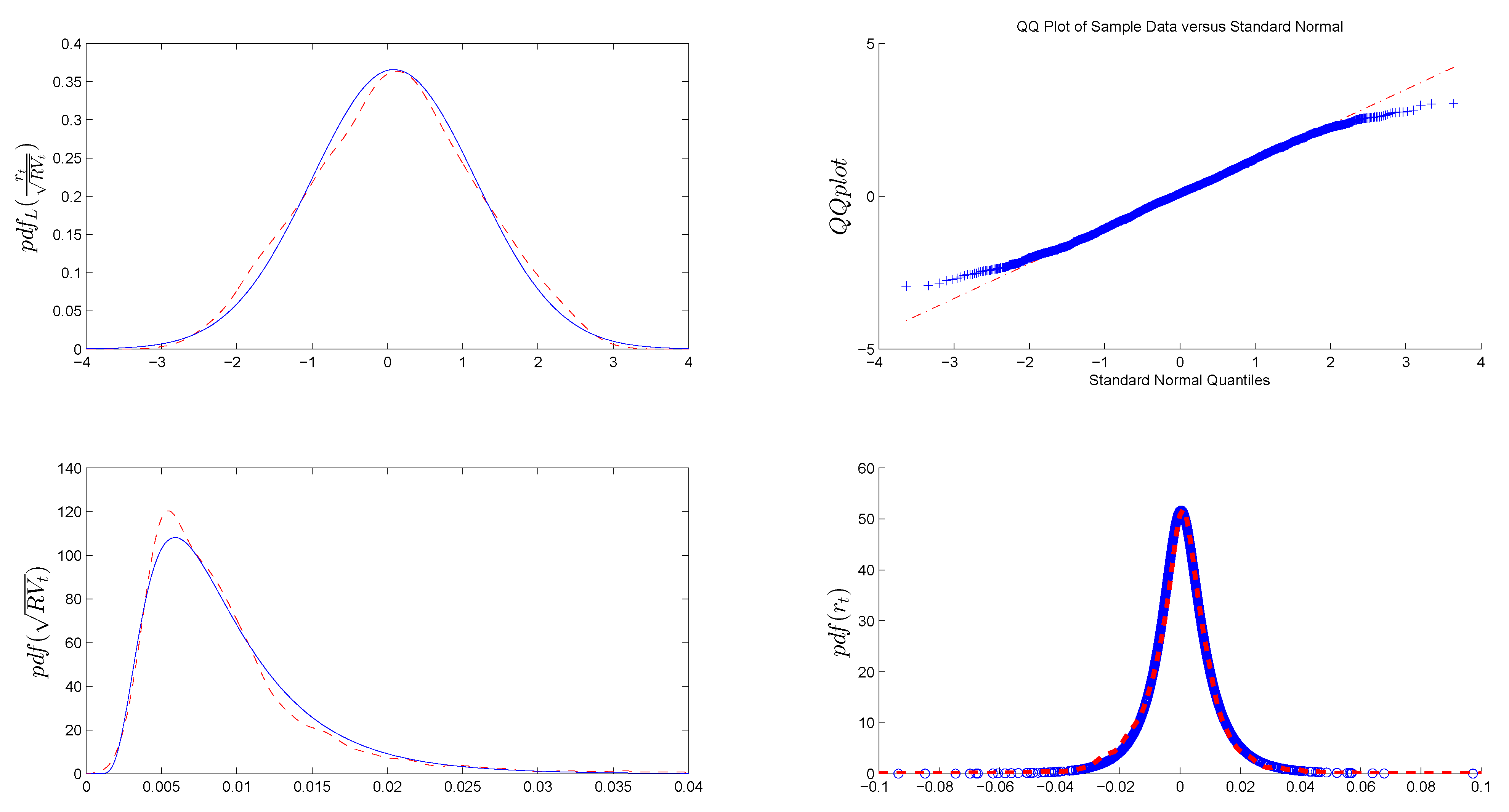
Appendix C
Conflicts of Interest
References
- R. Engle. “Autoregressive Conditional Heteroskedasticity With Estimates of the Variance of UK. Inflation.” Econometrica 50 (1982): 987–1008. [Google Scholar] [CrossRef]
- T. Bollerslev. “Generalized Autoregressive Conditional Heteroskedasticity.” J. Econom. 31 (1986): 307–327. [Google Scholar] [CrossRef]
- T. Bollerslev, R. Engle, and D. Nelson. “ARCH Models.” In Handbook of Econometrics, Vol.IV. Edited by R. Engle and D. McFadden. Amsterdam, The Netherlands: Elsevier Science B.V., 1994, Chapter 49; pp. 2959–3038. [Google Scholar]
- J. Hull, and A. White. “The Pricing of Options on Assets with Stochastic Volatilities.” J. Financ. 42 (1987): 281–300. [Google Scholar] [CrossRef]
- A. Melino, and S. Turnbull. “Pricing Foreign Currency Options with Stochastic Volatility.” J. Econom. 45 (1990): 239–265. [Google Scholar] [CrossRef]
- T. Andersen, T. Bollerslev, F. Diebold, and P. Labys. “Modeling and Forecasting Realized Volatility.” Econometrica 71 (2003): 579–625. [Google Scholar] [CrossRef]
- J. Maheu, and T. McCurdy. “Do High-frequency Measures of Volatility Improve Forecasts of Return Distributions? ” J. Econom. 160 (2011): 69–76. [Google Scholar] [CrossRef]
- T. Andersen, T. Bollerslev, and F. Diebold. “Roughing it Up: Disentangling Continuous and Jump Components in Measuring, Modeling and Forecasting Asset Return Volatility.” Rev. Econ. Stat. 89 (2007): 701–720. [Google Scholar] [CrossRef]
- M. McAleer, and M. Medeiros. “A multiple regime smooth transition heterogeneous autoregressive model for long memory and asymmetries.” J. Econom. 147 (2008): 104–119. [Google Scholar] [CrossRef]
- T. Andersen, T. Bollerslev, F. Diebold, and H. Ebens. “The Distribution of Realized Stock Return Volatility.” J. Financ. Econ. 61 (2001): 43–76. [Google Scholar] [CrossRef]
- T. Andersen, and T. Bollerslev. “Heterogeneous Information Arrivals and Return Volatility Dynamics: Uncovering the Long-Run in High Frequency Returns.” J. Financ. 52 (1997): 975–1005. [Google Scholar] [CrossRef]
- C. Granger, and A. Ding. “Varieties of Long Memory Models.” J. Econom. 73 (1996): 61–77. [Google Scholar] [CrossRef]
- P. Perron. “The Great Crash, the Oil Price Shock and the Unit Root Hypothesis.” Econometrica 57 (1989): 1361–1401. [Google Scholar] [CrossRef]
- E. Zivot, and D. Andrews. “Further Evidence on the Great Crash, the Oil-Price Shock, and the Unit-Root Hypothesis.” J. Bus. Econ. Stat. Am. Stat. Assoc. 10 (1992): 251–270. [Google Scholar]
- K. Choi, W. Yu, and E. Zivot. “Long Memory versus Structural Breaks in Modeling and Forecasting Realized Volatility.” J. Int. Money Financ. 29 (2010): 857–875. [Google Scholar] [CrossRef]
- F. Corsi. “A Simple Approximate Long-Memory Model of Realized Volatility.” J. Financ. Econom. 7 (2009): 174–196. [Google Scholar] [CrossRef]
- R. Giacomini, and H. White. “Tests of Conditional Predictive Ability.” Econometrica 74 (2006): 1545–1578. [Google Scholar] [CrossRef]
- M. Scharth, and M. Medeiros. “Asymmetric effects and long memory in the volatility of Dow Jones stocks.” Int. J. Forecast. 25 (2009): 304–327. [Google Scholar] [CrossRef]
- O. Barndorff-Nielsen, and N. Shephard. “Econometric analysis of realized volatility and its use in estimating stochastic volatility models.” J. R. Stat. Soc. 64 (2002): 253–280. [Google Scholar] [CrossRef]
- O. Barndorff-Nielsen, and N. Shephard. “Estimating quadratic variation using realized variance.” J. Appl. Econom. 17 (2002): 457–477. [Google Scholar] [CrossRef]
- O. Barndorff-Nielsen, P. Hansen, A. Lunde, and N. Shephard. “Designing realised kernels to measure the ex-post variation of equity prices in the presence of noise.” Econometrica 76 (2008): 1481–1536. [Google Scholar] [CrossRef]
- C. Brownlees, and G. Gallo. “Comparison of volatility measures: A risk management perspective.” J. Financ. Econ. 8 (2009): 29–56. [Google Scholar] [CrossRef]
- U. Muller, M. Dacorogna, R. Dav, R. Olsen, O. Pictet, and J. Ward. “Fractals and Intrinsic Time—A Challenge to Econometricians.” In Proceedings of the XXXIXth International AEA Conference on Real Time Econometrics, Luxembourg, 14–15 October, 1993.
- H. Tong. “On a Threshold Model.” In Pattern Recognition and Signal Processing. Edited by C. Chen. Amsterdam, The Netherlands: Sijthoff and Noordhoff, 1978, pp. 101–141. [Google Scholar]
- H. Tong, and K. Lim. “Threshold Autoregression, Limit Cycles and Cyclical Data.” J. R. Stat. Soc. Ser. B Methodol. 42 (1980): 245–292. [Google Scholar]
- B. Hansen. “Testing for Linearity.” J. Econ. Surv. 13 (1999): 551–576. [Google Scholar] [CrossRef]
- R. Davies. “Hypothesis Testing When a Nuisance Parameter is Present Only Under the Alternative.” Biometrika 64 (1977): 247–254. [Google Scholar] [CrossRef]
- R. Davies. “Hypothesis Testing When a Nuisance Parameter is Present Only Under the Alternative.” Biometrika 74 (1987): 33–43. [Google Scholar]
- B. Hansen. “Sample splitting and threshold estimation.” Econometrica 68 (2000): 575–603. [Google Scholar] [CrossRef]
- F. Diebold, and C. Chen. “Testing structural stability with endogenous breakpoint. A size comparison of analytic and bootstrap procedures.” J. Econom. 70 (1996): 221–241. [Google Scholar]
- D. Andrews. “Tests for parameter instability and structural change with unknown change point.” Econometrica 61 (1993): 821–856. [Google Scholar] [CrossRef]
- F. Corsi, S. Mittnik, C. Pigorsch, and U. Pigorsch. “The volatility of realized volatility.” Econom. Rev. 27 (2008): 46–78. [Google Scholar] [CrossRef]
- K. Chan. “Consistency and Limiting Distribution of the Least Squares Estimator of a Threshold Autoregressive Model.” Ann. Stat. 21 (1993): 520–533. [Google Scholar] [CrossRef]
- B. Hansen. “Inference in TAR models.” Stud. Nonlinear Dyn. Econom. 2 (1997): 1–14. [Google Scholar] [CrossRef]
- P. Franses, and D. Dijk. Non-Linear Time Series Models in Empirical Finance. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]
- K. Chan, J. Petrucelli, and H.T.S. Woolford. “A multiple threshold AR(1) model.” J. Appl. Probab. 22 (1985): 267–279. [Google Scholar] [CrossRef]
- J. Knight, and S. Satchell. “Some New Results for Threshold AR(1) Models.” J. Time Ser. Econom. 3 (2011): 1–42. [Google Scholar] [CrossRef]
- L. Glosten, R. Jagannathan, and D. Runkle. “On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks.” J. Financ. 48 (1993): 1779–1801. [Google Scholar] [CrossRef]
- L. Forsberg, and T. Bollerslev. “Bridging the Gap Between the Distribution of Realized (ECU) Volatility and ARCH Modeling (of the Euro): The GARCH-NIG Model.” J. Appl. Econ. 17 (2002): 535–548. [Google Scholar] [CrossRef]
- L. Stentoft. Option Pricing Using Realized Volatility. Aarhus, Denmark: CREATES Research Paper, 2008. [Google Scholar]
- G. Heber, A. Lunde, N. Shephard, and K. Sheppard. “Oxford-Man Institute’s realized library, Library version: 0.2.” Oxford, UK: Oxford-Man Institute, 2009. [Google Scholar]
- T. Andersen, T. Bollerslev, P. Frederiksen, and M. Nielsen. “Continuous-time models, realized volatilities, and testable distributional implications for daily stock returns.” J. Appl. Econom. 25 (2010): 233–261. [Google Scholar] [CrossRef]
- R. Dacco, and S. Satchell. “Why do Regime-switching Models Forecast so Badly? ” J. Forecast. 18 (1999): 1–16. [Google Scholar] [CrossRef]
- C. Ornthanalai. “Levy jump risk: Evidence from options and returns.” J. Financ. Econom. 112 (2014): 69–90. [Google Scholar] [CrossRef]
- P. Hansen, and A. Lunde. “A forecast comparison of volatility models: Does anything beat a GARCH(1,1)? ” J. Appl. Econom. 20 (2005): 873–889. [Google Scholar] [CrossRef]
- F. Corsi, N. Fusari, and D. Vecchia. “Realizing smiles: Pricing options with realized volatility.” J. Financ. Econ. 107 (2013): 284–304. [Google Scholar] [CrossRef]
- P. Christoffersen, B. Feunou, K. Jacobs, and N. Meddahi. “The Economic Value of Realized Volatility: Using High-Frequency Returns for Option Valuation.” J. Financ. Quant. Anal. 49 (2014): 663–697. [Google Scholar] [CrossRef]
- A. Patton, and I. Salvatierra. “Dynamic Copula Models and High Frequency Data.” J. Empir. Financ. 30 (2015): 120–135. [Google Scholar]
- D. Oh, and A. Patton. “High Dimension Copula-Based Distributions with Mixed Frequency Data.” J. Econom., 2015. Forthcoming. [Google Scholar]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pypko, S. Volatility Forecast in Crises and Expansions. J. Risk Financial Manag. 2015, 8, 311-336. https://doi.org/10.3390/jrfm8030311
Pypko S. Volatility Forecast in Crises and Expansions. Journal of Risk and Financial Management. 2015; 8(3):311-336. https://doi.org/10.3390/jrfm8030311
Chicago/Turabian StylePypko, Sergii. 2015. "Volatility Forecast in Crises and Expansions" Journal of Risk and Financial Management 8, no. 3: 311-336. https://doi.org/10.3390/jrfm8030311
APA StylePypko, S. (2015). Volatility Forecast in Crises and Expansions. Journal of Risk and Financial Management, 8(3), 311-336. https://doi.org/10.3390/jrfm8030311





