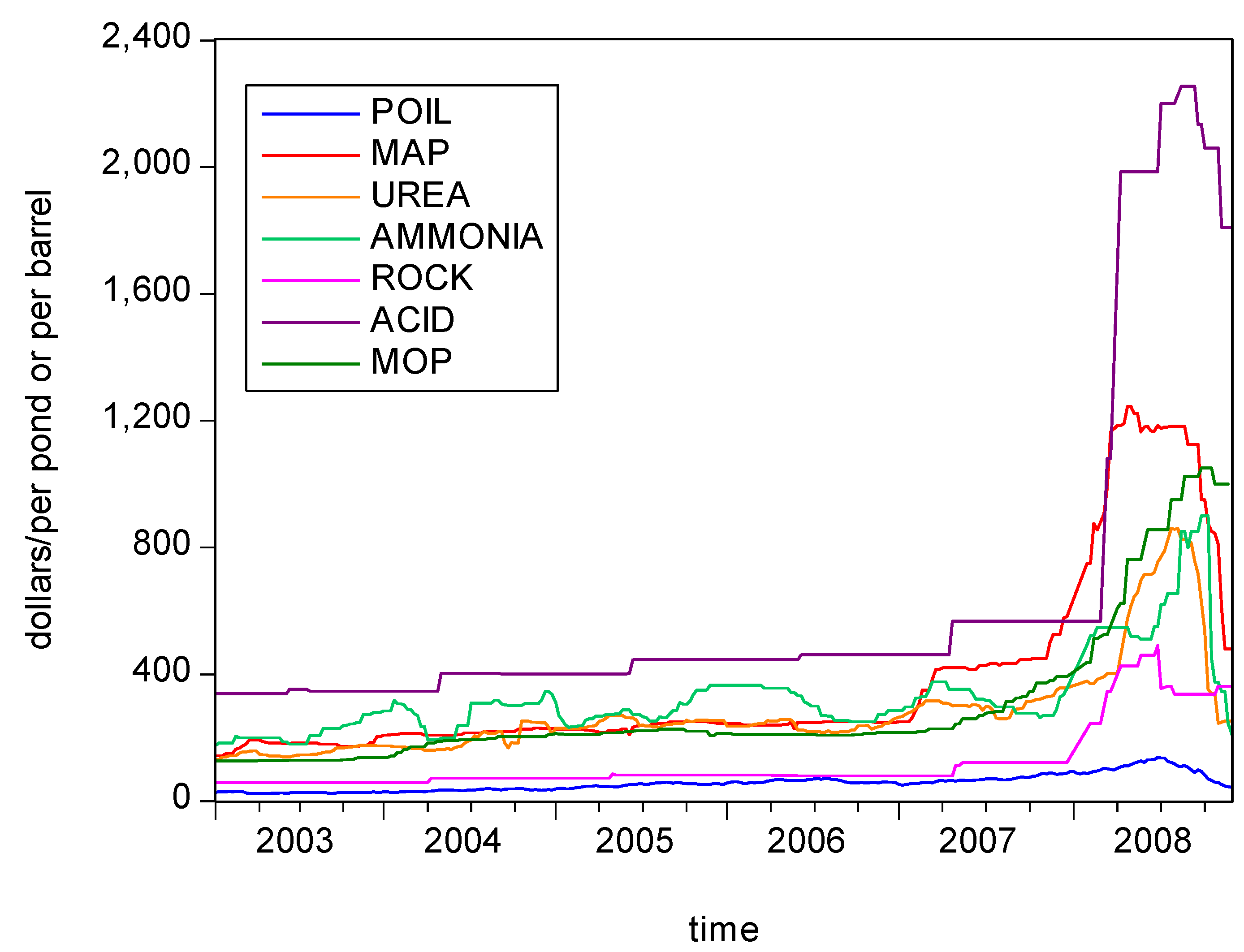
Both the autoregressive distributed lag (ARDL) model and the generalized autoregressive conditional heteroskedasticity (GARCH) model will be used to evaluate the effects of oil and global fertilizer prices, and to model the volatility in global fertilizer and crude oil prices. Before estimating the ARDL and GARCH models, the Lee and Strazicich (2003) approach will be used to capture the structural breakpoint in fertilizer prices, which should enable identification of alternative time periods for the volatility in fertilizer prices.
3.2 Autoregressive Distributed Lag Model
Fertilizer can be divided into organic fertilizer and chemical fertilizer, with the latter being a high user of energy. For instance, nitrogen fertilizer production relies mainly on coal and natural gas, so that a causal relationship might be deemed to exist between crude oil and fertilizers prices. Such a relationship may be determined by a Granger Causality test and the autoregressive distributed lag (hereafter ARDL) model. The ARDL model, in which the data determine the short-run dynamics, would seem to be one of the most widely used models for estimating time series energy demand relationships (Jones, 1993; Benten and Engsted, 2001; Jones,1993; Benten and Engsted,2001; Dimitropoulos et al., 2005; Hunt et al., 2005; Hunt and Ninomiya, 2003; Chen et al.,2010).
Hendry(2005) indicates that the ARDL model merges dynamics and interdependence with different illustrations grounded by linear relationships. In this model, the price of a specific fertilizer is interpreted by the lags of itself price and crude oil prices. A general ARDL model for the global fertilizer price can be shown as bellow:
where
is the global fertilizer price at time t, and
is the price of crude oil at time t.
The coefficient means the effect of the j-period lagged crude oil price on the fertilizer price, which implies that the fertilizer price can be predicted by the crude oil price. A test of the null hypothesis that each = 0 is a test of Granger non-causality.
All the variables included in the price should be stationary series to avoid spurious regression results, whereby the asymptotic standard normal results no longer hold. For this reason, the structural breakpoints of the crude oil price are estimated using the two-break minimum Lagrange Multiplier (LM) unit root test of Lee and Strazicich (2003). If and when the appropriate structural breakpoints are found, the fertilizer price equations will be estimated for different periods.
3.3 Conditional Mean and Conditional Volatility Models
Engle (1982) captured time-varying conditional volatility, or financial risk, through the autoregressive conditional heteroskedasticity (ARCH) model. Subsequent extensions, such as the generalized ARCH (GARCH) model of Bollerslev (1986), have been used to capture dynamic volatility for univariate and multivariate processes. The GARCH model is most widely used for symmetric shocks. In the presence of asymmetric shocks, whereby positive and negative shocks of equal magnitude have different impacts on volatility, the GJR model of Glosten et al. (1992) and the EGARCH model of Nelson (1991) are very useful. Further theoretical developments in specification, estimation and asymptotic theory have been suggested in Ling and Li (1997), Ling and McAleer (2002a, 2002b, 2003a, 2003b), and McAleer (2005).
The following model and discussion are based on McAleer (2005) and McAleer et al. (2007). The methods have been extended detect the volatility in patent growth by Chan et al. (2005a), in analyzing the volatility of USA ecological patents by Chan (2005b) and Marinova and McAleer (2003), in modelling the volatility of environment risk by Hoti et al. (2005), and the volatility of atmospheric carbon dioxide concentrations by McAleer and Chan (2006). However, there does not yet seem to have been any empirical analysis of such volatility models on global fertilizer prices, and hence no assessment of risk associated with such prices.
In this paper, we consider the stationary AR(1)-GARCH(1,1), or ARMA(p,q)-GARCH(1,1), model for the global fertilizer price series data, namely
:
where
is the unconditional shock (or movement in global fertilizer prices), and is given by:
and
0,
,
are sufficient conditions to ensure that the conditional variance
. Ling and McAleer (2003b) indicated equation (2) in the AR(1) process could be modified to incorporate a non-stationary ARMA(p,q) conditional mean and a stationary GARCH(r,s) conditional variance. In (2), the
(or ARCH) effect indicates the short run persistence of shocks, while the
(or GARCH) effect indicates the contribution of shocks to long run persistence (namely,
).
The parameters in equations (1) and (2) are typically estimated by the maximum likelihood method. Ling and McAleer (2003b) investigate the properties of adaptive estimators for univariate non-stationary ARMA models with GARCH(r,s) errors. The conditional log-likelihood function is given as follows:
As the GARCH process in equation (2) is a function of the unconditional shocks, the moments of
need to be investigated. Ling and Li (2002a) showed that the ARCH(p,q) model is strictly stationary and ergodic if the second moment is finite, that is,
. Ling and McAleer (2002b) showed that the Quasi MLE (QMLE) for GARCH(p,q) is consistent if the second moment is finite. Ling and Li (1997) demonstrated that the local QMLE is asymptotically normal if the fourth moment is finite, that is,
, while Ling and McAleer (2002b) proved that the global QMLE is asymptotically normal if the sixth moment is finite, that is,
. Using results from Ling and Li (1997), Bollerslev (1986), Nelson (1990), and Ling and McAleer (2002a, 2002b), the necessary and sufficient condition for the existence of the second moment of
for GARCH(1,1) is
and, under normality, the necessary and sufficient condition for the existence of the fourth moment is
.
For the univariate GARCH(p,q) model, several regularity conditions exist that enable the statistical validity of the model to be checked against the empirical data. Bougerol and Picard (1992) derived the necessary and sufficient condition, namely the log-moment condition or the negativity of a Lyapunov exponent, for strict stationarity and ergodicity (see Nelson (1990)). Using the log-moment condition, Elie and Jeantheau (1995) and Jeantheau (1998) established it was sufficient for consistency of the QMLE of GARCH(p,q) (see Lee and Hansen (1994) for the proof in the case of GARCH(1,1)), and Boussama (2000) showed that it was sufficient for asymptotic normality. Based on these theoretical developments, a sufficient condition for the QMLE of GARCH(1,1) to be consistent and asymptotically normal is given by the log-moment condition, namely
However, this condition is not straightforward to check in practice, even for the GARCH(1,1) model, as it involves the expectation of a function of a random variable and unknown parameters. The extension of the log-moment condition to multivariate GARCH(p,q) models has not yet been shown to exist, although Jeantheau (1998) showed that the ultivariate log-moment condition could be verified under the additional assumption that the determinant of the unconditional variance of in (1) is finite. Jeantheau (1998) assumed a multivariate log-moment condition to prove consistency of the QMLE of the multivariate GARCH(p,q) model. An extension of Boussama’s (2005b) log-moment condition to prove the asymptotic normality of the QMLE of the multivariate GARCH(p,q) process is not yet available.
The effects of positive shocks on the conditional variance,
, are assumed to be the same as the negative shocks in the symmetric GARCH model. In order to accommodate asymmetric behavior, Glosten et al. (1992) proposed the GJR model, for which GJR(1,1) is defined as follows:
where
,
,
,
are sufficient conditions for
and
is an indicator variable defined by
as
has the same sign as
. The indicator variable differentiates between positive and negative shocks, so that asymmetric effects in the data are captured by the coefficient
, with
0. The asymmetric effect,
, measures the contribution of shocks to both short run persistence,
, and to long run persistence,
.
Ling and McAleer (2002b) derived the unique strictly stationary and ergodic solution of a family of GARCH processes, which includes GJR(1,1) as a special case, a simple sufficient condition for the existence of the solution, and the necessary and sufficient condition for the existence of the moments. For the special case of GJR(1,1), Ling and McAleer (2002b) showed that the regularity condition for the existence of the second moment under symmetry of
is
and the condition for the existence of the fourth moment under normality of
is
while McAleer et al. (2007) showed that the weaker log-moment condition for GJR(1,1) was given by
which involves the expectation of a function of a random variable and unknown parameters.
An alternative model to capture asymmetric behavior in the conditional variance is the Exponential GARCH (EGARCH(1,1)) model of Nelson (1991), namely:
where the parameters
,
and
have different interpretations from those in the GARCH(1,1) and GJR(1,1) models.
As noted in McAleer et al. (2007), there are some important differences between EGARCH and the previous two models, as follows: (i) EGARCH is a model of the logarithm of the conditional variance, which implies that no restrictions on the parameters are required to ensure ; (ii) Nelson (1991) showed that ensures stationarity and ergodicity for EGARCH(1,1); (iii) Shephard (1996) observed that is likely to be a sufficient condition for consistency of QMLE for EGARCH(1,1); (iv) as the conditional (or standardized) shocks appear in equation (4), would seem to be a sufficient condition for the existence of moments; and (v) in addition to being a sufficient condition for consistency, is also likely to be sufficient for asymptotic normality of the QMLE of EGARCH(1,1).
Furthermore, EGARCH captures asymmetries differently from GJR. The parameters and in EGARCH(1,1) represent the magnitude (or size) and sign effects of the conditional (or standardized) shocks, respectively, on the conditional variance, whereas and represent the effects of positive and negative shocks, respectively, on the conditional variance in GJR(1,1).