Ensemble Learning and an Adaptive Neuro-Fuzzy Inference System for Cryptocurrency Volatility Forecasting

Abstract

The purpose of this study is to conduct an empirical comparative study of volatility models for three of the most popular cryptocurrencies. We study the volatility of the following cryptocurrencies: Bitcoin, Ethereum, and Litecoin. We consider the GARCH-type, boosting-family-tree-based ensemble learning, and ANFIS volatility models for these financial crypto-assets, which some have claimed capture stylized facts about cryptocurrency volatility well. We conduct comparative studies on in-sample and out-of-sample empirical analyses. The results show that tree-based ensemble learning delivers better forecast accuracy. Nevertheless, the performance of some GARCH-type volatility models is relatively close to that of the best model on both training and evaluation samples.

1. Introduction

Following the success of the first cryptocurrency, Bitcoin, the concept has arisen as an alternative to classic financial systems. Investors’ confidence in DeFi has brought about the fast-paced growth of digital asset classes such as Ethereum, stablecoins, smart contracts, and non-fungible tokens, among others. Many companies and markets support business transactions through digital wallets using cyptocurrencies as the payment mode Mallqui and Fernandes (2019). Surprisingly, DeFi’s popularity has also attracted the attention of centralized authorities, such as government authorities and central banks, and has inspired them to push forward the development of their own cryptocurrencies, which are called central bank digital currencies. These authorities have also started thinking about how cryptocurrencies contribute to the economy and addressing regulations for digital assets in, for example, the US, the UAE, and many other countries. Investors, government authorities, and academic researchers continue to pay more attention to cryptocurrencies. In particular, the modeling of cryptocurrencies has become another challenge for quantitative analysts.

Cryptocurrency prices are highly volatile Nadarajah (2017), so it is important to model and predict cryptocurrency volatility for risk management purposes. Empirical comparative studies on cryptocurrency prices and their volatilities have often been addressed in the literature. Works on cryptocurrency volatility modeling began by comparing various parametric GARCH-based models Chu et al. (2017); Conrad Christian and Eric (2018); Katsiampa (2017). As artificial intelligence has gained value in financial time–series modeling, research has been extended to machine-learning-based cryptocurrency volatility models Jiang (2020); Shen et al. (2021). Another direction of stock price volatility modeling consists of combining previous GARCH and machine learning volatility models with fuzzy logic theory, such as the evolving fuzzy GARCH and the neuro-fuzzy inference system named ANFIS.

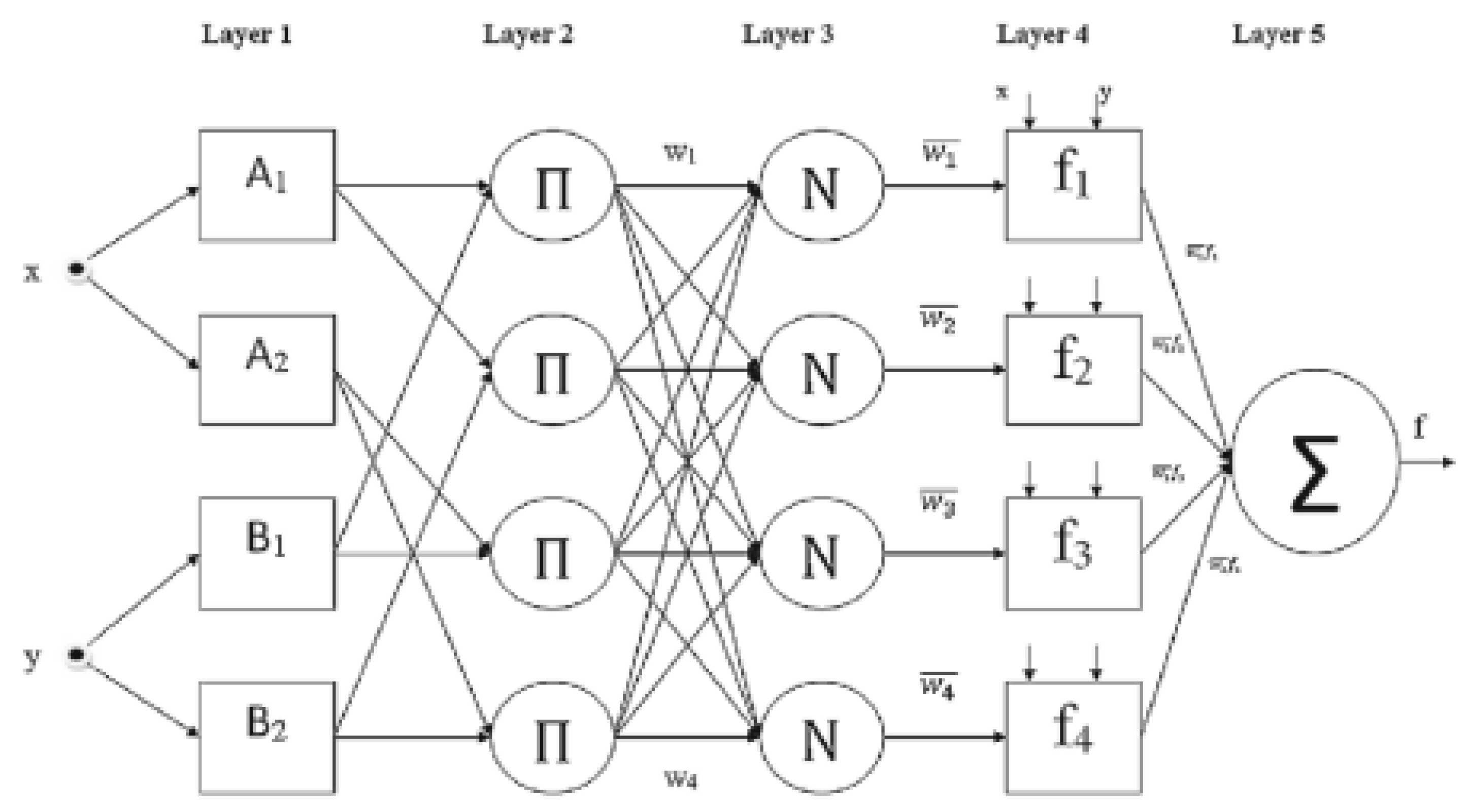
In this study, we enhance the work of previous empirical studies. We consider three volatility models, which are the GARCH family, ensemble learning, and ANFIS models, for three cryptocurrencies: Bitcoin, Ethereum, and Litecoin. We conduct an in-sample empirical analysis and an out-of-sample forecast accuracy evaluation of these volatility models for each cryptocurrency. To the best of our knowledge, comparative studies using these three types of volatility methods on these three financial crypto-assets have not yet appeared in the literature.

Some motivations for considering these models are as follows. GARCH-type models are well established for capturing various stylized facts concerning cryptocurrency return volatility, such as when capturing volatility clustering. ANFIS uses its flexibility to model nonlinearities. It has captured stylized facts on the volatility of financial variables well in previous work Conrad Christian and Eric (2018). The power of ANFIS in stock return volatility modeling leads us to consider it for cryptocurrency price volatility. We consider the boosting tree family of models to benefit from the various advantages of tree-based ensemble learning models. These models are based on regularization techniques and on the aggregation of several decision tree models. Moreover, they are known to be computationally fast compared with other kinds of machine learning methods. When cryptocurrency volatility modeling is reduced to the problem of function approximation, the strength of the boosting tree family appears most appropriate. The boosting tree family has delivered better accuracy in the forecasting of cryptocurrency volatility prediction in the literature.

This article is organized as follows. Section 2 presents the literature review, Section 3 presents the methodology, and the following section presents the empirical analysis. The last section provides concluding remarks.

2. Literature Review

Satoshi Nakamoto created Bitcoin in 2009 Satoshi (2009). This was the first cryptocurrency, and it has rapidly attracted the attention of investors and academics as an alternative to conventional currencies. Ten years later, we had a list of 1536 types of cryptocurrencies with a total market capitalization of USD 321 billion, of which Bitcoin occupied the most considerable share, followed by Ethereum and Litecoin Kristjanpoller and Minutolo (2018). Interest in cryptocurrencies never ceases. Our literature analysis will start with an analysis of works on Bitcoin prices and will later include Ethereum and Litecoin prices.

In the literature, many researchers have studied Bitcoin prices/returns, as well as their volatility. Studies have investigated potential factors driving Bitcoin’s price/return dynamics. These factors may come from the supply–demand side of Bitcoin markets, such as the Bitcoin trading volume, or from other financial markets, such as exchange rates or energy and index markets. They may also come from internet discussions about Bitcoin, which can be seen as a proxy for investor interest in Bitcoin; examples include the non-market-based factors of Google trends Kristoufek (2013); Michal et al. (2015), the volume of daily views on the Bitcoin entry on Wikipedia Guesmi et al. (2017), and others. The integration of these internal and external factors into Bitcoin’s price/return dynamics has been of interest. Google trends and Bitcoin trading volume have been stated Kristoufek (2013) as determinants for Bitcoin prices/returns. Econometric and automated models have been considered, and they range from linear to machine learning methodologies. Using parametric VAR and VECM dynamics to address the endogeneity problem and to examine the long-term relationship between the considered price series, significant effects of the macroeconomic and financial variables, oil prices, American financial market indices, and exchange rates have been found Guesmi et al. (2017).

Some studies focus on changes in Bitcoin price/return directions. They have used machine learning models and algorithms to address such issues. The authors of Madan (2014) predicted signs of future changes in Bitcoin prices using a machine learning algorithm. Similar work was conducted by Mallqui and Fernandes (2019). The authors of Rakotomarolahy (2021) considered daily explanatory variables (such as oil prices, American financial market indices, exchange rates, Google trends from web searches for the word Bitcoin, and the Bitcoin trading volume, which are common in the literature on Bitcoin return modeling) using logistic regression, discriminant analysis, and machine learning classification techniques; they found those variables to be predictors for Bitcoin return directions, with extreme gradient boosting ensemble learning being used for the dynamics.

We mention some related works on cryptocurrency market characteristics, such as the presence of structural breaks in cryptocurrencies Canh et al. (2019), the existence of persistence in the cryptocurrency market Caporale et al. (2018), the contagion effect on all other currencies da Gama Silva et al. (2019), the occurrence of herding behavior Bouri et al. (2019), and the “none” effect of new monetary policy on Bitcoin Vidal-Tomás and Ibañez (2018). Cryptocurrency risk analyses for hedging strategies and portfolio management purposes were conducted in Guesmi et al. (2017), Mba and Mwambi (2020), and Chu et al. (2017).

Cryptocurrency prices are known to be highly volatile. They largely depend on the scarcity of coins and people’s confidence in them, which affects their value and leads to strong upward and downward price fluctuations. Such strong fluctuations characterize the volatility of cryptocurrency price series Yu (2019), where companies holding large numbers of them are highly exposed to risks. To help companies manage these risks, predicting the volatility of cryptocurrencies is an essential way to shed light on their behavior and trading strategies.

To model cryptocurrency price volatility, researchers try to tackle various stylized facts. Several works have explored long-run memory in cryptocurrency volatility. Aurelio Bariviera (2017) found that the daily volatility of cryptocurrencies exhibited long-term memory over all periods. Similarly, volatility is characterized by long-run dependence behavior Charfeddine and Maouchi (2019), and Lahmiri et al. (2018) found such dependence with a high degree of randomness. The authors of Mensi et al. (2019) showed the existence of dual long-run memory in Bitcoin return and its volatility. Regarding the day-of-the-week effect, Aharon and Qadan (2019) addressed the existence of the day-of-the-week effect in cryptocurrency returns and volatility. In particular, Ma and Tanizaki (2019) showed the existence of high and significant volatility on Mondays and Thursdays.

For other effects and factor determinants of cryptocurrency volatilities, Balcilar et al. (2017) found that the volume cannot predict the volatility of a cryptocurrency. The authors of Bouri et al. (2018) confirmed this using copula models, where this financial stress effect limited the direction of the forecast. The authors of Yu (2019) and Baur and Dimpfl (2018) proved that leverage has a significant impact on the future volatility of cryptocurrencies. Regarding the momentum effect, Grobys and Sapkota (2019) showed that there is no significant dynamic reward. However, Cheng et al. (2019) found a strong dynamic effect on cryptocurrencies using DFA and MF-DFA. For the overreaction effect, Chevapatrakul and Mascia (2024) provided evidence of investor overreaction during days of sharp market declines and weeks of market recoveries. Regarding the spillover effect, Guesmi et al. (2017) stated that markets are characterized by return and volatility spillovers, and they are associated with strong positive correlations Canh et al. (2019). The authors of Aysan et al. (2018) studied the effect of geopolitical risk (GPR). They showed that Bitcoin returns and volatility are negatively and positively affected by GPR. They concluded that cryptocurrencies can be used as a hedging tool against GPR.

It is worth noting that most of the studies on cryptocurrency volatility modeling use GARCH-family models in their analysis. The authors of Katsiampa (2017) compared six GARCH models to model Bitcoin volatility while addressing possible asymmetry and nonlinearity, and they concluded that AR-CGARCH with long- and short-term components is an optimal model. The authors of Chu et al. (2017) fitted 12 GARCH models to each of the seven most popular cryptocurrencies and pointed out the power of IGARCH with persistent volatility and light structural changes. The authors of Ngunyi et al. (2019) used 13 GARCH-family models to forecast the volatilities of eight famous cryptocurrencies with 700 daily observations. The authors of Conrad Christian and Eric (2018) proposed the GARCH-MIDAS dynamics to capture the high-/low-frequency issues between the daily Bitcoin volatility and the monthly financial and macroeconomic variables when investigating the effect of the latter variables on the variable of interest. The authors of Walther et al. (2019) investigated the usefulness of exogenous factors in predicting 1-day, 7-day (one week), and 30-day (one month) cryptocurrency volatility. On a set of 17 different economic and financial factors, the average forecast was then combined using GARCH-MIDAS. Quyen Thieu (2017) derived a conditional heteroskedastic model with exogenous variables using the QMV estimation method and the semi-diagonal BEKK method with covariances.

However, the use of machine learning models started to emerge. The authors of Nakano et al. (2018) designed artificial neural network (ANN) classification models to extract meaningful trading signals from input technical indicators calculated from time–series performance data at 15-minute time intervals; in particular, the numerical results showed that the use of different technical indicators ultimately allowed overfitting to be avoided. The authors of Lukáš (2017) analyzed the realized volatility and predicted the log returns of BTCUSD and EURUSD exchange rates on a daily time scale using an artificial neural network and HARRVJ; they concluded that the EURUSD exchange rate is more volatile than that of BTCUSD. Xiangxi Jiang (2020) compared several neuron-based machine learning models (LSTM, MLP, GRU, and RNN) and found that the RNN performed better than other methods. Later, the use of machine learning exploded (see Khaldi et al. (2018, 2019); McNally et al. (2018); Shen et al. (2021); this is not an exhaustive list). The authors of Bouteska et al. (2024) compared several boosting and neuronal models and assessed the performance of the tree-based LightGBM model. For other works on tree-based ensemble learning models of volatility, we found Nasios and Vogklis (2022); Ying and Jungang (2017) for the boosting GBM, Ke et al. (2017) for the light boosting LightGBM, and Li et al. (2019) for the extreme boosting XGBM models. Few studies have investigated the combination of parametric and non-parametric methods for cryptocurrencies. We can mention the hybrid ANN-GARCH model with PCA preprocessing for predicting Bitcoin volatility Kristjanpoller and Minutolo (2018) and SVR-GARCH Herrera et al. (2018). Most of these studies were carried out on Bitcoin.

We see the changing behavior of cryptocurrency volatility dynamics for parametric specification, the power of tree-based ensemble learning models, and the limited use of hybrid volatility models on cryptocurrency.

In this research, we are interested in investigating how parametric models can capture stylized facts of cryptocurrency volatilities. The parametric models include models from the GARCH family, which are commonly used to forecast financial assets. We then compare their results with those of non-parametric models. We will consider two non-parametric methods, the hybrid ANFIS and the ensemble learning boosting types, such as the GBM, the XGBM, and the LightGBM, which are widely used in different areas of forecasting due to their strong generalization capabilities.

3. Cryptocurrency Volatility Models

Given any cryptocurrency price process $p_t$, and following Conrad Christian and Eric (2018); Khaldi et al. (2019), the daily log returns $r_t=log{p}_t-log{p}_{t-1}$ follow the random process

$${\displaystyle r_t={\mu }_t+{\epsilon }_{t}with{\epsilon }_t={\sigma }_t{z}_t,}$$

(1)

where ${\mu }_t$ is the conditional mean, ${\sigma }_t^2$ is the conditional variance of $r_t$, and $z_t$ is the innovation process. The conditional variance ${\sigma }_t^2$ is not constant and can be expressed in functional form as follows:

$${\displaystyle {\sigma }_t^2=f\left({\sigma }_{t-1}^2,{\sigma }_{t-2}^2,\dots ,{\sigma }_{t-1},{\sigma }_{t-2},\dots ,{\epsilon }_{t-1}^2,{\epsilon }_{t-2}^2,\dots ,{\epsilon }_{t-1},{\epsilon }_{t-2},\dots \right).}$$

(2)

The specification of the link function f depends on the method used (parametric or non-parametric). We will use the following volatility methods for the estimation of f: parametric GARCH-type models, three tree-based ensemble learning models of volatility (the GBM, the XGBM, and the LightGBM), and the hybrid ANFIS.

3.1. GARCH Models

We specify the link function f in relation (2) through parameters in GARCH models. We consider the following GARCH family processes that are frequently used when modeling the volatility of financial time series of cryptocurrency: the standard GARCH model (sGARCH) Bollerslev (1986), the threshold GARCH model (TGARCH) Zakoian (1994), the exponential GARCH model (EGARCH) Nelson (1991), and the Glosten–Jagannathan–Runkle GARCH model (GJR-GARCH) Glosten et al. (1993). We provide their mathematical expressions in

Table 1. Some parametric GARCH volatility models.

Model Name	Model Expression
sGARCH	${\sigma }_t^2=\omega +{\sum }_{i=1}^p{\alpha }_i{\epsilon }_{t-i}^2+{\sum }_{j=1}^q{\beta }_j{\sigma }_{t-j}^2$
TGARCH	${\sigma }_t=\omega +{\sum }_{i=1}^p{\alpha }_i\left[\left(1-{\gamma }_i\right)I\left({\epsilon }_{t-i}>0\right)-\left(1+{\gamma }_i\right)I\left({\epsilon }_{t-i}<0\right)\right]{\epsilon }_{t-i}+{\sum }_{j=1}^q{\beta }_j{\sigma }_{t-j}$
EGARCH	$log\left({\sigma }_t^2\right)=\omega +{\sum }_{j=1}^q{\beta }_{j}log\left({\sigma }_{t-j}^2\right)+{\sum }_{i=1}^p{\alpha }_i{\displaystyle \frac{{\epsilon }_{t-i}}{{\sigma }_{t-i}}}+{\sum }_{i=1}^p{\gamma }_i\left(\mid {\displaystyle \frac{{\epsilon }_{t-1}}{{\sigma }_{t-1}}}\mid \right)-\mathbb{E}\left(\mid {\displaystyle \frac{{\epsilon }_{t-1}}{{\sigma }_{t-1}}}\mid \right)$
GJR-GARCH	${\sigma }_t^2=\omega +{\sum }_{i=1}^p{\alpha }_i{\epsilon }_{t-i}^2+{\sum }_{i=1}^p{\gamma }_{i}I\left({\epsilon }_{t-i}<0\right)+{\sum }_{j=1}^j{\beta }_j{\sigma }_{t-j}^2$

.

In Table 1, $\left(\omega ,{\alpha }_i,{\beta }_j,{\gamma }_i\right)$ are parameters to be estimated, and I is an indicator function that is equal to 1 if ${\epsilon }_{t-i}<0$ and 0 otherwise.

3.2. Ensemble Learning Methods

Ensemble learning gradient tree boosting has been successfully used to overcome overfitting. This method is based on the summation of several binary trees to predict the output. We consider the gradient boosting model Friedman (2001) and two successful extensions of this ensemble learning method, which are the LightGBM and the extreme gradient boosting development Chen and Guestrin (2016).

3.2.1. Gradient Boosting Machine Model

Boosting uses the same general principle of constructing a family of models that are then aggregated using a weighted average of the estimates. Each model is an adaptive version of the previous one, giving more weight to poorly fitted or poorly predicted observations in the next estimation. Intuitively, this algorithm concentrates its efforts on the observations that are hardest to fit, while aggregating all models reduces the risk of overfitting. In the same spirit of adaptive approximation, Friedman proposed multiple additive regression trees (MART) and, later, the GBM, a family of algorithms based on a supposedly convex and differentiable loss function called l. The basic principle is the same as that for adaBoost Freund and Schapire (1997); here, a sequence of models is built in such a way that, at each step, each model added to the combination appears as a step towards a better solution. The main innovation is that this step is taken in the direction of the gradient of the loss function to improve the convergence properties. A second idea is to approach the gradient using a regression tree to avoid over-learning. The adaptive step-by-step model can be written as

$${\displaystyle {\widehat{f}}_m\left(x\right)={\widehat{f}}_{m-1}\left(x\right)+c_m\delta \left(x;{\gamma }_m\right),}$$

(3)

where $c_m$ parameters are $\delta \left(x;{\gamma }_m\right)$, and the parameter classifiers ${\gamma }_m$ are converted into a gradient descent as follows:

$${\displaystyle {\widehat{f}}_m\left(x\right)={\widehat{f}}_{m-1}\left(x\right)+{\gamma }_m\sum _{i=1}^n{\nabla }_{f_{m-1}}l\left(r_i;f_{m-1}\left(x_i\right)\right)}$$

(4)

where $l\left(y;f\left(x\right)\right)$ denotes the loss function, ${\nabla }_{f_{m-1}}$ denotes the gradient of the loss function, and $x_i=\left(r_{i-1},r_{i-2},\dots \right)$. The problem can be simplified by looking for a better descent step $\gamma$.

$${\displaystyle \underset{\gamma }{min}\sum _{i=1}^n\left[l\left(y_i,f_{m-1}\left(x_i\right)\right)-\gamma \frac{\delta l\left(y_i,f_{m-1}\left(x_i\right)\right)}{f_{m-1}\left(x_i\right)}\right].}$$

(5)

See

Table 2. Boosting algorithm for regression.

Let $X_0$ be the forecast;

Initialize ${\widehat{f}}_0=argmi{n}_{\gamma }{\sum }_{i=1}^{n}l\left(y_i,\gamma \right)$;

For $m=1\stackrel{‘}{a}M$  do

Calculate $r_{mi}=-{\left[l\left(y_i,f_{t-1}\left(x_i\right)\right)-\gamma {\displaystyle \frac{\delta l\left(y_i,f_{m-1}\left(x_i\right)\right)}{f_{m-1}\left(x_i\right)}}\right]}_{f=f_{m-1}}$; $i=1,\dots ,m$.

Add a regression tree ${\delta }_m$ to pairs ${\left(x_i,r_{mi}\right)}_{i=1,\dots ,m}$.

Calculate ${\gamma }_m$ by solving the following: $mi{n}_{\gamma }{\sum }_{i=1}^{n}l\left(y_i,f_{m-1}\left(x_i\right)+\gamma {\delta }_m\left(x_i\right)\right)$;

Update: ${\widehat{f}}_m\left(x\right)={\widehat{f}}_{m-1}\left(x\right)+{\gamma }_t{\delta }_t$;

End for;

Results: ${\widehat{f}}_M\left(X_0\right)$

.

3.2.2. Extreme Gradient Boosting Machine Model

More recently, Chen and Guestrin (2016) proposed an extension of boosting known as extreme gradient boosting. A new objective function L is considered by adding a regularization term to the differentiable convex loss function of order 1:

$${\displaystyle L\left(f\right)=\sum _{i=1}^{n}l\left({\widehat{y}}_i,y_i\right)+\sum _{m=1}^M\mathsf{\Omega }\left({\delta }_m\right)}$$

(6)

with

$${\displaystyle \mathsf{\Omega }\left(\delta \right)=\alpha \left|\delta \right|+\frac{1}{2}\beta {\parallel \omega \parallel }^2,}$$

(7)

where $\left|\delta \right|$ is the number of leaves in the regression tree $\delta$, $\omega$ is the vector of values assigned to each of its leaves, $\alpha$ is Lasso’s penalty coefficient, and $\beta$ is a ridge regularization coefficient.

The features of the Xgboost learning algorithm for preventing overfitting are the following: its shrinkage and the approximate greedy algorithm. The shrinkage controls the learning rate by scaling the contribution of each tree. A lower value for shrinkage implies a larger value for M. When finding the best split in the learning tree, Xgboost uses an approximate algorithm instead of the exact greedy algorithm based on the enumeration of all possible splits. The LightGBM model and algorithm can be found in Ke et al. (2017).

3.3. ANFIS Model

ANFIS is obtained by combining neural networks, fuzzy logic, and inference systems. A graphical representation is provided in Figure 1.

This architecture is based on adaptive networks and implements a fuzzy inference system of the Takagi–Sugeno type. Rule l: If x is $A_i$ and y is $B_j$, then $f_l=p_{l}x+q_{l}y+r_l$, where $p_l$, $q_l$ and $r_l$ are parameters of the consequences and $A_i$ and $B_i$ are fuzzy subsets that contain the premises. It contains five layers. The nodes of the first layer and the fourth layer, represented by squares in Figure 1, are adaptive and, therefore, trainable. Nodes in the circle cannot be trained and indicate fixed nodes.

• First layer: The first layer is used to assign each variable to its membership function. This corresponds to the fuzzification of the inputs. Each neuron in this layer is an adaptive neuron that produces a degree of membership in a fuzzy subset.

  $${\displaystyle O_i^1={\mu }_{A_i}\left(x\right),}$$

  (8)

  where x is the input to the neuron, and $A_i$ is the fuzzy set associated with this membership function. The output $O_i^1$ denotes the degree to which the given x satisfies the quantifier $A_i$. $O_i^1$ can take any type of function with a maximum equal to 1 and a minimum equal to 0.
• Second layer: This layer is a rule layer containing fixed neurons (circles) denoted by $\Pi$ in Figure 1. The neural potential (or degree of activation or rule weight) of each rule is determined here. Each neuron receives the input values ${\mu }_{A_i}\left(x\right)$ from the first layer and represents the fuzzy sets (or rules) of the respective input values. The degree of activation for the rules is generated by multiplying the input signals.

  $${\displaystyle O_i^2={\mu }_{A_i}\left(x\right){\mu }_{B_i}\left(y\right);i=1,2.}$$

  (9)
  Generally, any T-norm operator (operation on fuzzy subsets) can be used here to calculate the antecedents of rules by replacing the multiplication sign. This operator is the alternative to the AND connector.
• Third layer: The third layer normalizes the rule weights. Each neuron in this layer is a fixed neuron (circle) denoted by N in Figure 1

  $${\displaystyle O_i^3=\overline{{\omega }_i}=\frac{{\omega }_i}{{\sum }_{i=1}^4{\omega }_i};i=1,2,3,4.}$$

  (10)
• Fourth layer: This determines the consequences of the rules. The output layer calculates the overall output as the sum of all signals arriving at this layer. Every neuron in this layer is an adaptive neuron. This layer also receives normalized firing powers as inputs, as well as the original x and y inputs themselves, and it determines the consequences of the rules. This layer is called the defuzzification layer and returns the weighted neuron values for each rule as

  $${\displaystyle O_i^4=\overline{{\omega }_i}{f}_i=\overline{{\omega }_i}\left(p_{i}x+q_{i}y+r_i\right).}$$

  (11)
  Parameters $p_{i}x,q_{i}y,r_i$ are tuned during the learning process. They are called consequence parameters. For each rule, there is a weight for each input plus a bias. Consequently, the number of parameters for each rule is one more than the number of inputs.
• Fifth layer: This layer contains a single neuron and calculates the overall output as the sum of all of the signals arriving at this layer.

  $${\displaystyle O_i^5=\sum _i\overline{{\omega }_i}{f}_i.}$$

  (12)

For developments of ANFIS in general prediction tasks, see R (1993); Tan et al. (2017). For developments in specific cryptocurrencies, see Atsalakis et al. (2019); Karabiyik and Ergun (2021).

4. Results and Discussion

4.1. Preliminary Results

We use daily closing price data for Bitcoin, Ethereum, and Litecoin from 1 January 2017 to 31 January 2024 available on https://fr.investing.com/crypto/. We begin by exploring information about these cryptocurrencies; graphs and basic statistics of the prices/returns of the three cryptocurrencies are provided.

According to Figure 2, the three cryptocurrencies exhibit common behavior where their prices fluctuate in the same direction with different magnitudes of downward and upward trends. Precisely, from 2014 to earlier in 2017, we registered an exponentially increasing trend. However, this period was followed by remarkable variation with a decreasing trend, which continued until the beginning of the year 2018. Afterward, all three prices started to regain value and reached their maximum values around the middle of 2021. They then decreased sharply and appeared to stabilize around low levels through 2024. Overall variation in cryptocurrency prices usually comes from investor behaviors, financial markets, and economic conditions. However, the 2021 price fluctuation was amplified by the COVID-19 pandemic, particularly during the lockdown period. In addition, due to cryptocurrency’s dependence on power consumption, other sources of price variations may be related to the negative impacts of climate change around the world.

In the following, we will work on the log returns of cryptocurrency series. A summary of the statistics of the return series are given in

Table 3. Summary statistics of the three return series from 01-01-2017 to 31-01-2024.

	Bitcoin	Ethereum	Litecoin
Minimum	$-0.2159651$	$-0.2560768$	$-0.2114050$
Mean	$0.0006325$	$0.0009465$	$0.0004544$
Maximum	$0.0988464$	$0.1123083$	$0.2636085$
Variance	$0.0002904$	$0.0005088$	$0.0006209$
Standard deviation	$0.0170420$	$0.0225570$	$0.0249197$
Skewness	$-0.8287481$	$-0.5799587$	$0.6322128$
Kurtosis	$12.85501$	$9.84041$	$13.58340$

We see in Table 3 that the Bitcoin and Ethereum returns are left-skewed with excess kurtosis, while the Litecoin return is right-skewed with excess kurtosis. These results indicate the non-normality of the distribution for all three return series and suggest left-skewed and heavy-tailed distributions for Bitcoin and Ethereum returns but a right-skewed and heavy-tailed distribution for Litecoin returns. For a formal analysis, we perform a normality test and other important tests in

Table 4. Statistical tests of the three return series.

Test	Bitcoin	Ethereum	Litecoin
Jarque–Bera test	18,143 (<2.2 × ${10}^{-16}$)	10,604 (<2.2 × ${10}^{-16}$)	20,099 (< 2.2 × ${10}^{-16}$)
ADF test	−16.5 (≤0.01 )	−16.5 (≤0.01 )	−17.1 (≤0.01 )
Ljung–Box test	$5.3114\left(0.02119\right)$	$5.6674\left(0.01728\right)$	$4.9593\left(0.02595\right)$

.

We see in Table 4 that the normality, the presence of a unit root, and the non-autocorrelation of each return series are rejected according to the Jarque–Bera normality test, the ADF unit root test, and the Ljung–Box autocorrelation test, respectively. This highlights the stationarity and non-normality of the distribution and the autocorrelation of all three return series.

For forecast evaluation purposes, we split our data into two parts: the normal and full lockdown COVID-19 period from 01/01/2017 to 31/12/2021 for model training and the post-lockdown period from 01/01/2022 to 31/01/2024 for model evaluation. This subdivision is due to the strong price fluctuation during the COVID-19 pandemic. We use the RMSE and the relative squared error (RSE) measures to evaluate the prediction performance of both parametric and non-parametric volatility methods.

4.2. Model Building

We built all parametric and non-parametric models using the first part of the data or the training sample.

For the parametric models, we started by fitting $AR\left(p\right)$ for the conditional mean associated with its return series. We obtained $AR\left(2\right)$ for Bitcoin returns and $AR\left(1\right)$ for both Ethereum and Litecoin returns, where smaller values were preferred for the selection of the order p. To validate these models, we performed residual diagnostics, as shown in

Table 5. Residual diagnostics.

Test	Bitcoin	Ethereum	Litecoin
Box–Ljung test	2.238 × ${10}^{-5}$ (0.9965)	0.014166 (0.9053)	0.00015391 (0.9901)
ARCH-LM test	343.21 (2.2 × ${10}^{-16}$)	54.111 (2.61 × ${10}^{-7}$)	66.795 (1268 × ${10}^{-9}$)

. The Ljung–Box and ARCH-LM tests in Table 5 confirmed the non-autocorrelation of residuals and the presence of the arch effect.

For the conditional variance of each cryptocurrency, we fitted five GARCH-type models: sGARCH(4,1), TGARCH(4,1), EGARCH(4,1), IGARCH(4,1), and GJR-GARCH(4,1). These optimal orders were obtained by minimizing the Akaike information criterion (AIC). The distributions of the innovation process were taken as the normal distribution (norm), generalized error distribution (ged), Student’s t distribution (std), and skewed Student’s t distribution (sstd). The parameters were estimated using the maximum likelihood estimator method.

We computed the RMSE associated with all GARCH-type models. The results are reported in

Table 6. RMSE on the training sample.

		sGARCH	TGARCH	eGARCH	iGARCH	gjrGARCH
Bitcoin	norm	$0.006892$	$0.006708$	$0.005958$	$0.120344$	$0.007056$
	ged	$0.008329$	$0.006111$	$0.005941$	$0.078531$	$0.007567$
	std	$0.051635$	$0.008311$	$0.007529$	$0.067474$	$0.031229$
	sstd	$0.051635$	$0.008249$	$0.007571$	$0.067743$	$0.034910$
Ethereum	norm	$0.007698$	$0.008286$	$0.007267$	$0.159374$	$0.008370$
	ged	$0.008192$	$0.007472$	$0.007118$	$0.124355$	$0.008007$
	std	$0.018262$	$0.008360$	$0.008113$	$0.167782$	$0.019964$
	sstd	$0.018246$	$0.008360$	$0.008085$	$0.167992$	$0.020933$
Litecoin	norm	$0.007476$	$0.007186$	$0.008185$	$0.122884$	$0.014324$
	ged	$0.009459$	$0.010411$	$0.091296$	0.09792	$0.129459$
	std	$0.091447$	$0.066487$	$0.010838$	$0.127115$	$0.014893$
	sstd	$0.090980$	$0.067539$	$0.010629$	$0.126527$	$0.013587$

.

As shown by the RMSE in Table 6, the best-fitting volatility models are the eGARCH model with the generalized error distribution for both Bitcoin and Ethereum and the TGARCH model with the normal error distribution for Litecoin. After estimating parameters, we realized that many coefficients were not significant for the three models, and potential stationarity issues were raised for Bitcoin and Ethereum. Therefore, we refitted these models by removing non-significant coefficients. We obtained eGARCH(2,1) for Bitcoin, eGARCH(3,1) for Ethereum, and sGARCH(1,1) for Litecoin, as shown in

Table 7. Parameter estimates for the obtained GARCH types.

			$\mathit{\omega }$	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	${\mathit{\alpha }}_3$	${\mathit{\beta }}_1$	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$	${\mathit{\gamma }}_3$
Bitcoin	eGARCH(2,1)	Estimate	$-0.659497$	$-0.0087287$	$-0.046403$		$0.915460$	$0.151642$	$0.058880$
		p-value	$0.055644$	$0.837300$	$0.000000$		$0.000000$	$0.000061$	$0.004189$
Ethereum	eGARCH(3,1)	Estimate	$-0.681146$	$-0.036852$	$-0.039547$	$0.069783$	$0.905967$	$0.189331$	$-0.065186$	$0.163498$
		p-value	$0.003865$	$0.276418$	$0.360143$	$0.044434$	$0.000000$	$0.000049$	$0.254717$	$0.006867$
Litecoin	sGARCH(1,1)	Estimate	$0.000045$	$0.067425$			$0.873438$
		p-value	$0.000002$	$0.000000$			$0.000000$

.

In Table 7, we see that all estimates were statistically significant at the $5\%$ level, except for estimates of $\omega$ and ${\alpha }_1$ for Bitcoin and those of ${\alpha }_1$, ${\alpha }_2$, and ${\gamma }_2$ for Ethereum. We removed the non-significant coefficients from the model. When focusing on parameter estimates related to model asymmetry in EGARCH, the positivity of the ${\gamma }_1$ and ${\gamma }_2$ estimates for Bitcoin highlighted the greater impact of positive shocks on future volatility than negative shocks. We drew similar conclusions for Ethereum, as its remaining two asymmetry coefficients ${\gamma }_1$ and ${\gamma }_3$ were positive. We retained eGARCH(2,1) for Bitcoin, eGARCH(3,1) for Ethereum, and sGARCH(1,1) for Litecoin.

We conducted learning for the non-parametric ANFIS model and the three GBM, XGBM, and lightGBM tree-based ensemble learning models with the following specifications.

• GBM: Number of iterations = 100, maximum number of trees = 20, colsample by tree = 1, eta = $0.5$, gamma = 0, min child weight = 1, learning rate = $0.1$, and number of leaves = 31; the RMSE was used as an evaluation measure for learning.
• XGBM: Number of iterations = 100, maximum number of trees = 20, colsample by tree = 1, eta = $0.5$, gamma = 0, min child weight = 1, learning rate = $0.1$, and number of leaves = 31; the RMSE was used as an evaluation measure for learning.
• LIGHTGBM: Using the regression with the traditional gradient boosting decision tree (gbdt), learning rate = $0.1$, number of leaves = 31, 100 iterations, and RMSE as an evaluation measure on learning Sossi-Rojas et al. (2023).
• ANFIS: Method type = ANFIS, control parameters: number of labels = 7, number of iterations = 10 by steps of $0.1$, membership function = Gaussian, defuzzification method = the weighted average method (WAM), conjunction operator = ‘MIN’, disjunction operator = ‘MAX’, and implication function = type ZADEH.
• Simple RNN: Number of neurons = 10, activation: Tanh, number of training runs on the datasets = 50.

4.3. Evaluation

We evaluated the estimation and prediction performance of the parametric and non-parametric volatility methods obtained previously. We computed the RMSE on the training and test samples associated with the GARCH-type model, ANFIS, and the three boosting methods obtained previously.

Table 8. RMSE and RSE on the training and evaluation samples.

	Model	Full Lockdown		Post Full Lockdown
		RMSE	RSE	RMSE	RSE
Bitcoin	eGARCH	$0.005206$	$1.215836$	$0.002457$	$1.319523$
	GBM	$0.018291$	$0.968613$	$0.012240$	$0.950035$
	LIGHTGBM	$0.009962$	$0.287330$	$0.004706$	$0.140433$
	XGBM	$0.000306$	$0.000271$	$0.000306$	$0.000595$
	ANFIS	$0.020327$	$1.196356$	$0.013532$	$1.161172$
Ethereum	eGARCH	$0.007219$	$1.184622$	$0.004977$	$1.072735$
	GBM	$0.023876$	$0.927511$	$0.015296$	$0.380690$
	LIGHTGBM	$0.009962$	$0.161461$	$0.004837$	$0.038078$
	XGBM	$0.000296$	$0.000143$	$0.000306$	$0.000152$
	ANFIS	$0.025859$	$1.087909$	$0.016675$	$0.452373$
Litecoin	sGARCH	$0.007095$	$1.017795$	$0.005109$	$1.153713$
	GBM	$0.027105$	$0.977010$	$0.016986$	$0.945733$
	LIGHTGBM	$0.013973$	$0.259663$	$0.006556$	$0.140893$
	XGBM	$0.000323$	$0.000139$	$0.000367$	$0.000443$
	ANFIS	$0.031052$	$1.282286$	$0.023703$	$1.841533$

summarizes the in-sample and out-of-sample performance of the models.

As shown in Table 8, the XGBM model is the most accurate among all of the models, and it is recalled that this model is an improved version of the regularized and tree-based combined GBM model. Despite the difficulty of interpreting machine learning when capturing stylized facts about cryptocurrency price volatility, the XGBM adapts easily to cryptocurrency return volatility modeling when it occurs as a problem of function approximation. The RMSE and RSE loss functions on the training and test samples from the XGBM are largely small compared with those of the other two models, showing that the XGBM captures cryptocurrency features such as high volatility and heavy-tailed distributions. This performance of the improved GBM family in modeling the volatility of cryptocurrency series has been found in various studies Bouteska et al. (2024). The GARCH-type model is also not far from being a better predictor for financial data; in our case, this is confirmed, as it had the second smallest value after the XGBM. Many papers that we cited in the literature review addressed the performance of the GARCH model. A recent study on cryptocurrencies Khaldi et al. (2019) obtained the TGARCH model, and the difference from our results may come from our inclusion of new information due to the data size used and phenomena that occurred during this period.

5. Conclusions

This study sheds light on the dynamics of volatility in cryptocurrency markets. Using parametric and non-parametric volatility models, this study examined the volatility of the returns of Bitcoin, Ethereum, and Litecoin. The empirical results confirmed the non-normality and stationarity of the series. For all models used for cryptocurrency volatility forecasting, the tree-based ensemble learning XGBM model delivered the most accurate forecast. This highlighted the strength of the model based on the regularization and aggregation of several models. Apart from the success of this ensemble learning in various fields and challenges, such as the machine learning competition site Kaggle and the Knowledge Discovery Data Association Cup (KDDCup), it is computationally much faster than existing models Chen and Guestrin (2016). Our results reconfirm the strength of the XGBM for cryptocurrency volatility prediction.

The GARCH family, which was the first model applied to characterize the dynamics of cryptocurrency volatility and usually serves as the benchmark model in many studies, still provided challenging results. Its interpretability in capturing various stylized facts about volatility and its development as hybrid models would make it useful in volatility modeling.

The hybrid ANFIS volatility model needs to be explored in greater depth. We may improve it by using more advanced neural network architectures, more sophisticated fuzzy inference systems, and more efficient and scalable algorithms.