1. Introduction
Since the global financial crisis (GFC) of 2007–2008, the credit risk topic has become a greater concern in the financial industry. The high-financial-leverage nature of banks makes credit risk management a top priority. Unlike other institutions, banks adapt traditional asset and liabilities management into asset default and liabilities default management. Liquidity monitoring focuses on preventing liquidity defaults. Profitability is a key consideration, assessed primarily from the perspective of economic default (
Chen & Kuei, 2024). The consequences of the GFC on the global economy were initially reflected in the collapse of the value of institutions operating in the banking sector, demonstrating the importance of understanding the factors that influence banks’ value, which is commonly linked to stock price (
Amimakmur et al., 2024).
Worldwide, the phenomenon of M&A in the banking sector has constantly increased. While in the year 1985 there were only 247 deals, this number peaked in the year 2018, reaching over 2000 deals (
Statista, 2024). M&A benefit banks by raising capital, expanding, achieving a competitive advantage, enhancing financial operating performance and bringing financial stability (
Chakraborty & Das, 2024).
Montgomery and Takahashi (
2014) find that M&A lead to an increase in both shareholders’ wealth and the credit risk of banks involved in such transactions.
Hassan and Giouvris (
2020) observe that local bank-to-bank M&A create shareholder wealth, with local M&A associated with a reduction in credit risk, while cross-border M&A are linked to an increase in risk. Both papers rely on traditional conditional mean analysis techniques, including multivariate regression, robust regression, maximum likelihood regression and weighted least squares regression. However,
Wang et al. (
2024) clarify that these methods rely on assumptions of normality and homoscedasticity, which are often not met in real-world financial data. Given the high volatility and non-normal distribution of such data, these methods may be inadequate for estimation.
An alternative approach, quantile regression, offers more robust estimates and provides a comprehensive analysis of business performance changes in response to specific events. In particular,
Pop and Pop (
2024) observe that markets price risk differently for banks in the upper locations of the spread distribution, where market discipline is tougher for risker banks. Similarly,
Fich et al. (
2018) find that the characteristics related to the acquiring banks have varying effects on the distribution of abnormal returns. To understanding complex predictor–response relationships,
Cunningham et al. (
2020) consider quantile regression an ideal analytical tool, as it captures variations in predictor effects across different response quantiles.
While the traditional conditional mean models can address the question of “how horizontal M&A affects the relationship between credit risk and bank value”, they cannot answer an equally important question of “how horizontal M&A moderates this relationship across different quantiles of the bank value distribution”.
Therefore, this paper investigates the moderating effect of horizontal M&A on the relationship between credit risk and bank value within a quantile-based framework.
The current literature provides explanations about the relationship of credit risk with value in the context of M&A within banking industry. Our paper offers a deeper theoretical understanding of this relationship by capturing the heterogeneity in the predictor–response relationship across the distribution of response, providing a novel contribution to the theoretical literature. Empirically, our novel results cannot be captured using standard conditional mean estimations. We introduce quantile regression to uncover how lower-valued banks and higher-valued banks exhibit different sensitivities to credit risk in M&A activities, effectively addressing challenges related to violations of normality and homoscedasticity in the financial data. Practically, our novel findings guide investors in identifying rewarding investment opportunities, assist bank managers in balancing risk and value creation during M&A, and inform policymakers about regulating credit risk exposure in M&A activities within the banking sector.
The results of this paper reveal that credit risk has a significant negative effect on bank value across the entire distribution, with the magnitude of this effect decreasing from lower to upper locations. This indicates that lower-valued banks are more vulnerable to a steeper decline in value as a result of credit risk, compared to higher-valued banks. Horizonal M&A exhibit a stable and significant positive effect on bank value across the entire distribution, suggesting that horizontal M&A consistently enhance bank value, regardless of the bank’s valuation. However, the moderating effect of horizontal M&A significantly magnifies the negative impact of credit risk on bank value across the entire value distribution, but without statistically significant differences observed from lower to upper locations of the distribution. This implies that horizontal M&A amplify the adverse effect of credit risk on bank value uniformly, across banks, regardless of their valuation, assuming other factors remain constant.
Our results encourage investors to invest in banks that intend to merge and acquire, as such activities increase their wealth. However, simultaneously, they should carefully consider the credit risk profile of these banks because credit risk plays a significant counterfactor to value creation, especially for low-valued banks. We advise investors to utilize recent machine learning techniques, such as Decision Trees, to classify and categorize these investment opportunities based on credit risk and bank value. This will exclude investing in banks that are willing to undergo M&A with other banks when they are low-valued and experience high credit risk, and will prioritize those that are high-valued and experience low credit risk, as these represent the best investment opportunities. Additionally, for investors who hold a portfolio of bank stocks, we advise them to incorporate a fundamental-based diversification strategy, where they overweight banks actively involved in horizontal M&A and underweight low-valued, high-credit risk banks, as these are more vulnerable to significant declines in value. This enables investors to maximize their portfolio value while minimizing exposure to the adverse effects of credit risk and M&A activities.
For practitioners, the paper’s findings advise boards of directors in the banking sector to consider horizontal M&A as a growth strategy, as this enhances value across the entire banking sector. However, the findings emphasize the importance of implementing a tailored risk management strategy for lower-valued banks during M&A processes to minimize the adverse effects of credit risk. This approach ensures that M&A activities leverage the positive effects to the interest of shareholders. Additionally, the findings suggest that a board of directors utilize a credit risk–bank value monitoring tool that tracks both credit risk exposure and value simultaneously. This tool should adjust credit risk exposure based on the bank’s value, tightening exposure when value is low and loosening it when value is high, thereby balancing risk and reward more effectively.
Policymakers can benefit from our results by establishing a supportive framework that encourages healthy M&A activities in the banking sector, ensuring these activities contribute to growth while maintaining financial stability. We also suggest developing regulatory frameworks that address the impact of credit risk exposure on the banking sector, recognizing the increased vulnerability of lower-valued banks to greater declines in value due to credit risk; a vulnerability that becomes even more pronounced during M&A transactions. Approvals for M&A should be conditioned on banks demonstrating a low credit risk profile and/or strong valuation. Regulators should establish a dynamic capital buffer that is calibrated to credit risk exposure and bank value parameters, along with introducing event-specific capital buffers during M&A activities to safeguard against foreseen and unforeseen credit risks. Additionally, policymakers can establish a monitoring mechanism to track credit risk exposure and bank value simultaneously, ensuring that banks adhere to strict credit risk policies when their value fall below specified levels.
4. Empirical Results and Discussion
Table 2 summarizes the descriptive statistics for the dependent variable, independent variables, and controls. The variable M/B is expressed in logarithmic term; thus, values above zero correspond to a non-logarithmic M/B greater than one, while values below zero indicate it is less than one. Given that the average M/B is 0.39, it suggests that banks are generally valued at a premium compared to their book value. The values of standard deviation, minimum, maximum, skewness, and kurtosis for the M/B suggest a wide dispersion around the mean and the presence of outliers. The 10th percentile of the M/B is −0.09, suggesting that 10% of the bank-year observations in the panel data are valued at a discount compared to their book value. The high transition from the median to the 90th percentile indicates a substantial percentage of bank-year observations with high valuations. The average NCO is approximately zero, suggesting that banks generally incur small percentages of credit losses. However, the data reveal a dispersion around the NCO mean and highlight the presence of outliers. The upper percentile shows that at least 10% of the bank-year observations have incurred higher percentages of credit losses compared to the rest. The mean MA suggests that approximately 15% of bank-year observations involve M&A bidding activities. Given the binary nature of MA, elaborating on other descriptive statistics is not meaningful. Additionally, it makes the statistics of NCO × MA insubstantial for interpretation.
All the statistics of the controls in
Table 2 reveal a highly diverse sample of banks, ranging from those with assets in hundreds of millions to those exceeding trillions of dollars, and ranging from startup to mature institutions. The sample consists of both losing and profitable banks, with reasonable to extreme levels of leverage. It features liquid and illiquid, efficient and inefficient banks, and those specialized either in interest income or fee income. Additionally, it encompasses banks with and without growth capabilities, and those that move aligned to or against the market. The sample also includes banks that pay dividends despite losses, alongside those that receive tax credits. The macroeconomic environment experiences phases of expansion and recession. Despite the diversity in the sample and the varying macroeconomic conditions, all controls exhibit skewed distributions, with a high likelihood of outliers, as indicated by the skewness, kurtosis, and percentiles statistics.
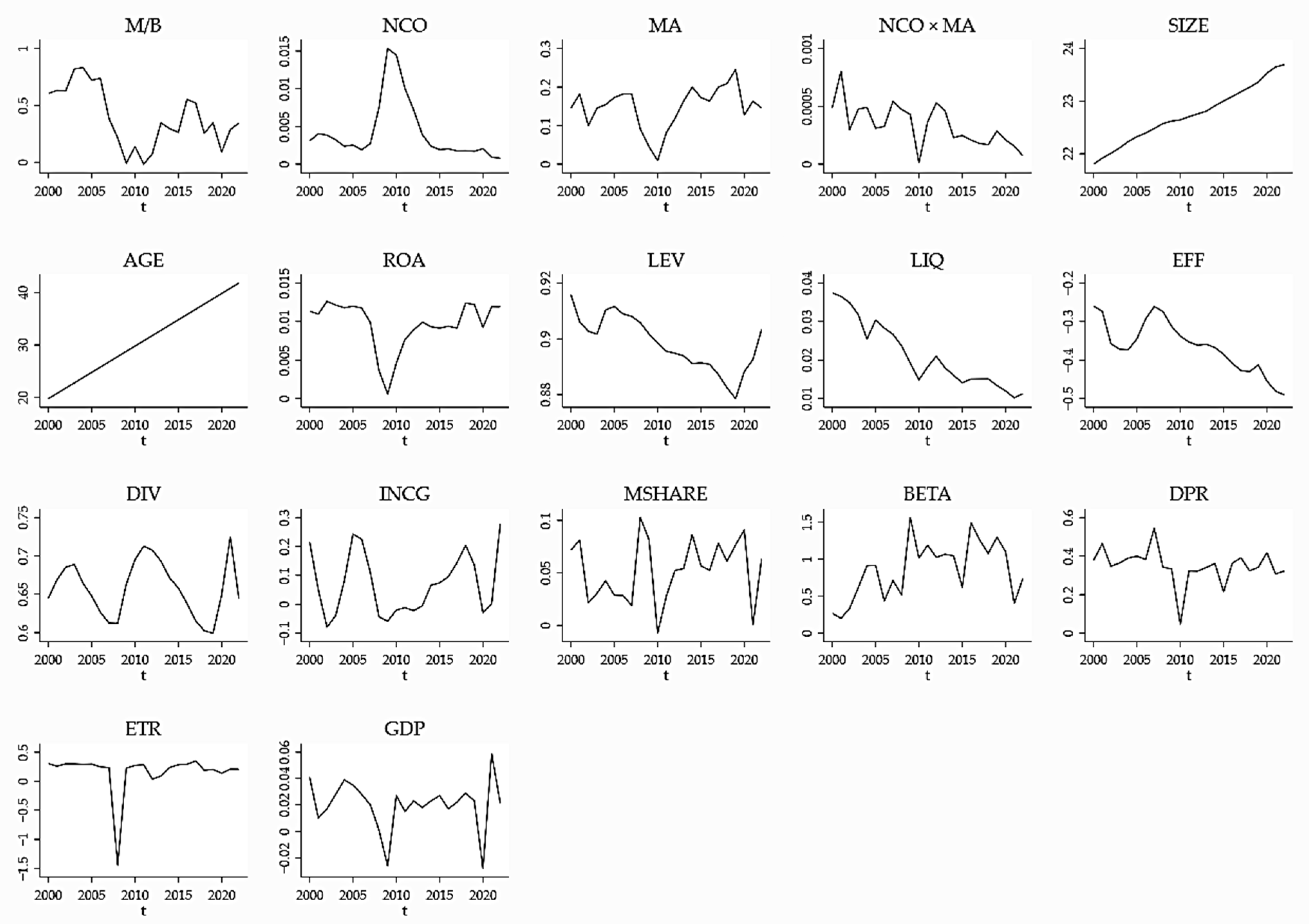
The K&T test in
Table 3 demonstrates that all variables are stationary, either by controlling for CD as detailed in the same table or by including time trends in SIZE and AGE, as illustrated in
Figure 1. Furthermore,
Table 4 verifies that all variables are free from multicollinearity, as indicated by the absence of very strong pairwise correlations and VIF values below five. These results permit performing linear regressions as presented in
Table 5.
Table 5 presents the coefficient results of OLS regression. While NCO and MA are statistically significant, NCO × MA is insignificant. Despite these results, the residuals obtained from OLS do not adhere to the Gauss theorem. They are homoscedastic, autocorrelated, and non-normally distributed. Therefore, quantile regression is preferable over OLS regression.
Table 6 presents the quantile regression coefficients. The independent variables show limited significant coefficients. NCO is significant between p10 and p60, while MA is significant between p20 and p80. NCO × MA is only significant at p70 and p90. Furthermore,
Table 7 evaluates the equality of coefficients across quantiles. Nearly half of the NCO and most of MA results are insignificant, and all NCO × MA results are insignificant.
Due to the endogeneity concerns highlighted by the LSDV results in
Table 5, which show the relevance of incorporating individual fixed effects into the model, incorporating these fixed effects increased the adjusted coefficient of determination (R
2) from 38.99% to 59.46%, providing a more accurate assessment of the predictors’ explanatory power on the variation in the M/B. Consequently,
Table 8 re-estimates the quantile regression using the MM-QR method, which incorporates individual fixed effects.
The results of
Table 8 are partially consistent with those in
Table 6. The variables NCO, MA, and NCO × MA become significant at all percentiles. The effect of NCO on the M/B is consistently negative across these percentiles. This negative impact of credit risk decreases in magnitude from the 10th percentile to the 90th percentile of bank value, suggesting a stronger detrimental effect on banks with lower valuations compared to those with higher valuations. The findings from
Table 8 align with the results in
Table 9, which indicate that the coefficients for NCO are not equal across different M/B percentiles. These findings strongly support H
1—the effect of credit risk on bank value varies significantly across quantiles of bank value. The consistent decrease in the negative effect of credit risk, as observed ascending through bank value percentiles, can be explained through the contributions of (
Fama & French, 1992,
1998). In asset-pricing models, the value premium suggests that stocks with higher valuations are less risky compared to those with lower valuations. In the banking sector, the risk–return principle exhibits an inverse shape. Investors accord higher valuations to banks with lower credit risk over those with higher credit risk (
Avramov et al., 2009). This anomaly is attributed to the fact that cumulative credit losses put banks in a financial distress phase (
Kanas et al., 2012). Additionally,
Jensen and Meckling (
1976) highlight that lower risk-taking incentives exist in highly profitable institutions. Yet, profitability stands as an important determinant in value creation for banks (
Handorf, 2011).
The findings on MA in
Table 8 are consistent with those in
Table 9. Bank value is positively affected by horizontal M&A. However, the magnitude of this effect remains positive and is relatively stable across all M/B percentiles. Thus, the posed H
2—the effect of horizontal mergers and acquisitions on bank value varies significantly across quantiles of bank value—cannot be supported, suggesting that the linear prediction of the success or failure of M&A is adequate as long as the Gauss theorem is not violated. The magnitude of the effect of horizontal M&A on bank value appears to be influenced by factors beyond the M/B of the acquiring banks, such as the size of acquirer.
Alexandridis et al. (
2017) show that the dynamics of wealth creation in M&A change based on acquirer size, with smaller banks outperforming large banks in wealth creation. This is supported by
DeYoung et al. (
2009), who suggest that the primary cause for large banks to engage in M&A is for building an empire, rather than wealth creation. In general, market power and operational synergies from M&A create value (
Krishnan & Yakimenko, 2022); managerial biases and skewed managerial incentives demolish it (
Sudarsanam, 2012). Our findings suggest that the potential advantages of horizontal M&A among banks surpass the drawbacks.
The findings of NCO × MA in
Table 8 are inconsistent with those in
Table 9. The moderating effect of horizontal M&A on the credit risk–bank value relationship is significant across all M/B percentiles. The interaction term shows negative signs across them all, meaning that horizontal M&A amplify the initial negative effect of credit risk on bank value across the distribution. The negative magnitude of the interaction term increases as moving from the 10th to the 90th percentile. However,
Table 9 shows that variations in the interaction term’s coefficients across M/B percentiles are not sufficient to be considered statistically different from one another. Thus, the posed H
3—the moderating effect of horizontal mergers and acquisitions on the credit risk–bank value relationship varies significantly across quantiles of bank value—cannot be supported. The rejection of H
2 and H
3 does not diminish the research contribution because H
1 is accepted. The three hypotheses should be viewed together in a moderating framework. The variation in the effect of NCO on the M/B across quantiles indicates that the credit risk–bank value relationship is not uniform across different bank value levels. Therefore, even if the effects of MA and NCOMA on the M/B are stable, the inclusion of NCO necessitates analyzing these effects across the quantiles of M/B. Furthermore, the non-Gaussian nature of the error term distribution, along with evidence of heteroskedasticity, autocorrelation, and fixed effects, justifies the use of Quantiles via Moments in this study. Given the lack of significant heterogeneity in the slopes of the moderator and the interaction term, and assuming the Gauss theorem holds, examining the posed H
3 in a quantile regression method is deemed more superior than linear methods due to the strong slope heterogeneity exhibited by the NCO. Yet, the findings imply that while horizontal M&A events by themselves enhance bank value, they diminish value when interacting with credit risk. The theoretical benefits of diversification and co-insurance effect, as outlined in (
Lewellen, 1971;
Markowitz, 1952), appear to be either absent in M&A among banks or, if present, exert a limited influence. Horizontal M&A either develop homogenized internal structures, eliminating potential diversification benefits (
Wang, 2024), or they generate diversification advantages that are subsequently offset by exploiting them to increase the riskiness of the loan portfolio post-M&A, aiming to generate higher returns and boost stock prices (
Knapp & Gart, 2014). However, this risky portfolio escalates credit losses, restricting profit making and impeding value creation (
Shirasu, 2018). Markets evaluate banks differently than other institutions, and they favor soundness over risk (
Avramov et al., 2009); thus, when M&A between banks lead to credit quality issues, markets react negatively and strongly (
Knapp et al., 2005).
The robustness of our MM-QR results is validated through a series of multiple checks: variables validity, conditional quantile validity, fixed effects validity, bootstrapping, and consistency validity. First, we confirm that the variables are free of multicollinearity and unit root issues, as addressed in
Table 3 and
Table 4 and
Figure 1, using correlation matrix and VIF (
Belsley et al., 1980), Pesaran’s CD test (
Pesaran, 2021), average line graphs (
Wang et al., 2018), and the K&T test (
Karavias & Tzavalis, 2014). Second, we illustrate that the conditional quantile regression of
Koenker and Bassett (
1978) outperforms conditional mean regression by effectively handling the non-Gaussian residuals (
Royston, 1983), heteroskedasticity (
Cook & Weisberg, 1983), and autocorrelation (
Drukker, 2003) in OLS and LSDV regressions, as presented in
Table 5. Third, using the Wald test (F-Statistic), we reveal in
Table 5 the necessity of including individual fixed effects in the conditional quantile regression to avoid issues in endogeneity and omitted variable bias. As such, necessity cannot be directly implemented in the
Koenker and Bassett (
1978) model due to incidental parameter bias (
Koenker et al., 2017). Therefore, we introduce the MM-QR of
Machado and Santos Silva (
2019), which can include individual fixed effects in the quantile regression model without such bias. Fourth, all results presented in
Table 6 and
Table 8 are derived via bootstrapping, ensuring robust estimates (
Efron & Tibshirani, 1994). Furthermore, the partial consistency of the MM-QR results in
Table 8 with those from the
Koenker and Bassett (
1978) quantile regression in
Table 6, as well as the OLS and LSDV results in
Table 5, and with similar outcomes of hypotheses testing using the Wald test in
Table 7 and
Table 9, further validate the robustness of our results.
Finally,
Table 8 reveals several statistically significant coefficients for control variables across all bank value percentiles. Although the equality of coefficients of these controls is not tested, it can be considered that there are initial relationships that need to be further examined. While AGE has an increased negative effect, EFF has a diminished negative impact. The static negative influence of both variables is aligned with
Pástor and Pietro (
2003), as investors value younger institutions higher due to their growth potential, and
Asimakopoulos and Athanasoglou (
2013), as markets react to expected efficiency gains from M&A activities. LEV, INCG, and GDP all have an increasing positive effect. The static impact of these variables is aligned with
Modigliani and Miller (
1958), as highly leveraged institutions are expected to yield higher returns;
Avramidis et al. (
2018), as markets incorporate the growth potential into stock valuations; and
Teixeira et al. (
2014), as banking activity correlates with the expansionary phase of the economy.
5. Conclusions
This paper aims to evaluate the moderating effect of horizontal mergers and acquisitions (M&A) on the relationship between credit risk and bank value across different quantiles of bank value. Furthermore, it investigates how credit risk and horizontal M&A influence bank value within these same quantiles. The most interest in predicting credit risk lies within quantiles, owing to non-linear processes and deviations from the Gauss theorem. Furthermore, the complex nature of M&A limits the ability to predict their outcomes linearly. To our knowledge, the existing literature has not provided an explanation of the credit risk and bank value relationship in the context of horizontal M&A that accounts for the potential non-linear behavior and the variability across different quantiles of bank value. This research bridges this gap, adopting a distinctive approach that utilizes the revolutionary Quantiles via Moments estimator to address endogeneity concerns, ensuring the robustness of our findings. Consequently, this study contributes to the academic field by revealing the non-linear dynamics of how credit risk and bank value interrelate under the conditions of horizontal M&A.
The findings indicate a significant variation in the effect of credit risk on bank value across the entire distribution of bank value. However, the results fail to provide statistical evidence to support a significant variation in the effect of horizontal M&A on bank value, as well as in their moderating effect on the relationship between credit risk and bank value, across the entire distribution of bank value. Given the significant non-linear behavior in the credit risk–bank value relationship, evaluating it within the scope of horizontal M&A using quantile analysis enhances the precision and accuracy for decision making. This remains valid despite the linear nature of M&A’s direct and moderating effects, as well as deviations from the Gauss theorem. The effect of credit risk on bank value is negative and becomes less pronounced for higher-valued banks; meanwhile, although the direct effect of horizontal M&A on bank value is positive, their moderating effect is negative, providing valuable implications for investors, practitioners, and policymakers.
Investors should assess the risk profile and value proposition of a bank before making investment decisions in banking stocks. They can include credit risk as a dynamic asset-pricing factor that rewards more for value stocks than growth stocks. Similarly, in horizontal M&A, they should consider credit risk as a dynamic pricing determinant for deal offers that potentially reduces the bidding offer and lowers it further for low-valued targets. Additionally, investors in banking stocks should diversify their portfolio not just across different banks but also across banks positioned at different quantiles of value to mitigates risks associated with fluctuations in bank value relative to credit risk.
For practitioners, it is crucial to integrate credit risk management along with bank value proposition. If their banks are valued lower, they should adopt a more stringent strategy to mitigate credit risk. Similarly, when incorporating horizontal M&A into their strategic growth plans, they should also be more stringent in mitigating credit risk.
Policymakers should acknowledge the varying effect of credit risk on bank value across different thresholds of value. It is advisable to implement a dynamic regulatory framework for the permissible percentage of exposure to credit risk in banks based on their value proposition. They should foster healthy M&A between banks as long as they do not compromise financial stability. It is advisable to establish capital buffers for horizontal M&A in the banking sector, designed to safeguard against both foreseen and unforeseen credit risk that may emerge after M&A. These buffers should be calibrated according to credit risk and bank value parameters.
This paper has two limitations that prevent the generalization of its results. First, due to the challenge of accessing data from banking sectors outside the U.S., the sample is limited to U.S. banks; thus, our findings may not be applicable to different jurisdictions. Second, given the complexities involved in applying non-market-based valuation techniques, the sample is limited to publicly traded banks; thus, our results may not extend to privately held banks. Hence, future researchers could broaden the scope of this study by considering banks on a global scale, incorporating non-listed banks, or undertaking both approaches.