Spatial Multivariate GARCH Models and Financial Spillovers
Abstract
1. Introduction
2. Matherials and Methods
2.1. Modelling and Inference
- is the vector of assets’ returns at time t,
- is the conditional covariance matrix,
- is the vector of the univariate conditional variances,
- is a squared matrix with the conditional standard deviations on the main diagonal and zero otherwise.
- is the positive definite conditional correlation matrix,
- is the conditional covariance matrix of the standardized residuals,
- is the unconditional covariance matrix of the standardized residuals,
2.1.1. Spatial DCC-GARCH
| = | . |
2.1.2. Estimation of the Multivariate Spatial GARCH(1,1) Model
- Compute the exogenous variables given the weights and the initially estimated variances ;
- Estimate the complete set of parameters and the new estimated variances according to Equation (16).
2.1.3. Spatial Weight Matrix
2.2. Financial Application: CoVaR
2.2.1. CoVaR Based on Filtered Historical Simulations (FHS)
- compute the residual (or devol) time series, dividing the returns by EWMA estimated volatility . This allows us to sample from approximately serially independent and identically distributed data;
- compute the estimated empirical distribution of (revol), multiplying the devol time series by the latest estimate of volatility and assigning to each of the possible outcome a weight ,
- estimate and by computing the empirical quantile of and , respectively.
2.2.2. Backtesting VaR and CoVaR
2.2.3. Tests Based on the Number of Violations
- the ex-post realized returns of institution i with ;
- the ex-ante Value-at-Risk forecasts at for time t, where q is the expected coverage;
- a sequence of violation for a given interval of the Value-at-Risk forecast:
2.2.4. Backtesting Based on Loss Functions
3. Results
3.1. Data
Spatial Weight Data
3.2. Empirical Results
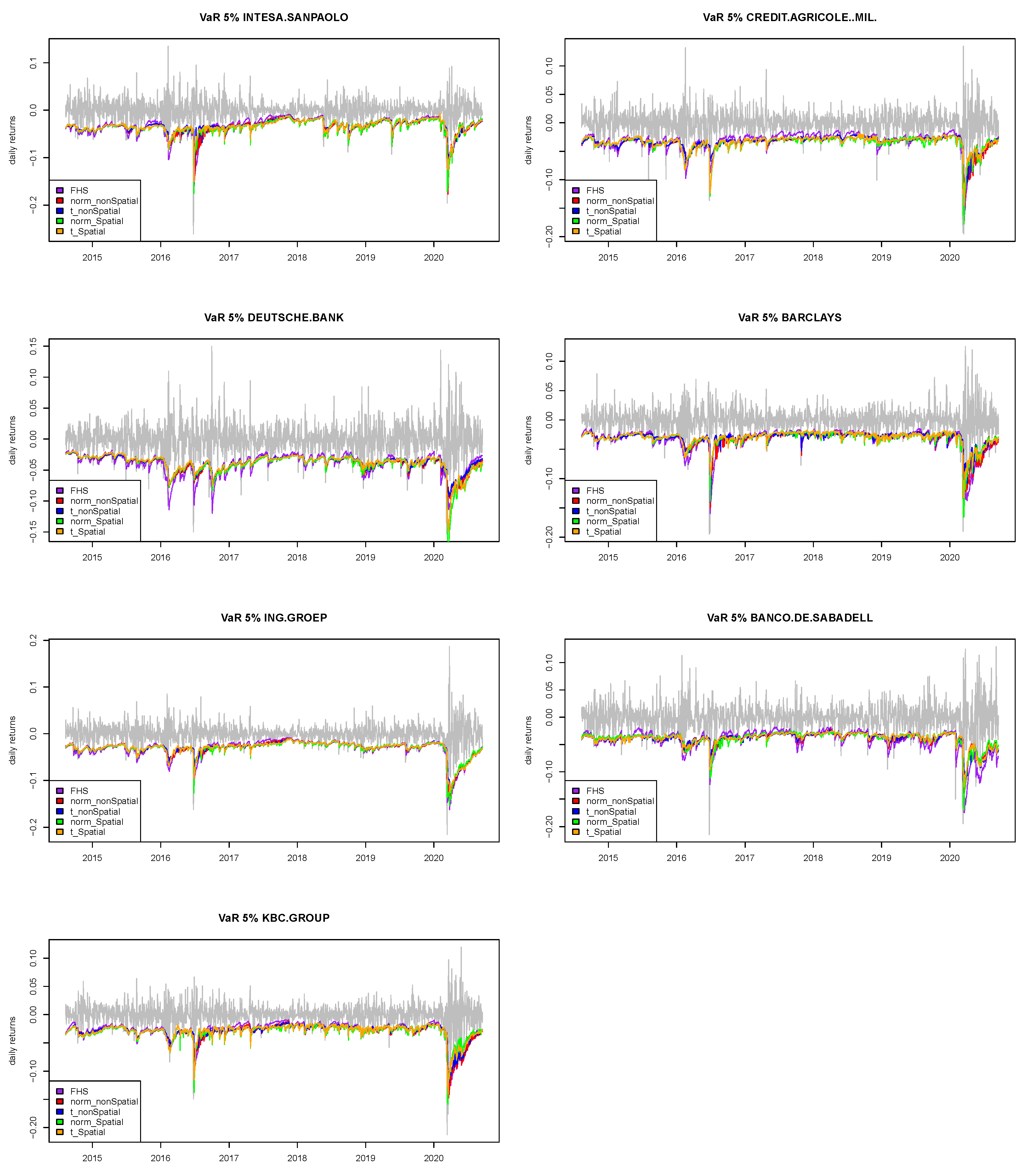
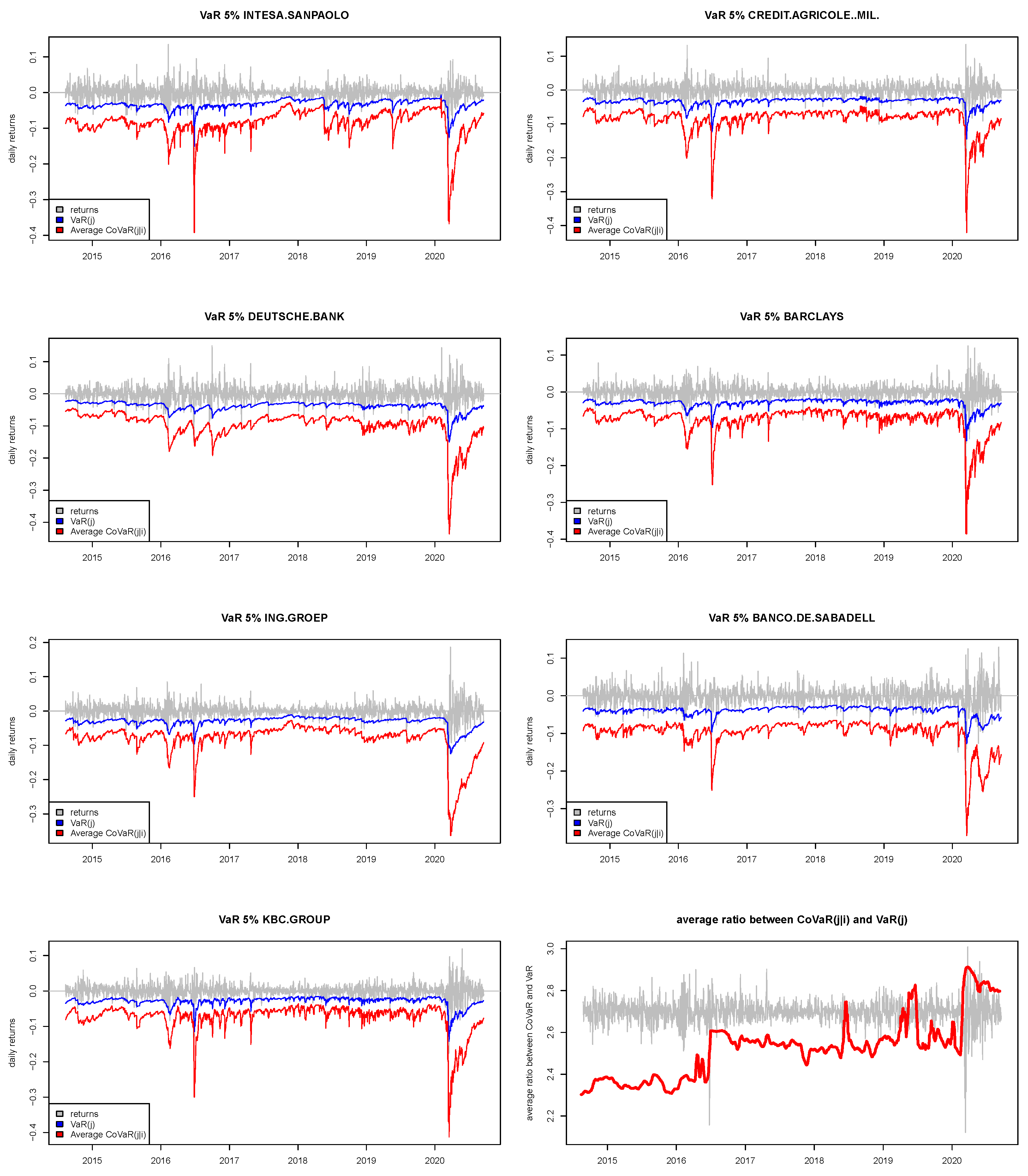
3.2.1. VaR and CoVaR
3.2.2. Backtesting Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| = | ||
| = | ++ | |
| = |
| 1 | |
| 2 | We use the convention that a higher value of r is preferable to a lower value, as in the cases when r represents returns or wealth. Other works consider a random variable x such that lower values of x are preferable, as in the case of losses (e.g., Artzner et al. 1999). The signs in the definitions then need to be changed accordingly. |
| 3 | The construction of a network of bilateral CoVaR is inspired by Adrian and Brunnermeier (2014). An alternative approach to extend CoVaR to a network dimension is proposed by Torri et al. (2021) and uses penalized multivariate quantile regression. |
| 4 | Under both Student t and Gaussian distribution it can be shown that for positive correlation is always greater than . Hence we consider a grid of values ranging from to infinity, such that the corresponding quantiles are equally spaced. In case of null or negative correlations, we use 0 as the lower value of the grid. |
| 5 | Central governments Institutions, Corporates, Retail, Equity, Securitization, and Other non-credit obligation assets. |
| 6 | In preliminary analyses we tested different orders of GARCH and we also considered an ARMA component, finding no relevant differences. We omit them for brevity. |
| 7 | We do not report the complete results for all the bivariate CoVaR estimations for brevity. The results are available upon request. |
References
- Abad, Pilar, Sonia Benito, and Carmen López. 2014. A comprehensive review of value at risk methodologies. The Spanish Review of Financial Economics 12: 15–32. [Google Scholar] [CrossRef]
- Adrian, Tobias, and Markus Brunnermeier. 2014. CoVaR. Staff Reports 348. New York: Federal Reserve Bank of New York. [Google Scholar] [CrossRef]
- Alexander, Carol, and Elizabeth Sheedy. 2008. Developing a stress testing framework based on market risk models. Journal of Banking & Finance 32: 2220–36. [Google Scholar]
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Aslam, Faheem, Paulo Ferreira, Khurrum Shahzad Mughal, and Beenish Bashir. 2021. Intraday volatility spillovers among european financial markets during COVID-19. International Journal of Financial Studies 9: 5. [Google Scholar] [CrossRef]
- Barone-Adesi, Giovanni, Kostas Giannopoulos, and Les Vosper. 2002. Backtesting derivative portfolios with filtered historical simulation (fhs). European Financial Management 8: 31–58. [Google Scholar] [CrossRef]
- Billio, Monica, Massimiliano Caporin, Lorenzo Frattarolo, and Loriana Pelizzon. 2021. Networks in risk spillovers: A multivariate garch perspective. Econometrics and Statistics, in press. [Google Scholar] [CrossRef]
- Billio, Monica, Mila Getmansky, Andrew W. Lo, and Loriana Pelizzon. 2012. Econometric measures of connectedness and systemic risk in the finance and insurance sectors. Journal of Financial Economics 104: 535–59. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1990. Modelling the coherence in short-run nominal exchange rates: A multivariate generalized arch model. The Review of Economics and Statistics 72: 498–505. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Robert F. Engle, and Jeffrey M. Wooldridge. 1988. A capital asset pricing model with time-varying covariances. Journal of Political Economy 96: 116–31. [Google Scholar] [CrossRef]
- Borovkova, Svetlana, and Rik Lopuhaa. 2012. Spatial GARCH: A spatial approach to multivariate volatility modeling. SSRN Electronic Journal. [Google Scholar] [CrossRef][Green Version]
- Caporin, Massimiliano. 2008. Evaluating value-at-risk measures in the presence of long memory conditional volatility. The Journal of Risk 10: 79–110. [Google Scholar] [CrossRef]
- Cesarone, Francesco, and Stefano Colucci. 2016. A quick tool to forecast value-at-risk using implied and realized volatilities. Journal of Risk Model Validation 10: 71–101. [Google Scholar] [CrossRef]
- Chen, Xiurong. 2017. Impact effects and spatial volatility spillover effects of sovereign credit rating downgrades–empirical analysis of multivariate spatial-bekk-garch model based on symbolic transfer entropy. Boletín Técnico 55: 614–23. [Google Scholar]
- Christoffersen, Peter, and Denis Pelletier. 2004. Backtesting Value-at-Risk: A Duration-Based Approach. Journal of Financial Econometrics 2: 84–108. [Google Scholar] [CrossRef]
- Conrad, Christian, and Menelaos Karanasos. 2010. Negative volatility spillovers in the unrestricted eccc-garch model. Econometric Theory 26: 838–62. [Google Scholar] [CrossRef]
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1: 223. [Google Scholar] [CrossRef]
- Dhaene, Geert, Piet Sercu, and Jianbin Wu. 2022. Volatility spillovers: A sparse multivariate garch approach with an application to commodity markets. Journal of Futures Markets 42: 868–87. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Marc Nerlove. 1989. The dynamics of exchange rate volatility: A multivariate latent factor arch model. Journal of Applied Econometrics 4: 1–21. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yılmaz. 2014. On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics 182: 119–34. [Google Scholar] [CrossRef]
- EBA. 2021. 2021 EU-Wide Stress Test—Methodological Note. Technical Report. La Défense: European Banking Authority. Available online: https://www.eba.europa.eu/sites/default/documents/files/document_library/RiskAnalysisandData/EU-wideStressTesting/2021/LaunchoftheST/962559/2021EU-widestresstest-MethodologicalNote.pdf (accessed on 3 September 2023).
- Engle, Robert. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert F., and Kenneth F. Kroner. 1995. Multivariate simultaneous generalized arch. Econometric Theory 11: 122–50. [Google Scholar] [CrossRef]
- Engle, Robert F., and Kevin Sheppard. 2001. Theoretical and Empirical Properties of Dynamic Conditional Correlation Multivariate Garch. Working Paper 8554. Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Engle, Robert F., Victor K. Ng, and Michael Rothschild. 1990. Asset pricing with a factor-arch covariance structure: Empirical estimates for treasury bills. Journal of Econometrics 45: 213–37. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Foglia, Matteo, Abdelhamid Addi, and Eliana Angelini. 2022. The eurozone banking sector in the time of COVID-19: Measuring volatility connectedness. Global Finance Journal 51: 100677. [Google Scholar] [CrossRef]
- Giacometti, Rosella, Gabriele Torri, and Sandra Paterlini. 2021. Tail risks in large portfolio selection: Penalized quantile and expectile minimum deviation models. Quantitative Finance 21: 243–61. [Google Scholar] [CrossRef]
- Giannopoulos, Kostas, and Radu Tunaru. 2005. Coherent risk measures under filtered historical simulation. Journal of Banking & Finance 29: 979–96. [Google Scholar]
- Girardi, Giulio, and A. Tolga Ergün. 2013. Systemic risk measurement: Multivariate garch estimation of CoVaR. Journal of Banking & Finance 37: 3169–80. [Google Scholar] [CrossRef]
- Gurrola-Perez, Pedro, and David Murphy. 2015. Filtered Historical Simulation Value-at-Risk Models and Their Competitors. London: Bank of England. [Google Scholar]
- Jeantheau, Thierry. 1998. Strong consistency of estimators for multivariate arch models. Econometric Theory 14: 70–86. [Google Scholar] [CrossRef]
- Jennrich, Robert I. 1970. An asymptotic χ2 test for the equality of two correlation matrices. Journal of the American Statistical Association 65: 904–12. [Google Scholar]
- Keiler, Sebastian, and Armin Eder. 2013. CDS Spreads and Systemic Risk: A Spatial Econometric Approach. Discussion Papers 01/2013. Frankfurt: Deutsche Bundesbank. [Google Scholar] [CrossRef]
- Koenker, Roger, and Gilbert Bassett, Jr. 1978. Regression quantiles. Econometrica: Journal of the Econometric Society 46: 33–50. [Google Scholar] [CrossRef]
- Koliai, Lyes. 2016. Extreme risk modeling: An evt–pair-copulas approach for financial stress tests. Journal of Banking & Finance 70: 1–22. [Google Scholar]
- Kupiec, Paul H. 1995. Techniques for verifying the accuracy of risk measurement models. The Journal of Derivatives 3: 73–84. [Google Scholar] [CrossRef]
- Li, Hong. 2020. Volatility spillovers across european stock markets under the uncertainty of brexit. Economic Modelling 84: 1–12. [Google Scholar] [CrossRef]
- Ling, Shiqing, and Michael McAleer. 2003. Asymptotic theory for a vector arma-garch model. Econometric Theory 19: 280–310. [Google Scholar] [CrossRef]
- Lopez, Jose Antonio. 1999. Methods for Evaluating Value-at-Risk Estimates. Economic Policy Review. San Francisco: Federal Reserve Bank of San Francisco, pp. 3–17. [Google Scholar] [CrossRef]
- Meucci, Attilio. 2005. Risk and Asset Allocation. Berlin: Springer, vol. 1. [Google Scholar]
- Rahman, Dima. 2014. Are banking systems increasingly fragile? Investigating financial institutions? CDS returns extreme co-movements. Quantitative Finance 14: 805–30. [Google Scholar] [CrossRef][Green Version]
- Rockafellar, R. Tyrrell, and Stan Uryasev. 2013. The fundamental risk quadrangle in risk management, optimization and statistical estimation. Surveys in Operations Research and Management Science 18: 33–53. [Google Scholar] [CrossRef]
- Torri, Gabriele, Rosella Giacometti, and Tomáš Tich ỳ. 2021. Network tail risk estimation in the european banking system. Journal of Economic Dynamics and Control 127: 104125. [Google Scholar] [CrossRef]
- Zhang, Wei-Guo, Guo-Li Mo, Fang Liu, and Yong-Jun Liu. 2018. Value-at-risk forecasts by dynamic spatial panel GJR-GARCH model for international stock indices portfolio. Soft Computing 22: 5279–97. [Google Scholar] [CrossRef]
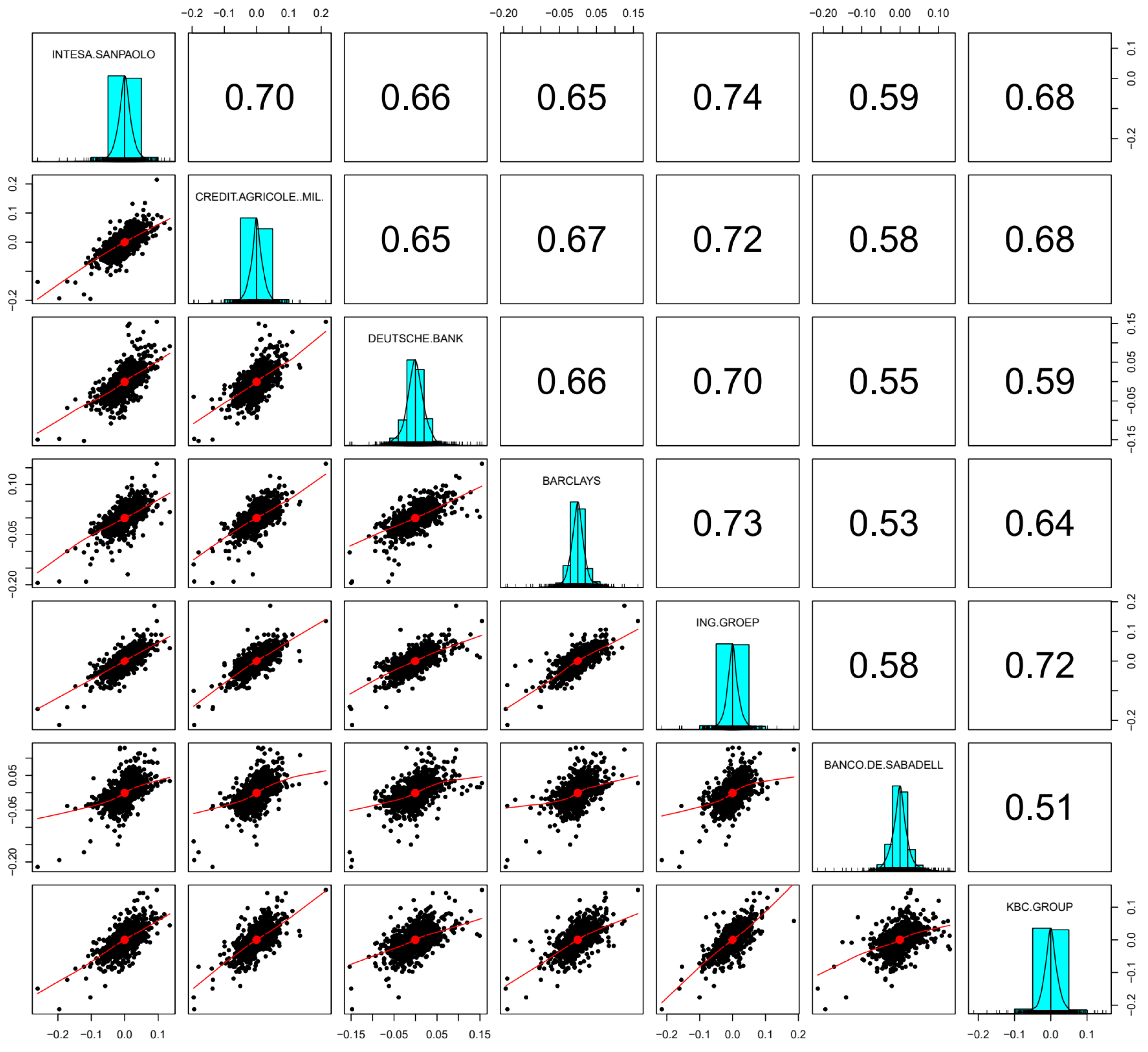

| Bank | Mean | StDev | Skewness | Kurtosis | ARCH Test (p-Value) |
|---|---|---|---|---|---|
| ISP | 0.0256 | −0.8101 | 11.6198 | < | |
| ACA | 0.0253 | −0.3810 | 11.2140 | < | |
| DB | 0.0244 | 0.1203 | 8.1958 | < | |
| BCS | 0.0235 | −0.6568 | 12.9321 | < | |
| ING | 0.0236 | −0.4705 | 11.4810 | < | |
| SAB | 0.0248 | −0.3435 | 10.9513 | < | |
| KBC | 0.0254 | −0.3002 | 10.0297 | < |
| Bank | ISP | ACA | DB | BCS | ING | SAB | KBC |
|---|---|---|---|---|---|---|---|
| ISP | 0 | 0.1482 | 0.1763 | 0.1221 | 0.1875 | 0.1873 | 0.1786 |
| ACA | 0.1453 | 0 | 0.1807 | 0.1745 | 0.1480 | 0.1562 | 0.1953 |
| DB | 0.1689 | 0.1766 | 0 | 0.1347 | 0.1306 | 0.2140 | 0.1753 |
| BCS | 0.1388 | 0.2025 | 0.1600 | 0 | 0.1668 | 0.1520 | 0.1799 |
| ING | 0.2130 | 0.1715 | 0.1549 | 0.1667 | 0 | 0.1596 | 0.1343 |
| SAB | 0.1834 | 0.1560 | 0.2188 | 0.1308 | 0.1375 | 0 | 0.1734 |
| KBC | 0.1761 | 0.1964 | 0.1804 | 0.1559 | 0.1165 | 0.1746 | 0 |
| Akaike | Bayes | Shibata | Hannan-Quinn | |
|---|---|---|---|---|
| GaussDCC | −39.18 | −38.96 | −39.18 | −39.09 |
| GaussSpDCC | −39.34 | −39.06 | −39.35 | −39.23 |
| tDCC | −39.96 | −39.71 | −39.98 | −39.87 |
| tSpDCC | −40.04 | −39.71 | −40.04 | −39.91 |
| GaussDCC | 0 | 0.065 | 0.907 | - | - | 0.016 | 0.885 | - |
| 19% | 57% | 97% | - | - | 74% | 97% | - | |
| GaussSpDCC | 0 | 0.059 | 0.722 | 0.062 | 0.109 | 0.024 | 0.858 | - |
| 37% | 29% | 81% | 31% | 12% | 93% | 99% | - | |
| tDCC | 0 | 0.066 | 0.893 | - | - | 0.014 | 0.915 | 5.90 |
| 27% | 69% | 96% | - | - | 95% | 99% | 100% | |
| tSpDCC | 0 | 0.048 | 0.720 | 0.051 | 0.115 | 0.015 | 0.924 | 6.15 |
| 27% | 32% | 74% | 25% | 11% | 92% | 100% | 100% |
| and —FHS | |||||||
| Bank | ISP | ACA | DB | BCS | ING | SAB | KBC |
| ISP | 0.034 | 0.065 | 0.076 | 0.060 | 0.064 | 0.083 | 0.068 |
| ACA | 0.064 | 0.033 | 0.081 | 0.057 | 0.064 | 0.078 | 0.064 |
| DB | 0.066 | 0.065 | 0.041 | 0.072 | 0.062 | 0.077 | 0.061 |
| BCS | 0.065 | 0.069 | 0.090 | 0.034 | 0.059 | 0.072 | 0.063 |
| ING | 0.065 | 0.071 | 0.076 | 0.061 | 0.032 | 0.078 | 0.066 |
| SAB | 0.067 | 0.066 | 0.077 | 0.058 | 0.065 | 0.042 | 0.063 |
| KBC | 0.065 | 0.067 | 0.076 | 0.061 | 0.066 | 0.079 | 0.028 |
| and —GaussDCC | |||||||
| Bank | ISP | ACA | DB | BCS | ING | SAB | KBC |
| ISP | 0.035 | 0.055 | 0.063 | 0.050 | 0.052 | 0.063 | 0.048 |
| ACA | 0.056 | 0.034 | 0.062 | 0.050 | 0.051 | 0.062 | 0.048 |
| DB | 0.056 | 0.055 | 0.039 | 0.051 | 0.051 | 0.062 | 0.047 |
| BCS | 0.055 | 0.054 | 0.063 | 0.032 | 0.051 | 0.061 | 0.047 |
| ING | 0.057 | 0.056 | 0.064 | 0.051 | 0.031 | 0.063 | 0.050 |
| SAB | 0.055 | 0.054 | 0.061 | 0.049 | 0.050 | 0.040 | 0.047 |
| KBC | 0.056 | 0.055 | 0.062 | 0.050 | 0.052 | 0.062 | 0.030 |
| and —GaussSpDCC | |||||||
| Bank | ISP | ACA | DB | BCS | ING | SAB | KBC |
| ISP | 0.035 | 0.057 | 0.064 | 0.050 | 0.052 | 0.063 | 0.048 |
| ACA | 0.056 | 0.035 | 0.064 | 0.050 | 0.052 | 0.062 | 0.048 |
| DB | 0.056 | 0.056 | 0.040 | 0.051 | 0.052 | 0.061 | 0.047 |
| BCS | 0.055 | 0.056 | 0.064 | 0.032 | 0.051 | 0.060 | 0.047 |
| ING | 0.058 | 0.058 | 0.065 | 0.051 | 0.032 | 0.063 | 0.050 |
| SAB | 0.056 | 0.056 | 0.062 | 0.049 | 0.051 | 0.039 | 0.047 |
| KBC | 0.057 | 0.057 | 0.063 | 0.050 | 0.053 | 0.061 | 0.030 |
| and —tDCC | |||||||
| Bank | ISP | ACA | DB | BCS | ING | SAB | KBC |
| ISP | 0.033 | 0.088 | 0.100 | 0.078 | 0.083 | 0.104 | 0.078 |
| ACA | 0.087 | 0.033 | 0.099 | 0.079 | 0.083 | 0.102 | 0.077 |
| DB | 0.087 | 0.087 | 0.038 | 0.081 | 0.083 | 0.101 | 0.075 |
| BCS | 0.085 | 0.085 | 0.101 | 0.031 | 0.082 | 0.100 | 0.075 |
| ING | 0.089 | 0.089 | 0.102 | 0.082 | 0.031 | 0.105 | 0.078 |
| SAB | 0.087 | 0.085 | 0.097 | 0.077 | 0.082 | 0.040 | 0.075 |
| KBC | 0.088 | 0.088 | 0.099 | 0.079 | 0.083 | 0.102 | 0.029 |
| and —tSpDCC | |||||||
| Bank | ISP | ACA | DB | BCS | ING | SAB | KBC |
| ISP | 0.033 | 0.087 | 0.098 | 0.075 | 0.081 | 0.100 | 0.075 |
| ACA | 0.085 | 0.034 | 0.097 | 0.076 | 0.081 | 0.098 | 0.075 |
| DB | 0.085 | 0.086 | 0.038 | 0.077 | 0.081 | 0.097 | 0.073 |
| BCS | 0.083 | 0.085 | 0.098 | 0.030 | 0.081 | 0.096 | 0.073 |
| ING | 0.087 | 0.088 | 0.100 | 0.078 | 0.031 | 0.100 | 0.076 |
| SAB | 0.085 | 0.084 | 0.095 | 0.074 | 0.080 | 0.039 | 0.073 |
| KBC | 0.086 | 0.087 | 0.097 | 0.076 | 0.081 | 0.098 | 0.029 |
| Panel A: Unconditional Coverage Test for , p-Value. | |||||
| Bank | FHS | GaussDCC | GaussSpDCC | tDCC | tSpDCC |
| ISP | 0.700 | 0.113 | 0.067 | 0.459 | 0.113 |
| ACA | 0.756 | 0.143 | 0.004 | 0.534 | 0.037 |
| DB | 0.534 | 0.670 | 0.589 | 0.270 | 0.122 |
| BCS | 0.670 | 0.789 | 0.327 | 0.756 | 0.589 |
| ING | 0.513 | 0.534 | 0.390 | 0.880 | 0.789 |
| SAB | 0.379 | 0.935 | 0.589 | 0.844 | 0.756 |
| KBC | 0.224 | 0.180 | 0.272 | 0.615 | 0.700 |
| Panel B: Conditional Coverage Test for , -Value. | |||||
| Bank | FHS | GaussDCC | GaussSpDCC | tDCC | tSpDCC |
| ISP | 0.001 | 0.002 | 0.125 | 0.017 | 0.119 |
| ACA | 0.033 | 0.002 | 0.017 | 0.007 | 0.069 |
| DB | 0.022 | 0.013 | 0.042 | 0.008 | 0.009 |
| BCS | 0.038 | 0.255 | 0.366 | 0.200 | 0.413 |
| ING | 0.001 | 0.002 | 0.012 | 0.001 | 0.013 |
| SAB | 0.455 | 0.997 | 0.655 | 0.882 | 0.774 |
| KBC | 0.023 | 0.095 | 0.156 | 0.079 | 0.035 |
| Panel A: Unconditional Coverage Test for . | |||||
| FHS | GaussDCC | GaussSpDCC | tDCC | tSpDCC | |
| Average exceedances | 12.0 | 18.9 | 17.1 | 4.4 | 5.0 |
| Average p-value | 0.047 | 0.000 | 0.000 | 0.639 | 0.472 |
| (% p-values < 0.05) | (88.1%) | (100%) | (100%) | (0%) | (0%) |
| Panel B: Conditional Coverage Test for . | |||||
| FHS | GaussDCC | GaussSpDCC | tDCC | tSpDCC | |
| Average p-value | 0.061 | 0.000 | 0.000 | 0.446 | 0.508 |
| (% p-values < 0.05) | (81.0%) | (100%) | (100%) | (0%) | (0%) |
| Panel A: Backtesting Based on Loss Function. (Investor’s Point of View). | |||||
| Bank | FHS | GaussDCC | GaussSpDCC | tDCC | tSpDCC |
| ISP | 4.11 | 4.06 | 3.97 | 4.08 | 3.96 |
| ACA | 4.21 | 4.24 | 4.14 | 4.24 | 4.18 |
| DB | 4.70 | 4.74 | 4.76 | 4.71 | 4.77 |
| BCS | 3.95 | 3.87 | 3.75 | 3.91 | 3.80 |
| ING | 3.74 | 3.74 | 3.70 | 3.77 | 3.72 |
| SAB | 4.92 | 4.85 | 4.83 | 4.89 | 4.87 |
| KBC | 3.54 | 3.61 | 3.48 | 3.55 | 3.47 |
| mean | 4.17 | 4.16 | 4.09 | 4.16 | 4.11 |
| Panel B: Backtesting Based on Loss Function. (Regulator’s Point of View). | |||||
| Bank | FHS | GaussDCC | GaussSpDCC | tDCC | tSpDCC |
| ISP | 1.24 | 1.15 | 1.05 | 1.29 | 1.16 |
| ACA | 1.44 | 1.35 | 1.17 | 1.44 | 1.33 |
| DB | 1.34 | 1.47 | 1.44 | 1.56 | 1.59 |
| BCS | 1.15 | 1.21 | 1.11 | 1.35 | 1.28 |
| ING | 1.06 | 1.11 | 1.05 | 1.19 | 1.12 |
| SAB | 1.45 | 1.58 | 1.60 | 1.63 | 1.64 |
| KBC | 1.14 | 1.09 | 0.97 | 1.10 | 1.02 |
| mean | 1.26 | 1.28 | 1.20 | 1.37 | 1.31 |
| Panel A: Backtesting Based on Loss Function. (Investor’s Point of View). | |||||
| FHS | GaussDCC | GaussSpDCC | tDCC | tSpDCC | |
| average loss | 0.392 | 0.465 | 0.414 | 0.393 | 0.371 |
| Panel B: Backtesting Based on Loss Function. (Regulator’s Point of View). | |||||
| FHS | GaussDCC | GaussSpDCC | tDCC | tSpDCC | |
| average loss | 0.233 | 0.359 | 0.307 | 0.153 | 0.142 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giacometti, R.; Torri, G.; Rujirarangsan, K.; Cameletti, M. Spatial Multivariate GARCH Models and Financial Spillovers. J. Risk Financial Manag. 2023, 16, 397. https://doi.org/10.3390/jrfm16090397
Giacometti R, Torri G, Rujirarangsan K, Cameletti M. Spatial Multivariate GARCH Models and Financial Spillovers. Journal of Risk and Financial Management. 2023; 16(9):397. https://doi.org/10.3390/jrfm16090397
Chicago/Turabian StyleGiacometti, Rosella, Gabriele Torri, Kamonchai Rujirarangsan, and Michela Cameletti. 2023. "Spatial Multivariate GARCH Models and Financial Spillovers" Journal of Risk and Financial Management 16, no. 9: 397. https://doi.org/10.3390/jrfm16090397
APA StyleGiacometti, R., Torri, G., Rujirarangsan, K., & Cameletti, M. (2023). Spatial Multivariate GARCH Models and Financial Spillovers. Journal of Risk and Financial Management, 16(9), 397. https://doi.org/10.3390/jrfm16090397







