Modeling the Optimal Combination of Proportional and Stop-Loss Reinsurance with Dependent Claim and Stochastic Insurance Premium
Abstract
1. Introduction
2. Reinsurance Contracts and Bivariate Models
2.1. Reinsurance Contracts
- (a)
- The proportional reinsurance contract:
- (b)
- The stop-loss reinsurance contract:
- (c)
- The combination of proportional and stop-loss reinsurance contracts:
2.2. Bivariate Models
- (a)
- Sarmanov’s Bivariate Exponential DistributionAs in Cossette et al. (2015) and Vernic (2016, 2017), the joint probability density function of X and Y under this distributional assumption is defined as follows:We assume that to ensure that their correlation coefficient is positive (Kang et al. 2021).
- (b)
- The Bivariate Exponential Distribution with the Farlie–Gumbel–Morgenstern (FGM) CopulaThe functional form of this copula is given bywith the corresponding copula density . The joint probability density functionof X and Y is determined by substituting , , , and . To make sure that they are positively correlated, the parameter θ of the FGM copula is assumed to belong to (Barges et al. 2009; Kang et al. 2021).
3. Formulation of Reinsurance Optimization Problem
3.1. Sarmanov’s Bivariate Exponential Distribution
- (a)
- If , the optimal combination of proportional and stop-loss reinsurance is derived by minimizingsubject towhere ,and
- (b)
- If , the optimal combination of proportional and stop-loss reinsurance is derived by minimizingsubject towhere
3.2. Bivariate Exponential Distribution with the FGM Copula
- (a)
- If , the optimal combination of proportional and stop-loss reinsurance is derived by minimizingsubject towhere ,and
- (b)
- If , the optimal combination of proportional and stop-loss reinsurance is derived by minimizingsubject towhere
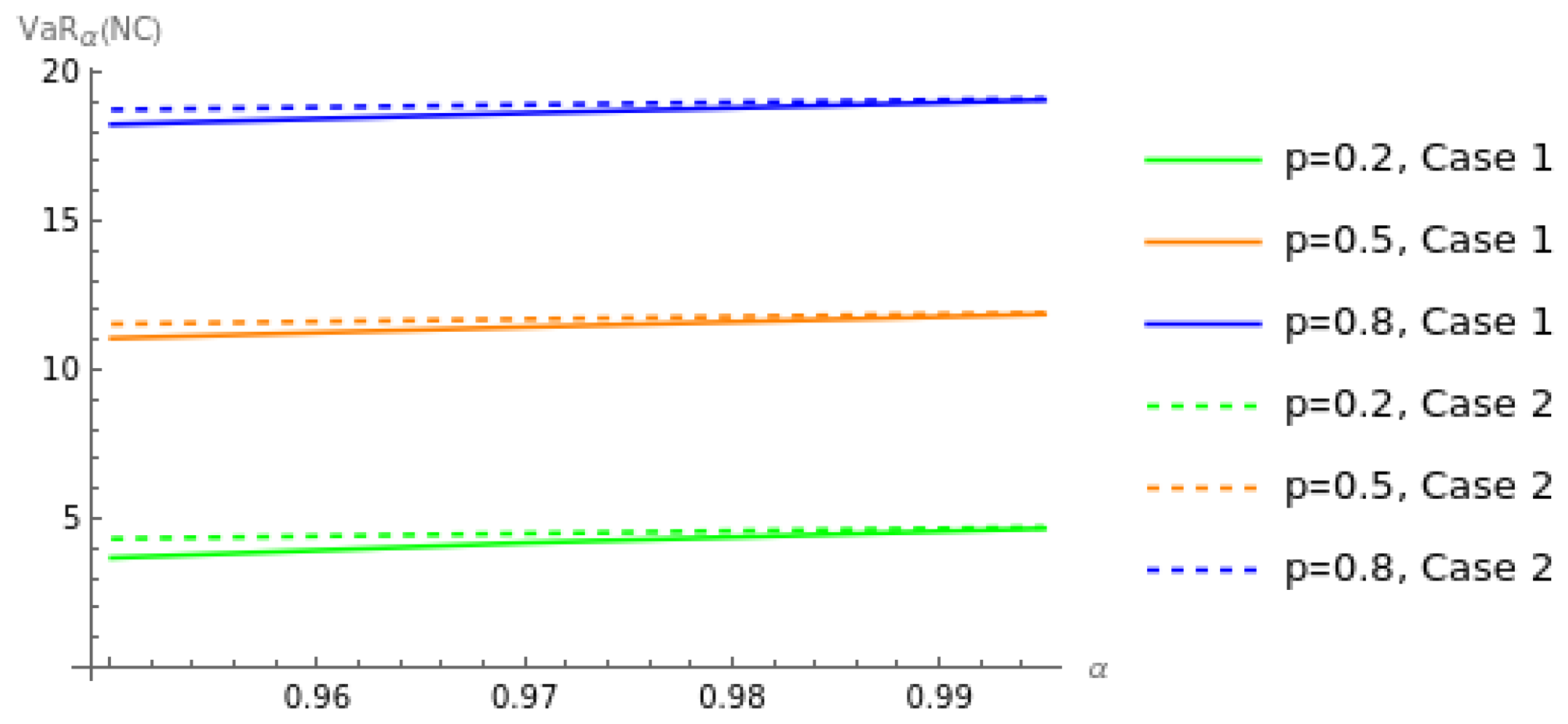
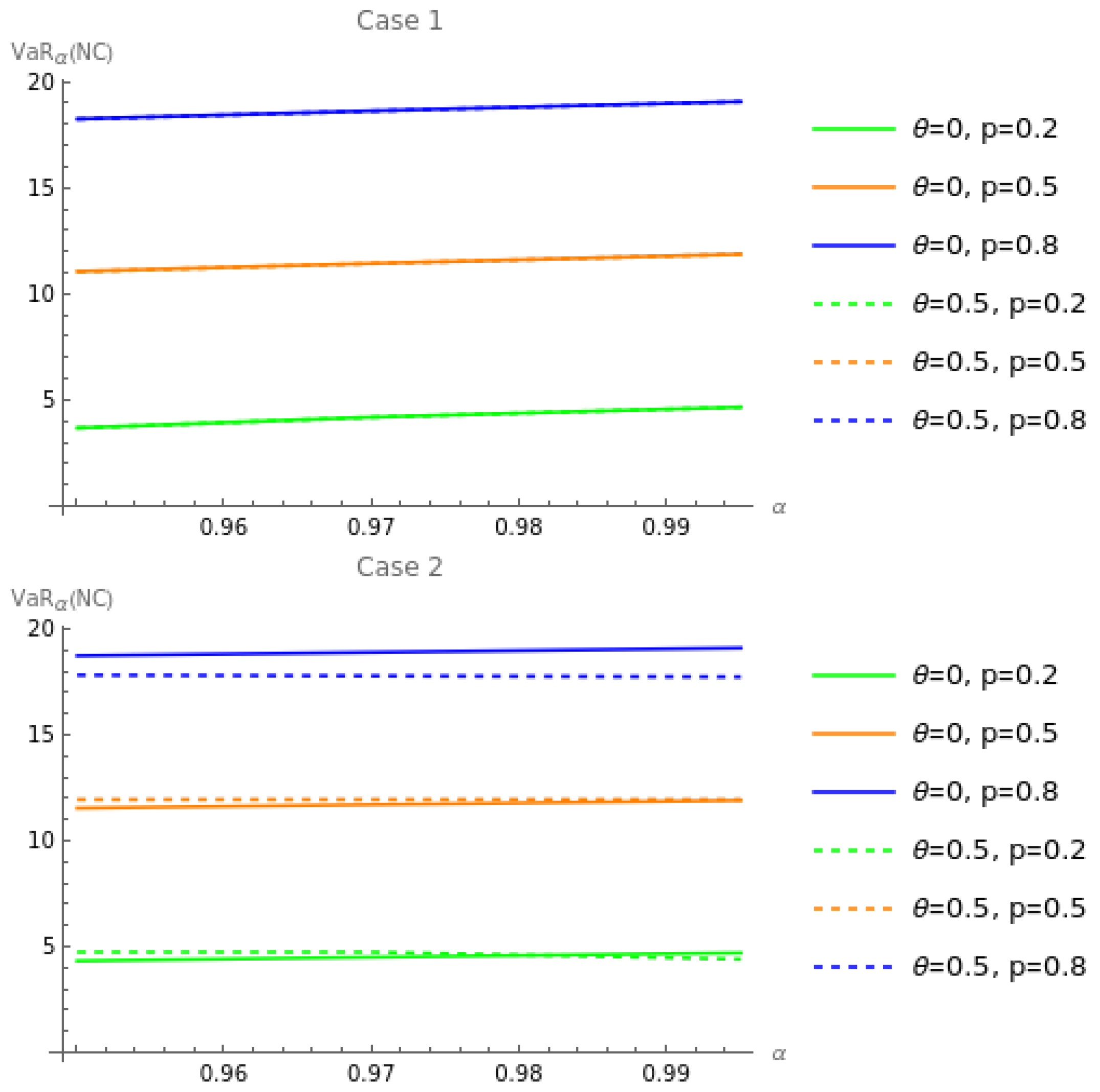
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Theorem 1
Appendix A.2. Proof of Theorem 2
| 1 | When X is a profit-and-loss (P&L) random variable denoting, e.g., a financial position or a financial asset return, the VaR of X at a given significance level is defined as the negative of its lower -quantile, i.e., ; see Artzner et al. (1999). |
References
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent Measures of Risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Bao, Zhen-hua. 2006. The Expected Discounted Penalty at Ruin in the Risk Process with Random Income. Applied Mathematics and Computation 179: 559–66. [Google Scholar] [CrossRef]
- Bao, Zhen-hua, and Zhong-xing Ye. 2007. The Gerber–Shiu Discounted Penalty Function in the Delayed Renewal Risk Process with Random Income. Applied Mathematics and Computation 184: 857–63. [Google Scholar] [CrossRef]
- Bargès, Mathieu, Hélène Cossette, and Étienne Marceau. 2009. TVaR-Based Capital Allocation with Copulas. Insurance: Mathematics and Economics 45: 348–61. [Google Scholar] [CrossRef]
- Borch, Karl. 1960. The Safety Loading of Reinsurance Premiums. Scandinavian Actuarial Journal 1960: 163–84. [Google Scholar] [CrossRef]
- Brachetta, Matteo, and Claudia Ceci. 2019. Optimal Excess-of-Loss Reinsurance for Stochastic Factor Risk Models. Risks 7: 48. [Google Scholar] [CrossRef]
- Cai, Jun, Christiane Lemieux, and Fangda Liu. 2016. Optimal Reinsurance from the Perspectives of Both an Insurer and a Reinsurer. ASTIN Bulletin: The Journal of the IAA 46: 815–49. [Google Scholar] [CrossRef]
- Cai, Jun, and Ken S. Tan. 2007. Optimal Retention for a Stop-Loss Reinsurance under the VaR and CTE Risk Measure. ASTIN Bulletin: The Journal of the IAA 37: 93–112. [Google Scholar] [CrossRef]
- Cai, Jun, Ken S. Tan, Chengguo Weng, and Yi Zhang. 2008. Optimal Reinsurance under VaR and CTE Risk Measures. Insurance: Mathematics and Economics 43: 185–96. [Google Scholar] [CrossRef]
- Champion, Brett, and Adam Strzebonski. 2008. Wolfram Mathematica Tutorial Collection: Constrained Optimization. Wolfram Library Archive. Available online: https://library.wolfram.com/infocenter/Books/8506 (accessed on 14 July 2022).
- Chen, Yanhong, and Yijun Hu. 2021. Optimal Reinsurance from the Perspectives of Both Insurers and Reinsurers under the VaR Risk Measure and Vajda Condition. Communications in Statistics: Theory and Methods 50: 3677–94. [Google Scholar] [CrossRef]
- Chi, Yichun. 2012. Optimal Reinsurance under Variance Related Premium Principles. Insurance: Mathematics and Economics 51: 310–21. [Google Scholar] [CrossRef]
- Chi, Yichun, and Ken S. Tan. 2011. Optimal Reinsurance under VaR and CVaR Risk Measures: A Simplified Approach. ASTIN Bulletin: The Journal of the IAA 41: 487–509. [Google Scholar]
- Cossette, Hélène, Etienne Marceau, and Samuel Perreault. 2015. On Two Families of Bivariate Distributions with Exponential Marginals: Aggregation and Capital Allocation. Insurance: Mathematics and Economics 64: 214–24. [Google Scholar] [CrossRef]
- Gajek, Lesław, and Dariusz Zagrodny. 2000. Insurer’s Optimal Reinsurance Strategies. Insurance: Mathematics and Economics 27: 105–12. [Google Scholar] [CrossRef]
- He, Xinya, Ailing Gu, and Haixiang Yao. 2022. Stochastic Differential Reinsurance and Investment Games with Delay under VaR Constraints. Communications in Statistics: Theory and Methods, in press. [Google Scholar]
- Kahn, Paul M. 1961. Some Remarks on a Recent Paper by Borch. ASTIN Bulletin: The Journal of the IAA 1: 265–72. [Google Scholar] [CrossRef]
- Kaluszka, Marek. 2004. Mean-Variance Optimal Reinsurance Arrangements. Scandinavian Actuarial Journal 2004: 28–41. [Google Scholar] [CrossRef]
- Kang, Yao, Dehui Wang, and Jianhua Cheng. 2021. Risk Models Based on Copulas for Premiums and Claim Sizes. Communications in Statistics: Theory and Methods 50: 2250–69. [Google Scholar] [CrossRef]
- Karageyik, Başak B., and Şule Şahin. 2017. Determination of the Optimal Retention Level Based on Different Measures. Journal of Risk and Financial Management 10: 4. [Google Scholar] [CrossRef]
- Khare, Shree, and Keven Roy. 2021. Quantifying the Role of Occurrence Losses in Catastrophe Excess of Loss Reinsurance Pricing. Risks 9: 52. [Google Scholar] [CrossRef]
- Liang, Zhibin, and Kam C. Yuen. 2016. Optimal Dynamic Reinsurance with Dependent Risks: Variance Premium Principle. Scandinavian Actuarial Journal 2016: 18–36. [Google Scholar] [CrossRef]
- Ohlin, Jan. 1969. On a Class of Measures of Dispersion with Application to Optimal Reinsurance. ASTIN Bulletin: The Journal of the IAA 5: 249–66. [Google Scholar] [CrossRef]
- Sari, Suci F., and Khreshna I. A. Syuhada. 2022. Tail Risk Measures-Based Optimal Reinsurance Model for Quota-Share Reinsurance. AIP Conference Proceedings 2471: 020010. [Google Scholar]
- Syuhada, Khreshna, Arief Hakim, and Suci Sari. 2021. The Combined Stop-Loss and Quota-Share Reinsurance: Conditional Tail Expectation-Based Optimization from the Joint Perspective of Insurer and Reinsurer. Risks 9: 125. [Google Scholar] [CrossRef]
- Tan, Ken S., Chengguo Weng, and Yi Zhang. 2009. VaR and CTE Criteria for Optimal Quota-Share and Stop-Loss Reinsurance. North American Actuarial Journal 13: 459–82. [Google Scholar] [CrossRef]
- Tan, Tao, Tao Chen, Lijun Wu, Yuhong Sheng, and Yijun Hu. 2020. VaR and CTE Based Optimal Reinsurance from a Reinsurer’s Perspective. Acta Mathematica Scientia 40: 1915–27. [Google Scholar] [CrossRef]
- Temnov, G. 2004. Risk Process with Random Income. Journal of Mathematical Sciences 123: 3780–94. [Google Scholar] [CrossRef]
- Vernic, Raluca. 2016. On the Distribution of a Sum of Sarmanov Distributed Random Variables. Journal of Theoretical Probability 29: 118–42. [Google Scholar] [CrossRef]
- Vernic, Raluca. 2017. Capital Allocation for Sarmanov’s Class of Distributions. Methodology and Computing in Applied Probability 19: 311–30. [Google Scholar] [CrossRef]
- Vidmar, Matija. 2018. Ruin under Stochastic Dependence between Premium and Claim Arrivals. Scandinavian Actuarial Journal 2018: 505–13. [Google Scholar] [CrossRef]
- Zhang, Nan, Zhuo Jin, Linyi Qian, and Rongming Wang. 2018. Optimal Quota-Share Reinsurance Based on the Mutual Benefit of Insurer and Reinsurer. Journal of Computational and Applied Mathematics 342: 337–51. [Google Scholar] [CrossRef]
- Zheng, Yanting, and Wei Cui. 2014. Optimal Reinsurance with Premium Constraint under Distortion Risk Measures. Insurance: Mathematics and Economics 59: 109–20. [Google Scholar] [CrossRef]
- Zhou, Ming, Hongbin Dong, and Jingfeng Xu. 2011. Optimal Combinational of Quota-Share and Stop-Loss Reinsurance Contracts under VaR and CTE with a Constrained Reinsurance Premium. Journal of Systems Science and Complexity 24: 156–66. [Google Scholar] [CrossRef]
| P | p | ||||||
|---|---|---|---|---|---|---|---|
| Value 1 | 1/15 | 1/10 | 0.6 | 60 | 0 | 0.2 | 0.950 |
| Value 2 | 0.2 | 0.5 | 0.970 | ||||
| Value 3 | 0.5 | 0.8 | 0.995 |
| p | ||||||
|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.950 | 0.222 | 274.595 | 9.763 | 3.733 |
| 0.970 | 0.118 | 168.979 | 0.000 | 4.235 | ||
| 0.995 | 0.017 | 2.629 | 9.131 | 4.718 | ||
| 0.5 | 0.950 | 0.074 | 3.347 | 0.000 | 11.111 | |
| 0.970 | 0.043 | 4.485 | 0.000 | 11.489 | ||
| 0.995 | 0.007 | 1.797 | 0.000 | 11.919 | ||
| 0.8 | 0.950 | 0.066 | 254.816 | 0.369 | 18.295 | |
| 0.970 | 0.037 | 2.995 | 0.183 | 18.677 | ||
| 0.995 | 0.006 | 1.439 | 0.024 | 19.117 | ||
| 0.2 | 0.2 | 0.950 | 0.223 | 0.000 | 0.000 | 3.731 |
| 0.970 | 0.118 | 262.698 | 0.000 | 4.233 | ||
| 0.995 | 0.017 | 124.323 | 0.000 | 4.717 | ||
| 0.5 | 0.950 | 0.074 | 1.215 | 1.781 | 11.107 | |
| 0.970 | 0.043 | 3.504 | 0.000 | 11.486 | ||
| 0.995 | 0.007 | 1.145 | 0.000 | 11.918 | ||
| 0.8 | 0.950 | 0.067 | 1.111 | 0.369 | 18.290 | |
| 0.970 | 0.037 | 3.528 | 0.184 | 18.674 | ||
| 0.995 | 0.006 | 5.633 | 0.025 | 19.116 | ||
| 0.5 | 0.2 | 0.950 | 0.224 | 336.420 | 6.758 | 3.727 |
| 0.970 | 0.119 | 185.575 | 0.000 | 4.230 | ||
| 0.995 | 0.018 | 95.837 | 0.000 | 4.716 | ||
| 0.5 | 0.950 | 0.075 | 7.452 | 3.298 | 11.100 | |
| 0.970 | 0.043 | 3.579 | 9.062 | 11.481 | ||
| 0.995 | 0.007 | 128.701 | 4.854 | 11.917 | ||
| 0.8 | 0.950 | 0.067 | 1.108 | 0.368 | 18.283 | |
| 0.970 | 0.027 | 1.057 | 0.000 | 18.692 | ||
| 0.995 | 0.006 | 1.146 | 0.026 | 19.114 |
| p | ||||||
|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.950 | 0.222 | 16.139 | 8.009 | 6.533 |
| 0.970 | 0.118 | 6.241 | 8.113 | 7.412 | ||
| 0.995 | 0.017 | 208.967 | 0.000 | 8.256 | ||
| 0.5 | 0.950 | 0.086 | 58.077 | 0.173 | 14.151 | |
| 0.970 | 0.047 | 96.293 | 0.059 | 14.641 | ||
| 0.995 | 0.007 | 5.997 | 0.003 | 15.191 | ||
| 0.8 | 0.950 | 0.076 | 57.978 | 0.557 | 19.798 | |
| 0.970 | 0.042 | 285.137 | 0.278 | 20.232 | ||
| 0.995 | 0.015 | 90.263 | 0.278 | 20.787 | ||
| 0.2 | 0.2 | 0.950 | 0.223 | 7.325 | 7.160 | 6.529 |
| 0.970 | 0.118 | 3.728 | 3.453 | 7.408 | ||
| 0.995 | 0.017 | 4.130 | 6.103 | 8.255 | ||
| 0.5 | 0.950 | 0.086 | 408.227 | 0.168 | 14.146 | |
| 0.970 | 0.047 | 3.238 | 0.061 | 14.637 | ||
| 0.995 | 0.007 | 7.070 | 0.003 | 15.190 | ||
| 0.8 | 0.950 | 0.076 | 1.591 | 0.556 | 19.793 | |
| 0.970 | 0.042 | 2.713 | 0.280 | 20.228 | ||
| 0.995 | 0.328 | 164.619 | 0.230 | 14.215 | ||
| 0.5 | 0.2 | 0.950 | 0.224 | 7.364 | 1.400 | 6.523 |
| 0.970 | 0.119 | 2.674 | 3.614 | 7.403 | ||
| 0.995 | 7.461 | 88.381 | 0.341 | 8.741 | ||
| 0.5 | 0.950 | 0.086 | 29.052 | 0.163 | 14.139 | |
| 0.970 | 0.047 | 8.165 | 0.057 | 14.631 | ||
| 0.995 | 0.007 | 4.847 | 0.002 | 15.189 | ||
| 0.8 | 0.950 | 0.076 | 1.741 | 0.555 | 19.785 | |
| 0.970 | 0.042 | 5.126 | 0.282 | 20.222 | ||
| 0.995 | 0.320 | 74.085 | 0.250 | 14.413 |
| p | ||||||
|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.950 | 0.089 | 45.344 | 0.000 | 4.375 |
| 0.970 | 0.052 | 3.982 | 1.970 | 4.551 | ||
| 0.995 | 0.008 | 5.311 | 1.101 | 4.760 | ||
| 0.5 | 0.950 | 0.034 | 39.610 | 8.265 | 11.590 | |
| 0.970 | 0.020 | 66.868 | 0.000 | 11.756 | ||
| 0.995 | 0.003 | 21.742 | 2.700 | 11.960 | ||
| 0.8 | 0.950 | 0.021 | 45.050 | 0.000 | 18.794 | |
| 0.970 | 0.012 | 45.050 | 0.000 | 18.958 | ||
| 0.995 | 0.002 | 43.975 | 0.000 | 19.160 | ||
| 0.2 | 0.2 | 0.950 | 0.168 | 0.000 | 0.000 | 3.993 |
| 0.970 | 0.191 | 3.169 | 0.000 | 3.883 | ||
| 0.995 | 0.220 | 0.000 | 0.000 | 3.744 | ||
| 0.5 | 0.950 | 0.203 | 0.000 | 0.000 | 9.568 | |
| 0.970 | 0.212 | 0.000 | 0.000 | 9.457 | ||
| 0.995 | 0.224 | 0.000 | 0.000 | 9.317 | ||
| 0.8 | 0.950 | 0.211 | 0.000 | 0.000 | 15.142 | |
| 0.970 | 0.217 | 0.000 | 0.000 | 15.030 | ||
| 0.995 | 0.224 | 0.000 | 0.000 | 14.891 | ||
| 0.5 | 0.2 | 0.950 | 0.055 | 6.555 | 0.000 | 4.537 |
| 0.970 | 0.062 | 7.436 | 0.000 | 4.501 | ||
| 0.995 | 0.072 | 6.159 | 0.000 | 4.456 | ||
| 0.5 | 0.950 | 2.549 | 10.966 | 3.279 | 12.000 | |
| 0.970 | 9.109 | 5.421 | 1.535 | 12.000 | ||
| 0.995 | 0.072 | 0.000 | 0.000 | 11.128 | ||
| 0.8 | 0.950 | 0.069 | 0.000 | 0.000 | 17.879 | |
| 0.970 | 0.071 | 7.624 | 2.454 | 17.844 | ||
| 0.995 | 0.073 | 2.006 | 1.189 | 17.799 |
| p | ||||||
|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.950 | 0.089 | 33.095 | 0.000 | 7.656 |
| 0.970 | 0.052 | 33.321 | 0.000 | 7.964 | ||
| 0.995 | 0.008 | 21.506 | 0.000 | 8.330 | ||
| 0.5 | 0.950 | 0.034 | 18.982 | 0.000 | 14.772 | |
| 0.970 | 0.020 | 73.940 | 0.000 | 14.984 | ||
| 0.995 | 0.003 | 39.198 | 0.000 | 15.243 | ||
| 0.8 | 0.950 | 0.021 | 48.792 | 0.000 | 20.378 | |
| 0.970 | 0.013 | 48.792 | 0.000 | 20.556 | ||
| 0.995 | 0.002 | 72.113 | 0.000 | 20.775 | ||
| 0.2 | 0.2 | 0.950 | 0.168 | 0.000 | 0.000 | 6.988 |
| 0.970 | 0.191 | 0.000 | 0.000 | 6.795 | ||
| 0.995 | 0.220 | 0.000 | 0.000 | 6.551 | ||
| 0.5 | 0.950 | 0.203 | 0.000 | 0.000 | 12.194 | |
| 0.970 | 0.212 | 0.000 | 0.000 | 12.053 | ||
| 0.995 | 0.224 | 0.000 | 0.000 | 11.875 | ||
| 0.8 | 0.950 | 0.211 | 4.411 | 0.000 | 16.418 | |
| 0.970 | 0.217 | 0.000 | 0.000 | 16.297 | ||
| 0.995 | 0.224 | 0.000 | 20.000 | 16.146 | ||
| 0.5 | 0.2 | 0.950 | 1.137 | 4.740 | 3.804 | 8.400 |
| 0.970 | 3.531 | 1.587 | 33.965 | 8.400 | ||
| 0.995 | 2.309 | 0.039 | 1.723 | 8.400 | ||
| 0.5 | 0.950 | 4.689 | 12.512 | 3.746 | 15.295 | |
| 0.970 | 3.176 | 11.521 | 5.801 | 15.294 | ||
| 0.995 | 0.073 | 2.702 | 5.736 | 14.182 | ||
| 0.8 | 0.950 | 0.069 | 1.914 | 3.072 | 19.386 | |
| 0.970 | 0.071 | 4.453 | 0.000 | 19.347 | ||
| 0.995 | 0.073 | 5.470 | 1.199 | 19.299 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sari, S.; Hakim, A.; Magdalena, I.; Syuhada, K. Modeling the Optimal Combination of Proportional and Stop-Loss Reinsurance with Dependent Claim and Stochastic Insurance Premium. J. Risk Financial Manag. 2023, 16, 95. https://doi.org/10.3390/jrfm16020095
Sari S, Hakim A, Magdalena I, Syuhada K. Modeling the Optimal Combination of Proportional and Stop-Loss Reinsurance with Dependent Claim and Stochastic Insurance Premium. Journal of Risk and Financial Management. 2023; 16(2):95. https://doi.org/10.3390/jrfm16020095
Chicago/Turabian StyleSari, Suci, Arief Hakim, Ikha Magdalena, and Khreshna Syuhada. 2023. "Modeling the Optimal Combination of Proportional and Stop-Loss Reinsurance with Dependent Claim and Stochastic Insurance Premium" Journal of Risk and Financial Management 16, no. 2: 95. https://doi.org/10.3390/jrfm16020095
APA StyleSari, S., Hakim, A., Magdalena, I., & Syuhada, K. (2023). Modeling the Optimal Combination of Proportional and Stop-Loss Reinsurance with Dependent Claim and Stochastic Insurance Premium. Journal of Risk and Financial Management, 16(2), 95. https://doi.org/10.3390/jrfm16020095






