Abstract
This article examines the asymmetric volatility spillover effects between Bitcoin and alternative coin markets at the disaggregate level. We apply a frequency connectedness approach to the daily data of 11 major cryptocurrencies for the period from 1 September 2017 to 2 March 2022. We try to uncover the existence of the “fear of missing out” psychological effect and “pump-and-dump schemes” in the crypto markets. To do that, we estimate the volatility spillovers from Bitcoin to altcoin and the cryptos’ own risk spillovers during bull and bear markets. The spillover results from Bitcoin to altcoin provide mixed results regarding the presence of this theory for major cryptocurrencies. However, the empirical findings carried out by the cryptos’ own spillover effects fully confirm the existence of a fear-of-missing-out effect and pump-and-dump schemes in all cryptocurrencies except for USDT.
Keywords:
asymmetric volatility spillover; bitcoin; altcoin; cryptocurrency; frequency connectedness JEL Classification:
C32; E42; E49; G14; G41
1. Introduction
Cryptocurrencies have drawn considerable interest from investors, policymakers, and regulators since Bitcoin was created by Satoshi Nakamoto (2008). With their widespread popularity among the public, they have become a popular topic in recent times among academicians, investors, portfolio managers, and regulators. Corbet et al. (2019) divided academic publications on cryptocurrencies into five main categories: bubble dynamics (Corbet et al. 2018b; Vranken 2017), regulation (Böhme et al. 2015; De Filippi 2014; Fletcher et al. 2021), cybercrime (Bernabe et al. 2019; Pinzón and Rocha 2016; Q. Wang et al. 2020), diversification (Chemkha et al. 2021; Urquhart and Zhang 2019), and efficiency (Khuntia and Pattanayak 2018; Nan and Kaizoji 2019; Vidal-Tomás and Ibañez 2018). However, we can extend the list of ranges from return-volume relationships and tail riskiness (Balcilar et al. 2017; Fousekis and Tzaferi 2021) to speculation (Blau 2018; Smaniotto and Neto 2020), as well as return-volatility transmissions between cryptocurrencies and other conventional financial markets (Bouri et al. 2018; Charfeddine et al. 2020; Corbet et al. 2018a).
Unlike other financial assets that are not traded on holidays, the crypto market is open 24 h a day including weekends. Thus, it is important to examine volatility spillover within crypto markets at multiple frequencies (Mensi et al. 2021). Rather than looking through the whole directional risk spillovers among crypto assets, as in other studies (i.e., Brandvold et al. 2015; Ciaian et al. 2018; Fasanya et al. 2021; Katsiampa et al. 2019; Koutmos 2018; Mensi et al. 2021; Sensoy et al. 2021; Yi et al. 2018), we concentrate on the accumulated risk spillovers from Bitcoin to other major alternative coins from the first day to longer periods. Our main motivation for doing so is the fact that price movements in the crypto market are largely determined by Bitcoin (Corbet et al. 2018a; Kumar et al. 2022; Yi et al. 2018). In addition, we examine the cryptos’ own risk spillovers at different frequencies. Indeed, our study is mainly related to two strands of studies in the crypto markets: studies investigating the relationship among crypto markets (Aslanidis et al. 2021; Fousekis and Tzaferi 2021) and studies examining the behavioral characteristics of cryptocurrency investors (Baur and Dimpfl 2018; J. N. Wang et al. 2021). This study differs from others in terms of the following aspects: The first aspect is the fact that the main risk coming from Bitcoin price movements to altcoins is neglected by these studies. When this fact is ignored, crypto investors cannot take full advantage of the study results. The second aspect is that we decompose the time domain into various frequencies, but we report the accumulated volatility spillover from Bitcoin to altcoins from the first trading day to the long-term investment horizon. In the third aspect, this study indeed provides different perspectives to test which kinds of investors (informed and uninformed) are dominant in the crypto market for the various altcoins under consideration. Lastly, we use a greater number of cryptos and try to select older major cryptocurrencies1 with higher market capitalization.
Volatility and volatility spillovers have become hot topics of finance research since the development of the conditional heteroscedasticity models of Engle (1982) and Bollerslev (1987). Subsequently, various generalized autoregressive conditional heteroscedasticity (GARCH) models2 have been formulized in the literature after recognizing that volatility propagates asymmetrically (Ang and Chen 2002; Baruník et al. 2017). Later, Cappiello et al. (2006) introduced the asymmetric dynamic conditional correlation DCC (ADCC) specification to account for both multivariate and asymmetries in the conditional variances and the conditional correlations. Based on the realized semivariances proposed by Barndorff-Nielsen et al. (2010), Baruník et al. (2016) propose a way to capture volatility spillovers that are due to bad and good volatility. As an alternative volatility spillover measurement approach, Diebold and Yilmaz (2009, 2012) developed a volatility spillover index (the DY index) based on forecast-error variance decompositions from vector autoregressions (VAR). This technique, however, assumes that the spillover effects among markets are the same across different investment horizons. Still, this assumption fails to model market reality. Baruník and Křehlík (2018) extend the time-domain DY index to the frequency domain to overcome this deficiency. Rather than focusing on frequency responses, this approach is interested in assessing shares of uncertainty in one variable due to shocks with varying persistence levels. In addition, the DY index is better than other ways of measuring volatility, such as multivariate asymmetric GARCH models, because it can measure the direction of the spillover effect in short-, medium-, and long-term financial cycles.
Against this background, the main goal of the present paper is to shed light on the existence of informed traders (or insiders) and uninformed noise traders in the cryptocurrency market. “Fear of missing out” (FOMO) and pump-and-dump schemes have attracted the attention of researchers in cryptocurrency markets (Baur and Dimpfl 2018; Delfabbro et al. 2021; Park and Chai 2020; J. N. Wang et al. 2021; Xu and Livshits 2019). FOMO is the fear a trader or investor experiences when they miss out on a potentially profitable investment or trading opportunity in the context of financial markets and trading. The FOMO feeling is most apparent when the value of an asset climbs dramatically in a short period. On the other hand, crypto pump-and-dump schemes occur when conspirators use misleading information to inflate the value of a currency, then sell it for a profit. In this respect, it is wise to assume that the greater the number of uninformed noise traders and fraudsters in a certain altcoin market, the greater the risk of spillovers from bitcoin (or altcoins’ prices) to related altcoins. The fact that bitcoin price crashes are followed by other altcoins in the cryptocurrency market confirms this argument.
Our study is strongly related to various studies, such as those by Demir et al. (2021) and Brik et al. (2022), in the cryptocurrency finance literature. Demir et al. (2021) investigated the asymmetric effect of Bitcoin on ETH, XRP, and LTC using the nonlinear autoregressive distributed lag (NARDL) model for the period of July 2015 to March 2019. Their results indicated that the price of Bitcoin impacts altcoin prices asymmetrically in the short run for all altcoins and a decline in Bitcoin price has a higher effect on altcoins than a rise in Bitcoin price. On the other hand, Brik et al. (2022) examined the return and volatility transmissions between Bitcoin and ten stable and nonstable major cryptocurrencies from 8 October 2018 to 17 August 2020 utilizing the VARMA-BEKK-GARCH model. They provided evidence that volatility transmission is bidirectional in the short and long runs for Bitcoin/Ethereum and Bitcoin/Bitcoin Cash but unidirectional in the short run for Bitcoin/Tether and Bitcoin/TrueUSD. Except for Bitcoin and TrueUSD, there is no long-term bidirectional volatility transmission. The main motivation for this study is to use asymmetric spillover measures to bring a different perspective to the issues that are frequently discussed in the finance literature. It is important for informed investors who want to invest in the crypto market to know in which altcoin market uninformed investors and fraudsters trade the most. Consequently, our work may be of interest to investors who want to recognize the risk coming from uninformed investors and adjust their investment strategy according to BTC price fluctuations.
We examine bitcoin and a set of 10 major altcoins with the largest market capitalization and find interesting results about the spillover from Bitcoin to altcoins during different market conditions. Our data span from 1 September 2017 to 2 March 2022. Our empirical results show that the short- and long-term risk spillovers sourced by Bitcoin are larger for BNB, ETH, LTC, and USDT during bullish market conditions. However, the short- and long-term risk spillovers from Bitcoin to TRON and XRP are greater during bearish market conditions. For ADA and DOGE, the risk spillover emanating from Bitcoin during a bearish market exceeds the risk spillover during a bullish market after the tenth day. Moreover, regarding the risk spread from Bitcoin to BCH and LINK, we do not observe any obvious difference between the bull and bear markets. In addition to this analysis, we examine the cryptocurrency’s own risk spillovers at various frequencies and volatility spillovers from BTC to altcoins during the pre- and post-COVID-19 periods. After COVID-19, the volatility spillover index from BTC to altcoins differs. For instance, the volatility spillover from BTC to BCH, DOGE, LINK, and TRX increased after the COVID-19 outbreak. The empirical findings clearly support FOMO and pump-and-dump schemes for all cryptocurrencies under consideration. Overall, we conclude that the FOMO of noise traders and the deployment of pump-and-dump schemes are inherent features of cryptocurrencies.
2. Methodology
This study uses the frequency connectedness approach developed by Baruník and Křehlík (2018) to examine the risk (volatility) spillover from Bitcoin to eight major cryptocurrencies. This technique is an extension of the time-domain spillover index developed by Diebold and Yilmaz (2012). We start by defining the model as
where is an N-dimensional covariance stationary stochastic process, is an × coefficient matrix, is an N-dimensional white noise or innovation process, and is the lag length. Utilizing lag-polynomial approximation (i.e., ), the VAR model can be written concisely as . The generalized forecast-error variance decomposition (FEVD) proposed by Koop et al. (1996) and Pesaran and Shin (1998), hereafter KPPS, can be computed using the moving average () representation,
where stands for infinite lag polynomials and is calculated recursively from . The H-step-ahead error variances in forecasting are originated from two sources. One of them is due to the corresponding variable’s () own variance, and others are due to the other variable’s () cross variance. Hence, the H-step-ahead generalized FEVD can be calculated as
where has -dimensional coefficients at lag and . represents how much of the future forecast error variance of the variable is due to innovations in variable at horizon . Since the rows of the variance decomposition matrix do not usually sum to one, we need to normalize each entry of the variance decomposition matrix by the row sum as
Now, and by construction. Using , we can construct several spillover measures (i.e., total, directional, net, and net pairwise). The total spillover index () can be constructed using the volatility contributions from the KPPS variance decomposition as
In addition to the total spillover index, it is possible to measure the spillover transmitted from the overall system to variable as
Similarly, the spillover transmitted from to the overall system as
The net spillover index for element is the difference
Lastly, the net pairwise spillover between markets and is simply the difference between the gross volatility shocks transmitted from market to market and those transmitted from to as
To measure the volatility spillover in the frequency domain, we follow Baruník and Křehlík (2018) and describe the spectral formulation of the variance decomposition. For this purpose, we utilize the Fourier transform of the coefficients (the impulse function used for the time domain) to obtain a frequency response function at a frequency ω ( with ). The power spectrum (Fourier transform of the filtered series) is
Therefore, Equation (7) illustrates how the variance of the N-dimensional stochastic process is distributed over the frequency components ω. Using the spectral representation for covariance, , we can define the variance decomposition on the frequency band as
where is the generalized causation spectrum,
which stands for the portion of the spectrum of the jth variable due to shocks in the kth variable at frequency . On the other hand,
is a weighting function, and it represents the power of the jth variable at , which sums through frequencies to a constant value of 2π. Baruník and Křehlík (2018) termed as frequency spillover. After normalizing the values of and , one can easily calculate alternative spillover indices (Equations (2)–(6)) in the frequency domain.
We define “good” or “bad” volatility3 spillover from Bitcoin to alternative cryptocurrencies when Bitcoin’s daily return4 is positive or negative, respectively. This is a good proxy for altcoin investors who observe downside (and upside) risk in the crypto market. Hence, we can formulate good and bad volatility spillovers at a given frequency as follows:
where and represent good and bad volatility spillover, and denotes the daily log return of Bitcoin.
3. Data and Descriptive Statistics
We employ daily prices for the eleven major cryptocurrencies (Bitcoin, Cardano, Binance Coin, Bitcoin Cash, Dogecoin, Ethereum, Chainlink, Litecoin, Tron, Tether, and Ripple). The data have daily frequencies and span from 1 September 2017 to 2 March 2022, with the equivalent of 1613 observations. Among them, 861 observations correspond to Bitcoin’s bullish periods and 752 to bearish periods. Furthermore, the World Health Organization (WHO) declared COVID-19 a global epidemic on 11 March 2020. For COVID-19 analysis, we split the whole dataset into two sub-periods (pre- and post-COVID-19) based on this declaration. We take the pre-COVID-19 period before the official declaration and the post-COVID-19 period after that announcement. Moreover, the selection of these cryptocurrencies is motivated by their large market capitalization and long trading periods in comparison to other crypto markets. The cryptocurrencies analyzed in this study account for nearly 75% of total crypto market capitalization.
Figure 1 plots the volatility series of corresponding cryptocurrencies and shows that the volatility series fluctuates over time. Moreover, all volatility series tend to appear in clusters. In other words, high-volatility sub-periods are followed by low-volatility periods for crypto assets. Moreover, we observe the co-movement of the volatility series, and this can be easily seen in the correlation heat map (see Figure 2). USDT volatility is the least correlated asset with other cryptos, and this is followed by DOGE, among other cryptocurrencies. The volatility of the USDT has also dropped dramatically since the end of 2020. We may argue that the sharp decrease in USDT volatility near the end of 2020 and its stabilization, as a result, are factors that weaken the link between it and other cryptocurrencies. On the other hand, BTC and ETH are the most correlated assets with other cryptos. The descriptive statistics for the crypto volatility series are shown in Table 1. LINK has the highest average volatility, while USDT has the lowest. Moreover, DOGE (USDT) has the greatest (lowest) volatility standard deviation. In addition, Jarque-Bera (JB) reveals that the normality hypothesis is rejected for all volatility series.
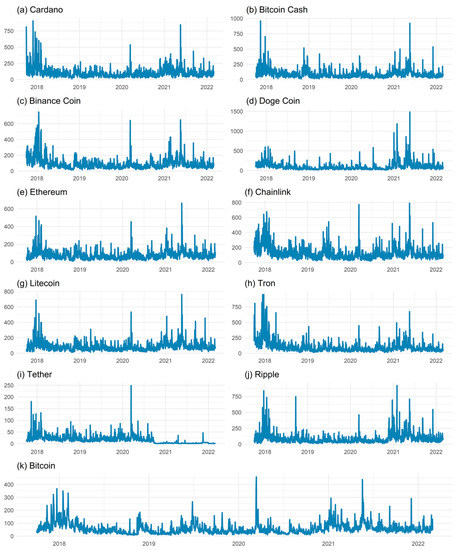
Figure 1.
The plot of cryptocurrency volatility series.

Figure 2.
Correlation heat map.

Table 1.
Descriptive statistics of volatility series.
4. Empirical Results and Discussion
We estimate two VAR models for eleven cryptocurrency volatility series. One is estimated when the Bitcoin return is positive (bullish market), whereas the other is estimated when the Bitcoin return is negative (bearish market). The lag length of both VAR models is determined using the Schwarz Information Criterion (SIC), and H has been set equal to 100. Frequency spillovers are assessed at the bands (0, 1], (1, 2], …, (10, 20], (20, 100], and (100, ∞] days. In accordance with Mensi et al. (2021), the short-term ranges between 1 and 5 days, the medium term, 5–20 days, and the long term, more than 20 days. Hence, we calculate the short-, medium-, and long-term risk spillovers from Bitcoin to other altcoins by summing up the volatility spillover in each band (Figure 3).
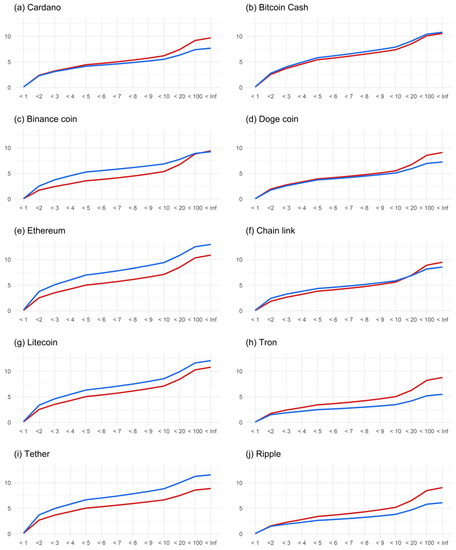
Figure 3.
Short- and long-term volatility spillover from Bitcoin to altcoins during bear and bull market conditions. Note: The horizontal axis denotes the frequency in days, while the vertical axis denotes cumulative spillover index. The red and blue line shows the volatility spillover from Bitcoin to altcoins when bitcoin returns are negative (bear market condition) and positive (bull market condition), respectively.
Figure 3 reveals mixed results regarding asymmetry. The short-, medium-, and long-term risk spillover from Bitcoin to BNB, ETH, LTC, and USDT is greater during a bull market than during a bear market. That means BNB, ETH, LTC, and USDT traders are more likely to encounter uninformed investors5 compared to other cryptocurrencies analyzed. Accordingly, these crypto traders should worry more about uninformed investors’ herding when making trading decisions because it is difficult to predict when the dump process starts and the overpriced coins will suddenly crash. This means a significant risk of loss of income for these investors. However, for TRON and XRP, the risk spillover is stronger in a bear market. In other words, informed investors are more dominant in these altcoin markets throughout all investment periods. Furthermore, our empirical findings show that the risk spillover from Bitcoin to ADA and DOGE during a bear market exceeds that during a bull market in the medium term. Lastly, the risk spillovers from Bitcoin to BCH and LINK during bull and bear market conditions are very close to each other. Hence, our empirical findings, except for BCH and LINK, are in line with Mensi et al. (2021), who found that cryptocurrencies are sensitive to frequencies.
In addition to the analysis carried out above, we report the asymmetric volatility spillovers of cryptocurrencies (Figure A1, Appendix A) explained by their own shocks. This can be justified by the following reasonable approach: Crypto investors generally follow the price of their invested coin rather than the bitcoin price. Similar to the previous analysis, we consider the period when the bitcoin price increases as a bullish market, whereas negative bitcoin returns represent a bearish market. Figure A1 shows that the risk spillovers of cryptos, except for USDT, on themselves are greater during a bull market than during a bear market. This can be explained by the well-known features of USDT. USDT is a fiat-collateralized stable coin where the actual US dollar currency backs each USDT in circulation. These results strongly confirm Baur and Dimpfl (2018), who found that positive shocks increase volatility more than negative shocks. In other words, the findings are compatible with uninformed investors’ FOMO and the presence of pump-and-dump schemes.
The empirical results in Figure 3 also provide evidence about the price formation of altcoins in the short, medium, and long runs. In fact, nearly 70% of the risk spillover from Bitcoin to altcoins takes place in the first 10 days, which can be seen as short-term. This finding concords with the empirical results from earlier studies, such as Ciaian et al. (2018) and Kumar et al. (2022). Among them, Ciaian et al. (2018) found that the prices of altcoins are driven by the development of Bitcoin in the short run but not in the long run. Likewise, Kumar et al. (2022) found that cryptocurrencies are more sensitive to crisis periods over short time horizons than those over longer ones.
We also investigate the spillover effects from BTC to altcoins before and after COVID-19 (Figure A2, Appendix A). This analysis brings a different perspective to the study because incredible price volatility has been observed in cryptocurrency prices since COVID-19. Moreover, during the COVID-19 pandemic, decentralized finance (DeFi) and decentralized apps (dApps) enjoyed a substantial gain in market share and popularity. This outbreak crisis also increased interest in cryptocurrency markets among ordinary and institutional investors, who have access to financial markets from their homes via fintech trading platforms, such as Robinhood (Katsiampa et al. 2022). These facts encourage us to expand this study to examine the asymmetry, including the COVID-19 health crisis. Our empirical findings show that the volatility spillover from BTC to BCH, DOGE, LINK, and TRX increased after the COVID-19 outbreak. Interestingly, ADA and XRP are two cryptocurrencies whose volatility spillover from BTC decreased after the COVID-19 outbreak.
5. Conclusions
In recent years, there has been an increase in empirical research on the fear of missing out (FOMO) on rewarding experiences. There are several studies in the literature that address this issue for stock markets. However, this topic has not yet been sufficiently investigated for cryptocurrencies. This study contributes to filling this gap by analyzing the asymmetric volatility of cryptocurrencies under different market conditions. This study examines the risk spillover from Bitcoin to 10 major cryptocurrencies using daily data from 1 September 2017 to 2 March 2022 and the frequency connectedness analysis of Baruník and Křehlík (2018).
This study attempts to uncover the behaviors of crypto traders by analyzing the risk spillover from Bitcoin to altcoins. Our findings show that BNB, ETH, LTC, and USDT volatility increase more in response to positive shocks than in response to negative shocks in the short, medium, and long terms. This can be explained by uniformed investors’ herding, fear of missing out on rising Bitcoin prices, and pump-and-dump schemes. In the short run, this is not the case for ADA and DOGE. For TRON and XRP, we find that the risk spillover is stronger in a bear market. This can be explained by the contrarian behavior of informed investors in these altcoin markets. In addition to this analysis, we investigate the cryptos’ own risk spillovers at different frequencies. These empirical findings strongly support the FOMO and pump-and-dump schemes for all cryptocurrencies except for USDT. Moreover, we employ the volatility spillover effects from BTC to altcoins, considering the COVID-19 crisis. The empirical findings show that the risk from BTC to ADA and XRP decreases after the post-covid period in comparison to the pre-pandemic period.
The results of this paper suggest that the impact of Bitcoin price movements on altcoin prices is mixed, meaning that the relationship between the two is not always predictable. This can make it difficult for investors to use Bitcoin price movements as a reliable indicator of altcoin performance. However, the presence of FOMO and pump-and-dump activity in the altcoin market suggests that individual altcoin prices may be more susceptible to manipulation and volatility spillover. As such, investors may want to be cautious when considering investments in altcoins and may want to thoroughly research the market and individual cryptocurrencies before making any investment decisions. It may also be beneficial for investors to diversify their portfolios by including a mix of Bitcoin and altcoins rather than putting all their eggs in one basket. Moreover, investors should also keep track of the latest developments in the cryptocurrency market, including any news or regulatory changes that could impact the market. This can help them stay informed and make informed investment decisions. Investors should also be wary of the fear of missing out and not make impulsive investment decisions based on hype or media coverage. Investors should also use reputable exchanges because they are less likely to engage in manipulative behavior or facilitate pump-and-dump schemes.
We point out that the results of this study are based on broad market analysis based on global data. The evidence we provide for the existence of fear of missing out and pump-and-dump schemes is limited to the altcoin market. Therefore, the psychological factors play a lesser role for cryptos with large market capitalization, such as Bitcoin. Moreover, our analysis results are valid for the broad market and may not apply to all individual exchanges.
Given that the price movements of altcoins are highly dependent on BTC and their own price history, future studies may extend our approach to analyze volatility spillover from other leading cryptocurrencies, such as ETH, ADA, and SOL, to various altcoins related to these platforms. Polygon, formerly known as Matic Network, for example, is a Layer-2 scaling solution for Ethereum that aims to enhance the network’s transaction processing speed while lowering transaction costs, often known as “gas prices.” In that respect, one may investigate the risk spillover from ETH to MATIC when the ETH price is going up and down. Another extension is to investigate the higher frequency (hour or minute) volatility connectedness of cryptocurrency to uncover FOMO and pump-and-dump strategies for the benefit of high-frequency traders.
Author Contributions
Conceptualization, M.B. and H.O.; methodology, H.O.; software, H.O.; validation, M.B. and H.O.; formal analysis, H.O.; investigation, H.O.; resources, H.O.; data curation, H.O.; writing—original draft preparation, M.B. and H.O.; writing—review and editing, M.B. and H.O.; visualization, M.B. and H.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Figure A1.
Short- and long-term volatility spillover from altcoins to themselves. Note: See note to Figure 3.
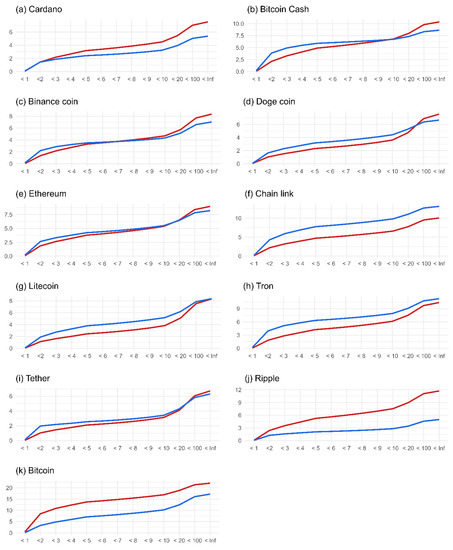
Figure A2.
Short- and long-term volatility spillover from Bitcoin to altcoins during pre- and post-COVID-19 period. Note: The horizontal axis denotes the frequency in days, while the vertical axis denotes cumulative spillover index. The red and blue line shows the volatility spillover from Bitcoin to altcoins during pre-COVID-19 and post-COVID-19 period, respectively.
Notes
| 1 | Bitcoin (BTC), Cardano (ADA), Binance Coin (BNB), Bitcoin Cash (BCH), Dogecoin (Doge), Ethereum (ETH), Chainlink (LINK), Litecoin (LTC), Tron (TRX), Tether (USDT), and Ripple (XRP). |
| 2 | See, e.g., Nelson (1991) for E-GARCH, Glosten et al. (1993) for leverage effect GARCH, and (Zakoian 1994) for TGARCH. |
| 3 | Following Garman and Klass (1980), we calculate the daily volatility series using the daily opening, closing, high, and low prices. Firstly, the daily volatility is calculated as , where , , , and show the minimum, the maximum, the close, and the opening price of the market i on day t, respectively. Second, we annualize the volatility series utilizing the formula . |
| 4 | We calculate the daily returns of Bitcoin by taking the logarithm of the close price divided by the open price as . The daily observations span from 1 September 2017, to 2 March 2022. |
| 5 | The behavior of informed investors is consistent with the basic suggestions of economic theory. They put more emphasis on investment knowledge and economic-related criteria than uninformed investors, who are more influenced by behavioral elements such as personality and sentiment (Jalilvand et al. 2018). Based on this fact, it is fair to think that uninformed investors are more open to market rumors with no economic justification. |
References
- Ang, Andrew, and Joseph Chen. 2002. Asymmetric correlations of equity portfolios. Journal of Financial Economics 63: 443–94. [Google Scholar] [CrossRef]
- Aslanidis, Nektarios, Aurelio F. Bariviera, and Alejandro Perez-Laborda. 2021. Are cryptocurrencies becoming more interconnected? Economics Letters 199: 109725. [Google Scholar] [CrossRef]
- Balcilar, Mehmet, Elie Bouri, Rangan Gupta, and David Roubaud. 2017. Can volume predict Bitcoin returns and volatility? A quantiles-based approach. Economic Modelling 64: 74–81. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Silja Kinnebrock, and Neil Shephard. 2010. Measuring Downside Risk—Realized Semivariance. In Volatility and Time Series Econometrics: Essays in Honor of Robert Engle. Oxford: Oxford Academic. [Google Scholar] [CrossRef]
- Baruník, Jozef, and Tomáš Křehlík. 2018. Measuring the frequency dynamics of financial connectedness and systemic risk. Journal of Financial Econometrics 16: 271–96. [Google Scholar] [CrossRef]
- Baruník, Jozef, Evžen Kočenda, and Lukáš Vácha. 2016. Asymmetric connectedness on the U.S. stock market: Bad and good volatility spillovers. Journal of Financial Markets 27: 55–78. [Google Scholar] [CrossRef]
- Baruník, Jozef, Evžen Kočenda, and Lukáš Vácha. 2017. Asymmetric volatility connectedness on the forex market. Journal of International Money and Finance 77: 39–56. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Thomas Dimpfl. 2018. Asymmetric volatility in cryptocurrencies. Economics Letters 173: 148–51. [Google Scholar] [CrossRef]
- Bernabe, Jorge Bernal, Jose Luis Canovas, Jose L. Hernandez-Ramos, Rafael Torres Moreno, and Antonio Skarmeta. 2019. Privacy-Preserving Solutions for Blockchain: Review and Challenges. IEEE Access 7: 164908–164940. [Google Scholar] [CrossRef]
- Blau, Benjamin M. 2018. Price dynamics and speculative trading in Bitcoin. Research in International Business and Finance 43: 493–99. [Google Scholar] [CrossRef]
- Böhme, Rainer, Nicolas Christin, Benjamin Edelman, and Tyler Moore. 2015. Bitcoin: Economics, technology, and governance. Journal of Economic Perspectives 29: 213–38. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1987. A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return. The Review of Economics and Statistics 69: 542–47. [Google Scholar] [CrossRef]
- Bouri, Elie, Mahamitra Das, Rangan Gupta, and David Roubaud. 2018. Spillovers between Bitcoin and other assets during bear and bull markets. Applied Economics 50: 5935–49. [Google Scholar] [CrossRef]
- Brandvold, Morten, Peter Molnár, Kristian Vagstad, and Ole Christian Andreas Valstad. 2015. Price discovery on Bitcoin exchanges. Journal of International Financial Markets, Institutions and Money 36: 18–35. [Google Scholar] [CrossRef]
- Brik, Hatem, el Ouakdi Jihene, and Ftiti Zied. 2022. Roles of stable versus nonstable cryptocurrencies in Bitcoin market dynamics. Research in International Business and Finance 62: 101720. [Google Scholar] [CrossRef]
- Cappiello, Lorenzo, Robert F. Engle, and Kevin Sheppard. 2006. Asymmetric dynamics in the correlations of global equity and bond returns. Journal of Financial Econometrics 4: 537–72. [Google Scholar] [CrossRef]
- Charfeddine, Lanouar, Noureddine Benlagha, and Youcef Maouchi. 2020. Investigating the dynamic relationship between cryptocurrencies and conventional assets: Implications for financial investors. Economic Modelling 85: 198–217. [Google Scholar] [CrossRef]
- Chemkha, Rahma, Ahmed BenSaïda, Ahmed Ghorbel, and Tahar Tayachi. 2021. Hedge and safe haven properties during COVID-19: Evidence from Bitcoin and gold. Quarterly Review of Economics and Finance 82: 71–85. [Google Scholar] [CrossRef]
- Ciaian, Pavel, Rajcaniova Miroslava, and Kancs d’Artis. 2018. Virtual relationships: Short- and long-run evidence from BitCoin and altcoin markets. Journal of International Financial Markets, Institutions and Money 52: 173–95. [Google Scholar] [CrossRef]
- Corbet, Shaen, Andrew Meegan, Charles Larkin, Brian Lucey, and Larisa Yarovaya. 2018a. Exploring the dynamic relationships between cryptocurrencies and other financial assets. Economics Letters 165: 28–34. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, and Larisa Yarovaya. 2018b. Datestamping the Bitcoin and Ethereum bubbles. Finance Research Letters 26: 81–88. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, Andrew Urquhart, and Larisa Yarovaya. 2019. Cryptocurrencies as a financial asset: A systematic analysis. International Review of Financial Analysis 62: 182–99. [Google Scholar] [CrossRef]
- De Filippi, Primavera. 2014. Bitcoin: A regulatory nightmare to a libertarian dream. Internet Policy Review 3. [Google Scholar] [CrossRef]
- Delfabbro, Paul, Daniel L. King, and Jennifer Williams. 2021. The psychology of cryptocurrency trading: Risk and protective factors. Journal of Behavioral Addictions 10: 201–7. [Google Scholar] [CrossRef]
- Demir, Ender, Serdar Simonyan, Conrado-Diego García-Gómez, and Chi Keung Marco Lau. 2021. The asymmetric effect of bitcoin on altcoins: Evidence from the nonlinear autoregressive distributed lag (NARDL) model. Finance Research Letters 40: 101754. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2009. Measuring financial asset return and volatility spillovers, with application to global equity markets. Economic Journal 119: 158–71. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2012. Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting 28: 57–66. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Fasanya, Ismail Olaleke, Oluwatomisin Oyewole, and Temitope Odudu. 2021. Returns and volatility spillovers among cryptocurrency portfolios. International Journal of Managerial Finance 17: 327–41. [Google Scholar] [CrossRef]
- Fletcher, Emily, Charles Larkin, and Shaen Corbet. 2021. Countering money laundering and terrorist financing: A case for bitcoin regulation. Research in International Business and Finance 56: 101387. [Google Scholar] [CrossRef]
- Fousekis, Panos, and Dimitra Tzaferi. 2021. Returns and volume: Frequency connectedness in cryptocurrency markets. Economic Modelling 95: 13–20. [Google Scholar] [CrossRef]
- Garman, Mark B., and Michael J. Klass. 1980. On the Estimation of Security Price Volatilities from Historical Data. The Journal of Business 53: 67–78. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Jalilvand, Abolhassan, Mojtaba Rostami Noroozabad, and Jeannette Switzer. 2018. Informed and uninformed investors in Iran: Evidence from the Tehran Stock Exchange. Journal of Economics and Business 95: 47–58. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi, Larisa Yarovaya, and Damian Zięba. 2022. High-Frequency connectedness between bitcoin and other top-traded crypto assets during the COVID-19 crisis. Journal of International Financial Markets, Institutions and Money 79: 101578. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi, Shaen Corbet, and Brian Lucey. 2019. High frequency volatility co-movements in cryptocurrency markets. Journal of International Financial Markets, Institutions and Money 62: 35–52. [Google Scholar] [CrossRef]
- Khuntia, Sashikanta, and J. K. Pattanayak. 2018. Adaptive market hypothesis and evolving predictability of bitcoin. Economics Letters 167: 26–28. [Google Scholar] [CrossRef]
- Koop, Gary, M. Hashem Pesaran, and Simon M. Potter. 1996. Impulse response analysis in nonlinear multivariate models. Journal of Econometrics 74: 119–47. [Google Scholar] [CrossRef]
- Koutmos, Dimitrios. 2018. Return and volatility spillovers among cryptocurrencies. Economics Letters 173: 122–27. [Google Scholar] [CrossRef]
- Kumar, Ashish, Najaf Iqbal, Subrata Kumar Mitra, Ladislav Kristoufek, and Elie Bouri. 2022. Connectedness among major cryptocurrencies in standard times and during the COVID-19 outbreak. Journal of International Financial Markets, Institutions and Money 77: 101523. [Google Scholar] [CrossRef]
- Mensi, Walid, Khamis Hamed Al-Yahyaee, Idries Mohammad Wanas Al-Jarrah, Xuan Vinh Vo, and Sang Hoon Kang. 2021. Does volatility connectedness across major cryptocurrencies behave the same at different frequencies? A portfolio risk analysis. International Review of Economics and Finance 76: 96–113. [Google Scholar] [CrossRef]
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 10 December 2022).
- Nan, Zheng, and Taisei Kaizoji. 2019. Market efficiency of the bitcoin exchange rate: Weak and semi-strong form tests with the spot, futures and forward foreign exchange rates. International Review of Financial Analysis 64: 273–81. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Park, Minjung, and Sangmi Chai. 2020. The effect of information asymmetry on investment behavior in cryptocurrency market. Paper presented at the Annual Hawaii International Conference on System Sciences, Maui, HI, USA, January 7–10. [Google Scholar]
- Pesaran, H. Hashem, and Yongcheol Shin. 1998. Generalized impulse response analysis in linear multivariate models. Economics Letters 58: 17–29. [Google Scholar] [CrossRef]
- Pinzón, Carlos, and Camilo Rocha. 2016. Double-spend Attack Models with Time Advantange for Bitcoin. Electronic Notes in Theoretical Computer Science 329: 79–103. [Google Scholar] [CrossRef]
- Sensoy, Ahmet, Thiago Christiano Silva, Shaen Corbet, and Benjamin Miranda Tabak. 2021. High-frequency return and volatility spillovers among cryptocurrencies. Applied Economics 53: 4310–28. [Google Scholar] [CrossRef]
- Smaniotto, Emanuelle Nava, and Giacomo Balbinotto Neto. 2020. Speculative trading in Bitcoin: A Brazilian market evidence. Quarterly Review of Economics and Finance 85: 47–54. [Google Scholar] [CrossRef]
- Urquhart, Andrew, and Hanxiong Zhang. 2019. Is Bitcoin a hedge or safe haven for currencies? An intraday analysis. International Review of Financial Analysis 63: 49–57. [Google Scholar] [CrossRef]
- Vidal-Tomás, David, and Ana Ibañez. 2018. Semi-strong efficiency of Bitcoin. Finance Research Letters 27: 259–65. [Google Scholar] [CrossRef]
- Vranken, Harald. 2017. Sustainability of bitcoin and blockchains. Current Opinion in Environmental Sustainability 28: 1–9. [Google Scholar] [CrossRef]
- Wang, Jying-Nan, Hung-Chun Liu, Shuang Zhang, and Yuan-Teng Hsu. 2021. How does the informed trading impact Bitcoin returns and volatility? Applied Economics 53: 3223–33. [Google Scholar] [CrossRef]
- Wang, Qin, Bo Qin, Jiankun Hu, and Fu Xiao. 2020. Preserving transaction privacy in bitcoin. Future Generation Computer Systems 107: 793–804. [Google Scholar] [CrossRef]
- Xu, Jiahua, and Benjamin Livshits. 2019. The anatomy of a cryptocurrency pump-and-dump scheme. Paper presented at the 28th USENIX Security Symposium, Santa Clara, CA, USA, August 14–16. [Google Scholar]
- Yi, Shuyue, Zishuang Xu, and Gang-Jin Wang. 2018. Volatility connectedness in the cryptocurrency market: Is Bitcoin a dominant cryptocurrency? International Review of Financial Analysis 60: 98–114. [Google Scholar] [CrossRef]
- Zakoian, Jean-Michel. 1994. Threshold heteroskedastic models. Journal of Economic Dynamics and Control 18: 931–55. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).