Co-Jumps, Co-Jump Tests, and Volatility Forecasting: Monte Carlo and Empirical Evidence
Abstract
:1. Introduction
2. Co-Jump Identification
2.1. Setup
2.2. Co-Jump Tests
2.2.1. BLT Co-Jump Test
2.2.2. JT Co-Jump Test
2.2.3. Univariate Jump Co-Exceedance Rule
3. Monte Carlo Experiments
4. Forecasting Methods
4.1. Forecasting Models
4.2. Co-Jump and Idiosyncratic Jump Variations
5. Setup of the Forecasting Experiment
- Set .
- Test for the null hypothesis of equal predictive ability among candidate models in Q with significance level . If the null hypothesis cannot be rejected, then the set SSM is the same as the set of all models. Otherwise, determine the worst model in the set Q.
- Remove the worst model from Q, and proceed to step 2.
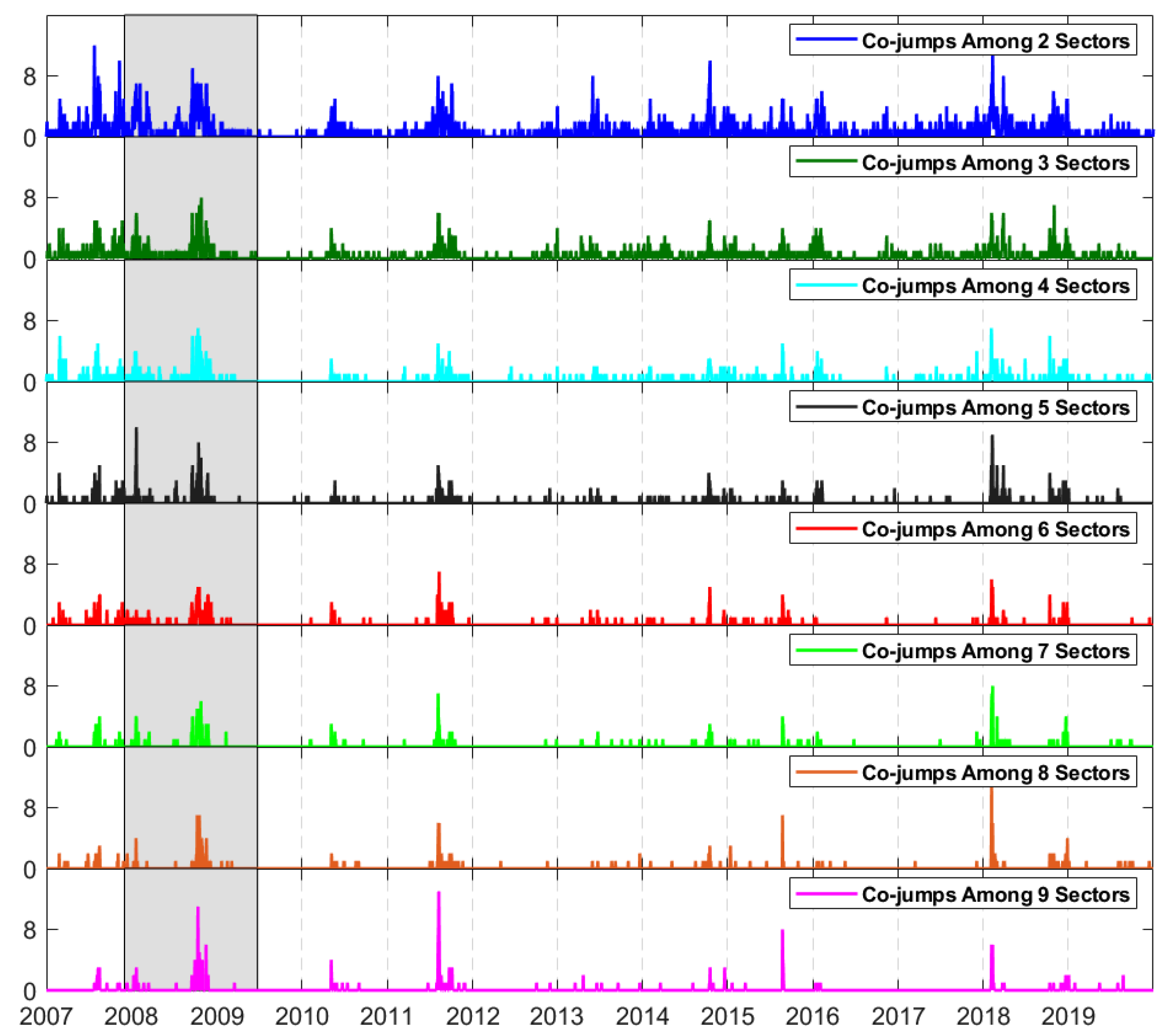
6. Data Description
7. Empirical Findings
8. Policy Implications
9. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | For literature in this area, see (Barndorff-Nielsen and Shephard 2006; Lee and Mykland 2007; Jiang and Oomen 2008; Aït-Sahalia et al. 2009; Huang and Tauchen 2005; Mancini 2009; Podolskij and Ziggel 2010; Corradi et al. 2018; Boswijk et al. 2018; Mukherjee et al. 2020, and the references cited therein). |
| 2 | Bandi and Russell (2008) show in the presence of market microstructure noise, realized variance does not identify daily integrated variance of the frictionless equilibrium. They propose a more general treatment of the effect of market microstructure noise on realized variance estimates. |
| 3 | We follow the parameter settings from Jacod and Todorov (2009). |
| 4 | Among 10 assets, co-jumps occur more frequently among a small portion of all assets (e.g., ) than a large portion of all assets (e.g., ) at each time. |
| 5 | Gilder et al. (2014) also implement the same approach. |
| 6 | One approach to measure jump variation is to use the difference between realized volatility and bipower variation, as shown in Equations (34) and (35). Another approach to examine the jump power variation is formed using power transformation of the instantaneous return, i.e., . Key papers in this area include (Ding et al. 1993; Ding and Granger 1996; Todorov and Tauchen 2010; Barndorff-Nielsen et al. 2008, and the references cited there in). |
| 7 | The co-exceedance rule of the LM test is utilized to identify co-jumps and idiosyncratic jumps among assets. |
| 8 | The set of models that consists of the best model(s). |
| 9 | Overall, the mean absolute forecasting errors in Table 13 are comparatively smaller with respect to results in the relevant literature (e.g., see Qiu et al. 2019). |
References
- Aït-Sahalia, Yacine, and Jean Jacod. 2009. Testing for jumps in a discretely observed process. The Annals of Statistics 37: 184–222. [Google Scholar] [CrossRef]
- Andersen, Torben G., and Jesper Lund. 1997. Estimating continuous-time stochastic volatility models of the short-term interest rate. Journal of Econometrics 77: 343–77. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, and Francis X. Diebold. 2007. Roughing it up: Including jump components in the measurement, modeling, and forecasting of return volatility. The Review of Economics and Statistics 89: 701–20. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2001. The distribution of realized exchange rate volatility. Journal of the American Statistical Association 96: 42–55. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2003. Modeling and forecasting realized volatility. Econometrica 71: 579–625. [Google Scholar] [CrossRef] [Green Version]
- Andersen, Torben G., Tim Bollerslev, Per Frederiksen, and Morten Ørregaard Nielsen. 2010. Continuous-time models, realized volatilities, and testable distributional implications for daily stock returns. Journal of Applied Econometrics 25: 233–61. [Google Scholar] [CrossRef] [Green Version]
- Bandi, Federico M., and Jeffrey R. Russell. 2008. Microstructure noise, realized variance, and optimal sampling. The Review of Economic Studies 75: 339–69. [Google Scholar] [CrossRef]
- Bandi, Federico M., and Roberto Reno. 2016. Price and volatility co-jumps. Journal of Financial Economics 119: 107–46. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2004. Power and bipower variation with stochastic volatility and jumps. Journal of Financial Econometrics 2: 1–37. [Google Scholar] [CrossRef] [Green Version]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2006. Econometrics of testing for jumps in financial economics using bipower variation. Journal of Financial Econometrics 4: 1–30. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Silja Kinnebrock, and Neil Shephard. 2008. Measuring Downside Risk-Realised Semivariance. Available online: https://ssrn.com/abstract=1262194 (accessed on 29 June 2022).
- Bibinger, Markus, and Lars Winkelmann. 2015. Econometrics of co-jumps in high-frequency data with noise. Journal of Econometrics 184: 361–78. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Tzuo Hann Law, and George Tauchen. 2008. Risk, jumps, and diversification. Journal of Econometrics 144: 234–56. [Google Scholar] [CrossRef] [Green Version]
- Boswijk, H. Peter, Roger J. A. Laeven, and Xiye Yang. 2018. Testing for self-excitation in jumps. Journal of Econometrics 203: 256–66. [Google Scholar] [CrossRef]
- Brandt, Michael W., and Christopher S. Jones. 2006. Volatility forecasting with range-based EGARCH models. Journal of Business & Economic Statistics 24: 470–86. [Google Scholar]
- Brownlees, Christian T., and Giampiero M. Gallo. 2006. Financial econometric analysis at ultra-high frequency: Data handling concerns. Computational Statistics & Data Analysis 51: 2232–45. [Google Scholar]
- Caporin, Massimiliano, Aleksey Kolokolov, and Roberto Renò. 2017. Systemic co-jumps. Journal of Financial Economics 126: 563–91. [Google Scholar] [CrossRef] [Green Version]
- Corsi, Fulvio. 2009. A simple approximate long-memory model of realized volatility. Journal of Financial Econometrics 7: 563–91. [Google Scholar] [CrossRef]
- Corsi, Fulvio, Davide Pirino, and Roberto Reno. 2010. Threshold bipower variation and the impact of jumps on volatility forecasting. Journal of Econometrics 159: 276–88. [Google Scholar] [CrossRef] [Green Version]
- Corradi, Valentina, Mervyn J. Silvapulle, and Norman R. Swanson. 2018. Testing for jumps and jump intensity path dependence. Journal of Econometrics 204: 248–67. [Google Scholar] [CrossRef]
- Ding, Zhuanxin, and Clive W. J. Granger. 1996. Modeling volatility persistence of speculative returns: A new approach. Journal of Econometrics 73: 185–215. [Google Scholar] [CrossRef]
- Ding, Zhuanxin, Clive W. J. Granger, and Robert F. Engle. 1993. A long memory property of stock market returns and a new model. Journal of Empirical Finance 1: 83–106. [Google Scholar] [CrossRef]
- Gençay, Ramazan, Michel Dacorogna, Ulrich A. Muller, Olivier Pictet, and Richard Olsen. 2001. An Introduction to High-Frequency Finance. Cambridge: Academic Press. [Google Scholar]
- Ghysels, Eric, and Arthur Sinko. 2011. Volatility forecasting and microstructure noise. Journal of Econometrics 160: 257–71. [Google Scholar] [CrossRef]
- Ghysels, Eric, Pedro Santa-Clara, and Rossen Valkanov. 2006. Predicting volatility: Getting the most out of return data sampled at different frequencies. Journal of Econometrics 131: 59–95. [Google Scholar] [CrossRef] [Green Version]
- Gilder, Dudley, Mark B. Shackleton, and Stephen J. Taylor. 2014. Cojumps in stock prices: Empirical evidence. Journal of Banking & Finance 40: 443–59. [Google Scholar]
- Hansen, Peter R., Asger Lunde, and James M. Nason. 2011. The model confidence set. Econometrica 79: 453–97. [Google Scholar] [CrossRef] [Green Version]
- Hansen, Peter R., and Asger Lunde. 2005. A forecast comparison of volatility models: Does anything beat a GARCH (1, 1)? Journal of Applied Econometrics 20: 873–89. [Google Scholar] [CrossRef] [Green Version]
- Harvey, Andrew, Esther Ruiz, and Neil Shephard. 1994. Multivariate stochastic variance models. The Review of Economic Studies 61: 247–64. [Google Scholar] [CrossRef] [Green Version]
- Hausman, Jerry A. 1978. Specification tests in econometrics. Econometrica: Journal of the Econometric Society 46: 1251–71. [Google Scholar] [CrossRef] [Green Version]
- Huang, Xin, and George Tauchen. 2005. The relative contribution of jumps to total price variance. Journal of Financial Econometrics 3: 456–99. [Google Scholar] [CrossRef]
- Jacod, Jean, and Viktor Todorov. 2009. Testing for common arrivals of jumps for discretely observed multidimensional processes. The Annals of Statistics 37: 1792–838. [Google Scholar] [CrossRef] [Green Version]
- Jiang, George J., and Roel CA Oomen. 2008. Testing for jumps when asset prices are observed with noise—A “swap variance” approach. Journal of Econometrics 144: 352–70. [Google Scholar] [CrossRef]
- Koopman, Siem Jan, Borus Jungbacker, and Eugenie Hol. 2005. Forecasting daily variability of the S&P 100 stock index using historical, realised and implied volatility measurements. Journal of Empirical Finance 12: 445–75. [Google Scholar]
- Lahaye, Jérôme, and Christopher Neely. 2020. The role of jumps in volatility spillovers in foreign exchange markets: Meteor shower and heat waves revisited. Journal of Business & Economic Statistics 38: 410–27. [Google Scholar]
- Lee, Suzanne S., and Per A. Mykland. 2007. Jumps in financial markets: A new nonparametric test and jump dynamics. The Review of Financial Studies 21: 2535–63. [Google Scholar] [CrossRef]
- Mancini, Cecilia. 2009. Non-parametric threshold estimation for models with stochastic diffusion coefficient and jumps. Scandinavian Journal of Statistics 36: 270–96. [Google Scholar] [CrossRef]
- Mancini, Cecilia, and Fabio Gobbi. 2012. Identifying the brownian covariation from the co-jumps given discrete observations. Econometric Theory 28: 249–73. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, Arpita, Weijia Peng, Norman R. Swanson, and Xiye Yang. 2020. Financial econometrics and big data: A survey of volatility estimators and tests for the presence of jumps and co-jumps. In Handbook of Statistics. Amsterdam: Elsevier, vol. 42, pp. 3–59. [Google Scholar]
- Müller, Ulrich A., Michel M. Dacorogna, Rakhal D. Davé, Richard B. Olsen, Olivier V. Pictet, and Jacob E. Von Weizsäcker. 1997. Volatilities of different time resolutions—Analyzing the dynamics of market components. Journal of Empirical Finance 4: 213–39. [Google Scholar] [CrossRef]
- Patton, Andrew J., and Kevin Sheppard. 2015. Good volatility, bad volatility: Signed jumps and the persistence of volatility. Review of Economics and Statistics 97: 683–97. [Google Scholar] [CrossRef] [Green Version]
- Podolskij, Mark, and Daniel Ziggel. 2010. New tests for jumps in semimartingale models. Statistical Inference for Stochastic Processes 13: 15–41. [Google Scholar] [CrossRef]
- Qiu, Yue, Xinyu Zhang, Tian Xie, and Shangwei Zhao. 2019. Versatile HAR model for realized volatility: A least square model averaging perspective. Journal of Management Science and Engineering 4: 55–73. [Google Scholar] [CrossRef]
- Todorov, Viktor, and George Tauchen. 2010. Activity signature functions for high-frequency data analysis. Journal of Econometrics 154: 125–38. [Google Scholar] [CrossRef]


| Jump Intensity | |
| Leverage Effect | |
| Jump Distribution | , where |
| Sampling Frequency | |
| Other Parameters |
| N | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| DGP1 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||||
| DGP2 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||||
| DGP3 | 0.1 | 0.3 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP4 | 0.2 | 0.3 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP5 | 0.1 | 0.4 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP6 | 0.2 | 0.4 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP7 | 0.1 | 0.3 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP8 | 0.2 | 0.3 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP9 | 0.1 | 0.4 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP10 | 0.2 | 0.4 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP11 | 0.1 | 0.3 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP12 | 0.2 | 0.3 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP13 | 0.1 | 0.4 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP14 | 0.2 | 0.4 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP15 | 0.1 | 0.3 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP16 | 0.2 | 0.3 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP17 | 0.1 | 0.4 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP18 | 0.2 | 0.4 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |||
| DGP19 | 0.1 | 0.1 | 0.3 | 0.3 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |
| DGP20 | 0.2 | 0.2 | 0.3 | 0.3 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |
| DGP21 | 0.1 | 0.1 | 0.4 | 0.4 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |
| DGP22 | 0.2 | 0.2 | 0.4 | 0.4 | 0 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |
| DGP23 | 0.1 | 0.1 | 0.3 | 0.3 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |
| DGP24 | 0.2 | 0.2 | 0.3 | 0.3 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |
| DGP25 | 0.1 | 0.1 | 0.4 | 0.4 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 | |
| DGP26 | 0.2 | 0.2 | 0.4 | 0.4 | −0.5 | 0.05 | 5 | 0.0144 | 0.5 | 10 |
| Case | BLT | JT | LM | LM–BNS |
|---|---|---|---|---|
| DGP1 | 0.0687 | 0.0220 | 0.0426 | 0.0014 |
| DGP2 | 0.0718 | 0.0143 | 0.0435 | 0.0010 |
| Case | BLT | JT | LM | LM–BNS |
|---|---|---|---|---|
| DGP3 | 0.0565 | 0.1892 | 0.0478 | 0.0015 |
| DGP4 | 0.0506 | 0.3751 | 0.0520 | 0.0022 |
| DGP5 | 0.0541 | 0.2486 | 0.0480 | 0.0017 |
| DGP6 | 0.0476 | 0.4510 | 0.0523 | 0.0028 |
| DGP7 | 0.0554 | 0.1771 | 0.0466 | 0.0019 |
| DGP8 | 0.0480 | 0.3982 | 0.0512 | 0.0027 |
| DGP9 | 0.0526 | 0.2178 | 0.0468 | 0.0022 |
| DGP10 | 0.0452 | 0.4543 | 0.0515 | 0.0034 |
| Case | BLT | JT | LM | LM–BNS |
|---|---|---|---|---|
| DGP11 | 0.9255 | 0.9451 | 0.9362 | 0.1702 |
| DGP12 | 0.9167 | 0.9836 | 0.9495 | 0.2121 |
| DGP13 | 0.9362 | 0.9670 | 0.9521 | 0.2606 |
| DGP14 | 0.9242 | 0.9891 | 0.9697 | 0.3409 |
| DGP15 | 0.9202 | 0.9451 | 0.9415 | 0.2340 |
| DGP16 | 0.9242 | 0.9836 | 0.9672 | 0.2020 |
| DGP17 | 0.9309 | 0.9560 | 0.9628 | 0.3085 |
| DGP18 | 0.9293 | 0.9891 | 0.9722 | 0.3409 |
| Case | BLT | JT | LM | LM–BNS |
|---|---|---|---|---|
| DGP19 | 0.9126 | 0.9394 | 0.9029 | 0.2087 |
| DGP20 | 0.8456 | 0.9798 | 0.9332 | 0.2166 |
| DGP21 | 0.9175 | 0.9697 | 0.9126 | 0.3155 |
| DGP22 | 0.8687 | 0.9798 | 0.9516 | 0.3433 |
| DGP23 | 0.8932 | 0.9596 | 0.9223 | 0.2524 |
| DGP24 | 0.8687 | 0.9747 | 0.9424 | 0.2097 |
| DGP25 | 0.9126 | 0.9697 | 0.9515 | 0.3350 |
| DGP26 | 0.8825 | 0.9798 | 0.9516 | 0.3295 |
| Model | Description |
|---|---|
| HAR-RV-C | Future RV depends on the lags of the continuous component of the RV. |
| HAR-RV-C-CJ | Future RV depends on the lags of the continuous component of RV and the co-jump variation. |
| HAR-RV-C-IJ | Future RV depends on the lags of the continuous component of the RV and the idiosyncratic jump variation. |
| HAR-RV-C-CJ-IJ | Future RV depends on the lags of the continuous component of RV, co-jump variation, and idiosyncratic jump variation. |
| Target Name | Description | Transformation | Frequency |
|---|---|---|---|
| XLF | Financial Sector SPDR Fund | Daily | |
| XLK | Technology Sector SPDR Fund | Daily | |
| XLP | Consumer Staples Select Sector SPDR Fund | Daily | |
| XLU | Utilities Select Sector SPDR Fund | Daily | |
| XLY | Consumer Discretionary Select Sector SPDR Fund | Daily |
| Sector | XLB | XLE | XLF | XLI | XLK | XLP | XLU | XLV | XLY | |
|---|---|---|---|---|---|---|---|---|---|---|
| Co-jump | Frequency (%) | 30.10% | 24.45% | 25.31% | 30.78% | 24.48% | 32.73% | 29.55% | 29.49% | 29.03% |
| Prop. (%) | 79.36% | 70.08% | 72.79% | 87.46% | 83.52% | 79.76% | 64.37% | 78.23% | 86.09% | |
| upside jump mean (%) | 0.63% | 0.78% | 0.72% | 0.56% | 0.57% | 0.43% | 0.61% | 0.49% | 0.55% | |
| downside jump mean (%) | −0.61% | −0.76% | −0.70% | −0.54% | −0.53% | −0.43% | −0.60% | −0.47% | −0.54% | |
| St. dev. | 0.0074 | 0.0090 | 0.0090 | 0.0064 | 0.0064 | 0.0052 | 0.0072 | 0.0055 | 0.0067 | |
| Ratio of JV to RV (%) | 27.96% | 22.71% | 23.50% | 28.58% | 22.74% | 30.40% | 27.45% | 27.39% | 26.97% | |
| Idiosyncratic jump | Frequency (%) | 15.01% | 17.42% | 14.82% | 10.39% | 10.36% | 15.19% | 24.05% | 16.56% | 10.36% |
| Prop. (%) | 20.64% | 29.92% | 27.21% | 12.54% | 16.48% | 20.24% | 35.63% | 21.77% | 13.91% | |
| upside jump mean (%) | 0.50% | 0.59% | 0.67% | 0.42% | 0.38% | 0.31% | 0.43% | 0.39% | 0.40% | |
| downside jump mean (%) | −0.51% | −0.59% | −0.62% | −0.43% | −0.39% | −0.31% | −0.45% | −0.40% | −0.38% | |
| St. dev. | 0.0056 | 0.0064 | 0.0077 | 0.0048 | 0.0042 | 0.0034 | 0.0047 | 0.0043 | 0.0043 | |
| Ratio of JV to RV (%) | 13.94% | 16.18% | 13.77% | 9.65% | 9.62% | 14.11% | 22.34% | 15.38% | 9.62% |
| Sector | HAR-RV-C | HAR-RV-C-CJ | HAR-RV-C-IJ | HAR-RV-C-CJ-IJ |
|---|---|---|---|---|
| Forecasting Period: 2008:11–2019:12 | ||||
| XLF | 0.6560 * | 1.0000 * | 0.6560 * | 0.6560 * |
| XLK | 0.2165 * | 0.4195 * | 0.1415 * | 1.0000 * |
| XLP | 0.1220 * | 0.1220 * | 0.0880 | 1.0000 * |
| XLU | 0.3860 * | 0.3860 * | 0.2975 * | 1.0000 * |
| XLY | 0.7780 * | 0.9385 * | 0.7780 * | 1.0000 * |
| Sector | HAR-RV-C | HAR-RV-C-CJ | HAR-RV-C-IJ | HAR-RV-C-CJ-IJ |
|---|---|---|---|---|
| Forecasting Period: 2008:11–2019:12 | ||||
| XLF | 0.7761 | 0.7765 | 0.7761 | 0.7768 |
| XLK | 0.6748 | 0.6758 | 0.6758 | 0.6763 |
| XLP | 0.6430 | 0.6441 | 0.6439 | 0.6443 |
| XLU | 0.6157 | 0.6189 | 0.6175 | 0.6200 |
| XLY | 0.7458 | 0.7470 | 0.7462 | 0.7470 |
| Sector | HAR-RV-C | HAR-RV-C-CJ | HAR-RV-C-IJ | HAR-RV-C-CJ-IJ |
|---|---|---|---|---|
| Forecasting Period: 2008:11–2019:12 | ||||
| XLF | 0.6765 | 0.6866 | 0.6823 | 0.6823 |
| XLK | 0.5680 | 0.5772 | 0.5649 | 0.5817 |
| XLP | 0.5567 | 0.5602 | 0.5556 | 0.5696 |
| XLU | 0.4927 | 0.4970 | 0.4914 | 0.5047 |
| XLY | 0.6804 | 0.6838 | 0.6802 | 0.6841 |
| Sector | HAR-RV-C | HAR-RV-C-CJ | HAR-RV-C-IJ | HAR-RV-C-CJ-IJ |
|---|---|---|---|---|
| Forecasting Period: 2008:11–2019:12 | ||||
| XLF | 0.2293 | 0.2251 | 0.2276 | 0.2267 |
| XLK | 0.2371 | 0.2348 | 0.2360 | 0.2320 |
| XLP | 0.2062 | 0.2056 | 0.2063 | 0.2031 |
| XLU | 0.2070 | 0.2061 | 0.2069 | 0.2042 |
| XLY | 0.2225 | 0.2211 | 0.2214 | 0.2205 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Yao, C. Co-Jumps, Co-Jump Tests, and Volatility Forecasting: Monte Carlo and Empirical Evidence. J. Risk Financial Manag. 2022, 15, 334. https://doi.org/10.3390/jrfm15080334
Peng W, Yao C. Co-Jumps, Co-Jump Tests, and Volatility Forecasting: Monte Carlo and Empirical Evidence. Journal of Risk and Financial Management. 2022; 15(8):334. https://doi.org/10.3390/jrfm15080334
Chicago/Turabian StylePeng, Weijia, and Chun Yao. 2022. "Co-Jumps, Co-Jump Tests, and Volatility Forecasting: Monte Carlo and Empirical Evidence" Journal of Risk and Financial Management 15, no. 8: 334. https://doi.org/10.3390/jrfm15080334
APA StylePeng, W., & Yao, C. (2022). Co-Jumps, Co-Jump Tests, and Volatility Forecasting: Monte Carlo and Empirical Evidence. Journal of Risk and Financial Management, 15(8), 334. https://doi.org/10.3390/jrfm15080334






