1. Introduction
A marketing campaign is a set of commercial operations all pursuing the same objective, which may concern the improvement of brand awareness and/or sales objectives (
Leppäniemi and Karjaluoto 2008). These operations can take different forms and be spread out over time or be concomitant. If in the past the majority of commercial operations were based on mass marketing, nowadays direct or even targeted marketing is more and more desired (
Koumétio et al. 2018;
Tekouabou et al. 2019). Companies use direct marketing strategies when they target customer segments by contacting them to achieve a specific sales campaign (
Moro et al. 2014). To facilitate the operational management of campaigns, they centralise remote interactions in a contact centre (
Feng et al. 2022). The latter contains all the strategic data on customers or potential customers for help, assistance, loyalty and the realisation of new business (
Ballings and Van den Poel 2015). Such centres allow communication with customers through different channels: postal mail, email, SMS or, better yet, telephone calls (on landline or mobile). Recently, the telephone has become one of the most widely used means of managing customer relations (
Moro et al. 2011,
2014), especially with the possibility of transmitting from the internet, using voice on internet protocol (VoIP) techniques, which have drastically reduced the cost of calls while ensuring greater security (
Butcher et al. 2007). This marketing technique implemented through a contact centre is called telemarketing because of the characteristic of remoteness (
Kotler and Keller 2016;
Moro et al. 2014). Telemarketing has proven to be more practical and efficient with the remote working conditions imposed to deal with the recent pandemic related to COVID-19 (
Sihombing and Nasib 2020). Telemarketing is becoming more and more reliable both for customers and for companies wanting to opt for this marketing strategy (
Butcher et al. 2007;
Feng et al. 2022). In addition to these different advantages, the technique allows for a rethinking of marketing by focusing on maximising the value of the customer throughout his or her life, thanks to the evaluation of the available information and the customisation of the targeting parameters (
Bhattacharyya et al. 2011;
Cioca et al. 2013). Thanks to technological evolution, notably, the processing capacities of machines and the volumes of storage, this information collected on customers is increasingly rich and varied (
Koumétio and Toulni 2021). On the other hand, the emergence of machine learning algorithms and data mining tools for which these data constitute the raw material (
Al-Garadi et al. 2020). These algorithms allow for a more efficient evaluation of these data to predict the results of the marketing campaigns, or even the complete automation of the operation (
Moro et al. 2014). The forecasts allow, in the majority of cases, an operational adjustment to build longer and closer relationships, according to the demand of the companies (
Rust et al. 2010).
The data collected and thus currently enriched for more realistic predictive targeting suffer from several problems, such as volume, complexity and especially heterogeneity, which negatively affect the performance of the algorithms (
Al-Garadi et al. 2020;
Koumétio and Toulni 2021). Thus, the classification algorithms currently used are limited not only by the data size, which makes them slower and weakens their performance, but by the feature scale difference, which makes them unstable, the data heterogeneity, and above all the non-numerical data, which require a more sophisticated or even complex preprocessing (
Al-Garadi et al. 2020;
Bhattacharyya et al. 2011;
Cioca et al. 2013). This should be set up, regulated, adjusted and transparently processed during the machine learning model design, especially for heterogeneous data, such as those of the UCI Portuguese bank telemarketing dataset (
Tekouabou et al. 2019). However, several works do not mention the preprocessing steps applied in their experiments (
Koumétio and Toulni 2021;
Moro et al. 2014;
Tekouabou et al. 2019;
Vafeiadis et al. 2015;
Vajiramedhin and Suebsing 2014). Moreover, previous works have examined conventional classification techniques as well as classical data mining methods (SVM, DT, KNN, NB, ANN, …) or emerging ensemble methods (RF, Bagging, GB, …). However, these methods present a problem of mismatch with multiple features and are prone to data leakage when re-training the machine learning model (
Turkmen 2021). Even though some studies involving these methods have achieved high performance, the experimental protocols are often very unreliable to really assess the feasibility of the performance achieved in these works (
Koumétio and Toulni 2021;
Moro et al. 2014;
Tekouabou et al. 2019;
Vafeiadis et al. 2015;
Vajiramedhin and Suebsing 2014). Among the works investigated on this problem, many have evoked the problem of execution time without really calculating it; this is the case of (
Farooqi and Iqbal 2019). However, the execution time is very important to evaluate the algorithmic complexity of a machine learning approach (
Cherif 2018;
Koumétio et al. 2018). On the other hand, the metrics often used to evaluate their performances are either unsuitable or insufficient to evaluate this type of problem (
Koumétio and Toulni 2021;
Tekouabou et al. 2019) (classification of imbalanced data
Marinakos and Daskalaki 2017). Of course, this is not to mention the sometimes depreciated and unreliable experimentation tools (SPSS, Rapidminer, WEKA), which allow for relatively dubious models.
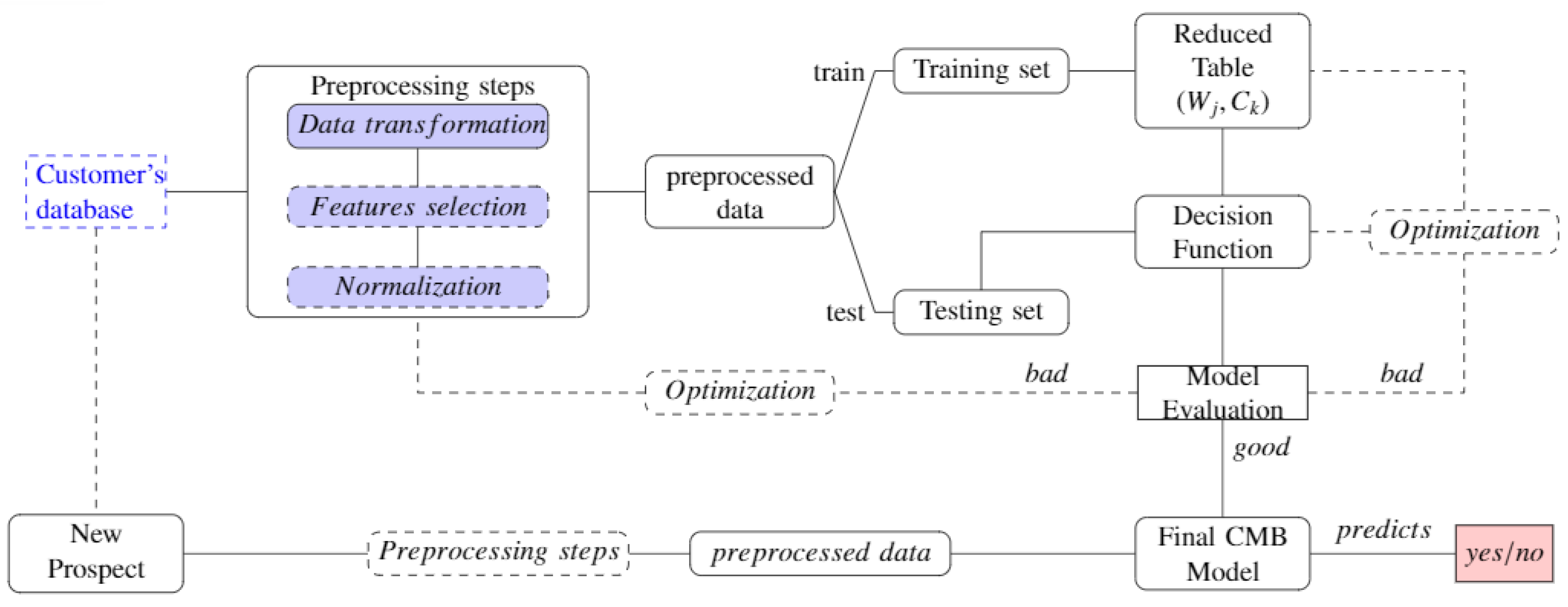
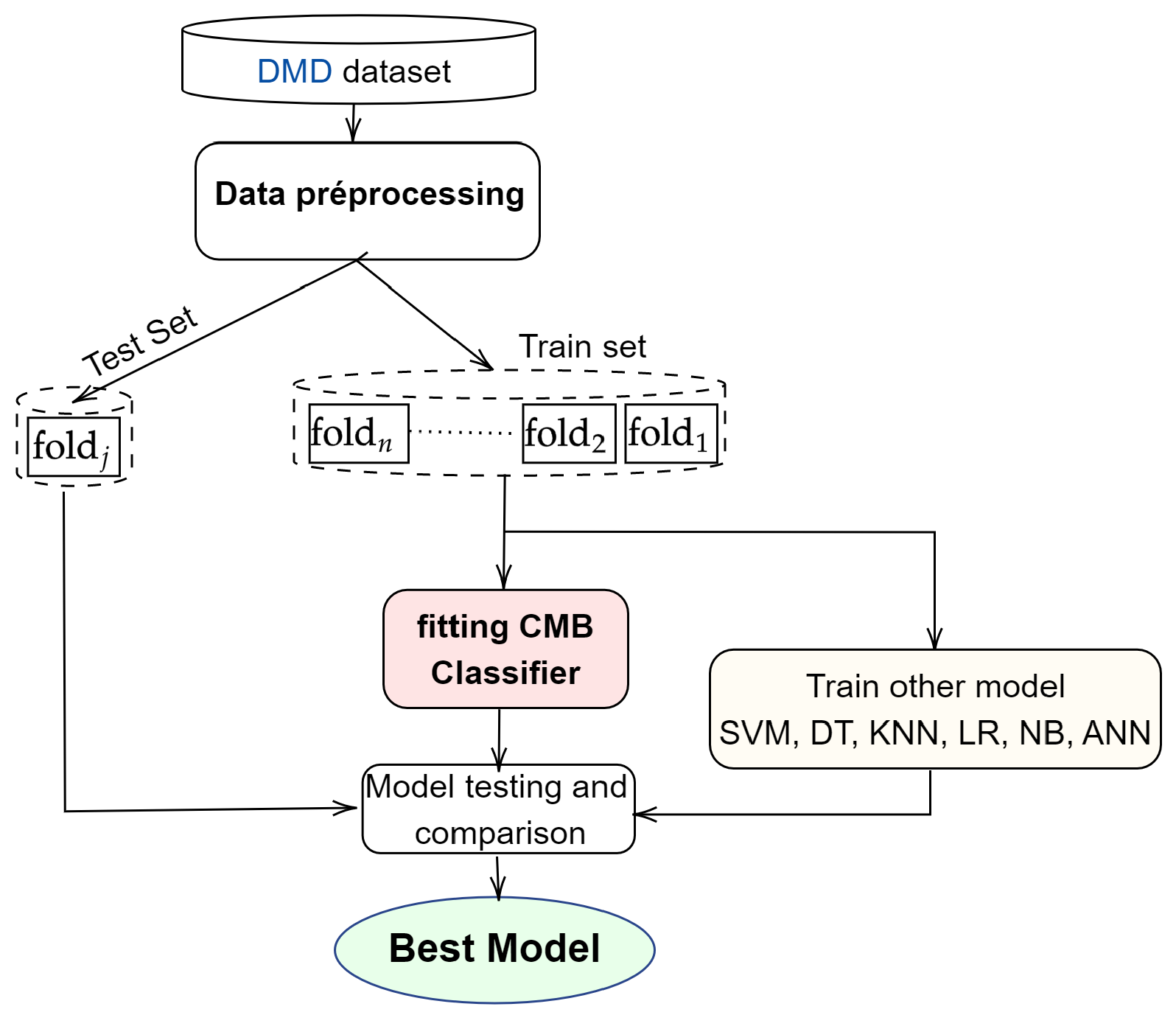
Hence, we propose in this paper a new approach based on membership classes (CMB). The CMB approach is devoted to achieving the best performance of realistic prediction by transforming the heterogeneous data used. Therefore, it will overcome the main challenge of current ML algorithms by well processing each type of these heterogeneous data. Optimising the transformation of this mosaic datasets’ features for better prediction performance is the first goal we seek to achieve during preprocessing. What makes our method different from other existing algorithms is that the preprocessing of nominal-type features that are difficult to process in the existing approaches so far simply involves imputing the missing values. The nominal features are directly used in the class membership-based (CMB) classification phase process. This and the elimination of non-significant attributes allow the processing time, which constitutes the second challenge of our approach. Generally, transformed data present a problem with different variable scales. Standardisation is an additional step in dealing with this problem, but it has an adverse or favourable effect on the performance of certain algorithms that are said to be unstable to variable scales, knowing that a very large-scale difference is more favourable for over-fitting. We have, therefore, created the proposed classification algorithm, which, from the reduced table of the training database, independently classifies each attribute before predicting the class of the individual. This is the third contribution of our paper.
Basically, the contribution of this paper is summarised in the following points:
The introduction of a novel approach that processes heterogeneous data by transforming separately each type of feature (numerical, Boolean, scaled and nominal), then a hybrid technique to replace missing values and implicitly select the most significant features. This helps to optimise the classification in terms of processing time and accuracy. Apart from the replacement of missing values, we do not transform nominal attributes in this step because they are directly treated in the classification; this allows reducing the processing time.
The construction of the reduced table of training data. For each class, this table contains the averages of transformed features and the favourable attributes for nominal features.
A simplification of the overall approach for the special case of binary classification. It incorporates a weighting scheme that improves the performance.
Proposing and following a clear and transparent design and implementation process to efficiently solve a real and concrete machine learning problem.
The successful implementation and use of the model designed to optimise the predictive performance of potential leads before a telemarketing bank campaign.
Following this work,
Section 2 and
Section 3 investigate the related works and depict the proposed method, which constructs a class membership-based approach, respectively. Then,
Section 4 analyses the experimental results performance of our model, while
Section 5 discusses these results. Finally,
Section 6 concludes our study.
2. Prior Literature Review
The banking telemarketing database was first used by (
Moro et al. 2011) in 2011, who processed this data with the RapidMiner tool. Its second version collected data from 2008 to 2012, and allowed the publication of the article (
Moro et al. 2014) and the data shared for research. Since then, this dataset has heavily affected the field of machine learning, occupying the seventh most popular data position on the UCI Machine Learning repository
1 It is a reference for the training and tuning of new models and even a pedagogical or research tool in data science. Thus, several articles using a multitude of approaches have been published on the subject of predicting the success of a telemarketing bank campaign (
Feng et al. 2022;
Govindarajan 2016;
Koumétio and Toulni 2021;
Tekouabou et al. 2019). The best papers published in this issue were selected by searching for “bank telemarketing” AND “machine learning” request in different databases (Google Scholars, WoS, and Scopus) and the list was completed by citation matching. The summary of these papers is presented in
Table 1. From the point of view of the type of learning, it is supervised learning and a very unbalanced classification problem (
Miguéis et al. 2017;
Thakar et al. 2018). The unbalanced classification often imposes the use of certain metrics, such as AUC,
-score, or
to determine the best model, especially since the target class is often a minority. This is one of the limitations of the majority of papers published on this problem. Some authors have used data-balancing techniques (SMOTE
Chawla et al. 2002; RAMO
Chen et al. 2010) before training the models (
Krawczyk 2016;
Marinakos and Daskalaki 2017). These approaches are limited by the fact that they create random instances that do not always reflect reality and, in addition, increase the processing time of the algorithms and thus the complexity of the models. On the other hand, since the data are heterogeneous, i.e., contain variables of several types, very few authors have shown transparent approaches allowing to understand the data pre-processing steps before training the models (
Koumétio et al. 2018;
Koumétio and Toulni 2021;
Tekouabou et al. 2019).
The methods used range from classical learning methods to deep learning methods and ensemble methods. While early works focused on simple learning methods, such as DT, SVM, NB, ANN, KNN or LR (
Elsalamony and Elsayad 2013;
Elsalamony 2014;
Karim and Rahman 2013;
Moro et al. 2011,
2014,
2015;
Vajiramedhin and Suebsing 2014), more complex approaches or combinations of several simple methods have since been used (
Amini et al. 2015;
Govindarajan 2016). These simple models have achieved the best performance in several works, although the experimental protocol often raises questions about the results. S. Moro et al. (
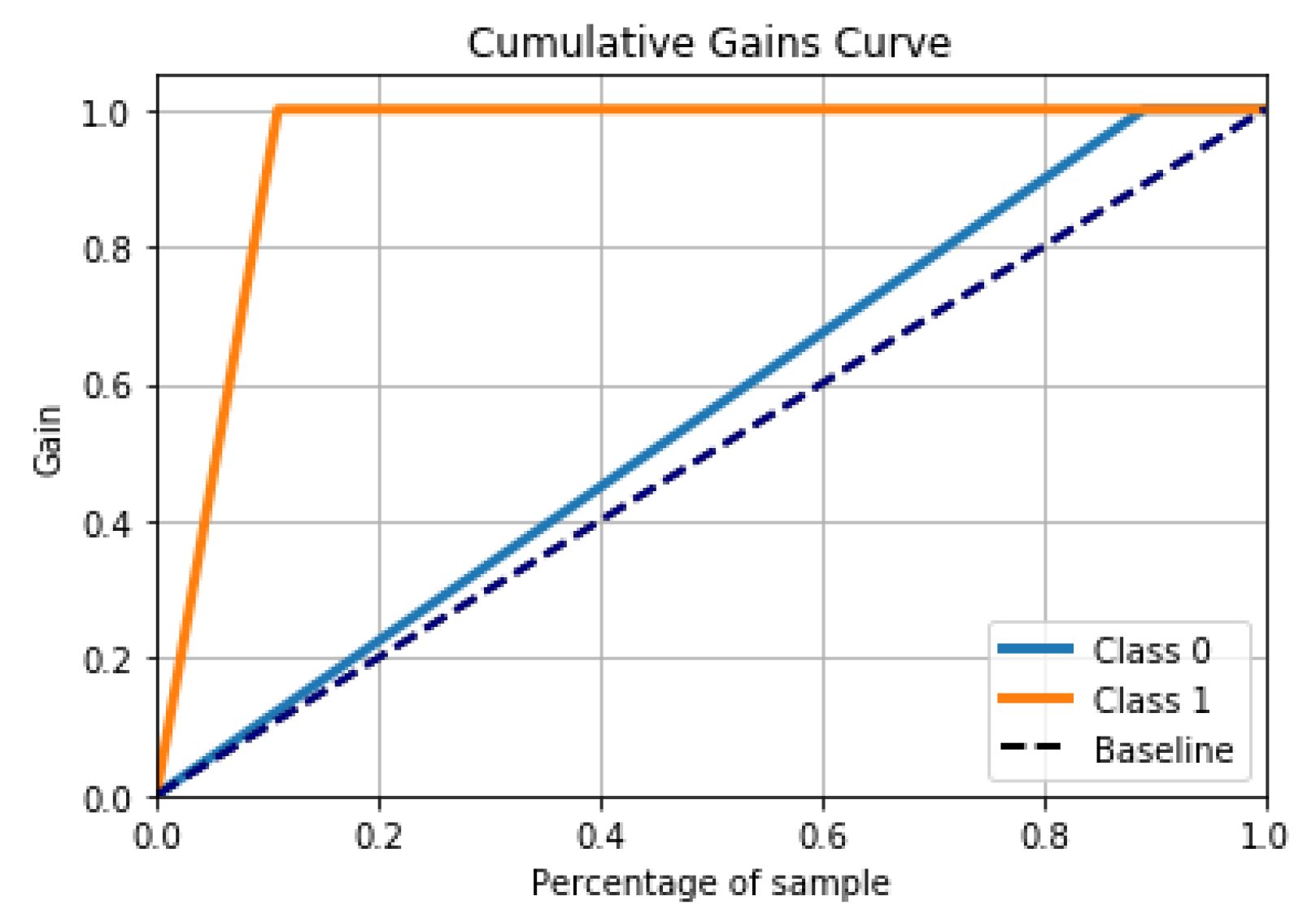
Moro et al. 2011,
2014,
2015) for example, used simple learning methods (DT, SVM, NB, ANN, LR, and KNN) but using the ALIFT chart to show the proportion of favourable prospects according to the model. Generally, the works on this topic pose a problem of performance reliability linked to the simulation tool (Rapid Miner). The DT model was found to perform better according to the results of (
Farooqi and Iqbal 2019;
Karim and Rahman 2013;
Koumétio et al. 2018;
Tekouabou et al. 2019;
Vajiramedhin and Suebsing 2014) and seems to be globally one of the best models for this problem by compromising performance and complexity. However, DT is still very much in favour of the over-fitting that would affect this performance in reality. Hence, (
Amini et al. 2015;
Elsalamony and Elsayad 2013;
Govindarajan 2016) have proposed ensemble methods to try to overcome these limitations. Other authors, on the other hand, have proposed their models based on the modification or improvement of classical models. This is the case of (
Tekouabou et al. 2019), who proposed an improvement of the KNN model, while (
Yan et al. 2020) proposed a model called the
network and (
Ghatasheh et al. 2020) the CostSensitive-MLP. (
Birant 2020) introduced a method called the class-based weighted decision jungle, which is very sensitive to class imbalance, while
Moro et al. (
2018) and
Lahmiri (
2017) used a divide-and-conquer strategy and two-step based system, respectively. Manipulation of this class imbalance was included in the approaches adopted by (
Krawczyk 2016;
Marinakos and Daskalaki 2017;
Miguéis et al. 2017;
Thakar et al. 2018) to overcome the problem. (
Elsalamony 2014;
Ładyżyński et al. 2019) used models based on artificial or deep neural networks, which are sometimes slow and unsuitable for this type of data. The ANN model provided the best scores in the work of (
Mustapha and Alsufyani 2019;
Selma 2020) with 98.93% and 95.00% for accuracy and the
score, respectively.
More recently, Feng et al. (
Feng et al. 2022) used Python frameworks to implement ensemble methods with dynamic selection to predict sales in this campaign.
Khalilpour Darzi et al. (
2021) introduced a correlation-augmented naive Bayes (CAN) algorithm as a novel Bayesian method supposed to be well adjusted for direct marketing prediction. However, the performance of his model is still quite limited compared to previous works and his model is a bit more complex. Moreover, the transparent problem of preprocessing heterogeneous data and interpretability of the constructed model still persists. This is the main motivation for the approach we propose in the next section.
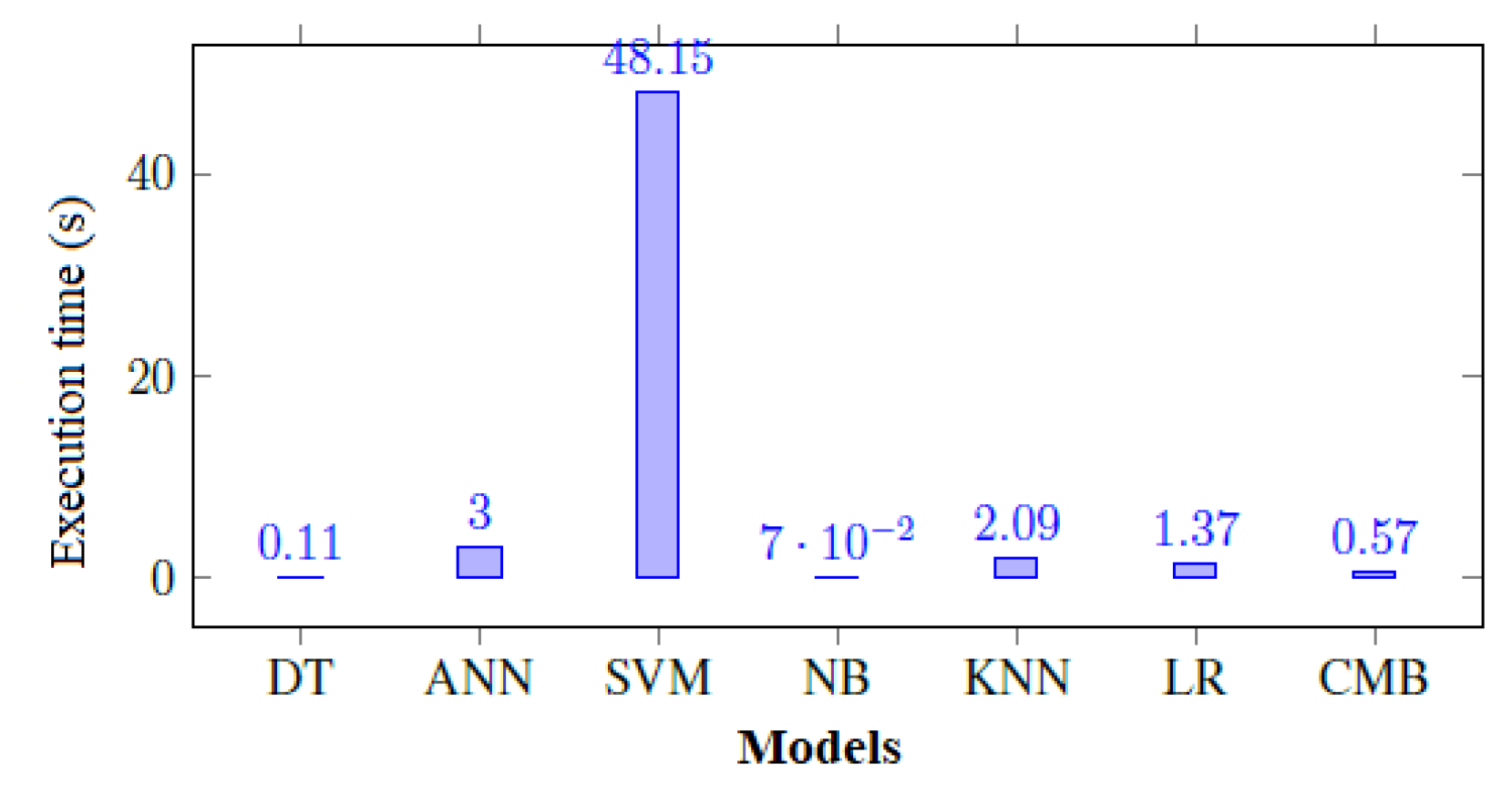
5. General Discussion
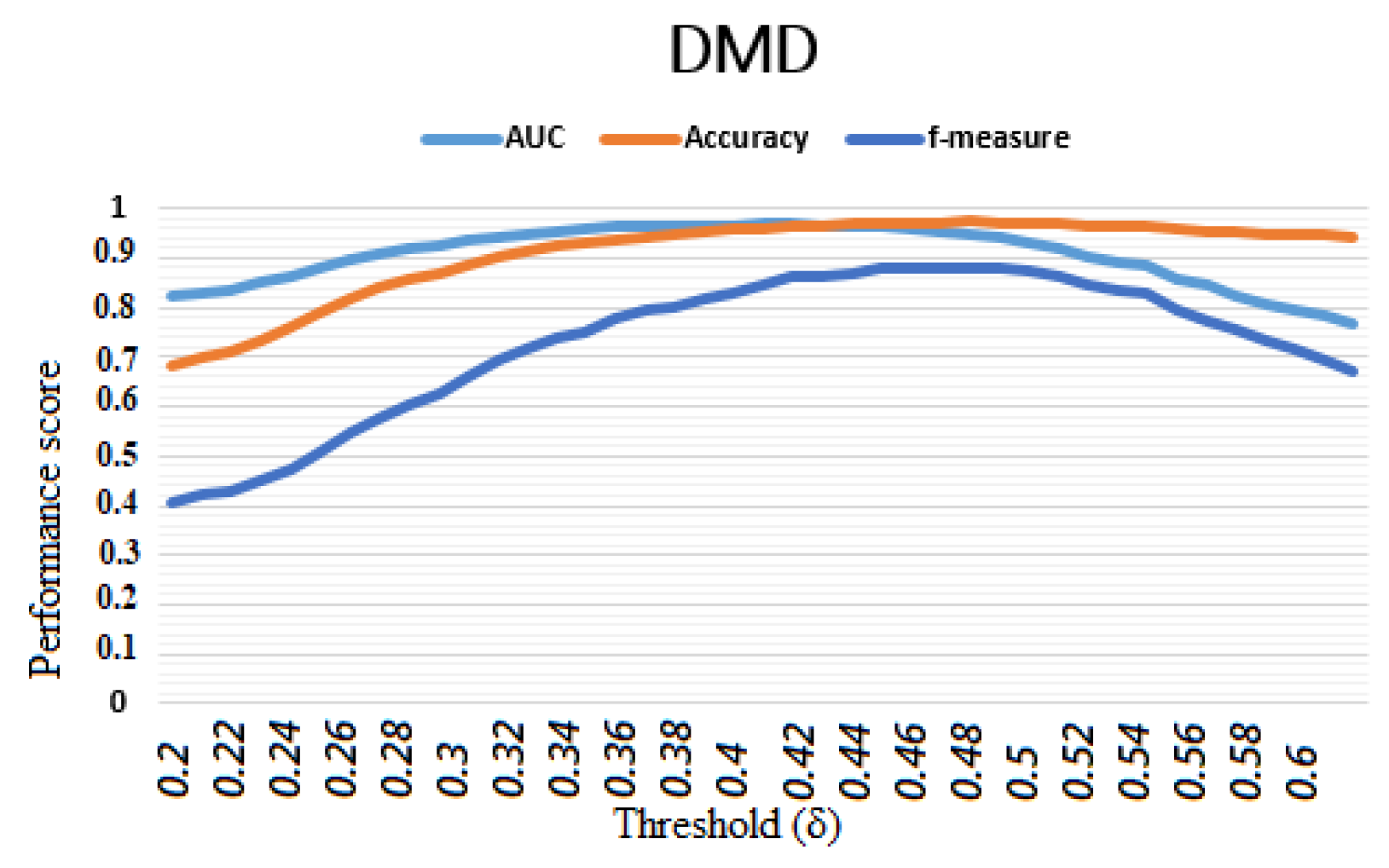
The use of machine learning methods has been widely discussed for over a decade (
Fawei and Ludera 2020;
Tekouabou et al. 2019). The search for the optimal model is still a challenge that researchers seek to address (
Koumétio and Toulni 2021). Indeed, the current work that addresses the limitations of yesterday’s work is setting the stage for tomorrow’s work. For the automatic targeting of customers in a banking telemarketing campaign, the use of machine learning approaches in previous work has not been able to show transparency in the processing of heterogeneous data, achieve optimal performance or use minimal resources. In this paper, we introduce a transparent classifier adapted to heterogeneous data that exploits nominal variables in the decision function. Note that these dummy variables are often either suppressed or coded arbitrarily in most works without really evaluating their impact on the final performance of the models. In many cases, their coding favours the learning model without necessarily reflecting reality, which leads to over-fitting. The results obtained in this study suggest that the application of the CMB approach to bank telemarketing data is able to predict the success of future prospecting with a high degree of accuracy compared to previous work. Furthermore, the fact that in addition to its better performance in terms of accuracy (97.3%), the model also gives a very close score for the AUC (95.9%) shows the stability of the model, which would be very unfavourable to over-fitting. Thus, this model based on the CMB approach presents globally two main advantages. The first of these advantages is the transparency in the pre-processing of the so-called heterogeneous data. Indeed, in previous works, the presence of non-numerical variables in the data set are often either ignored or treated arbitrarily, without this being mentioned in the work, which leads to models that are not correlated with reality and therefore to the production of the model. Moreover, the arbitrary coding of these variables is often the cause of over-fitting or the slowing down of the model, thus increasing its complexity (
Koumétio et al. 2018;
Moro et al. 2014;
Tekouabou et al. 2019). This is the case in the work of (
Wankhede et al. 2019) who used one hot encoding, which is known to multiply the variables and their processing time. In the CMB approach, the nominal variables are only processed by the decision function to optimise the processing time. On the other hand, the selection of the variables also contributes to optimising this processing time because 18 variables were significant to build a better model. Finally, still at the pre-processing level, the normalisation of the data allowed the scaling of the data to not only increase the performance, but also to stabilise the constructed model. The second advantage is the decision function, which deals directly with the nominal variables and contains only two parameters to be set in the optimisation process. This makes it very flexible and easy to optimise according to the training data, as we showed in
Section 4.3. The model is globally fast with a processing time lower than the average given by the state-of-the-art methods while keeping almost the best performance scores. The high values of the accuracy, AUC and
-measure with absolute deviations relatively less than five from each other prove that the model is less affected by the imbalance between the classes of the dataset compared to the works of (
Krawczyk 2016;
Marinakos and Daskalaki 2017). In addition, this function is easy to deploy in the real world and easily understood by bank marketers who do not necessarily have a great deal of knowledge of machine learning to use it or adapt it to new challenges. Although the CMB approach has many advantages, it is not without limitations related to our case study. One of them is related to the experimental protocol, which did not experiment with balancing the data by appropriate methods, such as SMOTE (
Chawla et al. 2002), RAMO (
Chen et al. 2010). The other is related to the use of certain variables, such as the call duration, which normally is only known after the call and therefore does not always reflect the reality in this database.
6. Conclusions
This paper presented and discussed the implementation on a Python platform of a class membership-based (CMB) approach to improve the prediction of call success in a commercial banking telemarketing campaign. The proposed approach provides a transparent process for preprocessing heterogeneous data and making optimal use of dummy variables that are often deleted or coded arbitrarily and/or in non-transparent ways during machine learning model building. The selection of meaningful features and normalisation not only improved performance, but also reduced processing time while stabilising the model for this data set. The use of a classification decision function directly incorporating the processing of categorical variables improved performance, reduced processing time, and furthermore, reduced the effects of class imbalance on the model performance and predictive risk. The constructed model was found to be more robust, stable, flexible and resistant to the effects of over-fitting. Its best performance reached 97.3%, 95.9% and 93.9% in terms of accuracy, AUC and -measure, respectively. Thus, the comparative analysis of our approach to classical machine learning algorithms and previous works showed that the CMB approach clearly overcomes the state-of-the-art works while offering, in addition, a relatively very low processing time. However, the approach is not yet suitable for other types of supervised machine learning problems, such as regression. Additionally, we have not yet experimented a combined approach with data- and time-variable balancing methods, which will be the focus of our future research.