Abstract
Movements in the India VIX are an important gauge of how the market’s risk perception shifts from day to day. This research attempts to forecast movements one day ahead of the India VIX using logistic regression and 11 ensemble learning classifiers. The period of study is from April 2009 to March 2021. To achieve the stated task, classifiers were trained and validated with 90% of the given sample, considering two-fold time-series cross-validation for hyper-tuning. Optimised models were then predicted on an unseen test dataset, representing 10% of the given sample. The results showed that optimal models performed well, and their accuracy scores were similar, with minor variations ranging from 63.33% to 67.67%. The stacking classifier achieved the highest accuracy. Furthermore, CatBoost, Light Gradient Boosted Machine (LightGBM), Extreme Gradient Boosting (XGBoost), voting, stacking, bagging and Random Forest classifiers are the best models with statistically similar performances. Among them, CatBoost, LightGBM, XGBoost and Random Forest classifiers can be recommended for forecasting day-to-day movements of the India VIX because of their inherently optimised structure. This finding is very useful for anticipating risk in the Indian stock market.
1. Introduction
The India VIX, an implied volatility of NIFTY 50 Index options, was created by the National Stock Exchange (NSE) of India in 2008. Its computation methodology is replicated from the Chicago Board Options Exchange (CBOE) implied Volatility Index (VIX) with permission from the CBOE. The India VIX is calculated using the implied volatilities of options trading on the NIFTY 50 Index. Daily changes in the VIX Index are of interest, not only for volatility trading but also for anticipating shifts in the market’s risk perceptions. () states that it is not only a ‘fear index’ but also the leading indicator of risk in the capital market, while () regards it as both a greed- and fear-based index. At an aggregate level, it captures how risky the market is at any point in time based on market participants’ perceptions.
According to the theory, in times of market turmoil, the market generally goes up or down sharply, and the VIX tends to increase. As market volatility moderates, the VIX decreases. However, in practice, the CBOE VIX Index is strongly and negatively associated with the S&P 500 Index’s returns but positively associated with the volume of the S&P 500 (). The India VIX Index and the NIFTY 50 Index move in opposite directions (; ). This relationship is strong when the market is falling. Additionally, the portfolio return can be maximised by tilting mid-cap to large-cap stocks when the VIX Index rises and tilting large-cap to mid-cap stocks when the VIX Index falls (; ).
Given the importance of the India VIX Index, it is essential to examine its movements. Although the magnitude of changes in the India VIX is also highly important, this study is limited to forecasting the direction of these changes. This focus is not only because it provides a good starting point for testing the performance of VIX forecasting using various machine learning algorithms but also because, in situations such as risk management and volatility trading, the direction of daily changes is of great interest.
In this study, the day-to-day movements of the India VIX are predicted by defining the classification problem, and the classification model is built by applying a standard classifier called logistic regression (; ) and a set of ensemble learning classifiers (; ; ; ; ). Ensemble learning is applied because, like stock market forecasting, VIX forecasting is time-series forecasting in which variables reveal temporal dependencies, and their relationship is likely to be non-linear (). These algorithms are trained, and their performance (; ) is compared and ranked. An accuracy score shows the overall performance of the classifier, while the area under the receiver operating characteristics (ROC) curve indicates the predictability of the individual classifier. Ranking () the trained classifiers reveals whether the classifiers’ predictability is significantly the same or different.
The rest of this paper is organised as follows: in Section 2, some previous studies are reviewed. Section 3 examines the research technique, while Section 4 discusses the modelling procedure. Next, Section 5 covers the models’ outcomes, and finally, Section 6 provides the conclusion and is followed by Appendix A.
2. Literature Review
Several previous studies on predicting the VIX using statistical techniques, including machine learning, are reviewed in this section to understand VIX forecasting techniques and their dynamics.
To judge the impact of trading volume on estimating a trend in stocks, logistic regression () was trained and used to test the significance of the previous five days’ trading volume for the selected stock. The study found that the current day’s stock market trend was statistically influenced by the third most recent day’s trading volume. The investigation emphasised the importance of incorporating the trading volume in day-to-day movements in stock market trends.
By extracting 33 technical indicators from stocks listed on the NSE of India, () used machine and deep learning algorithms to build classification models to predict stock movements. The authors applied the Boruta feature selection technique. After preparing numerous technical indicators from tick-by-tick stock prices of Maroc Telecom stocks for eight years, () used Random Forest, support vector machine (SVM) and gradient-boosting trees to predict variations in the Moroccan stock market ten minutes ahead. The results suggest that the Random Forest and gradient-boosting trees outperform SVM. With less time required to train and less computational complexity, the Random Forest and gradient-boosting trees are highly preferable for short-term forecasting.
() applied traditional statistical techniques to investigate the relationship between returns on the India VIX and returns on the NIFTY 50. Their result reveals bidirectional causality from the NIFTY 50 Index to the India VIX. In the long term, the India VIX causes movement in the NIFTY 50 Index, whereas in the short term, the NIFTY 50 Index causes movement in the India VIX. Furthermore, using SVM, Random Forest and artificial neural network (ANN) models, () developed staked models to predict S&P 500 volatility. The result revealed that the proposed models’ performance surpassed that of the other models based on generalised autoregressive conditional heteroskedasticity (GARCH) and exponential generalised autoregressive conditional heteroskedasticity (EGARCH) to forecast volatility.
Using an ANN, () developed a model characterised by a low forecasting error and substantial profit to forecast future VIX prices. This is an intra-day strategy in which the authors focused on open-to-close returns, considering non-lagged exogenous variables based on the data and information possessed by traders for making investments. The results revealed that when only the most recent exogenous variables, such as returns on BSE SENSEX, are used with the ANN, the model achieves a better result than the heterogeneous autoregressive and logistic specification models in terms of profitability.
() studied the effects of artificial intelligence and machine learning on service jobs in India based on crucial parameters, including compassion, physical, natural and logical parameters, noting their importance for people and machines in this sector. Their findings revealed that artificial intelligence and machine learning dominate more at the task than at the job level, and the logical aspect will be reduced in the coming year.
Using the fully modified least-squares method and the Johansen cointegration test, () investigated the influence of daily positive COVID-19 cases and deaths in the US on the CBOE VIX Index and the impact of the CBOE VIX Index on the stock indices of the US (measured by the symbol DJI), Germany (measured by the symbol DAX), France (measured by the symbol CAC40), England (measured by the symbol FTSE100), Italy (measured by the symbol MIB), China (measured by the symbol SSEC) and Japan (measured by the symbol Nikkei225). Their findings suggested a positive association between reported COVID-19 cases and the CBOE VIX Index and a positive influence of the CBOE VIX Index on most indices, except CAC40. Last, they found that newly reported cases had a higher impact than death cases in the US on the CBOE VIX Index during the same period.
During the pandemic, () investigated the influence of gold price volatility, oil price volatility and the VIX Index on the Turkish BIST 100 stock index, using the Toda-Yamamoto Causality test, variance decomposition methods and an impulse–response analysis. These techniques suggest that causality does not exist. However, they revealed that the influence of gold price volatility, oil price volatility and the VIX Index on the Turkish BIST 100 stock index decreased rapidly.
() studied the effect of COVID-19 lockdowns on the sharing economy, such as delivery services, entertainment, ride hailing, accommodation, entertainment and freelance work, and applied the difference-in-difference estimation method to evaluate this effect using Google trends data. Their results revealed a surge in activity for online deliveries, streaming services and freelance work; however, they also showed that the lockdowns decimated accommodation and transportation activities.
By using a plain linear autoregressive model with monthly volatility data from 2000 to 2017, () explored the forecasting-related association between stock volatility and implied volatility in the stock markets of five economically advanced nations (i.e., the UK, Japan, France, Germany and the USA). Results revealed that implied volatility of the stock market is significantly associated with stock volatility. However, results from markets outside the sample showed that implied volatility of the stock market is more crucial for stock than oil price volatility.
Generally, the volatility of a security price is computed from the close-to-close price only. Moreover, while computing these parameters, some authors believed that the security price has no drift, leading to the overestimation of volatility, whereas others assumed no opening price, leading to the underestimation of volatility. Using open, close, low and high stock prices, () computed a minimum-variance unbiased variance estimator independent of both the drift and the opening jumps of the underlying price movement.
() developed a fundamental analysis stock screening and ranking system to compute the performance of various supervised machine learning algorithms. First, Graham’s criterion was compared with the classification model in a stock screening scenario trade that allowed the long position only. Second, the regression performance was distinguished against classification models, allowing for including the short position. Finally, a regression model was used to perform stock ranking instead of just stock screening. Several fundamental variables were chosen as featured variables, and simple returns and categorical variables (i.e., buy, hold and sell based on returns) were selected as target variables for regression and classification, respectively. The results revealed that tuning the hyperparameters is crucial for optimal model performance. However, most models outperformed both Graham’s criterion and the given stock market index, and the best-calibrated model multi-folds the initial investment in stock screening.
() studied the association between the NIFTY 50 Index and the India VIX and found that both indices move in reverse directions. The statistical test indicates a significant relationship. This relationship is strong when the market is moving downwards. The author further argued that, by using a risk-mitigating technique when the India VIX increases, the performance of the portfolio consisting of stocks could be improved by shifting allocation from mid-cap to large-cap stocks and vice versa.
() examined the short-term association of the India VIX and returns on the NIFTY Index by applying the vector autoregression model to their data at five-minute intervals. In other words, the authors examined the risk–return trade-off concept, assuming a return on the stock market index and risk in the stock market, for which implied volatility is taken as a risk. From this, they revealed that the short-term association is not only negative but also asymmetric.
Considering technical indicators derived from price data, () utilised an ANN model to forecast daily upward and downward directional movements in the India VIX and found that the network can predict with up to 61% accuracy. On the other hand, using ANN models based on several backpropagation algorithms, () attempted to predict volatility in India’s stock market by predicting the volatility of NIFTY and gold returns, with the volatility of gold and NIFTY returns as the target variables. Using training data from 2013–2014, their results show that the model satisfactorily forecasted volatility for 2015. However, the forecasting accuracy of market volatility in 2008 was lower using the same sets of training data. () proposed a weight-constrained deep neural network for forecasting stock exchange index movements.
Considering daily data from March 2008 to December 2017, () studied the influence of returns on the NIFTY Index, foreign portfolio investment (FPI) in India, the S&P 500 Index and the CBOE VIX Index on the India VIX using the ARIMA GARCH model. The study’s outcome revealed the impacts of the NIFTY Index, FPI in India, the S&P 500 Index and the CBOE VIX Index on the India VIX Index. Specifically, they observed that because of increased investment in FPI, the India VIX Index has only decreased.
() studied the cointegration and non-linear causality among the implied volatility of the Indian stock market measured by the India VIX and the implied volatility of gold and oil. This study assumed that since India heavily imports resources such as gold and oil, the price fluctuations of these resources could influence inflation in India and the volatility of the Indian stock market. The results revealed that the implied volatilities of gold and oil positively impact the India VIX. The results also indicated an inverse bidirectional association between the implied volatility of oil and gold. Furthermore, using implied volatility indices, () investigated the short-term and long-term associations between the Indian and Chinese stock markets and gold and found that their associations are significantly bidirectional at both low and high frequencies, indicating that the stability of gold as a haven cannot be taken for granted.
() studied the symmetric thermal optimal path (TOPS) technique from 26 March 2004 to 19 June 2017 to analyse the robust interconnection trends between the VIX futures and the VIX spot. The authors noted that the VIX Index in the first few years dominated the VIX Index futures, in particular prior to the inception of VIX Index options. Furthermore, the authors recorded that most of the time, the TOPS detected an interspersed lead–lag association between the VIX futures and the VIX rather than dominance.
Using the composition of the VIX Index, () studied the predictability of cash flows and returns. The squared VIX Index was divided into variance risk premium (VRP) and expected return variations (ERV). Without introducing a powerful presumption on the dynamics of the return variations, the author examined the performance through the generalised method of moments technique with suitably selected instruments. The experiments’ results showed ERV’s short- and long-term cash flow reliability and VRP’s short term return reliability.
Taking implied volatility indices as a key risk measure, () applied the graph theory to study the information flow among the equities of Brazil, Russia, India, China and South Africa, US equities, and gold and oil commodities. The graph theory helped detect the dynamics of information integration among these countries. The results suggest that the exchange of information is unstable, and there is no consistency in the impact of the events; for example, some have global influence, while others only influence local markets.
() predict the binary movements of the CBOE VIX Index by applying an adaptive machine learning technique on economic predictors comprising 278 feature variables. The results depict that the applied algorithm achieved a maximum accuracy score of 62.2%. Their experiment also revealed that the weekly US unemployment report had the greatest impact on the outcome. Additionally, the technical indicators derived from the S&P 500 Index also seem to have predictive power. On the other hand, () examined the influence of various US macroeconomic variables on the binary movements of the CBOE VIX Index using a Light Gradient Boosted Machine (LightGBM), Extreme Gradient Boosting (XGBoost) and logistic regression and achieved a maximum accuracy score of 62%.
The literature review discovered that the predictability of ensemble machine learning to forecast the day-to-day movements of the VIX Index has not yet been studied in a classification setting. Most previous studies focus on predicting the VIX Index’s numerical values using various regressors. Only a few recent studies have tried to use classification techniques to predict the binary movements of the VIX Index, also indicating a shift in researchers’ attention to classification techniques. Regression models are more suitable for continuous data, while classification models are more helpful in classifying discrete and labelled data. Several researchers have cast doubt on regression models for time-series data because a regressor conducts a form of linear or non-linear extrapolation that is often unreliable in a practical setting and faces several challenges (; ; ).
Among the few classification models reviewed, two studies (; ) predicted the binary movement of the CBOE VIX Index, and another study () developed a binary classification model for India VIX with just one algorithm. However, more data are now available, and more advanced machine learning algorithms have been developed. Therefore, it is important to conduct a comprehensive study by applying the various ensemble machine learning algorithms with additional datasets to predict the India VIX Index’s binary movements, as machine learning algorithms require larger amounts of data. Keeping this in view, the research questions are as follows:
- How can we forecast the binary day-to-day movements of the India VIX using machine learning classifiers?
- How can we measure the performance of the classifiers?
- How can we say whether classifiers have similar performances?
- How do we know whether the models’ performances are acceptable?
To answer these research questions, the research objectives are as follows:
- To forecast the binary day-to-day movements of the India VIX, a standard classifier called logistic regression and 11 ensemble machine learning classifiers are trained.
- To measure the predictability of the classifiers, several metrics are applied.
- To distinguish the classifiers’ predictability, a statistical test is performed.
- To judge the predictability of the models in the context of the stock market, the performance of the developed models is compared with the past studies, and additionally, a basic classifier called logistic regression is trained for comparison.
3. Research Methodology
3.1. Description of the Models Used
In machine learning, the ensemble method combines the predictability of multiple predictors of the same or different algorithms. If the predictions of a combination of models, such as classifiers, are aggregated, the aggregated models produce a higher efficiency and accuracy than the best model alone. A combination of models is called an ensemble, and this method is called ensemble learning.
Out of 12 algorithms used, 11 were from an ensemble family, and 1 was logistic regression. Logistic regression is a fundamental and well-known classifier used to compare the predictability of ensemble learnings. The logistic regression uses the sigmoid function, which generates a probabilistic value ranging from zero to one. The ensemble learnings are based on combining numerous decision trees. They are listed in Table 1 and their library locations in Table 2. Thereafter, a brief description of each ensemble algorithm is depicted.

Table 1.
List of ensemble classifiers.

Table 2.
List of classifiers with their library.
I. Random Forest classifier: The Random Forest classifier () comprises numerous decision tree classifiers, each trained on a different random subset of the training set. After obtaining the predicted classes of all the individual decision trees, the predicted classes are combined using majority voting, and the class with the highest vote becomes the prediction of the estimator. Such a group of decision trees is called a Random Forest. Generally, a decision tree has low bias and high variance, and using a Random Forest, the model has low bias and low variance, which a machine learning model should also have.
II. Extremely randomised (Extra Trees) classifier: When a tree grows in a Random Forest, only a random subset of features in each node is considered a subdivision. Extra Trees () are likely to make trees more random using random thresholds for individual features instead of looking for the most likely thresholds, as do standard decision trees. The forest of overgrown randomised trees is called extremely randomised trees. This technique results in a higher bias for a lower variance. As discovering the most likely threshold for an individual feature across all nodes is the time-consuming task of growing a tree, a standard Random Forest is slower to train than extremely randomised trees. Less training time makes extremely randomised trees more efficient than a Random Forest.
III. Voting classifier: A voting classifier () trains on a set of models and predicts the class with the highest probability among all available classes. The predictions from the classifiers passed into the voting classifier are simply combined, and the predictions are made based on the most frequent voting patterns. The base estimators used in this study are logistic regression, a stochastic gradient descent classifier and a decision tree classifier.
The concept behind this technique requires combining numerous classifiers and generating the class labels. It uses weighted average predicted probabilities for soft voting and a majority vote for hard voting. Such a technique balances out the weakness of individual classifiers and behaves like a well-performing model. In soft voting, the predicted output class is the weighted average of the predicted probability assigned to that class. In hard voting, the predicted output class is the class with the most frequent votes. In other words, it is the highest predicted probability by each classifier.
IV. Stacking classifier: A stacking classifier () consists of two-layer estimators. The first layer contains multiple well-performing models used to predict the outputs on the same datasets. The second layer contains a meta-classifier, which takes all the models’ predictions from the first layer as an input and produces final predictions. In other words, it first combines or stacks the output of baseline estimators, then uses a final classifier to generate the final prediction. The base estimators are logistic regression, a linear support vector and a Random Forest classifier, and the meta-classifier is the Random Forest classifier used in this study.
V. Bagging classifier: This new version includes several works (; ; ). A bagging classifier is an ensemble meta-classifier in which the same baseline estimators are trained on different random subsets of the training set. There are two types of bagging techniques: pasting and bagging. In pasting, sampling is performed without replacement. In bagging, also called bootstrap aggregating, sampling is performed by replacement. After training all classifiers, the model predicts a new instance by aggregating the predictions of all classifiers. As in the case of the hard voting classifier, the aggregation function predicts the most frequent predictions. If trained on the original training set, each classifier would result in higher bias; however, aggregation reduces bias and variance. In this study, the decision tree classifier is used as the base estimator.
VI. Boosting classifier: Boosting refers to the technique that combines numerous weak or base learners by training them sequentially into a strong learner to enhance the classifier’s accuracy. In fact, each learner tries to correct its predecessor, and each added tree model sequentially tries to correct the prediction errors made by the preceding tree estimators. This process has three steps:
Step 1: The base learner reads the data and puts equal weight on each sample observation.
Step 2: Incorrect predictions with a higher weightage are assigned to the next base learner. This results in assigning higher weightage to the misclassified samples.
Step 3: Step 2 is repeated until the model can correctly classify the labels.
Among available boosting methods, AdaBoost and gradient boosting are the most popular.
A. AdaBoost classifier: To correct the predecessor, the classifier (, ; ) pays close attention to the training sample in which the predecessor is under-fitted, resulting in new models that focus more on the hard cases. In this study, the decision tree classifier is used as the base estimator.
B. Stochastic gradient boosting (Stochastic GBoosting) classifier: This classifier () tries to correct the predecessor by adding classifiers sequentially to an ensemble. However, it attempts to fit the new classifier to the residual errors made by the preceding classifier rather than tweaking the instance weights at every iteration by AdaBoost. When it is trained with a subsample hyperparameter value of 0.1, each tree is trained on 10% of the training samples, selected randomly. This considerably speeds up training. As a result, this technique trades a higher bias for lower variance.
VII. Other advance boosting classifiers:
A. Hist GBoosting classifier: Inspired by LightGBM, researchers () developed boosting classifiers based on a histogram, which buckets continuous feature values into discrete bins. This technique reduces memory usage and speeds up the training process. Generally, training gradient boosting is slow when the algorithms are dealing with a large number of samples, for example, when the sample size exceeds 10,000. Training the trees added to the ensemble can be surprisingly accelerated by discretising the continuous input features to several hundred unique features. Additionally, it tailors the training algorithm around input variables. Gradient boosting under such a modification is called a histogram-based gradient-boosting ensemble. Furthermore, it has inherent support for missing values. Some important advantages are the reduced cost of computing the gain for each split, decreased memory use, histogram subtraction for boosting execution and the reduced cost of communication for distributed learning.
B. XGBoost classifier: XGBoost () is the most popular and superior ensemble learning algorithm based on gradient-boosted decision trees designed for better execution and model efficiency. It is the preferred algorithm over any other tree-based algorithm.
C. LightGBM classifier: LightGBM (), a histogram-based algorithm, was developed to handle large sample sizes and higher feature dimensions.
D. CatBoost classifier: CatBoost (), an ensemble learning algorithm, is implemented using gradient boosting on decision trees. It was created by a team of researchers and engineers at Yandex, a technology company in Russia. It delivers a gradient-boosting structure that tries to solve categorical feature variables using a permutation-driven alternative to the typical algorithm. While it has good handling techniques for categorical data, it also works well with numerical, categorical and text features.
3.2. Feature Computation Techniques
This section describes the formulas utilised for deriving feature variables from the cleaned raw data.
I. Returns: Log return is computed as the difference in the natural log of consecutive days. Therefore, the current day log return is given by:
where the subscript i indicates current day, i − 1 indicates previous day and x is the entity to which log return is to be calculated.
II. Exponentially weighted moving average (EWMA): The EWMA computes the average by assigning weight w to the most recent observation and assigning weight wα to the next most recent observation. After that, the weights continue decreasing, as α is the decay factor that lies between zero and one. Since the sum of weights is equal to one, it is depicted in Equation (2) as the N moving period.
By applying the summation of geometric progression, Equation (2) becomes:
On rearranging Equation (3), the most recent weight, w, can be computed as:
Finally, for the given observations, the EWMA can be computed as the sum of the observations and their weights. It is defined by the following equation:
where x is the observation to which the EWMA is computed. Since α lies between zero and one, it gives more attention to the recent observations than the older ones. The value of α is taken as 0.5 in this study.
III. Exponentially weighted moving volatility (EWMV): Like Equation (5), the EWMV computes volatility by giving more importance to the recent observations. The equation is:
where x is the return to the entity from which the EWMV is computed. The assumption is that the expected return over the moving period is zero.
IV. Average true range (ATR): The ATR is the indicator of volatility and is computed as follows:
V. Drift-independent volatility (DIV): () used open, close, low and high stock prices to compute the minimum-variance unbiased variance estimator, which is independent of both the drift and the opening jumps of the underlying price movement. It is given by Equation (8) as follows:
where, V0 is defined as:
Vc is defined as:
VRS is given by () and ():
The mean of the open and closing price is defined as:
where c is lnC1 − lnO1, u is lnH1 − lnO1, o is lnO1 − lnC0 and d is lnL1 − lnO1.
The constant k is chosen to minimise the variance of the estimator V:
where α is set to 1.34, in practice, as suggested by (), who explain that α < 1.5 for all drift, and α = 0 when drift is zero. However, the authors further narrowed down the minimum value of α to 1.33.
C0 is the closing price of the previous day, O1 is the opening price of the current day, H1 is the current day’s high price during the trading interval, L1 is the current day’s low price during the trading interval, C1 is the closing price of the current period and ln is the natural log.
3.3. Data Transformation
Data transformation plays an important role in machine learning modelling and is an important step in pre-processing (; ). Before feeding data into the model, the data must be transformed to make them homogenous on the scale. The data are scaled using MinMaxScaler, which transforms the data within two defined boundary values: lower bound (LB) and upper bound (UB). LB and UB are chosen so that the model works optimally. The values of LB and UB are decided during the tuning process of the hyperparameters. The equation is as follows:
where is the scaled value, and is computed as:
3.4. Performance Evaluation
The performance of the classification models is measured by a confusion matrix and a classification report, specifically, a precision score, a recall score, an f1-score, an accuracy score, an ROC curve and a precision–recall curve (; ). These are standard measures of a classifier’s performance. Table 3 displays the nomenclature of the confusion matrix.

Table 3.
Confusion matrix.
In a confusion matrix, each column depicts a predicted class, and each row depicts an actual class. The first row indicates the negative class (depicted as 0). True negatives (TNs) were correctly classified as a negative class, while the remaining false positives (FPs) were wrongly classified as a positive class. The second row considers the positive class (depicted as 1). False negatives (FNs) were wrongly classified as a negative class, while the remaining true positives (TPs) were correctly classified as a positive class. A flawless classifier would only have classifications of TP and TN.
From the above confusion matrix, the performance evaluation parameters (; ) can be computed to assess the predictability of the classifiers. The accuracy score measures the overall accuracy and is the ratio of the accurately forecasted labels to the total labels. The precision score is the ratio of the number of TPs to the total number of TPs and FPs, while the recall score is the ratio of TPs to the total number of TPs and FNs. The f1-score is the harmonic mean of precision and recall. The ROC curve is the plot of the TP rate against the FP rate at various classification thresholds. The thresholds lie between zero and one. The area under the ROC curve (AUC) is an important measure and indicates the predictive power of the binary classifiers. An AUC of 50% indicates that the model’s output is random, and an AUC of less than 50% indicates that the model is ineffective. The precision–recall curve indicates a trade-off between precision and recall. A higher area under the precision–recall curve signifies a higher value for both precision and recall.
Furthermore, classifiers are ranked according to their predictability. () first computed hundreds of statistical parameters, and then based on a few important statistical values, they generated a class score and an overall score; subsequently, the classifiers were ranked. If the assigned rank was the same for multiple classifiers, they were statistically considered to be performing the same, which helped distinguish the respective performance of the classifiers.
4. Modelling Procedure
4.1. Data Collection
This study aimed to examine the various ensemble machine learning algorithms for predicting day-to-day upward and downward movements of the India VIX. To this end, the India VIX’s daily data are considered in this study. The period of study was from April 2009 to March 2021. The daily data of the India VIX Index and the NIFTY 50 Index for the given period were downloaded directly from the NSE of India portal, and the daily data of the CBOE VIX, S&P 500 and DJIA Indices were downloaded from Yahoo Finance using the yfinance module in Python. Subsequently, the data were pre-processed, and the feature variables were prepared.
4.2. Data Pre-Processing
There are minimal steps involved in data pre-processing. After downloading the data, they were checked for missing or null values. Several missing values for open, high and low for the India VIX were filled from the close value of the same day. There have been occasions when the US stock market was closed and the Indian stock market was open. In such situations, the missing values from the CBOE VIX, S&P 500 and DJIA Indices were filled using their most recent values. In other words, they were forward-filled.
4.3. Preparation of Feature Variables
Feature variables were prepared according to the feature computation techniques listed in Section 3.2, and a list of important feature variables is depicted in Table 4. The feature variables listed in Table 4 are also emphasised by the researchers. Values of open, high, low and closed, along with the EWMA of the India VIX, are considered feature variables. Because the India VIX is the option-implied volatility of tradable options on the NIFTY 50 Index, various volatilities of the NIFTY 50 Index were included in the feature variables. As few studies (; ; ) indicated an inverse relationship between the volatility index and the underlying index, log return on the NIFTY 50 Index is also included in the feature variables. Log return on the volume of the NIFTY 50 Index is also part of the feature variables, as emphasised by (). Lastly, as the study of () revealed that the US market affects the global market, log return on the S&P 500, log return on the DJIA and the first difference in the closing value of the CBOE VIX Index were also included in the list of feature variables. The models in the research paper generated the results after the closing of the US stock market, as US stock indices are included in the feature variables.

Table 4.
List of feature variables.
4.4. Feature Scaling
Since training machine learning algorithms requires scaling feature variables (; ), feature variables were scaled using MinMaxScaler, with the LB as +1 and the UB as +100, which gives better results for advanced ensemble learning algorithms. Therefore, the features are scaled between +1 and 100 using the MinMaxScaler method as explained in Section 3.3.
4.5. Target Variable
The target variable is one when tomorrow’s close values of the India VIX are higher than today’s and zero otherwise. The reflection period is assumed to be two days, as some important feature variables are already computed with longer rolling periods. Hence, the last two days of the computed features were considered to predict the present-day level of the India VIX. The definition of the target variable can be mathematically shown as follows:
The model can be shown as follows:
where y is the label that takes the value of either 0 or 1, X is the feature variable and subscript t denotes the time.
4.6. Execution of the Model
It is believed that advanced machine learning algorithms, such as ensemble learning, boost the accuracy of weak learners and are more suitable for financial time-series data (; ; ; ). Ensemble algorithms—Random Forest, Extra Trees, bagging, adaptive boosting, stacking, voting, gradient boosting, Hist GBoosting, XGBoost, LightGBM and CatBoost classifiers—and logistic regression were trained and tested on Windows 10 with a configuration of 10-core CPU, 32 GB RAM and 16 GB GPU. Data were divided into 90% and 10% for training and testing, respectively. The training sample was taken as 90% because machine learning algorithms require a large amount of data for training. The models were hyper-tuned using two-fold time-series cross-validation with a hyper-tuning algorithm called grid search cross-validation. Splitting is considered two-fold because more splitting of the training sample with the given sample size will result in the underfitting of the models. Two-fold time-series cross-validation similarly splits the training further into two subsamples of sub-training and validation, as stated in Figure 1. Next, the models were trained and validated for various combinations of parameters. During the hyper-tuning and validation process, the hyperparameters were selected so that the model achieves the highest average of the G-mean of f1-scores over the two given validation samples. The G-mean of f1-scores represents the geometric mean of f1-scores of both labels. The G-mean is an important measure, as it is highly sensitive to the individual element. If the value of any number decreases in the group of numbers, their G-mean drastically decreases. Similarly, if the f1-score of a label is too low or too high for another label, its G-mean will be lower.

Figure 1.
Two-fold time series cross-validation.
Since it was discovered that predictions were more prone to downward movements and that the count of ‘label 0’ was a little higher than the count of ‘label 1’ while hyper-tuning, there are class weights greater than one and class weights less than one respectively applied to upward and downward labels to balance out the accuracy of individual labels, which are depicted in Table 5. Class weights were converted into sample weights, which were applied during model training. Class weights were initially computed from the count of labels in the training sample, and subsequently, the one that gave the optimal result during validation was selected. Last, the optimal hyperparameters were selected while maximising the G-mean of the f1-scores, which further focused on producing balanced overall scores for both labels. Applying class weight and deciding based on the G-mean of the f1-score gave a balanced and robust performance. In practical settings, even in the case of binary classifiers, a balanced score results in better and more robust predictability. The validation results are shown in Table 6.

Table 5.
Class weights.

Table 6.
Two-fold time-series cross-validation (G-mean f1-score).
4.7. Optimal Models
As explained in the previous section, the models were trained and validated using two-fold time-series cross-validation, and the hyperparameters were captured for the optimal performance of the models. These are depicted in Table A1 in Appendix A. Class weights are displayed in Table 5. Lastly, optimal models were asked to predict unseen testing data. The results are displayed and explained in Section 5.
5. Findings
To evaluate the performance of the ensemble algorithms in forecasting the day-to-day movements of the India VIX Index, models were executed according to the procedures explained in the previous section. Table A1 in Appendix A depicts the lists of hyperparameters defining the models captured during the training and validation process. Since the average of the G-mean of the f1-scores is maximised during the validation, the validation scores are depicted in Table 6. Split0 and Split1 scores are the G-mean of the f1-scores from the first and second validation segments, respectively. The mean score is the mean of the Split0 and Split1 scores, which is the mean score maximised during validation. Similarly, Std score is the standard deviation of the Split0 and Split1 scores.
Table 7 shows the trained classifiers used to predict the unseen data, which included the testing dataset and various captured outputs. Table 8 displays ranked classifiers according to their performance. Table A2 in Appendix A depicts classification reports. The AUC plot, the area under the precision–recall curve plot and the confusion matrix are displayed in Figure A1, Figure A2 and Figure A3, respectively.

Table 7.
Summary result.

Table 8.
Ranking of the classifiers.
Out of the 300 trading days in the testing period, the India VIX decreased for 168 days and increased for 132 days. TN indicates the correctly predicted number of ‘Label 0’, and TP indicates the correctly predicted number of ‘Label 1’. ‘Label 0’ and ‘Label 1’ indicate downward and upward movements of the India VIX Index, respectively. It is evident from Table 7 that TP is comparatively less than TN, indicating that predicting upward movement is slightly difficult. To overcome this problem, a higher weight is assigned to ‘Label 1’.
Logistic regression correctly predicted 114 of Label 0 and 77 of Label 1, and achieved an accuracy score of 63.67%, an AUC of 69.04% and a precision–recall AUC of 63.44%, while maximising the G-mean of the f1-score, which attained 62.94%.
The Random Forest classifier correctly predicted 118 of Label 0 and 82 of Label 1, and achieved an accuracy score of 66.67%, an AUC of 67.77% and a precision–recall AUC of 66.38%, while maximising the G-mean of the f1-score, which attained 66.06%.
The Extra Trees classifier correctly predicted 112 of Label 0 and 80 of Label 1, and achieved an accuracy score of 64.00%, an AUC of 68.57% and a precision–recall AUC of 64.90%, while maximising the G-mean of the f1-score, which attained 63.47%.
The bagging classifier correctly predicted 118 of Label 0 and 81 of Label 1, and achieved an accuracy score of 66.33%, an AUC of 68.11% and a precision–recall AUC of 64.65%, while maximising the G-mean of the f1-score, which attained 65.68%.
The AdaBoost classifier correctly predicted 113 of Label 0 and 81 of Label 1, and achieved an accuracy score of 64.67%, an AUC of 67.98% and a precision–recall AUC of 62.87%, while maximising the G-mean of the f1-score, which attained 64.15%.
The stacking classifier correctly predicted 124 of Label 0 and 79 of Label 1, and achieved an accuracy score of 67.67%, an AUC of 69.48% and a precision–recall AUC of 65.48%, while maximising the G-mean of the f1-score, which attained 66.74%.
The voting classifier correctly predicted 118 of Label 0 and 80 of Label 1, and achieved an accuracy score of 66.00%, an AUC of 68.32% and a precision–recall AUC of 64.54%, while maximising the G-mean of the f1-score, which attained 65.30%.
The stochastic GBoosting classifier correctly predicted 115 of Label 0 and 75 of Label, 1 and achieved an accuracy score of 63.33%, an AUC of 68.72% and a precision–recall AUC of 65.32%, while maximising the G-mean of the f1-score, which attained 62.47%.
The Hist GBoosting classifier correctly predicted 122 of Label 0 and 75 of Label 1, and achieved an accuracy score of 65.67%, an AUC of 66.93% and a precision–recall AUC of 63.73%, while maximising the G-mean of the f1-score, which attained 64.57%.
The XGBoost classifier correctly predicted 118 of Label 0 and 81 of Label 1, and achieved an accuracy score of 66.33%, an AUC of 67.42% and a precision–recall AUC of 63.89%, while maximising the G-mean of the f1-score, which attained 65.68%.
The LightGBM classifier correctly predicted 118 of Label 0 and 81 of Label 1, and achieved an accuracy score of 66.33%, an AUC of 67.30% and a precision–recall AUC of 63.25%, while maximising the G-mean of the f1-score, which attained 65.68%.
The CatBoost classifier correctly predicted 120 of Label 0 and 80 of Label 1, and achieved an accuracy score of 66.67%, an AUC of 68.38% and a precision–recall AUC of 64.07%, while maximising the G-mean of the f1-score, which attained 65.91%.
It is evident from the above discussion that the models studied here performed well and that their accuracy scores are similar with minor variation. Their accuracy scores range from 63.33% to 67.67%. The stacking classifier achieved the highest accuracy score of 67.67% and an AUC of 69.48%. Its G-mean f1-score of 66.74% is also the highest. Though logistic regression and stochastic GBoosting achieved the lowest accuracy scores, logistic regression achieved the highest precision–recall AUC.
Furthermore, though classifiers have similar accuracies with minor variations, Table 8, which displays the classifier ranking based on the class score and overall score computed from several statistical parameters, distinguishes their performances. The CatBoost, LightGBM, XGBoost, voting, stacking, bagging and Random Forest classifiers are the top performers with assigned equal ranks, which signifies that though their respective performances seem to have few variations, their predictive power is significantly similar. When it is necessary to select the best classifiers among them, CatBoost, LightGBM and XGBoost can be recommended. However, the stacking classifier had the highest accuracy score because those three advanced boosting techniques are based on boosted trees and internally optimised algorithms. The Random Forest can also be recommended, as it is a tree-based bagging-optimised algorithm. Stacking is an ensemble of logistic regression, a linear support vector classifier (SVC) and Random Forest in this study, which makes models complicated and unorganised compared to advanced boosting algorithms.
The accuracy and findings of this research are much better and more comprehensive than those of previous studies (; ; ). In this regard, previous studies achieved a maximum accuracy score of 62.2%, while this research achieved an accuracy score of 67.67%. Additionally, this study comprehensively analyses various machine learning classifiers to recommend suitable algorithms. The predicted up and down counts of the previous studies are unbalanced, and the accuracy score could decrease by balancing. These findings are vital for investors and traders interested in anticipating risk in the Indian stock market: the NSE of India and the Bombay Stock Exchange.
6. Conclusions
This study aimed to investigate ensemble machine learning algorithms to predict the day-to-day movement of the India VIX, as the India VIX, believed to be a fear gauge, plays an important role in determining the risk of Indian stock markets. The India VIX is an important indicator of the market’s perception of risk, and its movements are a crucial gauge of how market perception shifts day to day.
In this research, the performance of several ensemble machine learning algorithms for predicting the day-to-day movements of the India VIX Index for the Indian stock market was studied since ensemble machine learning is known to perform better with financial time series. Eleven ensemble learning classifiers and a standard classifier called logistic regression were studied to achieve the stated task. In this regard, it was found that the models studied here performed well, with their overall accuracy scores being similar, with minor variations ranging from 63.33% to 67.67%. The performances of gradient boosting and logistic regression were the lowest, while the stacking classifier had the best performance. The trained models achieved better accuracy than previous studies.
Considering the classifiers’ performances outlined in Table 7 and their ranking from Table 8, CatBoost, LightGBM, XGBoost, voting, stacking, bagging and Random Forest classifiers are the best models, with significantly similar performances. Among them, CatBoost, LightGBM, XGBoost and Random Forest classifiers can be recommended for forecasting the day-to-day binary movements of the India VIX Index because of their inherently optimised structures. Therefore, it can be concluded that the day-to-day movement of the India VIX can be predicted with reasonably good accuracy using ensemble machine learning, even though stock market behaviour is inherently random.
7. Practical Implications
Whether moving upwards or downwards, the VIX is a crucial index for intra-day or short-term trades because the trading strategy could be based on expected volatility. The findings of this paper are useful to the following stakeholders and in the following circumstances:
- Traders: When volatility is expected to increase sharply, intra-day trades run the risk of stop-losses, quickly becoming triggered. To mitigate such risk, traders can either reduce their leverage or widen their stop-losses accordingly.
- Hedgers: For derivative contracts, such as a future contract where mart-to-market (MTM) is executed daily, institutional investors and proprietary desks face the risk of MTM being executed and, thereby, generating losses. To manage such risks, they can increase their hedge when volatility is expected to be higher and vice-versa.
- Volatility traders: They can take advantage of high validity by taking the long position on straddles and low validity by taking the short position on straddles. Implied volatility also anticipates options prices. When the volatility is expected to rise, the options price becomes more valuable, and when the volatility is expected to subside, the options price becomes less valuable. More precisely, the expected move in the implied volatility is used in conjunction with the outlook on the trend of the underlying index for volatility trading and hedging, as depicted in Table 9.
 Table 9. Options strategy for hedging and trading.
Table 9. Options strategy for hedging and trading. - Derivative trading: when the implied volatility index (the India VIX) is about to increase, buying calls on the India VIX is a better hedge than buying puts on the underlying stock index (the NIFTY 50 Index) because the implied volatility index is more sensitive. Hence, if the India VIX level is anticipated to be higher, buying calls on the India VIX and selling calls on the NIFTY 50 Index are recommended.
- Portfolio managers: The VIX also helps in selecting stocks to rebalance a portfolio. Portfolio managers can increase exposure to high-beta stocks when volatility is about to bounce from its peak level. Similarly, portfolio managers can increase exposure to low-beta stocks when volatility is about to bounce from its bottom level.
8. Academic Contributions
There is a shift in the research interest because, previously, traditional regression techniques were used for forecasting the numerical values of financial securities. However, this study has extensively researched forecasting the levels of financial securities using classification techniques. This research further develops the idea of day-to-day forecasting of binary movements in the India VIX and achieves accuracy at desirable levels. It initiates the research to anticipate the levels of the volatility index, which researchers can further extend to more complicated forecasting.
9. Limitations and Future Scope
This study is limited to the India VIX and forecasts the direction of binary day-to-day movements by only incorporating price variables. These techniques can be extended to other implied volatility indices. Other features, such as bond yields, commodity indices, repo rates, various interest rates and central bank announcements, could also be included. Including the economic policy uncertainty index as a feature variable could also be a great idea. Additionally, one could forecast the trinary movements in the India VIX and other volatility indices. It would be even better if the spikes in the India VIX could be predicted by developing imbalanced multiclass classification models, as spikes in the volatility index negatively impact the stock market. Ensemble learning algorithms could be trained with an empirical wavelet transform to improve forecasting accuracy. In the future, the India VIX could be predicted using an attention-based architecture called Transformer Neural Networks ().
Author Contributions
Data curation, conceptualisation, formal analysis, investigation, methodology, software, writing—original draft, validation, visualisation, writing—review and editing, A.P.; resources, investigation, writing—review and editing, validation, P.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The authors have declared that this research is based on publicly available data.
Acknowledgments
The authors have acknowledged that the Manuscript is reviewed by the anonymous reviewers and that reviewers’ contributions and suggestions have helped in improving the Manuscript.
Conflicts of Interest
The authors have declared that there are no conflicts of interest for this article.
Appendix A

Table A1.
Models’ hyperparameters.
Table A1.
Models’ hyperparameters.
| Logistic regression: penalty=‘elasticnet’, l1_ratio=0.3, solver=‘saga’, C=0.1, max_iter=20, tol=1e-08 |
| Random Forest: n_estimators=180, criterion=‘entropy’, max_depth=5, min_samples_split=2, min_samples_leaf=5, min_weight_fraction_leaf=0.01, max_features=29, min_impurity_decrease=0.01, max_leaf_nodes=7, max_samples=0.85, bootstrap=True, oob_score=True |
| Extra Trees: n_estimators=100, criterion=‘entropy’, max_depth=7, min_samples_split=17, min_samples_leaf=5, min_weight_fraction_leaf=0.001, max_leaf_nodes=19, max_features=29, min_impurity_decrease=0.001, bootstrap=True, oob_score=True |
Bagging: n_estimators=310, max_samples=0.85, max_features=32, bootstrap=True, bootstrap_features=False
|
AdaBoost: n_estimators=221, algorithm=‘SAMME’, learning_rate=0.01
|
Stacking: passthrough=True, estimators=[e1, e2], final_estimator=e3
|
Voting: voting=‘soft’, estimators=[e1, e2]
|
| Stochastic GBoosting: n_estimators=111, loss=‘deviance, learning_rate=0.5, subsample=0.45, criterion=‘friedman_mse, max_depth=2, min_samples_split=2, min_samples_leaf=2, min_weight_fraction_leaf=0.4, min_impurity_decrease=0.4, max_features=32, max_leaf_nodes=2, |
| Hist GBoosting: max_iter=300, loss=‘binary_crossentropy’, max_depth=2, min_samples_leaf=46, max_leaf_nodes=2, learning_rate=0.012, l2_regularization=1e-15, max_bins=200, tol=1e-8 |
| XGBoost: n_estimators=90, max_depth=4, learning_rate=0.01, objective=‘binary:logistic’, eval_metric=‘error’, booster=‘gbtree’, tree_method=‘approx’, gamma=13.6, reg_alpha=1.0, reg_lambda=1e-14, min_child_weight=7.7, subsample=0.55, colsample_bytree=0.9, importance_type=‘gain’, |
| LightGBM: n_estimators=625, objective=‘binary’, max_depth=2, num_leaves=3, learning_rate=0.001, subsample=0.05, colsample_bytree=0.95, boosting_type=‘gbdt’, reg_alpha=1.0, reg_lambda=10.0, min_child_weight=1e-08, min_child_samples=80, |
| CatBoost: n_estimators=3000, max_depth=4, learning_rate=0.001, min_child_samples=4, reg_lambda=30, bootstrap_type=‘Bayesian’, bagging_temperature=0, rsm=0.8, leaf_estimation_method=‘Gradient’, boosting_type=‘Plain’, langevin=True, score_function=‘L2’ |

Table A2.
Classification report.
Table A2.
Classification report.
| Logistic Regression | Random Forest | Extra Trees | ||||||||
| Precision | Recall | f1-Score | Precision | Recall | f1-Score | Precision | Recall | f1-Score | Support | |
| 0 | 0.67 | 0.68 | 0.68 | 0.70 | 0.70 | 0.70 | 0.68 | 0.67 | 0.67 | 168 |
| 1 | 0.59 | 0.58 | 0.59 | 0.62 | 0.62 | 0.62 | 0.59 | 0.61 | 0.60 | 132 |
| macro avg | 0.63 | 0.63 | 0.63 | 0.66 | 0.66 | 0.66 | 0.64 | 0.64 | 0.64 | 300 |
| weighted avg | 0.64 | 0.64 | 0.64 | 0.67 | 0.67 | 0.67 | 0.64 | 0.64 | 0.64 | 300 |
| Bagging | AdaBoost | Stacking | ||||||||
| Precision | Recall | f1-Score | Precision | Recall | f1-Score | Precision | Recall | f1-Score | Support | |
| 0 | 0.70 | 0.70 | 0.70 | 0.69 | 0.67 | 0.68 | 0.70 | 0.74 | 0.72 | 168 |
| 1 | 0.62 | 0.61 | 0.62 | 0.60 | 0.61 | 0.60 | 0.64 | 0.60 | 0.62 | 132 |
| macro avg | 0.66 | 0.66 | 0.66 | 0.64 | 0.64 | 0.64 | 0.67 | 0.67 | 0.67 | 300 |
| weighted avg | 0.66 | 0.66 | 0.66 | 0.65 | 0.65 | 0.65 | 0.67 | 0.68 | 0.68 | 300 |
| Voting | Stochastic GBoosting | Hist GBoosting | ||||||||
| Precision | Recall | f1-Score | Precision | Recall | f1-Score | Precision | Recall | f1-Score | Support | |
| 0 | 0.69 | 0.70 | 0.70 | 0.67 | 0.68 | 0.68 | 0.68 | 0.73 | 0.70 | 168 |
| 1 | 0.62 | 0.61 | 0.61 | 0.59 | 0.57 | 0.58 | 0.62 | 0.57 | 0.59 | 132 |
| macro avg | 0.65 | 0.65 | 0.65 | 0.63 | 0.63 | 0.63 | 0.65 | 0.65 | 0.65 | 300 |
| weighted avg | 0.66 | 0.66 | 0.66 | 0.63 | 0.63 | 0.63 | 0.65 | 0.66 | 0.65 | 300 |
| XGBoost | LightGBM | CatBoost | ||||||||
| Precision | Recall | f1-Score | Precision | Recall | f1-Score | Precision | Recall | f1-Score | Support | |
| 0 | 0.70 | 0.70 | 0.70 | 0.70 | 0.70 | 0.70 | 0.70 | 0.71 | 0.71 | 168 |
| 1 | 0.62 | 0.61 | 0.62 | 0.62 | 0.61 | 0.62 | 0.62 | 0.61 | 0.62 | 132 |
| macro avg | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 300 |
| weighted avg | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.67 | 0.67 | 0.67 | 300 |
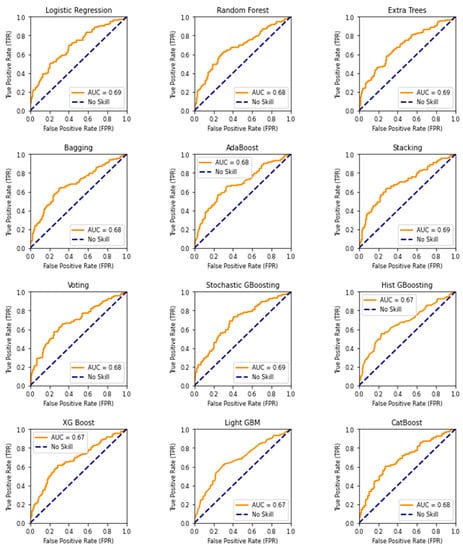
Figure A1.
ROC curve.
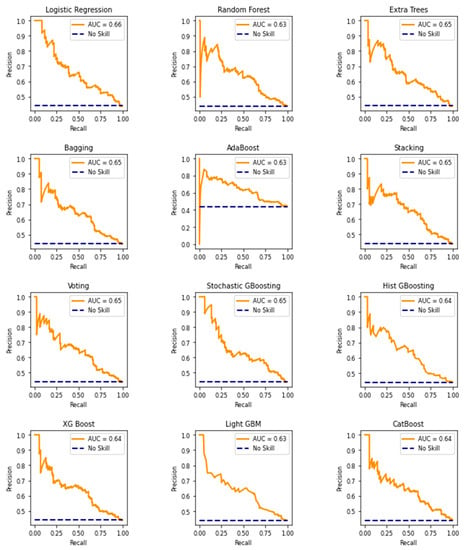
Figure A2.
Precision–recall curve.
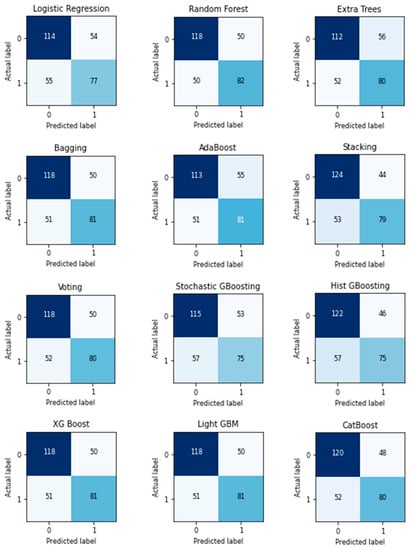
Figure A3.
Confusion matrix.
References
- Aliyeva, Aysel. 2022. Predicting Stock Prices Using Random Forest and Logistic Regression Algorithms. In 11th International Conference on Theory and Application of Soft Computing, Computing with Words and Perceptions and Artificial Intelligence—ICSCCW-2021. Edited by Rafik A. Aliev, Janusz Kacprzyk, Witold Pedrycz, Mo Jamshidi, Mustafa Babanli and Fahreddin M. Sadikoglu. Lecture Notes in Networks and Systems. Cham: Springer International Publishing, pp. 95–101. [Google Scholar] [CrossRef]
- Alvarez Vecino, Pol. 2019. A Machine Learning Approach to Stock Screening with Fundamental Analysis. Master’s thesis, Universitat Politècnica de Catalunya, de Catalunya, Spain. Available online: https://upcommons.upc.edu/handle/2117/133070 (accessed on 28 May 2022).
- Bai, Bing, Guiling Li, Senzhang Wang, Zongda Wu, and Wenhe Yan. 2021. Time Series Classification Based on Multi-Feature Dictionary Representation and Ensemble Learning. Expert Systems with Applications 169: 114162. [Google Scholar] [CrossRef]
- Bai, Yunfei, and Charlie Xiaowu Cai. 2022. Predicting VIX with Adaptive Machine Learning. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Ballestra, Luca Vincenzo, Andrea Guizzardi, and Fabio Palladini. 2019. Forecasting and Trading on the VIX Futures Market: A Neural Network Approach Based on Open to Close Returns and Coincident Indicators. International Journal of Forecasting 35: 1250–62. [Google Scholar] [CrossRef]
- Bantwa, Ashok. 2017. A Study on India Volatility Index (VIX) and Its Performance as Risk Management Tool in Indian Stock Market. SSRN Scholarly Paper. Rochester, NY, USA. Available online: https://papers.ssrn.com/abstract=3732839 (accessed on 28 May 2022).
- Batool, Maryam, Huma Ghulam, Muhammad Azmat Hayat, Muhammad Zahid Naeem, Abdullah Ejaz, Zulfiqar Ali Imran, Cristi Spulbar, Ramona Birau, and Tiberiu Horațiu Gorun. 2021. How COVID-19 Has Shaken the Sharing Economy? An Analysis Using Google Trends Data. Economic Research-Ekonomska Istraživanja 34: 2374–86. [Google Scholar] [CrossRef]
- Bouri, Elie, Anshul Jain, P. C. Biswal, and David Roubaud. 2017a. Cointegration and Nonlinear Causality amongst Gold, Oil, and the Indian Stock Market: Evidence from Implied Volatility Indices. Resources Policy 52: 201–6. [Google Scholar] [CrossRef]
- Bouri, Elie, David Roubaud, Rania Jammazi, and Ata Assaf. 2017b. Uncovering Frequency Domain Causality between Gold and the Stock Markets of China and India: Evidence from Implied Volatility Indices. Finance Research Letters 23: 23–30. [Google Scholar] [CrossRef]
- Breiman, Leo. 1996. Bagging Predictors. Machine Learning 24: 123–40. [Google Scholar] [CrossRef]
- Breiman, Leo. 2001. Random Forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef]
- Carr, Peter. 2017. Why Is VIX a Fear Gauge? Risk and Decision Analysis 6: 179–85. [Google Scholar] [CrossRef]
- Chakrabarti, Prasenjit, and K. Kiran Kumar. 2020. High-Frequency Return-Implied Volatility Relationship: Empirical Evidence from Nifty and India VIX. The Journal of Developing Areas 54. [Google Scholar] [CrossRef]
- Chandra, Abhijeet, and M. Thenmozhi. 2015. On Asymmetric Relationship of India Volatility Index (India VIX) with Stock Market Return and Risk Management. Decision 42: 33–55. [Google Scholar] [CrossRef]
- Chaudhuri, Tamal Datta, and Indranil Ghosh. 2016. Forecasting Volatility in Indian Stock Market Using Artificial Neural Network with Multiple Inputs and Outputs. arXiv arXiv:1604.05008. [Google Scholar] [CrossRef]
- Chen, Tianqi, and Carlos Guestrin. 2016. XGBoost: A Scalable Tree Boosting System. Paper presented at 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13–17; pp. 785–94. [Google Scholar] [CrossRef]
- Dai, Zhifeng, Huiting Zhou, Fenghua Wen, and Shaoyi He. 2020. Efficient Predictability of Stock Return Volatility: The Role of Stock Market Implied Volatility. The North American Journal of Economics and Finance 52: 101174. [Google Scholar] [CrossRef]
- Dixit, Gaurav, Dipayan Roy, and Nishant Uppal. 2013. Predicting India Volatility Index: An Application of Artificial Neural Network. International Journal of Computer Applications 70: 22–30. [Google Scholar] [CrossRef]
- Dorogush, Anna Veronika, Vasily Ershov, and Andrey Gulin. 2018. CatBoost: Gradient Boosting with Categorical Features Support. arXiv arXiv:1810.11363. [Google Scholar]
- Fernandes, Marcelo, Marcelo C. Medeiros, and Marcel Scharth. 2014. Modeling and Predicting the CBOE Market Volatility Index. Journal of Banking & Finance 40: 1–10. [Google Scholar] [CrossRef]
- Ferri, César, José Hernández-Orallo, and R. Modroiu. 2009. An Experimental Comparison of Performance Measures for Classification. Pattern Recognition Letters 30: 27–38. [Google Scholar] [CrossRef]
- Florian, Radu. 2002. Named Entity Recognition as a House of Cards: Classifier Stacking. Available online: https://apps.dtic.mil/sti/citations/ADA459582 (accessed on 28 May 2022).
- Freund, Yoav, and Robert E. Schapire. 1996. Experiments with a new boosting algorithm. icml 96: 148–156. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=d186abec952c4348870a73640bf849af9727f5a4 (accessed on 28 May 2022).
- Freund, Yoav, and Robert E. Schapire. 1997. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. Journal of Computer and System Sciences 55: 119–39. [Google Scholar] [CrossRef]
- Friedman, Jerome H. 2002. Stochastic Gradient Boosting. Computational Statistics & Data Analysis 38: 367–78. [Google Scholar] [CrossRef]
- Geurts, Pierre, Damien Ernst, and Louis Wehenkel. 2006. Extremely Randomized Trees. Machine Learning 63: 3–42. [Google Scholar] [CrossRef]
- Grima, Simon, Letife Özdemir, Ercan Özen, and Inna Romānova. 2021. The Interactions between COVID-19 Cases in the USA, the VIX Index and Major Stock Markets. International Journal of Financial Studies 9: 26. [Google Scholar] [CrossRef]
- Guryanov, Aleksei. 2019. Histogram-Based Algorithm for Building Gradient Boosting Ensembles of Piecewise Linear Decision Trees. In Analysis of Images, Social Networks and Texts. Edited by Wil M. P. van der Aalst, Vladimir Batagelj, Dmitry I. Ignatov, Michael Khachay, Valentina Kuskova, Andrey Kutuzov, Sergei O. Kuznetsov, Irina A. Lomazova, Natalia Loukachevitch, Amedeo Napoli and et al. Lecture Notes in Computer Science. Cham: Springer International Publishing, pp. 39–50. [Google Scholar] [CrossRef]
- Haghighi, Sepand, Masoomeh Jasemi, Shaahin Hessabi, and Alireza Zolanvari. 2018. PyCM: Multiclass Confusion Matrix Library in Python. Journal of Open Source Software 3: 729. [Google Scholar] [CrossRef]
- Han, Yechan, Jaeyun Kim, and David Enke. 2023. A Machine Learning Trading System for the Stock Market Based on N-Period Min-Max Labeling Using XGBoost. Expert Systems with Applications 211: 118581. [Google Scholar] [CrossRef]
- Hastie, Trevor, Saharon Rosset, Ji Zhu, and Hui Zou. 2009. Multi-Class AdaBoost. Statistics and Its Interface 2: 349–60. [Google Scholar] [CrossRef]
- Ho, Tin Kam. 1998. The Random Subspace Method for Constructing Decision Forests. IEEE Transactions on Pattern Analysis and Machine Intelligence 20: 832–44. [Google Scholar] [CrossRef]
- Hoang Vuong, Pham, Trinh Tan Dat, Tieu Khoi Mai, Pham Hoang Uyen, and Pham The Bao. 2022. Stock-Price Forecasting Based on XGBoost and LSTM. Computer Systems Science and Engineering 40: 237–46. [Google Scholar] [CrossRef]
- Ji, Qiang, Elie Bouri, and David Roubaud. 2018. Dynamic Network of Implied Volatility Transmission among US Equities, Strategic Commodities, and BRICS Equities. International Review of Financial Analysis 57: 1–12. [Google Scholar] [CrossRef]
- Kambeu, Edson. 2019. Trading Volume as a Predictor of Market Movement: An Application of Logistic Regression in the R Environment. International Journal of Finance & Banking Studies (2147-4486) 8: 57–69. [Google Scholar] [CrossRef]
- Ke, Guolin, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, and Tie-Yan Liu. 2017. Lightgbm: A Highly Efficient Gradient Boosting Decision Tree. Advances in Neural Information Processing Systems 30: 3149–57. [Google Scholar]
- Kumar, Parul, Sunil Kumar, and R. K. Sharma. 2022. An Impact of FPI Inflows, Nifty Returns, and S&P Returns on India VIX Volatility. World Review of Science, Technology and Sustainable Development 18: 289–308. [Google Scholar]
- Labiad, Badre, Abdelaziz Berrado, and Loubna Benabbou. 2016. Machine Learning Techniques for Short Term Stock Movements Classification for Moroccan Stock Exchange. Paper present at the 2016 11th International Conference on Intelligent Systems: Theories and Applications (SITA), Mohammedia, Morocco, October 19–20; pp. 1–6. [Google Scholar]
- Ledolter, Johannes, and Søren Bisgaard. 2011. Challenges in Constructing Time Series Models from Process Data. Quality and Reliability Engineering International 27: 165–78. [Google Scholar] [CrossRef]
- Livieris, Ioannis E., Theodore Kotsilieris, Stavros Stavroyiannis, and P. Pintelas. 2020. Forecasting Stock Price Index Movement Using a Constrained Deep Neural Network Training Algorithm. Intelligent Decision Technologies 14: 313–23. [Google Scholar] [CrossRef]
- Louppe, Gilles, and Pierre Geurts. 2012. Ensembles on Random Patches. In Machine Learning and Knowledge Discovery in Databases. Edited by Peter A. Flach, Tijl De Bie and Nello Cristianini. Lecture Notes in Computer Science. Berlin/Heidelberg: Springer, vol. 7523, pp. 346–61. [Google Scholar] [CrossRef]
- Mall, M., S. Mishra, P. K. Mishra, and B. B. Pradhan. 2011. A Study on Relation between India VIX and Nifty Returns. International Research Journal of Finance and Economics 69: 178–84. [Google Scholar]
- Molaei, Soheila Mehr, and Mohammad Reza Keyvanpour. 2015. An Analytical Review for Event Prediction System on Time Series. Paper present at the 2015 2nd International Conference on Pattern Recognition and Image Analysis (IPRIA), Rasht, Iran, March 11–12; pp. 1–6. [Google Scholar] [CrossRef]
- Naik, Nagaraj, and Biju R. Mohan. 2019. Stock Price Movements Classification Using Machine and Deep Learning Techniques-The Case Study of Indian Stock Market. In Engineering Applications of Neural Networks. Edited by John Macintyre, Lazaros Iliadis, Ilias Maglogiannis and Chrisina Jayne. Communications in Computer and Information Science. Cham: Springer International Publishing, pp. 445–52. [Google Scholar] [CrossRef]
- Onan, Mustafa, Aslihan Salih, and Burze Yasar. 2014. Impact of Macroeconomic Announcements on Implied Volatility Slope of SPX Options and VIX. Finance Research Letters 11: 454–62. [Google Scholar] [CrossRef]
- Patro, S. Gopal Krishna, and Kishore Kumar Sahu. 2015. Normalization: A Preprocessing Stage. arXiv arXiv:1503.06462. [Google Scholar] [CrossRef]
- Phillips, Peter C. B. 2005. Challenges of Trending Time Series Econometrics. Mathematics and Computers in Simulation 68: 401–16. [Google Scholar] [CrossRef]
- Prasad, Akhilesh, Priti Bakhshi, and Arumugam Seetharaman. 2022. The Impact of the U.S. Macroeconomic Variables on the CBOE VIX Index. Journal of Risk and Financial Management 15: 126. [Google Scholar] [CrossRef]
- Ramos-Pérez, Eduardo, Pablo J. Alonso-González, and José Javier Núñez-Velázquez. 2019. Forecasting Volatility with a Stacked Model Based on a Hybridized Artificial Neural Network. Expert Systems with Applications 129: 1–9. [Google Scholar] [CrossRef]
- Rogers, L. Christopher G., and Stephen E. Satchell. 1991. Estimating Variance From High, Low and Closing Prices. The Annals of Applied Probability 1: 504–12. [Google Scholar] [CrossRef]
- Rogers, L. Christopher G., Stephen E. Satchell, and Y. Yoon. 1994. Estimating the Volatility of Stock Prices: A Comparison of Methods That Use High and Low Prices. Applied Financial Economics 4: 241–47. [Google Scholar] [CrossRef]
- Ruta, Dymitr, and Bogdan Gabrys. 2005. Classifier Selection for Majority Voting. Information Fusion 6: 63–81. [Google Scholar] [CrossRef]
- Sadorsky, Perry. 2021. A Random Forests Approach to Predicting Clean Energy Stock Prices. Journal of Risk and Financial Management 14: 48. [Google Scholar] [CrossRef]
- Saranya, C., and G. Manikandan. 2013. A Study on Normalization Techniques for Privacy Preserving Data Mining. International Journal of Engineering and Technology (IJET) 5: 2701–4. [Google Scholar]
- Serur, Juan Andrés, José Pablo Dapena, and Julián Ricardo Siri. 2021. Decomposing the VIX Index into Greed and Fear. Serie Documentos de Trabajo-Nro 780. [Google Scholar] [CrossRef]
- Shaikh, Imlak, and Puja Padhi. 2016. On the Relationship between Implied Volatility Index and Equity Index Returns. Journal of Economic Studies 43: 27–47. [Google Scholar] [CrossRef]
- Sokolova, Marina, and Guy Lapalme. 2009. A Systematic Analysis of Performance Measures for Classification Tasks. Information Processing & Management 45: 427–37. [Google Scholar] [CrossRef]
- Tuna, Abdulkadir. 2022. The Effects of Volatilities in Oil Price, Gold Price and Vix Index on Turkish BIST 100 Stock Index in Pandemic Period. İstanbul İktisat Dergisi-Istanbul Journal of Economics 72: 39–54. [Google Scholar] [CrossRef]
- Ullal, Mithun S., Pushparaj M. Nayak, Ren Trevor Dais, Cristi Spulbar, and Ramona Birau. 2022. Nvestigating the Nexus between Artificial Intelligence and Machine Learning Technologies in the Case of Indian Services Industry. Business: Theory and Practice 23: 323–33. [Google Scholar] [CrossRef]
- Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention Is All You Need. In Advances in Neural Information Processing Systems. Long Beach: Curran Associates, vol. 30, pp. 5998–6008. Available online: https://proceedings.neurips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf (accessed on 28 May 2022).
- Wang, Yan, and Yuankai Guo. 2020. Forecasting Method of Stock Market Volatility in Time Series Data Based on Mixed Model of ARIMA and XGBoost. China Communications 17: 205–21. [Google Scholar] [CrossRef]
- Yang, Dennis, and Qiang Zhang. 2000. Drift-Independent Volatility Estimation Based on High, Low, Open, and Close Prices. The Journal of Business 73: 477–92. [Google Scholar] [CrossRef]
- Yang, Yan-Hong, and Ying-Hui Shao. 2020. Time-Dependent Lead-Lag Relationships between the VIX and VIX Futures Markets. The North American Journal of Economics and Finance 53: 101196. [Google Scholar] [CrossRef]
- Yun, Jaeho. 2020. A Re-Examination of the Predictability of Stock Returns and Cash Flows via the Decomposition of VIX. Economics Letters 186: 108755. [Google Scholar] [CrossRef]
- Zhang, Yanfang, Chuanhua Wei, and Xiaolin Liu. 2022. Group Logistic Regression Models with Lp,q Regularization. Mathematics 10: 2227. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).