Modeling and Simulating Cross Country Banking Contagion Risks
Abstract
:1. Introduction and Literature Review
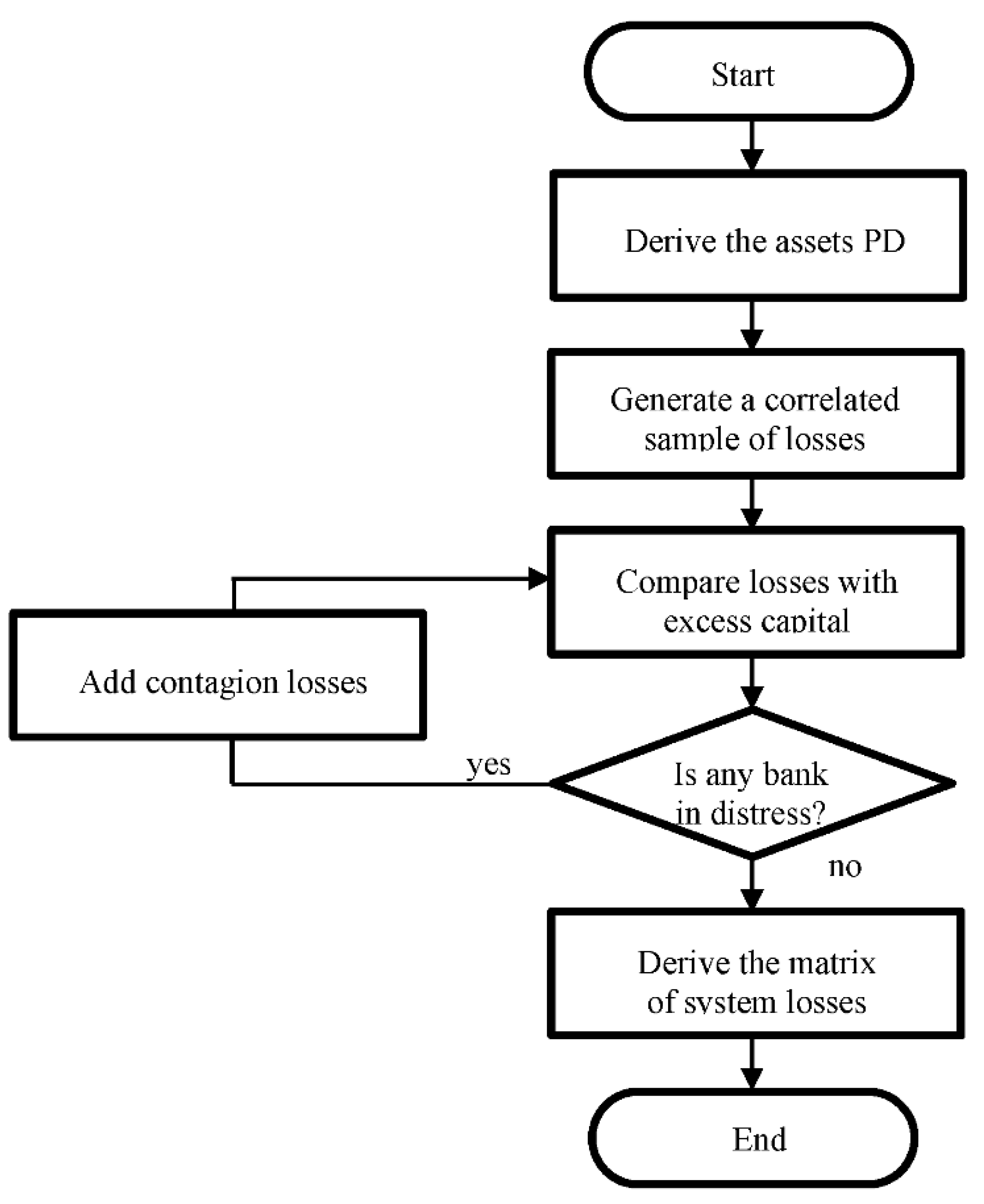
2. Methodology
3. Data and Results
4. Economic Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. The SYMBOL Model
| 1 | Source: ECB. |
| 2 | See the Appendix A for details. |
| 3 | The New York University Stern School Vlab SRISK documentation reports that “By default, the prudential capital requirement used in calculating such capital shortfalls is set to be 8% for firms in Africa, Asia and Americas and 5.5% for firms in Europe due to differences in accounting standards” (https://vlab.stern.nyu.edu/docs/srisk (accessed on 27 June 2021)). The scientific literature instead typically sets the minimum capital requirement to 8%, see, e.g., Brownlees and Engle (2017), Berger et al. (2019), and Chen et al. (2021) thus we kept this setting as reference for the estimations. |
| 4 | See the EBA 2020 EU-wide transparency exercise, in which for every bank in the sample is reported the exposure to each counterpart country, detailed by maturity classes. https://www.eba.europa.eu/risk-analysis-and-data/eu-wide-transparency-exercise (accessed on 27 June 2021). |
References
- Acemoglu, Daron, Asuman Ozdaglar, and Alireza Tahbaz-Salehi. 2015. Systemic risk and stability in financial networks. American Economic Review 105: 564–608. [Google Scholar] [CrossRef]
- Allen, Franklin, and Douglas Gale. 2000. Financial contagion. Journal of Political Economy 108: 1–33. [Google Scholar] [CrossRef]
- Andries, Alin Marius, and Nicu Sprincean. 2021. Cyclical behaviour of systemic risk in the banking sector. Applied Economics 53: 1463–97. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. 2005. An Explanatory Note on the Basel II IRB Risk Weight Functions. Available online: https://www.bis.org/bcbs/irbriskweight.pdf (accessed on 27 June 2021).
- Basel Committee on Banking Supervision. 2006. International Convergence of Capital Measurement and Capital Standards. Available online: https://www.bis.org/publ/bcbs128.pdf (accessed on 27 June 2021).
- Basel Committee on Banking Supervision. 2010. A Global Regulatory Framework for More Resilient Banks and Banking Systems. Available online: https://www.bis.org/publ/bcbs189_dec2010.pdf (accessed on 27 June 2021).
- Basel Committee on Banking Supervision 2013. Revised Basel III Leverage Ratio Framework and Disclosure Requirements. Available online: https://www.bis.org/publ/bcbs270.pdf (accessed on 27 June 2021).
- Battiston, Stefano, Domenico Delli Gatti, Mauro Gallegati, Bruce Greewald, and Joseph E. Stiglitz. 2012. Liaisons dangereuses: Increasing connectivity, risk sharing, and systemic risk. Journal of Economic Dynamics and Control 36: 1121–41. [Google Scholar] [CrossRef] [Green Version]
- Berger, Allen N., Raluca A. Roman, and John Sedunov. 2019. Did TARP reduce or increase systemic risk? The effects of government aid on financial system stability. Journal of Financial Intermediation 43: 100810. [Google Scholar] [CrossRef]
- Bikker, Jacob, and H aixia Hu. 2002. Cyclical Patterns in Profits, Provisioning and Lending of Banks. DNB Staff Reports, No. 86. Amsterdam: De Nederlandsche Bank. [Google Scholar]
- Brownlees, Christian, and Robert F. Engle. 2017. SRISK: A conditional capital shortfall measure of systemic risk. The Review of Financial Studies 30: 48–79. [Google Scholar] [CrossRef]
- Brusco, Sandro, and Fabio Castiglionesi. 2007. Liquidity coinsurance, moral hazard and financial contagion. Journal of Finance 62: 2275–302. [Google Scholar] [CrossRef]
- Chen, Lei, Hui Li, Frank Hong Liu, and Yue Zhou. 2021. Bank regulation and systemic risk: Cross country evidence. Review of Quantitative Finance and Accounting 57: 353–87. [Google Scholar] [CrossRef]
- De Lisa, Riccardo, Stefano Zedda, Francesco Vallascas, Francesca Campolongo, and Massimo Marchesi. 2011. Modelling Deposit Insurance Schemes’ losses in a Basel 2 framework. Journal of Financial Services Research 40: 123–41. [Google Scholar] [CrossRef]
- Demirgüç-Kunt, Asli, and Harry Huizinga. 2000. Financial Structure and Bank Profitability. Policy Research Working Paper Series 2430; Washington: The World Bank. [Google Scholar]
- Drehmann, Mathias, and Nikola Tarashev. 2013. Measuring the systemic importance of interconnected banks. Journal of Financial Intermediation 22: 586–607. [Google Scholar] [CrossRef] [Green Version]
- Elliott, Matthew, Benjamin Golub, and Matthew O. Jackson. 2014. Financial network and contagion. American Economic Review 104: 3115–53. [Google Scholar] [CrossRef] [Green Version]
- Elsinger, Helmut, Alfred Lehar, and Martin Summer. 2006. Using market information for banking system risk assessment. International Journal of Central Banking 2: 137–65. [Google Scholar] [CrossRef] [Green Version]
- European Commission. 2011a. Directorate-General for Economic and Financial Affairs, Public Finances in EMU 2011, European Economy 3. Available online: https://ec.europa.eu/economy_finance/publications/european_economy/2011/pdf/ee-2011-3_en.pdf (accessed on 27 June 2021).
- European Commission. 2011b. Directorate-General for Internal Market and Services: Commission Staff Working Document—Impact Assessment Accompanying the Proposal for a Directive of the European Parliament and of the Council Establishing a Framework for the Recovery and Resolution. Available online: https://www.eumonitor.eu/9353000/1/j9vvik7m1c3gyxp/vk9idfnk1qrb (accessed on 27 June 2021).
- European Commission. 2014. Directorate-General for Internal Market and Services, Commission Staff Working Document—Economic Review of the Financial Regulation Agenda. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX:52014SC0158&from=fr (accessed on 27 June 2021).
- Forbes, Kristin J., and Roberto Rigobon. 2002. No contagion, only interdependence: Measuring stock market comovements. The Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Frey, Rüdiger, and Juraj Hledik. 2014. Correlation and Contagion as Sources of Systemic Risk, SSRN. Available online: http://ssrn.com/abstract=2541733 (accessed on 27 June 2021).
- Furfine, Craig H. 2003. Interbank exposures: Quantifying the risk of contagion. Journal of Money, Credit and Banking 35: 111–28. [Google Scholar] [CrossRef]
- Galliani, Clara, and Stefano Zedda. 2015. Will the bail-in break the vicious circle between banks and their sovereign? Computational Economics 45: 597–614. [Google Scholar] [CrossRef]
- Giudici, Paolo, Peter Sarlin, and Alessandro Spelta. 2020. The interconnected nature of financial systems: Direct and common exposures. Journal of Banking and Finance 112: 105–49. [Google Scholar] [CrossRef]
- Gropp, Reint, Marco Lo Duca, and Jukka Vesala. 2009. Cross-border bank contagion in Europe. International Journal of Central Banking 5: 97–139. [Google Scholar]
- Hasman, Augusto, and Margarita Samartin. 2008. Information acquisition and financial contagion. Journal of Banking & Finance 32: 2136–47. [Google Scholar]
- Holopainen, Markus, and Peter Sarlin. 2017. Toward Robust Early-Warning Models: A Horse Race, Ensembles and Model Uncertainty. Quantitative Finance 17: 1–31. [Google Scholar] [CrossRef]
- Karimzadeh, Majid, S. M. Jawed Akhtar, and Behzad Karimzadeh. 2013. Determinants of profitability of banking sector in India. Transition Studies Review 20: 211–19. [Google Scholar] [CrossRef]
- Marchesi, Massimo, Marco Petracco Giudici, Jessica Cariboni, Stefano Zedda, and Francesca Campolongo. 2012. Macroeconomic Cost-Benefit Analysis of Basel III Minimum Capital Requirements and of Introducing Deposit Guarantee Schemes and Resolution Funds. Eur—Scientific and Technical Research Series; Luxembourg: European Commission Publication Office, ISBN 978–92-79-17781-1. [Google Scholar]
- Parrado-Martínez, Purificación, Pilar Gómez-Fernández-Aguado, and Antonio Partal-Ureña. 2019. Factors influencing the European bank’s probability of default: An application of SYMBOL methodology. Journal of International Financial Markets, Institutions and Money 61: 223–40. [Google Scholar] [CrossRef]
- Upper, Christian. 2011. Simulation methods to assess the danger of contagion in interbank markets. Journal of Financial Stability 7: 111–25. [Google Scholar] [CrossRef]
- Zedda, Stefano. 2015. Direct vs. side effects in financial contagion: What weights more? In Advances in Artificial Economics, Lecture Notes in Economics and Mathematical Systems. Edited by Frédéric Amblard, Francisco J. Miguel, Adrien Blanchet and Benoit Gaudou. Cham: Springer, vol. 676, pp. 131–38. [Google Scholar]
- Zedda, Stefano. 2017. Banking Systems Simulation: Theory, Practice, and Application of Modeling Shocks, Losses, and Contagion. Hoboken: John Wiley & Sons. [Google Scholar]
- Zedda, Stefano, and Giuseppina Cannas. 2020. Assessing banks’ systemic risk contribution and contagion determinants trough the leave-one-out approach. Journal of Banking and Finance 112: 105160. [Google Scholar] [CrossRef]
- Zedda, Stefano, and Simone Sbaraglia. 2020. Which interbank net is the safest? Risk Management 22: 65–82. [Google Scholar] [CrossRef]
- Zedda, Stefano, Jessica Cariboni, Massimo Marchesi, Marco Petracco Giudici, and Matteo Salto. 2012. The EU Sovereign Debt Crisis: Potential Effects on EU Banking Systems and Policy Options. Eur—Scientific and Technical Research Series; Luxembourg: European Commission Publication Office. [Google Scholar]
- Zhang, Xiaoming, Chunyan Wei, and Stefano Zedda. 2020. Analysis of China commercial banks’ systemic risk sustainability through the leave-one-out approach. Sustainability 12: 203. [Google Scholar] [CrossRef] [Green Version]
| Country | Assets PD % | Excess Capital US$ bn. | Total Assets US$ bn. | Correlation |
|---|---|---|---|---|
| Australia | 0.002125 | 87.4 | 2890.5 | 0.682 |
| Austria | 0.002055 | 49.5 | 840.4 | 0.500 |
| Belgium | 0.001357 | 19.8 | 560.4 | 0.688 |
| Canada | 0.001243 | 141.2 | 4755.0 | 0.532 |
| Denmark | 0.000555 | 35.3 | 1066.4 | −0.351 |
| Finland | 0.001082 | 37.4 | 723.1 | 0.551 |
| France | 0.001133 | 289.0 | 7960.4 | 0.672 |
| Germany | 0.001142 | 284.7 | 7990.2 | 0.853 |
| India | 0.002748 | 84.7 | 2290.0 | 0.582 |
| Ireland | 0.002415 | 22.3 | 285.6 | 0.198 |
| Italy | 0.001895 | 129.4 | 3130.0 | 0.827 |
| Japan | 0.000616 | 680.5 | 20,857.3 | 0.574 |
| Korea | 0.003001 | 75.2 | 2345.0 | 0.933 |
| Netherlands | 0.001017 | 96.0 | 2616.8 | 0.889 |
| Portugal | 0.002239 | 18.3 | 304.8 | 0.636 |
| Singapore | 0.002640 | 54.5 | 1024.0 | 0.976 |
| Spain | 0.001775 | 156.1 | 3877.8 | 0.468 |
| Sweden | 0.000810 | 38.6 | 926.2 | 0.427 |
| Switzerland | 0.001894 | 71.4 | 3032.5 | 0.667 |
| United Kingdom | 0.001020 | 285.2 | 7420.8 | 0.334 |
| United States | 0.004232 | 759.3 | 14,903.3 | 0.248 |
| Australia | Austria | Belgium | Canada | Denmark | Finland | France | Germany | India | Ireland | Italy | Japan | Korea | Netherlands | Portugal | Singapore | Spain | Sweden | Switzerland | United Kingdom | United States | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Australia | 0 | 18 | 238 | 3190 | 57 | 527 | 16,995 | 9629 | 9048 | 502 | 196 | 12,370 | 3783 | 2832 | 80 | 12,864 | 763 | 212 | 954 | 56,633 | 25,542 |
| Austria | 186 | 0 | 387 | 2597 | 1321 | 970 | 15,313 | 26,399 | 1361 | 556 | 2164 | 242 | 44 | 1600 | 11 | 24 | 2668 | 593 | 4436 | 5261 | 597 |
| Belgium | 602 | 225 | 0 | 3026 | 1182 | 71,338 | 83,592 | 37,481 | 2050 | 2004 | 6473 | 5953 | 634 | 39,662 | 145 | 1313 | 4408 | 745 | 1642 | 45,020 | 9185 |
| Canada | 4465 | 1338 | 3704 | 0 | 1224 | 461 | 28,371 | 31,745 | 1151 | 8650 | 1061 | 2652 | 1090 | 13,941 | 99 | 5487 | 1096 | 1057 | 989 | 96,988 | 85,668 |
| Denmark | 114 | 567 | 787 | 226 | 0 | 15,565 | 14,150 | 15,825 | 38 | 1724 | 259 | 78 | 1 | 668 | 5 | 23 | 888 | 35,873 | 175 | 11,316 | 2459 |
| Finland | 210 | 401 | 528 | 1173 | 12,983 | 0 | 10,792 | 6818 | 29 | 264 | 392 | 87 | 38 | 1012 | 1 | 1 | 219 | 45,560 | 341 | 11,177 | 5067 |
| France | 11,945 | 3506 | 69,783 | 24,768 | 8865 | 8314 | 0 | 124,951 | 28,536 | 31,604 | 162,329 | 108,616 | 7933 | 55,121 | 6564 | 11,242 | 90,326 | 7881 | 44,054 | 248,566 | 157,970 |
| Germany | 13,772 | 35,834 | 9726 | 17,261 | 8324 | 6568 | 293,141 | 0 | 19,982 | 24,837 | 84,979 | 34,661 | 4771 | 87,436 | 185 | 185 | 56,927 | 4647 | 17,261 | 234,695 | 134,718 |
| India | 28,236 | 573 | 1284 | 7489 | 106 | 638 | 25,107 | 14,959 | 0 | 7 | 278 | 54,829 | 24,675 | 7634 | 15 | 46,859 | 1029 | 997 | 5065 | 52,435 | 44,042 |
| Ireland | 789 | 582 | 10,615 | 1491 | 3131 | 264 | 55,575 | 30,737 | 73 | 0 | 38,913 | 328 | 97 | 24,421 | 170 | 142 | 3654 | 1288 | 843 | 67,912 | 24,198 |
| Italy | 258 | 10,303 | 2986 | 1537 | 411 | 774 | 84,116 | 60,329 | 3151 | 12,754 | 0 | 324 | 87 | 13,117 | 92 | 81 | 8608 | 292 | 2934 | 34,560 | 18,615 |
| Japan | 23,608 | 895 | 18,965 | 7519 | 5467 | 1759 | 93,445 | 18,446 | 56,224 | 207 | 8060 | 0 | 9774 | 11,328 | 725 | 48,747 | 2257 | 2059 | 3304 | 125,976 | 213,682 |
| Korea | 1605 | 419 | 145 | 570 | 39 | 1 | 4726 | 2494 | 7955 | 140 | 59 | 8164 | 0 | 507 | 88 | 2101 | 122 | 48 | 232 | 4122 | 23,232 |
| Netherlands | 13,335 | 948 | 31,748 | 9044 | 1031 | 1047 | 105,326 | 51,689 | 25,716 | 28,900 | 15,085 | 2577 | 958 | 0 | 701 | 23,210 | 9338 | 1344 | 12,840 | 183,463 | 28,937 |
| Portugal | 250 | 169 | 191 | 216 | 147 | 82 | 3700 | 453 | 150 | 441 | 62 | 842 | 191 | 238 | 0 | 712 | 3063 | 5 | 377 | 953 | 3836 |
| Singapore | 11,423 | 177 | 639 | 5432 | 18 | 0 | 7492 | 453 | 41,582 | 636 | 54 | 26,620 | 11,251 | 255 | 5795 | 0 | 140 | 529 | 5592 | 24,462 | 29,913 |
| Spain | 363 | 1555 | 3906 | 1971 | 1072 | 302 | 66,157 | 25,495 | 5500 | 6195 | 27,837 | 468 | 430 | 22,036 | 8971 | 813 | 0 | 322 | 3204 | 60,579 | 26,041 |
| Sweden | 329 | 630 | 674 | 1309 | 37,736 | 51,749 | 8046 | 8971 | 333 | 2520 | 279 | 2141 | 38 | 3888 | 0 | 0 | 331 | 0 | 1207 | 23,660 | 31,757 |
| Switzerland | 7119 | 3260 | 8320 | 3365 | 2241 | 2642 | 66,650 | 31,745 | 6581 | 4637 | 1955 | 2860 | 1773 | 11,238 | 9 | 5397 | 3038 | 1687 | 0 | 123,352 | 30,874 |
| United Kingdom | 96,838 | 8450 | 31,344 | 144,394 | 13,859 | 15,195 | 452,037 | 268,304 | 43,881 | 102,161 | 43,987 | 279,629 | 11,871 | 158,640 | 2394 | 38,365 | 40,834 | 20,271 | 204,928 | 0 | 391,974 |
| United States | 82,764 | 6292 | 5965 | 92,834 | 1367 | 32,996 | 201,161 | 56,226 | 32,952 | 43,120 | 4088 | 325,041 | 27,368 | 10,276 | 2333 | 27,616 | 16,134 | 52,715 | 10,717 | 324,512 | 0 |
| No Contagion | With Contagion | |
|---|---|---|
| Australia | 78.79 | 81.92 |
| Austria | 3.48 | 3.64 |
| Belgium | 4.88 | 6.68 |
| Canada | 53.57 | 54.35 |
| Denmark | 2.45 | 2.45 |
| Finland | 1.39 | 1.66 |
| France | 48.17 | 57.47 |
| Germany | 50.24 | 56.93 |
| India | 59.75 | 65.06 |
| Ireland | 0.55 | 2.13 |
| Italy | 30.65 | 33.73 |
| Japan | 54.20 | 55.73 |
| Korea | 96.25 | 99.56 |
| Netherlands | 12.50 | 15.92 |
| Portugal | 1.35 | 1.44 |
| Singapore | 8.95 | 14.65 |
| Spain | 37.59 | 37.98 |
| Sweden | 2.09 | 2.76 |
| Switzerland | 114.13 | 115.82 |
| United Kingdom | 29.93 | 35.77 |
| United States | 335.10 | 337.44 |
| Australia | Austria | Belgium | Canada | Denmark | Finland | France | Germany | India | Ireland | Italy | Japan | Korea | Netherlands | Portugal | Singapore | Spain | Sweden | Switzerland | United Kingdom | United States | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Australia | −4% | 0% | 0% | 0% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | 1% | −1% | 0% | 0% | 0% | 0% | 0% | 0% | 2% | 1% |
| Austria | 0% | −4% | 0% | 0% | 0% | 0% | 3% | −2% | 0% | 0% | −1% | 0% | −1% | 0% | 0% | 0% | 0% | 0% | 0% | 2% | 1% |
| Belgium | 1% | 0% | −27% | 0% | 0% | 0% | −5% | 1% | 2% | 1% | 2% | −2% | −1% | −3% | 0% | 1% | 2% | 0% | −2% | 20% | 14% |
| Canada | 0% | 0% | 0% | −1% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 0% |
| Denmark | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 0% |
| Finland | 4% | 0% | −1% | 5% | 3% | −16% | 17% | 4% | 2% | 2% | 0% | 32% | 1% | 1% | 0% | 1% | 1% | −6% | 0% | 36% | −12% |
| France | 0% | 0% | 0% | 1% | 0% | 0% | −16% | −3% | 1% | 1% | −2% | 3% | −2% | 0% | 0% | 0% | 0% | 0% | −2% | 9% | 5% |
| Germany | −1% | 0% | 0% | 0% | 0% | 0% | 2% | −12% | 0% | 0% | −3% | 1% | −2% | −1% | 0% | 0% | 0% | 0% | −1% | 5% | 4% |
| India | 0% | 0% | 0% | 0% | 0% | 0% | 2% | 0% | −8% | 0% | 0% | 0% | −4% | 0% | 0% | −2% | 0% | 0% | 0% | 3% | 7% |
| Ireland | 12% | 2% | 3% | 14% | 1% | 5% | 49% | 5% | 7% | −74% | −4% | 76% | 2% | −2% | 0% | 4% | 4% | 7% | 1% | 71% | −42% |
| Italy | 0% | 0% | 0% | 0% | 0% | 0% | −1% | −4% | 0% | 0% | −9% | 1% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 5% | 2% |
| Japan | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | −3% | −1% | 0% | 0% | 0% | 0% | 0% | 0% | 2% | 2% |
| Korea | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 0% | 0% | −3% | 0% | 0% | −1% | 0% | 0% | 0% | 1% | 1% |
| Netherlands | −1% | 1% | 0% | 0% | 0% | 0% | 5% | −8% | 0% | 1% | −2% | 1% | −1% | −21% | 0% | 0% | 0% | 0% | −1% | 8% | 7% |
| Portugal | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 0% | 2% | 0% | 0% | 1% | −1% | 0% | −6% | −4% | −1% | 0% | 0% | 4% | 3% |
| Singapore | −5% | 0% | 1% | 1% | 0% | 0% | 8% | 2% | −5% | 0% | 0% | −3% | −9% | −2% | 0% | −39% | 0% | 0% | −1% | 18% | 22% |
| Spain | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 0% | 0% | 0% |
| Sweden | 6% | 0% | 0% | 7% | 0% | 1% | 20% | 5% | 2% | 3% | 0% | 39% | 2% | 1% | 0% | 2% | 1% | −24% | 1% | 38% | −23% |
| Switzerland | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 1% |
| United Kingdom | 1% | 0% | 1% | 2% | 0% | 1% | 10% | 0% | 1% | 1% | 0% | 14% | 0% | −1% | 0% | 1% | 1% | 1% | −2% | −16% | 1% |
| United States | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% |
| Australia | Austria | Belgium | Canada | Denmark | Finland | France | Germany | India | Ireland | Italy | Japan | Korea | Netherlands | Portugal | Singapore | Spain | Sweden | Switzerland | United Kingdom | United States | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Australia | −4% | 0% | 0% | 0% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | 2% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 2% | 2% |
| Austria | 0% | −4% | 0% | 0% | 0% | 0% | 3% | 1% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 2% | 1% |
| Belgium | 1% | 0% | −27% | 1% | 0% | 0% | 6% | 5% | 3% | 1% | 4% | 4% | 0% | 0% | 0% | 2% | 2% | 0% | 1% | 20% | 14% |
| Canada | 0% | 0% | 0% | −1% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 0% |
| Denmark | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 0% |
| Finland | 5% | 0% | 0% | 6% | 3% | −16% | 18% | 5% | 2% | 2% | 1% | 32% | 1% | 1% | 0% | 2% | 1% | −6% | 1% | 36% | 3% |
| France | 1% | 1% | 0% | 1% | 0% | 0% | −16% | 3% | 1% | 1% | 0% | 5% | 0% | 1% | 0% | 1% | 1% | 0% | 0% | 9% | 7% |
| Germany | 0% | 0% | 0% | 0% | 0% | 0% | 4% | −12% | 1% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 5% | 4% |
| India | 1% | 0% | 0% | 0% | 0% | 0% | 2% | 1% | −8% | 0% | 0% | 2% | 0% | 0% | 0% | −1% | 0% | 0% | 0% | 3% | 7% |
| Ireland | 14% | 2% | 3% | 16% | 1% | 5% | 57% | 17% | 7% | −74% | 2% | 78% | 4% | 2% | 0% | 5% | 5% | 7% | 4% | 73% | 16% |
| Italy | 0% | 0% | 0% | 0% | 0% | 0% | 2% | 1% | 0% | 0% | −9% | 1% | 0% | 1% | 0% | 0% | 1% | 0% | 0% | 5% | 3% |
| Japan | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | −3% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 2% | 2% |
| Korea | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | 1% | −3% | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 1% |
| Netherlands | 1% | 1% | 0% | 1% | 0% | 0% | 9% | 2% | 1% | 1% | 1% | 2% | 0% | −21% | 0% | 0% | 1% | 0% | 0% | 8% | 7% |
| Portugal | 0% | 0% | 0% | 0% | 0% | 0% | 2% | 1% | 2% | 0% | 1% | 1% | 0% | 0% | −6% | −1% | 0% | 0% | 0% | 4% | 3% |
| Singapore | 2% | 0% | 1% | 1% | 0% | 0% | 9% | 3% | 2% | 0% | 1% | 7% | 1% | 0% | 0% | −39% | 0% | 0% | 0% | 18% | 23% |
| Spain | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 0% | 1% | 0% |
| Sweden | 6% | 0% | 0% | 7% | 1% | 1% | 20% | 5% | 2% | 3% | 0% | 39% | 2% | 1% | 0% | 2% | 1% | −24% | 1% | 38% | 1% |
| Switzerland | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 1% |
| United Kingdom | 2% | 0% | 1% | 3% | 0% | 1% | 13% | 4% | 2% | 1% | 1% | 16% | 1% | 1% | 0% | 1% | 1% | 1% | 0% | −16% | 9% |
| United States | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 1% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% |
| Australia | Austria | Belgium | Canada | Denmark | Finland | France | Germany | India | Ireland | Italy | Japan | Korea | Netherlands | Portugal | Singapore | Spain | Sweden | Switzerland | United Kingdom | United States | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Australia | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 0% | 0% | −1% | 0% | 0% | −1% | 0% | 0% | 0% | 0% | −1% |
| Austria | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −2% | 0% | 0% | −1% | 0% | −1% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| Belgium | −1% | 0% | 0% | −1% | 0% | 0% | −12% | −4% | 0% | 0% | −2% | −6% | −1% | −5% | 0% | −1% | 0% | 0% | −3% | −1% | −1% |
| Canada | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% |
| Denmark | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| Finland | 0% | 0% | −2% | 0% | 0% | −1% | −1% | −1% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −7% | −1% | −1% | −13% |
| France | −1% | 0% | −1% | 0% | 0% | 0% | −2% | −6% | −1% | 0% | −3% | −1% | −2% | −2% | 0% | −1% | −1% | 0% | −2% | −1% | −2% |
| Germany | −1% | 0% | 0% | −1% | 0% | 0% | −2% | −2% | 0% | 0% | −4% | 0% | −2% | −1% | 0% | 0% | 0% | 0% | −2% | −1% | 0% |
| India | −1% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | −1% | 0% | 0% | −2% | −4% | 0% | 0% | −2% | 0% | 0% | 0% | 0% | 0% |
| Ireland | −2% | 0% | 0% | −2% | 0% | 0% | −9% | −10% | −1% | −1% | −8% | −1% | −2% | −7% | 0% | −1% | −1% | −1% | −3% | −11% | −57% |
| Italy | 0% | 0% | 0% | 0% | 0% | 0% | −4% | −5% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 0% | −1% | 0% | 0% | 0% | 0% |
| Japan | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | −1% | 0% | 0% | −1% | 0% | 0% | 0% | 0% | −1% |
| Korea | −1% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 0% | 0% | 0% | 0% |
| Netherlands | −1% | 0% | −1% | −1% | 0% | 0% | −4% | −10% | −1% | 0% | −3% | −1% | −2% | −1% | 0% | 0% | −1% | 0% | −2% | −1% | 0% |
| Portugal | 0% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 0% | 0% | 0% | 0% | −1% | 0% | 0% | −4% | −2% | 0% | 0% | 0% | 0% |
| Singapore | −7% | 0% | 0% | −1% | 0% | 0% | −1% | −1% | −9% | 0% | 0% | −9% | −10% | −3% | 0% | −1% | 0% | 0% | −2% | 0% | −1% |
| Spain | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| Sweden | 0% | 0% | 0% | 0% | 0% | −2% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | −1% | −23% |
| Switzerland | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| United Kingdom | −2% | 0% | 0% | −1% | 0% | 0% | −3% | −4% | −1% | −1% | −1% | −2% | −1% | −2% | 0% | −1% | 0% | 0% | −2% | 0% | −8% |
| United States | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zedda, S.; Spinace-Casale, A. Modeling and Simulating Cross Country Banking Contagion Risks. J. Risk Financial Manag. 2021, 14, 351. https://doi.org/10.3390/jrfm14080351
Zedda S, Spinace-Casale A. Modeling and Simulating Cross Country Banking Contagion Risks. Journal of Risk and Financial Management. 2021; 14(8):351. https://doi.org/10.3390/jrfm14080351
Chicago/Turabian StyleZedda, Stefano, and Antonella Spinace-Casale. 2021. "Modeling and Simulating Cross Country Banking Contagion Risks" Journal of Risk and Financial Management 14, no. 8: 351. https://doi.org/10.3390/jrfm14080351
APA StyleZedda, S., & Spinace-Casale, A. (2021). Modeling and Simulating Cross Country Banking Contagion Risks. Journal of Risk and Financial Management, 14(8), 351. https://doi.org/10.3390/jrfm14080351







