Catch the Heterogeneity: The New Bank-Tailored Integrated Rating

Abstract

The purpose of this article is to develop a bank-oriented rating approach, tailored by incorporating the various heterogeneity dimensions characterizing financial institutions, named “Bank-Tailored Integrated Rating” (BTIR). BTIR is able to catch the financial cycle, including the pandemic crisis, and the ongoing change in banking normative from a microeconomic perspective, and it is inherently coherent with the challenging frontier of forecasting tail risk in financial markets in similar ways as in De Nicolò and Lucchetta (2017), although their approach is macroeconomic) since it considers the downside risk in the theoretical framework. The method employed was an innovative integrated rating (IR) statistical and econometrical panel pre-selection analysis that takes into account the characteristics of risk and the greater heterogeneity of the banks. The result is a challenge rating procedure delivering forward-looking preselection requested by the new International Financial Reporting Standard (IFRS-9). The future direction is extremely promising given the increase in idiosyncratic and systemic risks in financial markets.

1. Introduction

Since the great financial crisis of the years 2007–2008, a recurring sentiment is heard on the street: something is wrong with ratings. Although massive efforts have been made to update methods and regulations according to the emerging evidence and experience, the refrain continues. Even the opportunities to process massive bulk data through digital technologies seem unable to lead to a definitive solution of the puzzle. In fact, increasing the quantity of data does not seem an efficient way toward a solution. Now that economies are recovering from the COVID-19 disaster, a new test is underway: will the NPL increase abnormally?

The capital regulatory policies imposed on banking institutions increasingly reveal the need to consider the heterogeneity of regulated entities. It has become even more important to adapt the rating systems in light of the changes induced by the ongoing COVID-19 pandemic. It is clear that a standardized rating is no longer adequate for the needs of prudent risk management and guaranteeing bank stability (Acharya and Steffen 2020; Barnoussi et al. 2020). At the same time, the regulating framework should contribute to avoid the common errors of over/under-assessment of the risks inherent in the different business models recently applied by modern banks. This is the big challenge: avoiding standardization, while at the same time reliably capturing the risk queues. Using a heterogeneous and long dataset, we have succeeded in the intent to produce a reliable BTIR that solves the problems mentioned above. Rating systems play a critical role in the regulation framework for financial stability and in the managerial practices of the banking business. Unfortunately, a recent paper of Kolaric et al. (2017) suggests that the traditional ratings are biased by the “too big to fail” phenomenon, since they are based on homogeneous rating methodologies as adopted by risk rating agencies. Therefore, they are not completely reliable, as the level of non-performing loans demonstrates. Two activities in managing banking loan portfolios are critically related to the rating practices: (i) the firms’ appraisal, as the root of sound credit management, and (ii) the financial reporting, as a key driver to protect the investors’ wealth. Standard rating methodologies sometimes focus less on such key points, supposing that the use of a bulk dataset may circumvent the possible inaccuracies. In the meantime, they are missing the firm’s (bank’s) specific elements, which may distinguish the single entity.

The main motivation for this paper is supported by stylized facts: the unexpected, sometimes sudden, and quick failure of companies that had a very good credit rating just before the crash. This aspect deserves careful consideration and imposes a correction of the current rating methods. The natural and spontaneous questions are: was there a way to predict with a specific or more accurate rating? Which corporate factors were missed by the adopted methodology? Additionally, at the same time, should they take into account systemic or cyclical factors? A recent paper of Salvador et al. (2018) analyzes the adjustment of bank ratings which occurred in the United States, some European countries, and Japan as a result of the financial crisis. Their intuition is that there is a need to adjust rating procedures adopted by large agencies such as Fitch, Standard and Poor’s, and Moody’s. The authors limit themselves to observe that pro-cyclicality and macroeconomic factors, captured precisely by the great rating agencies, are nowadays more and more crucial. Indeed, they do not propose a rigorous statistical methodology and miss the firm-specific elements.

This paper contributes with an innovative-but-rigorous approach to take these elements into account directly, without necessarily having to draw on data already “filtered” by rating agencies (which could be less accurate than the macro-data directly collected). The paper is organized as follows. Section 2.1 provides proof of the need for BTIR according to the failure of other methods, as discussed by the literature on this topic. Section 2.2 introduces the basic model and the statistical procedure and algorithms we adopted. Indeed, BTIR is an extended version of integrated rating (IR), with a specific focus on banking business. Section 3 illustrates an empirical application of BTIR over a sample of 142 Italian banks to test the effective capability to fit better with risk and heterogeneity of the banking sector. Section 4 discusses the results and provides some insights for further developments of BTIR to better catch the financial cycle. In our example, we show how heterogeneity is important for banks’ ratings, but the systemic risk is implicitly considered. Therefore, a methodology to deal explicitly with the common factors (for instance, using as explanatory variables the factors of a VAR) could further improve BTIR. Finally, Section 5 concludes the paper.

2. Materials and Methods

2.1. Why BTIR Is Needed

Firm appraisal is the key component of any rating and scoring methodology. The actual capability to catch firm-specific components of the business performance is always a must. For rating methodologies, detecting the firm-specific components of business risks matters as well. In fact, the endogenous component of the corporate risk can be both at the root of the competitive advantage of the company and also its risk of default. Being selective is therefore a distinguishing element of a successful rating system, although (ab)uses of algorithms to process big data seem to lead in the opposite direction. Does it make sense to increase any dataset if its treatment is based on standardization? In fact, big data processing should facilitate to detect heterogeneity, a more precious goal than the reinforcement of the density functions around common evidence. Moreover, it should help to discover signals of the forthcoming discontinuities (indeed, a time-case of heterogeneity) instead of producing additional forecasts based on historical evidence. It may exacerbate the economic cycles, only, through time-correlated datasets. This is also the background pushing toward the new IFRS-9.

Our assumption is very simple: heterogeneity matters, and it should be explicitly included into rating methods. Stylized facts, firm appraisal rules, and IFRS-9 introduction are compliant with this assumption, as it follows below.

2.1.1. Stylized Facts: What the Evidence Shows

The severe crisis that began with the sudden and disastrous bankruptcy of Lehman Brothers on 15 September 2008 due to the subprime crisis has dusted off the difficulty of predicting and mitigating banking crises that subsequently have devastating effects on the real economy and total economic welfare. It is estimated that real product losses are conspicuous for all countries and with losses of tens of percentage points of annual GDP. Laeven and Valencia (2018) collect and document all the more or less serious global banking crises. This historical and current excursus allows to study the speed of crisis propagation and the response to further prevent it: a better monitoring system that certainly cannot leave the cyclical and macroeconomic variables out of the ratings, given that the failure of a bank has systemic effects. Wilms et al. (2018) identify 21 variables frequently used as determinants of the severity of banking crises but not yet included in the official ratings. The need to introduce a rating model closer to the new needs of the banking and financial market is therefore evident: our new “Bank-Tailored Integrated Rating” (BTIR) provides an important response in this direction.

A very important European episode is the case of the famous British bank that suddenly spread panic among savers within a few hours: the queues that formed outside Northern Rock, the country’s fifth-biggest mortgage lender, represented the first bank run in Britain since 1866.

Therefore, we wonder, could these painful bank runs be anticipated or mitigated?

Our research suggests that in an increasingly financial-integrated world and anchored in the real economy, it is essential to use macro-variables in ratings to make them more reliable.

Moreover, the bad bank situation has been quite relevant in the last years. Bad banks are those banks which own non-performing loans and that attempt to solve and recover the deficits. However, to retain those banks, the system should allow to manage and resell those loans to funds which often tend to speculate, with potential huge effects on the system. The European Central Bank (ECB) and the national systems have developed standards to recover the situation and lead to a major spread of the financial information of those banks, so that the market knows the content of those financial instruments and avoids another failure, as in the Lehman Brothers case. The major focus of the ECB and national system is to spread more information to all banks’ stakeholders and convey a sense of transparency to raise trust in the financial system. Trust is the key in the recovery from the financial crisis (Merton 2018); indeed, information to investors, clients, and all potential economic actors must be clear, complete, and transparent, and moreover, the system itself is implementing solutions in order to convey a sense of trust and transparency that was lacking after the financial crisis and the European Sovereign Debt crisis. Due to this mission shared by the entire European system, the ECB is working on directives that can lead to a major improvement of the non-performing loans situation in Europe, aggravated by the pandemic situation; on the one hand, banks will be given the opportunity to recover non-performing loans at the economic value and not at the market value, so that the weight on the balance sheet will definitely be lower. On the other hand, there is the insertion of a new accounting standard which focuses on the possibility for firms to have internal integrated rating focused on forward-looking information: IFRS-9. Barnoussi et al. (2020) underline that the banks need to reassess their loan assets, by updating their risk models with expectations about potential default rates and future macro-economic and financial developments.

The accuracy of the rating procedure is particularly required and fundamental in light of the serious problem of the non-performing loans (NPLs) and the consequent social damage of the credit crunch they generate. Our work provides solutions to this serious problem that risks slowing down economic development by obstructing the proper functioning of the intermediation process.

To our knowledge, no study has so far analyzed the possibility of preventing NPLs through a different rating system, while some studies suggest how to solve the problem of NPLs when it has already occurred. Our work fills this gap and suggests a way to prevent the future growth of non-performing loans.

It is more than self-evident that NPLs have recently become a serious and destabilizing factor for the European Banking Sector, destined to grow due to the pandemic situation, at least for the next few years. The European Banking Authority (2019) estimates that in December 2018, the stock of gross NPLs in the European Union (EU) banks stood at 658 billion euros, or 3.2% of total gross loans, and they remain high by historical standards, and about twice as high as those in other jurisdictions such as the USA and Japan (ESRB 2017). It is argued that NPLs reduce bank profitability, raise funding costs, and ultimately tie up bank capital that could otherwise be devoted to increasing lending in valuable projects (see, e.g., IMF 2015). This effect is dangerous and slows economic growth through the well-known phenomenon of the credit crunch.

Policymakers have resorted to a number of solutions, involving banks’ recapitalizations, Government’s guarantees of bank liabilities, and asset purchases programs, variously combined together (ECB 2017).

As already underlined above, after solving the problem, prevention is important, and this is precisely the purpose of our new and innovative “bank-tailored integrated rating” (BTIR).

2.1.2. Firms’ Appraisal

The main pitfalls in current rating systems are rooted in the firms’ appraisal processes. Indeed, ratios are considered per se, missing their connections (i.e., integration) inside the firms’ business. This leads to adopt ratios as influenced by exogenous risks, only, while the endogenous elements of the firms’ capabilities to craft the risk by integrating the different business components are missed.

Although in 2012 the European Commission focused on the need of a new supervisory method, by introducing the Single Supervisory Mechanism (SSM) led by the European Central Bank (ECB), which was made effective on 4 November 2014, shifting the supervision of 130 banks under ECB control, while the remaining banks shifted under the control of National Supervisory Authorities (NSAs), there is still a long way to go in the banks’ appraisal, as this new supervisory system has also led to some downsides (Fiordelisi et al. 2017). Indeed, the SSM is a day-to-day supervision led on two different levels that might create regulatory arbitrage conditions, and inconsistencies between ECB and NSAs are possible (Fiordelisi et al. 2017). Consequently, we do need a bank-integrated rating, that can diminish inconsistencies among banks.

The most recent literature on corporate performance assessment (Mantovani 2017) re-discovered Lintner (1965)’s model as an alternative approach to appraise firms and their performance, through the companies’ asset-side capability of the management in the long term. The analysis is useful to understand whether there is an appropriate allocation of financial resources, in line with the goodness of the performance, and it is important to assess company pay-out and managerial rents, as in Lambrecht and Myers (2012). The theoretical framework replaces the estimation of market risk premia for discounting rates with the use of the certainty equivalent approach. This substitution is possible, because the certainty equivalent of expected cash flows is discounted (at a free-risk rate) instead of the volatile expectations of cash flows (at a risky market rate). Furthermore, it requires a total risk-aversion input to estimate the certainty equivalent, instead of the adoption of the systematic risk-aversion, exactly as applied to a CAL portfolio, used as a benchmark. However, Leibowitz and Henriksson (1989) noted that a shortfall approach may be considered to proxy the risk-aversion by investors. Accordingly, focusing on a “confident equivalent” (i.e., the minimum threshold that may be overpassed, according to a certain confidence percentage) rather that Lintner’s “certainty equivalent” can be effective and sound, as Mantovani (2017) demonstrated. Determining both the threshold and the confidence is up to the investor, even before choosing the investment. Indeed, in banking analysis, the downside risk is particularly important, since “tail risk” is considered an important component in financial market analysis, as underlined by De Nicolò and Lucchetta (2017). The economic cycle may matter. The first to underline the importance of the cycle was Löffler (2004). This author proposes the Kalman filter procedure to distinguish between the cyclical component and the firm-specific component.

The cited current literature on risk assessment concentrates on corporate firms, and the “tail risk” analysis is mainly oriented to macroeconomic risk measures. This paper fills these gaps and contributes to the identification of a synthetic indicator of company performance and long-term creditworthiness, which is also able to take into consideration the investor’s risk-aversion and the downside risk component: the “bank-tailored integrated rating” (BTIR). This need arises from studies on rating modeling in order to make the implementation and use of the results easier within banking organizations. Indeed, it must be ensured that the indicator has three characteristics: (i) scientifically reliable and (ii) comprehensible to customers, and finally, (iii) consistent with the credit policies included in the new International Financial Reporting Standard (IFRS-9).

2.1.3. IFRS-9

The need for a different internal banking rating is consistent with the introduction of IFRS-9, which brought major changes to both firms and banks. The main elements introduced by this principle concern credit-risk and forward-looking information. This point is stressed by Barnoussi et al. (2020).

First, the introduction of the principle influences the credit cycle, by increasing the quantity and quality of information necessary for the appraisal of the application of funds. The consideration of the economic cycle clearly suggests, for the first time so decisively, the correctness in the introduction of macroeconomic variables in the rating indexes of banks and firms.

Second, IFRS-9 needs historical data, which are an important source of information about credit risk drivers and cash flow. Third, forward-looking events influence the credit risk drivers and should reflect possible differences in the future cash-flows. All this information leads to an efficient assessment of credit risk. Beyond micro-level data, IFRS-9 also needs to incorporate macroeconomic elements in the valuation. Accounting for forward-looking information, including macroeconomic factors, is one of the main innovative elements considered in the valuation of credit risk. Indeed, the macroeconomic framework in not only an element of the competitiveness of the environment in which the bank is set, but it becomes a fundamental influence of the merit of credit.

The forward-looking approach introduced a certain discontinuity in the already established banking system frameworks. For this and the above-listed reasons, the bank-tailored integrated rating purposely manages to incorporate the characteristics of the principle.

2.2. The Basic Model (from IR to BTIR)

In integrated rating (Mantovani et al. 2013), heterogeneity is considered both on the investor and the firm side. From the investor’s perspective, the expected return is computed by substituting the certainty equivalent, as in Lintner (1965), with the confident equivalent, which is jointly determined by a threshold bottom-return and its confidence, based on the investor’s profile, before picking the investment. From the firm’s perspective, the total risk of the corporate performance is considered meaningless and is exogenous or endogenous in nature, so that any firm-specific capability to control the corporate risk is considered. The actual implementation of IR estimates the total risk of the specific firm through the equation, as obtained by regressing the key proxies of corporate risks with the standard deviation of corporate returns.

Equation (1) explains the relationship between the expected return for a specific (i-th) investment and the confident equivalent return ($Rce$), supposing a 10% confidence level for the overall market:

$$\begin{gathered} Rce=E\left(R_i\right)-Z{\sigma }_i \\ E\left(R_i\right)=Rce+Z{\sigma }_i \\ \mathrm{Where}:Z={{\displaystyle \int }}_{-\infty }^{10\%}f\left(x\right)dx \\ \mathrm{and}{\sigma }_{it}={\beta }_0+{\beta }_1{X}_{1it}+\dots +{\beta }_n{X}_{nit}+{ϵ}_i \end{gathered}$$

(1)

Equation (1) indicates that the investor’s risk-aversion makes her/him accept an ex-post return below $Rce$ only once each 10 cases for the entire investment’s holding period. The confidence level adopted to estimate $Rce$ relates to the specific investor’s risk-aversion, which may change the confidence percentage accordingly. This equation is indeed a Shortfall Line according to Leibowitz and Henriksson (1989). According to the authors’ opinion, the Capital Allocation Line is a special case of a Shortfall Line if:

• The confidence is higher than 50%, since the Sharpe ratio is positive to back investors’ risk-aversion.
• A bottom threshold is determined at the risk-free rate.

If a reliable risk-free investment cannot be found, Fisher Black’s zero-beta model can be used to identify the market portfolio through an alternative CAL (Black 1972), replacing the risk-free rate with a zero-beta return (Mantovani 2017). In Black’s model, a market replicability of zero-beta return through the efficient frontier is adopted to determine the downside threshold-return without leading to an analytical estimation of the investors’ risk-aversion. In IR methodology, Black’s intuition is used, substituting the zero-beta return with the confident equivalent, provided that it is based on the investor’s profile (e.g., zero-beta with the market). Investments contributing both to the efficient frontier and outperforming the Shortfall Line, as determined by the confidence percentage fixed by the investor, can be found accordingly (Mantovani 2017).

Indeed, as with Linter’s certainty equivalent of a specific investment which moves towards the equilibrium, as proposed in classic CAPM, similarly, the explained confident equivalent for a specific investor directs to the equilibrium, as shown in Black’s zero-beta model.

The strong points of this methodology are:

• Risk-aversion is not punctual data.
• The expected return for a single investment is estimated without recurring to market data but using the confident equivalent of the specific investor, including the confidence.

To use the IR method, the degree of confidence to adopt is therefore required. This leads to investigate its relationship with the risk tolerance of the specific financial institution. The bank-specific/tailored integrated rating, detailed here, focuses on the development of a mathematical/econometric method that allows us to identify the best algorithm, to determine a fair degree of convexity and concavity (consequently, the correct degree of risk-aversion of the investor), which can be dynamic and adaptable, consequently to heterogeneous banks.

To take into account the characteristics of risk and greater heterogeneity of the banks, we propose a challenge procedure that clusters banks by risk and their own risk tolerance. These are the fundamentals of change of the original integrated rating and developing our new bank-tailored integrated rating, dedicated to the financial institutions combining the expectations of the IFRS-9 legislation. This further step allows us to design our “Bank-Tailored Integrated Rating” (BTIR). The approach is inherently coherent with the challenging frontier of forecasting tail risk in financial markets.

The proposed methodology considers different characteristics of the financial institution. Although our final aim is to introduce a preselection of variables, the starting point is identifying which are the ratios that impact the banks’ performance and trying to understand whether it is possible to cluster the selected banks, according to their risk level, which we have proxied through two ratios, that will be introduced later. This is aligned with the IR methodology for assessing the total risk of the company to feed the previous Equation (1) and to assess the expected return for the investment.

We move from a “simple” panel regression that considers different banking characteristics, inspired by Matthews et al. (2007), who consider the competitive ability of the UK banking system in the long run, investigating similar banking characteristics:

$$Y_{it}={\beta }_0+{\beta }_1{X}_{1it}+\dots +{\beta }_n{X}_{nit}+{ϵ}_i$$

(2)

where Y_it is a banks’ performance indicator and βs are the banks’ health key characteristics.

The independent variables are made up of indicators and indexes that inform about different characteristics of the bank. The indexes are chosen among a wide set of parameters, as used in the best practices of financial analysis of the bank performances. In particular, we considered 26 indexes concerning: asset quality, capital, operations, liquidity, and structure (see Appendix A). The set in the Appendix A were selected according to their capability to catch the best fittings of the panel regression.

The bank performances, as estimated through the regression, provide the expected level according to the actual status of the banks’ health. As in standard IR methodology, the expected level can be compared with the actual levels, chiefly those which are persistent over time. In standard IR methodology, the return on investment (ROI) is the adopted performance indicator, based on the traditional asset-side approaches in corporate finance. For BTIR, instead, the chosen explanatory variable to conduct the analysis is the return on equity (ROE). Indeed, ROE is the classic measurement of performance for banks, provided the specific nature of their business. However, to estimate the panel regression, we use a decomposed ROE measure, which considers four different drivers (as suggested by the ECB 2010): non-recurring assets, leverage, recurring revenues, and cost efficiency, through the formula:

$$ROE=\frac{Pre-Tax Profit}{Op. Income}\times \frac{Tot. Assets}{Equity}\times \frac{Net Revenue}{Tot. Assets}\times \frac{Op. Income}{Net Revenue}$$

(3)

The decomposed ROE considers difference characteristics of performance. For this reason, it is more suitable for the specific purposes of the BTIR methodology and analysis, since it avoids possible distortions due to the year-specific net income and methodological choices, as adopted by a specific database. Accordingly, any empirical evidence on ROE in this paper is based on figures computed by multiplying the above components.

After leading the regression, the resulting coefficients are used in the equation to compute a Threshold ROE [T(ROE)] for the single bank. To rank banks according to the BTIR, we firstly compare the results from the panel [T(ROE)] with each bank’s Permanent ROE [P(ROE)], computed as the average of the ROE ratio through years. A positive spread signals a favourable—and long-term—BTIR, while the larger the spread, the more superior the standing of the bank (given the same risk-aversion).

To score banks by including the risk-aversion in the ranking, a transformation is needed for the difference between Permanent-ROE and Threshold-ROE. Moreover, the transformation makes the results more comprehensible, and easy to use, to make them fruitful even for non-academic individuals. We state the following proposition:

Proposition 1.

Consider the bank (firm)“i”, it is possible to design its integrated rating IR based on a robust model ranking firms’ performance.

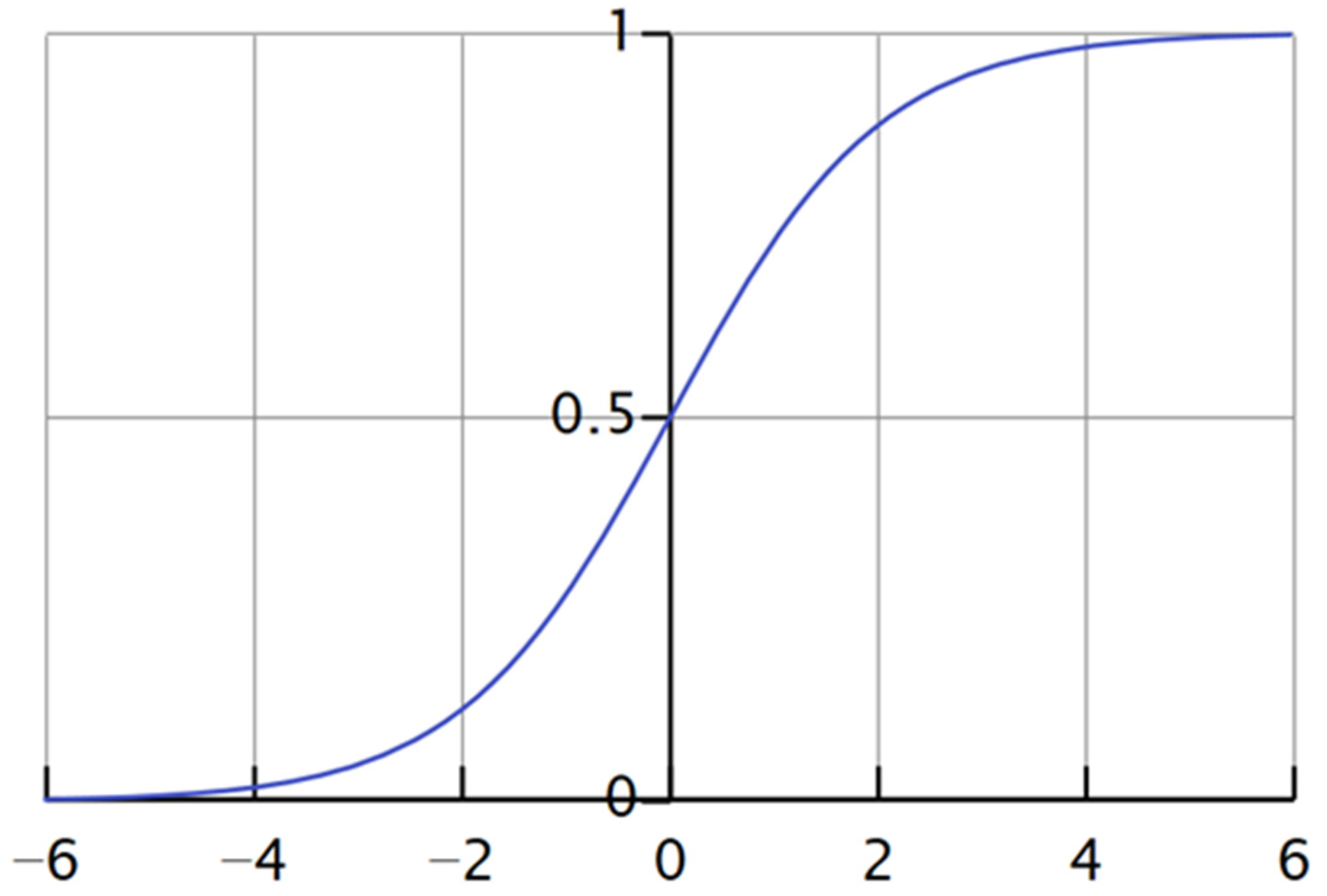
Proof of Proposition 1.

The logistic function spread in Mathematics and Statistics is a useful instrument in order to apply the transformation. The function is defined as (Blumen and Simon 1994):

$$f\left(x\right)=\frac{L}{1+e^{-k\left(x-x_0\right)}}$$

(4)

for all the real values of x with codomain [0, L > 0], with inflection point in x₀ and with slope k > 0. The simplest case is the logistic function (Blumen and Simon 1994), defined as in the codomain [0, 1], with inflection in x = 0:

$$f\left(x\right)=\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+1}$$

(5)

In the case of integrated rating, the variable is the difference between Permanent-ROE and Threshold-ROE, in a way that f(x) becomes an indicator in a close and limited interval, with a clear interpretation. The transformation belongs to the interval [−1, 1] and the preserving of the algebraic difference.

A useful modification of the logistic function (Blumen and Simon 1994) we propose here to embed the risk aversion into BTIR might be the following:

$$f\left(x\right)=\frac{2}{1+e^{-x}}-1$$

(6)

 □

Graphically, it is represented as follows in Figure 1.

The different steepening and shape of the curve reflects the risk-aversion filter, since the transformation is much more sensitive than the spread between ROE around the zero level.

In this case, f(x) is in the interval [−1, 1] with a unitary curve. A multiplying constant in the exponential component (e.g., e^(−2x)) changes the degree of the function slope, modifying the way in which the data might be discriminated, comparing them to more extreme values.

Then, it is straightforward to hypothesize the following distribution for the rating indicator:

• BTIR ∈ [−1, −1/2]: the bank has performed very poorly, and the rating leads to a negative merit of credit valuation.
• BTIR ∈ (−1/2, 0]: the bank has performed poorly, but it is not the only one in the sample.
• BTIR ∈ (0, 1/2]: the bank has performed in a good way, but it has not surpassed the expectations.
• BTIR ∈ (1/2, 1]: the bank has over-performed, compared to the benchmark.

The transformed positive [P(ROE) > T(ROE)] and negative [P(ROE) < T(ROE)] rating sub-samples are then cross-compared to widely used credit-risk indicators, namely “non-performing loans on gross loans” and “non-performing loans on total assets”, as defined according to the best practice of Bank Supervisor Authorities.

3. Results

Applying BTIR: Discussing Results from the Case of Italian Banks

This section illustrates a first simple procedure to deal with banks’ heterogeneity. Accordingly, it shows how to cluster banks. We would like to point out that systemic risk is implicitly considered, and clustering concerns the effective diversity of banks. Next, the systemic component is included, for example through the factors of a VAR, and we explain how to insert it. Indeed, our purpose is to demonstrate that the subset procedures are needed to consider the inevitable difference between banks.

We analyzed a sample of 142 Italian banks extracted by the ORBIS database (edited by Bureau Van Dijck). The selected banks have 2020 as the last year of accounts; moreover, they show details of their balance sheets for 10 years, so that the time span is from 2011 to 2020. To have the best representation for the BTIR, we have included in the sample only those banks that have the presence of complete balance sheets for an entire timespan of 10 years. In this way, we are able to have complete information about the different characteristics of the banks. Consequently, we monitored the very same 142 Italian banks for 10 years, where the ratios, directly extracted by the ORBIS database (apart from decomposed ROE), represent assets, debt, liquidity, and structural characteristics of the selected financial entities.

Table 1. Descriptive statistics for the 142 Italian banks (entire period 2011 to 2020). Authors’ development on data sourced from ORBIS—Bureau Van Dijck.

Variable	Obs.	Mean	SD	Min	Max
Net Interest/Average Assets	1420	1.776	0.596	−0.116	4.841
Non-Interest Expenses/Average Assets	1420	2.661	1.137	−4.801	11.471
Net Revenue	1420	48,804.492	873,656.77	−13,583,170	8,246,850
Solvency	1420	9.201	4.055	2.17	54.86
Total Assets	1420	25,760,148	1.217 × 108	37,127	1.296 × 109
Profit Margin	1420	12.591	20.75	−90.83	82.99
NPLs	1420	1,324,949	7,282,792.4	0	82,859,445
NPL/Gross Loans	1420	11.18	7.383	0	42.5
NCO/Average Gross Loans	1420	−0.854	1.279	−22.66	6.07
NCO/Net Income before Loans less provisions	1420	−67.26	128.141	−942.83	876.49
Impaired Loans/Equity	1420	89.546	73.745	0	843.8
Equity/Net Loans	1420	18.152	30.42	0	960.91
Net Loans/Total Assets	1420	61.552	17.082	0.03	96.14
ROA	1420	0.267	0.689	−6.06	8.01
Equity/Total Assets	1420	9.201	4.055	2.17	54.86
Equity/Total Liabilities	1420	10.401	6.198	2.22	121.52
Recurring Earning Power	1420	1.041	0.781	−5.56	10.08
Cost-to-Income	1420	64.463	38.454	−581.55	379.3
Equity	1420	1,595,479.3	7,328,320	3894	66,453,080
Pre-Tax Profit	1420	69,808.261	988,963.34	−15,200,211	9,256,061
Operating Income	1420	507,526.9	2,394,578.2	−2,190,685	24,911,694
NPLs/Total Assets	1420	0.074	0.051	0	0.366
Decomposed ROE	1420	0.044	0.122	−1.341	0.785

summarizes the key descriptive statistics of the sample. As may be observed, our sample is quite heterogeneous, so that we can observe that our banking rating system can be applied to all kinds of banks, no matter if they have quite different assets, debts, and liquidity structural characteristics. Indeed, this basic example is the origin of what the bank-tailored integrated rating is.

More details of the values in Table 1 can be found in Appendix B, stating details year by year.

Table 2. Pairwise correlations among key statistics of the 142 Italian banks. Authors’ development on data sourced from ORBIS—Bureau Van Dijck.

Variables	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)	(16)
(1) ROE	1.000
(2) NPLGrossLoans	−0.367 *	1.000
	(0.000)
(3) NPLsTotAssets	−0.404 *	0.919 *	1.000
	(0.000)	(0.000)
(4) NCOAvgGrossLoans	0.095 *	−0.282 *	−0.257 *	1.000
	(0.000)	(0.000)	(0.000)
(5) NCONetIncbefLo~v	0.046	−0.149 *	−0.174 *	0.515 *	1.000
	(0.081)	(0.000)	(0.000)	(0.000)
(6) ImpairedLoansE~y	−0.469 *	0.752 *	0.848 *	−0.213 *	−0.147 *	1.000
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
(7) EquityNetLoans	0.012	−0.079 *	−0.138 *	0.038	0.058 *	−0.191 *	1.000
	(0.648)	(0.003)	(0.000)	(0.153)	(0.029)	(0.000)
(8) EquityTotLiab	−0.077 *	0.019	−0.035	0.004	0.021	−0.264 *	0.300 *	1.000
	(0.004)	(0.468)	(0.190)	(0.866)	(0.435)	(0.000)	(0.000)
(9) ProfitMargin	0.726 *	−0.364 *	−0.386 *	0.072 *	0.056 *	−0.409 *	−0.005	0.027	1.000
	(0.000)	(0.000)	(0.000)	(0.006)	(0.035)	(0.000)	(0.855)	(0.305)
(10) NetInterestAv~s	−0.056 *	0.227 *	0.224 *	−0.114 *	−0.050	0.060 *	−0.093 *	0.282 *	−0.009	1.000
	(0.035)	(0.000)	(0.000)	(0.000)	(0.058)	(0.023)	(0.000)	(0.000)	(0.733)
(11) NonIntExpAvgAss	−0.386 *	0.283 *	0.239 *	−0.019	0.032	0.188 *	0.059 *	0.331 *	−0.445 *	0.351 *	1.000
	(0.000)	(0.000)	(0.000)	(0.486)	(0.221)	(0.000)	(0.026)	(0.000)	(0.000)	(0.000)
(12) ROA	0.821 *	−0.294 *	−0.321 *	0.075 *	0.028	−0.398 *	0.039	0.011	0.713 *	0.049	−0.446 *	1.000
	(0.000)	(0.000)	(0.000)	(0.005)	(0.299)	(0.000)	(0.140)	(0.682)	(0.000)	(0.066)	(0.000)
(13) CosttoInc	−0.242 *	0.041	0.034	−0.049	−0.081 *	0.058 *	0.073 *	0.179 *	−0.230 *	0.101 *	0.392 *	−0.326 *	1.000
	(0.000)	(0.125)	(0.199)	(0.065)	(0.002)	(0.028)	(0.006)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
(14) RecurrEarnPower	0.560 *	0.082 *	0.072 *	0.040	0.111 *	−0.016	−0.068 *	−0.096 *	0.455 *	0.177 *	−0.191 *	0.724 *	−0.404 *	1.000
	(0.000)	(0.002)	(0.007)	(0.132)	(0.000)	(0.535)	(0.011)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
(15) NetLoansTotAs~s	−0.232 *	−0.044	0.233 *	−0.031	−0.136 *	0.248 *	−0.385 *	−0.147 *	−0.186 *	0.220 *	−0.086 *	−0.131 *	−0.004	−0.095 *	1.000
	(0.000)	(0.101)	(0.000)	(0.250)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.001)	(0.000)	(0.886)	(0.000)
(16) Solvency	−0.085 *	0.054 *	−0.009	−0.003	0.014	−0.297 *	0.305 *	0.966 *	0.037	0.334 *	0.332 *	0.039	0.142 *	−0.051	−0.149 *	1.000
	(0.001)	(0.043)	(0.733)	(0.905)	(0.605)	(0.000)	(0.000)	(0.000)	(0.159)	(0.000)	(0.000)	(0.143)	(0.000)	(0.055)	(0.000)

*** p < 0.01, ** p < 0.05, * p < 0.1.

illustrates the pairwise correlations among the key index in Table 1 to be used in forthcoming steps. p-values for the significance of the correlation indexes are also reported. As may be observed, most correlations were evidenced as affordable.

Empirical results in Table 2 for the decomposed ROE are of interest for BTIR application. In fact, most of them are very significant, confirming that focusing on decomposed ROE to perform the panel regression for T-ROE estimations is a good choice.

From ORBIS, we extracted the ratios and indexes representing the independent variables involved in the regression. The only index that we have computed is the decomposed ROE (i.e., the dependent variable); in fact, we computed according to ECB (2010), following the method described previously.

The estimations were performed using a panel regression, whose coefficients will be instrumental to compute the Threshold-ROE, and therefore the measure of the rating.

Table 3. Panel regression (with fixed effects for banks and years) for T(ROE) discovery. We considered decomposed ROE (measured as addressed by ECB (2010)) as the dependent variable and ratios describing the major characteristics of the business of the banks as independent variables (directly extracted from ORBIS). The complete sample is made up of 142 Italian banks and the time span is from 2011 to 2020.

Independent Variables	Dependent Variable: Decomposed ROE
NPL/Gross Loans	−0.00300 *
	(−3.70)
NPLs/Total Assets	1.211 ***
	(4.57)
NCO/Average Gross Loans	0.000592
	(0.27)
NCO/Net Income before Loans less Provisions	−0.0000228
	(−0.89)
Impaired Loans/Equity	−0.000845 ***
	(−3.47)
Equity/Net Loans	−0.000108 *
	(−2.56)
Equity/Total Liabilities	0.0119 **
	(3.12)
Profit Margin	0.00148 ***
	(3.50)
Net Interest/Average Assets	−0.00136
	(−0.37)
Non-Interest Expenses/Average Assets	0.0113 ***
	(3.46)
ROA	0.107 ***
	(6.48)
Cost-to- Income	0.0000369
	(0.66)
Recurring Earning Power	0.000375
	(0.07)
Net Loans/Total Assets	−0.00107 ***
	(−7.17)
Solvency	−0.0267 ***
	(−4.91)
_cons	0.176 ***
	(6.83)
N	1420
adj. R2	0.8037

t statistics in parentheses. * p < 0.05, ** p < 0.01, *** p < 0.001.

shows the main estimation results of the panel regression.

As usual, when using data from financial reports, a certain level of endogeneity between the variables may exist and can affect the significance of the regression. However, this issue is less relevant for our purposes, since the panel regression is chiefly instrumental to determine the T(ROE) and to understand the correlation and importance of the variables part of the balance sheet, which should be paid more attention by the internal appraisers of the small and medium banks. Accordingly, the BTIR methodology (as the original IR) mainly requires good fittings from the regressions to assess the required performance given the business model adopted by the banks. Consequently, after investigating those correlations, we were able to proceed with the clustering of the banks according to the goodness of their performance (indeed, measured as the mix of the indexes resulting significant). For this reason, as we recognize the presence of endogeneity, it is not important to eliminate it completely: our main goal is to detect the most significant variables which allow us to create the rating. Nevertheless, a battery of robustness tests can be found in Appendix C.

The panel regression conveys that all the independent variables were significant, with a significance level of 1%, apart from Equity/Total Liabilities (5%), NPL/Gross Loans, Equity/Net Loans (10%), and NCO/Average Gross Loans, NCO/Net Income before Loans less Provisions, Recurring Earning Power, and Net Interest/Average Assets, which were not significant and, consequently, will not be used in the computation of the “Threshold-ROE”.

The panel estimates are interesting. The interpretation offered by Table 3 is that the variables linked to efficiency, such as ROA, cost to income, and recruiting, are fundamental. It seems important to consider the dynamic component of revenge. Interestingly, ROA seems more important in determining the improvement of the ROE rating. In an in-depth analysis, this is in line with the fact that ROA is a less static element than other capital variables and therefore can be effectively managed by bank managers.

For each bank included in the sample, we computed T-ROE by using the above regression equation. The results were then compared with the P-ROE computed sourcing data from the specific bank financial reports. While the positive spread separated 66 banks (46% of the sample) with good standing according to BTIR from the rest of the sample (76 banks, 54%), the exponential transformation provided a clearer picture of the sample distribution, as shown in Figure 2.

Based on the results depicted in Figure 2, it can be observed that all but 1 of the 142 banks included in the sample are very concentrated around the origin of the chart. In fact, none of the banks were included in the group with outstanding BTIR (i.e., BTIR ∈ (1/2, 1]). Similarly, none of those with negative BTIR show catastrophic performance (i.e., BTIR ∈ [−1, −1/2]). We may conclude that the sample is made up of “very normal” banks. Indeed, this is an ideal condition to test the actual capability of BTIR to catch the heterogeneity inside the sample. Given the above data concentration, only the algebraic sign will be used for the forthcoming discussions.

4. Discussion and Future Developments

In order to double check the goodness of the banks, we have considered two measures widely used in bank supervision and auditing: (i) non-performing loans/gross loans, where the four clusters are: “good”, for the interval [0 to 7%), “not so good”, for [8% to 15%), “bad”, for [16% to 23%), and “very bad”, for [24% to 30%], and (ii) non-performing loans/total assets, where the four clusters are: “good”, for the interval [0 to 6%), “not so good”, for [7% to 13%), “bad”, for [14% to 20%), and “very bad”, for [21% to 25%]. Considering the Financial Stability Report signed by (Banca d’Italia 2019), the level of Gross NPLs ratio was around 13.9% and that of Net NPLs was about 7% (both calculated in relation to total loans, including interbank and central bank exposures). In the Financial Stability Report, Banca d’Italia also projected the levels of both ratios for 2021, aiming at respectively 9.8% and 4.9%, always considering both significant and less significant institutions (i.e., less significant institutions are those banks that are not directly controlled by Central Banks). Consequently, we have set the clusters according to the averages shown in Financial Stability Reports, as these are representative of the Italian banking “population”.

Accordingly, we created eight different clusters of banks by matching each of the above indicators with figures of spreads between P(ROE) and T(ROE) and their transformation. The following schemes in

Table 4. Clustering banks according to BTIR and NPLs based on gross loans evidence (own computation): (a) results of the clustering in terms of absolute values, and (b) results of the clustering in terms of percentages composing the sample.

(a)
NPL/Gross Loans
	Good	Not Good	Bad	Very Bad	Total
Positive Rating	12	40	10	4	66
Negative Rating	27	37	12	0	76
Total	39	77	22	4	142
(b)
NPL/Gross Loans
	Good	Not Good	Bad	Very Bad	Total
Positive Rating	8%	28%	7%	3%	46%
Negative Rating	19%	26%	8%	0	54%
Total	27%	54%	15%	3%	100%

show the results for the two indicators taken as a benchmark.

The high relevance of the mismatching cluster “bad rating/good ratios” is evident (Table 4 and

Table 5. Clustering banks according to BTIR and NPLs based on gross loans evidence (own computation): (a) results of the clustering in terms of absolute values, and (b) results of the clustering in terms of percentages composing the sample.

(a)
NPL/Total Assets
	Good	Not Good	Bad	Very Bad	Total
Positive Rating	17	41	8	0	66
Negative Rating	35	35	5	1	76
Total	52	76	13	1	142
(b)
NPL/Total Assets
	Good	Not Good	Bad	Very Bad	Total
Positive Rating	12%	29%	6%	0%	46%
Negative Rating	25%	25%	4%	1%	54%
Total	36%	54%	9%	1%	100%

.): it represents about 55% of cases (64 banks out of 142) if gross loans are considered, while about 50% of cases (60 banks out of 142) if total assets are considered. The other mismatching cluster (“good rating/bad ratios”) represents only about 10% of cases if gross loans are considered and about 5% of cases for total assets. As a direct consequence, the two matching clusters involve 44% of cases when gross loans are considered and 49% when total assets are considered.

The above evidence is compliant with the general sentiment about ratings as “heard on the street” and provides some insights about it. In fact, both NPL/Gross Loans (Table 4) and NPL/Total Assets (Table 5) are punctual data with reduced capability to provide dynamic insights as well as suggestions on the persistence of the firms’ performance. This generates “surprise effects” on the dynamics of NPLs that the BTIR is able to catch in advance. In other words, the first mismatching cluster states the relevance of the risk of “anyway good” banks reverting into “anyway bad” banks as far as NPLs are concerned. There is a completely different story for the other mismatching cluster, which indicates the cases with good chances to recover from an unexpected increase of NPLs.

The gaps in figures among clusters based on Gross Loans or Total Assets are a direct consequence of the business models adopted by the specific bank. Total Assets are more significant for those intermediaries with superior relevance of monetary functions and security management in the business. Gross Loans significance is superior when loans represent a more relevant business area for the specific bank. Indeed, the small gaps shown by the empirical evidence are direct confirmation of the superior capability of BTIR to intercept the quality of the lending process of the banking system.

This evidence makes it clear that some more efforts in catching the heterogeneity of the business model are needed to improve BTIR even further. In fact, through this procedure, we adapted the integrated rating according to the banks’ characteristics, which allowed us to apply the IR methodology tailored to banks’ selected variables. As in standard IR, riskiness proved to be a crucial element that needs to be considered; indeed, banks are extremely riskier and more heterogeneous, when comparing them to normal enterprises. Past research already considered these special characteristics belonging to banks and they tried to select banks ex-ante, through a quantile regression, which provides an endogenous risk index (Koenker and Hallock 2001). Furthermore, more recent research preselected banks’ default risk in two different ways: (i) through a CoVAR to analyze which banks are riskier (Adrian and Brunnermeier 2016), and (ii) through a measure of tail risk, which indicates that banks are different from enterprises because of this excessive risk, named “tail risk” (De Nicolò and Lucchetta 2017).

Accordingly, to conduct a deeper bank and variable pre-selection, we may choose a VAR model that allows to extract the common factors, i.e., factor VAR. The VAR model is a powerful instrument to preselect the important $xs$, and it is not a usual instrument in this field, indeed it is usually applied in research about financial markets or corporate finance.

The BTIR is an important innovation which allows, through the factor VAR model, to consider the diversity across banks and the condition of global risk, by selecting the $xs$ through VAR factors.

Proposition 2.

Considering the bank “i”, it is possible to design its BTIR based on the robust extension of the IR model, preselecting the variables though a factor VAR methodology.

Proposition 2 underlines a challenging framework that consists in preselecting or clustering the relevant banks’ variables though a simple factor VAR model.

Indeed, this is our next goal in BTIR improvement.

5. Conclusions

This paper proposed an original extension of the integrated rating (IR) procedure (Mantovani et al. 2015), which was designed and used primarily for non-financial companies. The proposed “bank-tailored integrated rating” (BTIR) maintains the very same basic algorithms and theoretical background, although improvements are introduced to catch the bank heterogeneity in full. Accordingly, the approach is inherently coherent with the challenging frontier of forecasting tail risk in financial markets (De Nicolò and Lucchetta 2017), since it considers the downside risk in the theoretical framework.

We tested the efficacy of the BTIR over a sample of 142 banks, comparing BTIR results with those from indicators widely used by Bank Supervisor Authorities to assess the risks of the banking system as sourced from NPLs. The innovation we are proposing here consists in a clustering of banks according to their risk level and rating’s ranking, through a statistical procedure that takes into account the characteristics of risk and greater heterogeneity of the banks. The results were surprising: BTIR leads the standard indicators in warning about risks in more than one case, over two under investigation. The key driver of the superior BTIR capabilities relies on the caught heterogeneity of the analyzed banks through a simple panel regression, that clusters banks by heterogeneity and implicitly considers systemic risk. This occurs due to the selection process for the variables BTIR uses to estimate Threshold-ROE, as required by the investors in equity capital of the banking system, to compare with their Permanent-ROEs.

Nevertheless, the proposed methodology may be improved further, as this satisfactory test demonstrated. In fact, we are aware that by using balance sheets, we may bring about a slight loss in the quality of data, due to the potential errors in the balance sheets. This is why we are already working on future developments of the BTIR to embed a more sophisticated pre-selection of variables into the procedure, such as factor VAR (FAVAR). In the future, it is necessary to test whether a more sophisticated preselection model is better than a traditional VAR-based BTIR, as proposed in this paper. In fact, for simplicity, we believe that starting with a simple methodology is the first step of research.

The BTIR makes it possible to adapt the rating procedures to all banks, even those showing very different characteristics. In fact, the VAR allows to preselect and to evaluate markets with high systemic risk, avoiding errors due to general market conditions that may differ from country to country. In conclusion, the BTIR opens the door to a new research line of innovative ideas for the development of increasingly accurate ratings for banks, embedding the needs of macro- and micro-prudential policies.