An Innovative Job Evaluation Approach Using the VIKOR Algorithm

Abstract

Fairness is a key issue that requires the attention of human resource management practitioners. Having a robust methodical procedure for identifying the value of job positions in an enterprise is essential. Consequently, there is a need for a job evaluation system that ensures fair compensation for each position. A poorly defined job evaluation system creates the dilemma of mismatches between employees and their competencies for their responsibilities and, accordingly, their wages. This results in employee dissatisfaction, which ultimately exacerbates attrition, which is costly because of the loss of talented employees. This paper proposes a VIKOR algorithm as an innovative approach to job evaluations. Engineering-related positions in an international aviation company were analyzed to illustrate the appropriateness of the proposed approach for managing the job evaluation dilemma. The results indicate that 29 job grades would be appropriate for this firm. In addition, the proposed algorithm was found to be superior to other multiple-criteria decision-making techniques at managing the job evaluation dilemma.

1. Introduction

The feeling of fairness enhances employee morale, which can be reflected in improved organizational performance. It is clear that such feelings engender trust. Fairness, a key issue that should not be ignored in human resource management (HRM), has been defined as the ability to manage human resources with justice and honesty and without prejudice or bias (Lawson 2011). Therefore, “fairness is not an attitude … it’s a professional skill that must be developed and exercised” (Hume n.d.). Having a robust reward distribution system implies a fairness-based workplace environment (Datta 2012; Ostroff 1992; Balkin 1992; Miller 2001; Robbins 2016; Zhang et al. 2015). Consequently, having a fair reward mechanism in the employee promotion policies, along with a fair job evaluation (JE) system, is necessary (Koziol and Mikos 2019; Bosch 2015). Furthermore, JEs are seen as a methodical procedure for identifying the relative value of jobs in the enterprise to ensure fair compensation for each position (Armstrong and Taylor 2020).

JE appears to be simple; however, it is a sophisticated concept because of the subjectivity and complexity in job descriptions and analyses (Das and Garcia-Diaz 2001). The classic approaches to JEs have been implemented in various ways (i.e., quantitative and qualitative approaches) (Corominas et al. 2008). However, these approaches ignore the complexities in implementing JEs (Kahya 2006b). Multiple-criteria decision-making (MCDM) applications illustrate the practicality of adding sophisticated decision-making tools and techniques as an analytical dimension (Kahya 2006b; Kutlu et al. 2013, 2014). However, the practical integration of these tools to manage the complexity of such sophisticated processes has not been fully realized. The JE, a cornerstone of HRM, is a critical industrial relations issue; however, few studies have addressed it. To address this gap, this paper proposes the use of VIKOR (VlseKriterijuska Optimizacija I Komoromisno Resenje), an MCDM tool, as an innovative approach to JEs. Engineering-related positions in an international aviation company were analyzed to demonstrate the effectiveness of the proposed approach for managing the JE dilemma.

2. Background and Relevant Literature

2.1. Background

The many JE methods have been divided into two traditional categories: qualitative and quantitative JEs. These categories are also commonly known as non-analytical and analytical JEs, respectively (Koziol and Mikos 2019). The following four methods can be considered the most commonly known and used: ranking, grading, point factor rating, and factor comparison. The latter two are quantitative, and the former two are qualitative (Dubey 2015). The qualitative methods are older, while the quantitative methods are relatively more modern. These methods have been implemented under different names in various industries. Examples are Bedaux’s method, the Hay Guide Chart–Profile method, the Scheme of Geneva, the universal method, the National Joint Council, the JE questionnaire, and market-based JE (Adamus 2009).

The point factor method is the most used technique, and it is likely the most commonly accepted approach for analytical JEs (Armstrong and Taylor 2020) because of its simplicity and applicability (Kahya 2006b). Indeed, the point factor method has been widely applied because of its accuracy and the reliability of the outcomes (Bass and Barrett 1981; Das and Garcia-Diaz 2001). It can be considered an objective approach to the quantitative evaluation and analysis of jobs by rating several related factors in accordance with predetermined target measures (Dubey 2015). According to Armstrong and Taylor (2020), the value of a job, also known as job size, is represented by the contribution of each factor. Points are assigned to each factor, and their summation represents the worth of a specific job (i.e., its value or size) (Dubey 2015). The assigned points are based on the identified level of complexity for each job criterion (Adamus 2009). Specifically, each job is broken down into a set of elements or factors that reflect the workloads, required capabilities and competencies, and contributions of each factor.

When the point factor is applied, the weights of the selected factors can be generated by either the subjective judgments of the evaluation committee members or the application of models using optimization and/or statistical techniques (Kahya 2006b). The generation of weighted criteria using such models facilitates a firm’s creation of value-based job priorities (Kahya 2018). Having a set of weighted factors can also facilitate the job-pricing process (Weinberger 1995).

2.2. Relevant Literature

JEs have received little attention in the HRM literature; nevertheless, they have always been an attractive topic in mathematical modeling. For example, Ahmed (1989) discussed the importance of the JE process, especially in terms of factor weight allocation; thus, an effective linear programming model has been developed. To enhance objectivity, Gupta and Ahmed (1988) demonstrated an application of a linear-based goal-programming model to generate factor weights more precisely; however, the pre-emptive levels (goals) in their model were identified subjectively. This could lead to the generation of a mismatched weight for each level (Kahya 2018). Moreover, in LP/GP models, any increase in the number of factors for a set of jobs can increase the number of constraints (Kutlu et al. 2013). Das and Garcia-Diaz (2001) aimed to add reliability by developing a statistical JE model focused on determining the most appropriate evaluation factors. They used basic statistical analysis and linear correlation coefficients to more objectively quantify the value of the selected factors and jobs. Pittel (1999) developed a multiple regression-based model to generate updated factor weights on the basis of the market weight for each job. A mathematics-based point rating model has been developed to identify the most appropriate performance-based salary levels (Kareem et al. 2011).

The JE dilemma has often been considered an MCDM problem. Gupta and Chakraborty (1998) suggested that JE could be considered a managerial decision issue: specifically, an MCDM problem. Thus, they have developed a mathematical fuzzy-based MCDM model to address and to solve this issue objectively. In the same way, a JE system for 96 blue-collar jobs was developed through the use of questionnaires and interviews with Turkish metal industry executives. The focus was job factors and their corresponding weighting and levels (Kahya 2006a). The same context was also investigated through the analytic hierarchy process (AHP) (Kahya 2006b). The fuzzy analytic hierarchy process (F-AHP) was used, and the job scores were obtained through the Fuzzy Technique for Order Preference by Similarity to Ideal Solution (F-TOPSIS) (Kutlu et al. 2013). A similar approach was taken in another study (Kutlu et al. 2014). Yu and Tang (2011) aimed to improve the application of the point factor method by developing 12 operational steps for the JE procedure. This approach was enhanced by the use of statistical analysis applications and a modified AHP model. Practical compensation factors for JEs have been analytically identified within a hierarchical structure by using the interval analytic hierarchy process (IAHP), which considers the point-factor assumption (Chen and Jiang 2011). With the participation of 40 HRM professionals, the significance and influence of key JE factors and sub-factors were examined through the AHP (Doğan et al. 2014). An in-depth AHP was conducted, and statistical techniques were applied to enhance the applicability of the point factor as a JE method (Sun and Luo 2013).

3. VIKOR Algorithm

VIKOR has recently been applied and accepted academically as an authentic technique for solving MCDM problems. VIKOR applications have been used to address multifactorial problems in several research areas and industries (Mardani et al. 2016), such as manufacturing (Chatterjee et al. 2010; Devi 2011; Parameshwaran et al. 2015; Ghorabaee 2016), materiality assessment (Çalışkan 2013; Yazdani and Payam 2015), construction engineering and management (Peng 2015; Pamučar and Ćirović 2015; Tošić et al. 2015; Vahdani et al. 2013), sustainability (Quijano Hurtado et al. 2012; Martin-Utrillas et al. 2015), finance (Liu et al. 2016; Shen and Tzeng 2015; Safari et al. 2016), marketing (Chang et al. 2015), performance evaluation (Kuo and Liang 2012; Hsu 2015; Lee and Pai 2015), and HRM (Liu and Wu 2012; Mohammadi et al. 2014; Chou et al. 2014). For example, HR managers’ competencies have been measured by using VIKOR as a proposal for an effective and practical evaluation approach (Liu and Wu 2012). A project manager selection model was developed by incorporating the cybernetic analytic network process (CANP) and the quality function deployment (QFD), which were validated with the VIKOR method (Mohammadi et al. 2014). The performance of women in science and technology as intellectual HRs in 25 countries was evaluated with VIKOR (Chou et al. 2014).

The root of the VIKOR method is known as the $L_{p,i}$ metric, which can be defined as follows (Opricovic 1998; Opricovic and Tzeng 2004; Shojaei et al. 2018; El-Santawy 2012; Tzeng et al. 2005):

$$\begin{gathered} L_{p,i}={\left\{{\displaystyle \sum }_{j=1}^n{[u_j\left({\tilde{v}}_j^{+}-{\tilde{v}}_{ij}\right)/\left({\tilde{v}}_j^{+}-{\tilde{v}}_j^{-}\right)]}^p\right\}}^{\frac{1}{p}}, \\ 1\le p\le \infty \end{gathered}$$

(1)

where $u_j$ is the weight of criterion $j$; ${\tilde{v}}_j^{+}$ and ${\tilde{v}}_j^{-}$ represent the best and worst values within criterion $j$, respectively; and ${\tilde{v}}_{ij}$ is the value corresponding to alternative $i$ with respect to criterion $j$. The value of $p$ represents the tendency of the metric $L_p$ in that when $=1$, $L_{1,i}$ represents the extreme tendency for the maximum group utility. However, when $=\infty$, $L_{\infty ,i}$ represents the extreme tendency for the minimum regret (Shojaei et al. 2018; El-Santawy 2012; Tong et al. 2007; Yu 1973). Accordingly, VIKOR can be expressed in the form of a matrix in which the columns represent the criteria and the rows represent the alternatives. According to several applications in the literature (Opricovic and Tzeng 2004; Shojaei et al. 2018; El-Santawy 2012; Acuña-Soto et al. 2019; Huang et al. 2009), the VIKOR steps for solving an MCDM problem of m alternatives, (x₁, x₂, x₃, …, x_m), with respect to n criteria, (y₁, y₂, y₃, …, y_n), can be set as follows:

Step 1. Develop a decision matrix $\tilde{D}$ = (${\tilde{d}}_{ij}$)_m×n where m represents the number of alternatives and n represents the number of criteria; ${\tilde{d}}_{ij}$ is a real number that represents the value of the alternative x_i with respect to the criterion y_j:

$$\begin{gathered} \begin{array}{ccc}{y}_1& y_j& y_n\end{array} \\ \tilde{D}=\begin{array}{c}{x}_1\\ x_i\\ x_m\end{array} \left[\begin{array}{ccc}{\tilde{d}}_{11}& {\tilde{d}}_{1j}& {\tilde{d}}_{1n}\\ ⋮& ⋮& ⋮\\ {\tilde{d}}_{m1}& {\tilde{d}}_{mj}& {\tilde{d}}_{mn}\end{array}\right]. \end{gathered}$$

(2)

Step 2. Construct the normalized decision matrix $\tilde{N}$ = (${\tilde{n}}_{ij}$)_m×n in which ${\tilde{n}}_{ij}$ is calculated as follows:

$$\begin{gathered} {\tilde{n}}_{ij}=\frac{{\tilde{d}}_{ij}}{\sqrt{{\displaystyle \sum }{\tilde{d}}_{ij}^2}} where i=1, \dots , m; \\ for each j: j=1, \dots , n. \end{gathered}$$

(3)

Step 3. Determine the weight corresponding to each criterion $j$, u_j ϵ [0, 1]:

$$u_1,+u_2+\dots +u_j=1.$$

(4)

Step 4. Develop the weighted normalized decision matrix $\tilde{C}$ = (${\tilde{c}}_{ij}$)_m×n in which ${\tilde{c}}_{ij}$ is calculated as follows:

$${\tilde{c}}_{ij}=u_j\times {\tilde{n}}_{ij}.$$

(5)

Step 5. Find the positive ideal and negative solutions as follows:

$$K^{+}=\left\{{\tilde{c}}_1^{+}, \dots , {\tilde{c}}_n^{+}\right\} Positive ideal solution$$

(6)

$$K^{-}=\left\{{\tilde{c}}_1^{-}, \dots , {\tilde{c}}_n^{-}\right\} Negative ideal solution$$

(7)

where

$$\begin{gathered} {\tilde{c}}_i^{+}=\left\{\max \left({\tilde{c}}_{ij}\right) if j ϵ \ddot{J};\min \left({\tilde{c}}_{ij}\right) if j ϵ \stackrel{⃛}{J}\right\}, \\ j=1, \dots , n \end{gathered}$$

(8)

$$\begin{gathered} {\tilde{c}}_i^{-}=\left\{\min \left({\tilde{c}}_{ij}\right) if j ϵ \ddot{J};\max \left({\tilde{c}}_{ij}\right) if j ϵ \stackrel{⃛}{J}\right\}, \\ j=1, \dots , n \end{gathered}$$

(9)

$$\ddot{J} represents the set of benefit critria$$

$$\stackrel{⃛}{J} represents the set of cost critria.$$

Step 6. Find ${\widehat{S}}_i$ and ${\widehat{R}}_i$ where:

$${\widehat{S}}_i={\displaystyle \sum }_{j=1}^n\left({\tilde{c}}_j^{+}-{\tilde{c}}_{ij}\right); i=1, \dots , m$$

(10)

$${\widehat{R}}_i={max}_i\left({\tilde{c}}_j^{+}-{\tilde{c}}_{ij}\right); i=1, \dots , m.$$

(11)

Step 7. Calculate the ranking indexes (${\widehat{Q}}_i$) as follows:

$${\widehat{Q}}_i=\ddot{\lambda }\left[\frac{\left({\widehat{S}}_i-{\widehat{S}}^{-}\right)}{({\widehat{S}}^{+}-{\widehat{S}}^{-})}\right]+\left(1-\ddot{\lambda }\right)\left[\frac{\left({\widehat{R}}_i-{\widehat{R}}^{-}\right)}{({\widehat{R}}^{+}-{\widehat{R}}^{-})}\right]$$

(12)

$$\mathrm{where}{\widehat{S}}^{+}=ma{x}_i {\widehat{S}}_i; {\widehat{R}}^{+}=ma{x}_i {\widehat{R}}_i;$$

$${\widehat{S}}^{-}=mi{n}_i {\widehat{S}}_i; {\widehat{R}}^{-}=mi{n}_i {\widehat{R}}_i.$$

$\ddot{\lambda }$ ϵ [0, 1] is the weight for the strategy of maximum group utility (majority rule), and $(1-\ddot{\lambda ) }$ is the weight of the “regret”. Then, alternatives are sorted in descending order according to the ${\widehat{S}}_i, {\widehat{R}}_i,\mathrm{and}{\widehat{Q}}_i$ values. ${\widehat{S}}_i$ sorts the alternatives with respect to the maximum group utility (majority rule), and $\ddot{\lambda }$ > 0.5 should be used as a decision-making strategy. In contrast, ${\widehat{R}}_i$ sorts the alternatives with respect to the minimum “regret”; $\ddot{\lambda }$ < 0.5 should be used for this strategy. Usually, $\ddot{\lambda }$ = 0.5 is employed as a reflection of the “consensus” strategy. The best alternative, x₁, has the minimum ${\widehat{Q}}_i$ value, and the second best, x₂, has the second lowest value of ${\widehat{Q}}_i$, and so on. The x₁ alternative is considered a compromise if the following two conditions have been met:

• Condition (Condit.) 1: Acceptable advantage:

  Q(x₂) − Q(x₁) ≥ DQ

  where DQ = 1/(m − 1), m represents the total number of alternatives.
• Condit. 2: Acceptable stability in decision-making:
  The x₁ alternative must also be ranked best by ${\widehat{S}}_i \mathrm{and}/\mathrm{or}{\widehat{R}}_i$.
  If one of these conditions is not met, a set of compromise solutions is considered:
• Alternatives x₁ and x₂ represent the compromise solutions if only the “acceptable stability in decision-making” condition is not met, or
• Alternatives x₁, x₂, …, x_M represent the compromise solutions if the “acceptable advantage” condition is not met; x_M is identified by the relationship Q(x_M) − Q(x₁) < DQ, for maximum x_i.

It is worth noting that almost all VIKOR applications employ other MCDM tools, specifically, the AHP (Mardani et al. 2016; Rezaie et al. 2014; Wu et al. 2012; Chen and Chen 2010; Tsai and Chang 2013; Dincer and Hacioglu 2013). Thus, AHP is usually executed to generate the criteria weighting in MCDM models (Step 3, as illustrated above in the VIKOR steps). Indeed, AHP is a well-known MCDM tool that has been widely used to solve industrial issues. It was developed by Saaty (1977, 1987) to address the MCDM problem through mathematical operations and matrices to generate the weighting for the criteria and/or alternatives. In AHP, all the criteria and/or alternatives are involved in the pairwise comparisons using Saaty’s 1–9 scale of measurement. The general steps in the AHP, including Saaty’s scale, are summarized in

Table 1. AHP steps.

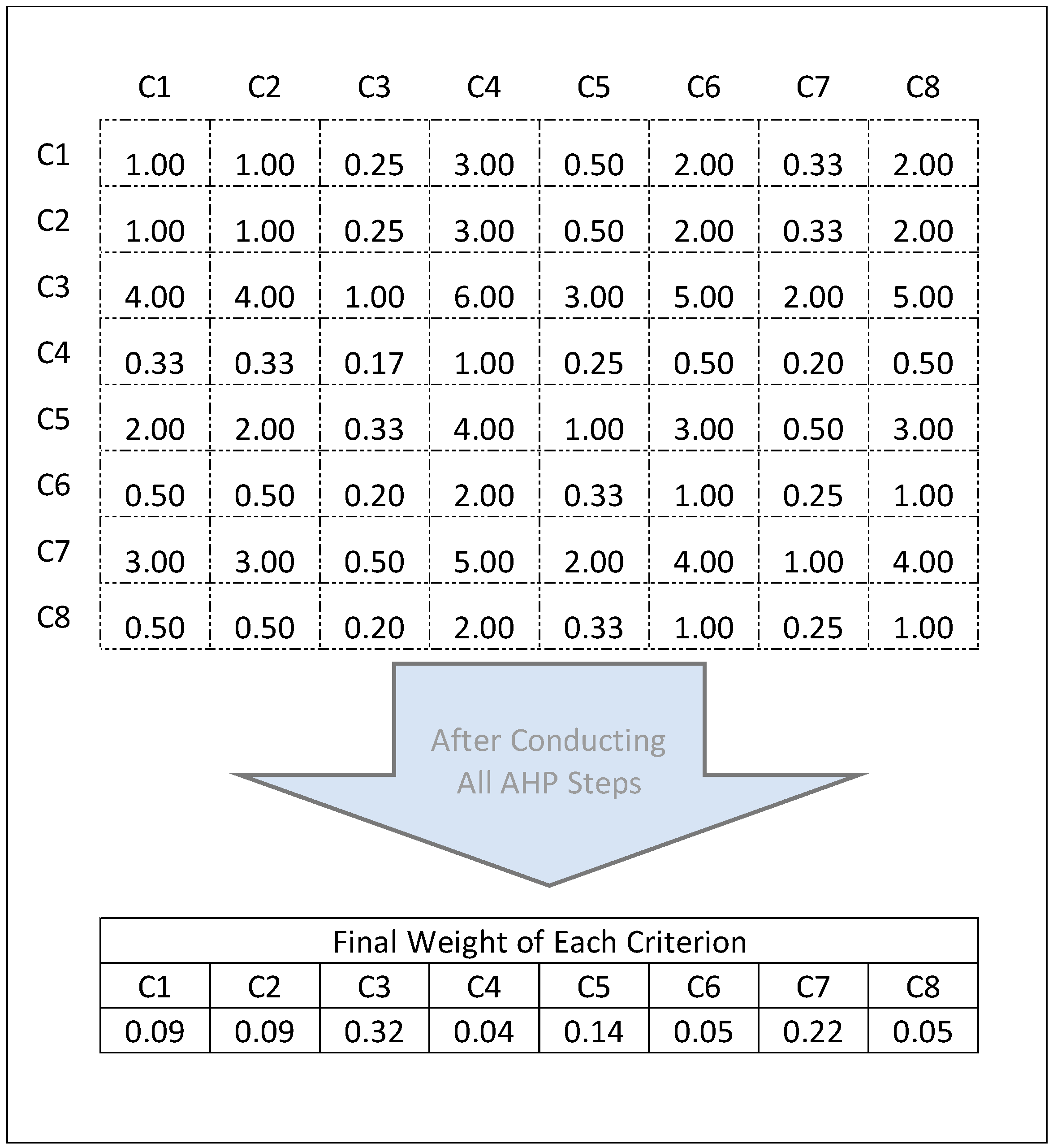
Step 1: List the goal, criteria, sub-criteria, and decision alternatives.

Step 2: Develop a pair-wise comparison matrix (size n × n) for each set of criteria, sub-criteria, or alternatives to be compared by using Saaty’s 1–9 scale of measurement.

Step 3: Develop a normalized matrix for each comparison by dividing each number in a column of the pairwise comparison matrix by its column sum.

Step 4: Develop the priority vector by averaging each row of the normalized matrix for each set of comparisons. Each element (criterion, sub-criterion, or alternative) will have a score.

Step 5: Calculate the overall priority (weights) by multiplying the criteria scores with respect to their corresponding goal (or by multiplying the sub-criteria scores with respect to their corresponding criterion; or by multiplying the alternative scores with respect to their corresponding criterion or sub-criterion).

Step 6: Calculate consistency ratio (CR) = consistency index CI/random index (RI), where CI = (λmax − n)/(n − 1); RI = 0.58, 0.90, 1.12, 1.24, 1.32, and 1.41 when n = 3, 4, 5, 6, 7, and 8, respectively; n is the size of the matrix (number of criteria or alternatives).

. Further details regarding the computations of the consistency ratio in the AHP can be found in (Al-Harbi 2001).

4. Application

The proposed VIKOR approach to JEs was applied to a leading international aviation company that provided engineering and maintenance services at more than 50 local and international airports. A group of experts representing 16 different departments (MD Office (MDO), Aircraft Maintenance (AM), Aircraft Component Maintenance (ACM), Supply Chain (SC), Power Plant Maintenance (PPM), Technical Training (TT), Technical Contract (TC), Information Technology (IT), Plants & Equipment Maintenance (PEM), Engineering (E), Safety & Technical Quality Assurance (STQA), Maintenance Control Center (MCC), Human Resources (HR), Finance (F), Technical Sales & Marketing (SM), and Administration (ADM)) were carefully selected. All experts were (1) skillful, professional, and well-educated; (2) occupying critical managerial or HRM positions; and (3) capable of dealing with different technical and managerial aviation issues. Expert opinions were used to rate the (1) JE criteria and (2) job position (JP) against each criterion. Saaty’s 1–9 scale of measurement was employed to perform the AHP pairwise comparisons to extract the weight for eight JE criteria: (C1) technical aviation knowledge, (C2) managerial knowledge, (C3) education, (C4) professional development level, (C5) work experience, (C6) communication skills, (C7) job responsibility, and (C8) decision-making skills. AHP was applied to facilitate the execution of Step 4 in the VIKOR algorithm. Thus, experts used linguistic terms to rate the importance of each JP with respect to each JE criterion (

Table 2. Linguistic terms used in performing VIKOR.

Criteria →	Technical Aviation Knowledge (C1)	Managerial Knowledge (C2)	Education (C3)	Professional Development (C4)	Work Experience (C5)	Communication Capabilities (C6)	Job Responsibilities (C7)	Decision Making Skills (C8)
Questions to be answered by Experts in order to Rate Each Job Position	To what extent do you think that “Technical Aviation Knowledge (C1)” is required for Job# x?	To what extent do you think that “Managerial Knowledge (C2)” is required for Job# x?	What is the minimum required level of education (i.e., degree) for Job# x?	What kind of professional development/training is more appropriate/suitable to be provided for Job# x?	What is the required level of experience for Job# x?	What kind of communication capabilities are required for Job# x?	To what extent do you think that “Job Responsibilities (C7)” are critical for Job# x?	To what extent do you think that “Decision Making Skills (C8)” are critical for Job# x?
Linguistic Terms Used for Rating Each Job Position (i.e. used when answering the corresponding question)	Considerably Required (CR)	Considerably Required (CR)	Bachelor with Preference of Higher Degree (BH)	Strategic & Decision Making (SD)	Very High Experience (>10)	Leading & Directing (L)	Extremely Critical (EC)	Extremely Critical (EC)
	Required (R)	Required (R)	Bachelor (B)	Advanced Managerial (AM)	High Experience (8–10)	Guiding & Controlling (G)	Critical (C)	Critical (C)
	Occasionally Required (OR)	Occasionally Required (OR)	Diploma (D)	Managerial (M)	Proper Experience (6–8)	Sending & Receiving (S)	Occasionally Critical (OC)	Occasionally Critical (OC)
	Rarely Required (RR)	Rarely Required (RR)	High School (HS)	Administrative (AD)	Acceptable Experience (4–6)	Basic (BA)	Rarely Critical (RC)	Rarely Critical (RC)
	Not Required (NR)	Not Required (NR)		Fundamental (F)	Little Experience (2–4)		Not Critical (NC)	Not Critical (NC)
					Minimum Experience (<2)
The Corresponding Numerical Rating Values for Each Linguistic Term	CR → 9 R → 7 OR → 5 RR → 3 NR → 1 2, 4, 6, and 8 are in-between judgmental rating values	CR → 9 R → 7 OR → 5 RR → 3 NR → 1 2, 4, 6, and 8 are in-between judgmental rating values	BH → 4 B → 3 D → 2 HS → 1	SD → 5 AM → 4 M → 3 AD → 2 F → 1	(>10) → 6 (8–10) → 5 (6–8) → 4 (4–6) → 3 (2–4) → 2 (<2) → 1	L → 6 G → 4 S → 2 BA → 1 5 and 3 are in-between judgmental rating values	EC → 9 C → 7 OC → 5 RC → 3 NC → 1 2, 4, 6, and 8 are in-between judgmental rating values	EC → 9 C → 7 OC → 5 RC → 3 NC → 1 2, 4, 6, and 8 are in-between judgmental rating values

; Conducting Step 1 in VIKOR). Expert involvement in this brainstorming exercise occurred during consecutive meetings to seek consensus in the AHP pairwise comparison and VIKOR Step 1 matrices. As a result of the large number of JPs to be compared and the complexity of the evaluation process, these consecutive meetings were held over a one-year time horizon. Figure 1 shows the weight extraction process for each criterion in the AHP. Figure 2 illustrates the process of using linguistic terms to rate each JP on the basis of each JE criterion.

It is worth noting that job evaluation criteria (also known as factors) are conventionally classified into four main categories: skills, responsibilities, efforts, and working conditions (Kahya 2006b). Usually, these criteria incorporate several sub-criteria from which companies select a customized set of criteria that suits their industry. Thus, a set of criteria (extracted from the literature) was presented to the experts in order to compare these criteria with the eight existing criteria that are being used in the company. The purpose of such an exercise is to explore to what extent a company’s criteria are aligned with those that are commonly accepted in literature. Just a few slight, trivial, and typographical changes have been corrected, which indicates that the company’s existing criteria are aligned with the literature, and accordingly, confirmed for the purpose of this study.

Additionally, it is very important herein to note that according to Yin (2017), case studies can be generalized analytically either using the replication logic when the research design incorporates two or more case studies; or by employing the approach of theory development when the research is designed based on a single case study as presented herein and as conducted previously in various MCDM research attempts (Siachou and Vlachos 2017; Narayanamurthy et al. 2018), including VIKOR applications (Luthra et al. 2017). Yin stressed that a case study should be considered as an “opportunity to shed empirical light on some theoretical concepts or principles … that is, analytic generalization”, and such a research design is relatively being considered as a unique form of validation, as it is entirely different from the classical statistical generalization. The constructive research approach belongs to the interventionist research paradigm (Morris et al. 2018), which is also known as a development research paradigm (De Villiers 2012). Dumay and Baard (2017) define interventionist research as a case study-based research approach through which researchers and practitioners (managers in organizations) work together in order to design and implement solutions in an interventional approach for the purpose of solving real-life issues. In turn, the constructive research approach aims at solving real-world issues through innovative employment of step-by-step practical procedures (i.e., constructions such as mathematical algorithms) in order to develop a kind of theoretical contribution corresponding to a certain field of knowledge (Lukka 2003). Indeed, under the umbrella of a constructive research approach, several research works have been conducted in order to develop empirical applications corresponding to the theory of MCDM (Antinmaa 2012; Morris et al. 2018; Lin et al. 2020; Tsolas 2020).

5. Results and Discussion

The contribution of the VIKOR algorithm to JE can be illustrated by an analysis of the results (Figure 3 and Figure 4). The current or customized applications of the VIKOR algorithm can be clarified by three processes embedded in the computations of the proposed model: (1) grade assignment, (2) job position assignment, and (3) job category adjustment. Thus, distinguishing among them is very important.

5.1. Grade Assignment

The grade assignment process emerged from the application of the VIKOR algorithm through which job positions are prioritized. As previously illustrated in the VIKOR steps, JPs are ranked in descending order by their Q scores. Therefore, for n JPs (J_i, J_i+1, … J_n), J_i is ranked first in Grade n only if the acceptable advantage condition and the acceptable stability in decision making are satisfied. Otherwise, J_i and J_i+1 are considered compromise solutions if only the acceptable stability condition is not satisfied. However, if the acceptable advantage condition is not satisfied, then the compromise solutions are represented by J_i, J_i+1, …, J_M for the maximum M that satisfies the following: Q_JM − Q_Ji < DQ, where DQ = 1/(J − 1) or 0.007692 in the current study.

Hence, Grade n is assigned to only one JP, J_#1 (CEO), which has the lowest Q value because both conditions (acceptable advantage and acceptable stability) are satisfied (Figure 3). It can also be observed that J_#87 (aircraft engineering director) has the second lowest Q value, which implies the immediate assigning of Grade n − 1. Moreover, because the associated value of Q_i+1 − Q_i = 0.00575 (i.e., = 0.053507 − 0.045577 = 0.00575), which is less than the value of DQ (i.e., 0.00575 < 0.007692), the acceptable advantage condition (Condit. 1) is not satisfied. It should be noted that the acceptable stability condition (Condit. 2) is satisfied. Accordingly, all JPs situated below J_#87 also represent a set of compromise solutions for Grade n − 1 as long as their corresponding values of Q_M − Q_i < DQ (i.e., <0.007692). Consequently, Grade n − 1 is assigned to J_#87 and three additional JPs (Figure 3). Their corresponding values, Q_M − Q_i, are less than DQ: specifically, “Q_M − Q_i”’s values for J_#2, J_#21, and J_#46 = 0.005752, which is less than DQ (<0.007692).

5.2. Job Position Assignment

Once the grade assignment process is completed, the job position assignment process can be applied with respect to two job-resizing actions. One of the outcomes is the creation of what can be referred to as VIKOR-based job-resizing actions: (1) upward-modulated and (2) downward-modulated. Accordingly, it can be clearly seen (Figure 4) that one of the director-level positions, J_#87 (aircraft engineering director), is situated above the vice president positions. Such an outcome reveals the necessity for creating a new vice president for aircraft engineering position. Consequently, four vice president positions are supposed to represent Grade n − 1 (Figure 4). It can be observed that almost all the director-level positions are assigned to Grades n − 2, n − 3, n − 4, and n − 5. However, the sole assistant vice president position (J_#32, assistant vice president for supply chain management) and two managerial job positions (J_#53, power plant logistics manager and J_#37, inventory manager) are situated in these director-level positions. This implies that two managerial positions (J_#53 and J_#37) have to be resized (upward-modulated action) through the creation of two director-level positions dedicated to power plant logistics and inventory management. Similarly, the sole assistant vice president position is supposed to be resized into a director-level position to manage the supply chain management department. Several upward-modulated actions and downward-modulated actions are illustrated in Figure 4.

5.3. Job Category Adjustment

The results indicate that most of the current managerial positions (before the application of the category adjustment process) corresponded to Grades n − 6, n − 7, n − 8, n − 9, n − 10, and n − 11. However, the proposal is for only Grades n − 6 and n − 7 to be assigned to the managerial category (Proposed Category column in Figure 4). The reason is that if Grade n − 8 is assigned to the managerial positions, then the proposed section manager category will have no representatives from seven departments (TC, TT, IT, PEM, E, STQA, and MCC). Therefore, the proposal is for Grade n − 8 to be assigned to the section manager category. It should be noted that assigning Grades n − 6 and n − 7 to the managerial positions satisfies the proposed condition that, as far as possible, at least one representative from each department should belong to each JP category. Such a condition is very important for ensuring the harmonization of the current and proposed departmental structures. By continuing the category adjustment process with respect to the proposed condition above, all JPs can then be assigned to their corresponding categories (Figure 4).

5.4. General Discussion

Since personal selection is a challenging dilemma, HR authorities in any firm are responsible for handling such an issue by considering different MCDM research attempts, including VIKOR applications (Krishankumar et al. 2020). Hence, although the issue of personal selection has commonly and traditionally been addressed using simplified criteria-oriented approaches (Thomas 2004; Blue et al. 2013; Thorndike 1949; Robertson and Smith 2001; Schmit and Ryan 1993), several research attempts have employed various sophisticated method-oriented approaches (Safari et al. 2014; Kabak et al. 2012; Islam and Rasad 2005; Gibney and Shang 2007; Boran et al. 2008). Indeed, Alguliyev et al. (2015) emphasized that personnel evaluation is a critical HRM issue due to its nature of multicriteria and its complexity through the existence of various quantitative as well as qualitative aspects, which imply that for such an evaluation process, subjective, unreliable, and/or invalid approaches “no longer suffice”. Hence, such an issue “is a complicated MCDM problem in which candidates must be prioritized in a rational manner and a suitable personnel must be selected” (Krishankumar et al. 2020). Therefore, VIKOR has been employed empirically in several HRM research works that incorporate personnel and/or job criteria in order to develop innovative models for handling such a dilemma (Alguliyev et al. 2015; Krishankumar et al. 2020). From this point of view, the applicability of VIKOR can be extended to handle the issue of job evaluation as a rational extension of the issue of personnel selection; particularly, because both of the issues are identical in a sense that any criterion in any of their different models can be mutually set for exchangeable employment.

In any MCDM problem, tools such as AHP, TOPSIS, VIKOR, ELECTRE, PROMETHEE, and DEA are effective and commonly employed to evaluate a various set of alternatives considering multiple and conflicting criteria (Chang et al. 2013; Yu et al. 2013; Paksoy et al. 2012) such as in the case of personnel and/or job evaluation problem (Krishankumar et al. 2020). These techniques can assist practitioners to be cognizant of as well as able to deal with the integrated assessments’ outcomes (Alguliyev et al. 2015). However, not all MCDM tools and techniques share the same applicability. For instance, AHP has always been criticized because it limits the proposed solution into a static form of a hierarchal structure (Hellebrandt et al. 2018) and due to the limited number of the involved criteria and alternatives in any AHP decision-making model (Shih et al. 2007). Likewise, as a rule of thumb in DEA applications, the number of alternatives should be greater than the total number of inputs and outputs (i.e., total number of criteria) in order to ensure accurate implementation of the DEA model (Alidrisi et al. 2019; Guevel 2020). However, among these MCDM approaches, it can be clearly noticed that TOPSIS and VIKOR are the most suitable and applicable for handling the personnel/job evaluation issue due to the capability of constructing an MCDM model with an unlimited number of criteria and alternatives, the clarity of the outcomes, and the ability to deal easily with different kinds of characteristics and decision alternatives (Parameshwaran et al. 2015). In particular, Alguliyev et al. (2015) stated that one of the attributes of VIKOR is that the aggregate function always generates the best results that are closed to the ideal solutions, which is not the case in TOPSIS. They clearly stated that VIKOR, specifically, is a useful MCDM method “in a situation where the decision-maker is not able or does not know how to express preference in the beginning of system design”. They concluded that “VIKOR ranks alternatives and determines the solution named compromise that is the closest to the ideal”.

6. Conclusions

A poorly defined JE system eventually creates the dilemma of mismatches between employee competencies and responsibilities and, consequently, wages. This results in employee dissatisfaction, which ultimately exacerbates staff attrition (i.e., employee turnover), which is costly because of the loss of talented employees. Indeed, the loss of human capital creates the conditions for a series of uncontrollable costs and expenses and the loss of potential opportunities. This paper argues that poorly defined and/or ill-managed job evaluation systems represent a key HRM issue that should be addressed. Thus, VIKOR has been proposed as a decision-analysis tool to manage the complexities of the JE process.

The results indicate that 29 grades are appropriate for the investigated aviation firm. This outcome was facilitated by the two implicit conditions in the VIKOR algorithm: acceptable advantage condition and acceptable stability condition. Thus, for such applications, VIKOR is superior to MCDM techniques. These two conditions represent the mechanism through which the grade assignment process was executed. The resulting ranked list of job titles with the corresponding grades indicates the necessity for conducting the job positions assignment process as an inevitable consequence of the Q score determined for each position. This was illustrated in the introduction of the two VIKOR-based job-resizing actions: (1) upward-modulated action and (2) downward-modulated action. For example, the upward-modulated action indicates that J_#73 (systems support analyst) deserves to be assigned Grade n − 10 as a “section manager” rather than an “analyst—in the specialist category” (which is relatively far below the top management positions). Inverse inferences can be made for the downward-modulated action. Such actions imply the need for category determinations to delineate the scope of each category, as illustrated above. In sum, this paper introduces VIKOR as a tool to improve the precision of JEs. The idea of matching the generated compromise solutions in the form of grades indicates the uniqueness of the technique in terms of its compatibility and flexibility.

The present study asserts that the proposed VIKOR algorithm helps to determine grades, to suggest suitable job positions within each grade, and to define the scope of each job category. However, JE or HRM issues should be examined in detail by practitioners, decision-makers, and/or academicians. For example, the acceptance of the upward-modulated action and the downward-modulated action requires the development of a new job description and analysis, and this, in turn, implies changes in the responsibilities and worth of each job. Decision-makers are responsible for these strategic HRM decisions because the consequences of modifying several job positions could lead to the very costly process of reforming the organizational structure. The costs of such a project must be carefully weighed against those associated with the loss of dissatisfied employees. Such issues offer several directions for future JE and HRM research and innovative managerial practices. Finally, HRM authorities and responsibilities for such a critical and huge strategic initiative/exercise should be carefully monitored and controlled in order to ensure a fair job evaluation process/project. Third parties might be employed to play their role as consultation agencies in order to handle such a managerial dilemma. MCDM applications should be expanded to consider various HRM practical issues such as job evaluation. Although many HRM aspects have been handled using various MCDM techniques such as AHP, TOPSIS, and DEA, there is still room for employing several tools, such as VIKOR, to handle job evaluation dilemmas in particular. Yet, only limited research attempts (i.e., MCDM applications) have shown such a contribution in the relevant literature.