Quantile Risk–Return Trade-Off
Abstract
1. Introduction
2. Data
2.1. Stock Returns
2.2. Risk Measures
3. Econometric Method
4. Empirical Analysis
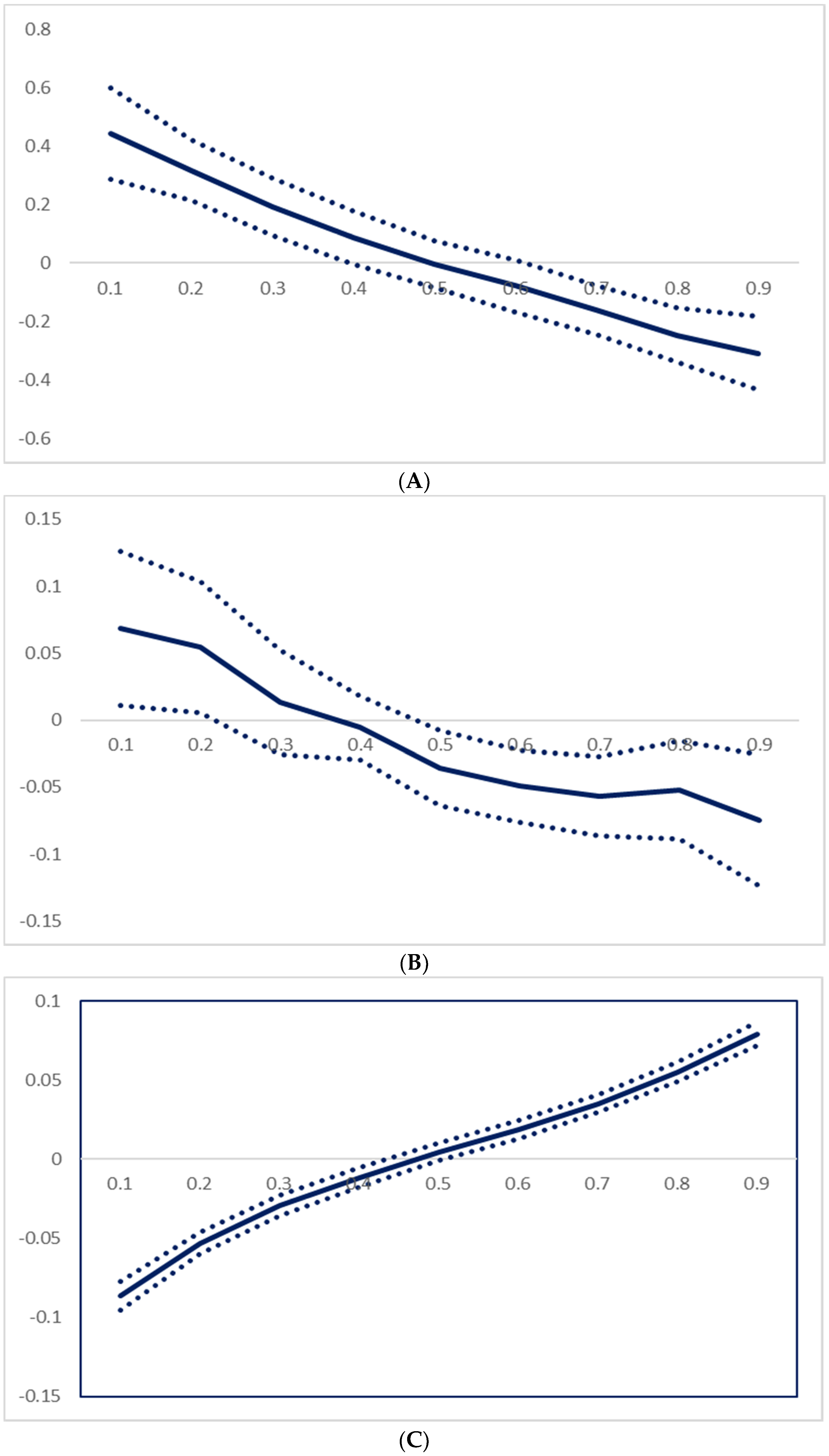
4.1. Market Portfolio
4.2. Industry Portfolios
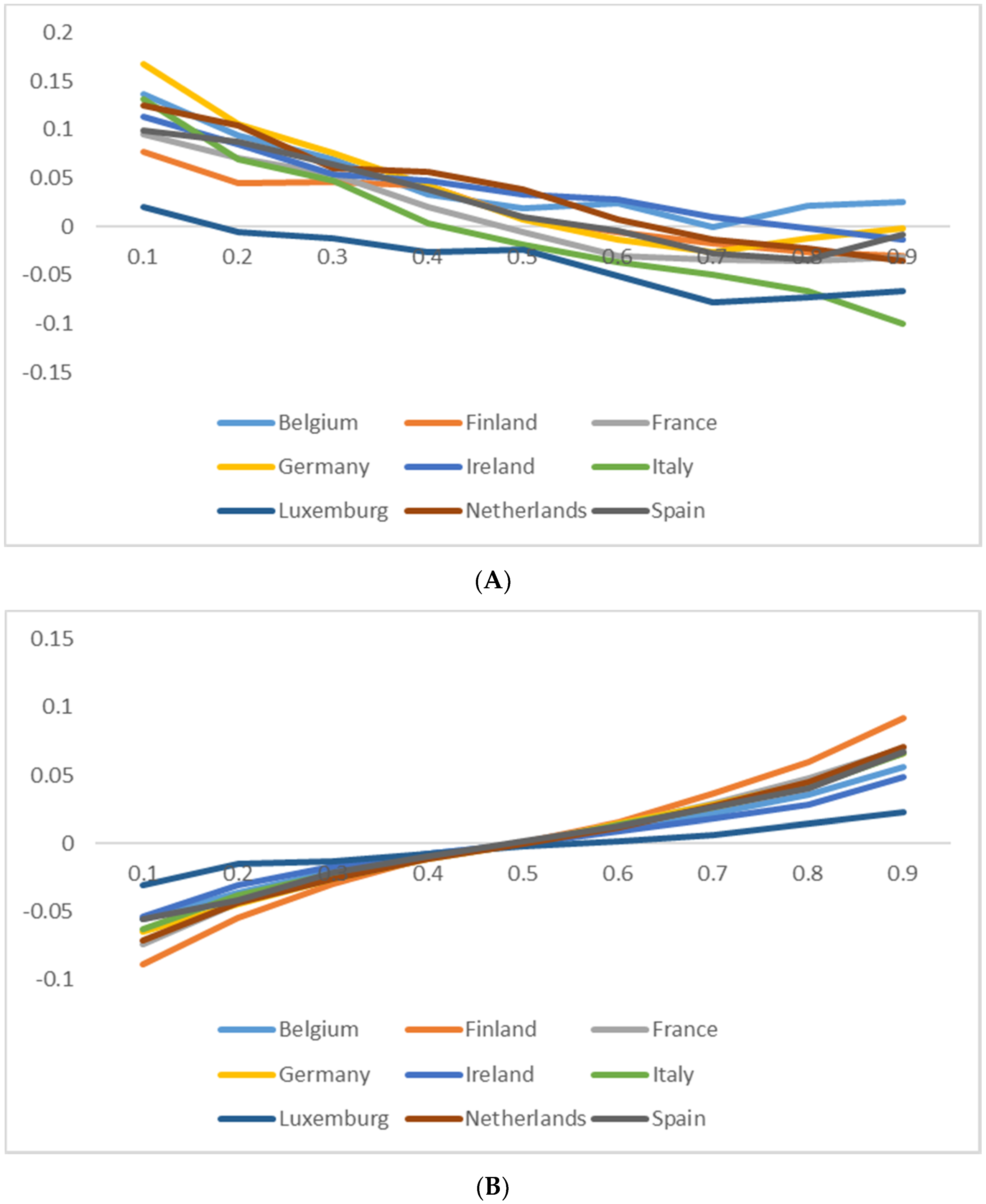
4.3. European Market Portfolios
4.4. Skewness and Kurtosis Effects
4.5. Subsample Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | The US stock returns and risk free interest rate are gratefully available from Kenneth French’s data library. The market portfolio is the value-weight return of all CRSP firms listed on NYSE, AMEX, or NASDAQ, cf. Fama and French (1993). |
| 2 | The Eurozone stock returns and euro LIBOR rate are available from DataStream. |
| 3 | The VIX data are available from CBOE’s webpage with VIX historical price data. |
| 4 | The quantile regression estimation follows Aslanidis and Christiansen (2014). |
References
- Adrangi, Bahram, Arjun Chatrath, Joseph Macri, and Kambiz Raffiee. 2019. Dynamic Responses of Major Equity Markets to the US Fear Index. Journal of Risk and Financial Management 12: 156. [Google Scholar] [CrossRef]
- Adrian, Tobias, Daniel Stackman, and Erik Vogt. 2019a. Global Price of Risk and Stabilization Policies. IMF Economic Review 67: 215–60. [Google Scholar] [CrossRef]
- Adrian, Tobias, Richard K. Crump, and Erik Vogt. 2019b. Nonlinearity and Flight-to-Safety in the Risk-Return Trade-Off for Stocks and Bonds. Journal of Finance 74: 1931–73. [Google Scholar] [CrossRef]
- Allen, David E., Michael McAleer, Robert Powell, and Abhay K. Singh. 2013. A Non-Parametric and Entropy Based Analysis of the Relationship between the VIX and S&P 500. Journal of Risk and Financial Management 6: 6–30. [Google Scholar]
- Aslanidis, Nektarios, and Charlotte Christiansen. 2014. Quantiles of the Realized Stock–Bond Correlation and Links to the Macroeconomy. Journal of Empirical Finance 28: 321–31. [Google Scholar] [CrossRef]
- Baillie, Richard T., and Ramon P. De Gennaro. 1990. Stock Returns and Volatility. Journal of Financial and Quantitative Analysis 25: 203–14. [Google Scholar] [CrossRef]
- Bali, Turan G. 2008. The Intertemporal Relation between Expected Returns and Risk. Journal of Financial Economics 87: 101–31. [Google Scholar] [CrossRef]
- Bali, Turan G., and Hao Zhou. 2016. Risk, Uncertainty, and Expected Returns. Journal of Financial and Quantitative Analysis 51: 707–35. [Google Scholar] [CrossRef]
- Bali, Turan G., Ozgur Demirtas, and Haim Levy. 2009. Is There an Intertemporal Relation between Downside Risk and Expected Returns? Journal of Financial and Quantitative Analysis 44: 883–909. [Google Scholar] [CrossRef]
- Bansal, Naresh, Robert A. Connolly, and Chris T. Stivers. 2020. The Nonlinear High-Volatility Phenomenon in Beta and Size Equity Premia. SSRN Working Paper. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2845610 (accessed on 3 March 2020).
- Campbell, John Y., and Ludger Hentschel. 1992. No News is Good News: An Asymmetric Model of Changing Volatility in Stock Returns. Journal of Financial Economics 31: 281–318. [Google Scholar] [CrossRef]
- Chan, Kakeung C., G. Andrew Karolyi, and Rene. M. Stulz. 1992. Global Financial Markets and the Risk Premium on US Equity. Journal of Financial Economics 32: 137–67. [Google Scholar] [CrossRef]
- Corhay, Albert, and Alireza T. Rad. 1994. Expected Returns and Volatility in European Stock Markets. International Review of Economics and Finance 3: 45–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the Relation between the Expected Value of the Volatility of the Nominal Excess Return on Stocks. Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Guo, Hui, and Christopher J. Neely. 2008. Investigating the Intertemporal Risk-Return Relation in International Stock Markets with the Component GARCH Model. Economics Letters 99: 371–74. [Google Scholar] [CrossRef]
- Kanas, Angelo. 2013. The Risk-Return Relation and VIX: Evidence from the S&P 500. Empirical Economics 44: 1291–314. [Google Scholar]
- Nelson, Daniel. 1991. Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica 45: 347–70. [Google Scholar] [CrossRef]
- Newey, Whitney K., and Kenneht D. West. 1987. A Simple, Positive Semi-Definite Heteroscedasticity and Autocorrelation Consistent Covariance Matrix. Econometrica 55: 703–8. [Google Scholar] [CrossRef]
- Savva, Christos, and Panayiotis Theodossiou. 2018. The Risk and Return Conundrum Explained: International Evidence. Journal of Financial Econometrics 16: 486–521. [Google Scholar] [CrossRef]
- Theodossiou, Panayiotis, and Unro Lee. 1995. Relationship between Volatility and Expected Returns across International Stock Markets. Journal of Business Finance and Accounting 22: 289–300. [Google Scholar] [CrossRef]

| Mean | Median | Maximum | Minimum | Std. Dev. | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|---|
| US MKT | 0.03 | 0.07 | 11.35 | −12 | 1.15 | −0.26 | 13.63 |
| NoDur | 0.04 | 0.06 | 10.24 | −9.87 | 0.95 | −0.19 | 13.49 |
| Durbl | 0.05 | 0.06 | 15.03 | −14.43 | 1.56 | −0.12 | 10.5 |
| Manuf | 0.05 | 0.08 | 10.83 | −11.11 | 1.18 | −0.29 | 12.76 |
| Enrgy | 0.04 | 0.03 | 19.33 | −19.73 | 1.59 | −0.21 | 17.94 |
| HiTec | 0.06 | 0.12 | 16.04 | −13.18 | 1.61 | 0.16 | 9.61 |
| Telcm | 0.04 | 0.06 | 14.5 | −9.67 | 1.3 | 0.08 | 12.5 |
| Shops | 0.05 | 0.08 | 10.99 | −10.61 | 1.17 | −0.07 | 9.68 |
| Hlth | 0.05 | 0.07 | 11.1 | −9.74 | 1.16 | −0.19 | 8.7 |
| Utils | 0.04 | 0.07 | 14.43 | −11.61 | 1.07 | 0.13 | 22.09 |
| Other | 0.04 | 0.07 | 12.24 | −13.38 | 1.38 | −0.15 | 14.98 |
| Belgium | 0 | 0.01 | 8.23 | −14.39 | 1.17 | −0.6 | 12.62 |
| Finland | 0 | 0 | 15.33 | −18.26 | 1.77 | −0.42 | 11.77 |
| France | 0 | 0.03 | 9.91 | −12.28 | 1.28 | −0.29 | 9.43 |
| Germany | 0 | 0.05 | 16.04 | −9.83 | 1.23 | −0.05 | 13.1 |
| Ireland | 0 | 0.01 | 9.09 | −13.38 | 1.32 | −0.76 | 11.18 |
| Italy | −0.01 | 0.01 | 10.47 | −17.43 | 1.36 | −0.69 | 13.19 |
| Luxemburg | −0.01 | 0 | 10.1 | −6.84 | 1.1 | −0.27 | 8.7 |
| Netherland | 0 | 0.03 | 9.29 | −10.66 | 1.25 | −0.42 | 9.83 |
| Spain | −0.01 | 0.03 | 11.74 | −14.2 | 1.31 | −0.38 | 10.9 |
| VIX | 19.42 | 17.38 | 82.69 | 9.14 | 8.12 | 2.22 | 11.37 |
| Skewness | −0.33 | −0.34 | 0.36 | −1.13 | 0.16 | −0.02 | 3.87 |
| Kurtosis | 4.34 | 4.32 | 5.3 | 4.23 | 0.1 | 2.18 | 13.4 |
| VSTOXX | 23.94 | 22.04 | 87.51 | 10.68 | 9.75 | 1.7 | 7.11 |
| Quantile | OLS | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|
| cons | −0.03 | 0.44 *** | 0.32 *** | 0.19 *** | 0.09 | 0.00 | −0.08 * | −0.16 *** | −0.25 *** | −0.31 *** |
| Mkt(−1) | −0.06 ** | 0.07 ** | 0.05 ** | 0.01 | −0.01 | −0.04 ** | −0.05 *** | −0.06 *** | −0.05 *** | −0.07 *** |
| VIX(−1) | 0.00 | −0.09 *** | −0.05 *** | −0.03 *** | −0.01 *** | 0.00 * | 0.02 *** | 0.04 *** | 0.06 *** | 0.08 *** |
| Pseudo R2 | 0.00 | 0.12 | 0.05 | 0.02 | 0.00 | 0.00 | 0.01 | 0.03 | 0.07 | 0.16 |
| Slope equality test | 1067.3 *** |
| Quantile | OLS | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|
| cons | −0.07 | 0.40 *** | 0.35 *** | 0.21 *** | 0.11 ** | 0.00 | −0.08 * | −0.21 *** | −0.34 *** | −0.39 *** |
| VIX(−1) | 0 | −0.09 *** | −0.06 *** | −0.03 *** | −0.01 *** | 0.00 | 0.02 *** | 0.04 *** | 0.06 *** | 0.09 *** |
| Pseudo R2 | 0 | 0.13 | 0.06 | 0.02 | 0 | 0.00 | 0.01 | 0.03 | 0.08 | 0.17 |
| Slope equality test | 832.1 *** |
| Industry | Quantile | 0.1 | 0.5 | 0.9 | Equality Test |
|---|---|---|---|---|---|
| NoDur | cons | 0.09 * | −0.02 | 0.04 | |
| R(−1) | 0.04 | −0.03 ** | −0.05 ** | ||
| VIX(−1) | −0.06 *** | 0.00 ** | 0.05 *** | ||
| Pseudo R2 | 0.08 | 0.00 | 0.10 | 694.1 ** | |
| Durbl | cons | 0.05 | 0.03 | −0.10 | |
| R(−1) | 0.07 *** | 0.02 | 0.03 | ||
| VIX(−1) | −0.09 *** | 0.00 | 0.10 *** | ||
| Pseudo R2 | 0.09 | 0.00 | 0.11 | 630.5 *** | |
| Manuf | cons | 0.32 *** | 0.04 | −0.23 *** | |
| R(−1) | 0.07 ** | −0.01 | −0.02 | ||
| VIX(−1) | −0.08 *** | 0.00 | 0.08 *** | ||
| Pseudo R2 | 0.10 | 0.00 | 0.14 | 1005.7 *** | |
| Enrgy | cons | −0.11 | −0.04 | 0.16 * | |
| R(−1) | 0.04 | −0.03 * | −0.06 ** | ||
| VIX(−1) | −0.08 *** | 0.00 | 0.08 *** | ||
| Pseudo R2 | 0.06 | 0.00 | 0.08 | 488.0 *** | |
| HiTec | cons | 0.11 | 0.06 | −0.23 *** | |
| R(−1) | 0.09 *** | 0.01 | −0.02 | ||
| VIX(−1) | −0.10 *** | 0.00 | 0.10 *** | ||
| Pseudo R2 | 0.09 | 0.00 | 0.12 | 962.7 *** | |
| Telcm | cons | 0.28 *** | −0.04 | −0.27 *** | |
| R(−1) | 0.04 ** | −0.01 | 0.00 | ||
| VIX(−1) | −0.08 *** | 0.01 * | 0.08 *** | ||
| Pseudo R2 | 0.11 | 0.00 | 0.13 | 957.1 *** | |
| Shops | cons | 0.07 | −0.02 | −0.14 ** | |
| R(−1) | 0.09 *** | 0.01 | −0.01 | ||
| VIX(−1) | −0.07 *** | 0.01 ** | 0.07 *** | ||
| Pseudo R2 | 0.08 | 0.00 | 0.12 | 920.4 *** | |
| Hlth | cons | −0.17 ** | −0.02 | 0.17 ** | |
| R(−1) | 0.09 *** | −0.02 * | 0.00 | ||
| VIX(−1) | −0.06 *** | 0.01 ** | 0.06 *** | ||
| Pseudo R2 | 0.05 | 0.00 | 0.08 | 348.4 *** | |
| Utils | cons | 0.08 | 0.04 | 0.06 | |
| R(−1) | 0.06 * | −0.03 * | −0.05 *** | ||
| VIX(−1) | −0.06 *** | 0.00 | 0.05 *** | ||
| Pseudo R2 | 0.08 | 0.00 | 0.09 | 598.3 *** | |
| Other | cons | 0.54 *** | 0.04 | −0.46 *** | |
| R(−1) | 0.03 | 0.00 | −0.03 | ||
| VIX(−1) | −0.10 *** | 0.00 | 0.10 *** | ||
| Pseudo R2 | 0.13 | 0.00 | 0.16 | 874.9 *** |
| Country | Quantile | 0.1 | 0.5 | 0.9 | Equality Test |
|---|---|---|---|---|---|
| Belgium | cons | 0.05 | 0.02 | −0.13 * | |
| R(−1) | 0.14 *** | 0.02 | 0.03 | ||
| VSTOXX(−1) | −0.06 *** | 0.00 | 0.06 *** | ||
| Pseudo R2 | 0.10 | 0.00 | 0.10 | 642.5 *** | |
| Finland | cons | 0.22 | −0.01 | −0.37 *** | |
| R(−1) | 0.08 ** | 0.01 | −0.03 | ||
| VSTOXX(−1) | −0.09 *** | 0.00 | 0.09 *** | ||
| Pseudo R2 | 0.09 | 0.00 | 0.12 | 821.7 *** | |
| France | cons | 0.33 *** | 0.02 | −0.28 *** | |
| R(−1) | 0.09 *** | −0.01 | −0.03 | ||
| VSTOXX(−1) | −0.07 *** | 0.00 | 0.07 *** | ||
| Pseudo R2 | 0.11 | 0.00 | 0.13 | 813.5 *** | |
| Germany | cons | 0.13 | 0.04 | −0.24 ** | |
| R(−1) | 0.17 *** | 0.01 | 0.00 | ||
| VSTOXX(−1) | −0.07 *** | 0.00 | 0.07 *** | ||
| Pseudo R2 | 0.10 | 0.00 | 0.12 | 675.9 *** | |
| Ireland | cons | −0.13 | 0.01 | 0.20 * | |
| R(−1) | 0.11 *** | 0.03 ** | −0.01 | ||
| VSTOXX(−1) | −0.05 *** | 0.00 | 0.05 *** | ||
| Pseudo R2 | 0.06 | 0.00 | 0.06 | 254.5 *** | |
| Italy | cons | −0.05 | 0.02 | −0.13 ** | |
| R(−1) | 0.13 *** | −0.02 | −0.10 *** | ||
| VSTOXX(−1) | −0.06 *** | 0.00 | 0.07 *** | ||
| Pseudo R2 | 0.07 | 0.00 | 0.11 | 616.9 *** | |
| Luxemburg cons | −0.46 *** | 0.05 * | 0.59 *** | ||
| R(−1) | 0.02 | −0.02 * | −0.07 ** | ||
| VSTOXX(−1) | −0.03 *** | 0.00 * | 0.02 *** | ||
| Pseudo R2 | 0.03 | 0.00 | 0.02 | 105.4 *** | |
| Netherland cons | 0.32 *** | 0.04 | −0.37 *** | ||
| R(−1) | 0.12 *** | 0.04 ** | −0.04 | ||
| VSTOXX(−1) | −0.07 *** | 0.00 | 0.07 *** | ||
| Pseudo R2 | 0.12 | 0.00 | 0.14 | 754.8 *** | |
| Spain cons | −0.13 | −0.01 | −0.19 ** | ||
| R(−1) | 0.10 *** | 0.01 | −0.01 | ||
| VSTOXX(−1) | −0.06 *** | 0.00 | 0.07 *** | ||
| Pseudo R2 | 0.08 | 0.00 | 0.10 | 399.4 *** | |
| Quantile | OLS | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|
| cons | 1.01 | 4.17 * | 2.02 | 0.78 | 0.73 | 0.92 | 0.22 | −0.87 | 0.13 | 1.14 |
| Mkt(−1) | −0.06 * | 0.07 ** | 0.05 * | 0.01 | −0.01 | −0.04 ** | −0.05 *** | −0.06 *** | −0.05 *** | −0.06 ** |
| VIX(−1) | 0.00 | −0.08 *** | −0.05 *** | −0.03 *** | −0.01 *** | 0.00 * | 0.02 *** | 0.03 *** | 0.05 *** | 0.08 *** |
| Skewness(−1) | −0.17 | 0.12 | 0.07 | −0.02 | −0.08 | −0.23 * | −0.19 | −0.22 | −0.42 * | −0.59 *** |
| Kurtosis(−1) | −0.25 | −0.86 | −0.39 | −0.14 | −0.16 | −0.23 | −0.08 | 0.15 | −0.11 | −0.37 |
| Pseudo R2 | 0.00 | 0.12 | 0.06 | 0.02 | 0.00 | 0.00 | 0.01 | 0.03 | 0.08 | 0.16 |
| Slope equality test | 988.0 *** |
| Industry | Quantile | 0.1 | 0.5 | 0.9 | Equality Test |
|---|---|---|---|---|---|
| NoDur | cons | 2.84 | −0.38 | 0.63 | |
| R(−1) | 0.05 * | −0.03 ** | −0.05 *** | ||
| VIX(−1) | −0.06 *** | 0.00 ** | 0.05 *** | ||
| Skewness(−1) | 0.01 | 0.03 | −0.29 | ||
| Kurtosis(−1) | −0.64 | 0.09 | −0.15 | ||
| Pseudo R2 | 0.08 | 0.00 | 0.11 | 920.1 *** | |
| Durbl | cons | −2.19 | −2.99 | 1.98 | |
| R(−1) | 0.07 ** | 0.02 | 0.02 | ||
| VIX(−1) | −0.09 *** | 0.00 | 0.10 *** | ||
| Skewness(−1) | 0.76 * | 0.16 | −0.38 | ||
| Kurtosis(−1) | 0.58 | 0.71 | −0.51 | ||
| Pseudo R2 | 0.09 | 0.00 | 0.11 | 1045.6 *** | |
| Manuf | cons | 4.96 * | 1.42 | 0.00 | |
| R(−1) | 0.07 *** | −0.01 | −0.03 | ||
| VIX(−1) | −0.08 *** | 0.00 | 0.08 *** | ||
| Skewness(−1) | −0.17 | −0.29 | −0.36 * | ||
| Kurtosis(−1) | −1.09 | −0.34 | −0.07 | ||
| Pseudo R2 | 0.11 | 0.00 | 0.14 | 1093.9 *** | |
| Enrgy | cons | 4.91 | 2.51 | 0.20 | |
| R(−1) | 0.05 * | −0.03 ** | −0.05 ** | ||
| VIX(−1) | −0.08 *** | 0.00 | 0.08 *** | ||
| Skewness(−1) | −0.29 | −0.35 | −0.32 | ||
| Kurtosis(−1) | −1.19 | −0.62 | −0.04 | ||
| Pseudo R2 | 0.06 | 0.00 | 0.08 | 491.1 *** | |
| HiTec | cons | 5.92 | −1.63 | 0.81 | |
| R(−1) | 0.09 *** | 0.01 | −0.02 | ||
| VIX(−1) | −0.09 *** | 0.00 | 0.10 *** | ||
| Skewness(−1) | 0.06 | 0.16 | −0.85 *** | ||
| Kurtosis(−1) | −1.36 | 0.40 | −0.29 | ||
| Pseudo R2 | 0.09 | 0.00 | 0.12 | 1099.3 *** | |
| Telcm | cons | 4.80 * | −0.67 | 1.36 | |
| R(−1) | 0.05 ** | −0.01 | 0.00 | ||
| VIX(−1) | −0.08 *** | 0.01 * | 0.08 *** | ||
| Skewness(−1) | −0.16 | 0.05 | −0.52 ** | ||
| Kurtosis(−1) | −1.06 | 0.15 | −0.41 | ||
| Pseudo R2 | 0.11 | 0.00 | 0.13 | 849.1 *** | |
| Shops | cons | 2.87 | −0.01 | 0.98 | |
| R(−1) | 0.10 *** | 0.00 | −0.01 | ||
| VIX(−1) | −0.07 *** | 0.01 ** | 0.07 *** | ||
| Skewness(−1) | 0.10 | −0.05 | −0.75 *** | ||
| Kurtosis(−1) | −0.65 | 0.00 | −0.32 | ||
| Pseudo R2 | 0.08 | 0.00 | 0.13 | 1095.0 *** | |
| Hlth | cons | 1.88 | −0.01 | −3.06 | |
| R(−1) | 0.10 *** | −0.03 ** | 0.00 | ||
| VIX(−1) | −0.05 *** | 0.01 ** | 0.06 *** | ||
| Skewness(−1) | 0.14 | −0.10 | −0.03 | ||
| Kurtosis(−1) | −0.47 | −0.01 | 0.74 | ||
| Pseudo R2 | 0.06 | 0.00 | 0.09 | 543.1 *** | |
| Utils | cons | 1.82 | 1.78 | 5.30 *** | |
| R(−1) | 0.07 ** | −0.03 ** | −0.06 ** | ||
| VIX(−1) | −0.06 *** | 0.00 | 0.05 *** | ||
| Skewness(−1) | 0.02 | −0.32 ** | −0.66 *** | ||
| Kurtosis(−1) | −0.41 | −0.43 | −1.26 *** | ||
| Pseudo R2 | 0.08 | 0.00 | 0.09 | 648.1 *** | |
| Other | cons | 5.24 * | −0.85 | −0.77 | |
| R(−1) | 0.05 | 0.00 | −0.03 | ||
| VIX(−1) | −0.09 *** | 0.00 | 0.10 *** | ||
| Skewness(−1) | −0.26 | 0.02 | −0.21 | ||
| Kurtosis(−1) | −1.12 * | 0.21 | 0.06 | ||
| Pseudo R2 | 0.13 | 0.00 | 0.16 | 1173.4 *** |
| Period | Quantile | 0.1 *** | 0.5 | 0.9 | Equality Test |
|---|---|---|---|---|---|
| 1990–2006 | cons | 0.29 *** | 0.01 | −0.20 ** | |
| Mkt(−1) | 0.14 *** | 0.02 | 0.01 | ||
| VIX(−1) | −0.07 *** | 0.00 | 0.07 *** | ||
| Pseudo R2 | 0.10 | 0.00 | 0.10 | 380.8 *** | |
| 1990–2006 | cons | 0.30 *** | 0.01 | −0.19 ** | |
| VIX(−1) | −0.07 *** | 0.00 | 0.07 *** | ||
| Pseudo R2 | 0.10 | 0.00 | 0.10 | 468.0 *** | |
| 2007–2020 | cons | 0.51 *** | −0.03 | −0.40 *** | |
| Mkt(−1) | 0.01 | −0.09 *** | −0.14 *** | ||
| VIX(−1) | −0.10 *** | 0.01** | 0.09 *** | ||
| Pseudo R2 | 0.14 | 0.01 | 0.22 | 524.5 *** | |
| 2007–2020 | cons | 0.53 *** | −0.04 | −0.50 *** | |
| VIX(−1) | −0.10 *** | 0.01 * | 0.09 *** | ||
| Pseudo R2 | 0.14 | 0.00 | 0.21 | 553.7 *** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aslanidis, N.; Christiansen, C.; Savva, C.S. Quantile Risk–Return Trade-Off. J. Risk Financial Manag. 2021, 14, 249. https://doi.org/10.3390/jrfm14060249
Aslanidis N, Christiansen C, Savva CS. Quantile Risk–Return Trade-Off. Journal of Risk and Financial Management. 2021; 14(6):249. https://doi.org/10.3390/jrfm14060249
Chicago/Turabian StyleAslanidis, Nektarios, Charlotte Christiansen, and Christos S. Savva. 2021. "Quantile Risk–Return Trade-Off" Journal of Risk and Financial Management 14, no. 6: 249. https://doi.org/10.3390/jrfm14060249
APA StyleAslanidis, N., Christiansen, C., & Savva, C. S. (2021). Quantile Risk–Return Trade-Off. Journal of Risk and Financial Management, 14(6), 249. https://doi.org/10.3390/jrfm14060249








