Abstract
Financial performance of firms is very important to bankers, shareholders, potential investors, and creditors. The inability of firms to meet their liabilities will affect all its stakeholders and will result in negative consequences in the wider economy. The objective of the study is to explore the applicability of a distress prediction model which uses the F-Score and its components to identify firms which are at high risk of going into default. The study incorporates a prediction model and vast literature to address the research questions. The sample of the study is collected from publicly listed firms of the United States. In total, 81 financially distressed firms wereextracted from the UCLA-LoPucki Bankruptcy Research Database during 2009–2017. This study found that the relationship of the F-Score and probability of firms going into financial distress is significant. This study also demonstrated that firms which are at risk of distress tend to record a negative cash flow from operations (CFO) and showed a greater decline in return on assets (ROA) in the year prior to default. This study extends the existing literature by supporting a model which has not been widely used in the area of financial distress predictions.
1. Introduction
When a firm goes into bankruptcy or when it defaults on its financial obligations, it will have negative impacts on its stakeholders such as lenders, creditors, customers, employees, and shareholders. Lenders and creditors will lose their capital loaned. The operations of customers’ businesses might be halted due to sudden interruptions in the supply of raw materials, which will adversely affect revenues, margins, and reputations. Employees will lose income, whereas shareholders might suffer losses from capital invested. In addition, these stakeholders are often debtors themselves and this affects their ability to meet financial obligations. Therefore, the bankruptcy of one firm not only affects its direct stakeholders, it will also have spillover effects on the economy as a whole, and its severity is dependent on the size of the company. Based on the above, it is evident that business failures will result in serious consequences to many parties. As such, in the past few decades, the area of bankruptcy and financial distress prediction has attracted the interests of many researchers. In the United States (US), businesses can declare bankruptcy by filing for Chapter 7 or Chapter 11 with the United States Courts. Chapter 7 is also known as liquidation bankruptcy, whereas Chapter 11 is known as reorganization bankruptcy (United States Courts 2017a, 2017b). Chapter 7 filings are for companies where reorganizations are not feasible and all of their assets will be liquidated to pay off debts. In contrast, Chapter 11 filings allow companies to restructure debts and revive their businesses.
After a few years of decline in the number of bankruptcy filings in the United States, the number of commercial bankruptcy filings increased again in 2016 (Brown 2017). The total assets involved in Chapter 7 and Chapter 11 filings in 2016 were in excess of $100 billion (Brown 2017). Based on the quantum of assets involved, it is evident that the cost associated with bankruptcies is high. These costs not only have to be borne by the distressed companies; they will also result in negative consequences to their creditors due to the inability of the distressed companies to meet their obligations. Furthermore, as the severity of economic crises is increasing, it is expected that the losses associated with bankruptcies will also be much higher. Therefore, it is very important for businesses to take proactive actions to minimize such losses. In order to do that, managers need to understand the factors which will lead to financial distress and have the tools available to enable them to make timely decisions. To date, many studies have been conducted to address the issue of financial distress predictions. Since the 1960s, many credit risk prediction models have been introduced. However, the performance of existing models is inconsistent (Tinoco and Wilson 2013) and thus, there is a need to continue to search for a better model that fits the current and future market environment. This study has primarily referenced the study conducted by Agrawal (2015), which demonstrated that the F-Score can be used to predict financial distress. The study tested the usability of the aggregate F-Score (Model 1) and the discrete variables that made up the F-Score (Model 2). The study by Agrawal (2015) was done using a sample of 270 Indian firms, which comprised of 135 defaulting firms and 135 non-defaulting firms.
However, the Indian market alone is small in size as compared to other markets such as the US market, and evidence from the Indian market is insufficient to be used as a representation of the global market. In addition, the operating environment for companies in India is also different from the US market. In India, access to capital is limited, which hinders the ability of firms to raise funds in times of necessity and in turn affects the survival of businesses. According to Sivabalan (2017), the market capitalization of US is close to $30.0 trillion, whereas the market capitalization of the Indian market is much lower at $2.3 trillion. With global market capitalization at close to $100 trillion (Edwards 2017), the US market represents about one third of the world’s equity market. The bankruptcies of any large public companies in the US will impact many stakeholders, including both domestic and international stakeholders. In addition, US is also a major import and export partner to many countries around the world and the negative consequences of bankruptcies in the US will spillover to other countries, creating a domino effect in the world economy. Thus, given its size and its significance to the global economy, this study has been conducted using data from companies listed in the US market.
The global economy has evolved over the years and the current business environment is very different as compared to the 1980s.Based on this background, the drivers of corporate failure might have changed as well and thus, there is a need to keep on exploring and find the best default prediction models by incorporating the most relevant variables for the current economic environment. The F-Score developed by (Piotroski 2000) is one potential model.
In addition to the commonly used ratios in existing bankruptcy prediction models, the F-Score also takes into account the quality of earnings of firms, which is represented by the accruals variable in the model. This is an important differentiating factor, as research by Janes (2005) showed that the addition of accruals can significantly improve the results of distress predictions. The study by Agrawal (2015) also provided significant evidence that the F-Score has default predictive ability for firms in India.
Piotroski (2000) first developed the F-Score as a measure to select good stocks for investments. The F-Score ranges between zero to nine and is the summation of scores based on nine financial variables. Piotroski (2000) demonstrated that companies with a high F-Score give better stock returns as compared to those with a low F-Score. As such, this implies that companies with a low F-Score will give low stock returns. According to Campbell et al. (2011), companies with a high probability of failure give low average stock returns as well.Given this similarity, we hypothesize that firms with a low F-Score have a higher tendency to be financially distressed as compared to the firms with a high F-Score.
This study contributes by providing evidence that the relationship of the F-Score and probability of firms going into financial distress is significant. This study also demonstrates that firms which are at risk of distress tend to record a negative cash flow from operations (CFO) and show a greater decline in return on assets (ROA) in the year prior to default. Finally, this study contributes to existing literature by examining the usefulness of the Piotroski’s F-Score and its components in predicting financial distress among firms in the United States.
2. Literature Review
2.1. A Review of Literature on Development of Default Prediction Models
The subject of bankruptcies prediction is a well-researched topic among finance researchers. Some of the earliest studies such as those done by Beaver (1966) and Altman (1968) found that analysis of financial ratios calculated from financial statements can be used to predict financial failure and the risk of bankruptcy.
The first notable bankruptcy prediction model was developed by Altman (1968) which is widely known as the Z-Score. In developing the Z-score, Altman (1968) used multivariate discriminant analysis and identified five variables which are most effective in predicting corporate bankruptcies. The five variables are the working capital/total assets ratio, retained earnings/total assets ratio, earnings before interest and taxes/total assets ratio, market value of equity/book value of total debt ratio, and sales/total assets ratio. The Z-score is made up of the weighted average combination of these five ratios. In the study by Altman (1968), 95% of all firms in the sample was correctly categorized into two groupings, i.e., bankrupt and non-bankrupt. Based on the findings in the study, the Z-Score’s predictive ability decreases as the number of years before bankruptcy increases.
Subsequently, in response to the changes in accounting standards in the 1970s, Altman et al. (1977) further researched and modified the Z-score to develop a new model for bankruptcy prediction named the Zeta model. The Zeta model was also developed by using multivariate discriminant analysis, which was the same technique used by Altman (1968). The Zeta model consisted of seven variables, namely return on assets, stability of earnings, interest coverage, cumulative profitability, liquidity, capitalization, and size. It was found that, in the year prior to bankruptcies, the accuracies of both the Z-score and Zeta models are about the same at 95% and 96%, respectively. However, when financial data between two to five years prior to bankruptcies were used, the Zeta model is more accurate in predicting bankruptcies than the Z-score (Altman et al. 1977).
The O-score is another prediction model which was developed by Ohlson (1980) to predict corporate bankruptcies. The O-score has nine variables which are mainly derived from the balance sheet and income statement. Ohlson (1980) is one of the first researchers to use conditional logistic regression analysis in studying bankruptcy risks. The O-Score was derived from a study of more than 2000 companies (Ohlson 1980), whereas the Z-Score was developed based on a study of 66 companies (Altman 1968). Until today, the Z-score, Zeta model, and O-score have remained as popular reference points for research in the area of financial distress and bankruptcy predictions. Even in recent years, researchers such as Le Maux and Morin (2011), Tinoco and Wilson (2013), and Agrawal (2015) have continued to show that the information contained in a company’s balance sheet, profit and loss statements, as well as cash flow statements can be used to predict the risk of payment defaults.
In the past decade, due to rapid advancements in technologies, many researchers had developed bankruptcy prediction models using advanced techniques such as neural networks (Odom and Sharda 1990; Salchenberger et al. 1992; Coats and Fant 1993; Yang et al. 1999; Kim and Kang 2010), genetic algorithms (Varetto 1998; Shin and Lee 2002), and decision trees (Pompe and Feelders 1997). These models are newer and were developed using modern statistical computation techniques. However, Adnan Aziz and Dar (2006) performed a comparison of available prediction models and found that there is no marked difference, in terms of prediction accuracy, between traditional statistical models and more advanced models, as mentioned above. This is consistent with the argument by Bandyopadhyay (2006), that there are no unifying agreements between researchers on which models have highest predictive accuracies. Adnan Aziz and Dar (2006) also found that accounting-based statistical models such as multivariate discriminant analysis and logistic models are most reliable.
The Z-Score and O-Score were developed more than 30 years ago. The fact that today’s businesses are still using these models in predicting financial distress in their day to day operations reflects the strong appeal of these prediction models to society, due to their relatively simplistic nature of their applications (Kumar and Kumar 2012). However, Kumar and Kumar (2012) revisited the Z-Score and O-Score by testing these models using the financial data of Texmo Industries for a five year period between 2005–2006 and 2009–2010. The study found that the O-Score performed slightly better than the Z-Score but the predictive abilities of both models are unsatisfactory.
2.2. Financial Ratios and Prediction of Financial Distress
According to Le Maux and Morin (2011), bankrupt companies usually exhibit similar financial attributes a few years prior to the event. Since the early 1960s, many studies such as those done by Altman (1968), Beaver (1966), Pongsatat et al. (2004), Kordestani et al. (2011), Tinoco and Wilson (2013), Almamy et al. (2016), Kliestik et al. (2018), Podhorska and Misankova (2016), Kovacova et al. (2019), and Pedro et al. (2018) had demonstrated that financial statements analysis can be used as a proactive approach in identifying and managing companies with a high tendency to go into financial distress. This is consistent with the findings by Jones (2017), which revealed that ratios calculated from financial statements are some of the strongest predictors of corporate bankruptcies, whereas external factors such as macroeconomic indicators, analyst recommendations, as well as industry variables are the weakest.
Earlier accounting-based models which are created to predict financial distress mostly used ratios calculated from balance sheet and profit and loss statements (Altman 1968; Ohlson 1980). Some of the common ratios used in the development of financial distress models are profitability ratios (Keasey and Mcguinness 1990; Pompe and Bilderbeek 2005), growth ratios (Shirata 1998), liquidity ratios (Altman 1968; Edmister 1972; Ohlson 1980; Houghton 1984), solvency ratios (Beaver 1966; Altman 1968; Ohlson 1980; Edmister 1972; Houghton 1984), and capital structure ratios (Castanias 1983).
The financial ratios used in both the Z-Score and Zeta model are calculated from data in the balance sheet and profit and loss statements only and do not contain information from cash flows statements. In more recent years, more and more researchers argued that relying on data from balance sheet and profit and loss statements alone to predict financial distress is insufficient. John (1976) argued that the data in the balance sheet and profit and loss statements are susceptible to manipulation. According to Kordestani et al. (2011), companies are unable to make many distortions in the cash flow statements and thus, this increases the reliability of the data.
Gentry et al. (1985) demonstrated that when cash flows variables were used in combination with accounting financial ratios, the accuracy of bankruptcies prediction is higher. Gentry et al. (1985) also found that dividend, investment, and receivables cash flows have significant importance in predicting bankruptcies. This is consistent with the study done by Almamy et al. (2016) which demonstrated that the predictive ability of the Z-Score increased when operating cash flow is added into the model.
In addition, Sloan (2005) demonstrated that improvements in earnings, which were driven by alteration of accruals, is not sustainable. Agrawal (2015) argued that other than the commonly used ratios, the quality of earnings is also a vital signal of firm’s financial position. This is consistent with the results by Janes (2005), which demonstrated that the use of accruals as variable can significantly improve the results of distress prediction models.
One such model which incorporates the above-mentioned variables is the F-Score by Piotroski (2000). Agrawal (2015) had shown that this model is useful in the prediction of defaults in Indian firms. Kolte et al. (2017) conducted a study to assess the applicability of the F-Score in predicting the bankruptcy of Kingfishers Airline. The results from the study showed that Kingfishers Airline’s F-Scores in the three years prior to its bankruptcy were low.Thus, this study contributes to existing literature by investigating the usefulness of the F-Score in predicting financial distress for public companies in United States.
3. Methodology
3.1. A Review of Statistical Techniques in Financial Distress and Bankruptcy Prediction Models
A review of literature revealed that the commonly used statistical techniques in developing accounting-based bankruptcy prediction models are multiple discriminant analysis, logistic regression, the probabilistic model, and linear probability (Altman and Saunders 1998). Of these four approaches, multiple discriminant analysis is the most widely used technique, followed by logistic regressions (Altman and Saunders 1998; Bandyopadhyay 2006). The Z-Score and Zeta models were developed using multiple discriminant analysis, whereas the O-Score is a logistic regression model.
However, the usage of discriminant analysis requires the independent variables to have a multivariate normal distribution (Angelini et al. 2008). According to the study done by Lennox (1999), cash flow and leverage have non-linear effects on the probability of bankruptcy of a firm. Thus, for bankruptcy prediction models incorporating cash flow and leverage variables, it is more suitable to adopt logistic regression analysis instead of discriminant analysis, as the logistic model does not require the variables to satisfy the assumption on normality.
Begley et al. (1996), Lennox (1999), and Mihalovič (2016) also showed that logistic and probabilistic models can predict bankruptcy more accurately than discriminant analysis. Begley et al. (1996), Lennox (1999), and Pongsatat et al. (2004) concluded that generally, the O-Score, which was developed using logistic analysis, has higher predictive accuracy as compared to the Z-Score. The strength of logistic models is further supported by Adnan Aziz and Dar (2006), who concluded that logistic regression models are one of the most reliable models in the area of bankruptcy prediction due to their stability and low Type 1 and Type 2 errors. Based on the above evidence, the most appropriate statistical technique for this study is the logistic regression model.
3.2. Sample Description and Statistical Technique
The sample of financially distressed firms for this study comprise of companies which had filed for Chapter 11 bankruptcy protection in the United States between January 2009 and September 2017. The list of companies was extracted from UCLA-LoPucki Bankruptcy Research Database and the original list consists of 306 large public companies.
It was deemed that companies in financial sector are unsuitable for this study, as the performance metrics for companies in these industries differ from other industries. On top of that, the variables in the F-Score do not take into account variables which are deemed important in measuring the performance of financial institutions such as the bank capital, loan ratio (Cleary and Hebb 2016), and net interest margin (Goyal and Bhatia 2016). At times of distressed, firms in the financial sector tend to receive government interventions in the form of bailouts or capital support as well (Cabrera et al. 2016; Dieckmann and Plank 2011; Kirshner 2015; Berger et al. 2016). Thus, companies in financial industries such as banks and insurance companies are excluded from this study. Subsequently, the financial data for remaining companies was extracted from Bloomberg and companies with incomplete financial information were excluded from this study. This includes
- Companies whereby financial data is unavailable for the period between one to three years prior to bankruptcy.
- Financial data available is insufficient to calculate all the ratios included in the F-Score.
As a result, the sample of financially distressed firms ended up with a total of 81 firms. Table 1 shows the year-wise distribution of the sample for financially distressed firms. The financial data for the variables used in this study was mainly collected from Bloomberg and the EDGAR database on the website of the Securities and Exchange Commission of the United States. The industry-wise distribution of the sample is as per Table 2. In the past 3 years, many firms in the Crude Petroleum and Natural Gas industry were negatively affected by the decline in global oil prices. Therefore, there is a high concentration of firms in this industry in our sample of financially distressed firms. The high number of bankrupt companies in year 2016 mainly comprised of companies in the crude petroleum and natural gas industries. Moreover, the worldwide oil price issue gave this industry more potential for being financially distressed and thus became an interesting case to examine (Ward 1994).

Table 1.
Year-Wise Distribution of Defaulting Firms.

Table 2.
Industry-Wise distribution of Distressed Firms.
The sample of non-distressed firms was formed by using matched-pair sampling technique. This technique has been used in many studies relating to financial distress, such as the studies done by Agrawal (2015), Beaver (1966), Altman (1968), and Begley et al. (1996). Matching pairs of non-distressed firms were chosen based on matching industries, the nearest total assets, and the financial year of reporting. The matching of industries was done using the Standard Industry Classification (SIC) Code in the United States. As such, the overall sample size became162 firms, which wasmade up of 81 distressed firms and 81 non-distressed firms.
In order for us to have a meaningful study, it is vital to ensure that the differences of the total assets of the 2 samples of companies are not statistically significant (Agrawal 2015). To confirm this, an independent samples t-test was performed. The results from the independent samples t-test and descriptive statistics for the total assets of the both distressed firms sample and non-distressed firms sample are presented in Table 3. As the p-value is at 0.944, which is greater than 0.05, this shows that the difference in total assets for the distressed firms sample and non-distressed firms sample are not statistically significant.

Table 3.
Descriptive Statistics and t-Test for Asset Size.
In addition, the overall sample was split into an estimation sample and a hold-out sample. Firms in the period from 2015 to 2017 were taken to represent the estimation sample, whereas the remaining firms from 2009 to 2014 were taken to represent the hold-out sample. Therefore, the estimation sample comprised of 57 distressed firms and 57 non-distressed firms. On the other hand, the hold-out sample comprised of 24 distressed firms and 24 non-distressed firms. As per a similar study done by Agrawal (2015), this study also used logistic regression to predict the probability of default for a firm based on the respective aggregate Piotroski’s F-Score for each firm and also the nine individual components that made up the aggregate F-Score. Based on logistic regression, the probability of an event happening was established as follows:
where
P (Y) = Probability of event Y happening
z = linear combination of independent variables as represented by:
β0 + β1×1 + β2X2 + β3X3 + … + βnXn + µ.
3.3. Variable Descriptions
Model 1 uses the aggregate Piotroski’s F-Score (Piotroski 2000) calculated as the total of the following independent variables.
where
F_Score = F_ROA + F_∆ROA + F_CFO + F_Accrual + F_∆Margin + F_∆Turnover + F_∆Leverage + F_∆Liquidity + F_Eq_Offer
F_ROA = 1 if Net Income/Total Assets is positive, 0 otherwise
F_∆ROA = 1 if current year’s ROA (Net Income/Total Assets) is higher than previous year’s ROA, 0 otherwise
F_CFO = 1 if Cash Flows From Operations/Total Assets is positive, 0 otherwise
F_Accrual = 1 if CFO (Cash Flows from Operations/Total Assets) > ROA (Net Income Before Extraordinary Items/Total Assets), 0 otherwise
F_∆Margin = 1 if current year’s Gross Margin Ratio is higher than previous year’s Gross Margin Ratio, 0 otherwise
F_∆Turnover = 1 if current year’s Asset Turnover Ratio is higher than previous year’s Asset Turnover Ratio, 0 otherwise
F_∆Leverage = 1 if current year’s Leverage Ratio is lower than previous year’s Leverage Ratio, 0 otherwise
F_∆Liquidity = 1 if current year’s Current Ratio is higher than previous year’s Current Ratio, 0 otherwise
F_Eq_Offer = 1 if the number of shares outstanding in the current year is not greater than the number of shares outstanding in the prior year, 0 otherwise.
Though the F-Score comprised of nine components, only seven components werebeing used in Model 2 as the variable ROA and Accruals were removed due to high multicollinearity. In addition, the linearity of all the remaining seven components of F-Score with respect of the logit of the outcome was assessed via the Box-Tidwell procedure (Box and Tidwell 1962). A Bonferroni correction was applied using all 15terms in the model, resulting in statistical significance being accepted when p< 0.00333 (Tabachnik and Fidell 2007). Based on this assessment, all the components were found to be linearly related to the logit of the outcome except CFO. Therefore, the CFO variable was recoded into a nominal variable. Thus, the components of the Piotroski’s F-Score used in Model 2 are ∆ROA, CFO, ∆Margin, ∆Turnover, ∆Leverage, ∆Liquidity and Eq_Offer.
Model 2 uses the individual components of the Piotroski’s F-Score, that is, ΔROA, CFO, ΔMargin, ΔTurnover, ΔLeverage, ΔLiquidity, and Eq_Offer. These are measured as follows:
F_Score = F_∆ROA + F_CFO + F_∆Margin + F_∆Turnover + F_∆Leverage + F_∆Liquidity + F_Eq_Offer
∆ROA = Current year’s ROA less previous year’s ROA
CFO = 1 if (Cash Flows from Operations/Total Assets) < 0, 0 otherwise.
∆Margin = Current year’s Gross Margin Ratio less previous year’s Gross Margin Ratio
∆Turnover = Current year’s Asset Turnover Ratio less prior year’s Asset Turnover Ratio
∆Leverage = Current year’s Leverage Ratio less prior year’s Leverage Ratio
∆Liquidity = Current year’s Current Ratio less prior year’s Current Ratio
Eq_Offer = number of shares outstanding in the current year less the number of shares outstanding in the prior year/number of shares outstanding in the prior year.
4. Results
Independent t-tests were run for Model 1 and Model 2 and the results together with their respective descriptive statistics arepresented in Table 4 and Table 5, respectively. It is observed that on average, distressed firms tend to have a lower Piotroski’s F-Score as compared to non-distressed firms. On the other hand, for Model 2, the decline in ROA for distressed firms is significantly greater than non-distressed firms. It is also observed that on average, distressed firms tend to record negative CFO as compared to non-distressed firms.

Table 4.
Model 1: Descriptive Statistics and Univariate t-test of Piotroski’s F-Score.

Table 5.
Model 2: Descriptive Statistics and Univariate t-test.
Logistic regression was run to determine the effects of Piotroski’s F-Score on the likelihood that a firm will be in financial distress. Both models exhibited a statistically significant chi-square value at a 0.01 level of significance. It was observed that the Nagelkerke R2 value of Model 2 is higher than Model 1, which implies that Model 2 explained 20.7% of the variations in the dependent variable in comparison to 11.1% in Model 1.
This study also found that the F-Score has a significant negative relationship with the probability of financial distress, which means that firms with a lower F-Score have ahigher probability to go into financial distress (See Table 6). These findings are consistent with the study done by Agrawal (2015). This finding provides a clear indication for bankers, shareholders, and creditors that they should avoid investing in or giving credit to those firms that have a low F-score. However, the distressed firms can also be identified by looking at individual measures such as ROA and CFO, as this study’s findings show that the decline in ROA for distressed firms is higher than non-distressed firms and they tend to record a negative CFO.

Table 6.
Result of Logistic Regression (estimated result).
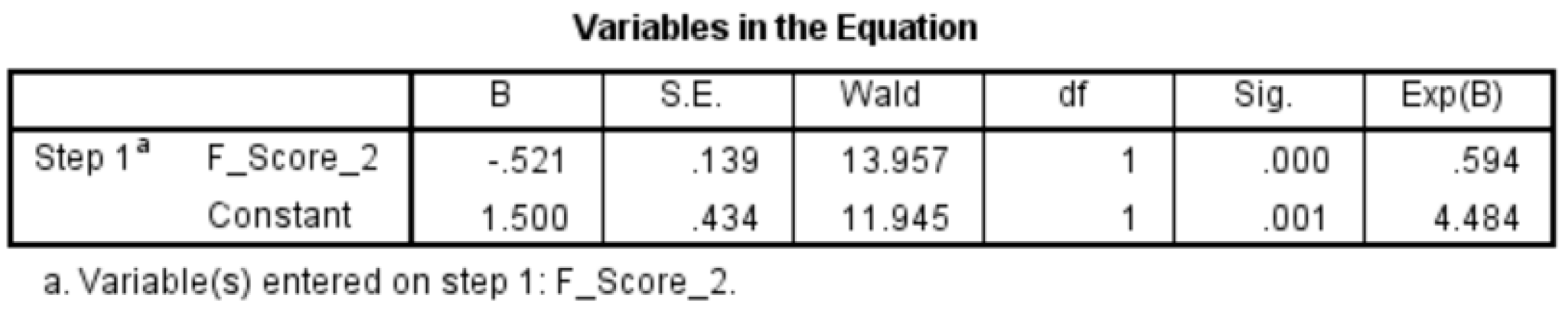
As it was found that there are collinearity issues with ROA and Accruals, a new aggregate F-Score (F-Score 2) was calculated and logistic regression was run for F-Score 2. It was found that the F-Score 2 also exhibited a statistically significant chi-square at the 0.00 significance level (please refer to Appendix A for results for SPSS). As this result is similar to the results for Model 1, these two variables were retained in the calculations of the aggregate F-Score in Model 1.
On top of that, in Model 2, ∆ROA was found to have a significant inverse relationship with probability of distress. This signifies that a greater decline in ROA is linked to a higher probability of distress. On the other hand, CFO has asignificant positive relationship with the probability of distress, which means that distressed firms tend to record a negative CFO. However, in the study by Agrawal (2015), ∆ROA and CFO were insignificant in relation to the probability of distress.
Table 7 and Table 8 shows the classification matrix of Model 1 and Model 2 and both models are shown to have the same predictive ability in the estimation sample. However, Model 1 has a higher overall accuracy of 79.2% in the hold-out sample as compared to 72.9% in Model 2. This shows that Model 1 is a better model in the prediction of financial distress.

Table 7.
Model 1: Logistic Regression Classification Matrix.

Table 8.
Model 2: Logistic Regression Classification Matrix.
5. Discussion
The finding in this study contradicts the results found by Agrawal (2015), which showed that the predictive ability of the model which uses the individual components of the F-Score (Model 2) is higher than when using the aggregate Piotroski’s F-Score (Model 1). However, the variables in Model 2 used in this study comprised of only seven components of the F-Score, whereas the Model 2 investigated in the study by Agrawal (2015) used all nine components as per the original F-Score introduced by Piotroski (2000). In this study, the variables ROA and Accruals wereremoved due to high multicollinearity with the ∆ROA variable. Thus, it is unfeasible to compare the predictive ability of Model 2 in this study versus Model 2 from the study by Agrawal (2015) due to the different components used in both models.
As there was insufficient evidence that fundamental analysis is useful for the Indian market (Aggarwal and Gupta 2009), it is difficult to explain the different findings between this study and the results found by Agrawal (2015). As Piotroski (2000) first modeled the F-Score using data from firms in the United States, it is possible that the aggregate F-Score is more suited for the US market.Nevertheless, the findings in this study and the study by Agrawal (2015) revealed that the F-Score can be useful in bankruptcy and financial distress prediction. The usage of the F-Score in predicting financial distress has not been widely researched and only Agrawal (2015) wasfound to have conducted a similar study for the Indian market. This study contributes to existing literature by providing evidence for the usefulness of the F-Score as a new financial distress prediction model.
6. Conclusions
Predicting a firm’s financial distress hasalways been a topic of interest for researchers and practitioners, as it affects bankers, shareholders, potential investors, and creditors. On many occasions, a group of firms’ inability to meet their liabilities negatively affects the economic stability of a country. Based on the current literature, researchers have mostly used accounting information based models to predict the financial distress of the firms. However, the findings using accounting information based models are not always consistent nor robust; as such, this study used alternative models that use Piotroski F scores forpredicting financial distress of a sample from the United States of America.
The results of this study present some significant implications for investment and lending decisions. It shall help bankers, shareholders, potential investors, and creditors in terms making investment decisions by knowing which companies might end up in financial distress in no time. However, it should also be highlighted that the current accounting-based models are simple and easy-to-use for predicting the likelihood of financial distress for any firm.
7. Limitation and Future Research
One of the limitations of this study is that the samples only include public listed companies in the US, with the average assets size in excess of $2 billion. In comparison with large corporations, small firms typically behave differently due to their size, lack of economies of scale, market power, and their ability to innovate. As such, the factors which can lead to bankruptcy and financial distress in smaller companies are different from larger companies. Therefore, it is uncertain if the F-Score is useful in predicting financial distress in smaller firms and more research can be done to explore this area.
In addition, as Piotroski (2000) first developed the F-Score to select best valued stocks for investments, the market value of equity is incorporated into the model as a means to capture market variable. Thus, the model is only useful for companies which are listed on stock exchanges and where the required information is available to the public. Moreover, the F-Score was developed using firms in the United States, whose financial market is one of the more transparent and robust markets in the world. In countries where there is poor transparency and regulations, the performance of the F-Score in distress predictions can be different.
Although the sample used in this study spanned across many industries, there is a heavy concentration in the oil and gas industry due to the collapse of oil price in the last few years. Additionally, the sample size used in this firm is relatively small. Moreover, the study did not consider the most recent year data in the analysis. Therefore, future studies should be conducted by including more companies from other industries with a larger sample size and various asset sizes. Plus, future studies can consider matching multiple healthy companies with a similar size but different F-scores instead of considering only one matching company. It is also proposed that future research can be conducted collecting data for sufficient number of years and running some time series analysis to see whether the study can have better conclusions about predicting firms’ financial distress. Finally, advanced data analysis techniques such as machine learning models can be used for bankruptcy prediction. Future studies can use alternative methods in predicting defaults and compare with the existing findings from the F-score models.
Author Contributions
M.R. carried out the literature review and the statistical analysis, and drafted the manuscript. C.L.S. helped with the data collections, data analysis, and discussion. M.A.K.M. participated in the discussion, and communicated with the editor. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Research Cell, Noakhali Science and Technology University.
Conflicts of Interest
The authors declare that they have no competing interests.
Appendix A
References
- Aziz, M. Adnan, and Humayon A. Dar. 2006. Predicting corporate bankruptcy: Where we stand? Corporate Governance: The International Journal of Business in Society 6: 18–33. [Google Scholar] [CrossRef]
- Aggarwal, Navdeep, and Mohit Gupta. 2009. Do High Book-to-Market Stocks Offer Returns to Fundamental Analysis in India? Decision 36: 304–941. [Google Scholar]
- Agrawal, Khushbu. 2015. Default Prediction Using Piotroski’s F-score. Global Business Review 16S 5: 175. [Google Scholar] [CrossRef]
- Almamy, Jeehan, John Aston, and Leonard N. Ngwa. 2016. An evaluation of Z-score using cash flow ratio to predict corporate failure amid the recent financial crisis: Evidence from the UK. Journal of Corporate Finance 36: 278–85. [Google Scholar] [CrossRef]
- Altman, Edward I. 1968. Financial ratios, discriminant analysis and the prediction of corporarte bankruptcy. The Journal of Finance 23: 589–609. [Google Scholar] [CrossRef]
- Altman, Edward I., and Anthony Saunders. 1998. Credit risk measurement: Developments over the last 20 years. Journal of Banking & Finance 21: 1721–42. [Google Scholar]
- Altman, Edward I., Robert G. Haldeman, and Paul Narayanan. 1977. Zeta Analysis: A new model to identify bankruptcy risk of corporations. Journal of Banking & Finance 1: 470–92. [Google Scholar]
- Angelini, Eliana, Giacomo di Tollo, and Andrea Roli. 2008. A neural network approach for credit risk evaluation. The Quarterly Review of Economics and Finance 48: 733–55. [Google Scholar] [CrossRef]
- Bandyopadhyay, Arindam. 2006. Predicting probability of default of Indian corporate bonds: Logistic and Z-score model approaches. The Journal of Risk Finance 7: 255–72. [Google Scholar] [CrossRef]
- Beaver, William H. 1966. Financial Ratios As Predictors of Failure. Journal of Accounting Research 4: 71–111. [Google Scholar] [CrossRef]
- Begley, Joy, Jin Ming, and Susan Watts. 1996. Bankruptcy classification errors in the 1980′s: An empirical analysis of Altman’s and Ohlson’s models. Review of Accounting Studies 1: 267–84. [Google Scholar] [CrossRef]
- Berger, Allen N., Christa H. S. Bouwman, Thomas Kick, and Klaus Schaeck. 2016. Bank liquidity creation following regulatory interventions and capital support. Journal of Financial Intermediation 26: 115–41. [Google Scholar] [CrossRef]
- Box, George E. P., and Paul W. Tidwell. 1962. Transformation of the Independent Variables. Technometrics 4: 531–50. [Google Scholar] [CrossRef]
- Brown, Linzee. 2017. BankruptcyData Releases Its Annual Corporate Bankruptcy Report. Available online: http://www.prweb.com/releases/2017/01/prweb13962074.htm (accessed on 13 January 2020).
- Cabrera, Matias, Gerald P. Dwyer, and Margarita Samartín-Saénz. 2016. Government finances and banks bailouts: Evidence from European stock markets. Journal of Empirical Finance 39: 169–79. [Google Scholar] [CrossRef]
- Campbell, John Y., Jens Dietrich Hilscher, and Jan Szilagyi. 2011. Predicting financial distress and the performance of distressed stocks. Journal of Investment Management 9: 14–34. [Google Scholar]
- Castanias, Richard. 1983. Bankruptcy risk and optimal capital structure. The Journal of Finance 38: 1617–35. [Google Scholar] [CrossRef]
- Cleary, Sean, and Greg Hebb. 2016. An efficient and functional model for predicting bank distress: In and out of sample evidence. Journal of Banking & Finance 6: 101–11. [Google Scholar]
- Coats, Pamela K., and L. Franklin Fant. 1993. Recognizing financial distress patterns using a neural network tool’. Financial Management 22: 142–55. [Google Scholar] [CrossRef]
- Dieckmann, Stephan, and Thomas Plank. 2011. Default risk of advanced economies: An empirical analysis of credit default swaps during the financial crisis. Review of Finance 16: 903–34. [Google Scholar] [CrossRef]
- Edmister, Robert O. 1972. An empirical test of financial ratio analysis for small business failure prediction. Journal of Financial and Quantitative Analysis 7: 1477–93. [Google Scholar] [CrossRef]
- Edwards, Jim. 2017. Global Market Cap is About to Hit $100 Trillion and Goldman Sachs Thinks the Only Way Is down. Business Insider Singapore. Available online: http://www.businessinsider.sg/global-market-cap-is-about-to-hit-100-trillion-2017-12 (accessed on 20 February 2020).
- Gentry, James A., Paul Newbold, and David T. Whitford. 1985. Predicting bankruptcy: If cash flow’s not the bottom line, what is? Financial Analysts Journal 41: 47–56. [Google Scholar] [CrossRef]
- Goyal, Shikha, and Ambika Bhatia. 2016. Analysis of Financial Ratios for Measuring Performance of Indian Public Sector Banks. International Journal of Engineering and Management Research (IJEMR) 6: 152–62. [Google Scholar]
- Houghton, KA. 1984. Accounting Data and the Prediction of Business Failure: The Setting of Priors and the Age Data. Journal of Accounting Research 22: 361–68. [Google Scholar] [CrossRef]
- Janes, Troy D. 2005. Accruals, Financial Distress, and Debt Covenants. Doctoral dissertation, University of Michigan, Ann Arbor, MI, USA. [Google Scholar]
- John, Argenti. 1976. Corporate Collapse: The Causes and Symptoms. London: McGraw-Hill Inc. [Google Scholar]
- Jones, Stewart. 2017. Corporate bankruptcy prediction: A high dimensional analysis. Review of Accounting Studies 22: 1366–422. [Google Scholar] [CrossRef]
- Keasey, Kevin, and Paul McGuinness. 1990. The failure of UK industrial firms for the period 1976–1984, logistic analysis and entropy measures. Journal of Business Finance & Accounting 17: 119–35. [Google Scholar]
- Kim, Myoung-Jong, and Dae-Ki Kang. 2010. Ensemble with neural networks for bankruptcy prediction. Expert Systems with Applications 37: 3373–79. [Google Scholar] [CrossRef]
- Kirshner, Jodie A. 2015. The bankruptcy safe harbor in light of government bailouts: Reifying the significance of bankruptcy as a backstop to financial risk. NYUJ Legislation & Public Policy 18: 795. [Google Scholar]
- Kliestik, Tomas, Maria Misankova, Katarina Valaskova, and Lucia Svabova. 2018. Bankruptcy prevention: New effort to reflect on legal and social changes. Science and Engineering Ethics 24: 791–803. [Google Scholar] [CrossRef] [PubMed]
- Kolte, Ashutosh, Arturo Capasso, and Matteo Rossi. 2017. Predicting financial distress of firms. A study on bankruptcy of Kingfisher Airlines. Paper presented at 10th Annual Conference of the EuroMed Academy of Business, Rome, Italy, September 13–15; pp. 735–49. [Google Scholar]
- Kordestani, Gholamreza, Mehrdad Bakhtiari, and Vahid Biglari. 2011. Ability of combinations of cash flow components to predict financial distress. Business: Theory and Practice 12: 277. [Google Scholar] [CrossRef]
- Kovacova, Maria, Tomas Kliestik, Katarina Valaskova, Pavol Durana, and Zuzana Juhaszova. 2019. Systematic review of variables applied in bankruptcy prediction models of Visegrad group countries. Oeconomia Copernicana 10: 743–72. [Google Scholar] [CrossRef]
- Kumar, Radha Ganesh, and Kishore Kumar. 2012. A comparison of bankruptcy models. International Journal of Marketing, Financial Services and Management Research 4: 76–86. [Google Scholar]
- Le Maux, Julien, and Danielle Morin. 2011. Black and white and red all over: Lehman Brothers’ inevitable bankruptcy splashed across its financial statements. International Journal of Business and Social Science 2: 39–65. [Google Scholar]
- Lennox, Clive. 1999. Identifying failing companies: A re-evaluation of the logit, probit and DA approaches. Journal of Economics and Business 51: 347–64. [Google Scholar] [CrossRef]
- Mihalovic, Matús. 2016. Performance comparison of multiple discriminant analysis and logit models in bankruptcy prediction. Economics and Sociology 9: 101. [Google Scholar] [CrossRef] [PubMed]
- Odom, Marcus D., and Ramesh Sharda. 1990. A neural network model for bankruptcy prediction. Paper presented at IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, June 17–21; pp. 163–68. [Google Scholar]
- Ohlson, James A. 1980. Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research 18: 109–31. [Google Scholar] [CrossRef]
- Pedro, Cristina Pereira, Joaquim J. S. Ramalho, and Jacinto Vidigal da Silva. 2018. The main determinants of banking crises in OECD countries. Review of World Economics 154: 203–27. [Google Scholar] [CrossRef]
- Piotroski, Joseph D. 2000. Value investing: The use of historical financial statement information to separate winners from losers. Journal of Accounting Research 38: 1–41. [Google Scholar] [CrossRef]
- Podhorska, Ivana, and Maria Misankova. 2016. Success of prediction models in Slovak companies. Global Journal of Business & Social Science Review 4: 54–59. [Google Scholar]
- Pompe, Paul P. M., and Jan Bilderbeek. 2005. The prediction of bankruptcy of small- and medium-sized industrial firms. Journal of Business Venturing 20: 847–68. [Google Scholar] [CrossRef]
- Pompe, Paul P. M., and A. J. Feelders. 1997. Using machine learning, neural networks, and statistics to predict bankruptcy. Computer-Aided Civil and Infrastructure Engineering 12: 267–76. [Google Scholar] [CrossRef]
- Pongsatat, Surapol, Judy Ramage, and Howard Lawrence. 2004. Bankruptcy prediction for large and small firms in Asia: A comparison of Ohlson and Altman. Journal of Accounting and Croporate Governance 1: 1–13. [Google Scholar]
- Salchenberger, Linda M., E. Mine Cinar, and Nicholas A. Lash. 1992. Neural networks: A new tool for predicting thrift failures. Decision Sciences 23: 899–916. [Google Scholar] [CrossRef]
- Shin, Kyung-Shik, and Yong-Joo Lee. 2002. A genetic algorithm application in bankruptcy prediction modeling. Expert Systems with Applications 23: 321–28. [Google Scholar] [CrossRef]
- Shirata, Cindy Yoshiko. 1998. Financial ratios as predictors of bankruptcy in Japan: An empirical research. Tsukuba College of Technology Japan 1: 1–17. [Google Scholar]
- Sivabalan, Srinivasan. 2017. Indian Stock Market Overtakes Canada in $2 Trillion Standoff. Bloomberg. Available online: https://www.bloomberg.com/news/articles/2017-11-30/indian-stock-market-overtakes-canada-in-2-trillion-standoff (accessed on 10 January 2020).
- Sloan, Richard G. 2005. Do stock prices fully reflect information in accruals and cash flows about future earnings? The Accounting Review 71: 289–315. [Google Scholar]
- Tabachnick, Barbara G., Linda S. Fidell, and Jodie B. Ullman. 2007. Using Multivariate Statistics. Boston: Pearson Education Limited. [Google Scholar]
- Tinoco, Mario Hernandez, and Nick Wilson. 2013. Financial distress and bankruptcy prediction among listed companies. International Review of Financial Analysis 30: 394–419. [Google Scholar] [CrossRef]
- United States Courts. 2017a. United States Courts. Available online: http://www.uscourts.gov/services-forms/bankruptcy/bankruptcy-basics/chapter-11-bankruptcy-basics (accessed on 5 January 2020).
- United States Courts. 2017b. United States Courts. Available online: http://www.uscourts.gov/services-forms/bankruptcy/b;ankruptcy-basics/chapter-7-bankruptcy-basics (accessed on 5 January 2020).
- Varetto, Franco. 1998. Genetic algorithms applications in the analysis of insolvency risk. Journal of Banking & Finance 22: 1421–39. [Google Scholar]
- Ward, Terry J. 1994. Cash Flow Information And The Prediction Of Financially Distressed Mining, Oil And Gas Firms: A Comparative Study. Journal of Applied Business Research (JABR) 10: 78–86. [Google Scholar] [CrossRef]
- Yang, Z. R., Marjorie B. Platt, and Harlan D. Platt. 1999. Probabilistic neural networks in bankruptcy prediction. Journal of Business Research 44: 67–74. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).