Economic Policy Uncertainty and Stock Return Momentum
Abstract
1. Introduction
2. Literature Review
2.1. Business Cycle
2.2. Market State
2.3. Macroeconomic Risk
2.4. Economic Policy Uncertainty
3. Methodology
β6TERMt−1 + β7IIPt−1 + β8 EPUt−1 + εt
4. Data and Variables
5. Empirical Findings and Interpretation
5.1. Descriptive Statistics
5.2. Business Cycle and Momentum
5.3. Four Factors Alpha and GRS Test
5.4. Portfolio Sorting of EPU and Momentum
5.5. Time Series Regression of Momentum and EPU
5.6. Macroeconomic Variables
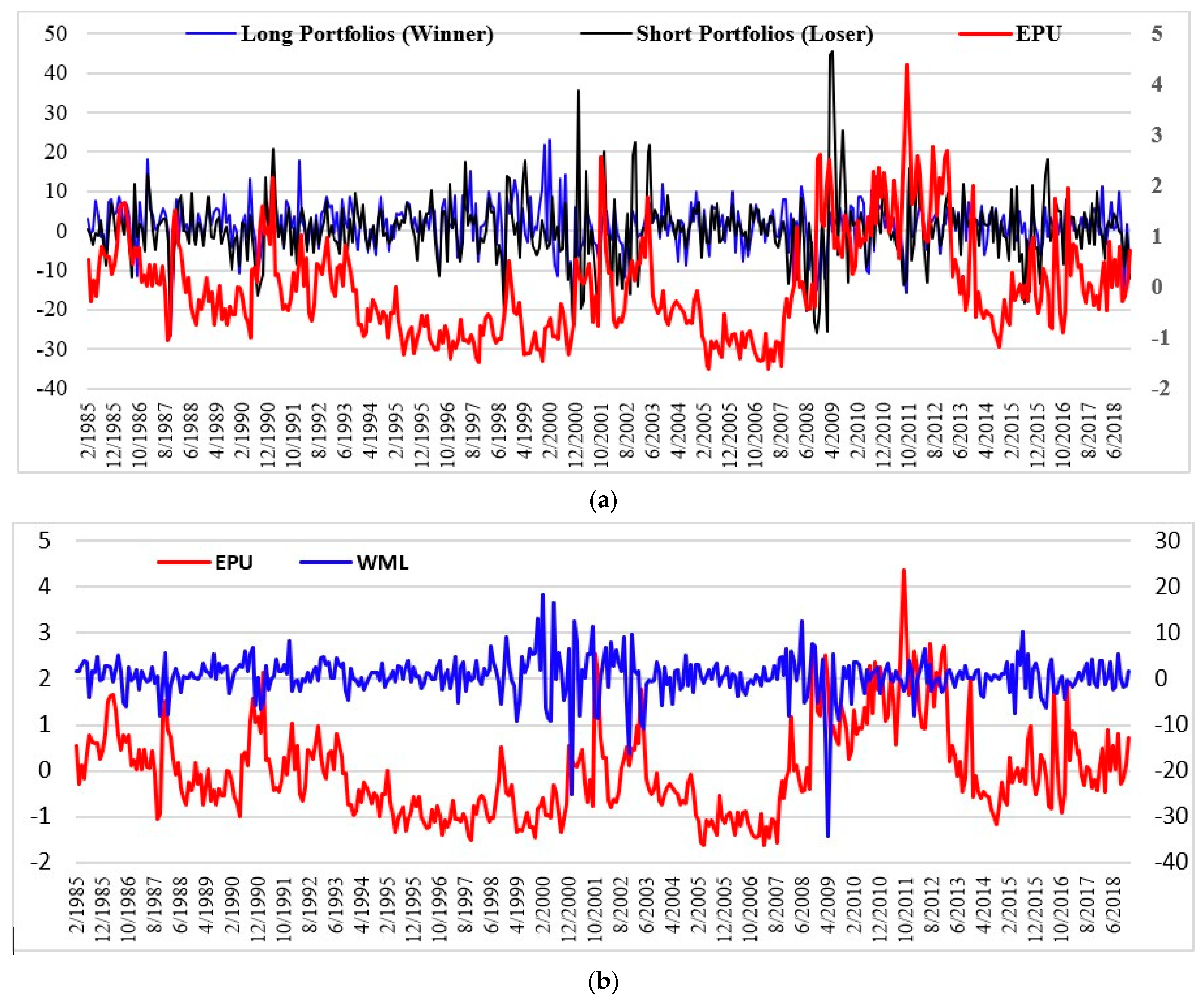
5.7. Time Series Evidence
5.7.1. Selection Order Criteria for Lags
5.7.2. VAR Model
5.7.3. Vector Error Correction Model
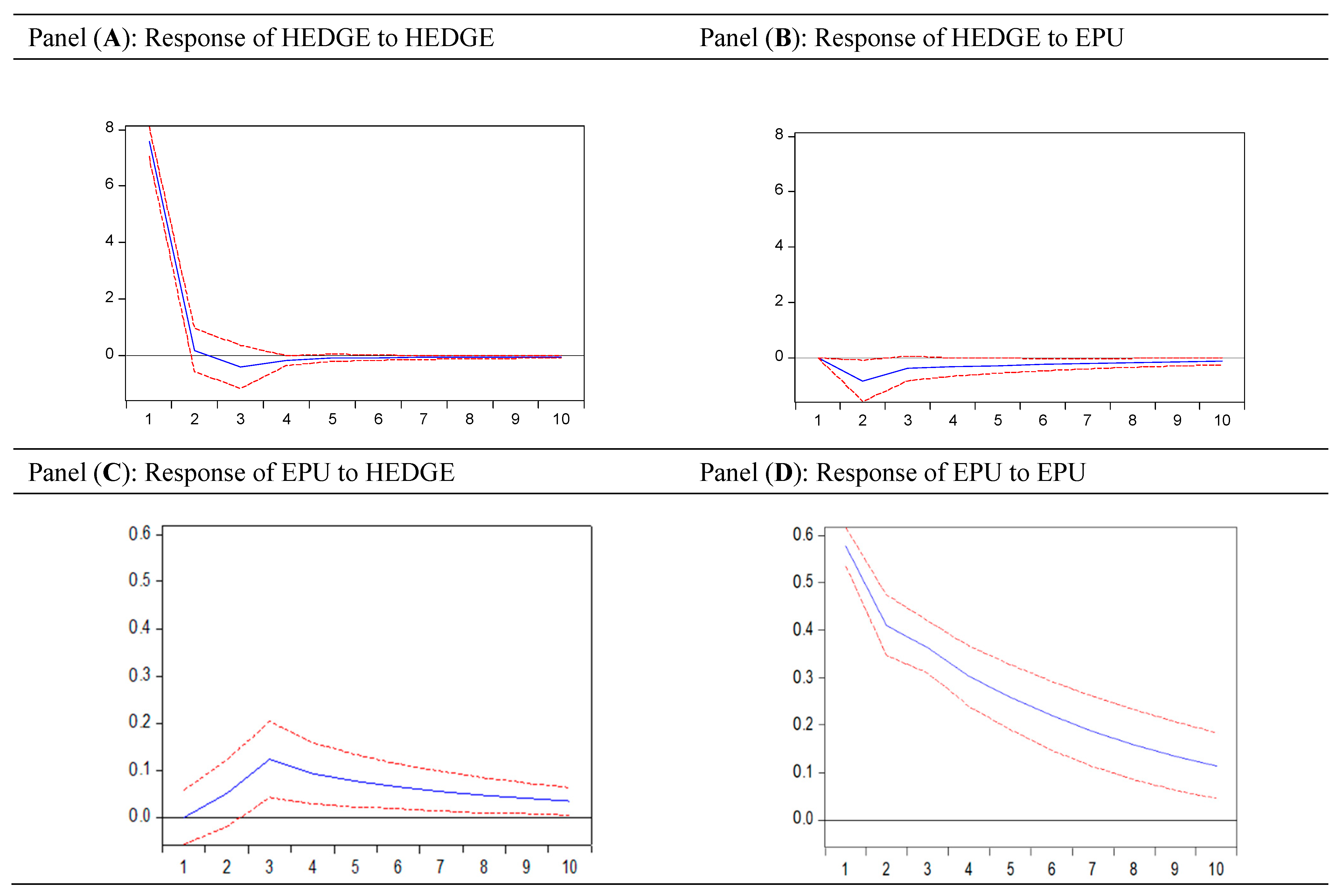
5.7.4. Impulse Response
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Addoum, Jawad M., Stefanos Delikouras, Da Ke, and Alok Kumar. 2019. Underreaction to political information and price momentum. Financial Management 48: 773–804. [Google Scholar] [CrossRef]
- Adjei, Frederick A., and Mavis Adjei. 2017. Economic policy uncertainty, market returns and expected return predictability. Journal of Financial Economic Policy 9: 242–59. [Google Scholar] [CrossRef]
- Al-Thaqeb, Saud Asaad, and Barrak Ghanim Algharabali. 2019. Economic policy uncertainty: A literature review. The Journal of Economic Asymmetries 20: e00133. [Google Scholar] [CrossRef]
- Antonakakis, Nikolaos, Ioannis Chatziantoniou, and George Filis. 2014. Dynamic spillovers of oil price shocks and economic policy uncertainty. Energy Economics 44: 433–47. [Google Scholar] [CrossRef]
- Antoniou, Antonios, Herbert Y. T. Lam, and Krishna Paudyal. 2007. Profitability of momentum strategies in international markets: The role of business cycle variables and behavioural biases. Journal of Banking & Finance 31: 955–72. [Google Scholar]
- Antoniou, Constantinos, John A. Doukas, and Avanidhar Subrahmanyam. 2013. Cognitive dissonance, sentiment, and momentum. Journal of Financial and Quantitative Analysis 48: 245–75. [Google Scholar] [CrossRef]
- Aretz, Kevin, Söhnke M. Bartram, and Peter F. Pope. 2010. Macroeconomic risks and characteristic-based factor models. Journal of Banking and Finance 34: 1383–99. [Google Scholar] [CrossRef]
- Avramov, Doron, and Tarun Chordia. 2006. Asset pricing models and financial market anomalies. The Review of Financial Studies 19: 1001–40. [Google Scholar] [CrossRef]
- Avramov, Doron, Si Cheng, and Allaudeen Hameed. 2016. Time-varying liquidity and momentum profits. Journal of Financial and Quantitative Analysis 51: 1897–923. [Google Scholar]
- Bahmani-Oskooee, Mohsen, and Majid Maki-Nayeri. 2019. Asymmetric effects of policy uncertainty on the demand for money in the United States. Journal of Risk and Financial Management 12: 1. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, Brandice Canes-Wrone, Steven J. Davis, and Jonathan Rodden. 2014. Why has US policy uncertainty risen since 1960? American Economic Review 104: 56–60. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, and Steven J. Davis. 2016. Measuring economic policy uncertainty. The Quarterly Journal of Economics 131: 1593–636. [Google Scholar] [CrossRef]
- Bernal, Oscar, Jean-Yves Gnabo, and Grégory Guilmin. 2016. Economic policy uncertainty and risk spillovers in the Eurozone. Journal of International Money and Finance 65: 24–45. [Google Scholar] [CrossRef]
- Brogaard, Jonathan, and Andrew Detzel. 2015. The asset-pricing implications of government economic policy uncertainty. Management Science 61: 3–18. [Google Scholar] [CrossRef]
- Carhart, Mark. M. 1997. On persistence in mutual fund performance. The Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Chan, Louis K. C., Narasimhan Jegadeesh, and Josef Lakonishok. 1999. The profitability of momentum strategies. Financial Analysts Journal 55: 80–90. [Google Scholar] [CrossRef]
- Chordia, Tarun, and Lakshmanan Shivakumar. 2002. Momentum, business cycle, and time-varying expected returns. The Journal of Finance 57: 985–1019. [Google Scholar] [CrossRef]
- Cooper, Michael J., Roberto C. Gutierrez, Jr., and Allaudeen Hameed. 2004. Market states and momentum. The Journal of Finance 59: 1345–65. [Google Scholar] [CrossRef]
- Du, Ding, Zhaodan Huang, and Bih-Shuang Liao. 2009. Why is there no momentum in the Taiwan stock market? Journal of Economics and Business 61: 140–52. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. Frence. 2012. Size, value, and momentum in international stock returns. Journal of Financial Economics 105: 457–72. [Google Scholar] [CrossRef]
- Friedman, Milton. 1953. Effects of Full Employment Policy on Economic Stability: A Formal Analysis. In Essays in Positive Economics. Chicago: University of Chicago Press, pp. 117–32. [Google Scholar]
- Galariotis, Emilios, and Konstantinos Karagiannis. 2020. Cultural dimensions, economic policy uncertainty, and momentum investing: International evidence. The European Journal of Finance, 1–18. [Google Scholar] [CrossRef]
- Griffin, John M., Xiuqing Ji, and J. Spencer Martin. 2003. Momentum investing and business cycle risk: Evidence from pole to pole. The Journal of Finance 58: 2515–47. [Google Scholar] [CrossRef]
- Gu, Ming, Minxing Sun, Yangru Wu, and Weike Xu. 2021. Economic policy uncertainty and momentum. Financial Management, 1–23. [Google Scholar] [CrossRef]
- Jegadeesh, Narasimhan, and Sheridan Titman. 1993. Returns to buying winners and selling losers: Implications for stock market efficiency. The Journal of Finance 48: 65–91. [Google Scholar] [CrossRef]
- Jegadeesh, Narasimhan, and Sheridan Titman. 2001. Profitability of momentum strategies: An evaluation of alternative explanations. The Journal of Finance 56: 699–720. [Google Scholar] [CrossRef]
- Jegadeesh, Narasimhan, and Sheridan Titman. 2011. Momentum. Annual Review of Financial Economics 3: 493–509. [Google Scholar] [CrossRef]
- Kelly, Bryan, Ľuboš Pástor, and Pietro Veronesi. 2016. The price of political uncertainty: Theory and evidence from the option market. The Journal of Finance 71: 2417–80. [Google Scholar] [CrossRef]
- Korajczyk, Robert A., and Ronnie Sadka. 2004. Are momentum profits robust to trading costs? The Journal of Finance 59: 1039–82. [Google Scholar] [CrossRef]
- Kumar, Ameet, Muhammad Ramzan Kalhoro, Rakesh Kumar, Niaz Hussain Ghumro, Sarfraz Ahmed Dakhan, and Vikesh Kumar. 2020. Decomposing the Effect of Domestic and Foreign Economic Policy Uncertainty Shocks on Real and Financial Sectors: Evidence from BRIC Countries. Journal of Risk and Financial Management 13: 315. [Google Scholar] [CrossRef]
- Kydland, Finn E., and Edward C. Prescott. 1977. Rules rather than discretion: The inconsistency of optimal plans. Journal of Political Economy 85: 473–91. [Google Scholar] [CrossRef]
- Lesmond, David A., Michael J. Schill, and Chunsheng Zhou. 2004. The illusory nature of momentum profits. Journal of Financial Economics 71: 349–80. [Google Scholar] [CrossRef]
- Liow, Kim Hiang, Wen-Chi Liao, and Yuting Huang. 2018. Dynamics of international spill overs and interaction: Evidence from financial market stress and economic policy uncertainty. Economic Modelling 68: 96–116. [Google Scholar] [CrossRef]
- Liu, Laura Xiaolei, and Lu Zhang. 2008. Momentum profits, factor pricing, and macroeconomic risk. The Review of Financial Studies 21: 2417–48. [Google Scholar] [CrossRef]
- Pástor, Ľuboš, and Pietro Veronesi. 2013. Political uncertainty and risk premia. Journal of Financial Economics 110: 520–45. [Google Scholar] [CrossRef]
- Phan, Dinh Hoang Bach, Susan Sunila Sharma, and Vuong Thao Tran. 2018. Can economic policy uncertainty predict stock returns? Global evidence. Journal of International Financial Markets, Institutions and Money 55: 134–50. [Google Scholar] [CrossRef]
- Rouwenhorst, K. Geert. 1999. Local return factors and turnover in emerging stock markets. The Journal of Finance 54: 1439–64. [Google Scholar] [CrossRef]
- Swinkels, Laurens. 2004. Momentum investing: A survey. Journal of Asset Management 5: 120–43. [Google Scholar] [CrossRef]
- Tsai, I-Chun. 2017. The source of global stock market risk: A viewpoint of economic policy uncertainty. Economic Modelling 60: 122–31. [Google Scholar] [CrossRef]
- Van der Ploeg, Frederick. 1989. The political economy of overvaluation. Economic Journal 99: 850–55. [Google Scholar] [CrossRef]
- Xavier, Gustavo, and Lucas N. C. Vasconcelos. 2019. The Impact of Foreign and Country-Specific Economic Policy Uncertainty on the Local Momentum Effect. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3187600 (accessed on 1 December 2020).
- Zaremba, Adam. 2019. The cross section of country equity returns: A review of empirical literature. Journal of Risk and Financial Management 12: 165. [Google Scholar] [CrossRef]
| 1 | The first component comprises search results gathered from 10 leading newspapers daily in the United States, where newspaper articles deliberating over economic policy are incorporated. An article is associated with economic uncertainty when words such as ‘uncertain,’ ‘economic,’ ‘legislation,’ and ‘federal reserve’ have be used at least once in the newspaper article. The second component is created by the inclusion of “tax code provisions” that are slated to elapse over the coming 10 years. The last component collects data from “Federal Reserve Bank of Philadelphia’s Survey of Professional Forecasters” to compute the level of dispersion among individual forecasters relating to macroeconomic policy variables. The weights assigned to the first, second, and third components are 0.5, 0.17, and 0.33, respectively. |
| 2 | For example, Jegadeesh and Titman (2001) using a sample of NASDAQ, NYSE, and AMEX listed stocks from 1990–1998, documented that past winners outperform past losers by approximately 1.39% per month. This is consistent with the results reported in Jegadeesh and Titman (1993), i.e., 1.31% per month. Later, Rouwenhorst (1999) using a sample of 20 emerging markets, found that the average return from the long-short momentum strategy is 0.39% per month. Griffin et al. (2003) reported that the average monthly momentum profit from a winner-minus-loser strategy is 0.59%, 0.77%, 1.63%, and 0.32% for the U.S, Europe, Africa, and Asia, respectively. It is worthwhile to note that the higher returns observed by Jegadeesh and Titman (1993, 2001), Rouwenhorst (1999), and Griffin et al. (2003) do not necessarily imply investor profits due to higher transactions costs (Swinkels 2004; Lesmond et al. 2004). Korajczyk and Sadka (2004) found that when price impact is ignored and transaction costs are proportional costs equal to the effective and quoted spreads, the momentum strategy earns significant profits. Similarly, Lesmond et al. (2004) failed to reject profitability in all momentum strategies, even after considering transaction cost aspects. |
| 3 | See www.policyuncertainty.com/index.html, accessed on 20 December 2020. |
| 4 | See mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html, accessed on 24 December 2020. |
| 5 | See fred.stlouisfed.org/, accessed on 24 December 2020. |
| 6 | See www.nber.org/cycles/cyclesmain.html, accessed on 22 December 2020. |
| 7 | M3 is utilized by the central bank to direct monetary policy to control inflation. This implies that M3 has an indirect impact on inflation via monetary policy. We examined the multicollinearity among macroeconomic variables in Table 9. VIF for the regression model in Table 9 turned out to be 1.24, 1.19, and 1.16 for inflation and money supply, respectively. To further clear our suspicion towards the relationship between inflation and money supply, we checked the correlation between the two variables, which turned out to −0.1261. |
| Variable | Obs. | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| HEDGE | 407 | 1.102 | 7.623 | −45.58 | 26.15 |
| MKTRF | 407 | 0.663 | 4.361 | −23.24 | 12.47 |
| SMB | 407 | 0.043 | 3.078 | −16.87 | 21.71 |
| HML | 407 | 0.192 | 2.867 | −11.10 | 12.90 |
| WML | 407 | 0.562 | 4.496 | −34.39 | 18.36 |
| EPU | 407 | 108.117 | 31.34 | 57.203 | 245.127 |
| Variables | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|
| (1) HEDGE | 1.000 | |||||
| (2) MKTRF | −0.208 * | 1.000 | ||||
| (3) SMB | 0.003 | 0.210 * | 1.000 | |||
| (4) HML | −0.190 * | −0.217 * | −0.266 * | 1.000 | ||
| (5) WML | 0.919 * | −0.171 * | 0.048 | −0.199 * | 1.000 | |
| (6) EPU | −0.115 * | 0.075 | 0.073 | −0.103 * | −0.140 * | 1.000 |
| Expansionary Period | Contractionary Period | ||
|---|---|---|---|
| December1982–July 1990 | 0.0149 (3.84) | August 1990–March 1991 | −0.0172 (−0.54) |
| April 1991–March 2001 | 0.0034 (0.53) | April 2001–November 2001 | −0.0216 (−0.52) |
| December 2001–December 2007 | 0.0032 (0.73) | January 2008–June 2009 | −0.0432 (−1.27) |
| (1) Long | (2) Short | (3) Hedge | |
|---|---|---|---|
| MKTRF | 1.176 *** (0.0364) | 1.269 *** (0.0457) | −0.092 * (0.0509) |
| SMB | 0.355 *** (0.0421) | 0.450 *** (0.0492) | −0.095 * (0.0530) |
| HML | −0.121 ** (0.0521) | −0.035 (0.0847) | −0.086 (0.0824) |
| WML | 0.498 *** (0.0317) | −1.036 *** (0.0476) | 1.534 *** (0.0582) |
| CONS | 0.031 (0.108) | −0.290 * (0.157) | 0.322 * (0.167) |
| N | 407 | 407 | 407 |
| Adj. R2 | 0.898 | 0.880 | 0.847 |
| F | 276.4 | 305.8 | 175.3 |
| Mean Alpha | t-Stat | p Value | Mean Adj. R2 | Mean SE | Mean |a| | SR | |
|---|---|---|---|---|---|---|---|
| J0 | 0.322 | 4.48 | 0.034 | 0.8469 | 0.1527 | 0.3218 | 0 |
| J1 | 0.321 | 4.42 | 0.035 | 0.8469 | 0.1527 | 0.3218 | 0.1084 |
| (1) | (2) | (3) | |
|---|---|---|---|
| Long | Short | Hedge | |
| MKTRF | 1.176 *** (0.0345) | 1.248 *** (0.0580) | −0.0723 (0.0616) |
| SMB | 0.494 *** (0.0541) | 0.343 *** (0.0973) | 0.151 (0.0968) |
| HML | −0.0287 (0.0467) | 0.222 ** (0.110) | −0.251 ** (0.118) |
| WML | 0.497 *** (0.0298) | −1.104 *** (0.0767) | 1.601 *** (0.0892) |
| CONS | 0.0391 (0.134) | −0.458 * (0.240) | 0.497 ** (0.246) |
| N | 204 | 204 | 204 |
| Adj. R2 | 0.910 | 0.895 | 0.867 |
| F | 365.9 | 232.4 | 87.74 |
| (1) Long | (2) Short | (3) Hedge | |
|---|---|---|---|
| MKTRF | 1.133 *** (0.0637) | 1.222 *** (0.0551) | −0.0892 (0.0769) |
| SMB | 0.239 *** (0.0598) | 0.399 *** (0.0615) | −0.160 ** (0.0693) |
| HML | −0.286 *** (0.106) | −0.373 *** (0.112) | 0.0872 (0.123) |
| WML | 0.518 *** (0.0601) | −1.057 *** (0.0547) | 1.575 *** (0.0665) |
| CONS | −0.0176 (0.157) | 0.0535 (0.173) | −0.0710 (0.194) |
| N | 203 | 203 | 203 |
| Adj. R2 | 0.896 | 0.870 | 0.826 |
| F | 114.3 | 223.0 | 159.9 |
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Long | Long | Short | Short | Hedge | Hedge | |
| EPU | 0.160 (0.354) | −0.0314 (0.103) | 1.037 + (0.599) | −0.150 (0.180) | −0.878 + (0.464) | 0.119 (0.186) |
| MKTRF | 1.176 *** (0.0364) | 1.269 *** (0.0458) | −0.0928 + (0.0511) | |||
| SMB | 0.355 *** (0.0421) | 0.453 *** (0.0488) | −0.0972 + (0.0527) | |||
| HML | −0.122 * (0.0516) | −0.0413 (0.0863) | −0.0809 (0.0835) | |||
| WML | 0.497 *** (0.0321) | −1.042 *** (0.0455) | 1.539 *** (0.0563) | |||
| CONS | 1.083 *** (0.299) | 0.0322 (0.108) | −0.0194 (0.426) | −0.286 + (0.156) | 1.102 ** (0.376) | 0.319 + (0.165) |
| N | 407 | 407 | 407 | 407 | 407 | 407 |
| adj. R2 | −0.002 | 0.897 | 0.012 | 0.880 | 0.011 | 0.847 |
| F | 0.203 | 221.3 | 3.003 | 270.2 | 3.572 | 159.9 |
| Hedge | |
|---|---|
| DIV | 11.43 (8.033) |
| INFLATION | 1.436 * (0.812) |
| M3 | −55.07 (287.9) |
| YIELD | −2.970 (2.313) |
| DEFAULT | −15.56 ** (7.059) |
| TERM | −4.938 ** (2.136) |
| IIP | 0.461 (0.713) |
| EPU | 0.0299 * (0.0171) |
| CONS | 0.600 (0.711) |
| N | 406 |
| Adj. R2 | 0.091 |
| F | 3.662 |
| Coef. | Std. Err. | p > z | 95% Conf. | Interval | |
|---|---|---|---|---|---|
| Panel (A): EPU as the dependent variable EPU | |||||
| L1. | 0.726 | 0.062 | 0.000 | 0.604 | 0.848 |
| L2. | −0.093 | 0.078 | 0.233 | −0.245 | 0.060 |
| L3. | 0.005 | 0.078 | 0.953 | −0.149 | 0.158 |
| L4. | 0.273 | 0.070 | 0.000 | 0.137 | 0.410 |
| HEDGE | |||||
| L1. | 0.155 | 0.159 | 0.328 | −0.156 | 0.467 |
| L2. | 0.421 | 0.158 | 0.008 | 0.112 | 0.730 |
| L3. | −0.090 | 0.152 | 0.555 | −0.388 | 0.208 |
| L4. | 0.326 | 0.140 | 0.020 | 0.051 | 0.600 |
| Constant | 9.477 | 4.574 | 0.038 | 0.513 | 18.441 |
| Panel (B): HEDGE as the dependent variable EPU | |||||
| L1. | −0.018 | 0.022 | 0.411 | −0.060 | 0.025 |
| L2. | −0.007 | 0.027 | 0.807 | −0.060 | 0.046 |
| L3. | 0.016 | 0.027 | 0.548 | −0.037 | 0.070 |
| L4. | −0.013 | 0.024 | 0.581 | −0.061 | 0.034 |
| HEDGE | |||||
| L1. | 0.088 | 0.055 | 0.112 | −0.021 | 0.196 |
| L2. | −0.019 | 0.055 | 0.725 | −0.127 | 0.088 |
| L3. | 0.013 | 0.053 | 0.813 | −0.091 | 0.116 |
| L4. | 0.161 | 0.049 | 0.001 | 0.066 | 0.257 |
| Constant | 3.837 | 1.592 | 0.016 | 0.717 | 6.956 |
| Cointegrating equation: | Cointegrating Equation (1) | |
| EPU (−1) | 1.000000 | |
| HEDGE (−1) | 51.09338 *** | |
| (5.35805) | ||
| C | −162.5485 | |
| Error Correction: | D(EPU) | D(HEDGE) |
| Cointegrating Equation (1) | 0.018317 *** | −0.018495 *** |
| (0.00508) | (0.00215) | |
| D (EPU (−1)) | −0.328359 *** | −0.009266 |
| (0.05121) | (0.02168) | |
| D (EPU (−2)) | −0.306039 *** | −0.014115 |
| (0.05164) | (0.02186) | |
| D (EPU (−3)) | −0.271631 *** | 0.036195 |
| (0.05208) | (0.02205) | |
| D (EPU (−4)) | −0.128718 *** | 0.054237 *** |
| (0.05032) | (0.02130) | |
| D (HEDGE (−1)) | −0.753648 *** | −0.031366 |
| (0.23890) | (0.10113) | |
| D (HEDGE (−2)) | −0.374986 * | −0.056872 |
| (0.20939) | (0.08864) | |
| D (HEDGE (−3)) | −0.386537 ** | −0.011666 |
| (0.16870) | (0.07142) | |
| D (HEDGE (−4)) | −0.093585 | 0.066331 |
| (0.12028) | (0.05092) | |
| C | −0.035858 | −0.008797 |
| (0.88857) | (0.37616) | |
| Adj. R2 | 0.152158 | 0.499365 |
| F | 8.976251 | 45.33162 |
| Panel (A): Response of EPU | Panel (B): Response of HEDGE | ||||
|---|---|---|---|---|---|
| Period | EPU | HEDGE | Period | EPU | HEDGE |
| 1 | 17.79262 | 0.000000 | 1 | 0.187222 | 7.529812 |
| 2 | 12.31028 | 1.372127 | 2 | −0.489499 | 0.178284 |
| 3 | 8.872394 | 3.830454 | 3 | −0.444385 | −0.225921 |
| 4 | 6.740064 | 2.612841 | 4 | 0.599574 | 0.217503 |
| 5 | 7.816250 | 4.093354 | 5 | 0.728219 | 0.584200 |
| 6 | 10.13712 | 4.158792 | 6 | −0.614950 | −0.396321 |
| 7 | 10.23387 | 3.871679 | 7 | −0.496040 | −0.053057 |
| 8 | 9.463814 | 3.647508 | 8 | −0.186526 | −0.015110 |
| 9 | 9.146190 | 3.840683 | 9 | −0.029423 | 0.035556 |
| 10 | 9.146403 | 3.925713 | 10 | −0.140596 | −0.147335 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goel, G.; Dash, S.R.; Mata, M.N.; Caleiro, A.B.; Xavier Rita, J.; Filipe, J.A. Economic Policy Uncertainty and Stock Return Momentum. J. Risk Financial Manag. 2021, 14, 141. https://doi.org/10.3390/jrfm14040141
Goel G, Dash SR, Mata MN, Caleiro AB, Xavier Rita J, Filipe JA. Economic Policy Uncertainty and Stock Return Momentum. Journal of Risk and Financial Management. 2021; 14(4):141. https://doi.org/10.3390/jrfm14040141
Chicago/Turabian StyleGoel, Garima, Saumya Ranjan Dash, Mário Nuno Mata, António Bento Caleiro, João Xavier Rita, and José António Filipe. 2021. "Economic Policy Uncertainty and Stock Return Momentum" Journal of Risk and Financial Management 14, no. 4: 141. https://doi.org/10.3390/jrfm14040141
APA StyleGoel, G., Dash, S. R., Mata, M. N., Caleiro, A. B., Xavier Rita, J., & Filipe, J. A. (2021). Economic Policy Uncertainty and Stock Return Momentum. Journal of Risk and Financial Management, 14(4), 141. https://doi.org/10.3390/jrfm14040141







