Volatility Spillovers among Cryptocurrencies
Abstract
:1. Introduction
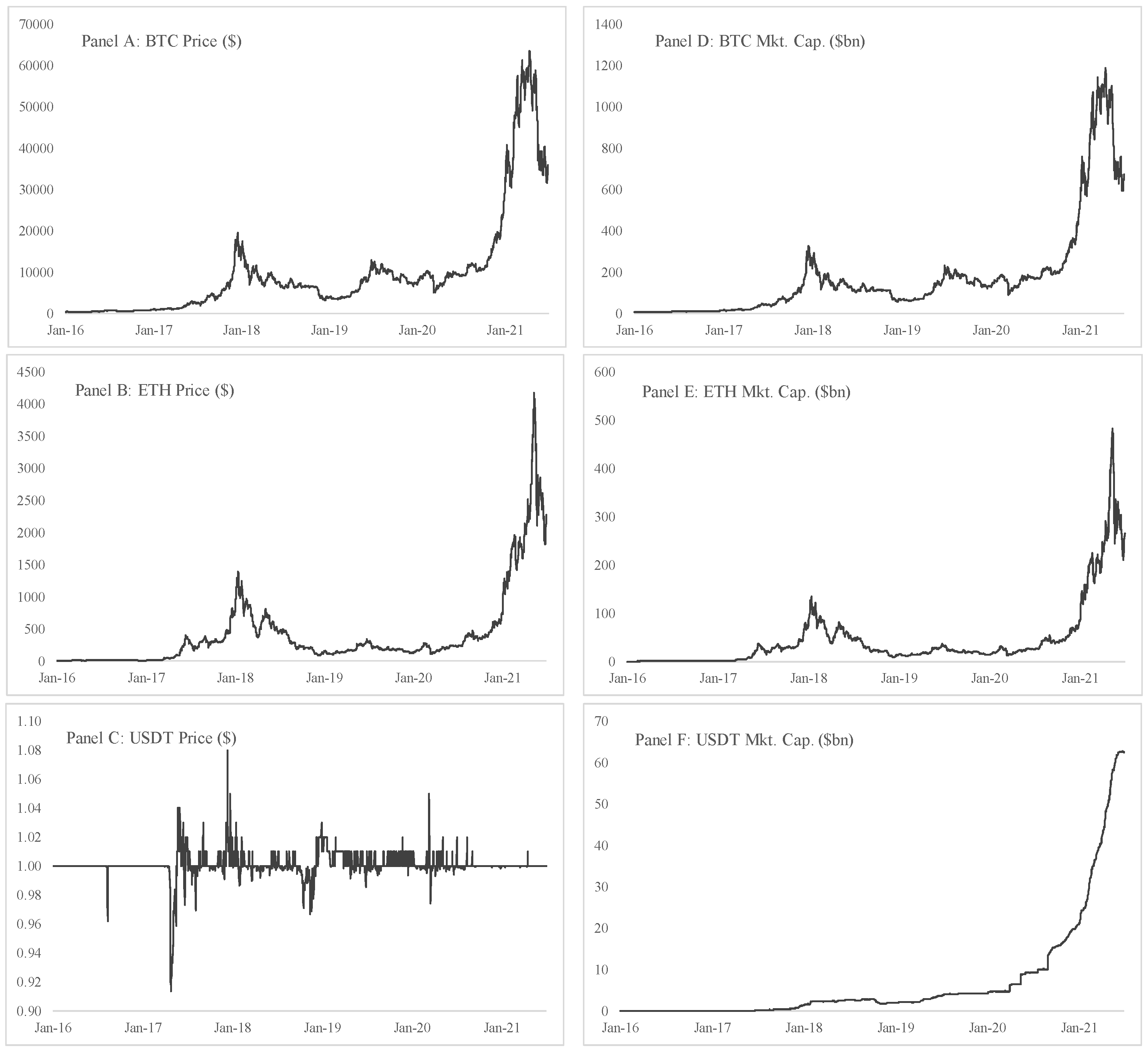
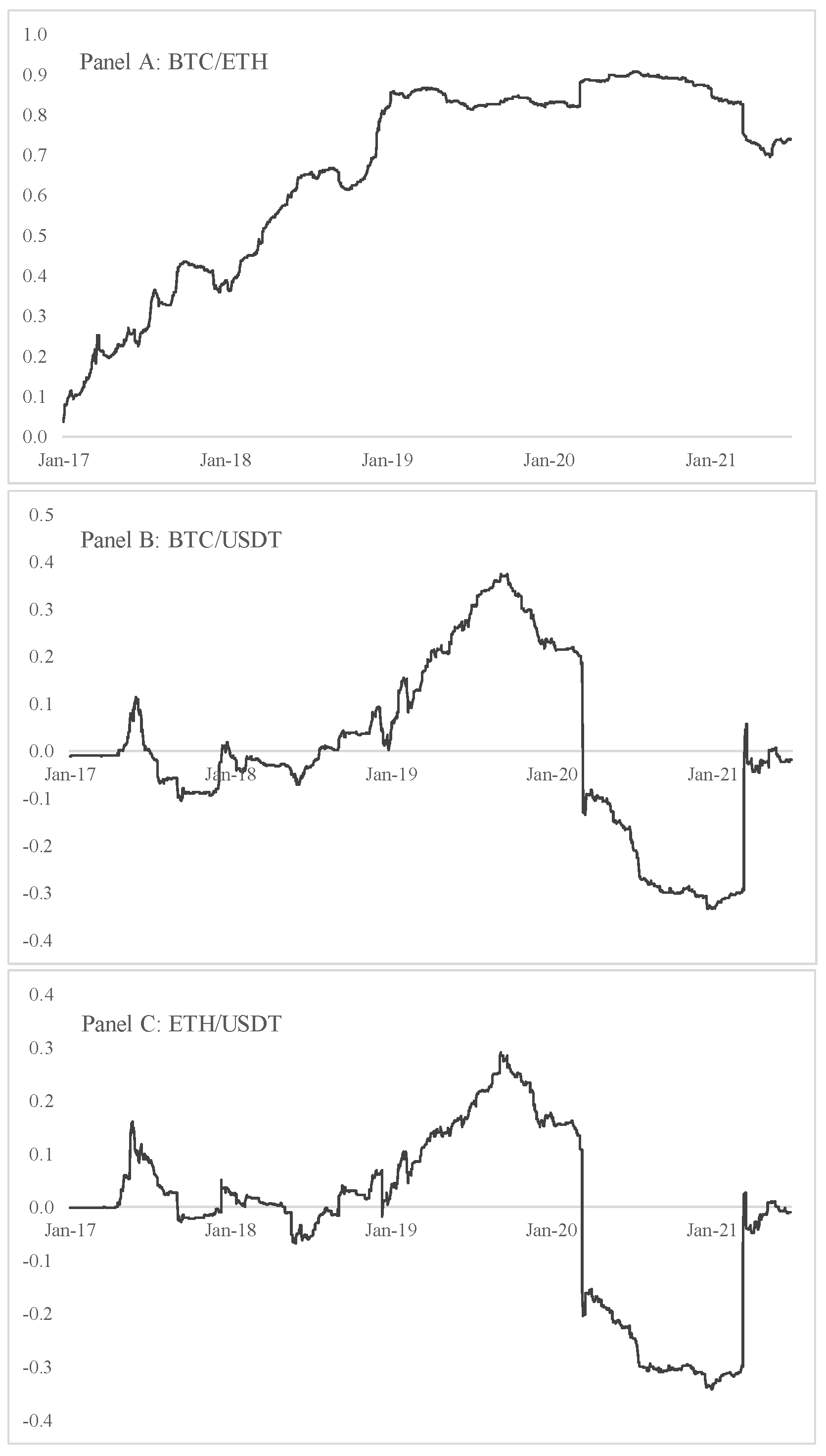
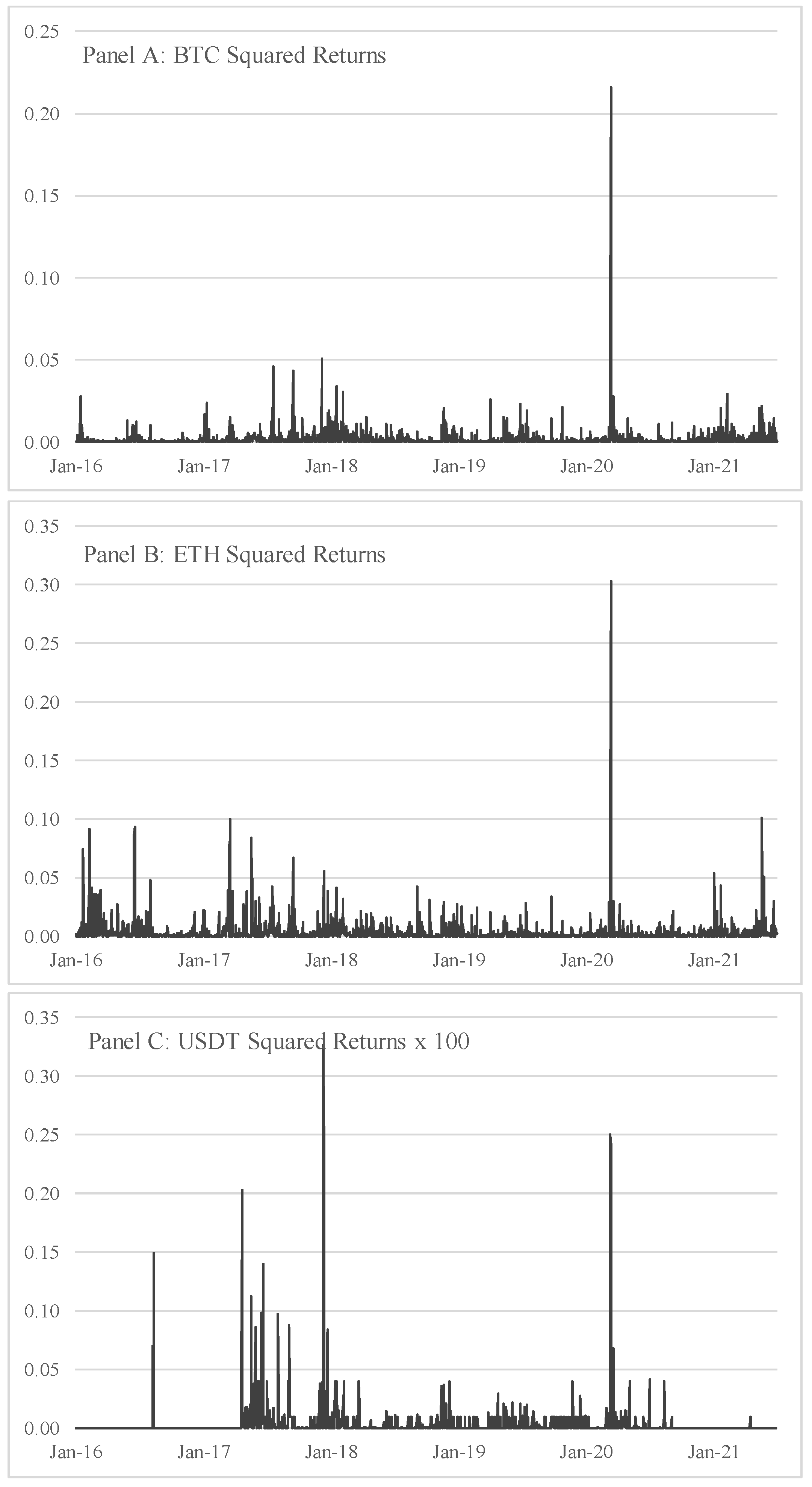
2. Data
3. Empirical Analysis
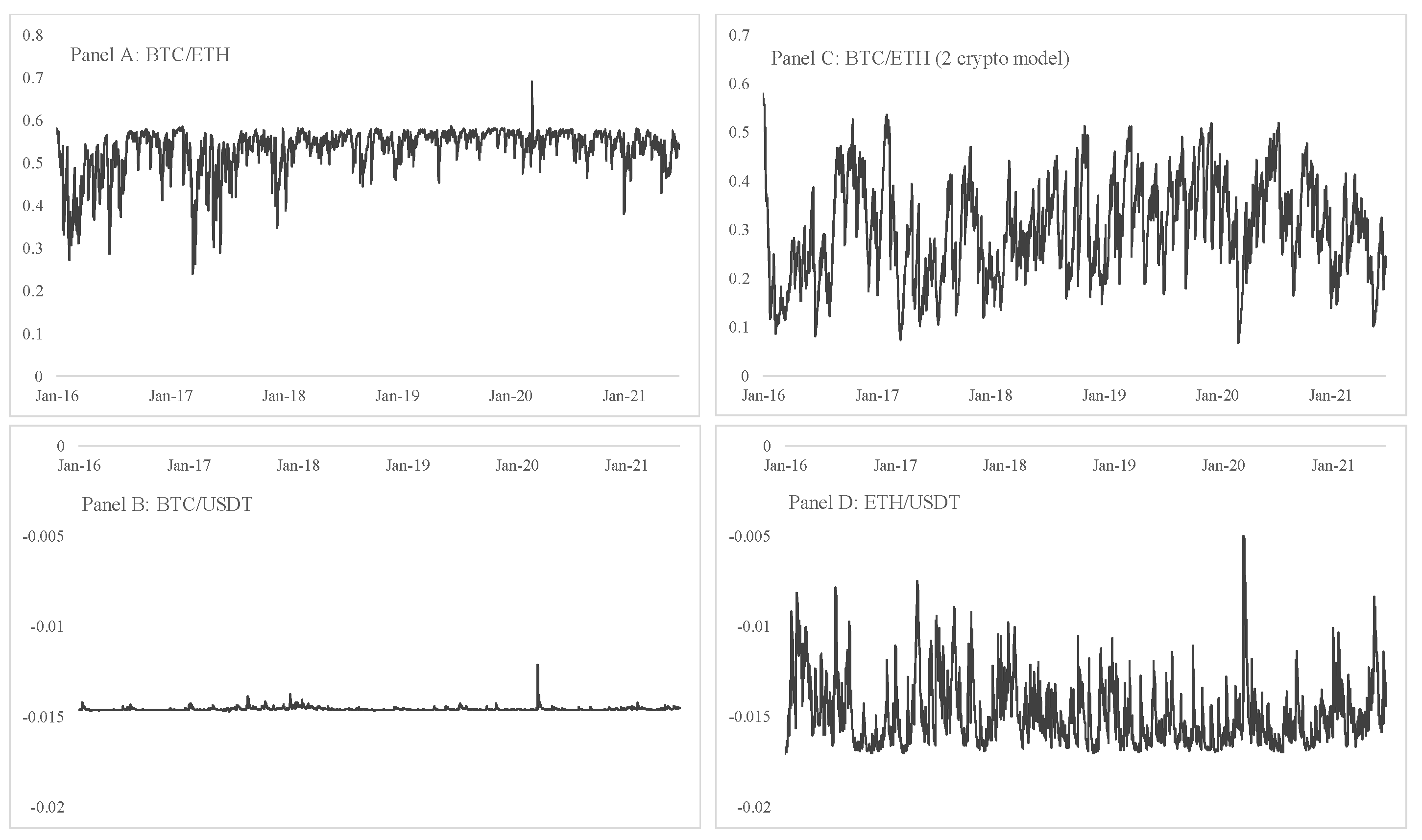
3.1. Application 1: Hedge Ratios
3.2. Application 2: Portfolio Weights
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | See: https://www.economist.com/finance-and-economics/2021/06/10/cryptocoins-are-proliferating-wildly-what-are-they-all-for (accessed on 13 September 2021). |
| 2 | Blockchain is a form of decentralised ledger technology that uses strong cryptography to confirm and link data entries. Cryptocurrencies utilise this technology to operate as decentralised virtual currencies, with blockchain thwarting the potential double-spending problem. |
| 3 | Source: https://coinmarketcap.com/ (accessed on 12 September 2021). |
| 4 | Coinmarketcap has closing prices for Tether from mid-March 2015, and for Ether from September 2015. Our sample starts on 1 January 2016 to coincide with the start of a quarter and ends on 30 June 2021 to coincide with the end of the most recent quarter. |
References
- Beneki, Christina, Alexandros Koulis, Nikolaos A. Kyriazis, and Stephanos Papadamou. 2019. Investigating volatility transmission and hedging properties between Bitcoin and Ethereum. Research in International Business and Finance 48: 219–27. [Google Scholar] [CrossRef]
- Bouri, Elie, Brian Lucey, and David Roubaud. 2020. The volatility surprises of leading cryptocurrencies: Transitory and permanent linkages. Finance Research Letters 33: 101188. [Google Scholar] [CrossRef]
- Bouri, Elie, David Gabauer, Rangan Gupta, and Aviral Kumar Tiwarid. 2021a. Volatility connectedness of major cryptocurrencies: The role of investor happiness. Journal of Behavioral and Experimental Finance 30: 100463. [Google Scholar] [CrossRef]
- Bouri, Elie, Luis A. Gil-Alana, Rangan Gupta, and David Roubaud. 2019. Modelling long memory volatility in the Bitcoin market: Evidence of persistence and structural break. International Journal of Finance and Economics 24: 412–26. [Google Scholar] [CrossRef] [Green Version]
- Bouri, Elie, Mahamitra Das, Rangan Gupta, and David Roubaud. 2018. Spillovers between Bitcoin and other assets during bear and bull markets. Applied Economics 50: 5935–49. [Google Scholar] [CrossRef] [Green Version]
- Bouri, Elie, Tareq Saeed, Xuan Vinh Vo, and David Roubaud. 2021b. Quantile connectedness in the cryptocurrency market. Journal of International Financial Markets, Institutions and Money 71: 101302. [Google Scholar] [CrossRef]
- Canh, Nguyen Phuc, Udomsak Wongchoti, Su Dinh Thanh, and Nguyen Trung Thong. 2019. Systematic risk in cryptocurrency market: Evidence from DCC-MGARCH model. Finance Research Letters 29: 90–100. [Google Scholar] [CrossRef]
- Caporale, Guglielmo Maria, Woo-Young Kang, Fabio Spagnolo, and Nicola Spagnolo. 2021. Cyber-attacks, spillovers and contagion in the cryptocurrency markets. Journal of International Financial Markets, Institutions and Money 74: 101298. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroskedasticity with estimates of the variance of UK inflation. Econometrica 50: 987–1008. [Google Scholar] [CrossRef]
- Engle, Robert F. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar]
- Gkillas, Konstantinos, and Paraskevi Katsiampa. 2018. An application of extreme value theory to cryptocurrencies. Economics Letters 164: 109–11. [Google Scholar] [CrossRef] [Green Version]
- Härdle, Wolfgang Karl, Campbell R. Harvey, and Raphael CG Reule. 2020. Understanding cryptocurrencies. Journal of Financial Econometrics 18: 181–208. [Google Scholar] [CrossRef]
- Ji, Qiang, Elie Bouri, Chi Keung Marco Lau, and David Roubaud. 2019. Dynamic connectedness and integration in cryptocurrency markets. International Review of Financial Analysis 63: 257–72. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi, Shaen Corbet, and Brian Lucey. 2019. Volatility spillover effects in leading cryptocurrencies: A BEKK-MGARCH analysis. Finance Research Letters 29: 68–74. [Google Scholar] [CrossRef] [Green Version]
- Koutmos, Dimitrios. 2018. Return and volatility spillovers among cryptocurrencies. Economics Letters 173: 122–27. [Google Scholar] [CrossRef]
- Kroner, Kenneth F., and Jahangir Sultan. 1993. Time dynamic varying distributions and dynamic hedging with foreign currency futures. Journal of Financial and Quantitative Analysis 28: 535–51. [Google Scholar] [CrossRef]
- Kroner, K. F., and V. K. Ng. 1998. Modelling asymmetric movements of asset prices. Review of Financial Studies 11: 817–44. [Google Scholar] [CrossRef]
- Kumar, Anoop S., and Suvvari Anandarao. 2019. Volatility spillover in crypto-currency markets: Some evidences from GARCH and wavelet analysis. Physica A: Statistical Mechanics and its Applications 524: 448–58. [Google Scholar]
- Kyriazis, Nikolaos A. 2019. A survey on empirical findings about spillovers in cryptocurrency markets. Journal of Risk and Financial Management 12: 170. [Google Scholar] [CrossRef] [Green Version]
- Ling, Shiqing, and Michael McAleer. 2003. Asymptotic theory for a vector ARMA-GARCH model. Econometric Theory 19: 278–308. [Google Scholar] [CrossRef] [Green Version]
- Liu, Yukun, and Aleh Tsyvinski. 2021. Risks and returns of cryptocurrency. Review of Financial Studies 34: 2689–727. [Google Scholar] [CrossRef]
- Moratis, George. 2021. Quantifying the spillover effect in the cryptocurrency market. Finance Research Letters 38: 101534. [Google Scholar]
- Naeem, Muhammad Abubakr, Elie Bouri, Zhe Peng, Syed Jawad Hussain Shahzad, and Xuan Vinh Vo. 2021. Asymmetric efficiency of cryptocurrencies during COVID19. Physica A: Statistical Mechanics and its Applications 565: 125562. [Google Scholar] [CrossRef]
- Qureshi, Saba, Muhammad Aftab, Elie Bouri, and Tareq Saeed. 2020. Dynamic interdependence of cryptocurrency markets: An analysis across time and frequency. Physica A: Statistical Mechanics and its Applications 559: 125077. [Google Scholar] [CrossRef]
- Sadorsky, Perry. 2012. Correlations and volatility spillovers between oil prices and the stock prices of clean energy and technology companies. Energy Economics 34: 248–55. [Google Scholar] [CrossRef]
- Sensoy, Ahmet, Thiago Christiano Silva, Shaen Corbet, and Benjamin Miranda Tabak. 2021. High-frequency return and volatility spillovers among cryptocurrencies. Applied Economics 53: 4310–28. [Google Scholar] [CrossRef]
- Smales, Lee A. 2019. Bitcoin as a safe haven: Is it even worth considering? Finance Research Letters 30: 385–93. [Google Scholar] [CrossRef]
- Smales, Lee A. 2020. One cryptocurrency to explain them all? Understanding the importance of Bitcoin in cryptocurrency returns. Economic Papers 39: 118–32. [Google Scholar] [CrossRef]
- Xu, Qiuhua, Yixuan Zhang, and Ziyang Zhang. 2021. Tail-risk spillovers in cryptocurrency markets. Finance Research Letters 38: 101453. [Google Scholar] [CrossRef]
- Yi, Shuyue, Zishuang Xu, and Gang-Jin Wang. 2018. Volatility connectedness in the cryptocurrency market: Is Bitcoin a dominant cryptocurrency? International Review of Financial Analysis 60: 98–114. [Google Scholar] [CrossRef]
| BTC | ETH | USDT | |
|---|---|---|---|
| Mean | 0.0022 | 0.0039 | 0.0000 |
| Median | 0.0021 | 0.0009 | 0.0000 |
| Std. Dev. | 0.040 | 0.060 | 0.006 |
| Maximum | 0.225 | 0.303 | 0.057 |
| Minimum | −0.465 | −0.551 | −0.049 |
| Skewness | −0.795 | −0.284 | 0.293 |
| Kurtosis | 14.96 | 10.48 | 20.76 |
| Observations | 2007 | 2007 | 2007 |
| BTC | ETH | USDT | |
|---|---|---|---|
| BTC | 1.000 | 0.668 | 0.341 |
| ETH | 0.581 | 1.000 | 0.319 |
| USDT | −0.015 | −0.017 | 1.000 |
| ARCH-LM Test | |||
|---|---|---|---|
| BTC Returns | |||
| F-Statistic | 0.259 | Prob. | 0.979 |
| Obs × R-squared | 2.077 | Prob. | 0.979 |
| ETH Returns | |||
| F-Statistic | 0.798 | Prob. | 0.589 |
| Obs × R-squared | 5.591 | Prob. | 0.588 |
| USDT Returns | |||
| F-Statistic | 1.191 | Prob. | 0.275 |
| Obs × R-squared | 1.192 | Prob. | 0.275 |
| BEKK | CCC | DCC | DCC (BTC/ETH) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coeff. | Std.Err. | Coeff. | Std.Err. | Coeff. | Std.Err. | Coeff. | Std.Err. | |||||
| Mean | ||||||||||||
| m10 | 0.002 | 0.001 | *** | 0.001 | 0.000 | ** | 0.000 | 0.000 | *** | 0.000 | 0.000 | |
| m11 | 0.044 | 0.023 | * | 0.950 | 0.009 | *** | 0.862 | 0.000 | *** | 0.989 | 0.000 | *** |
| m12 | −0.039 | 0.014 | *** | −0.061 | 0.013 | *** | −0.016 | 0.000 | *** | 0.000 | 0.000 | *** |
| m13 | 0.174 | 0.179 | −0.024 | 0.263 | −0.038 | 0.002 | *** | |||||
| m20 | 0.002 | 0.001 | ** | 0.004 | 0.002 | ** | 0.001 | 0.000 | *** | 0.002 | 0.001 | * |
| m21 | −0.082 | 0.041 | ** | −0.068 | 0.017 | *** | −0.004 | 0.000 | *** | -0.112 | 0.022 | *** |
| m22 | 0.045 | 0.040 | 1.027 | 0.008 | *** | 0.003 | 0.000 | *** | 0.139 | 0.018 | *** | |
| m23 | 0.343 | 0.228 | −0.028 | 0.267 | −0.008 | 0.003 | *** | |||||
| m30 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||||||
| m31 | 0.000 | 0.001 | 0.001 | 0.000 | ** | 0.000 | 0.000 | |||||
| m32 | −0.003 | 0.001 | ** | 0.000 | 0.000 | 0.000 | 0.002 | |||||
| m33 | −0.476 | 0.050 | *** | 0.045 | 0.271 | 1.000 | 0.004 | *** | ||||
| Variance | ||||||||||||
| c11 | 0.009 | 0.002 | *** | 0.001 | 0.000 | *** | 0.001 | 0.000 | *** | 0.000 | 0.000 | *** |
| c21 | 0.014 | 0.004 | *** | |||||||||
| c22 | 0.009 | 0.002 | *** | 0.002 | 0.000 | *** | 0.002 | 0.000 | *** | 0.002 | 0.000 | *** |
| c31 | 0.000 | 0.000 | * | |||||||||
| c32 | 0.000 | 0.000 | * | |||||||||
| c33 | 0.000 | 0.000 | 0.000 | 0.000 | *** | 0.000 | 0.000 | *** | ||||
| α11 | 0.405 | 0.063 | *** | 0.073 | 0.110 | 0.041 | 0.000 | *** | 0.020 | 0.191 | ||
| α12 | −0.096 | 0.128 | −0.003 | 0.107 | −0.005 | 0.005 | 0.000 | 0.000 | ||||
| α13 | −0.007 | 0.003 | ** | −0.276 | 2.600 | −0.013 | 15.851 | |||||
| α21 | −0.021 | 0.023 | −0.015 | 0.173 | −0.050 | 0.005 | *** | -0.048 | 0.013 | *** | ||
| α22 | 0.469 | 0.105 | *** | 0.073 | 0.161 | 0.063 | 0.000 | *** | 0.055 | 0.008 | *** | |
| α23 | −0.004 | 0.002 | * | −0.483 | 3.815 | −0.015 | 13.421 | |||||
| α31 | 0.061 | 0.249 | 0.001 | 0.001 | 0.002 | 0.000 | *** | |||||
| α32 | 0.207 | 0.329 | 0.000 | 0.001 | 0.000 | 0.000 | *** | |||||
| α33 | 0.460 | 0.080 | *** | 0.670 | 0.264 | 0.260 | 1.232 | |||||
| β11 | 0.907 | 0.026 | *** | 0.442 | 0.002 | *** | 0.464 | 0.000 | *** | 0.106 | 0.043 | ** |
| β12 | −0.013 | 0.055 | −0.003 | 0.001 | *** | −0.024 | 0.000 | *** | -0.001 | 0.000 | *** | |
| β13 | 0.002 | 0.001 | * | 0.083 | 0.645 | 0.019 | 0.078 | |||||
| β21 | 0.000 | 0.015 | 0.012 | 0.002 | *** | 0.060 | 0.000 | *** | 0.033 | 1.122 | ||
| β22 | 0.867 | 0.062 | *** | 0.444 | 0.001 | *** | 0.505 | 0.000 | *** | 0.525 | 0.000 | *** |
| β23 | −0.003 | 0.001 | * | −0.131 | 1.102 | −0.019 | 0.025 | |||||
| β31 | −0.051 | 0.062 | −0.004 | 0.000 | *** | −0.008 | 0.000 | *** | ||||
| β32 | −0.087 | 0.096 | −0.003 | 0.000 | *** | −0.001 | 0.000 | *** | ||||
| β33 | 0.938 | 0.012 | *** | 0.578 | 0.015 | *** | 0.479 | 0.000 | *** | |||
| ρ21 | 0.303 | 0.374 | ||||||||||
| ρ31 | −0.010 | 0.087 | ||||||||||
| ρ32 | −0.038 | 0.133 | ||||||||||
| θ1 | 0.102 | 0.057 | * | 0.168 | 0.036 | *** | ||||||
| θ2 | 0.693 | 0.146 | *** | 0.809 | 0.039 | *** | ||||||
| Log L | 26141 | 26369 | 24555 | 24205 | ||||||||
| AIC | −26.06 | −26.24 | −24.43 | −24.10 | ||||||||
| BEKK | CCC | DCC | |||||||
|---|---|---|---|---|---|---|---|---|---|
| BTC | ETH | USDT | BTC | ETH | USDT | BTC | ETH | USDT | |
| Q(20)r | 25.810 | 45.380 | 35.450 | 67.670 | 31.990 | 6.766 | 201.170 | 47.640 | 14.116 |
| p values | 0.172 | 0.000 | 0.018 | 0.000 | 0.043 | 0.997 | 0.000 | 0.000 | 0.824 |
| Q(20)r2 | 5.150 | 14.790 | 4.997 | 808.790 | 135.590 | 0.309 | 361.950 | 67.580 | 1.694 |
| p values | 0.990 | 0.780 | 0.999 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 1.000 |
| Mean | Std. Dev. | Min. | Max. | |
|---|---|---|---|---|
| Panel A: Dynamic Conditional Correlation | ||||
| BTC/ETH | 0.531 | 0.053 | 0.239 | 0.690 |
| BTC/USDT | −0.015 | 0.000 | −0.015 | −0.012 |
| ETH/USDT | −0.015 | 0.002 | −0.017 | −0.005 |
| Panel B: Hedge ratio (long/short) | ||||
| BTC/ETH | 0.955 | 0.088 | 0.638 | 2.676 |
| BTC/USDT | 0.000 | 0.000 | −0.008 | 0.000 |
| ETH/BTC | 0.297 | 0.047 | 0.006 | 0.355 |
| ETH/USDT | 0.000 | 0.000 | 0.000 | 0.000 |
| USDT/BTC | −1.226 | 0.916 | −7.263 | −0.002 |
| USDT/ETH | −2.279 | 1.762 | −10.072 | −0.093 |
| Panel C: Portfolio weights | ||||
| BTC/ETH | 0.022 | 0.017 | 0.000 | 0.107 |
| BTC/USDT | 0.998 | 0.022 | 0.025 | 1.000 |
| ETH/USDT | 0.999 | 0.000 | 0.996 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smales, L.A. Volatility Spillovers among Cryptocurrencies. J. Risk Financial Manag. 2021, 14, 493. https://doi.org/10.3390/jrfm14100493
Smales LA. Volatility Spillovers among Cryptocurrencies. Journal of Risk and Financial Management. 2021; 14(10):493. https://doi.org/10.3390/jrfm14100493
Chicago/Turabian StyleSmales, Lee A. 2021. "Volatility Spillovers among Cryptocurrencies" Journal of Risk and Financial Management 14, no. 10: 493. https://doi.org/10.3390/jrfm14100493
APA StyleSmales, L. A. (2021). Volatility Spillovers among Cryptocurrencies. Journal of Risk and Financial Management, 14(10), 493. https://doi.org/10.3390/jrfm14100493






