Univariate and Multivariate Machine Learning Forecasting Models on the Price Returns of Cryptocurrencies
Abstract
:1. Introduction
2. Study Design and Data Collection
3. Statistical Methods
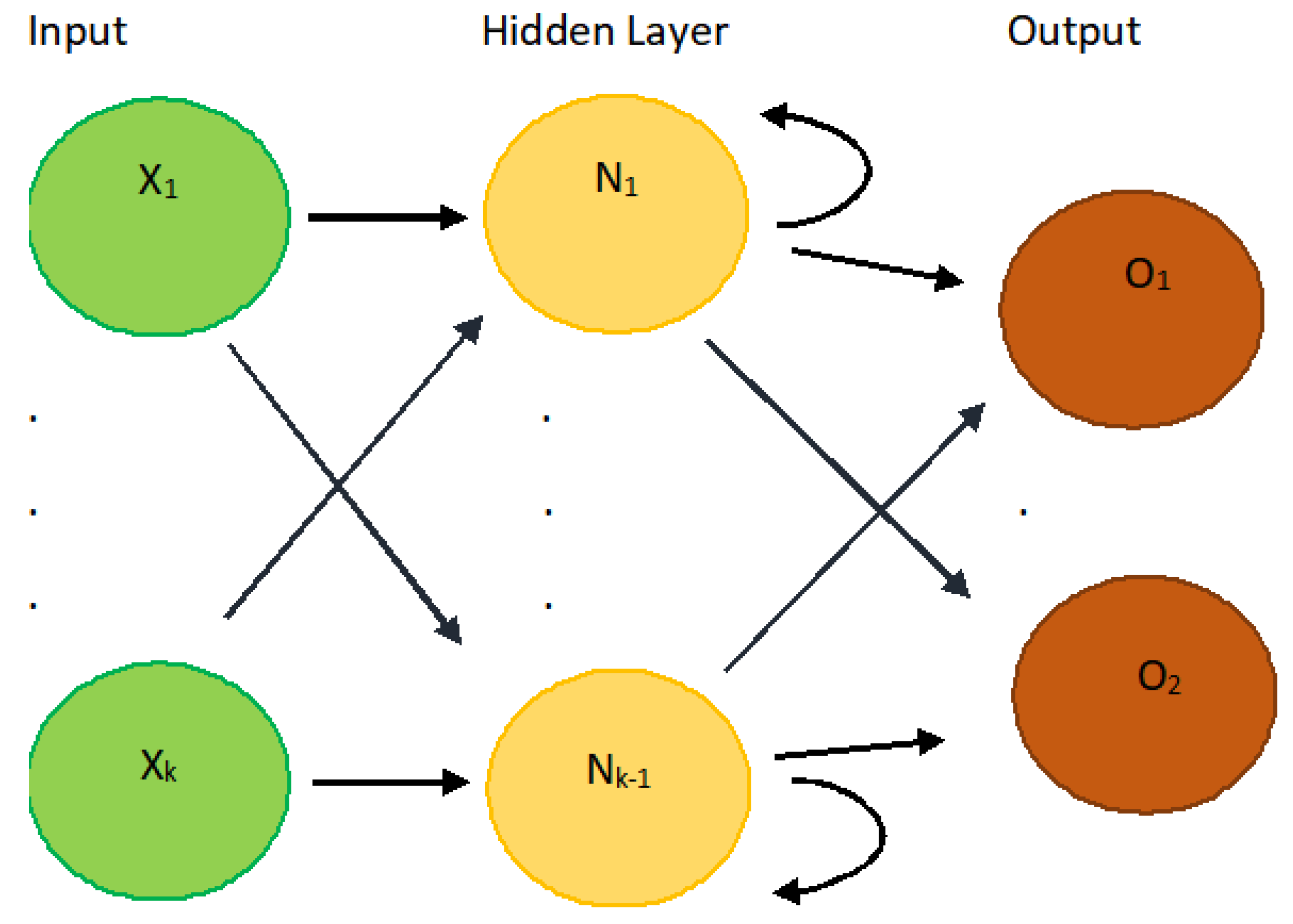
3.1. Univariate Machine Learning Methods
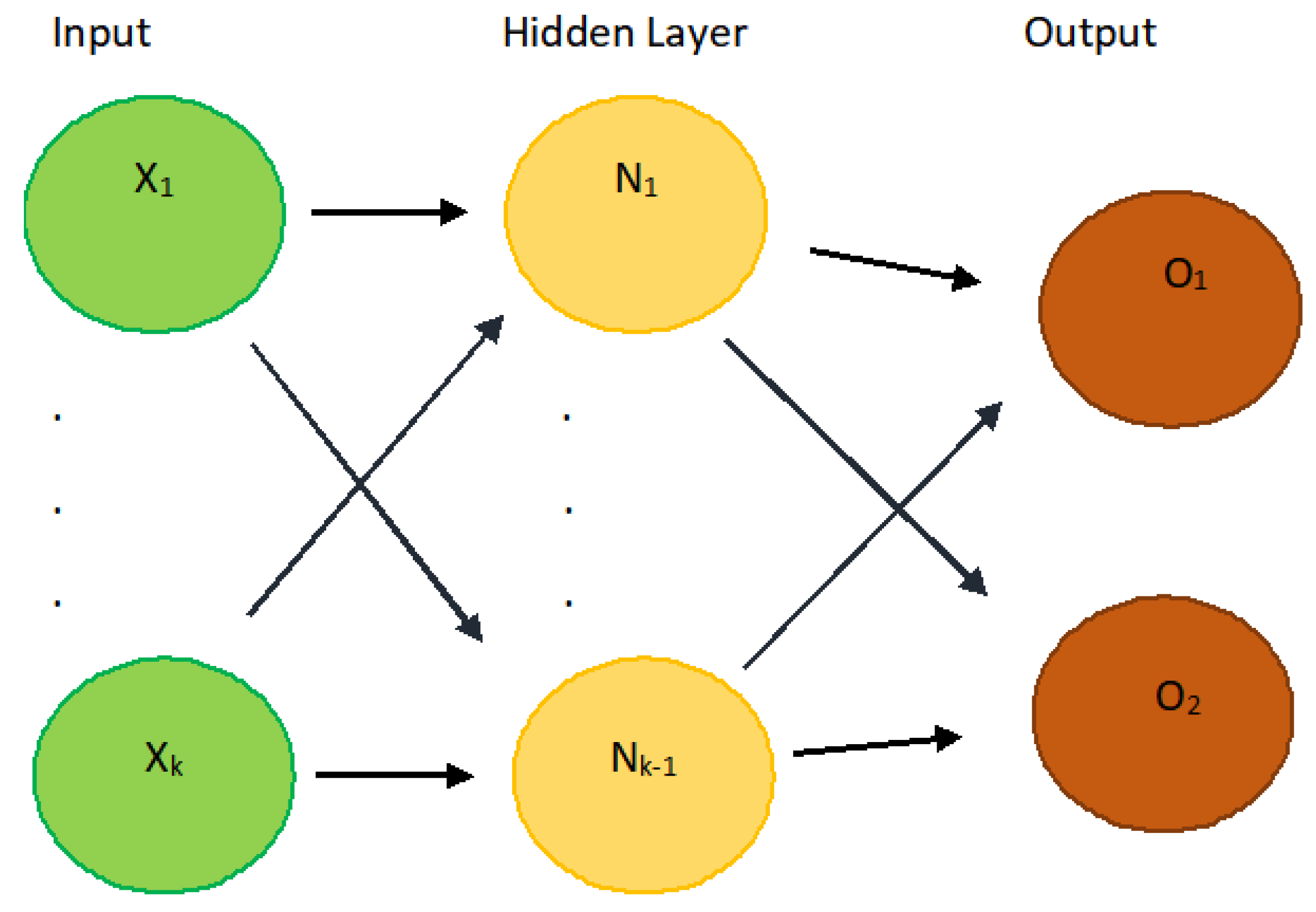
3.2. Multivariate Machine Learning Method
ETH(t) = BTC(t − 1) + ETH(t − 1) + USDT(t − 1) + XRP(t − 1) + BNB(t − 1) + ADA(t − 1) + FLOW(t − 1) + USDC(t − 1) + DOGE(t − 1) + UNI(t − 1) + ε(t)
USDT(t) = BTC(t − 1) + ETH(t − 1) + USDT(t − 1) + XRP(t − 1) + BNB(t − 1) + ADA(t − 1) + FLOW(t − 1) + USDC(t − 1) + DOGE(t − 1) + UNI(t − 1) + ε(t)
XRP(t) = BTC(t − 1) + ETH(t − 1) + USDT(t − 1) + XRP(t − 1) + BNB(t − 1) + ADA(t − 1) + FLOW(t − 1) + USDC(t − 1) + DOGE(t − 1) + UNI(t − 1) + ε(t)
BNB(t) = BTC(t − 1) + ETH(t − 1) + USDT(t − 1) + XRP(t − 1) + BNB(t − 1) + ADA(t − 1) + FLOW(t − 1) + USDC(t − 1) + DOGE(t − 1) + UNI(t − 1) + ε(t)
ADA(t) = BTC(t − 1) + ETH(t − 1) + USDT(t − 1) + XRP(t − 1) + BNB(t − 1) + ADA(t − 1) + FLOW(t − 1) + USDC(t − 1) + DOGE(t − 1) + UNI(t − 1) + ε(t)
FLOW(t) = BTC(t − 1) + ETH(t − 1) + USDT(t − 1) + XRP(t − 1) + BNB(t − 1) + ADA(t − 1) + FLOW(t − 1) + USDC(t − 1) + DOGE(t − 1) + UNI(t − 1) + ε(t)
USDC(t) = BTC(t − 1) + ETH(t − 1) + USDT(t − 1) + XRP(t − 1) + BNB(t − 1) + ADA(t − 1) + FLOW(t − 1) + USDC(t − 1) + DOGE(t − 1) + UNI(t − 1) + ε(t)
DOGE(t) = BTC(t − 1) + ETH(t − 1) + USDT(t − 1) + XRP(t − 1) + BNB(t − 1) + ADA(t − 1) + FLOW(t − 1) + USDC(t − 1) + DOGE(t − 1) + UNI(t − 1) + ε(t)
UNI(t) = BTC(t − 1) + ETH(t − 1) + USDT(t − 1) + XRP(t − 1) + BNB(t − 1) + ADA(t − 1) + FLOW(t − 1) + USDC(t − 1) + DOGE(t − 1) + UNI(t − 1) + ε(t)
3.3. Forecast Evaluation
4. Data Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Akyildirim, Erdinc, Ahmet Goncu, and Ahmet Sensoy. 2021. Prediction of cryptocurrency returns using machine learning. Annals of Operations Research 297: 3–36. [Google Scholar] [CrossRef]
- Diebold, F. X., and R. S. Mariano. 1995. Comparing Predictive Accuracy. Journal of Business and Economic Statistics 13: 253–63. [Google Scholar]
- Hyndman, Rob J., and George Athanasopoulos. 2021. Forecasting: Principles and Practice, 3rd ed. Melbourne: OTexts. [Google Scholar]
- Hyun, Steve, Jimin Lee, Jong-Min Kim, and Chulhee Jun. 2019. What Coins lead in the Cryptocurrency Market? Using Copula and Neural Networks Model. Journal of Risk and Financial Management 12: 132. [Google Scholar] [CrossRef] [Green Version]
- Katsiampa, Paraskevi. 2017. Volatility estimation for Bitcoin: A comparison of GARCH models. Economics Letters 158: 3–6. [Google Scholar] [CrossRef] [Green Version]
- Katsiampa, Paraskevi. 2019. An empirical investigation of volatility dynamics in the cryptocurrency market. Research in International Business and Finance 50: 322–35. [Google Scholar] [CrossRef]
- Kim, Jong Min, Chulhee Jun, and Junyoup Lee. 2021. Forecasting the volatility of the cryptocurrency market using GARCH and Stochastic Volatility. Mathematics 9: 1614. [Google Scholar] [CrossRef]
- Kim, Jong Min, Seong-Tae Kim, and Sangjin Kim. 2020. On the Relationship of Cryptocurrency Price with US Stock and Gold Price using Copula Models. Mathematics 8: 1859. [Google Scholar] [CrossRef]
- Mostafa, Fahad, Pritam Saha, Mohammad R. Islam, and Nguyet Nguyen. 2021. GJR-GARCH Volatility Modeling under NIG and ANN for Predicting Top Cryptocurrencies. Journal of Risk and Financial Management 14: 421. [Google Scholar] [CrossRef]
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 1 September 2021).
- Petropoulos, Fotios, and Spyros Makridakis. 2020. Forecasting the novel coronavirus COVID-19. PLoS ONE 15: e0231236. [Google Scholar] [CrossRef] [PubMed]
- Phillip, Andrew, Jennifer Chan, and Shelton Peiris. 2019. On long memory effects in the volatility measure of Cryptocurrencies. Finance Research Letters 28: 95–100. [Google Scholar] [CrossRef]
- Plakandaras, Vasilios, Elie Bouri, and Rangan Gupta. 2021. Forecasting bitcoin returns: Is there a role for the US–China trade war? Journal of Risk 23: 3. [Google Scholar]
- Shahzad, Syed Jawad Hussain, Elie Bouri, Mobeen Ur Rehman, and David Roubaud. 2021. The Hedge Asset for Brics Stock Markets: Bitcoin, Gold, or Vix. Kiel: The World Economy. [Google Scholar]
- Swamidass, Paul M. 2000. Holt’s Forecasting Model. In Encyclopedia of Production and Manufacturing Management. Boston: Springer. [Google Scholar]
- Wang, Pengfei, Wei Zhang, Xiao Li, and Dehua Shen. 2019. Is cryptocurrency a hedge or a safe haven for international indices? A comprehensive and dynamic perspective. Finance Research Letters 31: 1–18. [Google Scholar] [CrossRef]
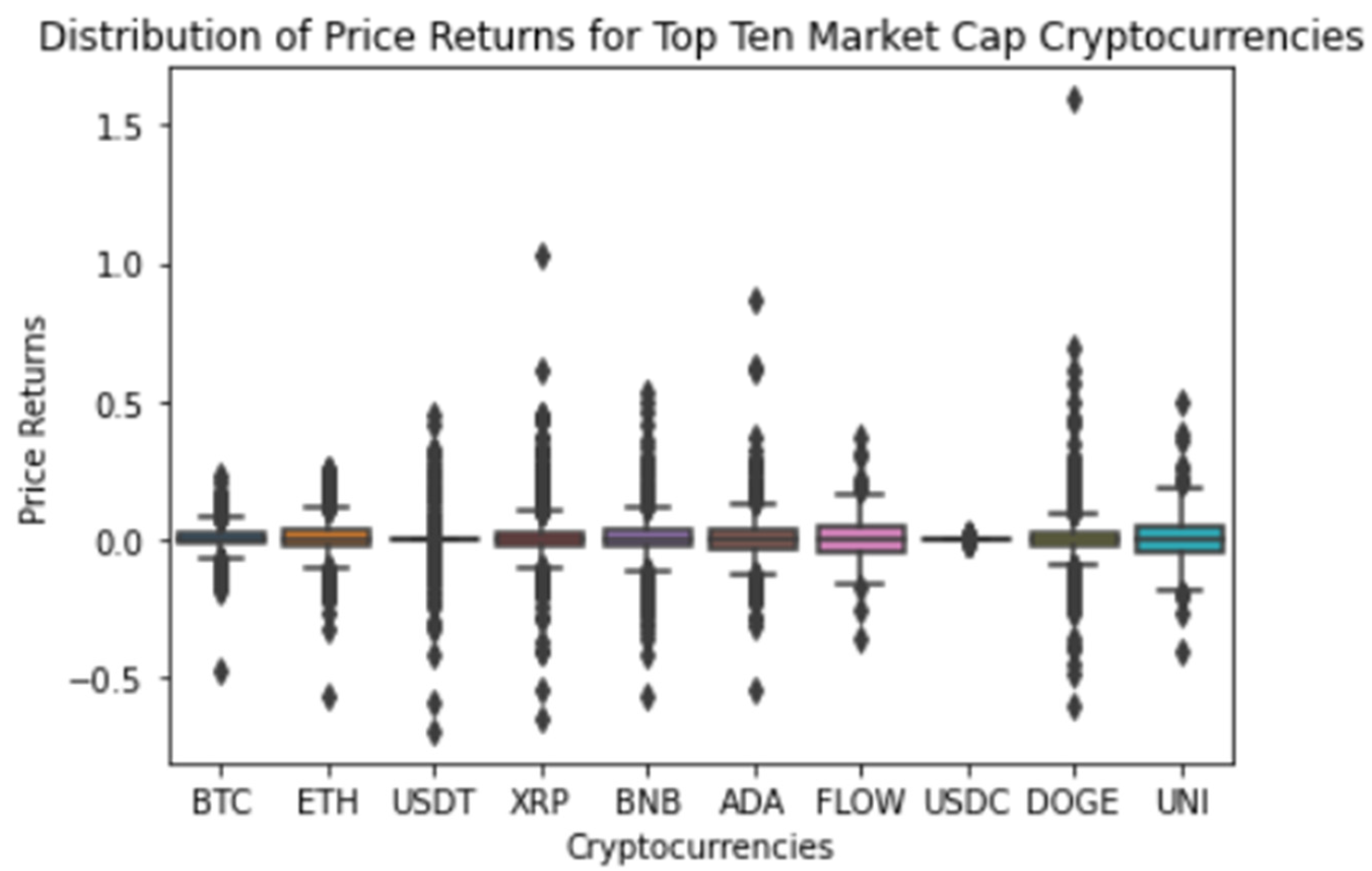
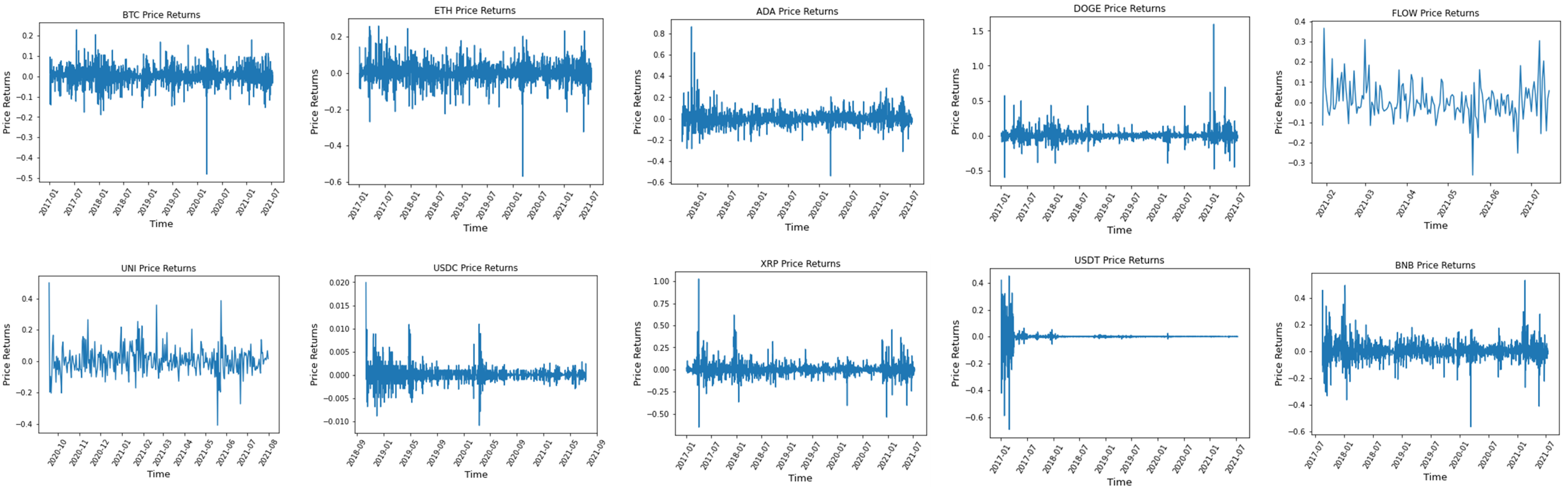
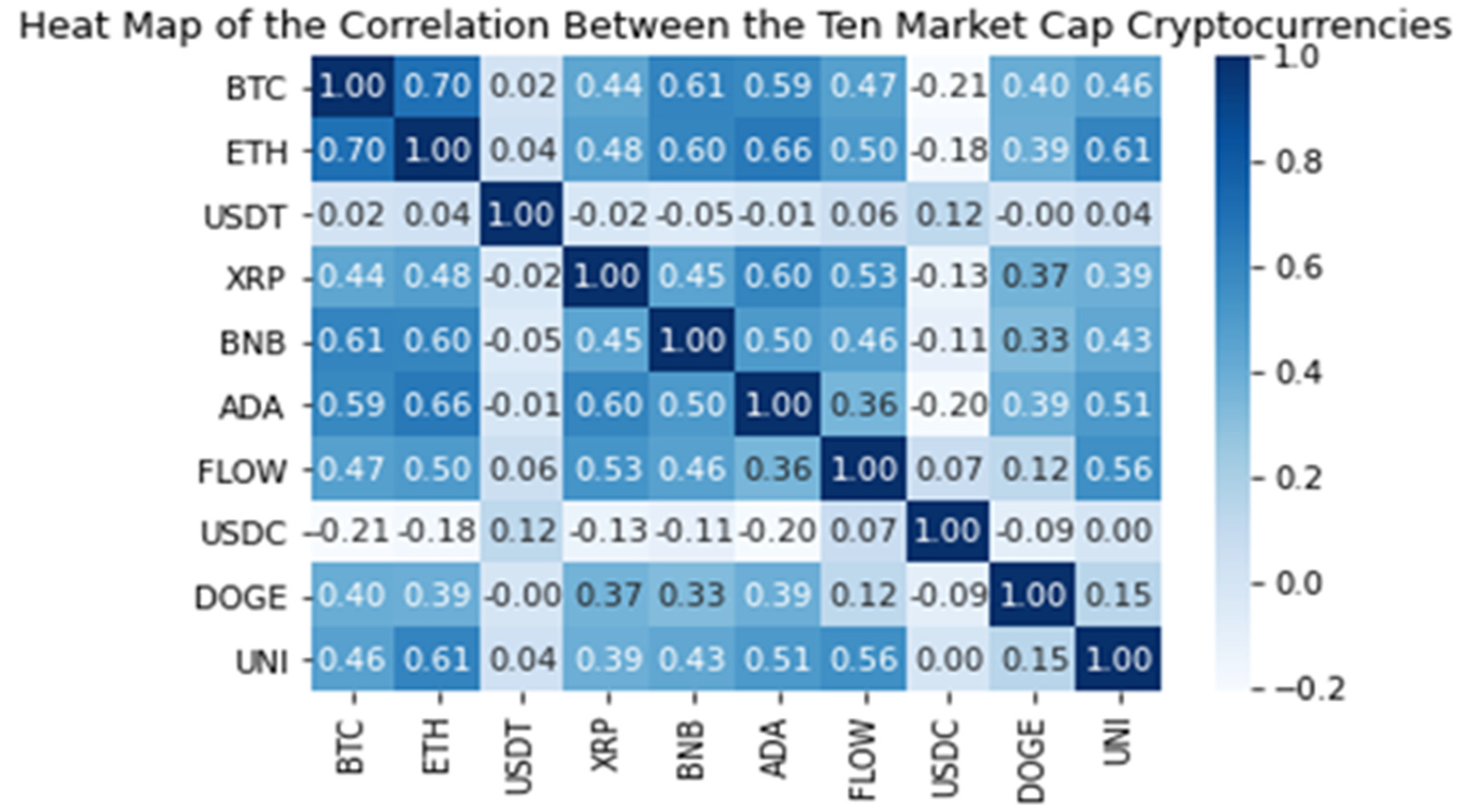
| Size | Mean | SD | Min | Q1 | Median | Q3 | Max | Kurtosis | Skewness | |
|---|---|---|---|---|---|---|---|---|---|---|
| BTC | 1654 | 0.002 | 0.044 | −0.480 | −0.016 | 0.003 | 0.022 | 0.228 | 11.016 | −0.811 |
| ETH | 1654 | 0.003 | 0.058 | −0.570 | −0.023 | 0.002 | 0.031 | 0.260 | 8.165 | −0.483 |
| USDT | 1654 | 0.000 | 0.046 | −0.693 | −0.001 | 0.000 | 0.001 | 0.454 | 77.596 | −2.135 |
| XRP | 1654 | 0.003 | 0.079 | −0.653 | −0.027 | −0.001 | 0.024 | 1.028 | 28.286 | 1.868 |
| BNB | 1423 | 0.004 | 0.072 | −0.566 | −0.026 | 0.001 | 0.032 | 0.533 | 11.162 | 0.325 |
| ADA | 1382 | 0.003 | 0.076 | −0.539 | −0.032 | 0.001 | 0.034 | 0.862 | 20.509 | 1.734 |
| FLOW | 167 | 0.006 | 0.092 | −0.362 | −0.042 | −0.003 | 0.043 | 0.367 | 3.057 | 0.464 |
| USDC | 1008 | 0.000 | 0.002 | −0.011 | −0.001 | 0.000 | 0.001 | 0.020 | 17.396 | 1.571 |
| DOGE | 1654 | 0.004 | 0.088 | −0.601 | −0.025 | −0.001 | 0.023 | 1.594 | 71.995 | 4.226 |
| UNI | 300 | 0.005 | 0.092 | −0.408 | −0.047 | −0.002 | 0.050 | 0.501 | 5.082 | 0.730 |
| 70% | RMSE | ||||||
|---|---|---|---|---|---|---|---|
| DNN | RNN | LSTM | ARIMA | FORECASTX | HOLTS | Multivariate LSTM | |
| BTC | 0.120 | 0.107 | 0.045 | 0.049 | 0.046 | 0.046 | 0.046 |
| ETH | 0.153 | 0.080 | 0.087 | 0.066 | 0.061 | 0.061 | 0.055 |
| XRP | 0.003 | 0.011 | 0.012 | 0.002 | 0.002 | 0.003 | 0.001 |
| USDT | 0.146 | 0.140 | 0.092 | 0.086 | 0.079 | 0.080 | 0.068 |
| BNB | 0.079 | 0.100 | 0.069 | 0.075 | 0.069 | 0.070 | 0.060 |
| ADA | 0.094 | 0.125 | 0.215 | 0.074 | 0.068 | 0.068 | 0.053 |
| DOGE | 0.167 | 0.185 | 0.001 | 0.001 | 0.093 | 0.090 | 0.093 |
| USDC | 0.008 | 0.045 | 0.122 | 0.132 | 0.001 | 0.001 | 0.001 |
| FLOW | 0.347 | 0.127 | 0.095 | 0.097 | 0.120 | 0.119 | 0.103 |
| UNI | 0.381 | 0.111 | 0.104 | 0.104 | 0.095 | 0.096 | 0.072 |
| 80% | RMSE | ||||||
| DNN | RNN | LSTM | ARIMA | FORECASTX | HOLTS | Multivariate LSTM | |
| BTC | 0.042 | 0.067 | 0.041 | 0.045 | 0.042 | 0.043 | 0.044 |
| ETH | 0.085 | 0.084 | 0.088 | 0.065 | 0.059 | 0.059 | 0.064 |
| XRP | 0.001 | 0.005 | 0.008 | 0.001 | 0.001 | 0.001 | 0.001 |
| USDT | 0.164 | 0.143 | 0.116 | 0.099 | 0.090 | 0.090 | 0.080 |
| BNB | 0.087 | 0.083 | 0.079 | 0.086 | 0.079 | 0.079 | 0.070 |
| ADA | 0.086 | 0.142 | 0.212 | 0.081 | 0.074 | 0.073 | 0.061 |
| DOGE | 0.123 | 0.148 | 0.001 | 0.001 | 0.107 | 0.102 | 0.117 |
| USDC | 0.008 | 0.050 | 0.146 | 0.154 | 0.001 | 0.001 | 0.001 |
| FLOW | 0.566 | 0.194 | 0.107 | 0.110 | 0.139 | 0.139 | 0.124 |
| UNI | 0.387 | 0.212 | 0.111 | 0.118 | 0.107 | 0.107 | 0.081 |
| 90% | RMSE | ||||||
| DNN | RNN | LSTM | ARIMA | FORECASTX | HOLTS | Multivariate LSTM | |
| BTC | 0.070 | 0.077 | 0.047 | 0.050 | 0.046 | 0.048 | 0.031 |
| ETH | 0.117 | 0.083 | 0.075 | 0.069 | 0.063 | 0.063 | 0.056 |
| XRP | 0.001 | 0.010 | 0.010 | 0.001 | 0.001 | 0.001 | 0.001 |
| USDT | 0.250 | 0.143 | 0.130 | 0.109 | 0.098 | 0.102 | 0.030 |
| BNB | 0.196 | 0.080 | 0.081 | 0.093 | 0.122 | 0.092 | 0.046 |
| ADA | 0.092 | 0.259 | 0.165 | 0.081 | 0.072 | 0.072 | 0.034 |
| DOGE | 0.119 | 0.119 | 0.001 | 0.001 | 0.117 | 0.111 | 0.050 |
| USDC | 0.004 | 0.052 | 0.136 | 0.159 | 0.001 | 0.001 | 0.001 |
| FLOW | 0.242 | 0.136 | 0.120 | 0.117 | 0.138 | 0.231 | 0.130 |
| UNI | 0.097 | 0.107 | 0.441 | 0.082 | 0.077 | 0.074 | 0.055 |
| 70% | MAD | ||||||
|---|---|---|---|---|---|---|---|
| DNN | RNN | LSTM | ARIMA | FORECASTX | HOLTS | Multivariate LSTM | |
| BTC | 0.061 | 0.063 | 0.029 | 0.031 | 0.029 | 0.030 | 0.036 |
| ETH | 0.096 | 0.071 | 0.056 | 0.042 | 0.041 | 0.041 | 0.045 |
| XRP | 0.066 | 0.065 | 0.056 | 0.050 | 0.047 | 0.049 | 0.048 |
| USDT | 0.001 | 0.008 | 0.006 | 0.001 | 0.001 | 0.003 | 0.001 |
| BNB | 0.045 | 0.044 | 0.043 | 0.047 | 0.043 | 0.045 | 0.044 |
| ADA | 0.055 | 0.106 | 0.161 | 0.053 | 0.048 | 0.049 | 0.039 |
| DOGE | 0.143 | 0.125 | 0.064 | 0.062 | 0.056 | 0.058 | 0.055 |
| USDC | 0.005 | 0.030 | 0.001 | 0.001 | 0.000 | 0.006 | 0.001 |
| FLOW | 0.106 | 0.121 | 0.079 | 0.081 | 0.067 | 0.065 | 0.076 |
| UNI | 0.270 | 0.134 | 0.067 | 0.066 | 0.066 | 0.066 | 0.059 |
| 80% | MAD | ||||||
| DNN | RNN | LSTM | ARIMA | FORECASTX | HOLTS | Multivariate LSTM | |
| BTC | 0.388 | 0.056 | 0.030 | 0.034 | 0.030 | 0.031 | 0.034 |
| ETH | 0.063 | 0.068 | 0.066 | 0.046 | 0.043 | 0.043 | 0.049 |
| XRP | 0.086 | 0.122 | 0.073 | 0.061 | 0.056 | 0.057 | 0.055 |
| USDT | 0.001 | 0.009 | 0.004 | 0.001 | 0.001 | 0.001 | 0.001 |
| BNB | 0.053 | 0.064 | 0.051 | 0.055 | 0.050 | 0.051 | 0.047 |
| ADA | 0.064 | 0.124 | 0.146 | 0.059 | 0.053 | 0.053 | 0.043 |
| DOGE | 0.137 | 0.070 | 0.072 | 0.077 | 0.067 | 0.067 | 0.069 |
| USDC | 0.005 | 0.054 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| FLOW | 0.091 | 0.108 | 0.077 | 0.089 | 0.079 | 0.073 | 0.094 |
| UNI | 0.400 | 0.110 | 0.076 | 0.052 | 0.076 | 0.075 | 0.062 |
| 90% | MAD | ||||||
| DNN | RNN | LSTM | ARIMA | FORECASTX | HOLTS | Multivariate LSTM | |
| BTC | 0.039 | 0.068 | 0.034 | 0.036 | 0.034 | 0.036 | 0.028 |
| ETH | 0.067 | 0.059 | 0.056 | 0.048 | 0.047 | 0.048 | 0.044 |
| XRP | 0.096 | 0.098 | 0.090 | 0.064 | 0.066 | 0.071 | 0.028 |
| USDT | 0.002 | 0.005 | 0.005 | 0.001 | 0.001 | 0.001 | 0.001 |
| BNB | 0.136 | 0.081 | 0.058 | 0.056 | 0.100 | 0.069 | 0.038 |
| ADA | 0.075 | 0.075 | 0.098 | 0.051 | 0.052 | 0.053 | 0.029 |
| DOGE | 0.125 | 0.097 | 0.090 | 0.081 | 0.089 | 0.203 | 0.046 |
| USDC | 0.008 | 0.057 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| FLOW | 0.093 | 0.107 | 0.091 | 0.071 | 0.089 | 0.080 | 0.109 |
| UNI | 0.096 | 0.128 | 0.543 | 0.039 | 0.059 | 0.058 | 0.050 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, D.; Kim, J.-M. Univariate and Multivariate Machine Learning Forecasting Models on the Price Returns of Cryptocurrencies. J. Risk Financial Manag. 2021, 14, 486. https://doi.org/10.3390/jrfm14100486
Miller D, Kim J-M. Univariate and Multivariate Machine Learning Forecasting Models on the Price Returns of Cryptocurrencies. Journal of Risk and Financial Management. 2021; 14(10):486. https://doi.org/10.3390/jrfm14100486
Chicago/Turabian StyleMiller, Dante, and Jong-Min Kim. 2021. "Univariate and Multivariate Machine Learning Forecasting Models on the Price Returns of Cryptocurrencies" Journal of Risk and Financial Management 14, no. 10: 486. https://doi.org/10.3390/jrfm14100486
APA StyleMiller, D., & Kim, J.-M. (2021). Univariate and Multivariate Machine Learning Forecasting Models on the Price Returns of Cryptocurrencies. Journal of Risk and Financial Management, 14(10), 486. https://doi.org/10.3390/jrfm14100486







