1. Introduction
The Black–Scholes model assume that financial returns are independent. On the other hand, empirical evidence shows that returns exhibit dependency or long-range dependence (see,
Cont 2001;
Ding et al. 1993). Furthermore, keeping in mind the diversification of the portfolio where correlation is a crucial factor in the selection criteria, we assume that, in extreme events, investors could also diversify their portfolios by selecting low clustering markets.
Extremes in financial markets are actively discussed because they can have a massive influence on both the economy and the society. This study discusses the property of financial returns and provides insight into the distribution of financial returns data, which is still openly debated in the literature. The aim of this study is to investigates the dependency structure of extreme returns in a variety of stock market indices for developed and emerging markets. Using the interval estimator that was introduced by
Ferro and Segers (
2003) for a range of threshold values help us better understand the dependency structure of financial returns. In turn, using the estimated extremal index and the dependency structure will shed light on behavior of the financial returns. To our knowledge, a numerical investigation of the clustering extremes behaviour of the developed and emerging stock market indices has not been carried out in the literature; hence we are making preliminary progress in this direction.
The paper is divided into six sections. The next section is a brief literature review. Then, we discuss the methods used to measure clustering. After that, we describe the data used in this study and its limitations. The fifth section present the empirical results, which include a summary table of the main results as well as all the indices’ figures. Then we provide a discussion and we conclude the paper with final remarks and a discussion of future research.
2. Literature Review
It is crucial for investors, regulators, and practitioners to understand the behaviour and statistical proprieties of financial returns data. Some of the common stylised statistical properties of financial returns data as discussed by
Cont (
2001) include the absence of autocorrelations, heavy tails, the gain or loss of asymmetry, aggregational Gaussianity, intermittency, volatility clustering, conditional heavy tails, slow decay of autocorrelation in absolute returns leverage effect, volume/volatility correlation and asymmetry in time scales. Several studies in the literature have estimated the extremal index in financial return data. For example,
Longin (
2000) applies the block method estimator to the S&P500 index and finds that
θ < 1. Furthermore,
Hamidieh et al. (
2009) use the interval estimator on crude oil prices, the S&P500 index and Intel’s stock price. The findings are similar to the results obtained by
Ferro and Segers (
2003).
Robert et al. (
2009) use the sliding block method and the interval estimator on the negative log returns of the FTSE100 index. Finally,
Miranda (
2020) applies the block method, run method and found that the interval estimator method produces clear results on the PSI20 index and that
θ < 1. Now, we will provide a brief review of the extremal index used with financial returns data. Let
ξ1,
ξ2, … be a sequence of independent identically distributed (IID) random variables (RVs) with distribution function
F. Define
Mn as the maximum of the first
n by:
The limiting distribution of maxima in an independent sequence is shown in the following theorem:
Theorem 1. Letbe a sequence of IID RVs. If there exist constants, and some non-degenerate distribution functionsuch thatthen,is a generalized extreme value (GEV) distribution.
See, for example,
Fisher and Tippett (
1928),
Leadbetter (
1983) and
Embrechts et al. (
2013). Now, let (
ξn) be a stationary sequence and
Mn be the corresponding maximum values. let, (
) be the associated IID sequence and (
) the corresponding maximum values. Then, there exists
θ ∈ (0, 1] such that
If and only if
is called the extremal index of the sequence (
ξn); see
Leadbetter (
1983). If
≤ 1, then the process suggests clustering. If
= 1, the process has no clustering or this is the case of the IID observations. There are several methods used to estimate the extremal index, but the most widely known and used approaches are the blocks estimator and the run estimator. The blocks estimator method is based on the results found by
Hsing et al. (
1988). The blocks estimator divides the data into
p blocks of size
q, where
n = pq. Then, for each block the maximum is computed as
. By using the following equation, we can then estimate the extremal index.
where,
I is an indicator function,
B is the number of blocks with at least one exceedance of the threshold value
u and
N is the number of observations that exceed a threshold value
u.
Robert et al. (
2009) showed that better results could be obtained by taking the maxima of the sliding block
p =
n −
q + 1 instead of taking the joint block
p =
n/
q.
O’Brien (
1987) proposed the run estimator which can be estimated by the following equation
where,
Ai,n = (
ξi > u,
ξi+1 ≤
un, …,
ξi+r ≤
u), and
N is defined as described before. More details about these methods can be found in the literature by
Smith and Weissman (
1994) and
Embrechts et al. (
2013).
These methods require the run length and block size parameters, which may be challenging to estimate. In order to obtain good results, both methods require a large threshold and an optimal choice of block size and run length. Furthermore, studies
Ferreira (
2018) and
Embrechts et al. (
2013) summarise and compare the approaches used in estimating the extremal index. We used an approach by
Ferro and Segers (
2003) (the interval estimator method) that does not require these parameters. Furthermore,
Miranda (
2020) applied the run, block and interval estimators to financial returns data of the PSI-20 and observed that the difference in terms of bias for the Intervals estimator presents values closer to the runs estimator. However, the region of stability is greater in the intervals estimator. The interval approach is based on the limited result of the number of exceedances threshold and on the convergence of the inter-exceedance times (time between two successive exceedances) of threshold
u by the sequence (
ξn) (see
Ferro and Segers 2003;
Ferro 2003).
3. Methodology
In our application, we estimated the extremal index value by using the interval estimator method for financial returns data. Define the financial return data as a sequence (ξ
n)
n≥1. Let
be the number of returns exceeding threshold u by the sequence (ξ
n). Let 1
≤ S1 ≤ … ≤ SN ≤ n be the observed exceedance times and,
Ti = Si + 1 − Si be the time between two successive exceedances, where
i = 1, …, N − 1. Then, the extremal index
θ can be estimated using the following equations:
By combining (6) and (7), we obtain the following equation:
is defined as the interval estimator for the extremal index developed by
Ferro and Segers (
2003). More information on this method can be found in
Ferro and Segers (
2003) and
Ferro (
2003). It is worth mentioning that
Ferro and Segers’ (
2003) interval estimator method is limited in its selection of the optimal threshold value. We compute this value numerically and plot the estimated extremal index values verses the range of threshold values. Since optimal threshold selection is openly discussed in the literature, a common choice for the threshold is to use a high quantile value, which we also use to estimate the extremal index.
We follow the
IMF Fund (
2017) classification for selecting the countries. There are different financial systems, models, and internal/external factors that should be considered in comparing countries. However, we believe that the stock prices and, consequently the financial returns, will reflect most of these differences in the clustering behaviour.
4. Data1
We explore the dependency structure of extreme returns in a time series of daily logarithmic returns
Rn of 16 equity indices from different countries. These indices include both developed and emerging markets. The list of the countries and indices can be found in
Table 1. The data are obtained from
Trading Economics (
2017), and we use the daily log return for the period from 1 July 1997 to 16 January 2017. The average number of observations is (
n = 5000). We chose 1 July 1997 as the start of the period because the data for most of the indices in this study are available from 1997 onwards.
The natural asset model that led to the Black–Scholes Model for option pricing is
Here,
corresponds to a sequence of IID random variables with
and unit variance. In the limit
, so that
(
fixed), it is shown that the asset prices follow a log-normal distribution:
Based on the applicability of this model, the extremal index for financial returns data should behave like those of IID observations. In order to meet the assumptions of this model, should be equal to 1 since no clustering appear for IID data. In our analysis , and we analyse the dependency or clustering of the maximum financial returns as
5. Results
In this section, we examine the extremal index for all the indices at different threshold values as illustrated in
Figure 1,
Figure 2,
Figure 3,
Figure 4 and
Figure 5. The results show a stable region of the plot of
. An accurate result of
depends on the choice of the optimal threshold value. Arguably, a natural choice of the threshold value is a high quantile. Furthermore, we present an empirical results obtained by estimating the extremal index for daily financial returns in developed and emerging markets, as presented in
Table 2.
We found that all the indicess’ extremes show clustering for the corresponding extremal index value of all sample countries with large threshold values. Moreover, using the 0.99 quantile of the indices of the S&P500, FTSE100, CAC40, MICEX markets result in . Notably, the results show that, even though it is an emerging market, China has lower clustering when compared to the developed economies in the sample. Finally, both Brazil and Malaysia show higher clustering than developed economies, which is expected as they are emerging markets.
6. Discussion
The empirical results in this study suggest that for the overall the values of the extremal index in all indices
≤ 0.46. This for the 0.95 and 0.99 quantiles, as seen in
Miranda (
2020),
Hamidieh et al. (
2009),
Robert et al. (
2009) and
Alokley (
2015). The results show that, for developed countries,
> 0.25; this indicates clustering for the 0.99 threshold. Our result of the S&P500 is in agreement with
Hamidieh et al. (
2009), who estimated the extremal index and found that
= 0.33 with 95% confidence by using the Maxspectrum and Ferro–Segers estimates. Furthermore,
Alokley (
2015) estimates a close result. However,
Longin (
2000) investigate the stock market returns of the S&P500 using the blocks method and find that
= 0.72 was minimal for one-day returns. Moreover, our results for the FTSE100 are 0.35, 0.28 for the 0.95 and 0.99, respectively. These results are close to the results of
Robert et al. (
2009), who investigated the FTSE100 index and found that
= 0.33. Both results agree with
Alokley (
2015) findings. Furthermore, our findings for the PSI20 show a stable region of
values from 0.2 to 0.3, as shown in
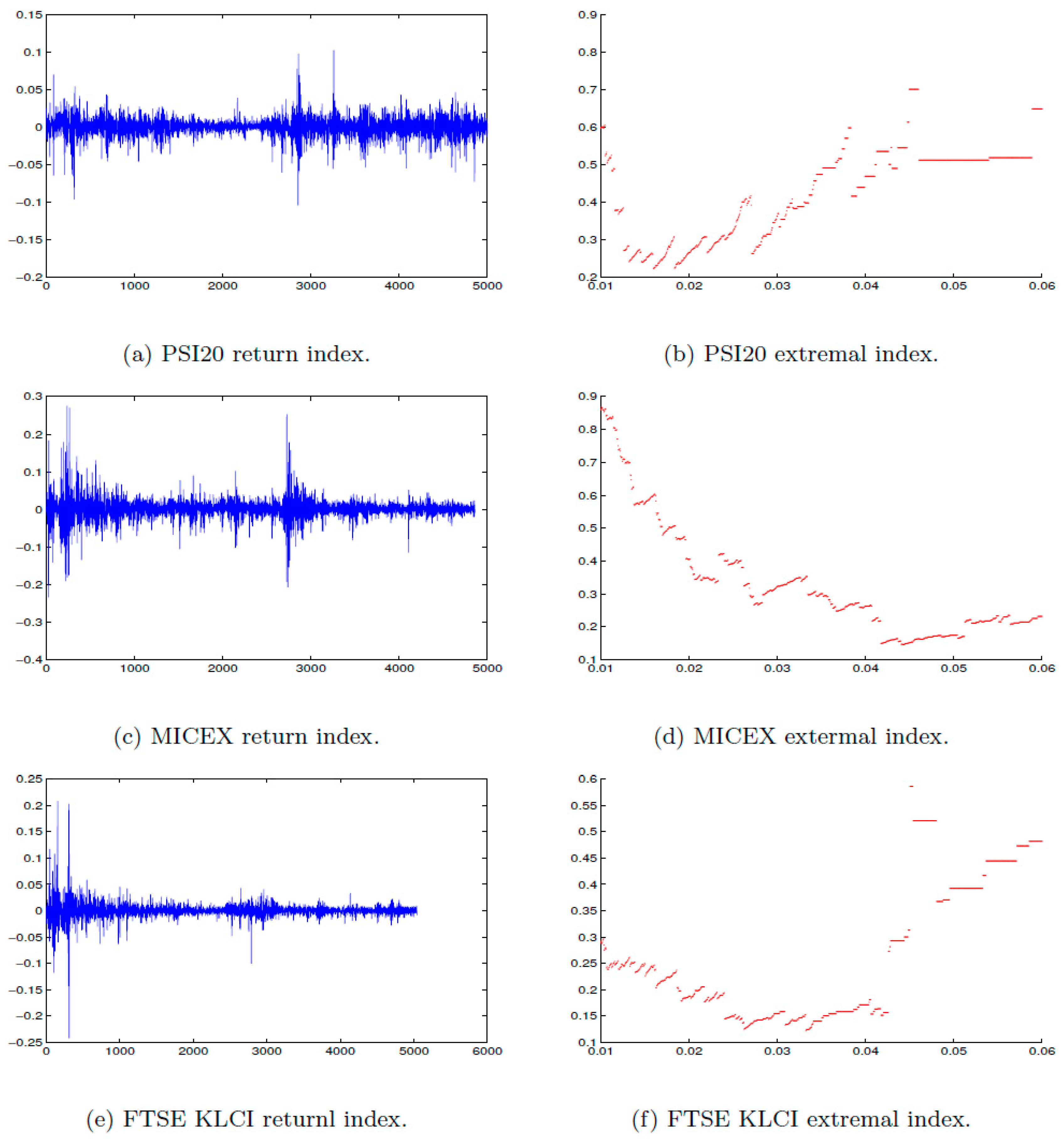
Figure 5b; this result is in agreement with
Miranda (
2020).
Furthermore, as expected, the degree of clustring is higher, on average, for emerging markets, especially FTSE KLCA and IBOVESVA. Overall, the IBOVESPA Index (Brazil Stock Market) and the FTSE KLCI Index (Malaysian Stock Market) show more clustering with a 0.99 quantile. To our knowledge, no previous study has investigated the clustering of emerging markets; hence our results may shed light on the behaviour of clustring in these markets. Our findings also show that most of the indices in the emerging markets behave similarly to the developed markets. The final result that is relevant to our financial application is the following: the exceedances of the high threshold for financial return data in all the countries exhibit clustering and do not behave as IID data. Therefore, the Black–Scholes model does not apply to financial return data.
Authors should discuss the results and how they can be interpreted in perspective of previous studies and of the working hypotheses. The findings and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted.
7. Conclusions
In this paper, we attempt to better understand the behaviour of financial returns data in developed and emerging markets. Empirical results suggest that the degree of clustering in stock market returns is high for both emerging and developed economies. Selecting low clustering markets can be help to overcome extreme financial events. It is also worth mentioning that the results depend on the threshold value used to estimate . Our results’ limitations are mainly related to the optimal threshold value, since this study used a range of thresholds in the pursuit of accurate and dependable findings.
Future research can explore the following areas: (1) It might be of interest to determine which financial model could explain this empirical behavior since no clustering occurs for IID data. (2) An investigation could be carried out to better understand the clustering of volatility. (3) It is also useful to apply this method to investigate the behaviour of the oil markets returns. Estimating an accurate as a measure of clustering will help investors and portfolio managers diversify their portfolios, and will also help policymakers to regulate financial markets.
Author Contributions
Conceptualization, S.A.A. and M.S.A.; methodology, S.A.A.; software, S.A.A.; validation, S.A.A., M.S.A.; formal analysis, S.A.A.; investigation, S.A.A.; resources, M.S.A.; data curation, M.S.A.; writing–original draft preparation, M.S.A.; writing–review and editing, M.S.A.; visualization, S.A.A.; supervision, ALOKLEYX.S.; project administration, M.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alokley, Sara Ali. 2015. Understanding Extremes and Clustering in Chaotic Maps and Financial Returns Data. Ph.D. thesis, University of Exeter, Exeter, UK. [Google Scholar]
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1: 223–36. [Google Scholar] [CrossRef]
- Ding, Zhuanxin, Clive W. J. Granger, and Robert F. Engle. 1993. A long memory property of stock market returns and a new model. Journal of Empirical Finance 1: 83–106. [Google Scholar] [CrossRef]
- Embrechts, Paul, Claudia Klüppelberg, and Thomas Mikosch. 2013. Modelling Extremal Events: For Insurance and Finance. Berlin: Springer Science & Business Media, vol. 33. [Google Scholar]
- Ferreira, Marta Susana. 2018. Heuristic tools for the estimation of the extremal index: A comparison of methods. REVSTAT 16: 115–36. [Google Scholar]
- Ferro, Christopher A. T. 2003. Statistical Methods for Cluster of Extreme Values. Ph.D. thesis, University of Lancaster, Lancaster, UK. [Google Scholar]
- Ferro, Christopher A. T., and Johan Segers. 2003. Inference for clusters of extreme values. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 65: 545–56. [Google Scholar] [CrossRef]
- Fisher, Ronald Aylmer, and Leonard Henry Caleb Tippett. 1928. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Mathematical Proceedings of the Cambridge Philosophical Society 24: 180–90. [Google Scholar] [CrossRef]
- Hamidieh, Kamal, Stilian Stoev, and George Michailidis. 2009. On the estimation of the extremal index based on scaling and resampling. Journal of Computational and Graphical Statistics 18: 731–55. [Google Scholar] [CrossRef]
- Hsing, Tailen, Jürg Hüsler, and Malcolm Ross Leadbetter. 1988. On the exceedance point process for a stationary sequence. Probability Theory and Related Fields 78: 97–112. [Google Scholar] [CrossRef]
- IMF Fund. 2017. World Economic Outlook Data, April 2017 ed. Washington: IMF Fund. [Google Scholar]
- Leadbetter, M. Ross. 1983. Extremes and local dependence in stationary sequences. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 65: 291–306. [Google Scholar] [CrossRef]
- Longin, Francois M. 2000. From value at risk to stress testing: The extreme value approach. Journal of Banking & Finance 24: 1097–130. [Google Scholar]
- Miranda, Maria Cristina Souto. 2020. Extremal index estimation: Application to financial data. In Handbook of Research on Accounting and Financial Studies. Hershey: IGI Global, pp. 96–130. [Google Scholar]
- O’Brien, George L. 1987. Extreme values for stationary and markov sequences. The Annals of Probability 15: 281–91. [Google Scholar] [CrossRef]
- Robert, Christian Y., Johan Segers, and Christopher A. T. Ferro. 2009. A sliding blocks estimator for the extremal index. Electronic Journal of Statistics 3: 993–1020. [Google Scholar] [CrossRef]
- Smith, Richard L., and Ishay Weissman. 1994. Estimating the extremal index. Journal of the Royal Statistical Society. Series B (Methodological) 56: 515–28. [Google Scholar] [CrossRef]
- Trading Economics. 2017. Index Daily Closing. Available online: Tradingeconomics.com (accessed on 16 January 2017).
| 1 | The authors are willing to share their raw data set in Excel format with those wishes to replicate the results of this study. |
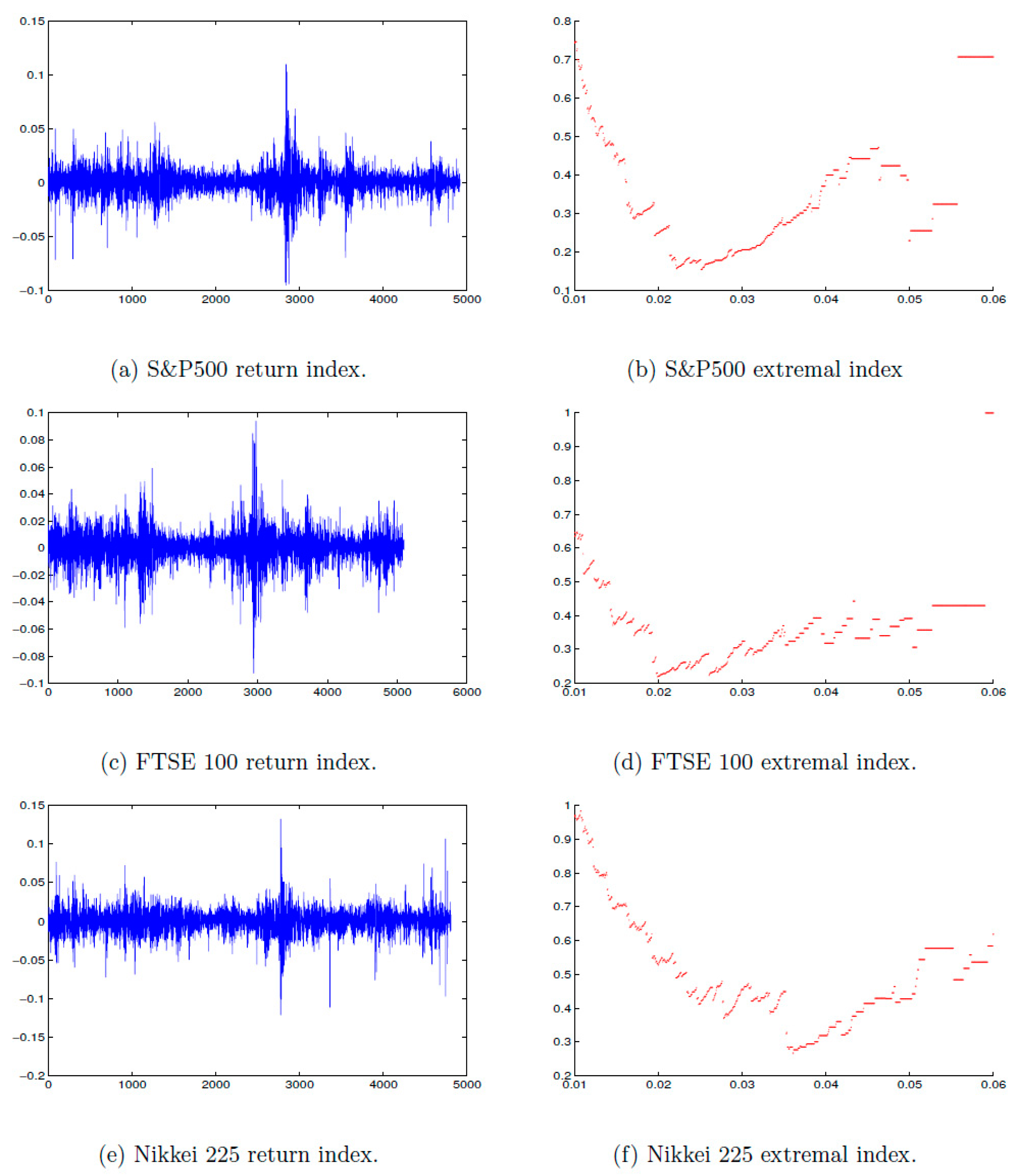
Figure 1.
Daily log returns of (a) S&P 500, (c) FTSE 100, (e) Nikkei 225 for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) S&P 500, (d) FTSE 100, (f) Nikkei 225 at a range of threshold u.
Figure 1.
Daily log returns of (a) S&P 500, (c) FTSE 100, (e) Nikkei 225 for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) S&P 500, (d) FTSE 100, (f) Nikkei 225 at a range of threshold u.
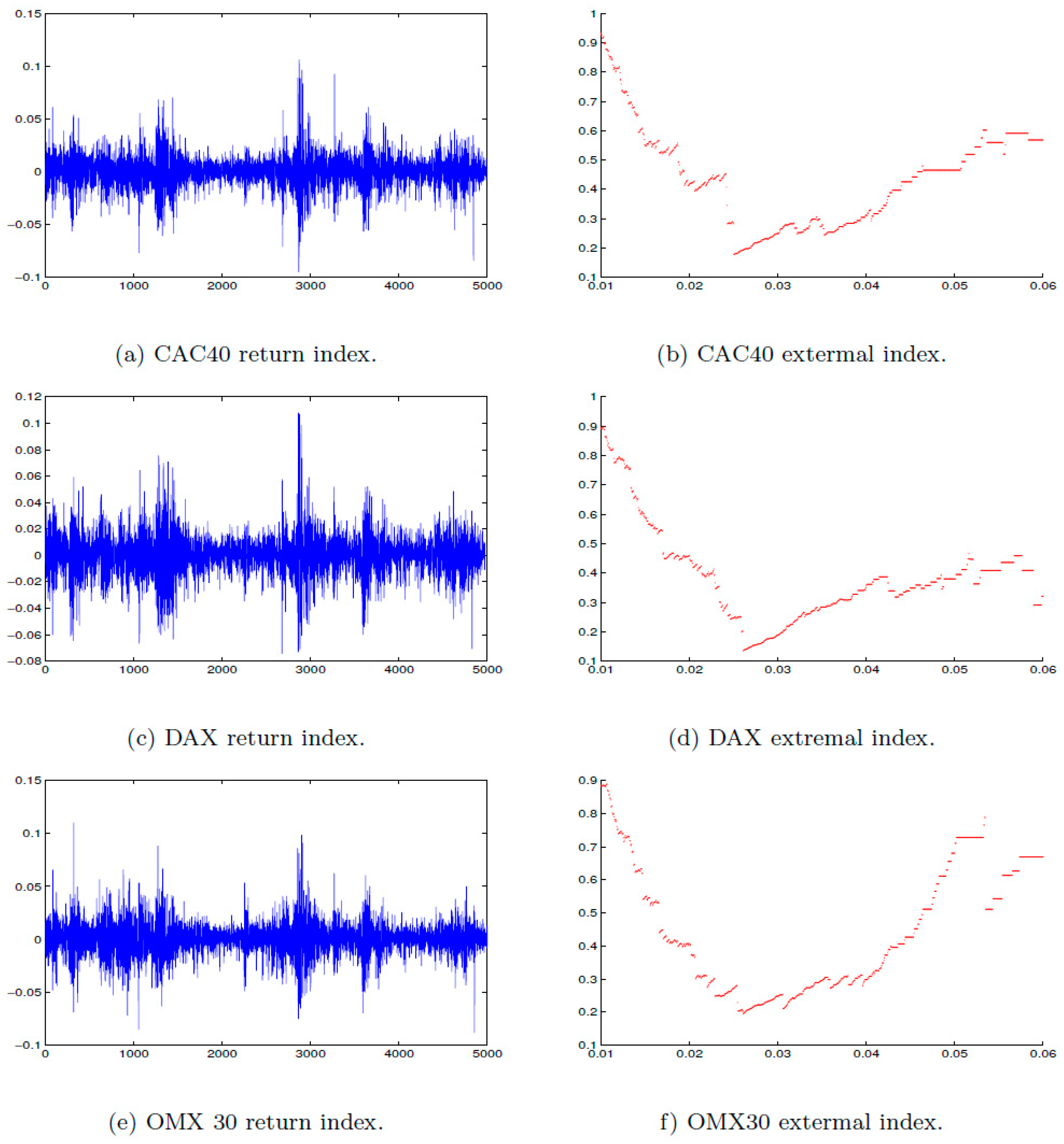
Figure 2.
Daily log returns of (a) CAC40, (c) DAX, (e) OMX 30 for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) CAC 40, (d) DAX, (f) OMX 30 at a range of threshold u.
Figure 2.
Daily log returns of (a) CAC40, (c) DAX, (e) OMX 30 for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) CAC 40, (d) DAX, (f) OMX 30 at a range of threshold u.
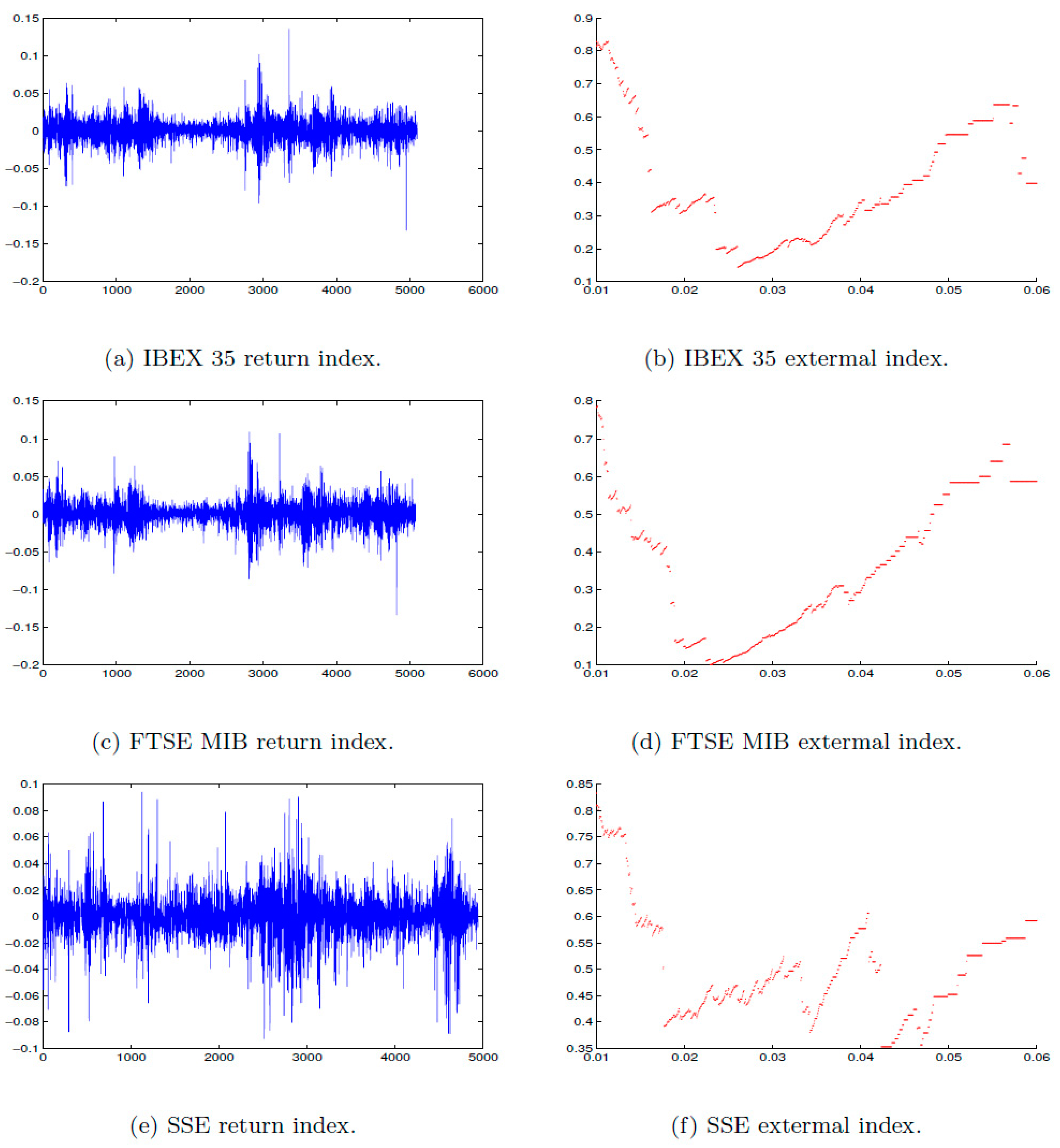
Figure 3.
Daily log returns of (a) IBEX 35, (c) FTSE MIB, (e) SSE for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) IBEX 35, (d) FTSE MIB, (f) SSE at a range of threshold u.
Figure 3.
Daily log returns of (a) IBEX 35, (c) FTSE MIB, (e) SSE for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) IBEX 35, (d) FTSE MIB, (f) SSE at a range of threshold u.
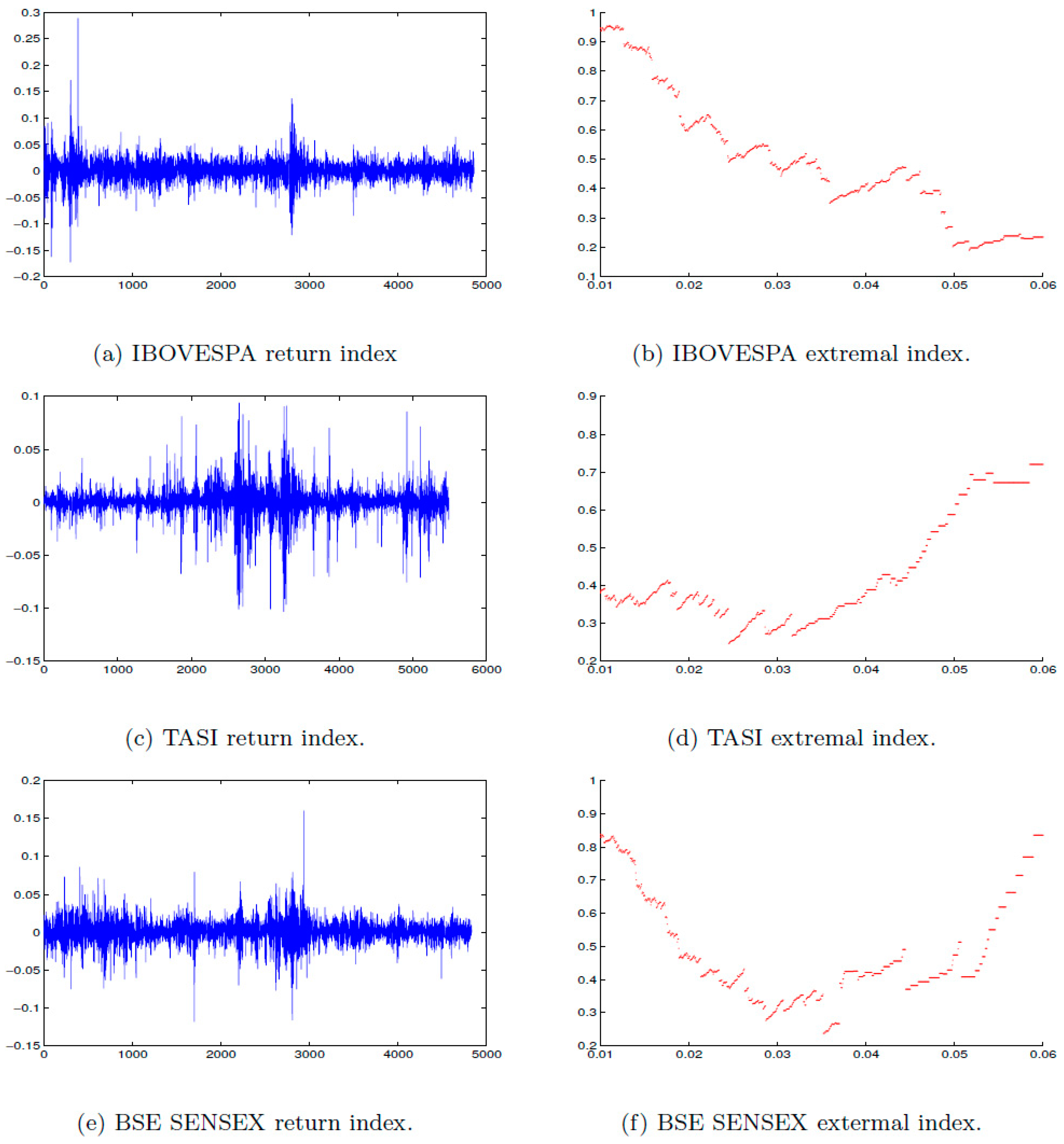
Figure 4.
Daily log returns of (a) IBOVESPA, (c) TASI, (e) BSE SENSEX for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) IBOVESPA, (d) TASI, (f) BSE SENSEX at a range of threshold u.
Figure 4.
Daily log returns of (a) IBOVESPA, (c) TASI, (e) BSE SENSEX for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) IBOVESPA, (d) TASI, (f) BSE SENSEX at a range of threshold u.
Figure 5.
Daily log returns of (a) PSI20, (c) MICEX, (e) FTSE KLCI for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) PSI20, (d) MICEX, (f) FTSE KLCI at a range of threshold u.
Figure 5.
Daily log returns of (a) PSI20, (c) MICEX, (e) FTSE KLCI for the period from 1 July 1997 to 16 January 2017, that consists of an average of (n = 5000) observations. The estimated extremal index of (b) PSI20, (d) MICEX, (f) FTSE KLCI at a range of threshold u.
Table 1.
Country stock indices.
Table 1.
Country stock indices.
| Country | Index Code | Index |
|---|
| Developed economies | | |
| France | CAC40 | CAC 40 Index |
| Germany | DAX | DAX Index |
| Italy | FTSE MIB | FTSE MIB Index |
| Japan | Nikkei 225 | Nikkei 225 Index |
| USA | S&P500 | S&P500 Index |
| UK | FTSE 100 | FTSE 100 Index |
| Spain | IBEX 35 | IBEX 35 Index |
| Sweden | OMX 30 | OMX Stockholm Index |
| Emerging markets | | |
| Brazil | IBOVESPA | Brazil BOVESPA Index |
| China | SSE | Shanghai Stock Exchange Index |
| India | BSE SENSEX | Mumbai SENSEX 30 Index |
| Malaysia | FTSE KLCI | Kuala Lumpur Comp Index |
| Russia | MICEX | Moscow Interbank Currency Exchange Index |
| Saudi Arabia | TASI | Tadawul Stock Index |
| Portugal | PSI20 | Portuguese Stock Index |
Table 2.
The estimated extremal index θ for developed and emerging markets.
Table 2.
The estimated extremal index θ for developed and emerging markets.
| Country | Index | 0.95 | 0.99 |
|---|
| u | θ | u | θ |
|---|
| Developed economies | | | | | |
| France | CAC40 | 0.0222 | 0.4304 | 0.0387 | 0.2878 |
| Germany | DAX | 0.0237 | 0.3011 | 0.0398 | 0.3434 |
| Italy | FTSE MIB | 0.0242 | 0.1137 | 0.0389 | 0.2709 |
| Japan | Nikkei 225 | 0.0234 | 0.4481 | 0.0386 | 0.2938 |
| USA | S&P500 | 0.0180 | 0.2975 | 0.0347 | 0.2770 |
| UK | FTSE 100 | 0.0183 | 0.3519 | 0.0313 | 0.2835 |
| Spain | IBEX 35 | 0.0233 | 0.3553 | 0.0380 | 0.3037 |
| Sweden | OMX 30 | 0.0240 | 0.2532 | 0.0416 | 0.3315 |
| Emerging markets | | | | | |
| Brazil | IBOVESPA | 0.0302 | 0.4631 | 0.0517 | 0.1939 |
| China | SSE | 0.0249 | 0.4544 | 0.0421 | 0.4484 |
| India | BSE SENSEX | 0.0239 | 0.3884 | 0.0391 | 0.3994 |
| Malaysia | FTSE KLCI | 0.0104 | 0.2750 | 0.0337 | 0.1271 |
| Russia | MICEX | 0.0352 | 0.2933 | 0.0692 | 0.2897 |
| Saudi Arabia | TASI | 0.0185 | 0.3794 | 0.0366 | 0.3344 |
| Portugal | PSI20 | 0.0185 | 0.2303 | 0.0299 | 0.3553 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).